Samacheer Kalvi 10th Maths Guide Chapter 3 Algebra Ex 3.16

Students can download Maths Chapter 3 Algebra Ex 3.16 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.16

1. In the

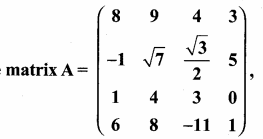
write (i) The number of elements
(ii) The order of the matrix
(iii) Write the elements a₂₂, a₂₃, a₂₄, a₃₄, a₄₃, a₄₄.
Answer:
(i) The number of elements is 16
(ii) The order of the matrix is 4 × 4
(iii) Elements corresponds to

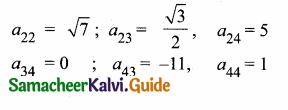
Question 2.
If a matrix has 18 elements, what are the possible orders it can have? What if it has 6 elements?
Answer:
The possible orders of the matrix having 18 elements are

The possible orders of the matrix having 6 elements are

Question 3.
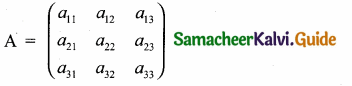
Construct a 3 × 3 matrix whose elements are given by
(i) a_ij = |i – 2j|
Answer:
a_ij = |i – 2j|
The general 3 × 3 matrices is

a₁₁ = |1 – 2(1)| = |1 – 2| = | – 1| = 1
a₁₂ = |1 – 2(2)| = |1 – 4| = | – 3| = 3
a₁₃ = |1 – 2(3)| = |1 – 6| = | – 5| = 5
a₂₁ = |2 – 2(1)| = |2 – 2| = 0 = 0
a₂₂ = |2 – 2(2)| = |2 – 4| = | – 2| = 2
a₂₃ = |2 – 2(3)| = |2 – 6| = | – 4| = 4
a₃₁ = |3 – 2(1)| = |3 – 2| = | 1 | = 1
a₃₂ = |3 – 2(2)| = |3 – 4| = | – 1 | = 1
a₃₃ = |3 – 2(3)| = |3 – 6| = | – 3 | = 3
The required matrix

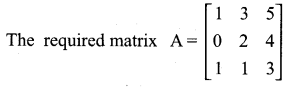
(ii) a_ij = \(\frac{(i+j)^{3}}{3}\)
Answer:
a₁₁ = \(\frac{(1+1)^{3}}{3}\) = \(\frac{2^{3}}{3}\) = \(\frac { 8 }{ 3 } \)
a₁₂ = \(\frac{(1+2)^{3}}{3}\) = \(\frac { 27 }{ 3 } \) = 9
a₁₃ = \(\frac{(1+3)^{3}}{3}\) = \(\frac { 64 }{ 3 } \) = \(\frac { 64 }{ 3 } \)
a₂₁ = \(\frac{(2+1)^{3}}{3}\) = \(\frac { 27 }{ 3 } \) = 9
a₂₂ = \(\frac{(2+2)^{3}}{3}\) = \(\frac { 64 }{ 3 } \) = \(\frac { 64 }{ 3 } \)
a₂₃ = \(\frac{(2+3)^{3}}{3}\) = \(\frac { 125 }{ 3 } \) = \(\frac { 125 }{ 3 } \)
a₃₁ = \(\frac{(3+1)^{3}}{3}\) = \(\frac { 64 }{ 3 } \) = \(\frac { 64 }{ 3 } \)
a₃₂ = \(\frac{(3+2)^{3}}{3}\) = \(\frac { 125 }{ 3 } \) = \(\frac { 125 }{ 3 } \)
a₃₃ = \(\frac{(3+3)^{3}}{3}\) = \(\frac { 216 }{ 3 } \) = 72
The required matrix

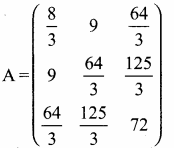
Question 4.
If 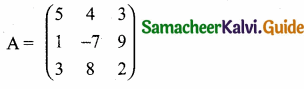 then find the tranpose of A.
Answer:

transpose of A = (A^T)

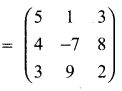
Question 5.
If 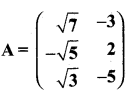then find the tranpose of – A
Answer:

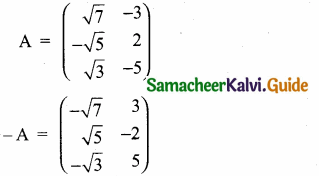
Transpose of – A = (-A^T) =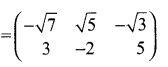

Question 6.
If A = 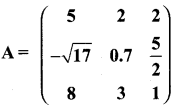then verify (AT)T = A
Answer:

Hence it is verified

Question 7.
Find the values of x, y and z from the following equations
(i)

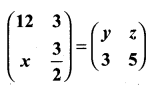
Answer:
Since the given matrices are equal then all the corresponding elements are equal.
y = 12, z = 3, x = 3
The value of x = 3, y = 12 and z = 3

(ii)

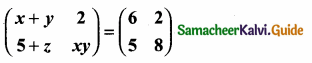
Answer:
x + y = 6 ……(1)
5 + z = 5
z = 5 – 5 = 0
xy = 8
y = \(\frac { 8 }{ x } \)
Substitute the value of y = \(\frac { 8 }{ x } \) in (1)
x + \(\frac { 8 }{ x } \) = 6
x² + 8 = 6x
x² – 6x + 8 = 0
(x – 4) (x – 2) = 0
∴ x – 4 = 0 or x – 2 = 0
x = 4 or x = 2
y = \(\frac { 8 }{ 4 } \) = 2 or y = \(\frac { 8 }{ 2 } \) = 4

∴ The value of x, y and z are 4, 2, 0 (or) 2, 4, 0

(iii)

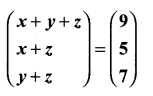
Solution:
x + y + z = 9 ……….(1)
x + z = 5 ……….(2)
y + z = 7 ……….(3)

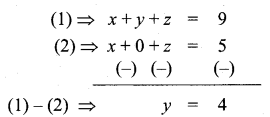
Substitute the value of y = 4 in (3)
y + z = 7
4 + z = 7
z = 7 – 4
= 3
Substitute the value of z = 3 in (2)
x + 3 = 5
x = 5 – 3
= 2
∴ The value of x = 2 , y = 4 and z = 3