Samacheer Kalvi 10th Maths Guide Chapter 3 Algebra Ex 3.18

Students can download Maths Chapter 3 Algebra Ex 3.18 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.18

Question 1.
Find the order of the product matrix AB if

Answer:
Given A = [a_ij]_p×q and B = [a_ij]_q×r
Order of product of AB = p × r
Order of product of BA is not defined. Number columns in r is not equal to the number of rows in P.
∴ Product BA is not defined.

Question 2.
A has ‘a’ rows and ‘a + 3 ’ columns. B has ‘6’ rows and ‘17 – b’ columns, and if both products AB and BA exist, find a, b?
Solution:
A has a rows, a + 3 columns.
B has b rows, 17 – b columns
If AB exists a × a + 3
b × 17 – b
a + 3 = 6 ⇒ a – 6 = -3 ………… (1)
If BA exists 6 × 17-6
a × a + 3
17 – 6 = a ⇒ a + 6 = 17 …………. (2)
(1) + (2) ⇒ 2a = 14 ⇒ a = 7
Substitute a = 7 in (1) ⇒ 7 – b = -3 ⇒ b = 10
a = 7, b = 10

Question 3.
A has ‘a’ rows and ‘a + 3 ’ columns. B has rows and ‘b’ columns, and if both products AB and BA exist, find a,b?
Answer:

1. Order of matrix AB = 3 × 3
2. Order of matrix AB = 4 × 2
3. Order of matrix AB = 4 × 2
4. Order of matrix AB = 4 × 1
5. Order of matrix AB = 1 × 3

Question 4.

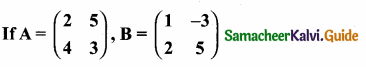
find AB, BA and check if AB = BA?
Answer:

Question 5.
Given that


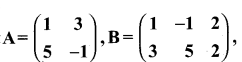
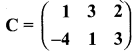
verify that A(B + C) = AB + AC
Answer:

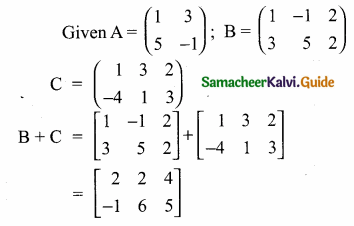
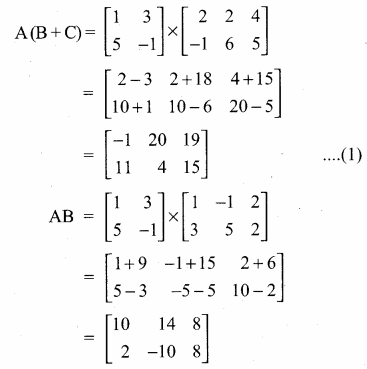
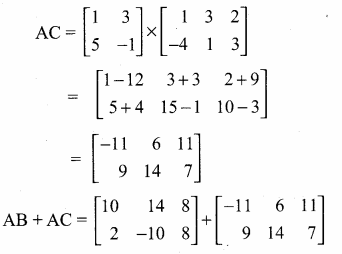
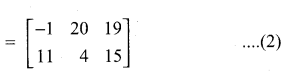
From (1) and (2) we get
A (B + C) = AB + AC

Question 6.
Show that the matrices

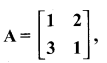
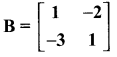
satisfy commutative property AB = BA
Answer:

From (1) and (2) we get
AB = BA. It satisfy the commutative property.

Question 7.

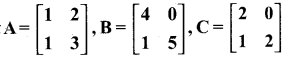
Show that (i) A(BC) = (AB)C
(ii) (A-B)C = AC – BC
(iii) (A-B)^T = A^T – B^T
Answer:



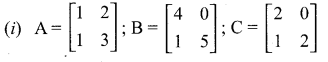
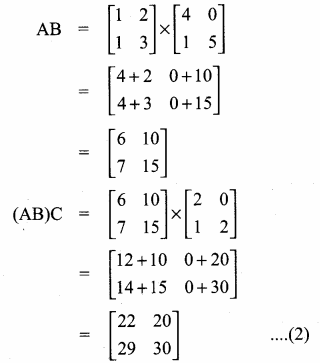
From (1) and (2) we get
A(BC) = (AB)C

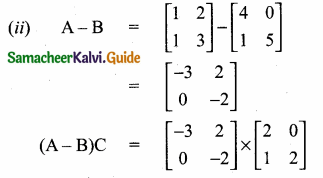
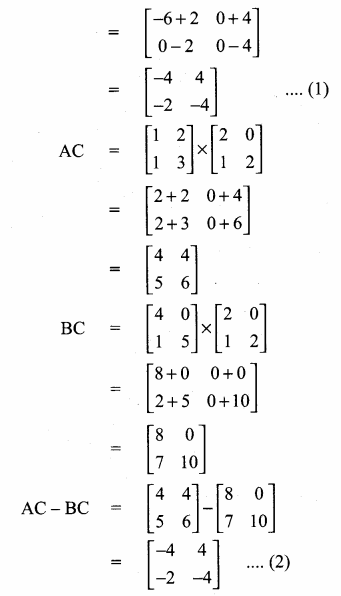
From (1) and (2) we get
(A – B) C = AC – BC


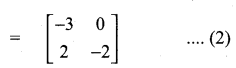
From (1) and (2) we get
(A-B)^T = A^T – B^T

Question 8.

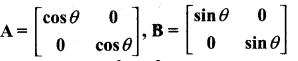
then snow that A² + B² = I.
Answer:

Question 9.

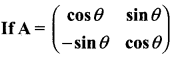
prove that AA^T = I.
Answer:

AA^T = I
∴ L.H.S. = R.H.S.

Question 10.
Verify that A² = I when

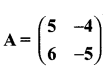
Answer:

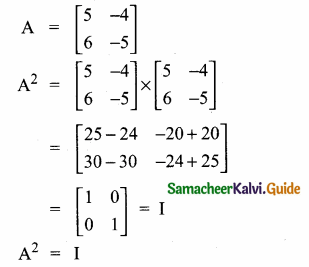
∴ L.H.S. = R.H.S.

Question 11.

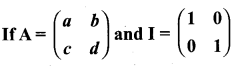
show that A² – (a + d)A = (bc – ad)I₂.
Answer:

L.H.S. = R.H.S.
A² – (a + d) A = (bc – ad)I₂

Question 12.

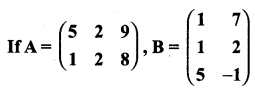
verify that (AB)^T = B^T A^T
Answer:


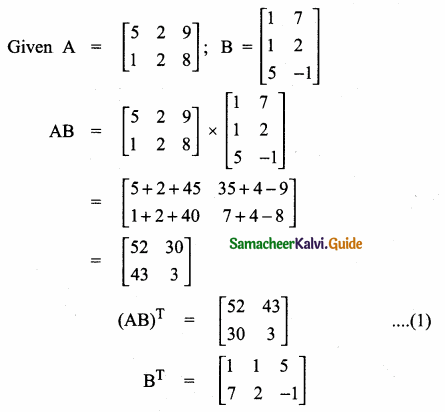
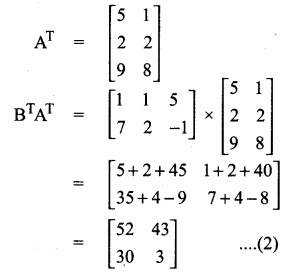
From (1) and (2) we get, (AB)^T = B^T A^T

Question 13.

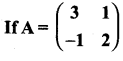
show that A² – 5A + 7I₂ = 0
Answer:


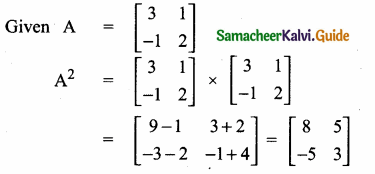
L.H.S. = R.H.S.
∴ A² – 5A + 7I₂ = 0