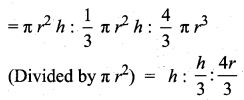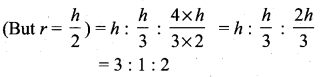Students can download Maths Chapter 7 Mensuration Ex 7.5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 7 Mensuration Ex 7.5
Multiple Choice Questions
Question 1.
The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is
(1) 60π cm2
(2) 68π cm2
(3) 120π cm2
(4) 136π cm2
Solution:
(4) 13671 cm2
Hint:
Here, h = 15 cm, r = 8 cm
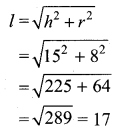
C.S.A of a cone = πrl sq. units. = π × 8 × 17 = 136π cm3
Question 2.
If two solid hemispheres of same base radius r units are joined together along with their bases, then the curved surface area of this new solid is
(1) 4πr2 sq. units
(2) 6πr2 sq. units
(3) 3πr2 sq. units
(4) 8πr2 sq. units
Answer:
(1) 4πr2 sq. units
Hint:
When you joined two hemispheres together, the solid sphere is formed
C.S.A of the new solid = C.S.A of a sphere = 4πr2 sq. units.
![]()
Question 3.
The height of a right circular cone whose radius is 5 cm and slant height is 13 cm will be
(1) 12 cm
(2) 10 cm
(3) 13 cm
(4) 5 cm
Solution:
(1) 12 cm
Hint:
Here r = 5 cm and l = 13 cm
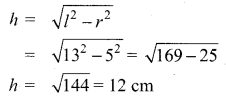
Question 4.
If the radius of the base of a right circular cylinder is halved keeping the same height, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is _________
(1) 1 : 2
(2) 1 : 4
(3) 1 : 6
(4) 1 : 8
Answer:
(2) 1 : 4
Hint:
Let the radius of the cylinder be “r” and the height be “h”
Radius of the new cylinder = \(\frac{r}{2}\) (Height will be same)
Volume of the new cylinder : Volume of the original cylinder
= \(\pi r_{1}^{2} h: \pi r_{2}^{2} h\) (πh is same)
= \(r_{1}^{2}: r_{2}^{2}\)
= \(\left(\frac{r}{2}\right)^{2}: r^{2}\)
= \(\frac{r^{2}}{4}: r^{2}=\frac{1}{4}: 1\)
= 1 : 4
![]()
Question 5.
The total surface area of a cylinder whose radius is \(\frac{1}{3}\) of its height is _______
(1) \(\frac{9 \pi h^{2}}{8}\) sq. units
(2) 24πh2 sq.units
(3) \(\frac{8 \pi h^{2}}{8}\) sq.units
(4) \(\frac{56 \pi h^{2}}{8}\) sq.units
Answer:
(3) \(\frac{8 \pi h^{2}}{8}\) sq.units
Hint:
Let the height of the cylinder be “h”
Radius of the cylinder = \(\frac{1}{3}\) h
T.S.A of the cylinder = 2πr(h + r)
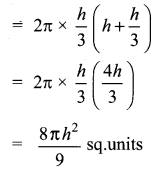
Question 6.
In a hollow cylinder, the sum of the external and internal radii is 14 cm and the width is 4 cm. If its height is 20 cm, the volume of the material in it is
(1) 5600π cm3
(2) 11200π cm3
(3) 56π cm3
(4) 3600π cm3
Solution:
(2) 112007π cm3
Hint:
Here, let the external radius be “R” and the internal radius be “r”
R + r = 14 ……(1)
Width (R – r) = 4 ……(2)
Height of the hollow cylinder = 20 cm
Volume of the hollow cylinder = πh × (R2 – r2)
= πh(R + r) (R – r)
= π × 20 (14) × 4
= π × 1120
= 1120π cm3
![]()
Question 7.
If the radius of the base of a cone is tripled and the height is doubled then the volume is ______
(1) made 6 times
(2) made 18 times
(3) made 12 times
(4) unchanged
Answer:
(2) made 18 times
Hint:
Radius of a cone = r
Height of a cone = h
Volume of the cone = \(\frac{1}{3}\) πr2h cu. units
When the radius is increased three-time (tripled) and the height is doubled
Radius is 3r and the height is 2h
Volume of the new cone
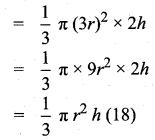
Volume is increased 18 times.
Question 8.
The total surface area of a hemisphere is how many times the square of its radius.
(1) π
(2) 4π
(3) 3π
(4) 2π
Solution:
(3) 3π
Hint:
T.S.A of the hemisphere = 3πr2
The square of the radius is 3π times.
![]()
Question 9.
A solid sphere of radius x cm is melted and cast into a shape of a solid cone of the same radius. The height of the cone is _______
(1) 3x cm
(2) x cm
(3) 4x cm
(4) 2x cm
Answer:
(3) 4x cm
Hint:
Radius of a sphere = Radius of a cone = x cm
Volume of a cone = Volume of a sphere
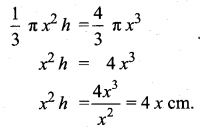
Question 10.
A frustum of a right circular cone is of height 16cm with radii of its ends as 8cm and 20cm. Then, the volume of the frustum is
(1) 3328π cm3
(2) 3228π cm3
(3) 3240πcm3
(4) 3340π cm3
Solution:
(1) 3328π cm3
Hint:
Here, h = 16 cm, r = 8 cm, R = 20 cm
Volume of the frustum
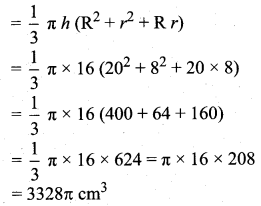
![]()
Question 11.
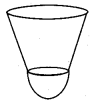
A shuttlecock used for playing badminton has the shape of the combination of ______
(1) a cylinder and a sphere
(2) a hemisphere and a cone
(3) a sphere and a cone
(4) frustum of a cone and a hemisphere
Answer:
(4) frustum of a cone and a hemisphere
Hint:
Question 12.
A spherical ball of radius r1 units is melted to make 8 new identical balls each of radius r2 units. Then r1 : r2 is _______
(1) 2 : 1
(2) 1 : 2
(3) 4 : 1
(4) 1 : 4
Answer:
(1) 2 : 1
Hint:
Volume of the first sphere : Volume of second sphere = 8 : 1
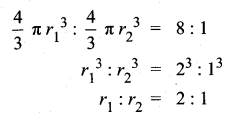
![]()
Question 13.
The volume (in cm3) of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is ________
(1) \(\frac{4}{3} \pi\)
(2) \(\frac{10}{3} \pi\)
(3) 5π
(4) \(\frac{20}{3} \pi\)
Answer:
(1) \(\frac{4}{3} \pi\)
Hint:
Radius of the sphere = 1 cm
Volume of the Sphere = \(\frac{4}{3}\) πr3 cu. units
= \(\frac{4}{3}\) × π × 1 × 1 × 1 cm3
= \(\frac{4}{3}\) π cm3
Question 14.
The height and radius of the cone of which the frustum is a part are h1 units and r1 units respectively. Height of the frustum is h2 units and the radius of the smaller base is r2 units. If h2 : h1 = 1 : 2 then r2 : r1 is ______
(1) 1 : 3
(2) 1 : 2
(3) 2 : 1
(4) 3 : 1
Answer:
(2) 1 : 2
Hint:
h2 : h1 = 1 : 2
h1 : h2 = 2 : 1
Ratio of their volumes
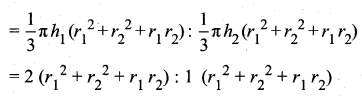
Volume is 2 : 1 the ratio of their radius also 2 : 1
r1 : r2 = 2 : 1 But r2 : r1 = 1 : 2
![]()
Question 15.
The ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height is
(1) 1 : 2 : 3
(2) 2 : 1 : 3
(3) 1 : 3 : 2
(4) 3 : 1 : 2
Solution:
(4) 3 : 1 : 2
Hint:
Volume of (cylinder : cone : sphere)