Students can download 11th Business Maths Chapter 2 Algebra Ex 2.7 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 2 Algebra Ex 2.7
Samacheer Kalvi 11th Business Maths Algebra Ex 2.7 Text Book Back Questions and Answers
Choose the correct answer.
Question 1.
If nC3 = nC2 then the value of nC4 is:
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(d) 5
Hint:
Given that nC3 = nC2
We know that if nCx = nCy then x + y = n or x = y
Here 3 + 2 = n
∴ n = 5
Question 2.
The value of n, when np2 = 20 is:
(a) 3
(b) 6
(c) 5
(d) 4
Answer:
(c) 5
Hint:
nP2 = 20
n(n – 1) = 20
n(n – 1) = 5 × 4
∴ n = 5
![]()
Question 3.
The number of ways selecting 4 players out of 5 is:
(a) 4!
(b) 20
(c) 25
(d) 5
Answer:
(d) 5
Hint:
5C4 = 5C1 = 5
Question 4.
If nPr = 720(nCr), then r is equal to:
(a) 4
(b) 5
(c) 6
(d) 7
Answer:
(c) 6
Hint:
Given nPr = 720(nCr)
\(\frac{n !}{(n-r) !}=720 \frac{n !}{r !(n-r) !}\)
1 = \(\frac{720}{r !}\)
r! = 720
r! = 6 × 5 × 4 × 3 × 2 × 1
r! = 6!
r = 6
![]()
Question 5.
The possible outcomes when a coin is tossed five times:
(a) 25
(b) 52
(c) 10
(d) \(\frac{5}{2}\)
Answer:
(a) 25
Hint:
Number of possible outcomes When a coin is tossed is 2
∴ When five coins are tossed (same as a coin is tossed five times)
Possible outcomes = 2 × 2 × 2 × 2 × 2 = 25
Question 6.
The number of diagonals in a polygon of n sides is equal to:
(a) nC2
(b) nC2 – 2
(c) nC2 – n
(d) nC2 – 1
Answer:
(c) nC2 – n
![]()
Question 7.
The greatest positive integer which divide n(n + 1) (n + 2) (n + 3) for all n ∈ N is:
(a) 2
(b) 6
(c) 20
(d) 24
Answer:
(d) 24
Hint:
Put n = 1 in n(n + 1) (n + 2) (n + 3)
= 1 × 2 × 3 × 4
= 24
Question 8.
If n is a positive integer, then the number of terms in the expansion of (x + a)n is:
(a) n
(b) n + 1
(c) n – 1
(d) 2n
Answer:
(b) n + 1
![]()
Question 9.
For all n > 0, nC1 + nC2 + nC3 + …… + nCn is equal to:
(a) 2n
(b) 2n – 1
(c) n2
(d) n2 – 1
Answer:
(b) 2n – 1
Hint:
Sum of binomial coefficients 2n
i.e., nC0 + nC1 + nC2 + nC3 + ……. + nCn = 2n
nC1 + nC2 + nC3 + ……. + nCn = 2n – nC0 = 2n – 1
Question 10.
The term containing x3 in the expansion of (x – 2y)7 is:
(a) 3rd
(b) 4th
(c) 5th
(d) 6th
Answer: (c) 5th
Hint:
First-term contains x7.
The second term contains x6.
The fifth term contains x3.
![]()
Question 11.
The middle term in the expansion of \(\left(x+\frac{1}{x}\right)^{10}\) is:
(a) 10C4 \(\left(\frac{1}{x}\right)\)
(b) 10C5
(c) 10C6
(d) 10C7 x2
Answer:
(b) 10C5
Hint:
x is x, a = \(\frac{1}{x}\), n = 10 which is even.
So the middle term is
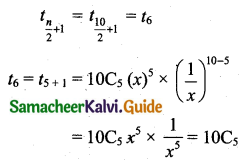
Question 12.
The constant term in the expansion of \(\left(x+\frac{2}{x}\right)^{6}\) is:
(a) 156
(b) 165
(c) 162
(d) 160
Answer:
(d) 160
Hint:
Here x is x, a is \(\frac{2}{x}\) (Note that each term x will vanish)
∴ Constant term occurs only in middle term
n = 6
∴ middle term = \(t_{\frac{6}{2}+1}\) = t3+1
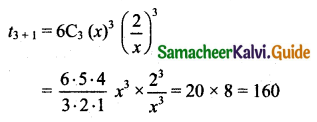
![]()
Question 13.
The last term in the expansion of (3 + √2 )8 is:
(a) 81
(b) 16
(c) 8
(d) 2
Answer:
(b) 16
Hint:
(√2)8 = \(\left(2^{\frac{1}{2}}\right)^{8}\) = 24 = 16
Question 14.
If \(\frac{k x}{(x+4)(2 x-1)}=\frac{4}{x+4}+\frac{1}{2 x-1}\) then k is equal to:
(a) 9
(b) 11
(c) 5
(d) 7
Answer:
(a) 9
Hint:
\(\frac{k x}{(x+4)(x-1)}=\frac{4}{x+4}+\frac{1}{2 x-1}\)
kx = 8x – 4 + x + 4
kx = 9x
k = 9
![]()
Question 15.
The number of 3 letter words that can be formed from the letters of the word ‘NUMBER’ when the repetition is allowed are:
(a) 206
(b) 133
(c) 216
(d) 300
Answer:
(c) 216
Hint:
Number of letters in NUMBER is 5
From 5 letters we can form 3 letter ways = 6 × 6 × 6 = 216.
Question 16.
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is:
(a) 18
(b) 12
(c) 9
(d) 6
Answer:
(a) 18
Hint:
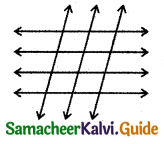
To form a parallelogram we need 2 parallel lines from 4 and 2 intersecting lines from 3.
Number of parallelograms = 4C2 × 3C2
= \(\frac{4 \times 3}{2 \times 1} \times 3\)
= 18
![]()
Question 17.
There are 10 true or false questions in an examination. Then these questions can be answered in
(a) 240 ways
(b) 120 ways
(c) 1024 ways
(d) 100 ways
Answer:
(c) 1024 ways
Hint:
For each question, there are two ways of answering it.
for 10 questions the numbers of ways to answer = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 210
= 1024 ways
Question 18.
The value of (5C0 + 5C1) + (5C1 + 5C2) + (5C2 + 5C3) + (5C3 + 5C4) + (5C4 + 5C5) is:
(a) 26 – 2
(b) 25 – 1
(c) 28
(d) 27
Answer:
(a) 26 – 2
Hint:
(5C0 + 5C1 + 5C2 + 5C3 + 5C4 + 5C5) + (5C1 + 5C2 + 5C3 + 5C4)
= 25 + (5C0 + 5C1 + 5C2 + 5C3 + 5C4 + 5C5) – (5C0 + 5C5)
= 25 + 25 – (1 + 1) (∵ Adding and subtracting of 5C0 and 5C5)
= 2(25) – 2 (∵ 5C0 = 5C5 = 1)
= 26 – 2
![]()
Question 19.
The total number of 9 digit number which has all different digit is:
(a) 10!
(b) 9!
(c) 9 × 9!
(d) 10 × 10!
Answer:
(c) 9 × 9!
Hint:
Here we can use the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
They are in 10 in total. We have to form a nine-digit number.

The first place from the left can be filled up by anyone of the digits other than zero in 9 ways. The second place can be filled up by anyone of the remaining (10 – 1) digits (including zero) in 9 ways, the third place in 8 ways, fourth place in 7 ways, fifth place in 6 ways, sixth place in 5 ways, seventh place in 4 ways, eighth place in 3 ways and ninth place in 2 ways.
∴ The number of ways of making 9 digit numbers = 9 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 = 9 × 9!
Question 20.
The number of ways to arrange the letters of the word “CHEESE”:
(a) 120
(b) 240
(c) 720
(d) 6
Answer:
(a) 120
Hint: Here there are 6 letters.
The letter C occurs one time
The letter H occurs one time
The letter E occurs three times
The letter S occurs one time
Number of arrangements = \(\frac{6 !}{1 ! 1 ! 3 ! 1 !}=\frac{6 !}{3 !}=\frac{6 \times 5 \times 4 \times 3 !}{3 !}\) = 120
![]()
Question 21.
Thirteen guests have participated in a dinner. The number of handshakes that happened in the dinner is:
(a) 715
(b) 78
(c) 286
(d) 13
(b) 78
Hint:
To handshakes, we need two guests.
Number of selecting 2 guests from 13 is 13C2 = \(\frac{13 \times 12}{2 \times 1}\) = 78
Question 22.
The number of words with or without meaning that can be formed using letters of the word “EQUATION”, with no repetition of letters is:
(a) 7!
(b) 3!
(c) 8!
(d) 5!
Answer:
(c) 8!
Hint:
There are 8 letters.
From 8 letters number of words is formed = 8P8 = 8!
![]()
Question 23.
Sum of binomial coefficient in a particular expansion is 256, then number of terms in the expansion is:
(a) 8
(b) 7
(c) 6
(d) 9
Answer:
(a) 8
Hint:
Sum of binomial coefficient = 256
i.e., 2n = 256
2n = 28
n = 8
Question 24..
The number of permutation of n different things taken r at a time, when the repetition is allowed is:
(a) rn
(b) nr
(c) \(\frac{n !}{(n-r) !}\)
(d) \(\frac{n !}{(n+r) !}\)
Answer:
(b) nr
![]()
Question 25.
The sum of the binomial coefficients is:
(a) 2n
(b) n2
(c) 2n
(d) n + 17
Answer:
(a) 2n