Students can download 11th Business Maths Chapter 3 Analytical Geometry Ex 3.1 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 3 Analytical Geometry Ex 3.1
Samacheer Kalvi 11th Business Maths Analytical Geometry Ex 3.1 Text Book Back Questions and Answers
Question 1.
Find the locus of a point which is equidistant from (1, 3) and x-axis.
Solution:
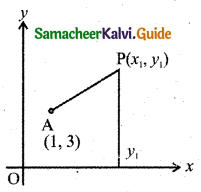
Let P(x1, y1) be any point on the locus.
Let A be the point (1, 3)
The distance from the x-axis on the moving pint P(x1, y1) is y1.
Given that AP = y1
AP2 = \(y_{1}^{2}\)
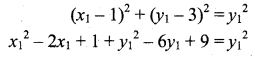
∴ The locus of the point (x1, y1) is x2 – 2x – 6y + 10 = 0
Question 2.
A point moves so that it is always at a distance of 4 units from the point (3, -2).
Solution:
Let P(x1, y1) be any point on the locus.
Let A be the point (3, -2)
Given that PA = 4
PA2 = 16
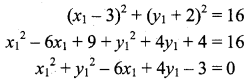
∴ The locus of the point (x1, y1) is x2 + y2 – 6x + 4y – 3 = 0
Question 3.
If the distance of a point from the points (2, 1) and (1, 2) are in the ratio 2 : 1, then find the locus of the point.
Solution:
Let P(x1, y1) be any point on the locus.
Let A(2, 1) and B(1, 2) be the given point.
Given that PA : PB = 2 : 1
i.e., \(\frac{P A}{P B}=\frac{2}{1}\)
PA = 2PB
PA2 = 4PB2
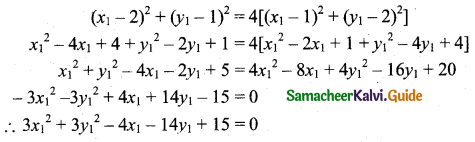
∴ The locus of the point (x1, y1) is 3x2 + 3y2 – 4x – 14y + 15 = 0
Question 4.
Find a point on the x-axis which is equidistant from the points (7, -6) and (3, 4).
Solution:
Let P(x1, 0) be any point on the x-axis.
Let A(7, -6) and B(3, 4) be the given points.
Given that PA = PB
PA2 = PB2
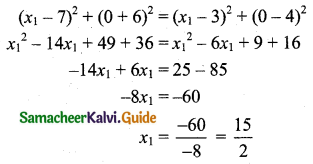
∴ The required point is \(\left(\frac{15}{2}, 0\right)\)
Question 5.
If A(-1, 1) and B(2, 3) are two fixed points, then find the locus of a point P so that the area of triangle APB = 8 sq.units.
Solution:
Let the point P(x1, y1).
Fixed points are A(-1, 1) and B(2, 3).
Given area (formed by these points) of the triangle APB = 8
⇒ \(\frac{1}{2}\) [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] = 8
⇒ \(\frac{1}{2}\) [x1(1 – 3) + (-1) (3 – y1) + 2(y1 – 1)] = 8
⇒ \(\frac{1}{2}\) [-2x1 – 3 + y1 + 2y1 – 2] = 8
⇒ \(\frac{1}{2}\) [-2x1 + 3y1 – 5] = 8
⇒ -2x1 + 3y1 – 5 = 16
⇒ -2x1 + 3y1 – 21 = 0
⇒ 2x1 – 3y1 + 21 = 0
∴ The locus of the point P(x1, y1) is 2x – 3y + 21 = 0.