Students can download 11th Business Maths Chapter 5 Differential Calculus Ex 5.7 Questions and Answers, Notes, Samcheer Kalvi 11th Business Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 11th Business Maths Solutions Chapter 5 Differential Calculus Ex 5.7
Samacheer Kalvi 11th Business Maths Differential Calculus Ex 5.7 Text Book Back Questions and Answers
Question 1.
Differentiate the following with respect to x.
(i) xsin x
(ii) (sin x)x
(iii) (sin x)tan x
(iv) \(\sqrt{\frac{(x-1)(x-2)}{(x-3)\left(x^{2}+x+1\right)}}\)
Solution:
(i) Let y = xsin x
Taking logarithm on both sides we get,
log y = log(xsin x)
log y = sin x log x
Differentiating with respect to x,
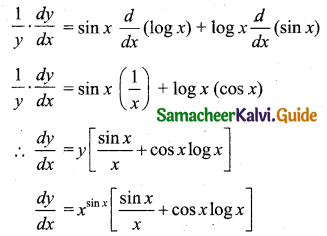
(ii) Let y = (sin x)x
Taking logarithm on both sides we get,
log y = x log(sin x)
Differentiating with respect to x,
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x \(\frac{d}{d x}\) log(sin x) + log(sin x) \(\frac{d}{d x}\) (x)
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x \(\frac{1}{\sin x}\) (cos x) + log(sin x) (1)
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = x cot x + log(sin x)
\(\frac{d y}{d x}\) = y[x cot x + log(sin x)]
\(\frac{d y}{d x}\) = (sin x)x [x cot x + log(sin x)]
![]()
(iii) Let y = (sin x)tan x
Taking logarithm on both sides we get,
log y = tan x log(sin x)
Differentiating with respect to x,
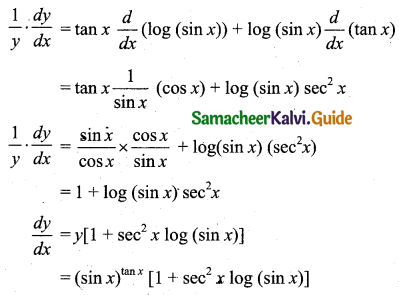
(iv) Let y = \(\sqrt{\frac{(x-1)(x-2)}{(x-3)\left(x^{2}+x+1\right)}}\)
y = \(\left(\frac{(x-1)(x-2)}{(x-3)\left(x^{2}+x+1\right)}\right)^{\frac{1}{2}}\)
Taking logarithm on both sides we get,
log y = \(\frac{1}{2}\) {[log(x – 1) + log(x – 2)] – [(log(x – 3) + log(x2 + x + 1)]}
log y = \(\frac{1}{2}\) [log(x – 1) + log(x – 2) – log(x – 3) – log(x2 + x + 1)]
Differentiating with respect to x,
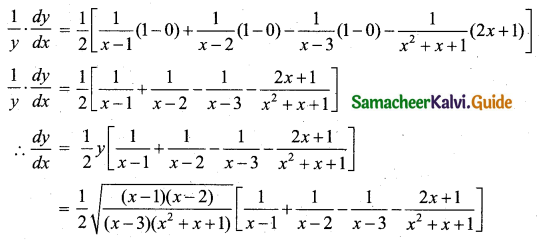
![]()
Question 2.
If xm . yn = (x + y)m+n, then show that \(\frac{d y}{d x}=\frac{y}{x}\)
Solution:
xm . yn = (x + y)m+n
Taking logarithm on both sides we get,
m log x + n log y = (m + n) log(x + y)
Differentiating with respect to x,
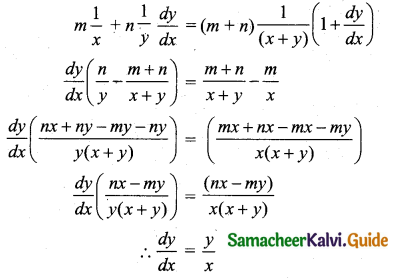
Hence proved.