Samacheer Kalvi 11th Maths Guide Chapter 11 Integral Calculus Ex 11.13

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 11 Integral Calculus Ex 11.13 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 11 Integral Calculus Ex 11.13

Choose the correct or the most suitable answer from given four alternatives.

Question 1.
If ∫ f(x) dx = g(x) + c. then ∫ f(x) g (x)dx
(1) ∫ (f(x)² dx
(2) ∫ f(x) g(x) dx
(3) ∫ f'(x) g(x) dx
(4) ∫ (g(x))² dx
Answer:
(1) ∫ (f(x)² dx

Explaination:
Given ∫ f (x) dx = g (x) + c
\(\frac{\mathrm{d}}{\mathrm{d} x}\) ∫ f(x)dx = \(\frac{\mathrm{d}}{\mathrm{d} x}\) (g(x) + c)
∫ \(\frac{\mathrm{d}}{\mathrm{d} x}\) (f(x)) dx = g'(x)
∫ d(f(x)) = g'(x)
f(x) = g(x)
∴ ∫ f(x) g'(x) dx = ∫ f(x) f(x) dx
= ∫ [f(x)]² dx

Question 2.
If \(\int \frac{3^{\frac{1}{x}}}{x^{2}}\) dx = k\(\left(3^{\frac{1}{x}}\right)\) + c, then the value of k is
(1) log 3
(2) – log 3
(3) \(-\frac{1}{\log 3}\)
(4) \(\frac{1}{\log 3}\)
Answer:
(3) \(-\frac{1}{\log 3}\)

Explaination:

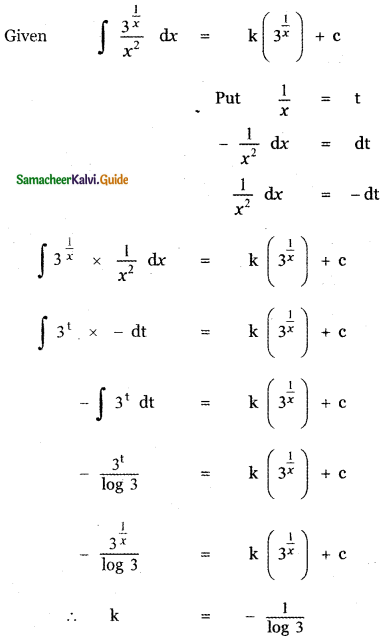
Question 3.
If ∫ f'(x) e^x2 dx = (x – 1)e^x2 + c, then f(x) is
(1) 2x³ – \(\frac{x^{2}}{2}\) + x + c
(2) \(\frac{x^{3}}{2}\) + 3x² + 4x + c
(3) x³ + 4x² + 6x + c
(4) \(\frac{2 x^{3}}{3}\) – x² + x + c
Answer:
(4) \(\frac{2 x^{3}}{3}\) – x² + x + c

Explaination:
Given ∫ f'(x) e^x2 dx = (x – 1)e^x2 + c
Differentiating both sides with respect to x we have

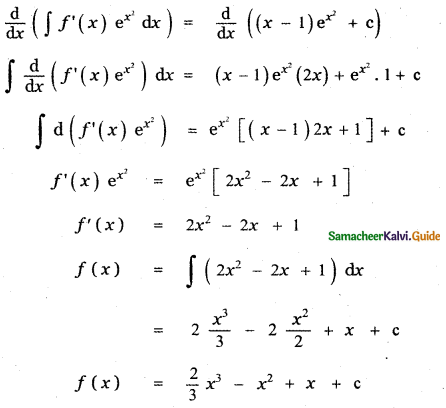
Question 4.
The gradient (slope) of a curve at any point (x, y) is \(\frac{x^{2}-4}{x^{2}}\). If the curve passes through the point (2, 7), then the equation of the curve is
(1) y = x + \(\frac{4}{x}\) + 3
(2) y = x + \(\frac{4}{x}\) + 4
(3)y = x² + 3x + 4
(4) y = x² – 3x + 6
Answer:
(1) y = x + \(\frac{4}{x}\) + 3

Explaination:


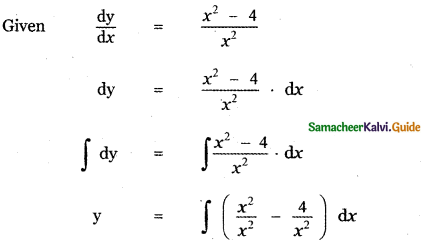
Given, this curve passes through the point (2, 7)
∴ 7 = 2 + \(\frac{4}{2}\) + c
7 = 2 + 2 + c
c = 7 – 4 = 3
∴ The required equation is
y = x + \(\frac{4}{x}\) + 3

Question 5.

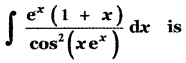
(1) cot (xe^x) + c
(2) sec (xe^x) + c
(3) tan (xe^x) + c
(4) cos (xe^x) + c
Answer:
(3) tan (xe^x) + c

Explaination:

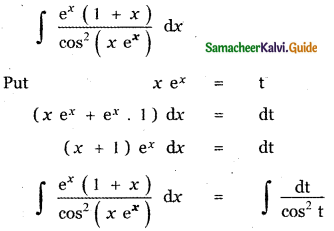
= ∫sec² t
= tan t + c
= tan (x e^x) + c

Question 6.

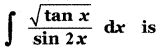
(1) \(\sqrt{\tan x}+\mathbf{c}\)
(2) \(2 \sqrt{\tan x}+\mathbf{c}\)
(3) \(\frac{1}{2} \sqrt{\tan x}+c\)
(4) \(\frac{1}{4} \sqrt{\tan x}+c\)
Answer:
(1) \(\sqrt{\tan x}+\mathbf{c}\)

Explaination:

Question 7.
∫sin³ dx is
(1)
(2)
(3)
(4)
Answer:
(3)

Explaination:
∫sin³ dx
sin 3x = 3 sin x – 4 sin³ x
4 sin³ x = 3 sin x – sin 3x
sin³ x = \(\frac{1}{4}\)(3 sin x – sin 3x)

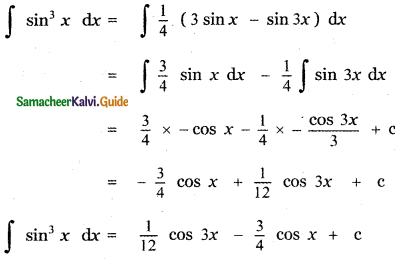
Question 8.

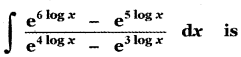
(1) x + c
(2) \(\frac{x^{3}}{3}\) + c
(3) \(\frac{3}{x^{3}}\) + c
(4) \(\frac{1}{x^{2}}\) + c
Answer:
(2) \(\frac{x^{3}}{3}\) + c

Explaination:

Question 9.

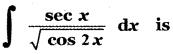
(1) tan^-1 (sin x) + c
(2) 2 sin^-1 (tan x) + c
(3) tan^-1 (cos x) + c
(4) sin^-1 (tan x) + c
Answer:
(4) sin^-1 (tan x) + c

Explaination:

Question 10.

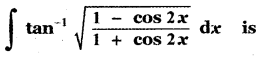
(1) x² + c
(2) 2x² + c
(3) \(\frac{x^{2}}{2}\) + c
(4) – \(\frac{x^{2}}{2}\) + c
Answer:
(3) \(\frac{x^{2}}{2}\) + c

Explaination:

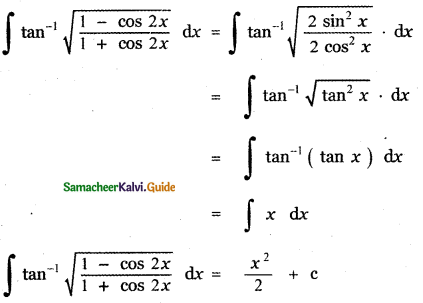
Question 11.
∫2^3x+5 dx is
(1)
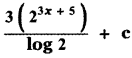
(2)
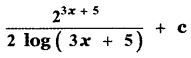
(3)
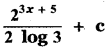
(4)
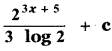
Answer:
(4)

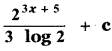
Explaination:
∫2^3x+5 dx
Put 3x + 5 = t
3 dx = dt
dx = \(\frac{1}{3}\) dt

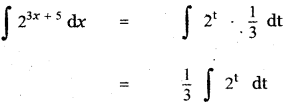
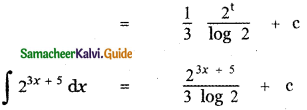
Question 12.

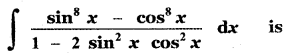
(1) \(\frac{1}{2}\) sin 2x + c
(2) –\(\frac{1}{2}\) sin 2x + c
(3) \(\frac{1}{2}\) cos 2x + c
(4) –\(\frac{1}{2}\) cos 2x + c
Answer:
(2) –\(\frac{1}{2}\) sin 2x + c

Explaination:

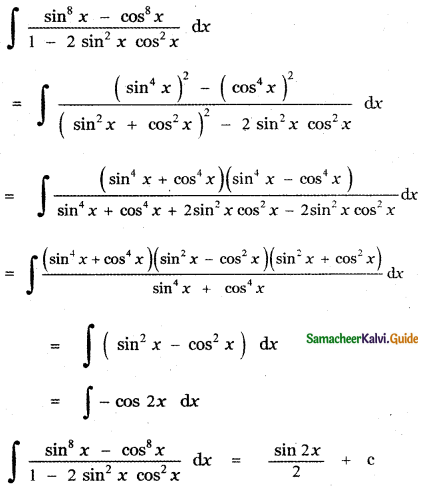
Question 13.

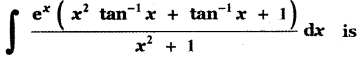
(1) e^x tan^-1 (x + 1) + c
(2) tan^-1 (e^x) + c
(3) e^x \(\frac{\left(\tan ^{-1} x\right)^{2}}{2}\) + c
(4) e^x tan^-1 x + c
Answer:
(4) e^x tan^-1 x + c

Explaination:

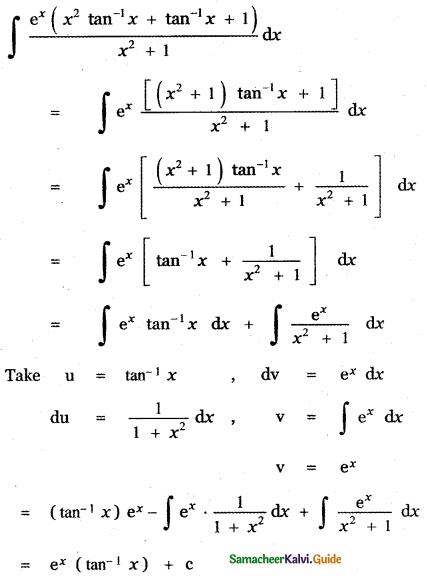
Question 14.

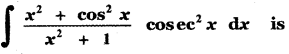
(1) cot x + sin^-1 x + c
(2) – cot x + tan^-1x + c
(3) – tan x + cot^-1 x + c
(4) – cot x – tan^-1x + c
Answer:
(4) – cot x – tan^-1x + c

Explaination:

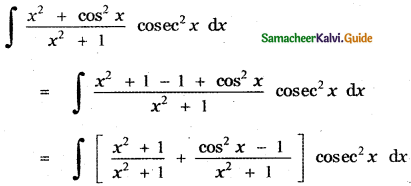
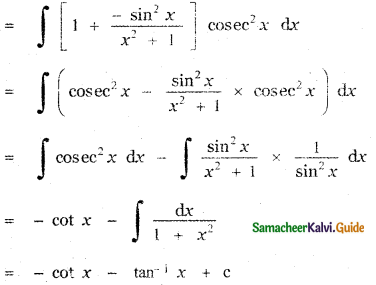
Question 15.
∫x² cos x dx is
(1) x² sin x + 2x cos x – 2 sin x + c
(2) x² sin x – 2x cos x – 2 sin x + c
(3) – x² sin x + 2x cos x + 2 sin x + c
(4) – x² sin x – 2x cos x + 2 sin x + c
Answer:
(1) x² sin x + 2x cos x – 2 sin x + c

Explaination:
\(\int x^{2} \cos x d x\)
By Bernoullis formula dv = cosxdx
u = x² v = sinx
u’ = 2x v₁ = -cos x
u” = 2 v₂ = -sinx
= uv – u’v₁ + u”v₂
= x²sin x + 2x cos x – 2 sin x + c

Question 16.

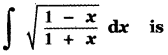
(1)
(2)
(3)
(4)
Answer:
(1)

Explaination:

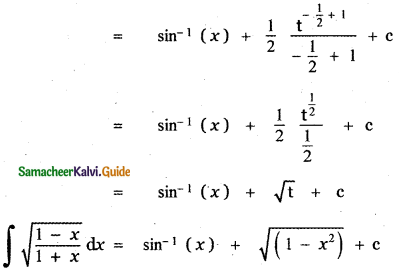
Question 17.
\(\int \frac{d x}{e^{x}-1}\) is
(1) log |e^x| – log |e^x – 1| + c
(2) log |e^x| + log |e^x – 1| + c
(3) log |e^x – 1| – log |e^x| + c
(4) log |e^x + 1| – log |e^x| + c
Answer:
(3) log |e^x – 1| – log |e^x| + c

Explaination:

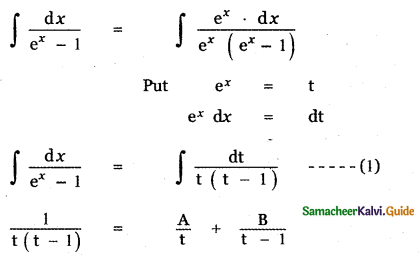
Question 18.
∫e^-4x cos x dx is
(1) \(\frac{e^{-4 x}}{17}\) [4 cos x – sin x] + c
(2) \(\frac{e^{-4 x}}{17}\) [- 4 cos x – sin x] + c
(3) \(\frac{e^{-4 x}}{17}\) [4 cos x + sin x] + c
(4) \(\frac{e^{-4 x}}{17}\) [- 4 cos x – sin x] + c
Answer:
(2) \(\frac{e^{-4 x}}{17}\) [- 4 cos x – sin x] + c

Explaination:

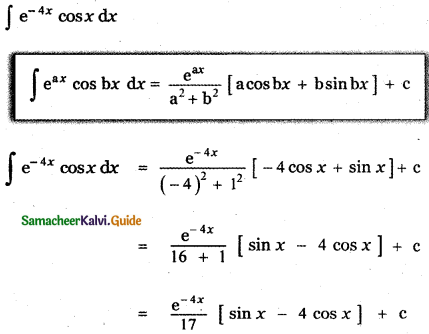
Question 19.

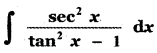
(1)
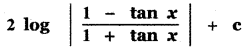
(2)
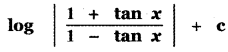
(3)
(4)
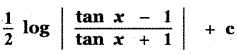
Answer:
(4)

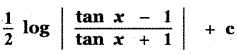
Explaination:

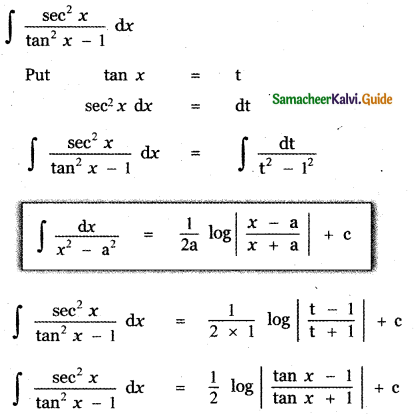
Question 20.
∫e^-7x sin 5x dx is
(1) \(\frac{e^{-7 x}}{74}\) [- 7 sin 5x – 5 cos 5x] + c
(2) \(\frac{e^{-7 x}}{74}\) [7 sin 5x + 5 cos 5x] + c
(3) \(\frac{e^{-7 x}}{74}\) [7 sin 5x – 5 cos 5x] + c
(4) \(\frac{e^{-7 x}}{74}\) [- 7 sin 5x + 5 cos 5x] + c
Answer:
(1) \(\frac{e^{-7 x}}{74}\) [- 7 sin 5x – 5 cos 5x] + c

Explaination:

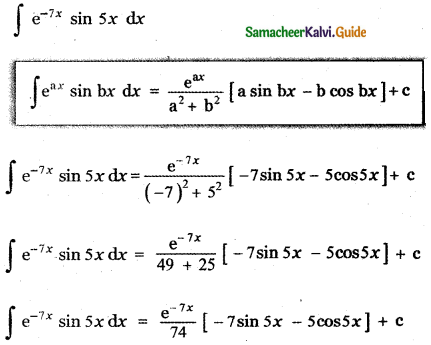
Question 21.
∫x² e^x/2 dx is
(1)
(2)
(3)
(4)
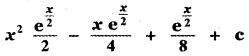
Answer:
(3)

Explaination:

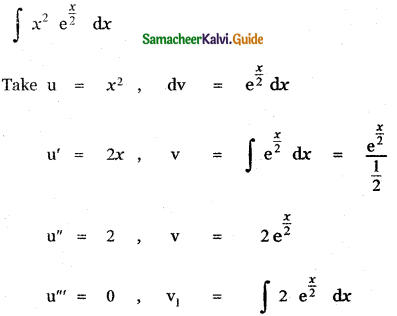
Question 22.

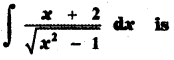
(1)
(2)
(3)
(4)
Answer:
(4)

Explaination:

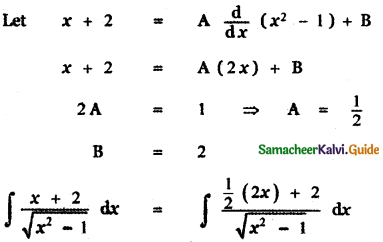
Question 23.

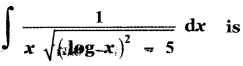
(1)
(2)
(3)
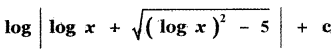
(4)
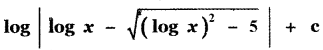
Answer:
(3)

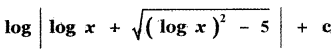
Explaination:

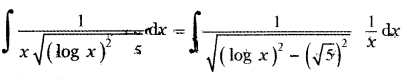
Question 24.
∫sin √x dx is
(1) 2(- √x cos √x + sin √x) + c
(2) 2(- √x cos √x + sin √x) + c
(3) 2(- √x sin √x – cos √x) + c
(4) 2(- √x sin √x + cos √x) + c
Answer:
(1) 2(- √x cos √x + sin √x) + c

Explaination:

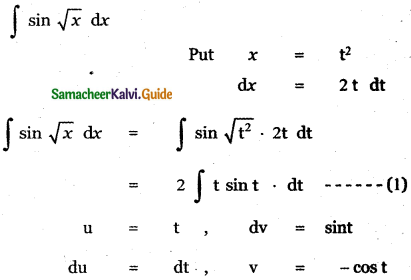
Question 25.

(1)
(2)
(3)
(4)
Answer:
(4)

Explaination: