Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 5 Binomial Theorem, Sequences and Series Ex 5.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.2
Question 1.
Write the first 6 terms of the sequence whose nth terms are given below and classify them as Arithmetic progression Geometric progression, Arithmetic – geometric progression, Harmonic progression and none of them.
(i) \(\frac{1}{2^{n+1}}\)
Answer:
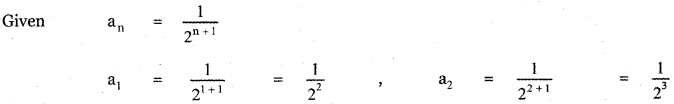

![]()
(ii) 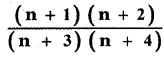
Answer:

(iii) \(4\left(\frac{1}{2}\right)^{n}\)
Answer:


![]()
(iv) \(\frac{(-1)^{n}}{n}\)
Answer:

(v) \(\frac{2 n+3}{3 n+4}\)
Answer:

![]()
(vi) 2018
Answer:
The nth term an = 2018
a1 = 2018,
a2 = 2018,
a3 = 2018,
a4 = 2018,
a5 = 2018,
a6 = 2018,
∴ The given sequence is 2018, 2018, 2018, 2018, 2018, 2018, ………….
This is a œnstant sequence which has same common ratio and common difference.
Hence this is an A. P, G . P and AGP.
(vii) \(\frac{3 n-2}{3^{n-1}}\)
Answer:

![]()
Question 2.
Write the first 6 terms of the sequences whose nth term an is given below
(i) 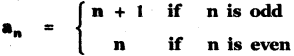
n = 1, an = n + 1, a1 = 1 + 1 = 2
n = 2, an = n, a2 = 2
n = 3, an = n + 1, a3 = 3 + 1 = 4
n = 4, an = n, a4 = 4
n = 5, an = n + 1, a5 = 5 + 1 = 6
n = 6, an = n, a6 = 6
∴ The first six terms are 2, 2, 4, 4, 6, 6
(ii) 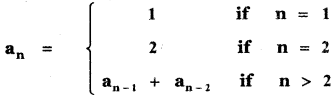
n = 1, a1 = 1, n = 2, a2 = 2
n = 3, an = an+1 + an-2, a3 = a3 – 1 + a3 – 2 = a2 + a1 = 2 + 1 = 3
n = 4, an = an+1 + an-2, a4 = a4 – 1 + a4 – 2 = a3 + a2 = 3 + 2 = 5
n = 5, an = an+1 + an-2, a5 = a5 – 1 + a5 – 2 = a4 + a3 = 5 + 3 = 8
n = 6, an = an+1 + an-2, a6 = a6 – 1 + a6 – 2 = a5 + a4 = 8 + 5 = 13
∴ The first six terms are 1, 2, 3, 5, 8, 13
(iii) 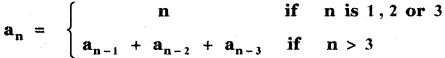
Answer:
n = 1, an = n, a1 = 1
n = 2, an = n, a2 = 1
n = 3, an = n, a3 = 1
n = 4, an = an-1 + an-2 + an-3
a4 = a4-1 + a4-2 + a4-3
a4 = a3 + a2 + a1
a4 = 3 + 2 + 1 = 6
n = 5, an = an-1 + an-2 + an-3
a5 = a5-1 + a5-2 + a5-3
a5 = a4 + a3 + a2
a5 = 6 + 3 + 2 = 11
n = 6, an = an-1 + an-2 + an-3
a6 = a6-1 + a6-2 + a6-3
a6 = a5 + a4 + a3
a6 = 11 + 6 + 3 = 20
∴ The first six terms are 1, 2, 3, 6, 11, 20
![]()
Question 3.
Write the nth term of the following sequences.
(i) 2, 2, 4, 4, 6, 6, ……………..
Answer:
The odd terms are a1 = 2, a3 = 4, a5 = 6
The even terms are a2 = 2, a4 = 4, a6 = 6
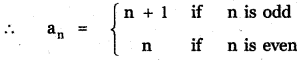
(ii) 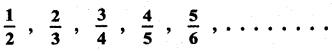
Answer:
![]()
The terms in the numerator are 1 , 2 , 3, 4
a = 1 , d = 2 – 1 = 1
an = a + (n – 1) d
an = 1 + (n – 1)(1) = 1 + n – 1 = n
an = n
The terms in the denominator are 2 , 3 , 4 , 5 , 6 .
a = 2, d = 3 – 2 = 1
an = a + (n – 1) d
an = 2 + (n – 1) (1) = 2 + n – 1 = n + 1
an = n + 1
∴ The nth term of the given sequence is an = \(\frac{n}{n+1}\) for all n ∈ N
(iii) ![]()
Answer:
![]()
The terms in the numerator are 1, 3, 5, 7, 9, ………….
a = 1 , d = 3 – 1 = 2
an = a + (n – 1) d
an = 1 + (n – 1)2
an = 1 + 2n – 2 = 2n – 1
The terms in the denominator are 2, 4, 6, 8, 10, …………..
a = 2, d = 4 – 2 = 2
an = a + (n – 1) d
an = 2 + (n – 1)(2)
an = 2 + 2n – 2 = 2n
∴ The nth term of the given sequence is an = \(\frac{2 n-1}{2 n}\) for all n ∈ N
![]()
(iv) 6, 10, 4, 12, 2, 14, 0, 16, – 2 …………………
Answer:
The given sequence is 6, 10, 4, 12, 2, 14, 0, 16, – 2 ……………..
The odd terms are a1 = 6, a3 = 4 , a5 = 2 , a7 = 0, a9 = – 2
∴ an = n – 7, n is odd
The even terms are a2 = 10, a4 = 12 , a6 = 14 , a8 = 16
∴ an = 8 + n, n is even.
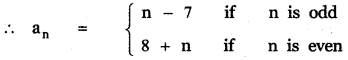
Question 4.
The product of three increasing numbers in a G.P is 5832 . If we add 6 to the second number and 9 to the third number, then resulting numbers form an A.P. Find the numbers in G.P.
Answer:
Let the increasing numbers in G.P be \(\), a, ar.
Given \(\frac{a}{r}\) × a × ar = 5832 ⇒ a3 = 5832 = 183 ⇒ a = 18
Also given \(\frac{a}{r}\), a + 6, ar + 9 form an A.P.
∴ 2(a + b) = \(\frac{a}{r}\) + (ar + 9)
⇒ (a + 6) + (a + 6) = \(\frac{a}{r}\) + (ar + 9)
⇒ (a + 6) – \(\frac{a}{r}\) = (ar + 9) – (a + 6)
⇒ a + 6 – \(\frac{a}{r}\) = ar + 9 – a – 6
⇒ a + 6 – \(\frac{a}{r}\) = ar – a + 3
Substituting the value of a = 18, we get
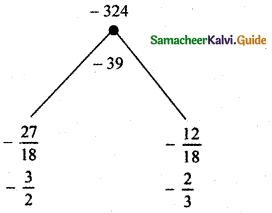

39r = 18r2 + 18
18r2 – 39r + 18 = 0
(2r – 3)(3r -2) = 0
2r – 3 = 0 or 3r – 2 = 0
r = \(\frac{3}{2}\) or r = \(\frac{2}{3}\)
![]()
Case (i) When a = 18, r = \(\frac{3}{2}\) the numbers in G.P are
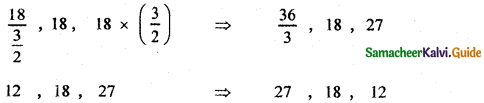
Case (ii) When a = 18, r = \(\frac{2}{3}\)
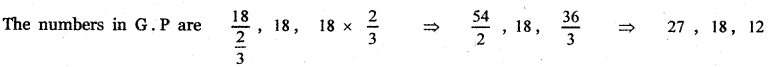
Question 5.
Write the nth term of the sequence \(\frac{3}{1^{2} \cdot 2^{2}}, \frac{5}{2^{2} \cdot 3^{2}}, \frac{7}{3^{2} \cdot 4^{2}}\), …………….. as a difference of two terms.
Answer:
![]()
The terms in the numerator are 3,5, 7
which forms an A. P with first term a = 3 and common difference d = 5 – 3 = 2
nth term tn = a + (n – 1) d
= 3 + (n – 1)(2)
= 3 + 2n – 2 = 2n + 1
tn = 2n + 1
The terms in the denominator are 12 . 22, 22 . 32, 32 . 42 ……………….
nth term tn = n2 . (n + 1)2
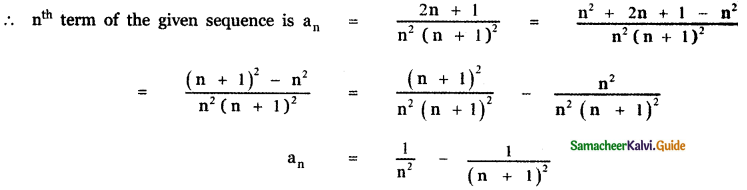
Question 6.
If tk is the kth term of a G.P then show that tn – k, tk, tn + k also form a G.F for any positive integer k.
Answer:
Given tk is the kth term of a G.P. We have nth term of a G.P is tn = arn-1

![]()
Question 7.
If a, b, c are in geometric progression and if a1/x = b1/y = c1/z are in Arithmetic progression.
Answer:

Question 8.
The A.M of two numbers exceeds their G.M by 10 and H.M by 16. Find the numbers.
Answer:
Let the numbers be a and b

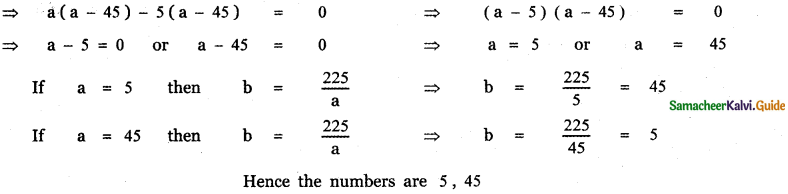
![]()
Question 9.
If the roots of the equation (q – r)x2 + (r – p)x + (p – q) = 0 are equal then show that p , q and r are in A. P.
Answer:
The roots are equal ⇒ ∆ = 0
(i.e.) b2 – 4ac = 0
Hence, a = q – r ; b = r – p ; c = p – q
b2 – 4ac = 0
⇒ (r – p)2 – 4(q – r)(p – q) = 0
r2 + p2 – 2pr – 4[qr – q2 – pr + pq] = 0
r2 + p2 – 2pr – 4qr + 4q2 + 4pr – 4pq = 0
(i.e.) p2 + 4q2 + r2 – 4pq – 4qr + 2pr = 0
(i.e.) (p – 2q + r)2 = 0
⇒ p – 2q + r = 0
⇒ p + r = 2q
⇒ p, q, r are in A.P.
Question 10.
If a , b , c are respectively the pth, qth and rth terms of a G . P show that (q – r) log a + (r – p) log b + (p – q) log c = 0
Answer:
Let A be first term and R be the jmnon ratio of the G.P.
Given a = pth term of the G.P
General term of a G. P with first term A and common ratio R is tn = ARn – 1
∴ a = tp = ARP – 1
log a = log ARp-1 = log A + log Rp-1 = log A + (p – 1) log R
b = qth term of the G.P
b = tq = ARq-1
log b = log ARq-1 = log A + log Rq-1 = log A + (q – r)log R
c = rth term of the G.P
c = tr = ARr-1
log c = log ARr-1 = log A + log Rr-1 = log A + (r – 1) log R
![]()
(q – r) log a + (r – p) log b + (p – q) log c
= (q – r) [log A + (p – 1) log R] + (r – p) [ log A + (q – 1) log R ] + (P – q) [ log A + (r – 1) log R]
= (q – r) log A + (q – r) (p – 1 ) log R + (r – p) log A + (r – p) (q – 1) log R + (P – q) log A + (p – q) (r – 1 ) log R
= [ q – r + r – p + p – q ] log A + [ (q – r) (p – 1) + (r – p) (q – 1) + (p – q)(r – 1)] log R
= 0 × log A + [pq – q – rp + r + rq – r – pq + p + pr – p – rq + q] log R
= 0 × log R = 0
∴ (q – r) log a + (r – p) log b + (p – q) log c = 0