Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 6 Two Dimensional Analytical Geometry Ex 6.4 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.4
Question 1.
Find the combined equation of the straight lines whose separate equations are x – 2y – 3 = 0 and x + y + 5 = 0.
Answer:
Separate equations are x – 2y – 3 = 0; x + y + 5 = 0
So the combined equation is (x – 2y – 3) (x + y + 5) = 0
x2 + xy + 5x – 2y2 – 2xy – 10y – 3x – 3y – 15 = 0
(i.e) x2 – 2y2 – xy + 2x – 13y – 15 = 0
![]()
Question 2.
Show that 4x2 + 4xy + y2 – 6x – 3y – 4 = 0 represents a pair of parallel lines.
Answer:
The equation of the given pair of straight lines is
4x2 + 4xy + y2 – 6x – 3y – 4 = 0 ………. (1)
Compare this equation with the equation
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 ………. (2)
a = 4, 2h = 4, b = 1, 2g = -6,
2f = -3, c = – 4
The condition for parallelism is
h2 – ab = 0
22 – (4) (1) = 4 – 4 = 0
∴ The given pair of straight lines represents a pair of parallel straight lines.
Question 3.
Show that 2x2 + 3xy – 2y2 + 3x + y + 1 = 0 represents a pair of perpendicular straight lines.
Answer:
Comparing the given equation with the general form a = 2,h = 3/2, b = -2,g= 3/2, f = 1/2 and c = 1
Condition for two lines to be perpendicular is a + b = 0. Here a + b = 2 – 2 = 0
⇒ The given equation represents a pair of perpendicular lines.
![]()
Question 4.
Show that equation 2x2 – xy – 3y2 – 6x + 19y – 20 = 0 represents a pair of intersecting lines. Show further that the angle between them is tan-1(5)
Answer:
The equation of the given pair of lines is
2x2 – xy – 3y2 – 6x + 19y – 20 = 0 —- (1)
Compare this equation with the equation
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 —- (2)
a = 2 , 2h = – 1, b = – 3, 2g = – 6, 2f = 19, c = – 20
h2 – ab = \(\left(-\frac{1}{2}\right)^{2}\) – (2)(-3)
= \(\frac{1}{4}\) + 6 ≠ 0
∴ The given line (1) is not parallel.
∴ They are intersecting lines.
Let θ be the angle between the lines.
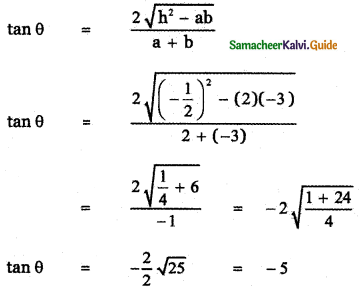
Taking the acute angle θ = tan-1 (5)
Question 5.
Prove that the equation to the straight lines through the origin each of which makes an angle α with the straight line y = x is x2 – 2xy sec 2α + y2 = 0
Answer:
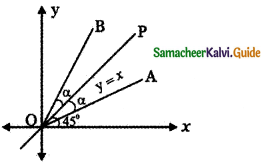
Let OP be the given line y = x having slope
m = 1 = tan 45°
Given that OA is the line making angle α with the line y = x.
![]()
Slope of the line OA = tan (45° – α)
The equation of OA is the equation of the line passing through the point (0, 0) having slope tan (45° – α).
y – 0 = tan(45°- α) (x – 0)
y = x tan (45°- α)
x tan (45° – α) – y = 0
Also given the line OB makes an angle α with the line y = x.
![]()
Slope of the line OB = tan(45° + α)
The equation of OB is the equation of the line passing through the point (0, 0) having slope tan(45° + α)
y – 0 = tan (45° + α) (x – 0)
y = x tan (45° + α)
x tan (45° + α) – y = 0 ………. (2)
The combined equation is
(x tan(45°- α) – y) (x tan(45°+ α) – y) = 0
x2tan(45° – α) tan(45° + α) – xy tan (45° – α) – xy tan(45° + α) + yz = 0
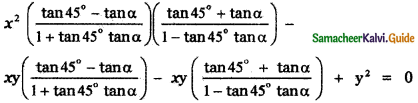
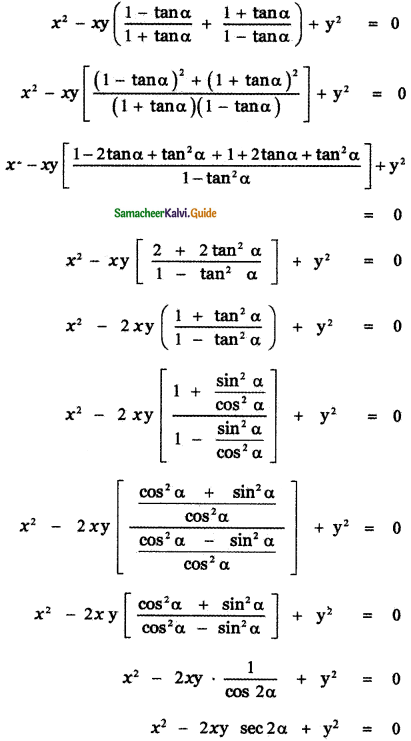
![]()
Question 6.
Find the equation of the pair of straight lines passing through the poInt (1,3) and
perpendicular to the lines 2x -3y + 1 = 0 and 5x + y – 3 = 0.
Answer:
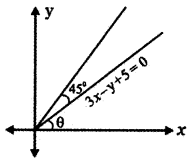
Equation of a line perpendicular to 2x – 3y + 1 = 0 is of the form 3x + 2y + k = 0.
It passes through (1, 3) ⇒ 3 + 6 + k = 0 ⇒ k = – 9
So the line is 3x + 2y – 9 = 0
The equation of a line perpendicular to 5x + y – 3 = 0 will be of the form x – 5y + k = 0.
It passes through (1, 3) ⇒ 1 – 15 + k = 0 ⇒ k = 14
So the line is x – 5y + 14 = 0.
The equation of the lines is 3x + 2y – 9 = 0 and x – 5y + 14 = 0
Their combined equation is (3x + 2y – 9)(x – 5y + 14) = 0
(i.e) 3x2 – 15xy + 42x + 2xy – 10y2 + 28y – 9x + 45y – 126 = 0
(i.e) 3x2 – 13xy – 10y2 + 33x + 73y – 126 = 0
Question 7.
Find the separate equation of the following pair of straight lines.
(i) 3x2 + 2xy – y2 = 0
(ii) 6(x – 1)2 + 5(x – 1) (y – 2) – 4(y – 3)2 = 0
(iii) 2x2 – xy – 3y2 – 6x + 19y – 20 = 0
Answer:
(i) Factorising 3x2 + 2xy – y2 we get
3x2 + 3xy – xy – y2 = 3x (x + y) – y (x + y)
= (3 x – y)(x + y)
So 3x2 + 2xy – y2 = 0 ⇒ (3x – y) (x + y) = 0
⇒ 3x – y = 0 and x + y = 0
![]()
(ii) 6(x – 1)2 + 5 ( x – 1) (y – 2) – 4(y – 3 )2 = 0
Let X = x – 1 and Y = y – 2
∴ The given equation becomes
6X2 + 5XY – 4Y2 = 0
6X2 + 8 XY – 3XY – 4Y2 = 0
2X(3X + 4Y) – Y (3X + 4Y) = 0
(2X – Y) (3X + 4Y) = 0
2X – Y = 0 and 3X + 4Y = 0
Substituting for X and Y , we have
2X – Y = 0 ⇒ 2(x – 1) – (y – 2) = 0
⇒ 2x – 2 – y + 2 = 0
⇒ 2x – y = 0
3X + 4Y = 0 ⇒ 3 (x – 1) + 4 ( y – 2 ) = 0
⇒ 3x – 3 + 4y – 8 = 0
⇒ 3x + 4y – 11 = 0
∴ The separate equations are
2x – y = 0 and 3x + 4y – 11 = 0
(iii) 2x2 – xy – 3y2 – 6x + 19y – 20 = 0
The given equation is
2x2 – xy – 3y2 – 6x + 19y – 20 = 0 ……… (1)
2x2 – xy – 3y2 = 2x2 – 3xy + 2xy – 3y2
= x (2x – 3y) + y (2x – 3y )
= (x + y) (2x – 3y)
Let the separate equation of the straight lines be
x + y + 1 = 0 and 2x – 3y + m = 0 …….. (A)
(1) ⇒ 2x2 – xy – 3y2 – 6x + 19y – 20 = (x + y + 1) (2x – 3y + m)
Equating the coeffident of x , y and constant term on both sides, we have
-6 = m + 2l ………. (2)
19 = m – 3l ………. (3)
lm = – 20 ………. (4)
Solving equations (2), (3) and (4) we have
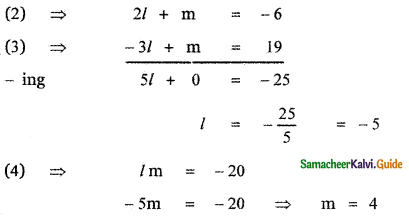
Substituting the values of l and m in equation (A) the required separate equations of the lines are
x + y – 5 = 0 and 2x – 3y + 4 = 0
![]()
Question 8.
The slope of one of the straight lines ax2 + 2hxy + by2 = 0 is twice that of the other, show that 8h2 = 9ab.
Answer:
The equation of the given straight line is
ax2 + 2hxy + by2 = 0 ………… (1)
Given that the slopes of the straight lines are m and 2m

Question 9.
The slope of one of the straight lines ax2 + 2h xy + by2 = 0 is three times the other, show that 3h2 = 4ab.
Answer:
The equation of the given straight line is
ax2 + 2hxy + by2 = 0 ……….. (1)
Given that the slopes of the lines are m and 3m.

![]()
Question 10.
A ∆ OPQ is formed by the pair of straight lines x2 – 4xy + y2 = 0 and the line PQ. The equation of PQ is x + y – 2 = 0, Find the equation of the median of the triangle ∆ OPQ drawn from the origin O
Answer:
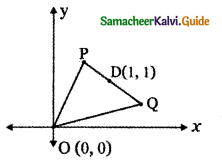
The equation of the given pair of lines is
x2 – 4xy + y2 = 0 ……….. (1)
The equation of the line PQ is
x + y – 2 = 0
y = 2 – x ……….. (2)
To find the coordinates of P and Q, .
Solve equations (1) and (2)
(1) ⇒ x2 – 4x ( 2 – x) + ( 2 – x)2 = 0
x2 – 8x + 4x2 + 4 – 4x + x2 = 0
6x2 – 12x + 4 = 0
3x2 – 6x + 2 = 0
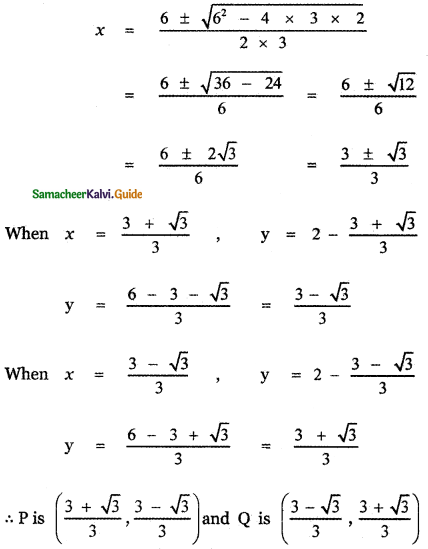
The midpoint of PQ is

The equation of the median drawn from 0 is the equation of the line joining 0 (0, 0) and D (1, 1)
![]()
∴ The required equation is x = y
![]()
Question 11.
Find p and q, if the following equation represents a pair of perpendicular lines
6x2 + 5xy – py2 + 7x + qy – 5 = 0
Answer:
The equation of the given pair of straight lines is
6x2 + 5xy – py2 + 7x + qy – 5 = 0 ……….. (1)
Given that equation (1) represents a pair of perpendicular straight lines.
∴ Coefficient of x2 + coefficient of y2 = 0
6 – p = 0 ⇒ p = 6
6x2 + 5xy – 6y2 = 6x2 + 9xy – 4xy – 6y2
= 3x(2x + 3y) – 2y (2x + 3y)
= (2x + 3y) (3x – 2y)
Let the separate equation of the straight lines be
2x + 3y + 1 = 0 and 3x – 2y + m = 0
6x2 + 5xy – 6y2 + 7x + qy – 5
= (2x + 3y + 1)(3x – 2y + m)
Comparing the coefficients of x , y and constant terms on both sides
2m + 3l = 7 ………… (2)
3m – 2l = q ……….. (3)
lm = – 5 …….. (4)
Equation (4) ⇒ l = 1, m = – 5
or l = – 1, m = 5
When l = 1, m = – 5 , equation (2) does not satisfy.
∴ l = – 1 , m = 5
Substituting in equation (3)
3 (5) – 2(-1) = q ⇒ q = 17
∴ The required values are p = 6, q = 17
Question 12.
Find the value of k, if the following equation represents a pair of straight lines. Further, find whether these lines are parallel or intersecting
12x2 + 7xy – 12y2 – x +7y + k = 0
Answer:
The equation of the given pair of straight lines is
12x2 + 7xy – 12y2 – x + 7y + k = 0 ………. (1)
Compare this equation with the equation
ax2 + 2hxy + by2 + 2gx + 2f y + c = 0 ……….. (2)
a = 12, 2h = 7 , b = – 12 ,
2g = – 1, 2f = 7, k = c
a = 12, h = \(\frac{7}{2}\), b = – 12,
g = \(-\frac{1}{2}\), f = \(\frac{7}{2}\), c = k
The condition for a second degree equation in x and y to represent a pair of straight lines is
abc + 2fgh – af2 – bg2 – ch2 = 0
Substituting the values
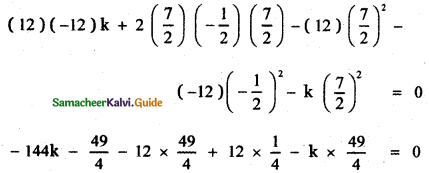

Coefficient of x2 + coefficient of y2 = 12 – 12 = 0
∴ The given pair of straight lines are perpendicular and hence they are intersecting lines.
![]()
Question 13.
For what values of k does the equation
12x2 + 2kxy + 2y2 +11x – 5y + 2 = 0 represent two straight lines.
Answer:
The given equation of the pair of straight line is
12x2 + 2kxy + 2y2 + 11x – 5y + 2 = 0 ……… (1)
Compare this equation with the equation
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 ………. (2)
a = 12, 2h = 2k, b = 2,
2g = 11, 2f = – 5 , c = 2 ,
a =12, h = k, b = 2,
g = \(\frac{11}{2}\), f = –\(\frac{5}{2}\), c = 2,
The condition for a second degree equation in x and y to represent a pair of straight lines is
abc + 2fgh – af2 – bg2 – ch2 = 0
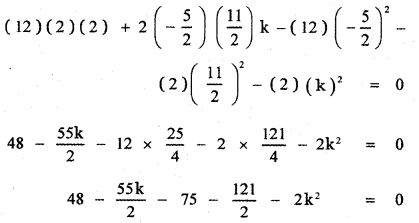
96 – 55k – 150 – 121 – 4k2 = o
– 4k2 – 55k – 175 = 0
4k2 + 55k + 175 = 0

∴ The given equation represents a pair of straight lines when
k = – 5 and k = \(\frac{-35}{4}\)
![]()
Question 14.
Show that the equation 9x2 – 24xy + 16y2 – 12x + 16y – 12 = 0 represents a pair of parallel lines. Find the distance between them.
Answer:
The given equation of the pair of straight line is
9x2 – 24xy + by2 – 12x + 16y – 12 = 0 ………… (1)
9x2 – 24xy + 16y2 = 9x2 – 12xy – 12xy + 16y2
= 3x (3x – 4y) – 4y (3x – 4y)
= (3x – 4y) (3x – 4y)
Let the separate equation of the straight lines be
3x – 4y + 1 = 0 and 3x – 4y + m = 0
9x2 – 24xy + 16y2 – 12x + 16y – 12
= (3x – 4y + l) ( 3x – 4y + m )
Comparing the coefficients of x , y and constant terms on both sides
3l + 3m = – 12
l + m = – 4 ……….. (2)
– 4l – 4m = 16
l + m = – 4 ………… (3)
lm = – 12 ……….. (4)
(l – m)2 = (l + m)2 – 4lm
= (- 4)2 – 4 × – 12
= 16 + 48 = 64
l – m = √64 = 8
l – m = 8 ………… (5)
Solving equations (2) and (5 ), we have
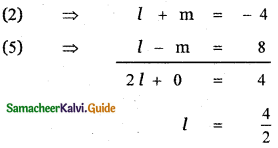
(2) ⇒ 2 + m = – 4 ⇒ m = – 6
∴ l = 2 and m = – 6
∴ The separate equation of the straight lines are
3x – 4y – 6 = 0 and 3x – 4y + 2 = 0
The distance between the parallel lines is given by
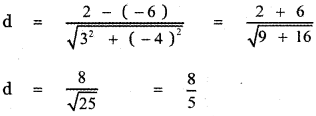
∴ The given pair of straight lines are parallel and the distance between them is \(\frac{8}{5}\) units
![]()
Question 15.
Show that the equation 4x2 + 4xy + y2 – 6x – 3y – 4 = 0 represents a pair of parallel lines. Find the distance between them.
Answer:
The given equation of pair of straight lines is
4x2 + 4xy + y2 – 6x – 3y – 4 = 0 ………. (1)
4x2 + 4xy + y2 = (2x + y)2
Let the separate equation of the lines be
2x + y + l = 0 ……….. (2)
2x + y + m = 0 ………. (3)
4x2 + 4xy + y2 – 6x – 3y – 4 = (2x + y + l) (2x + y + m)
Comparing the coefficients of x , y and constant terms on both sides we have
2l + 2m = – 6
l + m = – 3 ……… (4)
l + m = – 3 ……… (5)
l m = – 4 ……… (6)
(l – m)2 = (l + m)2 – 4lm
(l – m )2 = (- 3)2 – 4 × – 4
(l – m)2 = 9 + 16 = 25
l – m = 5 ………… (7)
Solving equations (4) and (7)
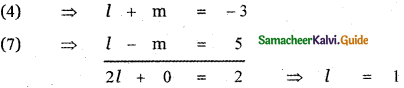
(4) ⇒ l + m = – 3 ⇒ m = – 4
∴ The separate equation of the straight lines are
2x + y + 1 =0 and 2x + y – 4 = 0
The distance between the parallel lines is
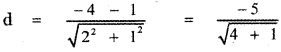
d = \(\frac{5}{\sqrt{5}}\) = \(\sqrt{5}\)
∴ The given equation represents a pair of parallel straight lines and the distance between the parallel lines is \(\sqrt{5}\) units.
![]()
Question 16.
Prove that one of the straight lines given by ax2 + 2hxy + by2 = 0 will bisect the angle between the coordinate axes if (a + b)2 = 4h2
Answer:
The equation of the given pair of straight lines is
ax2 + 2hxy + by2 = 0 ……… (1)
Let m1 and m2, be the slopes of the separate straight lines.
Given that one of the straight lines of (1) bisects the angle between the coordinate axes.
∴ The angle made by that line with x-axis 45°.
Slope of that line m1 = tan 45°
m1 = 1

Squaring on both sides
(a + b)2 = (- 2h)2
(a + b)2 = 4h2
Question 17.
If the pair of straight lines x2 – 2kxy – y2 = 0 bisects the angle between the pair of straight lines x2 – 2lxy – y2 = 0. Show that the later pair also bisects the angle between the former.
Answer:
The equations of the given pair of straight lines are
x2 – 2kxy – y2 = 0 ………… (1)
x2 – 2lxy – y2 = 0 ………… (2)
Given that the pair x2 – 2kxy – y2 = 0 bisects the angle between the pair x2 – 2lxy – y2 = 0
∴ The equation of the bisector of the pair
x2 – 2lxy – y2 = 0 is the pair x2 – 2kxy – y2 = 0
The equation of the bisector of x2 – 2lxy – y2 = 0 is
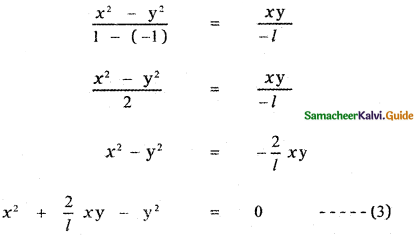
Equation (3) and Equation (1) represents the same straight lines. ∴ The coefficients are proportional.
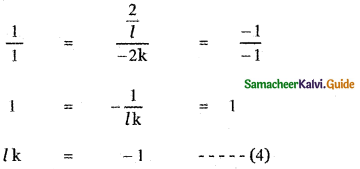
To show that the pair x2 – 2lxy – y2 = 0 bisects the angle between the pair x2 – 2kxy – y2 = 0, it is enough to prove the equation of the bisector of x2 – 2kxy – y2 = 0 is x2 – 2lxy – y2 = 0
The equation of the bisector of x2 – 2kxy – y2 = 0 is
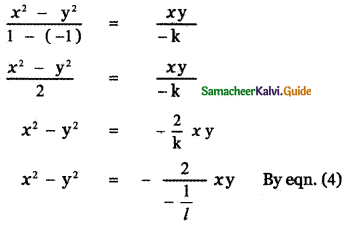
x2 – y2 = 2lxy .
x2 – 2lxy – y2 = 0
∴ The pair x2 – 2lxy – y2 = 0 bisects the angle between the pair x2 – 2kxy – y2 = 0
![]()
Question 18.
Prove that the straight lines joining the origin to the points of intersection of 3x2 + 5xy – 3y2 + 2x + 3y = 0 and 3x – 2y – 1 = 0 are at right angle.
Answer:
Homogenizing the given equations 3x2 + 5xy – 3y2 + 2x + 3y = 0 and 3x – 2y – 1 = 0
(i.e) 3x – 2y = 1.
We get (3x2 + 5xy – 3y2) + (2x + 3y)( 1) = 0
(i.e) (3x2 + 5xy – 3y2) + (2x + 3y)(3x – 2y) = 0
3x2 + 5xy – 3y2 + bx2 – 4xy + 9xy – 6y2 = 0
9x2 + 10xy – 9y2 = 0
Coefficient of x2 + coefficient of y2 = 9 – 9 = 0
⇒ The pair of straight lines are at right angles.