Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 Matrices and Determinants Ex 7.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.2
Question 1.
without expanding the determinant,
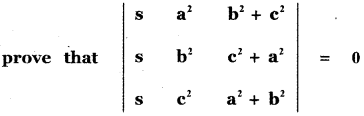
Answer:

= s (a2 + b2 + c2) × 0
since two columns are equal.
= 0
![]()
Question 2.
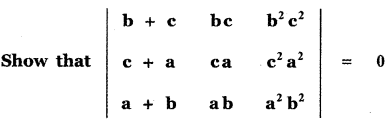
Answer:

![]()
Question 3.
Prove that
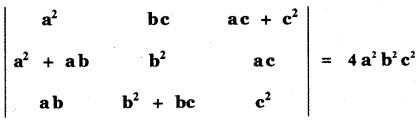
Answer:


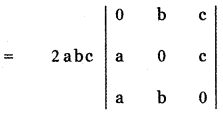
= 2abc [0 – b(0 – ac) + c(ab – 0)]
= 2 abc [ abc + abc ]
= 2 abc × 2abc
Δ = 4 a2b2c2
![]()
Question 4.
Prove that
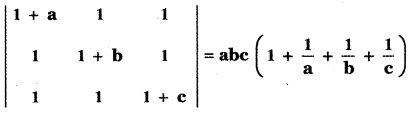
Answer:
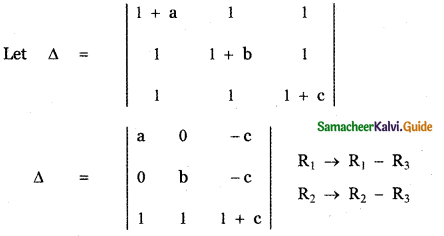
= a [b(1 + c) + c (1)] – 0 – c [0 – b]
= a[b + bc + c] + bc
= ab + abc + ac + bc
= abc + ab + bc + ac
= abc
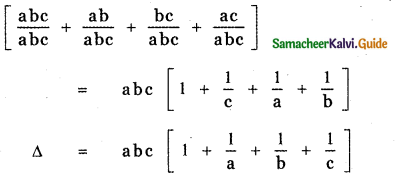
![]()
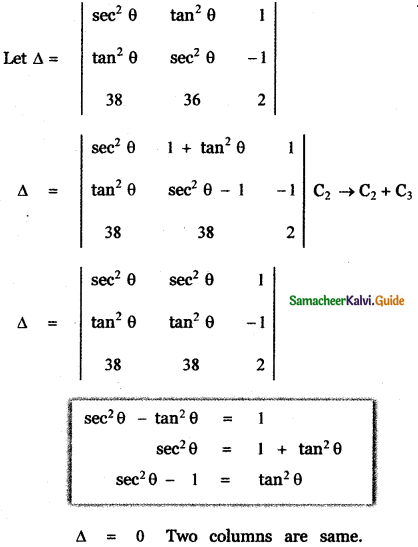
Question 5.

Answer:
![]()
Question 6.
show that \(\left| \begin{matrix} x\quad +\quad 2a & y\quad +\quad 2b & z\quad +\quad 2c \\ x & y & z \\ a & b & c \end{matrix} \right| \) = 0
Answer:
Let Δ = \(\left| \begin{matrix} x\quad +\quad 2a & y\quad +\quad 2b & z\quad +\quad 2c \\ x & y & z \\ a & b & c \end{matrix} \right| \)
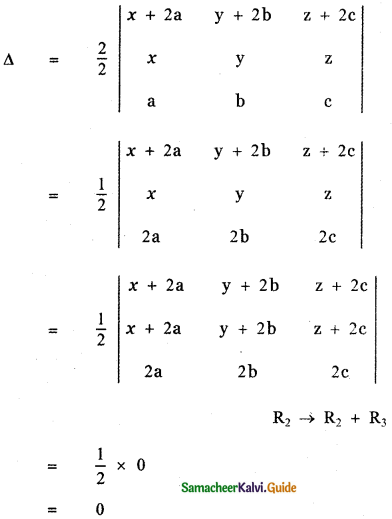
![]()
Question 7.
Write the general form of a 3 × 3 skew- symmetric matrix and prove that its determinant is 0.
Answer:
A square matrix A = [ aij ]3 × 3 is a skew – symmetric matrix if aij = – aij for all i,j and the elements on the main diagonal of a skew – symmetric matrix are zero.

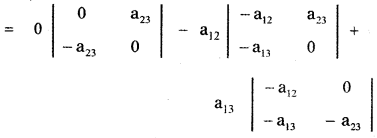
= 0 – a12 (0 + a13 a23) + a13 (a12 a23 – 0)
= – a12 a13 a23 + a13 a12 a23
= 0
Hence the determinant of a skew – symmetric matrix is 0.
![]()
Question 8.
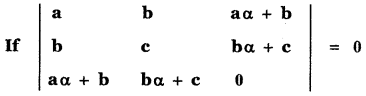
Prove that a, b, c are in G. P or α is a root of ax2 + 2bx + c = 0.
Answer:


![]()
Question 9.
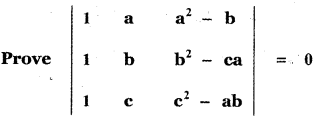
Answer:
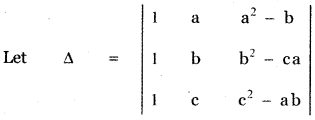
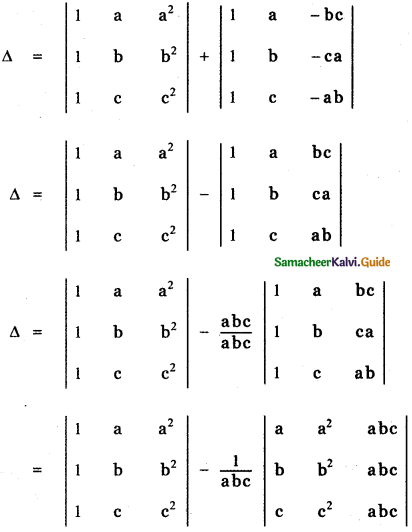
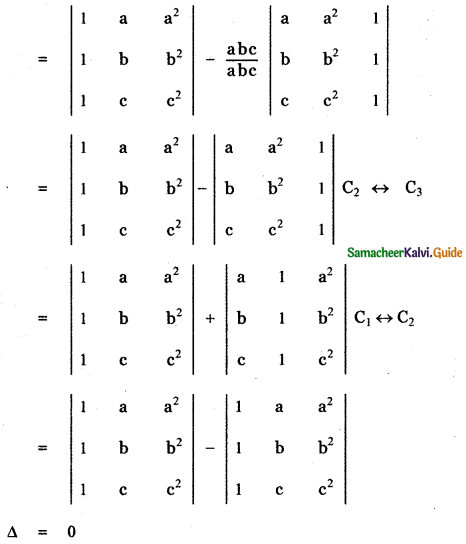
![]()
Question 10.
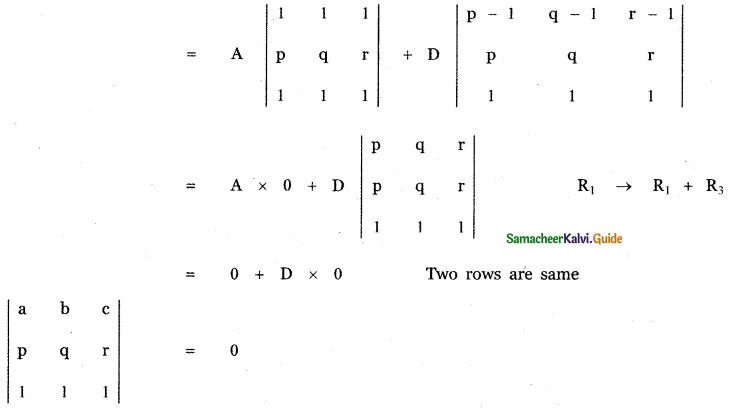
If a, b, c are pth, qth and rth terms of an A.P, find the value of \(\left| \begin{matrix} a & b & c \\ p & q & r \\ 1 & 1 & 1 \end{matrix} \right| \)
Answer:
Given a, b, c are pth, qth and rth terms of an A.P.
tp = a = A + (p – 1)D,
tq = b = A + (q – 1)D,
tr = c = A + (r – 1) D
where A – first term , D – Common difference of the AP.
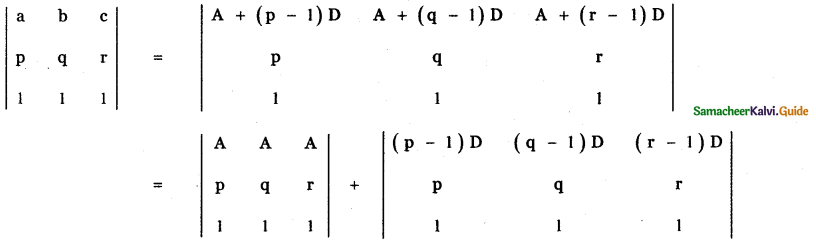
![]()
Question 11.
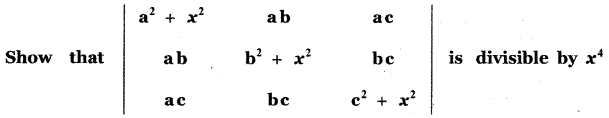
Answer:


![]()
Question 12.
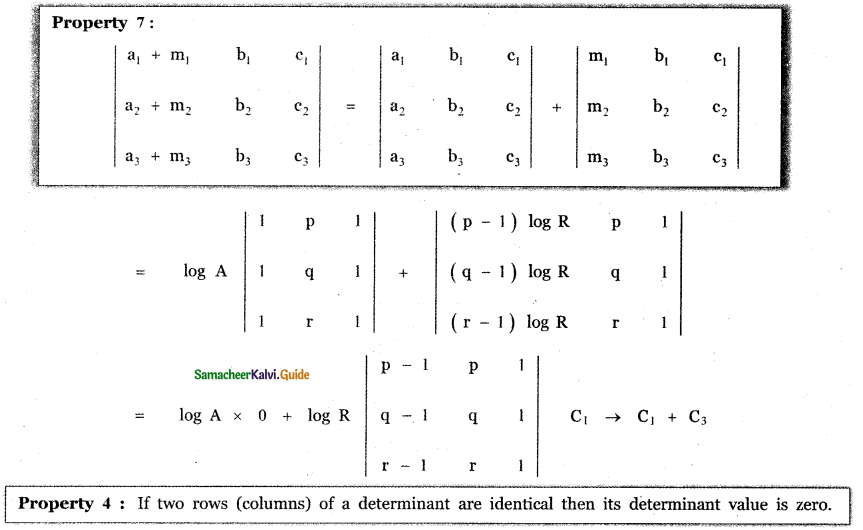
If a , b , c , are all positive, and are pth, qth and rth terms of a G.P., show that \(\left| \begin{matrix} log\quad a & p & 1 \\ log\quad b & q & 1 \\ log\quad c & r & 1 \end{matrix} \right| \) – 0
Answer:
Given a, b, c are the pth, qth and rth terms of a G.P.
∴ a = ARp-1, b = ARq-1, c = ARr-1
where A is the first term , R – common ratio.


![]()
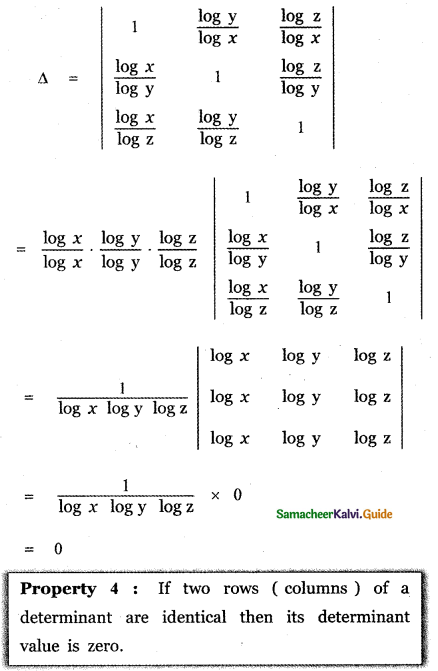
Question 13.
Find the value of
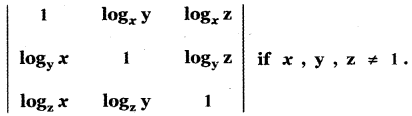
Answer:

![]()
Question 14.
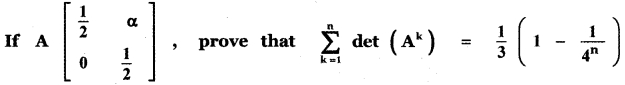
Answer:
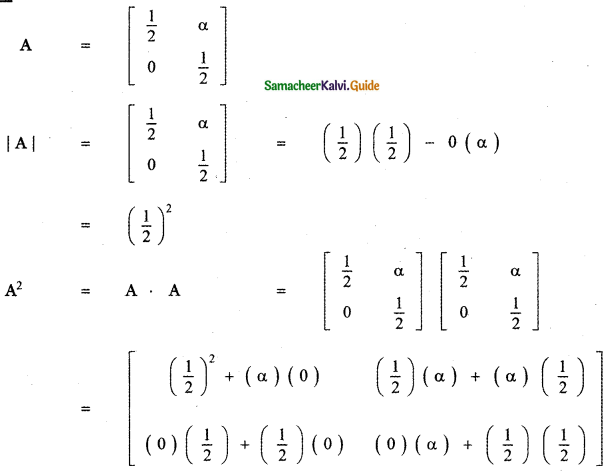

![]()


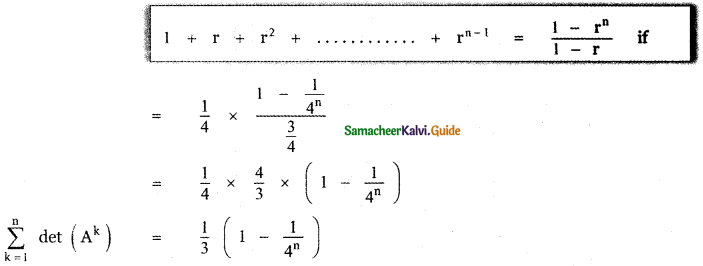
![]()
Question 15.
Without expanding, evaluate the following determinants:
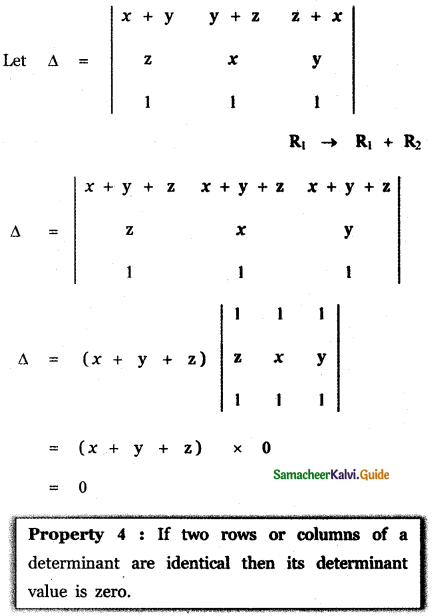
(i) \(\left| \begin{matrix} 2 & 3 & 4 \\ 5 & 6 & 8 \\ 6x & 9x & 12x \end{matrix} \right| \)
(ii) \(\left| \begin{matrix} x\quad +\quad y & y\quad +\quad z & z\quad +\quad x \\ z & x & y \\ 1 & 1 & 1 \end{matrix} \right| \)
Answer:
(i) \(\left| \begin{matrix} 2 & 3 & 4 \\ 5 & 6 & 8 \\ 6x & 9x & 12x \end{matrix} \right| \)

(ii) \(\left| \begin{matrix} x\quad +\quad y & y\quad +\quad z & z\quad +\quad x \\ z & x & y \\ 1 & 1 & 1 \end{matrix} \right| [
![]()
Question 16.
If A is a Square, matrix, and |A| = 2, find the value of |A AT|.
Answer:
|A| = 2 (Given) |AT| = 2
Now |AAT| = |A| |AT| = 2 × 2 = 4.
Question 17.
If A and B are square matrices of order 3 such that |A| = -1 and |B| = 3, find the value of |3 AB|.
Answer:
Given |A| = -1 : |B| = 3
Given A and B are square matrices of order 3.
∴ |kAB| = k3 |AB|
Here k = 3 ∴ |3AB| = 33 |AB|
= 27 |AB|
= 27 (-1) (3)
= -81
Question 18.
If λ = – 2, determine the value of
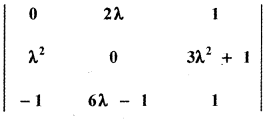
Answer:

Expanding along the first row
Δ = 0 + 4 [4 × 0 – (- 1 ) ( 13)] + [4 × -13 – 0 × – 1]
= 4 [0 + 13] + 1 [- 52 + 0]
= 52 – 52 = 0
![]()
Question 19.
Determine the roots of the equation
[latex]\left| \begin{matrix} 1 & 4 & 20 \\ 1 & -2 & 5 \\ 1 & 2x & { 5x }^{ 2 } \end{matrix} \right| \) = 0
Answer:
\(\left| \begin{matrix} 1 & 4 & 20 \\ 1 & -2 & 5 \\ 1 & 2x & { 5x }^{ 2 } \end{matrix} \right| \) = 0 ………… (1)
Put x = -1 then (1) ⇒
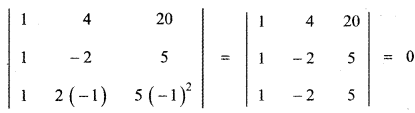
∴ x = – 1 satisfies equation (1)
Hence x = – 1 is a root of equation (1)
Put x = 2 then ……….. (1)
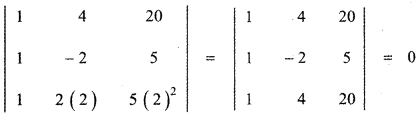
[Property 4: If two rows (columns) of a determinant are identical then its determinant value is zero.]
∴ x = 2 satisfies equation (1)
Hence x = 2 is a root of equation (1)
Hence the required roots are x = -1 , 2
Question 20.
Verify that det (AB) = (det A) (det B) for
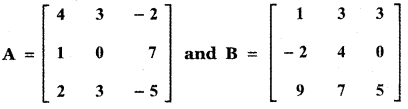
Answer:
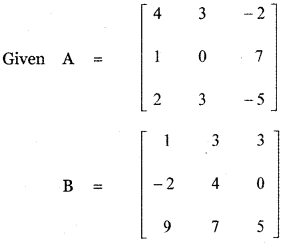

![]()
= 4 [-10 (0 – 9 × 19) – 5 (0 + 17 × 19) + 1 (32 × 9 + 17 × 26)]
= 4 [1710 – 5 × 323 + 288 + 442]
= 4 [1710 – 1615 + 730]
= 4 [2440 – 1615]
= 4 × 825
det (AB) = 3300 …….. (1)
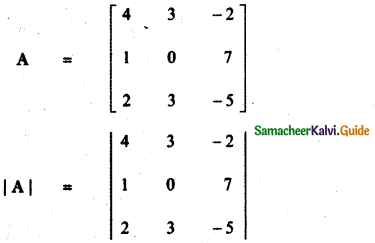
= 4(0 – 21) – 3 (- 5 – 14) – 2 (3 – 0)
= -84 – 3 × – 19 – 6
= -84 + 57 – 6
= -90 + 57
det A = -33 ………… (2)
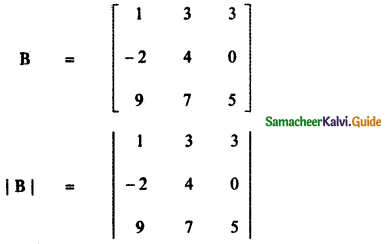
= 1 (20 – 0) – 3 (- 10 – 0) + 3 (-14 – 36)
= 20 + 30 + 3 × – 50
= 50 – 150
det A = – 100 ……….. (3)
From equations (2) and (3)
(det A) (det B) = – 33 × – 100
(detA) (det B) = 3300 ………… (4)
From equations (1) and (4), we have
det (AB) = (det A) (det B)
![]()
Question 21.
Using cofactors of elements of second row, evaluate |A|, where A = \(\left[ \begin{matrix} 5 & 3 & 8 \\ 2 & 0 & 1 \\ 1 & 2 & 3 \end{matrix} \right] \)
Answer:

|A| = a21 A21 + a22 A22 + a23 A23
= 2 × 7 + 0 × 7 + 1 × – 7
= 14 – 7
|A| = 7