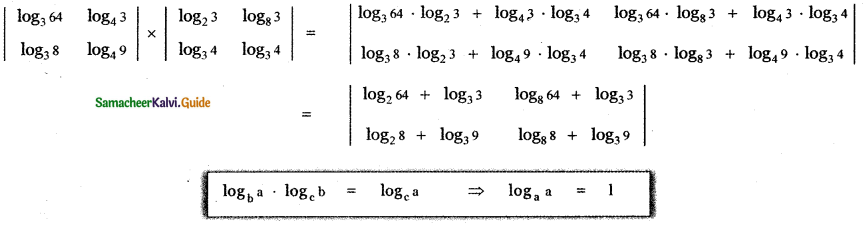Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 7 Matrices and Determinants Ex 7.4 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.4
Question 1.
Find the area of the triangle whose vertices are (0, 0), (1, 2) and (4, 3)
Answer:
The given points are (0, 0), (1, 2) and (4, 3)
Area of the triangle with vertices
(x1, y1), (x2, y2) and (x3, y3) is
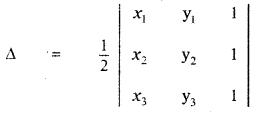
∴ The area of the triangle with vertices
(0, 0), (1, 2) and (4, 3) is
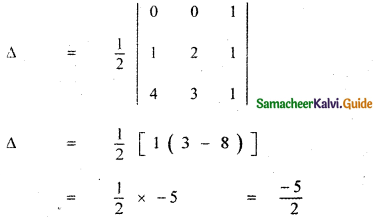
Area cannot be negative. Taking positive value, we have
Required area Δ = \(\frac{5}{2}\) sq.units.
![]()
Question 2.
If (k, 2), (2, 4) and (3, 2) are vertices of the triangle of area 4 square units then determine the value of k.
Answer:
Given Area of the triangle with vertices (k, 2), (2, 4) and (3, 2) is 4 square units.
The area of the triangle with vertices
(x1, y1) , (x2, y2) and (x3, y3) is
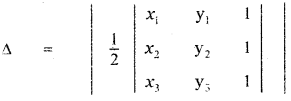
Given Δ = 4, (x1, y1) = (k , 2), (x2, y2) = (2 , 4) and (x3, y3) = (3 , 2)
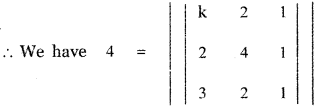
± 4 = k(4 – 2) – 2 (2 – 3) + 1(4 – 12)
± 4 = k × 2 – 2 × – 1 – 8
± 4 = 2k + 2 – 8
± 4 = 2k – 6
2k – 6 = 4 or 2k – 6 = -4
2k = 4 + 6 or 2k = – 4 + 6
2k = 10 or 2k = 2
k = 5 or k = 1
Required values of k are 1, 5.
![]()
Question 3.
Identify the singular and non – singular matrices.
(i) \(\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right] \)
(ii) \(\left[ \begin{matrix} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{matrix} \right] \)
(iii) \(\left[ \begin{matrix} 0 & a\quad -\quad b & k \\ b-\quad a & 0 & 5 \\ -k & -5 & 0 \end{matrix} \right] \)
Answer:
(i) \(\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right] \)
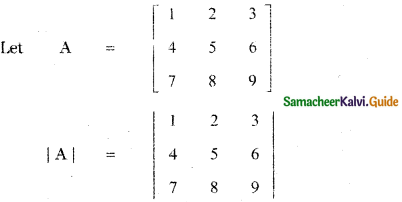
|A| = 1 (45 – 48) – 2(36 – 42) + 3(32 – 35)
|Al = – 3 – 2 × – 6 + 3 × – 3
|A| = – 3 + 12 – 9
|A| = – 12 + 12 = 0
∴ A is a singular matrix.
![]()
(ii) \(\left[ \begin{matrix} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{matrix} \right] \)
Answer:
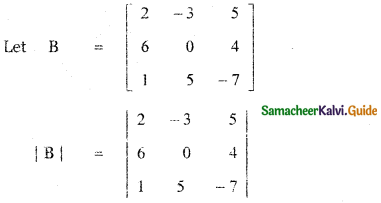
|B| = 2(0 – 20) + 3 (- 42 – 4) + 5(30 – 0)
|B| = -40 + 3 × – 46 + 150
|B| = -40 – 138 + 150
|B| = -178 + 150 ≠ 0
∴ B is non singular.
(iii) \(\left[ \begin{matrix} 0 & a\quad -\quad b & k \\ b-\quad a & 0 & 5 \\ -k & -5 & 0 \end{matrix} \right] \)

|C| = 0 – (a – b) (0 + 5k) + k(-5 (b – a) – 0)
|C| = -5k (a – b) – 5k (b – a)
|C| = -5k (a – b) + 5k(a – b)
|C| = o
∴ C is a singular matrix.
![]()
Question 4.
Determine the values of a and b so that the following matrices are singular:
(i) A = \(\left[ \begin{matrix} 7 & 3 \\ -2 & a \end{matrix} \right] \)
(ii) B = \(\left[ \begin{matrix} b\quad -\quad 1 & 2 & 3 \\ 3 & 1 & 2 \\ 1 & -2 & 4 \end{matrix} \right] \)
Answer:
(i) A = \(\left[ \begin{matrix} 7 & 3 \\ -2 & a \end{matrix} \right] \)
|A| = \(\left[ \begin{matrix} 7 & 3 \\ -2 & a \end{matrix} \right] \)
|A| = 7a + 6
Given that A is singular
∴ |A| = 0
7a + 6 = 0 ⇒ a = \(\frac{-6}{7}\)
(ii) B = \(\left[ \begin{matrix} b\quad -\quad 1 & 2 & 3 \\ 3 & 1 & 2 \\ 1 & -2 & 4 \end{matrix} \right] \)
|B| = \(\left[ \begin{matrix} b\quad -\quad 1 & 2 & 3 \\ 3 & 1 & 2 \\ 1 & -2 & 4 \end{matrix} \right] \)
= (b – 1 )(4 + 4) – 2(12 – 2) + 3(- 6 – 1)
= 8 (b – 1) – 20 – 21
= 8b – 8 – 41
|B| = 8b -49
Given that B is singular
∴ |B| = 0
8b – 49 = 0 ⇒ b = \(\frac{49}{8}\)
![]()
Question 5.
If cos 2θ = 0, determine
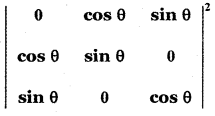
Answer:
Given cos 2θ = 0

![]()
Question 6.
Find the value of the product
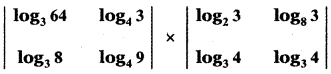
Answer: