Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Physics Guide Pdf Chapter 11 Waves Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 11 Waves
11th Physics Guide Waves Book Back Questions and Answers
![]()
I. Multiple choice questions:
Question 1.
A student tunes his guitar by striking a 120 Hertz with a tuning fork, and simultaneously plays the 4th string on his guitar. By keen observation, he hears the amplitude of the combined sound oscillating thrice per second. Which of the following frequencies is the most likely the frequency of the 4th string on his guitar?
(a) 130
(b) 117
(c) 110
(d) 120
Answer:
(b) 117
Hint:
Frequency of the fourth string can be derived from harmonic series generated by the strings.
Frequencies of first 4 strings are 120, 119, 118, 117 Hz.
f4 = 117Hz
Question 2.
A transverse wave moves from a medium A to a medium B. In medium A, the velocity of the transverse wave is 500 ms-1 and the wavelength is 5 m. The frequency and the wavelength of the wave in medium B when its velocity is 600 ms-1, respectively are:
(a) 120 Hz and 5 m
(b) 100 Hz and 5 m
(c) 120 Hz and 6 m
(d) 100 Hz and 6 m
Answer:
(d) 100 Hz and 6 m
Hint:
vA = 500 ms-1; λA = 5 m
∴ Frequency in medium B
fB = \(\frac{v_{\mathrm{A}}}{\lambda_{\mathrm{A}}}\) = \(\frac { 500 }{ 5 }\) = 100 Hz
Wavelength in medium B is
λB = \(\frac{v_{\mathrm{B}}}{f_{\mathrm{B}}}\) = \(\frac { 600 }{ 100 }\) = 6m
![]()
Question 3.
For a particular tube, among six harmonic frequencies below 1000 Hz, only four harmonic frequencies are given: 300 Hz, 600 Hz, 750 Hz and 900 Hz. What are the two other frequencies missing from this list?
(a) 100 Hz, 150 Hz
(b) 150 Hz, 450 Hz
(c) 450 Hz, 700 Hz
(d) 700 Hz, 800 Hz
Answer:
(b) 150 Hz, 450 Hz
Hint: Fundamental frequency f0 = 150 Hz
From the series of frequencies we get
f1 = 2f0
f2 = 3f0
= 3 x 150
= 450 Hz
Question 4.
Which of the following options is correct?

Options for (1), (2) and (3), respectively are:
(a) (b), (c) and (a)
(b) (c), (a) and (b)
(c) (a), (b) and (c)
(d) (b), (a) and (c)
Answer:
(a) (b), (c) and (a)
Question 5.
Compare the velocities of the wave forms given below, and choose the correct option.
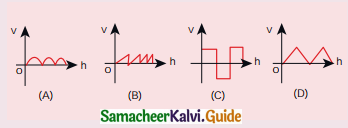
where, vA, vB, vC and vD are velocities given in (a), (b), (c) and (d), respectively.
(a) vA > vB > vD > vC
(b) vA < vB < vD < vC
(c) vA = vB = vD = vC
(d) vA > vB = vD > vC
Answer:
(c) vA = vB = vD = vC
Hint:
The amplitude of the velocity waves is same in all four cases.
Question 6.
A sound wave whose frequency is 5000 Hz travels in air and then hits the water surface. The ratio of its wavelengths in water and air is:
(a) 4.30
(b) 0.23
(c) 5.30
(d) 1.23
Answer:
(a) 4.30
Hint:
Frequency = 5000 Hz
Speed of sound in air vair = 332 m/s
Speed of sound in water vwater = 1450 m/s
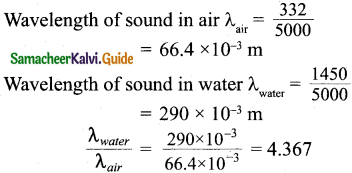
Question 7.
A person standing between two parallel hills fires a gun and hears the first echo after t1 sec and the second echo after t2 sec. The distance between the two hills is:
(a) \(\frac{v\left(t_{1}-t_{2}\right)}{2}\)
(b) \(\frac{v\left(t_{1} t_{2}\right)}{2\left(t_{1}+t_{2}\right)}\)
(c) v(t1 + t2)
(d) \(\frac{v\left(t_{1}+t_{2}\right)}{2}\)
Answer:
(d) \(\frac{v\left(t_{1}+t_{2}\right)}{2}\)
Hint:
For first echo 2d1 = vt1
For second echo 2d2 = vt2
∴ d = d1 + d2 = \(\frac{v\left(t_{1}+t_{2}\right)}{2}\)
![]()
Question 8.
An air column in a pipe which is closed at one end, will be in resonance with the vibrating body of frequency 83 Hz. Then the length of the air column is:
(a) 1.5 m
(b) 0.5 m
(c) 1.0 m
(d) 2.0 m
Answer:
(c) 1.0 m
Hint:
l = \(\frac { λ }{ 4 }\); f = 83 Hz
v = 332 m/s
λ = \(\frac { v }{ f }\)
= \(\frac { 332 }{ 83 }\)
= 4 m
l = \(\frac { λ }{ 4 }\) = \(\frac { 4m }{ 4 }\) = 1m = 1.0 m
Question 9.
The displacement y of a wave travelling in the x direction is given by y = (2 x 10-3) sin (300t – 2x + \(\frac { π }{ 4 }\)), where x and y are measured in metres and t in second. The speed of the wave is:
(a) 150 ms-1
(b) 300 ms-1
(c) 450 ms-1
(d) 600 ms-1
Answer:
(a) 150 ms-1
Hint:
The given equation is similar to
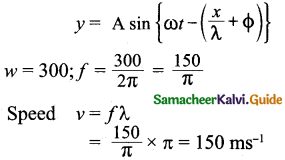
Question 10.
Consider two uniform wires vibrating simultaneously in their fundamental notes. The tensions, densities, lengths and diameter of the two wires ,are in the ratio 8:1, 1:2, (x : y) and 4 : 1 respectively. If the note of the higher pitch has a frequency of 360 Hz and the number of beats produced per second is 10, then the value of (x : y) is:
(a) 36 : 35
(b) 35 : 36
(c) 1 : 1
(d) 1 : 2
Answer:
(a) 36 : 35
Hint:
No. of beats = 10
Frequency of higher pitch f1 = 360 Hz
Frequency of lower pitch f2 = 360 – 10 = 350 Hz
x : y = Ratio of length
l ∝ f
l1 : l2 = x : y = f1 : f2
= 360 : 350
= 36 : 35
![]()
Question 11.
Which of the following represents a wave:
(a) (x – vt)³
(b) x(x + vt)
(c) \(\frac { 1 }{ (x +vt) }\)
(d) sin(x + vt)
Answer:
(d) sin(x + vt)
Hint:
Wave must have a wave function.
Since y = a sin ωt
Question 12.
A man sitting on a swing which is moving to an angle of 60° from the vertical is blowing . a whistle which has a frequency of 2.0 k Hz. The whistle is 2.0 m from the fixed support point of the swing. A sound detector which detects the whistle sound is kept in front of the swing. The maximum frequency the sound detector detected is:
(a) 2.027 kHz
(b) 1.914 kHz
(c) 9.14 kHz
(d) 1.011 kHz
Answer:
(a) 2.027 kHz
Hint:

Question 13.
Let y = \(\frac{1}{1+x^{2}}\) at t = 0 be the amplitude of the wave propagating in the positive x-direction. At t = 2s, the amplitude of the wave propagating becomes y = \(\frac{1}{1+(x-2)^{2}}\). Assume that the shape of the wave does not
change during propagation. The velocity of the wave is:
(a) 0.5 ms-1
(b) 1.0 ms-1
(c) 1.5 ms-1
(d) 2.0 ms-1
Answer:
(b) 1.0 ms-1
Hint:
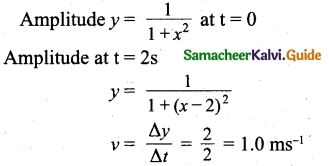
Question 14.
A uniform rope having mass m hangs vertically from a rigid support. A transverse wave pulse is produced at the lower end. Which of the following plots shows the correct variation of speed v with height h from the lower end?
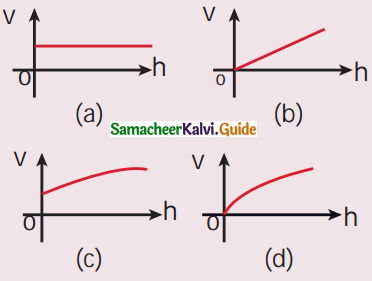
Answer:
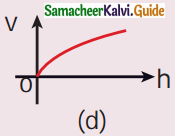
Hint:
Speed varies exponentially with height h.
Question 15.
An organ pipe A closed at one end is allowed to vibrate in its first harmonic and another pipe B open at both ends is allowed to vibrate in its third harmonic. Both A and B are in resonance with a given tuning fork. The ratio of the length of A and B is:
(a) \(\frac { 8 }{ 3 }\)
(b) \(\frac { 3 }{ 8 }\)
(c) \(\frac { 1 }{ 6 }\)
(d) \(\frac { 1 }{ 2 }\)
Answer:
(d) \(\frac { 1 }{ 2 }\)
Hint:
First harmonic of a closed organ pipe
LC = \(\frac { 3 λ }{ 4 }\)
Third harmonic of an open organ pipe
L0 = \(\frac { 3 λ }{ 2 }\)
\(\frac{\mathrm{L}_{\mathrm{C}}}{\mathrm{L}_{\mathrm{O}}}\) = \(\frac { 3 π }{ 4 }\) x \(\frac { 3 }{ 3λ }\)
= \(\frac { 2 }{ 4 }\)
= \(\frac { 1 }{ 2 }\)
∴ \(\frac{\mathrm{L}_{\mathrm{C}}}{\mathrm{L}_{\mathrm{O}}}\) = \(\frac { 1 }{ 2 }\)
![]()
II. Short Answer Questions:
Question 1.
What is meant by waves?
Answer:
The disturbance which carries energy and momentum from one point in space to another point in space without the transfer of the medium is known as a wave.
Question 2.
Write down the types of waves.
Answer:
Waves can be classified into two types –
- Transverse waves
- Longitudinal waves
Question 3.
What are transverse waves? Give one example.
Answer:
In transverse wave motion, the constituents of the medium oscillate or vibrate about their mean positions in a direction perpendicular to the direction of propagation (direction of energy transfer) of waves.
Example: light (electromagnetic waves)
Question 4.
What are longitudinal waves? Give one example.
Answer:
The direction of vibration of particles in a medium is parallel to the direction of propagation of the wave.
Example: Sound waves traveling in air.
Question 5.
Define wavelength.
Answer:
For transverse waves, the distance between two neighbouring crests or troughs is known as the wavelength. For longitudinal waves, the distance between two neighbouring compressions or rarefactions is known as the wavelength. The SI unit of wavelength is meter.
Question 6.
Write down the relation between frequency, wavelength and velocity of a wave.
Answer:
Velocity of the wave is v = λf.
![]()
Question 7.
What is meant by the interference of waves?
Answer:
Interference is a phenomenon in which two waves moving in the same direction superimpose to form a resultant wave of greater, lower or the same amplitude.
Question 8.
Explain the beat phenomenon.
Answer:
When two or more waves superimpose each other with slightly different frequencies, then a sound of periodically varying amplitude at a point is observed. This phenomenon is known as beats. The number of amplitude maxima per second is called beat frequency. If we have two. sources, then their difference in frequency gives the beat frequency. Number of beats per second n = |f1 – f2| per second
Question 9.
Define intensity of sound and loudness of sound.
Answer:
“Loudness is defined as the degree of the sensation of sound produced in the ear or the perception of sound by the listener”. The intensity of sound is defined as “the sound power transmitted per unit area placed normal to the propagation of sound wave”.
Question 10.
Explain Doppler Effect.
Answer:
When the source and the observer are in relative motion with respect to each other and to the medium in which sound propagates, the frequency of the sound wave observed is different from the frequency of the source. This phenomenon is called Doppler Effect.
Question 11.
Explain red. shift and blue shift in Doppler Effect.
Answer:
If the spectral lines of the star are found to shift towards red end of the spectrum (called redshift) then the star is receding away from the Earth. If the spectral lines of the star are found to shift towards the blue end of the spectrum (called blue shift) then the star is approaching Earth.
Question 12.
What is meant by end correction in resonance air column apparatus?
Answer:
Since the antinodes are not exactly formed at the open end, we have to include a correction, called end correction e. It is calculated, by assuming that antinode is formed at a small distance above the open end e = 0.3 d.
![]()
Question 13.
Sketch the function y = x + a. Explain your sketch.
Answer:
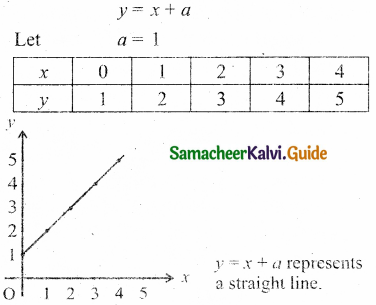
Question 14.
Write down the factors affecting velocity of sound in gases.
Answer:
(i) Effect of pressure: Speed of sound is independent of pressure for a fixed temperature.
(ii) Effect of temperature: Speed of sound varies directly to the square root of temperature in kelvin. Speed of sound in air increases by 0.61 ms-1 per degree celcius rise in temperature.
(iii) Effect of density: Velocity of sound in a gas is inversely proportional to the square root of the density of the gas.
(iv) Effect of moisture (humidity): Speed of sound increases with rise in humidity.
(v) Effect of wind: In the direction along the wind blowing, the speed of sound to wind blowing, the speed of sound decreases.
Question 15.
What is meant by an echo? Explain.
Answer:
An echo is a repetition of sound produced by the reflection of sound waves from a wall, mountain or other obstructing surfaces. The minimum distance from a sound-reflecting wall to hear an echo at 20°C is 17.2 meter.
![]()
III. Long Answer Questions:
Question 1.
Discuss how ripples are formed in still water.
Answer:
Suppose we drop a stone in a trough of still water, we can see a disturbance produced at the place where the stone strikes the water surface. We find that this disturbance spreads out (diverges out) in the form of concentric circles of ever-increasing radii (ripples) and strikes the boundary of the trough. This is because some of the kinetic energy of the stone is transmitted to the water molecules on the surface.
Actually, the particles of the water (medium) themselves do not move outward with the disturbance. This can be observed by keeping a paper strip on the water surface. The strip moves up and down when the disturbance (wave) passes on the water surface. This shows that the water molecules only undergo vibratory motion about their mean positions.
Question 2.
Briefly explain the difference between traveling waves and standing waves.
Answer:
Progressive waves:
- Crests and troughs ate formed in transverse progressive waves. Compression and rarefaction are formed in longitudinal progressive waves. These waves move forward or backward in a medium i.e., they will advance in a medium with a definite velocity.
- All the particles in the medium vibrate in such a way that the amplitude of the vibration for all particles is the same.
- These waves carry energy while propagating.
Stationary waves:
- Crests and troughs are formed in transverse stationary waves. Compression and rarefaction are formed in longitudinal stationary waves. These waves neither move forward nor backward in a medium i.e., they will not advance in a medium.
- Except at nodes, all other particles of the medium vibrate such that the amplitude of vibration is different for different particles. The amplitude is minimum or zero at nodes and maximum at antinodes.
- These waves do not transport energy.
![]()
Question 3.
Show that the velocity of a traveling wave produced in a string is v = \(\sqrt{\frac{T}{\mu}}\)
Answer:
Let us consider an elemental segment in the string as shown in the Figure. Let A and B be two points on the string at an instant of time. Let dl and dm be the length and mass of the elemental string, respectively. By definition, linear mass density, μ is
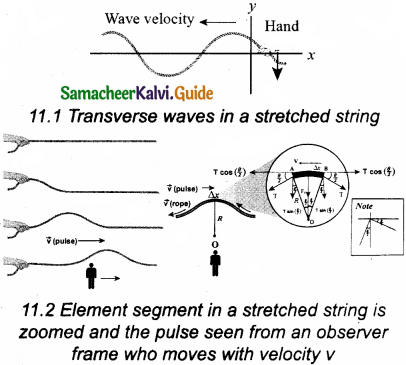
μ = \(\frac { dm }{ dl }\) … (1)
dm = μ dl … (2)
Consider an elemental string AB having a curvature which looks like an arc of a circle with centre at O, radius R and the arc subtending an angle θ at the origin O as shown in Figure. The angle 0 can be written in terms of arc length and radius as \(\frac { dl }{ R }\) = θ. The centripetal acceleration supplied by the tension in the string is
acp = \(\frac{v^{2}}{\mathrm{R}}\) … (3)
Then, centripetal force can be obtained when mass of the string (dm) is included in equation (3)
Fcp = \(\frac{(dm)v^{2}}{\mathrm{R}}\) … (4)
Experienced by elemental string can be calculated by substituting equation (2) in equation (4) we get the centripetal force as
\(\frac{(dm)v^{2}}{\mathrm{R}}\) = \(\frac{\mu v^{2} d l}{R}\) … (5)
The tension T acts along the tangent of the elemental segment of the string at A and B. Since the arc length is very small, variation in the tension force can be ignored. T can be resolved into horizontal component T cos (\(\frac { θ }{ 2 }\)) and vertical component T sin (\(\frac { θ }{ 2 }\)).
The horizontal components at A and B are equal in magnitude but opposite in direction. Hence, they cancel each other. Since the elemental arc length AB is taken to be very small, the vertical components at A and B appears to acts vertical towards the centre of the arc and hence, they add up. The net radial force Fr is
Fr = 2Tsin(\(\frac { θ }{ 2 }\)) … (6)
Since the amplitude of the wave is very small when it is compared with the length of the string, the sine of small angle is approximated
as sin (\(\frac { θ }{ 2 }\)) ≈ \(\frac { θ }{ 2 }\). Hence, equation (6) can be written as,
Fr = 2T x \(\frac { θ }{ 2 }\) = Tθ … (7)
But θ = \(\frac { dl }{ R }\), therefore substituting in equation (7), we get
Fr = T \(\frac { dl }{ R }\) … (8)
Applying Newton’s second law to the elemental string in the radial direction, under equilibrium, the radial component of the force is equal to the centripetal force. By equating equation (5) and equation (8), we get,
T \(\frac { dl }{ R }\) = μv²dl
v = \(\sqrt{\frac{\mathrm{T}}{\mu}}\) measured in ms-1
Question 4.
Describe Newton’s formula for velocity of sound waves in air and also discuss the Laplace’s correction.
Answer:
Newton assumed that when sound propagates in air, the formation of compression and rarefaction takes place in a very slow manner so that the process is isothermal in nature. It is found that, the heat produced during compression (pressure increases, volume decreases), and heat lost during rarefaction (pressure decreases, volume increases) occur over a period of time such in a way that the temperature of the medium remains constant. Hence, by treating the air molecules to form an ideal gas, the changes in pressure and volume obey Boyle’s law, Mathematically
PV= Constant …(1)
Differentiating equation (1), we get
PdV + Vdp = 0
(or) P = – V\(\frac { dp }{ dv }\) = BT … (2)
where, BT is an isothermal bulk modulus of air.
v = \(\sqrt{\frac{\mathrm{B}}{\rho}}\) … (3)
Substituting equation (2) in equation (3), the speed of sound in air is
vT = \(\sqrt{\frac{\bar{B}_{\mathrm{T}}}{\rho}}\) = \(\sqrt{\frac{\mathrm{P}}{\rho}}\)
Since P is the pressure of air whose value at NTP (Normal Temperature and Pressure) is 76 cm of mercury, we have
P = (0.76 x 13.6 x 10³ x 9.8)Nm-2
ρ = 1.293 kg m-3.
Here p is density of air. Then the speed of sound in air at normal temperature and pressure (NTP) is

But the speed of sound in air at 0°C is experimentally observed as 332 ms-1 that is close up to 16% more than theoretical value.
Laplace correction: Laplace satisfactorily corrected this discrepancy by assuming that when the sound propagates through a medium, the particles oscillate very rapidly such that the compression and rarefaction occur very fast. Hence the exchange of heat produced due to compression and cooling effect due to rarefaction do not take place, because, air (medium) is a poor conductor of heat. Since, temperature is no longer considered as a constant here, propagation of sound is an adiabatic process. By adiabatic considerations, the gas obeys Poisson’s law (not Boyle’s law as Newton assumed), that is
PV’ = Constant … (4)
where, γ = \(\frac{\mathrm{C}_{\mathrm{p}}}{\mathrm{C}_{\mathrm{v}}}\), that is the ratio between specific heat at constant pressure and specific heat at constant volume.
Differentiating equation (4) on both the sides, we get
Vγ dP + P (γVγ-1 dV) = 0
or, γP = – V\(\frac { dp }{ dv }\) = BA … (5)
where, BA is the adiabatic bulk modulus of air.
v = \(\sqrt{\frac{\mathrm{B}}{\rho}}\)
Now, substituting equation (5) in equation (6), the speed of sound in air is

Since air contains mainly, nitrogen, oxygen, hydrogen etc, (diatomic gas), we take γ = 1.47. Hence, speed of sound in air is vA = (\(\sqrt{1.4}\))(280ms-1) = 331.30 ms-1, which is very much closer to experimental data.
Question 5.
Write short notes on reflection of sound waves from plane and curved surfaces.
Answer:
When the sound waves hit the plane wall, they bounce off in a manner similar to that of light. When a loudspeaker is kept at an angle with respect to a wall (plane surface), then the waves coming from the source (assumed to be a point source) can be treated as spherical wave fronts. Hence, the reflected wave front on the plane surface is also spherical, such that its centre of curvature can be treated as the image of the sound source (virtual or imaginary loud speaker) that can be assumed to be at a position behind the plane surface. These are shown in figures.
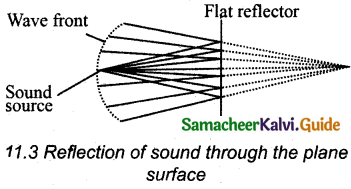
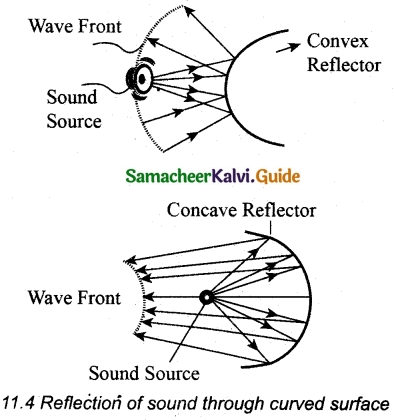
The behaviour of sound is different when it is reflected from different surfaces-convex or concave or plane. The sound reflected from a convex surface is spread out and so it is easily attenuated and weakened. Whereas, if it is reflected from the concave surface it will converge at a point and this can be easily amplified. The parabolic reflector (curved reflector) that is used to focus the sound precisely to a point is used in designing the parabolic mics which are known as high directional microphones.
We know that any surface (smooth or rough) can absorb sound. For instance, the sound produced in a big hall or auditorium or theatre is absorbed by the walls, ceilings, floor, seats etc. To avoid such losses, a curved sound board (concave board) is kept in front of the speaker, in such a way that the board reflects the sound waves of the speaker towards the audience. This method will minimize the spreading of sound waves in all possible direction in that hall it also enhances the uniform distribution of sound throughout the hall. Hence a person sitting at any position in that hall can hear the sound without any disturbance.
Question 6.
Briefly explain the concept of the superposition principle.
Answer:
When two or more waves in a medium overlap, their total displacement is the vector sum of the individual displacements.
Let us consider two functions which characterize the displacement of the waves, for example,
y1 = A1 sin(kx – ωt)
and y2 = A2 sin(kx – ωt)
Since both y1 and y2 satisfy the wave equation (solutions of wave equation) then their algebraic sum
y = y1 + y2
also satisfies the wave equation. It is meant that the displacements are additive.
![]()
Question 7.
Explain how the interference of waves is formed.
Answer:
Interference is a phenomenon in which two waves superimpose to form a resultant wave of greater, lower, or the same amplitude.
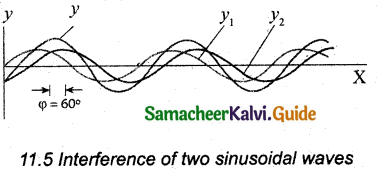
Let us consider two harmonic waves having identical frequencies, constant phase difference φ, and same waveform (can be treated as coherent source), but having amplitudes A1 and A2, then
y1 = A1 sin(kx – ωt) … (1)
y2 = A2 sin(kx – ωt) … (2)
Suppose they move simultaneously in a particular direction, then interference occurs (i.e., the overlap of these two waves). Mathematically y = y1 + y2 … (3)
Hence by substituting equation (1) and equation (2) in equation (3), we get

By squaring and adding equation (5) and (6), we get,
A² = A1² + A2² + 2A1A2cosφ … (8)
Since, intensity is square of the amplitude (I – A²), we get,
I = I1 + I2 + 2\(\sqrt{\mathrm{I}_{1} \mathrm{I}_{2}} \cos \varphi\) … (9)
This means the resultant intensity at any point depends on the phase difference at that point.
Question 8.
Describe the formation of beats.
Answer:
When two or more waves superimpose each other with slightly different frequencies, then a sound having periodically varying amplitude at a point is observed. This phenomenon is known as beats. The number of amplitude maxima per second is called beat frequency. If we have two sources, then their difference in frequency gives the beat frequency.
Number-of beats per second
n = \(\left|f_{1}-f_{2}\right|\) Per second
Question 9.
What are stationary waves? Explain the formation of stationary waves and also write down the characteristics of stationary waves.
Answer:
When the wave hits the rigid boundary it bounces back to the original medium and can interfere with the original waves. A pattern is formed, that is known as standing waves or waves stationary. Let us consider two harmonic progressive waves (formed by strings) that have the same amplitude and same velocity but move in opposite directions. Then the displacement of the first wave (incident wave) is
y1 = A sin(kx – ωt) … (1)
(waves move toward right)
The displacement of the second wave (reflected wave) is
y2 = A sin(kx + ωt) … (2)
(waves move toward left)
both will interfere with each other by the principle of superposition, the net displacement is
y = y1 + y2 … (3)
By substituting equation (1) and equation (2) in equation (3), we get
y = \(\left\{\begin{array}{l}
\mathrm{A} \sin (k x-\omega t) \\
+\mathrm{A} \sin (k x+\omega t)
\end{array}\right.\) … (4)
Using trigonometric identity, we rewrite equation (4) as
y(x, t) = 2A cos(ωt) sin(kx) … (5)
This represents a stationary wave or standing wave, It is meant that this wave does not move either forward or backward, whereas progressive or travelling waves will move forward or backward. In addition, the displacement of the particle in equation (5) can be written in more compact form,
y(x, t) = A’cos(cot)
where, A’ = 2A sin(Ax). It is implied implying that the particular element of the string executes simple harmonic motion with amplitude equals to A’. The maximum of this amplitude occurs at positions for which
sin(kx) = 1
⇒ kx = \(\frac { π }{ 2 }\), \(\frac { 3π }{ 2 }\), \(\frac { 5π }{ 2 }\), … = nπ
where m takes half-integer or half-integral values. The position of maximum amplitude is known as an antinode. Expressing wave number in terms of wavelength, let us represent the anti-nodal positions as
xm = (\(\frac { 2m+1 }{ 2 }\)) \(\frac { λ }{ 2 }\) … (6)
where, m = 0, 1, 2 ….
For m = 0 we have maximum at
x0 = \(\frac { λ }{ 2 }\)
For m = 1 we have maximum at
x0 = \(\frac { 3λ }{ 4 }\)
For m = 2 we have maximum at
x2 = \(\frac { 5λ }{ 4 }\)
and so on.
The distance between two successive antinodes can be computed by,
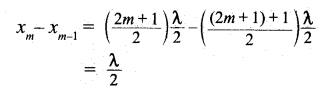
Similarly, the minimum of the amplitude A’ also occurs at some points in the space, and these points can be determined by setting
sin(kx) = 0
⇒ kx = 0, π, 2π, 3π, … = nπ
where n takes integer or integral values. It is noted that the elements at these points do not vibrate (not move), and the points are called nodes. The nth nodal positions is given by,
xn = n\(\frac { λ }{ 2 }\) … (7)
where, n = 0, 1, 2, …
For n = 0 we have minimum at
xo = 0
For n = 1 we have minimum at
x1 = \(\frac { λ }{ 2 }\)
For n = 2 we have maximum at
x2 = λ
and so on.
The distance between any two successive nodes can be calculated as
xn – xn-1 – n\(\frac { λ }{ 2 }\) – (n-1)\(\frac { λ }{ 2 }\) = \(\frac { λ }{ 2 }\)
Characteristics of stationary waves:
- Stationary waves are characterized by the confinement of a wave disturbance between two rigid boundaries. It is meant that the wave does not move forward or backward in a medium (does not advance), it remains steady at its place. Hence, they are called “stationary waves or standing waves”.
- Certain points in the region in which the wave exists have maximum amplitude, called anti-nodes. At certain points, the amplitude is minimum or zero, called nodes.
- The distance between two consecutive nodes (or) anti-nodes is \(\frac { λ }{ 2 }\).
- The distance between a node and its neighboring anti-node is \(\frac { λ }{ 4 }\).
- The transfer of energy along the standing wave is zero.
![]()
Question 10.
Discuss the law of transverse vibrations in stretched strings.
Answer:
There are three laws of transverse vibrations of stretched strings that are given as follows:
(i) The law of length: For a given wire with tension T (which is fixed) and mass per unit length µ. (fixed) the frequency varies inversely with the vibrating length. Therefore,
f ∝ \(\frac { 1 }{ f }\) ⇒ f = \(\frac { C }{ l }\)
⇒ l x f = C, when C is a constant.
(ii) The law of tension: For a given vibrating length l (fixed) and mass per unit length µ (fixed) the frequency varies directly with the square root of the tension T,
f ∝ \(\sqrt{T}\)
⇒ f = A\(\sqrt{T}\), when A is a constant.
(iii) The law of mass: For a given vibrating length l (fixed) and tension T (fixed) the frequency varies inversely with the square root of the mass per unit length μ,
f ∝ \(\frac{1}{\sqrt{\mu}}\) when B is a constant.
Question 11.
Explain the concepts of frequency, harmonics and detail.
Answer:
(i) The fundamental frequency is the lowest natural frequency.
(ii) If natural frequencies are written as integral multiples of the fundamental frequency, then the frequencies are said to be in harmonics. So, the first harmonic is v1 = v1, (the fundamental frequency is called first harmonics), the second harmonics is v2 = 2v1 the third harmonics is v3 = 3v1, and so on.
(iii) The frequency higher than the fundamental frequency can be produced by blowing air strongly at the open end. Such frequencies are called overtones.
First overtone, (f2 = 3f1) since here, the frequency is three times the fundamental frequency it is called third harmonic. Second overtone, (f3 = 5f1) and since n = 5 here, this is called fifth harmonic.
Question 12.
What is a sonometer? Give its construction and working. Explain how to determine the frequency of tuning fork using a sonometer.
Answer:
Sonometer is used for sound-related measurements. Using this device, The following quantities can be determined.
(i) The frequency of the tuning fork or frequency of the alternating current.
(ii) The tension in the string.
(iii) The unknown hanging mass.
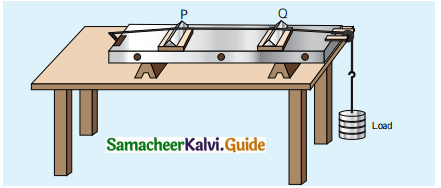
Construction: The sonometer is made up of a hollow box that is one meter long with a uniform metallic thin string attached to it. One end of the string is connected to a hook and the other end is connected to a weight hanger through a pulley as shown in Figure. Since only one string is used, it is also known as monochord. The weights are added to the free end of the wire to increase the tension of the wire. Two adjustable wooden knives are put over the board, and their positions are adjusted to change the vibrating length of the stretched wire.
Procedure: A transverse stationary or standing wave is produced. So, at the knife edges P and Q, nodes are formed. In between the knife edges, anti-nodes are formed.
If the length of the vibrating element is l then
l = \(\frac { λ }{ 2 }\) ⇒ λ = 2l
Let f be the frequency of the vibrating element, T the tension in the string, and p the mass per unit length of the string.
Then using the the equation v = \(\sqrt{\frac{\mathrm{T}}{\mu}}\) measured in ms-1, we get,
f = \(\frac { v }{ λ }\) = \(\frac { 1 }{ 2l }\)\(\sqrt{\frac{\mathrm{T}}{\mu}}\) in Hertz.
Let ρ be the density of the material of the string and d be the diameter of the string. Then the mass per unit length μ,

Question 13.
Write short notes on intensity and loudness.
Answer:
The intensity of sound is defined as “the sound power transmitted per unit area taken normal to the propagation of the sound wave”. The intensity of sound is inversely proportional to the square of the distance from the source.
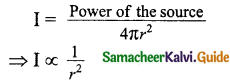
This is known as the inverse square law of sound intensity. Two sounds with the same intensities need not have the same loudness. For example, the sound heard during the explosion of balloons in a silent closed room is very loud when compared to the same explosion happening in a noisy market.
If the intensity of sound is increased then loudness also increases. Loudness depends on both intensities of the sound wave and sensitivity of the ear.
![]()
Question 14.
Explain how overtones are produced in a,
(a) closed organ pipe
(b) Open organ pipe
Answer:
(a) Closed organ pipes: If one end of a pipe is closed, the wave reflected at this closed-end is 180° out of phase with the incoming wave. So, there is no displacement of the particles at the closed end. Hence, nodes are formed at the closed end and anti-nodes are formed at the open end.
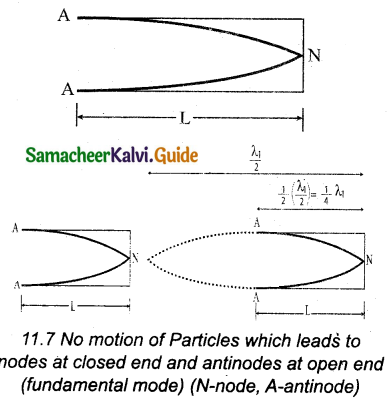
Consider the simplest mode of vibration of the air column called the fundamental mode. Anti-node is formed at the open end and node at the closed end. From the above figure, let L be the length of the tube and the wavelength of the wave produced. For the fundamental mode of vibration, we have,
– L = \(\frac{\lambda_{1}}{4}\) (or)
Wave length λ1 = 4L
The frequency of the note emitted is
f1 = \(\frac{v}{\lambda_{1}}\) = \(\frac { v }{ 4L }\)
which is called the fundamental note.
The frequencies higher than the fundamental frequency can be produced by blowing air strongly at the open end. Such frequencies are called overtones.
The second mode of vibration in open pipes is shown in the figure.
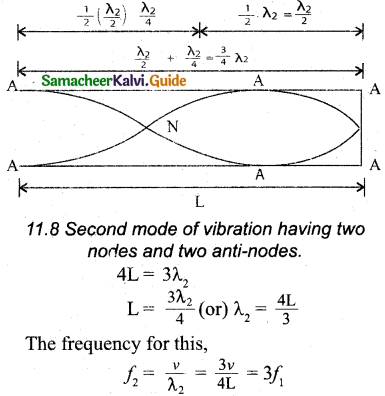
is called the first overtone, since here, the frequency is three times the fundamental frequency it is called third harmonic. The Figure shows the third mode of vibration having three nodes and three anti-nodes.
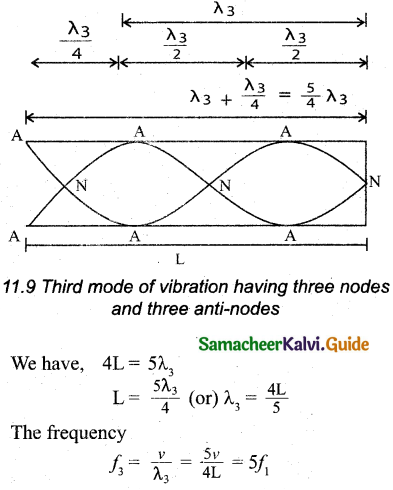
is called the second overtone, and since n = 5 here, this is called fifth harmonic. Hence, the closed organ pipe has only odd harmonics and the frequency of the nth harmonic is fn = (2n+l)f1. Hence, the frequencies of harmonics are in the ratio,
f1 : f2 : f3 : f4 = 1 : 3 : 5 : 7 : …
(b) Open organ pipes:
The flute is an example of an open organ pipe. It is a pipe with both ends are opened. At both open ends, anti-nodes are formed. Consider the simplest mode of vibration of the air column called fundamental mode. Since anti-nodes are formed at the open end, a node is formed at the mid-point of the pipe.
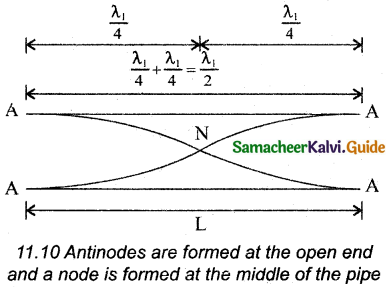
From above Figure, if L be the length of the tube, the wavelength of the wave produced is given by
L=\(\frac{\lambda_{1}}{2}\) (or) λ1 = 2L
The frequency of the note emitted is
f1 = \(\frac{v}{\lambda_{1}}\) = \(\frac { v }{ 2L }\)
That is called the fundamental note.
The frequencies higher than the fundamental frequency can be produced by blowing air strongly at one of the open ends. Such frequencies are called overtones.
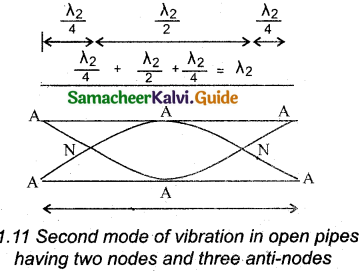
The second mode of vibration in open pipes is shown in figure. It has two nodes and three anti-nodes,
∴ L = λ2 (or) λ2 = L
The frequency,
f2 = \(\frac{v}{\lambda_{2}}\) = \(\frac { v }{ L }\) = 2 x \(\frac { v }{ 2L }\) = 2f1
is called first over tone. Since n = 2 here, it is called the second harmonic.
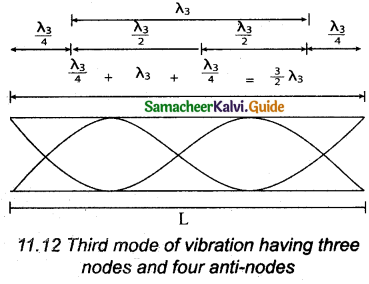
The Figure above shows the third mode of vibration having three nodes and four anti-nodes
∴ L = \(\frac { 3 }{ 2 }\)λ3 (or) λ3 = \(\frac { 2L }{ 3 }\)
The frequency,
f3 = \(\frac{v}{\lambda_{3}}\) = \(\frac { 3v }{ 2L }\) = 31
is called second over tone. Since n = 3 here, it is called the third harmonic.
Hence, the open organ pipe has all the harmonics, and the frequency of the nth harmonic is fn = nf1.
Hence, the frequencies of harmonics are in the ratio f1 : f2 : f3 : f4 = 1 : 2 : 3 : 4 : …
Question 15.
How will you determine the velocity of sound using the resonance air column apparatus?
Answer:
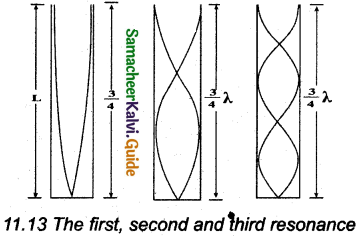
The resonance air column apparatus is used to measure the speed of sound in air at room temperature.
Construction:
(i) It consists of a cylindrical glass tube of one-meter length whose one end A is open and another end B is connected to the water reservoir R through a rubber tube as shown in Figure.
(ii) This cylindrical glass tube is mounted on a vertical stand with a scale attached to it. The tube is partially filled with water and the water level can be adjusted by raising or lowering the water in the reservoir R.
(iii) The surface of the water will act as a closed-end and others as the open end. Hence, it behaves like a closed organ pipe, forming nodes at the surface of water and antinodes at the closed end.
(iv) When a vibrating tuning fork is brought near the open end of the tube, longitudinal waves are formed inside the air column.
(v) These waves move downward as shown in Figure, and reach the surfaces of water and get reflected and produce standing waves.
(vi) The length of the air column is varied by changing the water level until a loud sound is produced in the air column.
(vii) At this particular length the frequency of waves in the air column resonates with the frequency of the tuning fork (natural frequency of the tuning fork).
(viii) At resonance, the frequency of sound waves produced is equal to the frequency of the tuning fork. This will occur only when the length of the air column is proportional to (\(\frac { 1 }{ 4 }\))th of the wavelength of the sound waves produced. \(\frac { 1 }{ 4 }\)λ = L1 … (1)
But since the antinodes are not exactly formed at the open end, a Correction is to include. It is called end correction e, by assuming that the antinode is formed at some small distance above the open end. Including this end correction, the first resonance is \(\frac { 1 }{ 4 }\)λ = L1 + e … (2)
Now the length of the air column is increased to get the second resonance. Let L2 be the length at which the second resonance occurs. Again taking end correction into account, we have
\(\frac { 3 }{ 4 }\)λ = L2 + e … (3)
In order to avoid end correction, let us make the difference of equation (3) and equation (2), we get
\(\frac { 3 }{ 4 }\)λ – \(\frac { 1 }{ 4 }\)λ = (L2 + e) – (L1 + e)
⇒ \(\frac { 1 }{ 2 }\)λ = L2 – L1 = ∆L
⇒ λ = 2∆L
The speed of the sound in air at room temperature can be calculated by using the formula
v = fλ = 2f∆L.
![]()
Question 16.
What is meant by the Doppler effect? Discuss the following cases.
(i) Source in motion and Observer at rest
- Source moves towards the observer
- Source moves away from the observer
(ii) Observer in motion and Source at rest.
- The observer moves towards Source
- Observer resides away from the Source
(iii) Both are in motion
- Source and Observer approach each other
- Source and Observer resides from each other
- Source chases Observer
- Observer chases Source
Answer:
When the source and the observer are in relative motion with respect to each other and to the medium in which sound is propagated, the frequency of the sound wave observed is different from the frequency of the source. This phenomenon is called Doppler Effect.
(i) Source in motion and the observer at rest:
(a) Source moves towards die observer:
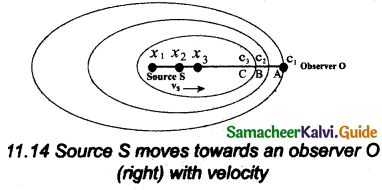
Suppose a source S moves to the right (as shown in Figure) with a velocity vs and let the frequency of the sound waves produced by the source be fs. It is assumed that the velocity of sound in a medium is v.
The compression (sound wavefront) produced by the source S at three successive instants of time are shown in the Figure. When S is at position x1 the compression is at C1. When S is at position x2, the compression is at C2 and similarly for x3 and C3.
It is assumed that if C1 reaches the observer’s position A then at that instant C2 reaches point B and C3 reaches point C as shown in the Figure. Obviously it is seen that the distance between compressions C2 and C3 is shorter than the distance between C1 and C2.
It is meant that the wavelength decreases when the source S moves towards the observer O. But frequency is inversely related to wavelength and therefore, frequency increases.
Calculation:
Let λ be the wavelength of the source S as measured by the observer when S is at position x1 and λ’ be the wavelength of the source observed by the observer when S moves to position x2.
Then the change in wavelength is ∆λ = λ – λ’ = vst, where t is the time taken by the source to travel between x1 and x2 Therefore,
λ’ = λ – vst … (1)
But t = \(\frac { λ }{ v }\) … (2)
On substituting equations (2) in equation (1), we get.
λ’ = λ(1 – \(\frac{v_{s}}{v}\))
Since frequency is inversely proportional to wavelength, we have
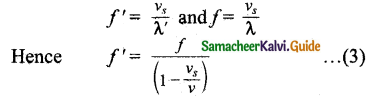
Since, \(\frac{v_{s}}{v}\) << 1, by using the binomial expansion and retaining only first order in \(\frac{v_{s}}{v}\), we get
f ‘ = f(1 + \(\frac{v_{s}}{v}\)) … (4)
(b) Source moves away from the observer Since the velocity of the source is opposite in direction when compared to case (a), hence by changing the sign of the velocity of the source in the above case i.e., by substituting (vs → – v ) in equation (1), we get
f ‘= \(\frac{f}{\left(1+\frac{v_{s}}{v}\right)}\) … (5)
Using binomial expansion again, we get
f ‘= f(1 – \(\frac{v_{s}}{v}\)) … (6)
(ii) Observer in motion and source at rest:
(a) Observer moves towards Source:
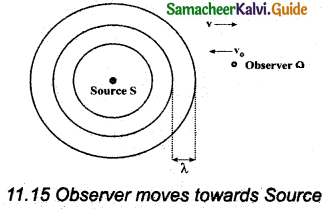
We can assume that the observer O moves towards the source S with velocity vo. The source S is at rest and the velocity of sound waves (with respect to the medium) produced by the source is v.
From the Figure, It is observed that both vo and v are in opposite direction. Then, their relative velocity is vr = v + vo. The wavelength of the sound wave is λ = \(\frac { v }{ f }\), which means the frequency observed by the observer O is f ‘ = \(\frac{v_{r}}{\lambda}\). Then
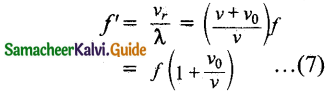
(b) Observer recedes away from the Source: If the observer O is moving away (receding away) from the source S, then velocity v0 and v move in the same direction. Hence, their relative velocity is vr = v – v0. Hence, the frequency observed by the observer O is
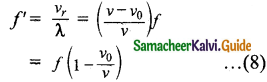
(iii) Both are in motion:
(a) Source and observer approach each other:

Let vs and vo be the respective velocities of source and observer approaching each other as shown in Figure. In order to calculate the apparent frequency observed by the observer, let us have a dummy (behaving as observer or source) in between the source and observer. Since the dummy is at rest, the dummy (observer) observes the apparent frequency due to approaching source as given in equation f ‘ =\(\frac{f}{\left(1-\frac{v_{s}}{v}\right)}\)
fd = \(\frac{f}{\left(1-\frac{v_{s}}{v}\right)}\) … (1)
The true observer approaches the dummy from the other side at that instant of time. Since the source (true source) comes in a direction opposite to the true observer, the dummy (source) is treated as a stationary source for the true observer at that instant. Hence, apparent frequency when the true observer approaches the stationary source (dummy source), f’ = f(1 + \(\frac{v_{0}}{v}\)).
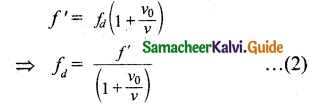
Since this is true for any arbitrary time, therefore, comparing equation (1) and equation (2), we get

(b) Source and observer recede from each other:

It is noticed that the velocity of the source and the observer each point in opposite directions with respect to the case in (a) and hence, we substitute (vs → – vs) and (v0 → – v0) in equation (3), and therefore, the apparent frequency observed by the observer when the source and observer recede from each other is f’ = \(\left(\frac{v-v_{0}}{v+v_{s}}\right)\)f
(c) Source chases the observer:

Only the observer’s velocity is oppositely directed when compared to case (a). Therefore, substituting (v0 → – v0) in equation (3), we get f’ = \(\left(\frac{v-v_{0}}{v-v_{s}}\right)\)f
(d) Observer chases the source:

Only the source velocity is oppositely directed when compared to case (a). Therefore, substituting (vs → – vs) in equation (3), we get f’ = \(\left(\frac{v+v_{0}}{v+v_{s}}\right)\)f
IV. Numerical Problems:
Question 1.
The speed of a wave in a certain medium is 900 m/s. If 3000 waves pass over a certain point of the medium in 2 minutes, then compute its wavelength?
Answer:
Given:

Question 2.
Consider a mixture of 2 mol of helium and 4 mol of oxygen. Compute the speed of sound in this gas mixture at 300 K.
Answer:
Number of molecules of helium = 2
Number of molecules of oxygen = 4
When helium and oxygen are mixed, hence the molecular weight of the mixture of gases is given by

In addition, helium is monoatomic,
\(\mathrm{C}_{v_{2}}\) = \(\frac { 2R }{ 2 }\)
Oxygen is diatomic \(\mathrm{C}_{v_{1}}\) = \(\frac { 5R }{ 2 }\)
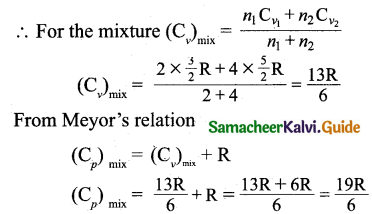
Ratio of specific heat capacitors of a mixture of gases is
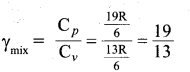
According to Laplace, the speed of sound in a gas is

∴ The speed of sound = 400.9 m/s
![]()
Question 3.
A ship in a sea sends SONAR waves straight down into the seawater from the bottom of the ship. The signal reflects from the deep bottom bedrock and returns to the ship after 3.5 s. After the ship moves to 100 km it sends another signal which returns back after 2 s. Calculate the depth of the sea in each case and also compute the difference in height between two cases.
Answer:
In the first case
time = 3.5s
Velocity sound in sea water = 1450 m/s
Distance 2d = v x t
= 1450 x 3.5 = 5,075 m
Depth of the sea d = \(\frac { 5075 }{ 2 }\) = 2537.5 m
In the second case,
time = 2s
Velocity of sound in water = 1450 m/s
Distance 2d = vt
= 1450 x 2
= 2900 m
Depth of the sea d = \(\frac { 2900 }{ 2 }\) = 1450
Difference ∆d = 2537.5 – 1450 = 1087.5
= 1087.5 m
Question 4.
A sound wave is transmitted into a tube as shown in the figure. The sound wave splits into two waves at point A which recombine at point B. Let R be the radius of the semi-circle which is varied until the first minimum. Calculate the radius of the semi-circle if the wavelength of the sound is 50.0 m.
Answer:
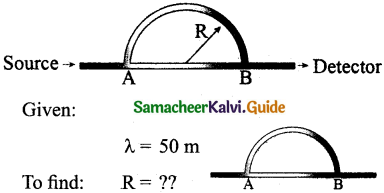
Path difference = πR – 2R
[Here AB = 2R; Semicircle path = πR]
Formula:
Path difference = (2n – 1)\(\frac { λ }{ 2 }\) (for minimum n – 1)
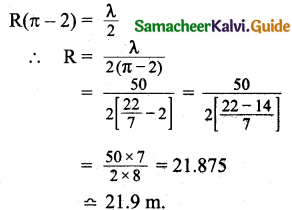
Question 5.
N tuning forks are arranged in order of increasing frequency and any two successive tuning forks give n beats per second when sounded together. If the last fork gives double the frequency of the first (called as octave), Show that the frequency of the first tuning fork is f = (N – 1)n.
Answer:
f,f + n,f+ 2n, … f + (m – 1)n
f + (N – 1)n = 2f
n = \(\frac { f }{ N-1 }\)
(or) f = n(N – 1)
Question 6.
Let the source propagate a sound wave whose intensity at a point (initially) be I. Suppose we consider a case when the amplitude of the sound wave is doubled and the frequency is reduced to one-fourth. Calculate now the new intensity of sound at the same point?
Answer:
Given:

Question 7.
Consider two organ pipes of the same length in which one organ pipe is closed and another organ pipe is open. If the fundamental frequency of closed pipe is 250 Hz. Calculate the fundamental frequency of the open pipe.
Answer:
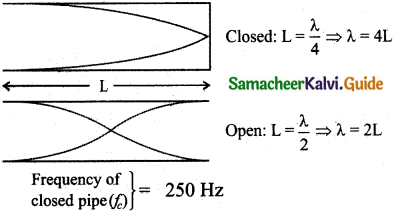
Formula:
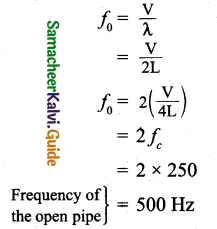
Question 8.
Police in a siren car moving with a velocity of 20 ms-1 chases a thief who is moving in a car with a velocity v0ms-1. The police car sounds at frequency 300 Hz, and both of them move towards a stationary siren of frequency 400 Hz. Calculate the speed at which the thief is moving.
Answer:
Velocity of sound v = 330 m/s
Velocity of a police siren car vs = 20 m/s
Frequency of a police siren car f = 300 Hz
Let the velocity of the thief be v m/s
The frequency of police siren heard by a thief is
f1 = \(\left(\frac{330-v}{330-20}\right)\) x 300
= \(\left(\frac{330-v}{310}\right)\) x 300 Hz
Frequency of stationary siren = 400 Hz
Frequency of stationaiy siren heard by a thief
f2 = \(\left(\frac{330+v}{330}\right)\) x 400
If there are no beats then

Question 9.
Consider the following function,
(a) y = x² + 2 α tx
(b) y = (x + vt)²
which among the above function can be characterized as a wave?
Answer:
Given:
Formula:
For the function to be a wave function \(\frac { (dy/dx) }{ (dy/dt) }\) should be a constant.
For function (a):

Hence, function
(a) does not describe a wave.
(b) satisfies wave function.
![]()
V. Conceptual Questions:
Question 1.
Why is it that transverse waves cannot be produced in a gas? Can the transverse waves be produced in solids and liquids?
Answer:
They travel in the form of crests and troughs and so involve a change in shape. They can be produced in a medium that has elasticity in shape. As gas has no elasticity of shape, hence transverse waves cannot be produced in a gas. Transverse waves can be produced in solids anion the surface of liquids.
Question 2.
Why is the roar of our national animal different from the sound of a mosquito?
Answer:
The pitch of the sound of our national animal lion is higher than that of mosquitoes. In addition, the frequency of sound waves generated by our national animal is more than the frequency of sound waves generated by mosquitoes.
Question 3.
A sound source and listener are both stationary and a strong wind is blowing. Is there a Doppler effect?
Answer:
When both source and listener are stationary, there is no relative motion between the source and the observer. Hence there is no Doppler effect.
Question 4.
In an empty room, why is it that a tone sounds louder than in the room having things like furniture, etc.
Answer:
When a room has furniture reverberation time can be suitably decreased since furniture has a large absorption coefficient of sound. So a tone sounds with lesser amplitude and intensity. Whereas in an empty room, reverberation time will be more than a room having things like furniture.
![]()
Question 5.
How do animals sense the impending danger of hurricanes?
Answer:
Hurricane produces a shock wave which has a speed greater than the speed of sound. It travels with a supersonic sound that can be easily sensed by animals using the Doppler effect. The multiple reflections of sound can be easily sensed by animals.
Question 6.
Is it possible to realize whether a vessel kept under the tap is about to fill with water?
Answer:
Yes. The frequency of a note generated by an air column is inversely proportional to its length. Consequently, as the length of the air column decreases, the frequency increases, i.e., the note becomes more shrill. In our case, when a vessel kept under the top is about to fill with water, as the water level rises, the length of the air column in the vessel goes on decreasing and the emitted sound becomes more and more shrill. Hence it is realised.