Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.2
Question 1.
Solve the following . equations by using Cramer’s rule
(i) 2x + 3y = 7; 3x + 5y = 9
(ii) 5x + 3v = 17; 3x + 7y = 31
(iii) 2x + y – z = 3; x + y + z – 1; x – 2y – 3z = 4
(iv) x + y + z = 6; 2x + 3y – z = 56; x – 2y – 3z = -7
Solution:
The equations are
2x + 3y = 7
3x + 5y = 9
Here Δ = \(\left|\begin{array}{ll}
2 & 3 \\
3 & 5
\end{array}\right|\) = 10 – 9 = 1
≠ 0
∴ We can apply Cramer’s Rule

∴ x = 8; y = -3
![]()
(ii) The equations are
5x + 3y = 17
3x + 7y = 31
Here Δ = \(\left|\begin{array}{ll}
5 & 3 \\
3 & 7
\end{array}\right|\) = 35 – 9 = 26
≠ 0
We can apply Cramer’s Rule
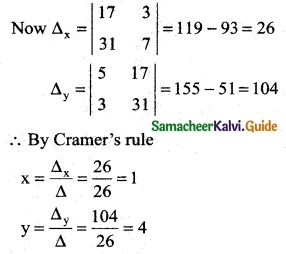
∴ x = 1; y = 4
(iii) The equations are
2x + y – z = 3
x + y + z = 1
x – 2y – 3z = 4
Here Δ = \(\left|\begin{array}{ccc}
2 & 1 & -1 \\
1 & 1 & 1 \\
1 & -2 & -3
\end{array}\right|\)
= 2 (-3 + 2) – 1 (-3 – 1) – 1 (-2 – 1)
= 2 (-1) -1 (-4) -1 (-3)
= -2 + 4 + 3
Δ = 5 ≠ 0
∴ We can apply Cramer’s Rule and the system is consistant and it has unique solution.
Δx = \(\left|\begin{array}{ccc}
3 & 1 & -1 \\
1 & 1 & 1 \\
4 & -2 & -3
\end{array}\right|\)
= 3 (-3 + 2) – 1 (-3 – 4) – 1 (-2 – 4)
= 3 (-1) -1 (-7) -1 ( 6)
= -3 + 7 + 6 = 10
Δy = \(\left|\begin{array}{ccc}
2 & 3 & -1 \\
1 & 1 & 1 \\
1 & 4 & -3
\end{array}\right|\)
= 2 (- 3 – 4) -3 (-3 – 1) -1 (4 – 1)
= 2 (-7) – 3 (-4) – 1 (3)
= -14 + 12 – 3
= -5
Δz = \(\left|\begin{array}{ccc}
2 & 1 & 3 \\
1 & 1 & 1 \\
1 & -2 & 4
\end{array}\right|\)
= 2 (4 + 2) – 1 (4 – 1) + 3 (- 2 – 1)
= 2 (6) – 1(3) + 3 (-3)
= 12 – 3 – 9 = 0
∴ By Cramer’s rule
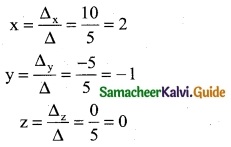
∴ (x, y, z) = (2, -1, 0)
![]()
(iv) The equations are
x + y + z = 6
2x + 3y – z = 5
6x – 2y – 3z = -7
Here Δ = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
2 & 3 & -1 \\
6 & -2 & -3
\end{array}\right|\)
= 1 (-9 – 2) -1 (-6 + 6) + 1 (-4 – 18)
= 1 (-11) – 1 (0) +1 (-22)
= -11 – 22
= -33 ≠ 0
∴ We can apply Cramer’s Rule and the system is consistent and it has unique solution.
Now,
Δx = \(\left|\begin{array}{ccc}
6 & 1 & 1 \\
5 & 3 & -1 \\
-7 & -2 & -3
\end{array}\right|\)
= 6 (- 9 – 2) – 1 (- 15 – 7) + 1 (- 10 + 21)
= 6 (-11) – 1 (-22)+ 1 (11)
= -66 + 22 + 11
= -33
Δy = \(\left|\begin{array}{ccc}
1 & 6 & 1 \\
2 & 5 & -1 \\
6 & -7 & -3
\end{array}\right|\)
= 1 (-15 – 7) – 6 (- 6 + 6) + 1 (- 14 – 30)
= 1 (-22) – 6 (0) + 1 (-44)
= -66
Δz = \(\left|\begin{array}{ccc}
1 & 1 & 6 \\
2 & 3 & 5 \\
6 & -2 & -7
\end{array}\right|\)
= 1 (- 21 + 10) – 1 (- 14 – 30) + 6 (- 4 – 18)
= 1 (-11) – 1 (-44) + 6 (-22)
= -11 + 44 – 132
= -99
∴ By Cramer’s rule
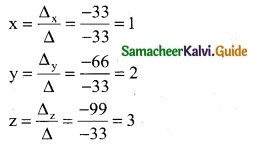
(x, y, z) = (1, 2, 3)
![]()
(v) The equations are
x + 4y + 3z = 2
2x – 6y + 6z = -3
5x – 2y + 3z = -5
Here Δ = \(\left|\begin{array}{ccc}
1 & 4 & 3 \\
2 & -6 & 6 \\
5 & -2 & 3
\end{array}\right|\)
= 1 (-18 + 12) -4 (6 -30) + 3 (-4 + 30)
= 1 (-6) – 4 (-24) + 3 (26)
= -6 + 96 + 78
= 168 ≠ 0
We can apply Cramer’s Rule and the system is consistent and it has unique solution.
Δx = \(\left|\begin{array}{ccc}
2 & 4 & 3 \\
-3 & -6 & 6 \\
-5 & -2 & 3
\end{array}\right|\)
= 2 (-18 + 12) – 4 (-9 + 30) + 3 (6 – 30)
= 2 (-6) -4 (21) + 3 (-24)
= -12 – 84 – 72
= -168
Δy = \(\left|\begin{array}{ccc}
1 & 2 & 3 \\
2 & -3 & 6 \\
5 & -5 & 3
\end{array}\right|\)
= 1 (-9 + 30) – 2 (6 – 30) + 3 (-10 + 15)
= 1(21) – 2 (-24) + 3 (5)
= 21 + 48 + 15
= 84
Δz = \(\left|\begin{array}{ccc}
1 & 4 & 2 \\
2 & -6 & -3 \\
5 & -2 & -5
\end{array}\right|\)
= 1 (30 – 6) – 4 (-10 +15) + 2 (-4 + 30)
= 1 (24) – 4 (5) + 2 (26)
= 24 – 20 + 52
= 56
∴ By Cramer’s rule
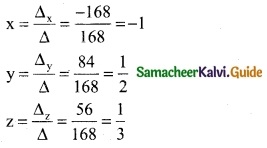
(x, y, z) = (-1, \(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 3 }\))
![]()
Question 2.
A commodity was produced by using 3 units of labour and 2 units of capital, the total cost is Rs 62. If the commodity had been produced by using 4 units of labour and one unit of capital, the cost is Rs 56. What is the cost per unit of labour and capital? (Use determinant method).
Solution:
Let ‘x’ be the cost per unit of labour
Let ‘y’ be the capital
∴ 3x + 2y = 62
4x + y = 56

∴ The cost per unit of labour is Rs 10 and Cost per unit of capital is Rs 16
![]()
Question 3.
A total of Rs 8,600 was invested in two accounts. One account earned 4\(\frac { 3 }{ 4 }\)% annual interest and the other earned 6\(\frac { 1 }{ 2 }\)% annual interest. If the total interest for one year was Rs 431.25, how much was invested in each accout? (Use determinant method)
Solution:
Let the two investments be x and y
Given that
x + y = 8600 ……. (1)
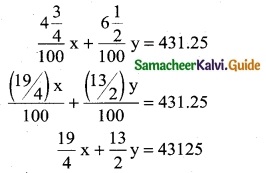
Multiply by 4 (both sides)
19x + 26y = 172500 ……….. (2)
Here Δ = \(\left|\begin{array}{ll}
1 & 1 \\
19 & 26
\end{array}\right|\) = 26 – 19 = 7 ≠ 0
∴ We can apply Cramer’s Rule
Δx = \(\left|\begin{array}{ll}
8600 & 1 \\
172500 & 26
\end{array}\right|\)
= 223600 – 172500
= 51100
Δy = \(\left|\begin{array}{ll}
1 & 8600 \\
19 & 172500
\end{array}\right|\)
= 172500 – 163400
= 9100
By Cramer’s Rule
x = \(\frac { Δ_x }{ Δ }\) = \(\frac { 51100 }{ 7 }\) = 7300
y = \(\frac { Δ_y }{ Δ }\) = \(\frac { 9100 }{ 7 }\) = 1300
∴ Amount invested at 4\(\frac { 3 }{ 4 }\)% is Rs 7,300 and
Amount invested at 6\(\frac { 1 }{2 }\)% is Rs 1,300
![]()
Question 4.
At marina two types of games viz., Horse riding and Quad Bikes riding are available on hourly rent. Keren and Bentia spent Rs 780 and Rs 560 during the month of May
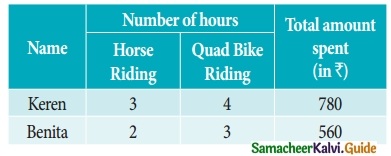
Find the hourly charges for the two games (rides). (Use determinant method).
Solution:
let the hourly charges for horse riding be x and let the hourly charges for Quad Bikes riding be y.
For Keren
3x + 4y = 780 ……… (1)
For Benita
2x + 3y = 560 ……… (2)
Here Δ = \(\left|\begin{array}{ll}
3 & 4 \\
2 & 3
\end{array}\right|\) = 9 – 8 = 1 ≠ 0
∴ We can apply Cramer’s Rule

∴ The hourly charges for horse riding is Rs 100 and Quad Bikes riding is Rs 120
![]()
Question 5.
In a market survey three commodities A, B and C were considered. In finding out the index number some fixed weights were assigned to the three varieties in each of the commodities. The table below provides the information regarding the consumption of three commodities according to the three varieties and also the total weight received by the commodity.
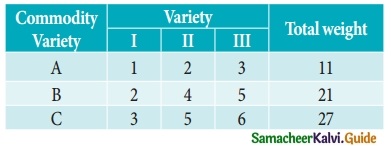
Find the weights assigned to the three varieties by using Cramer’s Rule.
Solution:
Let x, y and z be are consumption of three commodities A, B and C respectively.
Given that
x + 2y + 3z = 11 ……… (1)
2x + 4y + 5z = 21 ……… (2)
3x + 5y + 6z = 27 ……… (2)
Here Δ = \(\left|\begin{array}{ccc}
1 & 2 & 3 \\
2 & 4 & 5 \\
3 & 5 & 6
\end{array}\right|\)
= 1 (24 – 25) – 2 (12 – 15) + 3 (10- 12)
= 1 ( 1) 2 ( 3) + 3 (- 2)
= -1 + 6 – 6 = -1 ≠ 0
∴ We can apply Cramer’s Rule
Now Δx = \(\left|\begin{array}{ccc}
11 & 2 & 3 \\
21 & 4 & 5 \\
27 & 5 & 6
\end{array}\right|\)
= 11 (24 – 25) -2 (126 – 135) + 3 (105 – 108)
= 11(-1) -2 (-9)+ 3 (-3)
= -11 + 18 – 9
= -2
Δy = \(\left|\begin{array}{ccc}
1 & 11 & 3 \\
2 & 21 & 5 \\
3 & 27 & 6
\end{array}\right|\)
= 1 (126 – 135) -11 (12 – 15) + 3 (54 – 63)
= 1 (-9) -11 (-3) + 3 (-9)
= -9 + 33 – 27
= -3
Δz = \(\left|\begin{array}{ccc}
1 & 2 & 11 \\
2 & 4 & 21 \\
3 & 5 & 27
\end{array}\right|\)
= 1 (108 – 105) – 2 (54 – 63) + 11 (10 – 12)
= 1(3) – 2 (-9) + 11 (-2)
= 3 + 18 – 22 = -1
By Cramer’s Rule
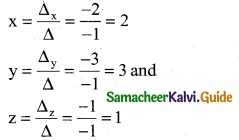
∴ (x, y, z) = (2, 3, 1)
![]()
Question 6.
A total of Rs 8,500 was invested in three interest-earning accounts. The interest rates were 2%, 3%, and 6%, if the total simple interest for one year was Rs 380 and the amount invested at 6% was equal to the sum of the amounts in the other two accounts, then how much was invested in each account? (use Cramer’s rule)
Solution:
Let the amount invested at 2%, 3%, and 6% are x, y, and z respectively.
x + y + z = 8500 ………. (1)
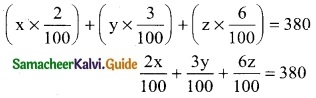
2x + 3y + 6z = 38000 ………. (2)
x + y = z
x + y – z = 0 ……… (3)
Here Δ = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
2 & 3 & 6 \\
1 & 1 & -1
\end{array}\right|\)
= 1 (-3 – 6) -1 (-2 – 6) + 1 (2 – 3)
= 1 (-9) -1 (-8) + 1 (-1)
= -9 + 8 – 1 = -2
≠ 0
∴ We can apply Cramer’s Rule
Δx = \(\left|\begin{array}{ccc}
8500 & 1 & 1 \\
38000 & 3 & 6 \\
0 & 1 & -1
\end{array}\right|\)
= 8500 (-3 – 6) -1 (-38000 – 0) + 1 (38000 – 0)
= 8500 (-9) + 38000 + 38000
= -76500 + 76000
= -500
Δy = \(\left|\begin{array}{ccc}
1 & 8500 & 1 \\
2 & 38000 & 6 \\
1 & 0 & -1
\end{array}\right|\)
= 1(-38000 – 0) – 8500 (-2 – 6) + 1 (0 – 38000)
= -38000 + 68000-38000
= 68000 – 76000
= -8000
Δz = \(\left|\begin{array}{ccc}
1 & 1 & 8500 \\
2 & 3 & 38000 \\
1 & 1 & 0
\end{array}\right|\)
= (0 – 38000) -1 (0 – 38000) + 8500 (2 – 3)
= -38000 + 38000 – 8500
= -8500
By Cramer’s Rule
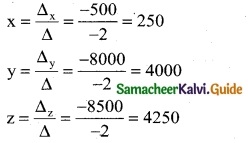
∴ Amount invested at 2% is Rs 250; Amount invested at 3% is Rs 4,000 and Amount invested at 6% is Rs 4,250
![]()