Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 4 Differential Equations Ex 4.5 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.5
Question 1.
\(\frac { d^2y }{dx^2}\) – 6\(\frac { dy }{dx}\) + 8y = 0
Solution:
Given (D2 – 6D + 8) y = 0, D = \(\frac{d}{d x}\)
The auxiliary equations is
m2 – 6m + 8 = 0
(m – 4)(m – 2) = 0
m = 4, 2
Roots are real and different
The complementary function (C.F) is (Ae4x + Be2x)
The general solution is y = Ae4x + Be2x
![]()
Question 2.
\(\frac { d^2y }{dx^2}\) – 4\(\frac { dy }{dx}\) + 4y = 0
Solution:
The auxiliary equations A.E is m2 – 4m + 4 = 0
(m – 2)2 = 0
m = 2, 2
Roots are real and equal
The complementary function (C.F) is (Ax + B) e2x
The general solution is y = (Ax + B) e2x
![]()
Question 3.
(D² + 2D + 3) y = 0
Solution:
The auxiliary equation is m² + 2m + 3 = 0
Here a = 1, b = 2, c = 3

The complementary function is
eax (Acosßx + Bsinßx)
∴ C.F = e-x [Acos√2x + Bsin √2x]
∴ The general solution is
y = e-x (Acos√2x + Bsin√2x)
Question 4.
\(\frac { d^2y }{dx^2}\) – 2k\(\frac { dy }{dx}\) + k²y = 0
Solution:
Given (D2 – 2kD + k2)y = 0, D = \(\frac{d}{d x}\)
The auxiliary equations is m2 – 2km + k = 0
⇒ (m – k)2 = 0
⇒ m = k, k
Roots are real and equal
The complementary function (C.F) is (Ax + B) ekx
The general solution is y = (Ax + B) ekx
![]()
Question 5.
(D² – 2D – 15) y = 0
Solution:
The auxiliary equation is
m² – 2m + 15 = 0
m² + 3m – 5m – 15 = 0
m (m + 3) – 5 (m + 3) = 0
(m + 3) (m – 5) = 0
m = -3, 5
Roots are real and different
∴ The complementary function is
Aem1x + Bem2x
C.F = Ae-3x + Be5x
∴ The general solution is
y = (Ae-3x + Be5x) ………… (1)
\(\frac { dy }{dx}\) = Ae-3x (-3) + Be5x (5)
\(\frac { dy }{dx}\) = -3Ae-3x + 5Be5x ………… (2)
\(\frac { d^2y }{dx^2}\) = 9Ae-3x + 25Be5x ……….. (3)
when x = 0; \(\frac { dy }{dx}\) = 0
-3 Ae° + 5Be° = 0
-3A + 5B = 0 ………. (4)
when x = 0; \(\frac { d^2y }{dx^2}\) = 2
Eqn (3) ⇒ 9Ae° + 25Be° = 2
9A + 25B = 2 ……… (5)
Solving equation (4) & (5)

![]()
Question 6.
(4D² + 4D – 3) y = e2x
Solution:
The auxiliary equation is
4m² + 4m – 3 = 0
4m² + 6m – 2m – 3 = 0
2m (2m + 3) – 1 (2m + 3) = 0
(2m + 3) (2m – 1) = 0
2m = -3; 2m = 1
m = -3/2, 1/2
Roots are real and different
The complementary function is
Aem1x + Bem2x

![]()
Question 7.
\(\frac { d^2y }{dx^2}\) + 16y = 0
Solution:
Given (D2 + 16) y =0
The auxiliary equation is m2 + 16 = 0
⇒ m2 = -16
⇒ m = ± 4i
It is of the form α ± iβ, α = 0, β = 4
The complementary function (C.F) is e0x [A cos 4x + B sin 4x]
The general solution is y = [A cos 4x + B sin 4x]
![]()
Question 8.
(D² – 3D + 2) y = e3x which shall vanish for x = 0 and for x = log 2
Solution:
(D² – 3D + 2) y = e3x
The auxiliary equation is
m² – 3m + 2 =0
(m – 1) (m – 2) = 0
m = 1, 2
Roots are real and different
The complementary function is
C.F = Aem1x + Bem2x
C.F = Ax + Be2x

when x = log 2; y = 0
Aelog 2 + Be2log 2 + \(\frac { e^{3xlog2} }{2}\) = 0
Aelog 2 + Belog (2)² + \(\frac { e^{log2³} }{2}\) = 0
2A + 4B + \(\frac { 8 }{2}\) = 0
2A + 4B + 4 = 0
2A + 4B = -4 ……… (3)
Solving equation (2) & (3)
Eqn (2) × 2 ⇒ 2A + 2B = -1

![]()
Question 9.
(D² + D – 2) y = e3x + e-3x
Solution:
The auxiliary equation is
m² + m – 6 = 0
(m + 3) (m – 2) = 0
Roots are real and different
The complementary function is
C.F = Aem1x + Bem2x
C.F = Ae-3x + Be2x

Question 10.
(D² – 10D + 25) y = 4e5x + 5
Solution:
The auxiliary equation is
m² – 10m + 25 = 0
(m – 5) (m – 5) = 0
m = 5, 5
Roots are real and equal
C.F = (Ax + B) emx
C.F = (Ax + B) e5x
P.I(1) = x. \(\frac { 4 }{2D-10}\) e5x
Replace D by 5, 2D – 10 = 0 when D = 5

![]()
Question 11.
(4D² + 16D +15) y = 4e\(\frac { -3 }{2}\)x
Solution:
The auxiliary equation is 4m² + 16m + 15 = 0
4m² + 16m + 10m + 15 = 0
2m (2m + 3) + 5 (2m + 3) = 0
(2m + 3) (2m + 5) = 0
2m = -3, -5
∴ m = -3/2, -5/2
Roots are real and different
C.F = (Ax + B) em1x + Bem2x
C.F = Ae-3/2 x + Be-5/2 x

Question 12.
(3D² + D – 14) y – 13 e2x
Solution:
The auxiliary equation is 3m² + m – 14 = 0
3m² – 6m + 7m – 14 = 0
3m (m – 2) + 7 (m – 2) = 0
(m – 2) (3m + 7) = 0
m = 2; 3m = -7
m = 2, -7/3
Roots are real and different
C.F = (Ax + B) em1x + Bem2x
C.F = Ae2x + Be-7/3 x

![]()
Question 13.
Suppose that the quantity demanded Qd = 13 – 6p + 2\(\frac { dp }{dt}\) + \(\frac { d^2p }{dt^2}\) = and quantity supplied Qd = -3 + 2p where is the price. Find the equilibrium price for market clearence.
Solution:
For market clearance, the required condition is Qd = Qs
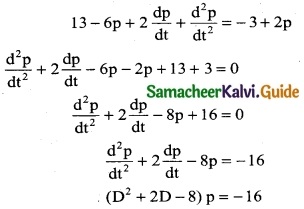
The auxiliary equation is
m² + 2m – 8 = 0
(m + 4) (m – 2) = 0
m = -4, 2
Roots are real and different

![]()