Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 5 Numerical Methods Miscellaneous Problems Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 5 Numerical Methods Miscellaneous Problems
Question 1.
If f (x) = eax then show that f(0), Δf(0), Δ²f(0) are in G.P
Solution:
Given f(x) = eax
f(0) = e° = 1 ……… (1)
Δf(x) = ea(x+h) – eax
= e ax+ah – eax
= eax. eah – eax
= eax (eah – 1)
Δf(0) = e° (eah – 1)
= (eah – 1) …….. (2)
Δ²f(x)= Δ [Δf(x)]
= Δ [ea(x+h) – eax]
[ea(x+h+h) – ea(x+h)] – [ea(x+h) – eax]
= ea(x+2h) – ea(x+h) – ea(x+h) + eax
Δ²f(0) = Δ [Δf(x)]
= ea(2h) – ea(h) – ea(h) + e0
= e2ah – eah – eah + 1
= (eah)² – 2eah + 1
= [eah – 1]² ………… (3)
from (1), (2) & (3)
[t2]² =[Δf(0)]² = (eah – 1)²
t1 × t3 = f(0) × Δ²f(0)
= (1)(eah – 1)² = (eah – 1)²
⇒ [Δf(0)]² = f(0) × Δ²f(0)
∴ f(0), Δf(0), Δ²f(0) an is G.P.
![]()
Question 2.
Prove that
(i) (1 + Δ) (1 – ∇) = 1
(ii) Δ∇ = Δ – ∇
(iii) EV = Δ = ∇E
Solution:
(i) LHS = (1 + Δ) (1 – ∇)
= (E) (E-1) = E1-1
= E° = 1
= RHS
Hence proved.
(ii) LHS = Δ∇
= (E – 1)(1 – E-1)
= E – EE-1 + E-1
= E – 1 – 1 – E-1
= E – 2 – E-1 ………… (1)
RHS = Δ – ∇
= (E – 1) -(1 – E-1)
= E – 1 – 1 + E-1
= E – 2 + E-1 ………. (2)
from (1) & (2) LHS = RHS
Hence proved.
![]()
(iii) E∇ = EE-1Δ [∵ ∇ = E-1Δ]
= Δ ……… (1)
∇E = E-1 ΔE
= E-1 EΔ
= Δ ………. (2)
from (1) (2)
E∇ = Δ = ∇E
Question 3.
A second degree polynomial passes though the point (1, -1) (2, -1) (3, 1) (4, 5). Find the polynomial.
Solution:
Points are (1, -1), (2, -1), (3, 1) and (4, 5)

we will use Newton’s backward interpolation formula to find the polynomial.

= 5 + (x – 4) (4) + (x – 4) (x – 3) + 0
= 5 + 4x – 16 + x² – 7x + 12
y(x) = x² – 3x + 1
![]()
Question 4.
Find the missing figures in the following table
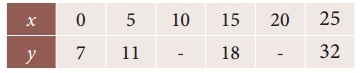
Solution:
Here y0 = 7; y1 = 11; y2 = ?; y3 = 18; y4 = ?; y5 = 32
Since only four values of f(x) are given, the polynomial which fits the data is of degree three. Hence fourth differences are zeros.
Δ4yk = 0
(ie) (E – 1)4 yk = 0
(i.e) (E4 – 4E³ + 6E² – 4E + 1)yk = 0 ……….. (1)
Put k = 0 in (1)
(E4 – 4E³ + 6E² – 4E + 1)y0 = 0
E4 y0 – 4E3 y0 + 6E² y0 – 4E y0 + y0 = 0
y4 – 4y3 + 6y2 – 4y1 + y0 = 0
y4 – 4(18) + 6y2 – 4(11) + 7 = 0
y4 – 72 + 6y2 – 44 + 7 = 0
y4 + 6y2 = 109
(2)
Put k = 1 in (1)
(E4 – 4E3 + 6E² – 4E + 1)y1 = 0
[E4 y1 – 4E y1 + 6E² y1 – 4Ey1 + y] = 0
y5 – 4y4 + 6y3 – 4y2 + y1 = 0
32 – 4 (y4) + 6(18) — 4(y2) + 11 = 0
32 – 4y4 + 108 – 4y2 + 11 = 0
-4y4 – 4y2 + 151 = 0
4y4 + 4y2 = 151 ,……. (3)
Solving equation (1) & (2)
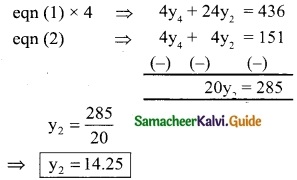
Substitute y2 = 14.25 in eqn (1)
y4 + 6(14.25) = 109
y4 + 25.50 = 109
y4 = 109 – 85.5
∴ y4 = 23.5
∴ Required two missing values are 14.25 and 23.5.
![]()
Question 5.
Find f (0.5) if f(-1) = 202, f(0) = 175, f(1) = 82 and f(2) = 55
Solution:
From the given data

Here we have to apply Newton’s forward interpolation formula, since the value of f(x) is required near the beginning of the table.
y(x= x0+nh) =f(x0) + \(\frac { n }{1!}\) Δf(x0) + \(\frac { n(n-1) }{2!}\) Δ²f(x0) + \(\frac { n(n-1)(n-2) }{3!}\) Δ³f(x0) + ………
Given:
x = 0.5 and h = 1
x0 + nh = x
-1 + n(1) = 0.5
n = 1 + 0.5
∴ n = 1.5

= 202 – 40.5 – 24.75 – 8.25
= 202 – 73.5
f(0.5) = 128.5
![]()
Question 6.
From the following data find y at x = 43 and x = 84
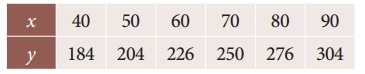
Solution:
To find y at x = 43
Since the value of y is required near the beginning of the table, we use the Newton’s forward interpolation formula.
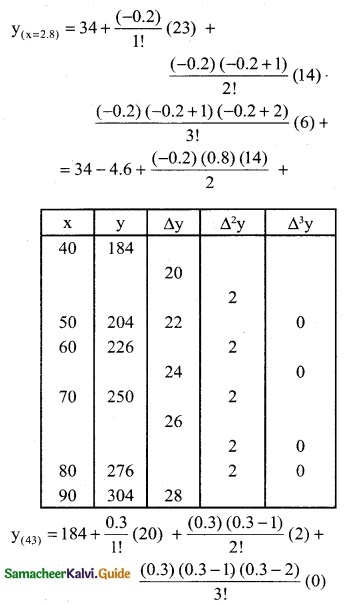
= 184 + (0.3) (20) + (0.3) (-0.7)
= 184 + 6.0 – 0.21
= 190 + 0.21
y(x=43) = 189.79
To find y at x = 84
Since the value of y is required at the end of the table, we apply backward interpolation formula.
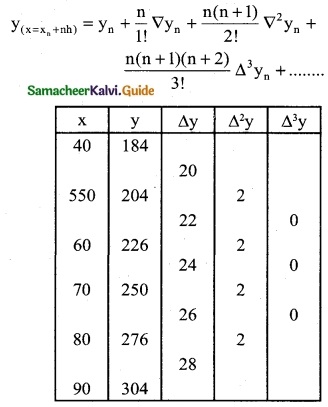
xn + nh = x
90 + n(10) = 84
10n = 84 – 90
10n = -6
∴ n = -0.6
y(x=84) = 304 + \(\frac { (0.6) }{1!}\) (28) + \(\frac {(0.6)(-0.6 + 1) }{2!}\)(2) +
= 304 + (0.6) (28) + \(\frac { (-0.6)(0.4) }{2}\) + 2
= 304 – 16.8 – 0.24
= 304 – 17.04
= 286.96
![]()
Question 7.
The area A of circle of diameter ‘d’ is given for the following values
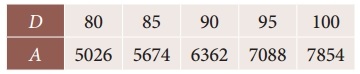
Find the approximate values for the areas of circles of diameter 82 and 91 respectively.
Solution:
To find A at D = 82
Since the value of A is required near the beginning of the table. We use the Newton’s forward interpolation formula.
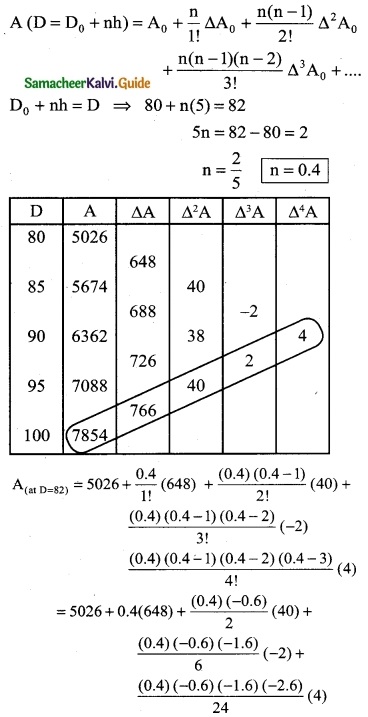
= 5026 + 259.2 – 4.8 – 0.128 – 0.1664
= 5285.2 – 5.0944
= 5280.1056
A = 5280.11
To find Δ at D = 91
Since the value of A is required near the beginning of the table. We use the Newton’s forward interpolation formula.

= 7854 – 1378.8 + 28.8 + 0.096 + 0.0576
= 7882.9536 – 1378.8
= 6504.1536
= 6504.15
![]()
Question 8.
If u0 = 560, u1 = 556, u2 = 520, u4 = 385, show that u3 = 465
Solution:
U0 = 560; U1 = 556; U2 = 520; U4 = 385
Since only four values of U are given, the polynomial which fits the data is of degree three. Hence fourth differences are zeros.
Δ4U0
(E – 1)4 U0 = 0
⇒ (E4 – 4E³ + 6E² – 4E + 1) U0 = 0
⇒ E4U0 – 4E³U0 + 6E²U0 – 4EU0 + U0 = 0
U4 – 4U3 + 6U2 – 4U1 + U0 = 0
385 – 4(U3) + 6 (520) – 4 (556) + 560 = 0
385 – 4(U3) + 3120 – 2224 + 560 = 0
1841 – 4U3 = 0
4U3 = 1841 ⇒ U3 = \(\frac { 1841 }{4}\)
U3 = 460.25
![]()
Question 9.
From the following table obtain a polynomial of degree y in x
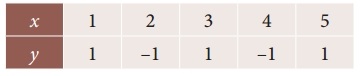
Solution:
We will use Newton’s backward interpolation formula to find the polynomial.
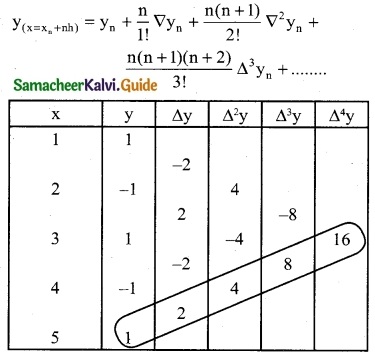
To find y in terms of x
xn + nh = x
5 + n(1) = x
∴ n = x – 5
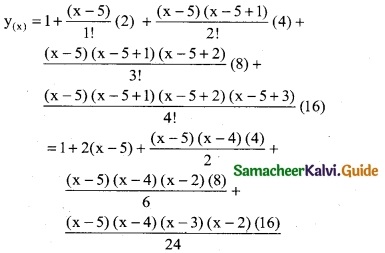
= 1 + 2x – 10 + 2 (x² – 9x + 20) + \(\frac { 4 }{3}\) (x – 5) (x² – 7x + 12) + \(\frac { 2 }{3}\)(x² – 9x + 20)(x² – 5x + 6)
= 1 + 2x – 10 + 2x² – 18x + 40 + \(\frac { 4 }{3}\)
[x³ – 7x² + 12x – 5x² + 35x – 60] + \(\frac { 2 }{3}\) [x4 – 5x³ + 6x² – 9x³ + 45x² – 54x + 20x² – 100x + 120]

![]()
Question 10.
Using Lagrange’s interpolation formula find a polynominal which passes through the points (0, -12), (1, 0), (3, 6) and (4, 12).
Solution:
We can construct a table using the given points.

Here x0 = 0; x1 = 1; x2 = 3; x3 = 4,
y0 = -12; y1 = 0; y2 = 6; y3 = 12

= (x³ – 7x² + 12x – x² + 7x – 12) – (x³ – 5x² + 4x) + (x³ – 4x² + 3x)
= (x³ – 8x² + 19x – 12) – (x³ – 5x² + 4x) + (x³ – 4x² + 3x)
= x³ – 8x² + 19x – 12 – x³ + 5x² – 4x + x³ – 4x² + 3x
∴ y = x³ – 7x² + 18x – 12
![]()