Samacheer Kalvi 12th Business Maths Guide Chapter 6 Random Variable and Mathematical Expectation Ex 6.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 6 Random Variable and Mathematical Expectation Ex 6.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 6 Random Variable and Mathematical Expectation Ex 6.1

Question 1.
Construct cumulative distribution function for the given probability distribution.

Solution:
F(0) = P(x ≤ 0) = p(0) = 0.3
F(1) = P(x ≤ 1) = p(0) + p(1)
= 0.3 + 0.2 = 0.5
F(2) = P(x ≤ 2) = P(0) + P(1) + P(2)
= 0.3 + 0.2 + 0.4 = 0.9
F(3) = P(x ≤ 3) = P(0) + P(2) + P(3) + P(4)
= 0.3 + 0.2 + 0.4 + 0.1 = 1

Question 2.
Let X be a discrete random variable with the following p.m.f

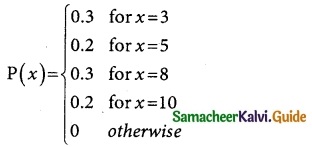
Find and plot the c.d.f. of X.
Solution:
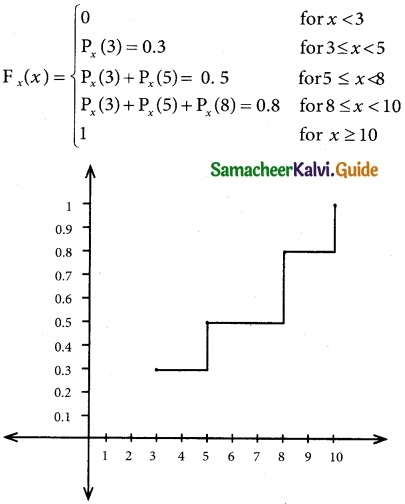
F(3) = P(x ≤ 3) = P(3) = 0.3
F(5) = P(x ≤ 5) = P(x = 3) + (x = 5)
= 0.3 + 0.2 = 0.5
F(8) = P(x ≤ 8) = P(3) + P(5) + P(8)
= 0.3 + 0.2 + 0.3
= 0.8
F(10) = P(x ≤ 10)
= P(3) + P(5) + P(8) + P(10)
= 0.3 + 0.2 + 0.3 + 0.2
= 1

Question 3.
The discrete random variable X has the following probability function.

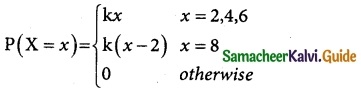
where k is a constant. Show that k = \(\frac { 1 }{18}\)
Solution:
From the data
P(x = 2) = kx
= 2k
P(x = 4) = kx
= 4k
P(x = 6) = kx
= 6k
P(x = 8) = k(x – 2)
= k(8 – 2) = 6k
Since P(X = x) is a probability mass function
\(\sum_{x=2}^{8}\) P(X = x) = 1
\(\sum_{i=2}^{∞}\) P(xi) = 1
(i.e) P(x = 2) + P(x = 4) + P(x = 6) + P(x = 8) = 1
2k + 4k + 6k + 6k = 1
18k = 1
∴ k = \(\frac { 1 }{18}\)

Question 4.
The discrete random variable X has the probability function

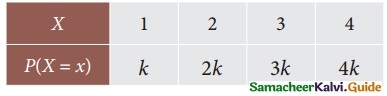
Solution:
From the data
P(x = 1) = k
p(x = 2) = 2k
p(x = 3) = 3k
P(x = 4) = 4k
Since P(X = x) is a probability Mass function
\(\sum_{x=1}^{4}\) P(X = x) = 1
\(\sum_{i=1}^{∞}\) P(x_i) = 1
p(x = 1) + P(x = 2) + P(x = 3) + P(x = 4) = 1
P(x = 1) + P(x = = 2) + P(x = 3) + P(x = 4) = 1
k + 2k + 3k + 4k = 1
10k = 1
k = \(\frac { 1 }{10}\)
∴ k = 0.1

Question 5.
Two coins are tossed simultaneously. Getting a head is termed as success. Find the t probability distribution of the number of successes.
Solution:
Let X is the random variable which counts the Number of Heads when the coins are tossed the outcomes are stated below

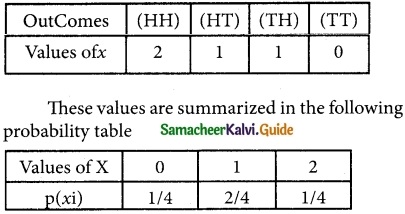
Question 6.
The discrete random variable X has the probability function.

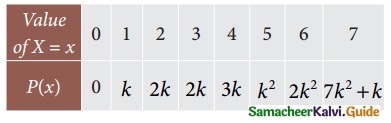
(i) Find k
(ii) Evaluate p( x < 6), p(x ≥ 6)and p(0 < x < 5) (iii) If P(X ≤ x) > 1, 2 then find the minimum value of x.
Solution:
(i) Since the condition of Probability Mass function
\(\sum_{i=2}^{∞}\) P(x_i) = 1
\(\sum_{i=0}^{7}\) P(x_i) = 1
P(x = 0) + P(x = 1) + P(x = 2) + P(x = 3) + P(x = 4) + P P(x = 6) + p(x = 7) = 1
0 + k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
10k² + 9k – 1 = 0
10k² + 10k – k – 1 = 0
10k(k + 1) -1(k + 1) = 0
(k + 1)(10k – 1) = 0
k + 1 = 0; 10k – 1 = 0
k = -1 10k = 1
k = \(\frac { 1 }{10}\)
k = -1 is not possible

(ii) P(x < 6)
P(x < 6) = P(x = 0) + P(x = 1) + P(x = 2)+ P(x = 3) + p(x = 4) + P(x = 5)
= 0 + k + 2k +2k + 3k + k²
= 8k + k²

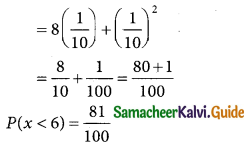
P(x ≥ 6) = P(x = 6) + p(x = 7)
= 2k² + 7k² + k
= 9k² + k

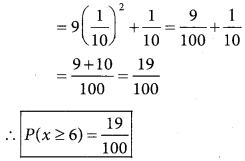
P(0 < x < 5)
= P(x = 1) + P(x = 2) + p(x = 3) + P(x = 4)
= k + 2k + 2k + 3k
= 8k = 8(\(\frac { 1 }{10}\))
∴ P(0 < x < 5) = \(\frac { 8 }{10}\)

(iii) We want the minimum value of x for which P(X ≥ x) > \(\frac { 1 }{2}\)
Now P(X ≤ 0) = 0 < \(\frac { 1 }{2}\)
P(X ≤ 1) = P(x = 0) + P(X = 1) = 0 + k = k
\(\frac { 1 }{10}\) < \(\frac { 1 }{2}\)
P( X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)
= 0 + k + 2k = 3k
\(\frac { 3 }{10}\) \(\frac { 1 }{2}\)
P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 2) + P(X = 3)
= 0 + k + 2k + 2k = 5k
= \(\frac { 5 }{10}\) = \(\frac { 1 }{2}\)
P(X ≤ 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 2) + P(X = 3) + P(X = 4)
= 0 + k + 2k + 2k + 3k = 8k
= \(\frac { 8 }{10}\) > \(\frac { 1 }{2}\)
This Shows that the minimum value of X for which P(X ≤ x) > \(\frac { 1 }{2}\) is 4

Question 7.
The distribution of a continuous random variable X in range (-3, 3) is given by p.d.f.

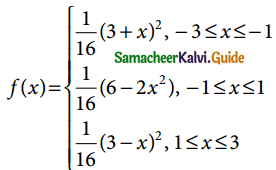
Verify that the area under the curve is unity.
Solution:
Since(-3, 3) in the range of given p.d.f
Area under the curve A = \(\int_{-∞}^{∞}\) f(x)dx = \(\int_{-3}^{3}\) f(x)dx

Hence the Area under the curve is unity

Question 8.
A continuous random variable X has the following distribution function:

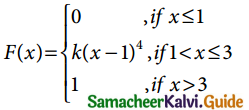
Find (i) k and (ii) the probability density function.
Solution:
(i) Here F(3) – F(1) = 1
K(3 – 1)⁴ – O = 1
K(2)⁴ = 1
K(16) = 1
k = \(\frac { 1 }{16}\)

(ii) The Probability density function
f(x) = \(\frac { d(F(x)) }{dx}\) = \(\left\{\begin{array}{l}
4 k(x-1)^{3}, 1<x \leq 3 \\
0 \text { else where }
\end{array}\right.\)

Question 9.
The length of time (in minutes) that a certain person speaks on the telephone is found to be random phenomenon, with a probability function specified by the probability density function f(x) as

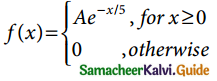
(a) Find the value of A that makes f (x) a p.d.f.
(b) What is the probability that the number of minutes that person will talk over the phone is (i) more than 10 minutes, (ii) less than 5 minutes and (iii) between 5 and 10 minutes.
Solution:
(a) Since f(x) is a probability density Function

b (i) more than 10 minutes

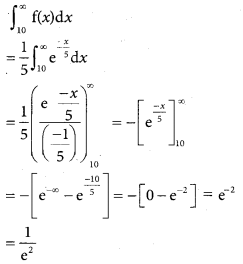
Question 10.
Suppose that the time in minutes that a person has to wait at a certain station for a train is found to be a random phenomenon with a probability function specified by the distribution function

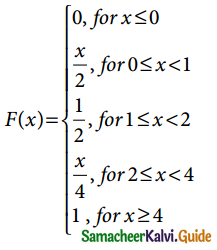
(a) Is the distribution function continuous? If so, give its probability density function?
(b) What is the probability that a person will have to wait (i) more than 3 minutes, (ii) less than 3 minutes and (iii) between 1 and 3 minutes?
Solution:
(i) Yes, the distribution function is continuous on [0, 4]
The probability density function

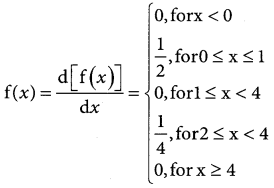
(b) The probability that a person will have to wait
(i) more than 3 minutes

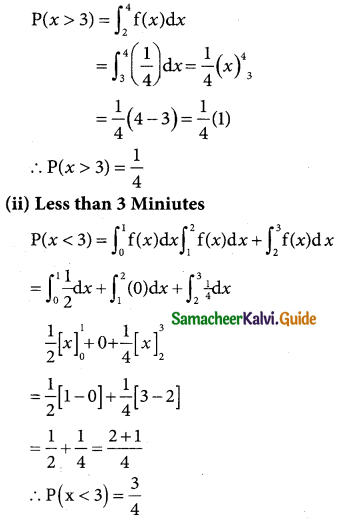
(iii) between 1 and 3 minutes

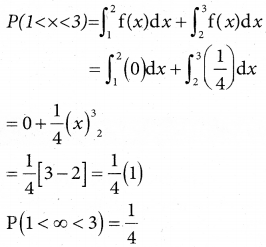
Question 11.
Define random variable.
Solution:
A random variable (r.v.) is a real valued function defined on a sample space S and taking values in (-∞, ∞) or whose possible values are numerical outcomes of a random experiment.

Question 12.
Explain What are the types of random variable.
Solution:
Random variables are classified into two types namely discrete and continuous random variables these are important for practical applications in the field of Mathematics and Statistics.

Question 13.
Define dicrete random Variable
Solution:
A variable which can assume finite number of possible values or an infinite sequence of countable real numbers is called a discrete random variable.

Question 14.
What do you understand by continuous random variable?
Solution:
A random variable X which can take on any value (integral as well as fraction) in the interval is called continuous random variable.

Question 15.
Describe what is meant by a random variable
Solution:
If S is a sample space with a probability measure and x is a real valued function defined over the elements of S then x is called a random variable A random variable is also called a change variable.

Question 16.
Distinguish between discrete and continuous random variable
Solution:

Question 17.
Explain the distribution function of random variable
Solution:
The discrete cumulative distribution function or distribution function of a real valued discrete random variable X takes the countable number of points x₁, x₂, …. with corresponding probabilities p(x₁), p(x₂),… and then the cumulative distribution function is defined by
F_x(x) = P(X ≤ x), for all x ∈ R
i.e. F_x (x) = \(\sum_{x \leq x}\) p(x_i)

Question 18.
Explain the terms (i) probability Mass function (ii) probability density function and (iii) probability
Solution:
(i) If X is a discrete random variable with distinct values x₁, x₂, …. x_n, …, then the function, denoted by P_x(x) and defined by

This is defined to be the probability mass function or discrete probability function of X.

(ii) The probability that a random variable X takes a value in the interval [t₁, t₂] (open or closed) is given by the integral of a function called the probability density function f_x(x):
P(t₁ ≤ X ≤ t₂) = \(\int_{t_{1}}^{t_{2}}\) f_x(x)dx.

(iii)The probability distribution of a random variable X is defined only when we have the various values oft the various values of the random variable e.g. x₁, x₂ …… x_n togather with respective probabilities p₁, p₂, p₃ …… p₄ satisfying
\(\sum_{i=1}^{n}\) Pi = 1

Question 19.
What are the properties of (i) discrete random variable and (ii) Continuous random variable
Solution:
(i) The probability mass function p(x) must satisfy the following conditions
(i) p(x_i) ≥ 0 ∀ i,
(ii) \(\sum_{i=1}^{∞}\) p(x_i) = 1

(ii) The probability density functions/)(x) or simply ; by/(x) must satisfy the following conditions.
(i) f(x) ≥ 0 ∀ x and
(ii) \(\int_{-∞}^{∞}\) f(x) dx = 1

Question 20.
State the Properties of distribution function.
Solution:
The function F_x(x) or simply F(x) has the following properties.
(i) 0 ≤ F(x) ≤ 1, -∞ < x < ∞
(ii) F(-∞) = \(\lim _{x \rightarrow-\infty}\) F(x) = 0 and F(+∞) = \(\lim _{x \rightarrow ∞}\) F(x) = 1.
(iii) F(.) is a monotone, non-decreasing function; ; that is, F(a) < F(b) for a < b.
(iv)F(.) is continuous from the right; that is, \(\lim _{h \rightarrow 0}\) F(x + h) = F(x).
(v) F(x) = \(\frac { d }{dx}\) F(x) = f(x) ≥ 0;
(vi) F'(x) = \(\frac { d }{dx}\) F(x) = f(x) ⇒ dF(x) = f(x)dx
dF(x) is known as probability differential of X.
(vii) P(a ≤ x ≤ b) = \(\int_{a}^{b}\) f(x)dx = \(\int_{-∞}^{b}\) f(x)dx – \(\int_{-∞}^{a}\) f(x)dx
= P(X ≤ b) – P(X ≤ a)
= F(b) – F(a)