Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 9 Applied Statistics Ex 9.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 9 Applied Statistics Ex 9.2
Question 1.
Define Index Number.
Solution:
Index Numbers are the indicators which reflect the changes over a specified period of time in price of different commodities, production, sales, cost of living etc.
“An Index Number is a device which shows by its variations the change in a magnitude which is not capable of accurate measurements in it-self or of direct valuation in practice”. – Whel-don
“An Index number is a statistical measure of fluctuations in a variable arranged in the form of a series and using a base. Period for maxing H comparisons” – Lawrence J Kalpan.
![]()
Question 2.
State the uses of Index Number.
Solution:
(1) Index number is an important tool for formulating decision and management p policies.
(2) It helps in studying the trends and tendencies.
(3) It determines the inflation and deflation in an Economy.
Question 3.
Mention the classification of Index Number.
Solution:
Index number can be classified as follows,
(i) Price Index Number:
It measures the general changes in the retail or wholesale price level of a particular or group of commodities.
(ii) Quantity Index Number:
These are indices of measure the changes in the quantity of goods manufactured in a factory.
(iii) Cost of living Index Number:
These are intended to study the effect of change in the price level on the cost of living of different classes of people.
Question 4.
Define Laspeyre’s Price index number.
Solution:
Laspeyre’s Price index number
P\(_{ 01 }^{L}\) ⥪ \(\frac { Σp_1q_0 }{Σp_0q_0}\) × 100
where P1 = Current year price
p0 = base year price
q0 = base year quantity
Question 5.
Explain Paasche’s price index number.
Solution:
Paasches price index number
P\(_{ 01 }^{L}\) = \(\frac { Σp_1q_1 }{Σp_0q_1}\) × 100
where P1 = current year price
q1 = current year quantity
p0 = base year price
q0 = base year quantity
![]()
Question 6.
Write note on Fisher’s price index number.
Solution:
Fishers price index number
PF = \(\sqrt { P^L×P^P}\)
P\(_{ 01 }^{F}\) = \(\sqrt { \frac{Σp_1p_0×Σp_1q_1}{Σp_0q_0×Σp_0q_1}}\) × 100
where P1 = current year price
q1 = current year quantity
p0 = base year price
q0 = base year quantity
Question 7.
State the test of adequacy of index number.
Solution:
There are two tests which are used to test the adequacy for an index number. The two tests are as follows
(i) Time Reversal Test
(ii) Factory Reversal Test
Question 8.
Define Time Reversal Test.
Solution:
It is an important test for testing the consistency of a good index number. This test maintains time consistency by working both forward and backward with respect to time (here time refers to base year and current year). Symbolically the following relationship should be satisfied. P01 × p10 = 1
Fisher’s index number formula satisfies the above relationship
P\(_{ 01 }^{F}\) = \(\sqrt { \frac{Σp_1p_0×Σp_1q_1}{Σp_0q_0×Σp_0q_1}}\)
when the base year and current year are interchanged, we get
P\(_{ 10 }^{F}\) = \(\sqrt { \frac{Σp_0q_1×Σp_0q_0}{Σp_1q_1×Σp_1q_0}}\)
P\(_{ 01 }^{F}\) × P\(_{ 10 }^{F}\) = 1
Question 9.
Explain factor reversal test.
Solution:
This is another test for testing the consistency of a good index number. The product of price index number and quantity index number from the base year to the current year should be equal to the true value ratio. That is, the ratio between the total value of current period and total
value of the base period is known as true value ratio. Factor Reversal Test is given by,
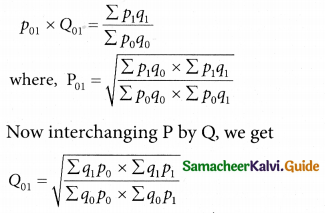
where P01 is the relative change in price
Q01 is the relative change in quantity.
Question 10.
Define true value ratio.
Solution:
\(\frac { Σp_1q_1 }{Σp_0q_0}\) is the ratio of the total value in the current period to the total value in the base period and this ratio is called the true value ratio.
![]()
Question 11.
Discuss about cost of Living Index Number.
Solution:
Cost of living index numbers are generally designed to represent the average change over time in the prices paid by the ultimate consumer for a specified quantity of goods and services cost of living index number is also known as consumer price index number.
It is well known that a given change in the level of prices (retail) affects the cost of living of different classes of people in different manners. The general index number fails to reveal this. Therefore it is essential to construct a cost of living index number which helps us in determining the effect of rise and fall in prices on different classes of consumers living in different areas.
Question 12.
Define family budget method.
Solution:
In this method, the weights are calculated by multiplying prices and quantity of the base year.
(i.e.) V = Σp0q0. The formula is given by,
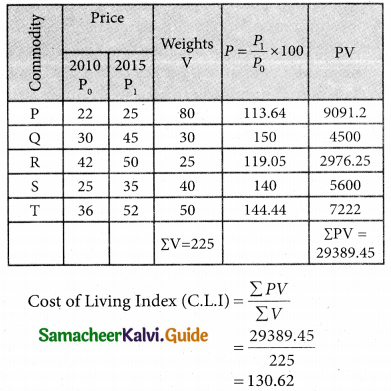
Cost of Living Index Number = \(\frac { Σpv }{Σv}\)
where P = \(\frac { p_1 }{p_0}\) × 100 is the price relative.
v = Σp0q0 is the value relative.
Question 13.
State the uses of cost of Living Index Number.
Solution:
(i) It indicates whether the real wages of workers are rising or falling for a given time.
(ii) It is used by the administrators for regulating dearness allowance or grant of bonus to the workers.
Question 14.
Calculate by a suitable method, the index number of price from the following data:
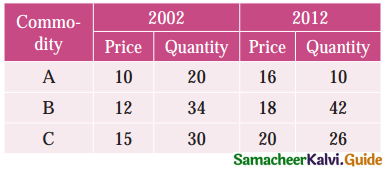
Solution:
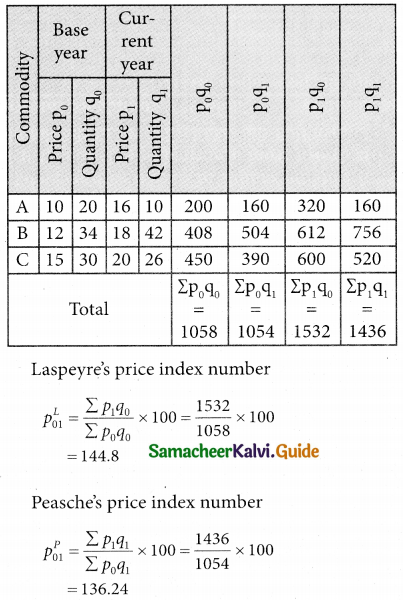
Question 15.
Calculate price index number for 2005 by (a) Laspeyre’s (b) Paasche’s method
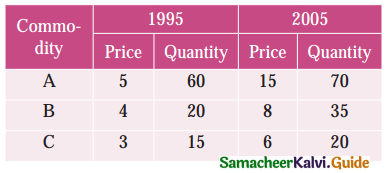
Solution:
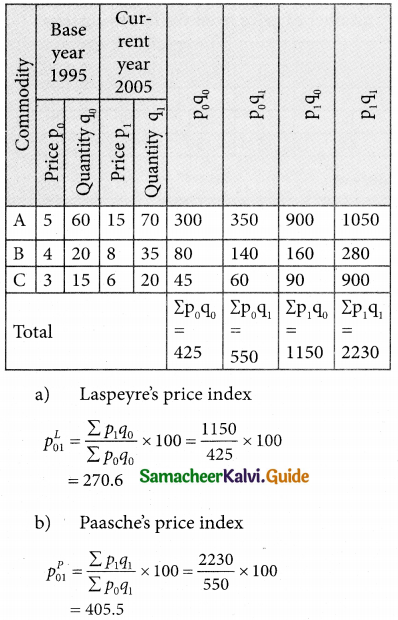
![]()
Question 16.
Calculate price index number for 2005 by (a) Laspeyre’s (b) Paasche’s method
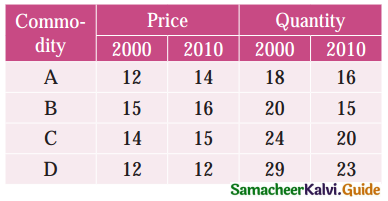
Solution:
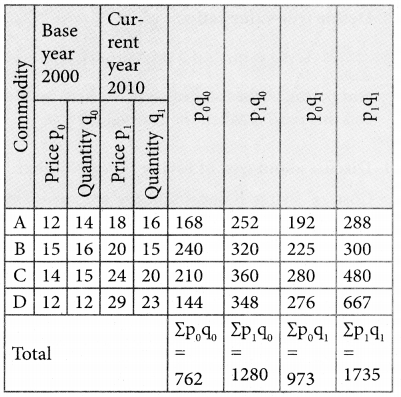

Question 17.
Using the following data, construct Fisher’s Ideal index and show how it satisfies Factor Reversal Test and Time Reversal Test?
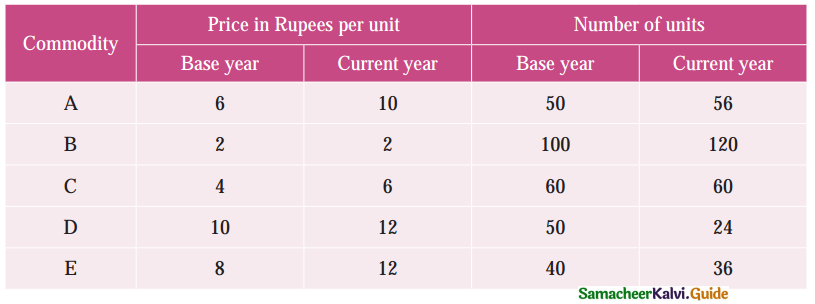
Solution:
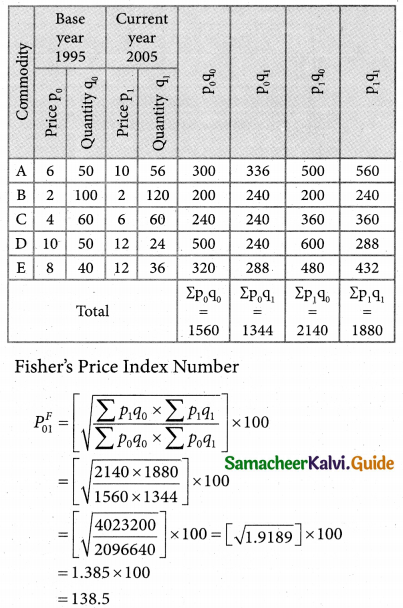

![]()
Question 18.
Using the following data, construct Fisher’s Ideal index and show how it satisfies Factor Reversal Test and Time Reversal Test?
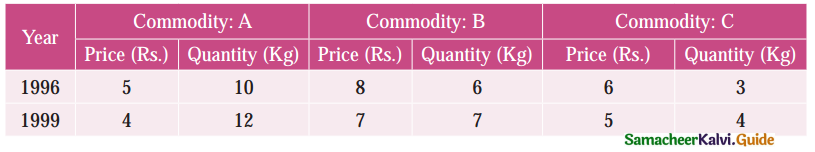
Solution:
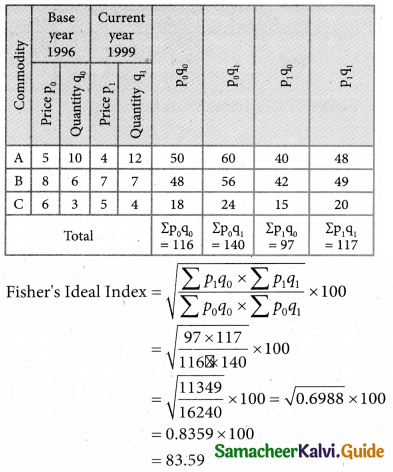
Question 19.
Calculate Fisher’s index number to the following data. Also show that it satisfies Time Reversal Test.
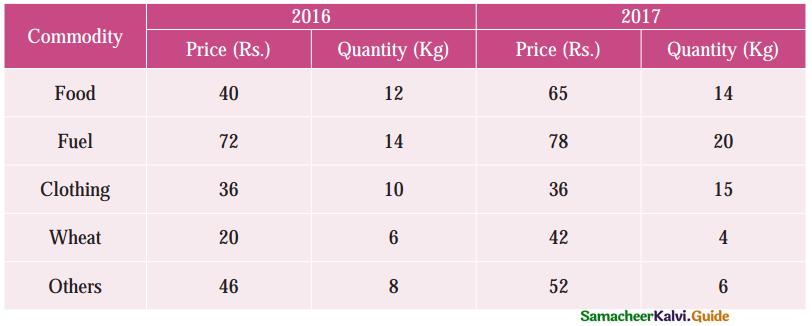
Solution:
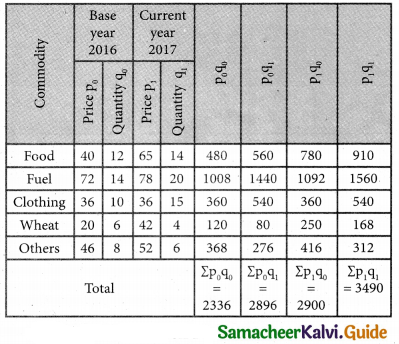

Question 20.
Th following are the group index numbers and the group weights of an average working class family’s budget. Construct the cost of living index number:

Solution:
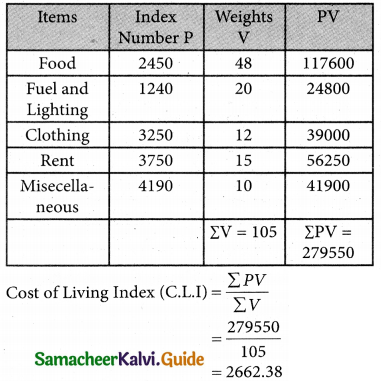
Question 21.
Construct the cost of living Index number for 2015 on the basis of 2012 from the following data using family budget method.
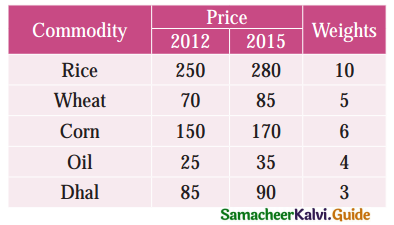
Solution:
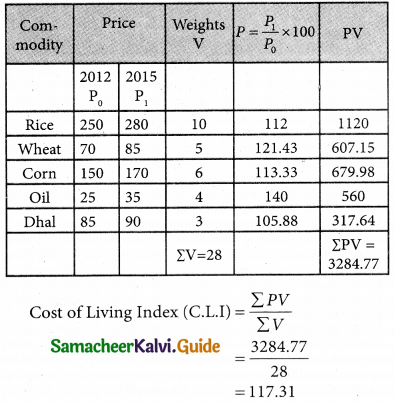
![]()
Question 22.
Calculate the cost of living index by aggregate expenditure method:
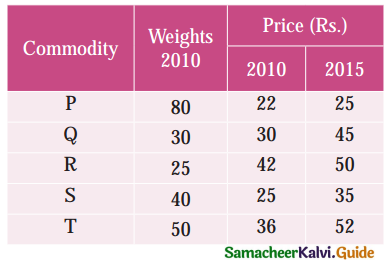
Solution: