Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 Applications of Matrices and Determinants Ex 1.6 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.6
Question 1.
Test for consistency and if possible, solve the following systems of equations by rank method.
(i) x – y + 2z = 2, 2x + y + 4z = 7, 4x – y + z = 4
Solution:
Matrix form

The system is consistent.
ρ(A) ρ[A|B] = 3 = n
it has unique solution.
Writing the equivalent equations from echelon form
x – y + 2z = 2 ………… (1)
3y = 3 ⇒ y = 1
-7z = -7
z = 1
(1)⇒ x – y + 2z = 2
x – 1 + 2 = 2
x = 1
∴ Solution is x = 1, y = 1, z = 1
![]()
(ii) 3x + y + z = 2, x – 3y + 2z = 1, 7x – y + 4z = 5
Solution:
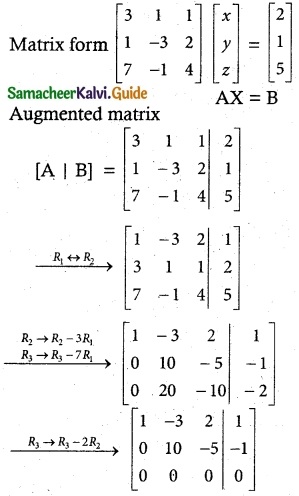
ρ(A) = 2 ρ[A | B] = 2
ρ(A) = ρ[A | B] = 2 < n
The system is consistent. It has infinitely many solution.
Writing the equivalent equations from echelon form.
x – 3y + 2z = 1 ………. (1)
10y – 5z = -1 ………. (2)
Put z = t.
(2) ⇒ 10y – 5z = -1
10y = -1 + 5z = 5t – 1

![]()
(iii) 2x + 2y + z = 5, x – y + z = 1, 3x + y + 2z = 4
Solution:
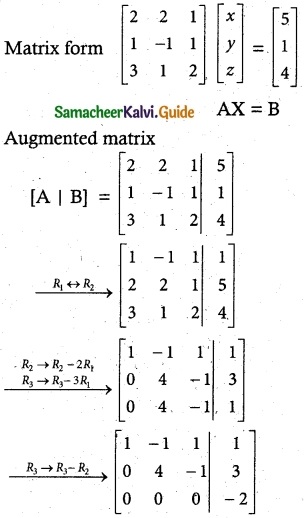
ρ(A) = 2 ρ[A | B] = 3
ρ(A) ≠ ρ[A | B] = 2 < n
∴ The system is inconsistent. It has no solution.
![]()
(iv) 2x – y + z = 2, 6x – 3y + 3z = 6, 4x – 2y + 2z = 4
Solution:
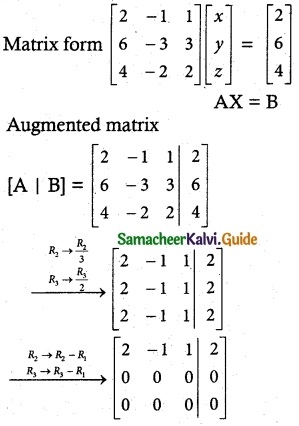
ρ(A) = 1 ρ[A | B] = 1
ρ(A) = ρ[A | B] = 1 < n.
∴ The system reduces into a single equation.
∴ It is consistent and has infinitely many solutions.
Writing the equivalent equations from echelon form
2x – y + z = 2
Put y = s, z = t
2x – s + t = 2
2x = 2 + s – t
x = \(\frac {2+s-t}{2}\)
(x, y, z) = (\(\frac {2+s-t}{2}\), s, t) ∀ s, t ∈ R
![]()
Question 2.
Find the value of k for which the equations kx – 2y + z = 1, x – 2ky + z = -2, x – 2y + kz = 1 have
(i) no solution
(ii) unique solution
(iii) infinitely many solution.
Solution:

[∵ 2 – k – k² = -(k² + k – 2)
= -(k + 2)(k – 1)
= (k + 2)(1 – k)]
case (i)
If k = 1
ρ(A) = 2, ρ(A | B) = 3.
ρ(A) ≠ ρ(A | B)
The system is inconsistent and it has no solution.
Case (ii)
If k ≠ 1, k ≠ -2
ρ(A) = 3, ρ(A | B) = 3 = n
The system is consistent and it has unique solution.
Case (iii)
If k = -2
ρ(A) = 2, ρ(A | B) = 2
The system is consistent and it has infinitely many solution.
![]()
Question 3.
Investigate the values of λ and µ the system of linear equations 2x + 3y + 5z = 9, 7x + 3y – 5z = 8, 2x + 3y + λz = µ, have
(i) no solution
(ii) a unique solution
(iii) an infinite number of solutions.
Solution:

Case (i)
If λ = 5, µ ≠ 9
ρ(A) = 2, ρ(A | B) = 3
ρ(A) ≠ ρ(A | B)
The system is inconsistent. It has no solution.
Case (ii)
If λ = 5, µ ≠ 9
ρ(A) = 3, ρ(A | B) = 3
ρ(A) = ρ(A | B) = 3 = n
The system is consistent. It has unique solution.
Case (iii)
If λ = 5, µ = 9
ρ(A) = 2, ρ(A | B) =2
ρ(A) = ρ(A | B) = 2 < n
The system is consistent. It has infinitely many solution.
![]()