Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 Ordinary Differential Equations Ex 10.1 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.1
Question 1.
For each of the following equations, determine its order, degree (if exists)
(i) \(\frac { dy }{ dx }\) + xy = cot x
(ii) (\(\frac { d^3y }{ dx^3 }\))2/3 – 3 \(\frac { d^2y }{ dx^2 }\) + 5\(\frac { dy }{ dx }\) + 4 = 0
(iii) (\(\frac { d^2y }{ dx^2 }\))2 + (\(\frac { dy }{ dx }\))² = x sin (\(\frac { d^2y }{ dx^2 }\))
(iv) \(\sqrt{\frac { dy }{ dx }}\) – 4 \(\frac { dy }{ dx }\) – 7x = 0
(v) y(\(\frac { dy }{ dx }\)) = \(\frac { x }{ (\frac { dy }{ dx })+(\frac { dy }{ dx })^3 }\)
(vi) x²\(\frac { d^2y }{ dx^2 }\) + [1 + (\(\frac { dy }{ dx }\))²]1/2 = 0
(vii) (\(\frac { d^2y }{ dx^2 }\))³ = \(\sqrt{1+(\frac { dy }{ dx })}\)
(viii) \(\frac { d^2y }{ dx^2 }\) = xy + cos (\(\frac { dy }{ dx }\))
(ix) \(\frac { d^2y }{ dx^2 }\) + 5 \(\frac { dy }{ dx }\) + ∫ ydx = x³
(x) x = exy(\(\frac { dy }{ dx }\))
Solution:
(i) \(\frac { dy }{ dx }\) + xy = cot x
In the given equation, the highest order derivative is \(\frac { dy }{ dx }\) only its power is 1
∴ Its order = 1 & degree = 1
![]()
(ii) (\(\frac { d^3y }{ dx^3 }\))2/3 – 3 \(\frac { d^2y }{ dx^2 }\) + 5\(\frac { dy }{ dx }\) + 4 = 0
Taking power 3 on both sides, we get
(\(\frac { d^3y }{ dx^3 }\))2 = (3 \(\frac { d^2y }{ dx^2 }\) – 5\(\frac { dy }{ dx }\) – 4)³
In the equation (1), the highest order derivative is \(\frac { d^3y }{ dx^3 }\) and its power is 2.
∴ Its order = 3 & degree = 2
(iii) (\(\frac { d^2y }{ dx^2 }\))2 + (\(\frac { dy }{ dx }\))² = x sin (\(\frac { d^2y }{ dx^2 }\))
In the equation, the highest order derivative is \(\frac { d^2y }{ dx^2 }\) and its order is 2.
It has a term sin (\(\frac { d^2y }{ dx^2 }\)), so its degree is not defined or degree does not exist.
![]()
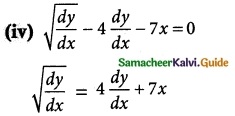
on squaring both sides,
\(\frac { dy }{ dx }\) = 16 (\(\frac { dy }{ dx }\))² + 49 x² + 56x \(\frac { dy }{ dx }\)
clearly, it is a differential equation of order = 1 & degree = 2.

In this equation, the highest order derivative is \(\frac { dy }{ dx }\) & its power is 4.
∴ Its order = 1 & degree = 4
![]()

In this equation, the highest order derivative is \(\frac { d^2y }{ dx^2 }\) & its power is 2.
∴ Its order = 2 & degree = 2

In this equation, the highest order derivative is \(\frac { d^2y }{ dx^2 }\) & its power is 6.
∴ Its order = 2 & degree = 6
![]()
(viii) \(\frac { d^2y }{ dx^2 }\) = xy + cos (\(\frac { dy }{ dx }\))
In this equation, the highest order derivative is \(\frac { d^2y }{ dx^2 }\) & its power is 2.
It has a term cos(\(\frac { dy }{ dx }\)), so its degree is not defined or degree does not exist.
(ix) \(\frac { d^2y }{ dx^2 }\) + 5 \(\frac { dy }{ dx }\) + ∫ ydx = x³
differentiating with respect to x, we get
\(\frac { d^3y }{ dx^3 }\) + 5 \(\frac { d^2y }{ dx^2 }\) + y = 3x²
In this equation the highest order derivative is \(\frac { d^3y }{ dx^3 }\) & its power is 1
∴ Its order = 3 & degree = 1
(x) x = exy(\(\frac { dy }{ dx }\))
In this equation the highest order derivative is \(\frac { dy }{ dx }\) & its order is 1
It has the term exy(\(\frac { dy }{ dx }\))
So its degree is not defined or degree does not exist.
![]()