Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 Complex Numbers Ex 2.7 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.7
Question 1.
Write in polar form of the following complex numbers.
(i) 2 + i2 √3
Solution:
Let z + i2√3 = r (cos θ + i sin θ)
equating real and imaginary parts
r cos θ = 2 (+ve)
r sin θ = 2√3 (+ve)
r² cos² θ + r² sin² θ = (2)² + (2√3)²
r² = 4 + 12 = 16
|z| = r = 4
since cos cos θ and sin θ are positive ‘θ’ lies in 1st quadrant.
cos θ = \(\frac{1}{2}\), sin θ = \(\frac{√3}{2}\)
∴ θ = sin θ = \(\frac{π}{3}\) (or) θ = tan-1 |\(\frac{y}{x}\)|
= tan-1 |\(\frac{2√3}{2}\)|
= tan-1 √3 = \(\frac{π}{3}\)
∴ argument = 2kπ + \(\frac{π}{3}\)
∴ Polar form is z = r (cos θ + i sin θ)
2 + 2i√3 = 4 (cos (2kπ + \(\frac{π}{3}\)) + i sin(2kπ +\(\frac{π}{3}\))) k ∈ z
![]()
(ii) 3 – i √3
Solution:
Let z = 3 – i √3 = r (cos θ + i sin θ)
equating real and imaginary parts
r cos θ = 3 (+ve)
r sin θ = -√3 (-ve)
r² cos² θ + r² sin² θ = (3)² + (-√3)²
r² = 9 + 3 = 12
|z| = r = 2√3
since cos cos θ positive and sin θ in -ve so lies in IV quadrant.
cos θ = \(\frac{√3}{2}\), sin θ = \(\frac{-1}{2}\), θ = \(\frac{-π}{6}\)
argument = 2kπ – \(\frac{π}{6}\), k ∈ Z
polar from z = r(cos θ + i sin θ)
3 – i√3 = 2√3 (cos (2kπ – \(\frac{π}{6}\)) + i sin(2kπ – \(\frac{π}{6}\))) k ∈ Z
(iii) -2 – i 2 = r (cos θ + i sin θ)
Solution:
Let z = -2 – i2 = r(cos θ + i sin θ)
equating real and imaginary parts
r cos θ = -2
r sin θ = -2
r² cos² θ + r² sin² θ = (-2)² + (-2)²
r² = 4 + 4 = 8
r² = 8
|z| = r = 2√2
cos θ = \(\frac{-2}{2√2}\) = \(\frac{-1}{√2}\), sin θ = \(\frac{-2}{2√2}\) = \(\frac{-1}{√2}\)
since cos θ and sin θ both are in -ve so lies in III quadrant.
argument = 2kπ – 3\(\frac{π}{4}\)
as θ = \(\frac{π}{4}\) – π = –\(\frac{3π}{4}\)
polar from z = r(cos θ + i sin θ)
-2 – i2 = 2√2 (cos (2kπ – \(\frac{3π}{4}\)) + i sin(2kπ – \(\frac{3}{4}\))) k ∈ Z
(iv) \(\frac{i-1}{cos{\frac{π}{3}}+isin{\frac{π}{3}}}\)
Solution:
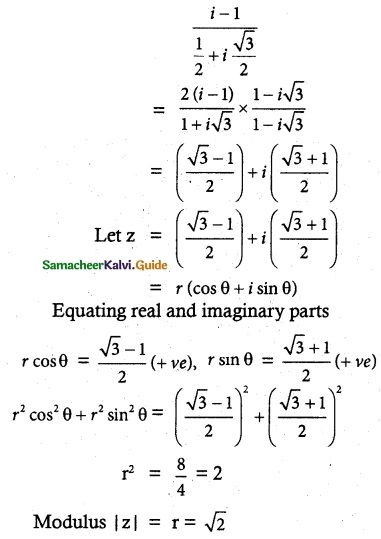
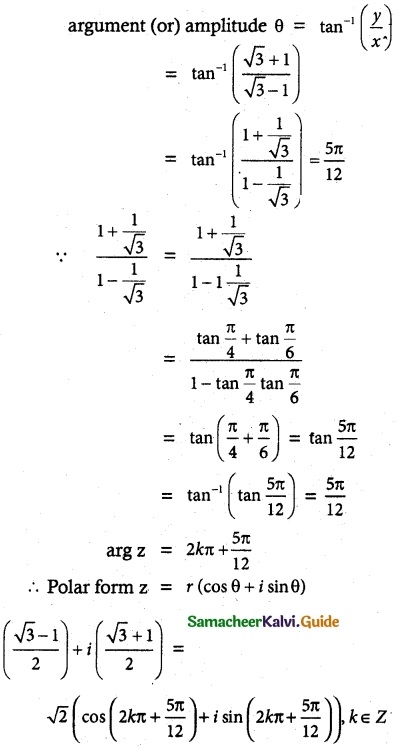
![]()
Question 2.
Find the rectangular form of the complex numbers
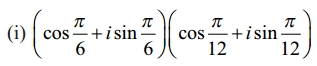
Solution:

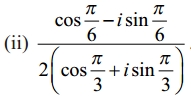
Solution:

![]()
Question 3.
\(\left(x_{1}+i y_{1}\right)\left(x_{2}+i y_{2}\right)\left(x_{3}+i y_{3}\right) \cdots\left(x_{n}+i y_{n}\right)=a+i b\), show that
![]()
Solution:
Let (x1 + iy1) (x2 + iy2) (x3 + iy3) …… (xn + iyn) = a + ib
Taking modulus
|(x1 + iy1) (x2 + iy2) (x3 + iy3) …… (xn + iyn)| = |a + ib|
|x1 + iy1| |x2 + iy2| |x3 + iy3| …… |xn + iyn| = |a + ib|
\(\sqrt{x_{1}^{2}+y_{1}^{2}} \sqrt{x_{2}^{2}+y_{2}^{2}} \sqrt{x_{3}^{2}+y_{3}^{2}} \ldots \sqrt{x_{n}^{2}+y_{n}^{2}}\) = \(\sqrt{a^2+b^2}\)
Squaring on both sides
\(\left(x_{1}^{2}+y_{1}^{2}\right)\left(x_{2}^{2}+y_{2}^{2}\right)\left(x_{3}^{2}+y_{3}^{2}\right) \ldots\left(x_{n}^{2}+y_{n}^{2}\right)\) = a² + b²
Hence proved
![]()
(ii) \(\sum_{r=1}^{n}\) tan-1 (\(\frac{y_r}{x_r}\)) = tan-1 (\(\frac{b}{a}\)) + 2kπ, k ∈ Z
Solution:
Let (x1 + iy1) (x2 + iy2) (x3 + iy3) …… (xn + iyn) = a + ib
Taking arguments
arg [(x1 + iy1) (x2 + iy2) (x3 + iy3) …… (xn + iyn)] = arg (a + ib)
arg (x1 + iy1) + arg(x2 + iy2) + arg (x3 + iy3) …… + arg(xn + iyn) = arg(a + ib)
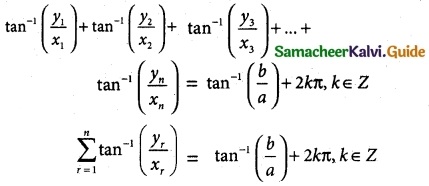
Question 4.
Given \(\frac{1+z}{1-z}\) = cos 2θ + i sin 2θ, show that To prove that z = i tan θ.
Solution:

Squaring on both sides
(1 + x)² + y² = (1 – x)² + y²
1 + 2x + x² + y² = 1 – 2x + x² +y²
x = 0
∴ z = 0 + iy = iy

∴ y = tan θ
hence z = iy
z = i tan θ
![]()
Question 5.
If cos α + cos β + cos γ = sin α + sin β + sin γ = 0. then show that
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ) and
(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ).
Solution:
Let a = cos α + i sin α = eiα
b = cos β + i sin β = eiβ
c = cos γ + i sin γ = eiγ
a + b + c = (cos α + cos β + cos γ) + i (sin α + sin β + sin γ)
⇒ a + b + c = 0 + i 0
⇒ a + b + c = 0
If a + b + c = 0 then a3 + b3 + c3 = 3abc
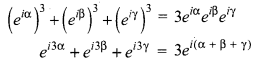
(cos 3α + i sin 3α + cos 3β + i sin 3β + cos 3γ + i sin 3γ) = 3 [cos (α + β + γ) + i sin (α + β + γ)]
(cos 3α + cos 3β + cos 3γ) + i (sin 3α + sin 3β + sin 3γ) = 3 cos (α + β + γ) + i 3sin(α + β + γ)
Equating real and Imaginary parts
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ)
(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ)
![]()
Question 6.
If z = x + iy and arg \(\left(\frac{z-i}{z+2}\right)\) = \(\)\frac{π}{4}, then show that x² + y³ + 3x – 3y + 2 = 0.
Solution:

2y – x – 2 = x² + 2x + y² – y
x² + y² + 2x + x – y – 2y + 2 = 0
⇒ x² + y² + 3x – 3y + 2 = 0
Hence proved
![]()