Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.4 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.4
Question 1.
Find the equations of the two tangents that can be drawn from (5, 2) to the ellipse 2x² + 7y² = 14.
Solution:
2x2 + 7y2 = 14
(÷ by 14) ⇒ \(\frac{x^{2}}{7}+\frac{y^{2}}{2}\) = 1
comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
we get a2 = 7 and b2 = 2
The equation of tangent to the above ellipse will be of the form
y = mx + \(\sqrt{a^{2} m^{2}+b^{2}}\) ⇒ y = mx + \(\sqrt{7 m^{2}+2}\)
Here the tangents are drawn from the point (5, 2)
⇒ 2 = 5m + \(\sqrt{7 m^{2}+2}\) ⇒ 2 – 5m = \(\sqrt{7 m^{2}+2}\)
Squaring on both sides we get
(2 – 5m)2 = 7m2 + 2
25m2 + 4 – 20m – 7m2 – 2 = 0
18m2 – 20m + 2 = 0
(÷ by 2) ⇒ 9m2 – 10m + 1 = 0
(9m – 1) (m – 1) = 0
‘ m = 1 (or) m = 1/9
When m = 1, the equation of tangent is
y = x + 3 or x – y + 3 = 0
When m = \(\frac{1}{9}\) the equation of tangent is 9
y = \(=\frac{x}{9}+\sqrt{\frac{7}{81}+2}\) (i.e.) y = \(\frac{x}{9}+\frac{13}{9}\)
9y = x + 13 or x – 9y + 13 = 0
![]()
Question 2.
Find the equations of tangents to the hyperbola \(\frac {x^2}{16}\) – \(\frac {y^2}{64}\) = 1 which are parallel to 10x – 3y + 9 = 0.
Solution:
Equation of Hyperbola \(\frac {x^2}{16}\) – \(\frac {y^2}{64}\) = 1
∴ a² = 16, b² = 64
Tangent is parallel to the line
10x – 3y + 9 = 0 is
10x – 3y + k = 0
∴ 3y = 10x + k
y = \(\frac {10}{3}\)x + \(\frac {k}{3}\)
∴ m = \(\frac {10}{3}\) c = \(\frac {k}{3}\)
Condition that the line y = mx + c to be tangent to the hyperbola is
c² = a²m² – b²
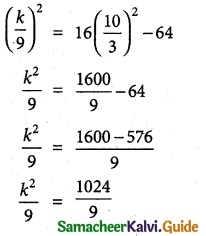
k² = 1024
k = ±32
∴ Equation of tangent
⇒ 10x – 3y ± 32 = 0
![]()
Question 3.
Show that the line x – y + 4 = 0 is a tangent to the ellipse x² + 3y² = 12. Also find the co-ordinates of the point of contact.
Solution:
The given ellipse is x2 + 3y2 = 12
(÷ by 12) ⇒ \(\frac{x^{2}}{12}+\frac{y^{2}}{4}\) = 1
(ie.,) Here a2 = 12 and b2 = 4
The given line is x – y + 4 = 0
(ie.,) y = x + 4
Comparing this line with y = mx + c
We get m = 1 and c = 4
The condition for the line y = mx + c
To be a tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 is c2 = a2m2 + b2
LHS = c2 = 42 = 16
RHS: a2m2 + b2 = 12( 1 )2 + 4 = 16
LHS = RHS The given line is a tangent to the ellipse. Also the point of contact is
\(\left(\frac{-a^{2} m}{c}, \frac{b^{2}}{c}\right)=\left[-\left(\frac{12(1)}{4}\right), \frac{4}{4}\right]\) (i.e.,) (-3, 1)
![]()
Question 4.
Find the equation of the tangent to the parabola y² = 16x perpendicular to 2x + 2y + 3 = 0.
Solution:
Equation of the parabola
y² = 16x
4 a = 16
a = 4
Tangent is perpendicular to the line
2x + 2y + 3 = 0 is 2x – 2y + k = 0
2x – 2y + k = 0
2y = 2x + k
y = x + \(\frac {k}{2}\)
m = 1 c = \(\frac {k}{2}\)
Condition that the line y = mx + c to be tangent to the parabola is
c = \(\frac {a}{m}\)
\(\frac {k}{2}\) = \(\frac {4}{1}\)
k = 8
Equation of the tangent
2x – 2y + 8 = 0
÷ by 2 ⇒ x – y + 4 = 0
![]()
Question 5.
Find the equation of the tangent at t = 2 to the parabola y² = 8x (Hint: use parametric form).
Solution:
y2 = 8x
Comparing this equation with y2 = 4ax
we get 4a = 8 ⇒ a = 2
Now, the parametric form for y2 = 4ax is x = at2, y = 2at
Here a = 2 and t = 2
⇒ x = 2(2)2 = 8 and y = 2(2) (2) = 8
So the point is (8, 8)
Now eqution of tangent to y2 = 4 ax at (x1, y1) is yy1 = 2a(x + x1)
Here (x1, y1) = (8, 8) and a = 2
So equation of tangent is y(8) = 2(2) (x + 8)
(ie.,) 8y = 4 (x + 8)
(÷ by 4) ⇒ 2y = x + 8 ⇒ x – 2y + 8 = 0
Aliter
The equation of tangent to the parabola y2 = 4ax at ‘t’ is
yt = x + at2
Here t = 2 and a = 2
So equation of tangent is
(i.e.,) y(2) = x + 2(2)2
2y = x + 8 ⇒ x – 2y + 8 = 0
Question 6.
Find the equations of the tangent and normal to hyperbola 12x² – 9y² = 108 at θ = \(\frac {π}{3}\) .
(Hint: use parametric form)
Solution:
(i) Equation of the tangent to hyperbola be

⇒ 4x – 3y = 6
⇒ 4x – 3y – 6 = 0
![]()
(ii) Equation of the normal to hyperbola be
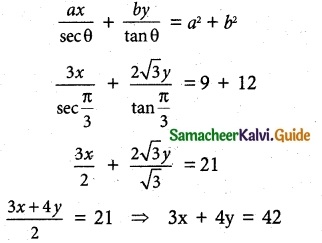
⇒ 3x + 4y – 42 = 0
Question 7.
Prove that the point of intersection of the tangents at ‘t1‘ and ‘t2‘ on the parabola y² = 4ax is [at1t2, a(t1 + t2)].
Solution:
Equation of the tangent of parabola y² = 4ax be
at t1 yt1 = x + at1² ……….. (1)
at t2 yt2 yt = x + at2² ……….. (2)
(1) – (2) ⇒ y(t1 – t2) = a(t1² – t2²)
y(t1 – t2) = a(t1 + t2)(t1 – t2)
y = a(t1 + t2)
(1) ⇒ t1a(t1 + t2) = x + at1²
x = at1² + at1t2 – at1²
x = at1t2
Point of intersection be [at1t2, a(t1 + t2)]
![]()
Question 8.
If the normal at the point ‘t1‘ on the parabola y² = 4ax meets the parabola again at the point t2 then prove that t2 = -(t1 + \(\frac {2}{t_1}\))
Solution:
Equation of normal to y2 = 4at’ t’ is y + xt = 2at + at3.
So equation of normal at ‘t1’ is y + xt1 = 2at1 + at13
The normal meets the parabola y2 = 4ax at ‘t2’ (ie.,) at (at22, 2at2)
⇒ 2at2 + at1t22 = 2at1 + at13
So 2a(t2 – t1) = at13 – at1t22
⇒ 2a(t2 – t1) = at1(t12 – t22)
⇒ 2(t2 – t1) = t1(t1 + t2)(t1 – t2)
⇒ 2= -t1(t1 + t2)
⇒ t1 + t2 = \(\frac{-2}{t_{1}}\)
⇒ t2 = \(-t_{1}-\frac{2}{t_{1}}=-\left(t_{1}+\frac{2}{t_{1}}\right)\)
![]()