Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.7 Textbook Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.7
Question 1.
Find the non-parametric form of vector equation and Cartesian equation of the plane passing through the point (2, 3, 6) and parallel to the .straight lines.
\(\frac { x-1 }{ 2 }\) = \(\frac { y+1 }{ 3 }\) = \(\frac { z-3 }{ 1 }\) and \(\frac { x+3 }{ 2 }\) = \(\frac { y-3 }{ -5 }\) = \(\frac { z+1 }{ -3 }\)
Solution:

![]()
Question 2.
Find the non-parametric form of vector equation and Cartesian equations of the plane passing through the points (2, 2, 1), (9, 3, 6) and perpendicular to the plane 2x + 6y + 6z = 9.
Solution:

Cartesian equation
3x + 4y – 5z = 9
3x + 4y – 5z – 9 = 0
Question 3.
Find parametric form of vector equation and Cartesian equations of the plane passing through the points (2, 2, 1), (1, -2, 3) and parallel to the straight line passing through the points (2, 1, -3) and (-1, 5, -8)
Solution:

Cartesian equation
-12x + 11y + 16z = 14
12x – 11y – 16z = -14
12x – 11y – 16z + 14 = 0
![]()
Question 4.
Find the non-parametric form of vector equation and Cartesian equation of the plane passing through the point (1, -2, 4) and perpendicular to the plane x + 2y – 3z = 11 and parallel to the line \(\frac { x+7 }{ 3 }\) = \(\frac { y+3 }{ -1 }\) = \(\frac { z }{ 1 }\)
Solution:
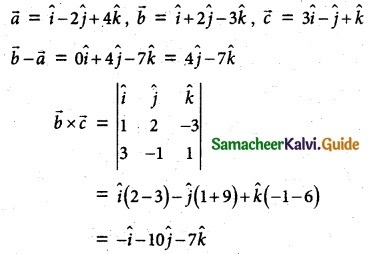
Non parametric form
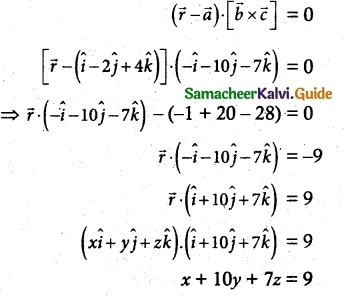
Which is the required Cartesian equation of the place.
Question 5.
Find the parametric form of vector equation and Cartesian equations of the plane containing
the line \(\overline { r }\) = (\(\hat { i }\) – \(\hat { j }\) + 3\(\hat { k }\)) + t(2\(\hat { i }\) – \(\hat { j }\) + 4\(\hat { k }\) ) and perpendicular to plane \(\overline { r }\) (\(\hat { i }\) + 2\(\hat { j }\) + \(\hat { k }\)) = 8
Solution:

Cartesian equation
9x – 2y – 5z = -4
9x – 2y – 5z + 4 = 0
![]()
Question 6.
Find the parametric vector non-parametric vector and Cartesian form of the equations of the plane passing through the three non- collinear points (3, 6, -2), (-1, -2, 6) and (6, 4, -2).
Solution:
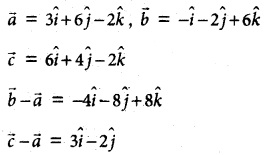

Cartesian equation
⇒ \(\overline { r }\)(2\(\hat { i }\) + 3\(\hat { j }\) + 4\(\hat { k }\)) = 16
⇒ 2x + 3y + 4z – 16 = 0
Question 7.
Find the non-parametric form of vector equation and Cartesian equations of the plane
\(\overline { r }\) = (6\(\hat { i }\) – \(\hat { j }\) + \(\hat { k }\)) + s(\(\hat { -i }\) + 2\(\hat { j }\) + \(\hat { k }\)) + t(\(\hat { -5i }\) – 4\(\hat { j }\) – 5\(\hat { k }\))
Solution:

Cartesian equation:
3x + Sy – 7z = 6
3x + 5y – 7z – 6 = 0
![]()