Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 Geometry Ex 5.2 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 5 Geometry Ex 5.2
Question 1.
Fill in the blanks:
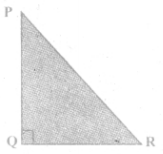
(i) If in a ∆ PQR, PR2 = PQ2 + QR2, then the right angle of ∆ PQR is at the vertex _______ .
Answer:
Q
Hint:
![]()
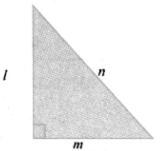
(ii) If ‘l‘ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l2 = _______ .
Answer:
n2 – m2
Hint:
(iii) If the sides of a triangle are in the ratio 5:12:13 then, it is _______ .
Answer:
a right angled triangle
Hint:
132 = 169
52 = 25
122 = 144
169 = 25 + 144
∴ 132 = 52 + 122
(iv) The medians of a triangle cross each other at _______ .
Answer:
Centroid
(v) The centroid of a triangle divides each medians in the ratio _______ .
Answer:
2 : 1
![]()
Question 2.
Say True or False.
(i) 8, 15, 17 is a Pythagorean triplet.
Answer:
True
Hint:
172 = 289
152 = 225
82 = 64
64 + 225 = 289 ⇒ 172 = 152 + 82
(ii) In a right angled triangle, the hypotenuse is the greatest side.
Answer:
True
Hint:

(iii) In any triangle the centroid and the incentre are located inside the triangle.
Answer:
True
![]()
(iv) The centroid, orthocentre, and incentre of a triangle are collinear.
Answer:
True
(v) The incentre is equidistant from all the vertices of a triangle.
Answer:
False
Question 3.
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem.
(i) 8, 15, 17
Answer:
Take a = 8 b = 15 and c = 17
Now a2 + b2 = 82 + 152 = 64 + 225 = 289
172 = 289 = c2
∴ a2 + b2 = c2
By the converse of Pythagoras theorem, the triangle with given measures is a right angled triangle.
∴ Ans: yes
![]()
(ii) 12, 13, 15
Answer:
(ii) 12, 13. 15
Take a = 12,b = 13 and c = 15
Now a2 + b2 = 122 + 132 = 144 + 169 = 313
152 = 225 ≠ 313
By the converse of Pythagoras theorem, the triangle with given measures is not a right angled triangle.
∴ Ans: No.
(iii) 30, 40, 50
Answer:
Take a = 30, b = 40 and c = 50
Now a2 + b2 = 302 + 402 = 900 + 1600 = 2500
C2 = 502 = 2500
∴ a2 + b2 = c2
By the converse of Pythagoras theorem, the triangle with given measures is a right
angled triangle.
∴ Ans: yes
(iv) 9, 40, 41
Answer:
Take a = 9, b = 40 and c = 41
Now a2 + b2 = 92 + 402 = 81 + 1600 = 1681
c2 = 412 = 1681
∴ a2 + b2 = c2
By the converse of Pythagoras theorem, the triangle with given measures is a right
angled triangle.
∴ Ans: yes
![]()
(v) 24, 45, 51
Answer:
Take a = 24,b = 45 and c = 51
Now a2 + b2 = 242 + 452 = 576 + 2025 = 2601
c2 = 512 = 2601
∴ a2 + b2 = c2
By the converse of Pyhtagoreas theorem, the triangle with given measure is a right angled triangle.
∴ Ans: yes
Question 4.
Find the unknown side in the following triangles.
(i)
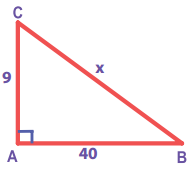
Answer:
From ∆ ABC, by Pythagoras theorem
BC2 = AB2 + AC2
Take AB2 + AC2 = 92 + 402 = 81 + 1600 = 1681
BC2 = AB2 + AC2 = 1681 = 412
BC2 = 412 ⇒ BC = 41
∴ x = 41
![]()
(ii)
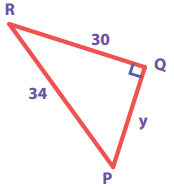
Answer:
From ∆ PQR, by Pythagoras theorem.
PR2 = PQ2 + QR2
342 = y2 + 302
⇒ y2 = 342 – 302
= 1156 – 900
= 256 = 162
y2 = 162 ⇒ y = 16
(iii)
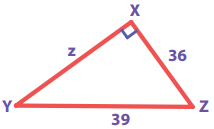
Answer:
From ∆ XYZ, by Pythagoras theorem,
= YZ2 = XY2 + XZ2
⇒ XY2 = YZ2 – XZ2
Z2 = 392 – 362
= 1521 – 1296
= 225 = 152
z2 = 152
⇒ z = 15
![]()
Question 5.
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height.
Answer:
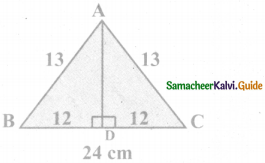
In an isosceles triangle the altitude dives its base into two equal parts.
Now in the figure, ∆ABC is an isosceles triangle with AD as its height
In the figure, AD is the altitude and ∆ABD is a right triangle.
By Pythagoras theorem,
AB2 = AD2 + BD2
⇒ AD2 = AB2 – BD2
= 132 – 122 = 169 – 144 = 25
AD2 = 25 = 52
Height: AD = 5cm
Question 6.
Find the distance between the helicopter and the ship.
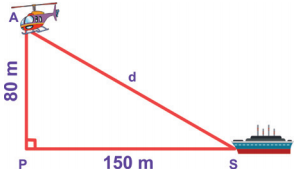
Answer:
From the figure AS is the distance between the helicopter and the ship.
∆ APS is a right angled triangle, by Pythagoras theorem,
AS2 = AP2 + PS2
= 802 + 1502 = 6400 + 22500 = 28900 = 1702
∴ The distance between the helicopter and the ship is 170 m
![]()
Question 7.
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12cm, SM = 8cm, find CS.
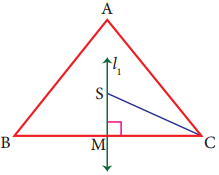
Answer:
Given l1, is the perpendicular bisector of BC.
∴ ∠SMC = 90°and BM = MC
BC = 12cm
⇒ BM + MC = 12cm
MC + MC = 12cm
2MC = 12
MC = \(\frac{12}{2}\)
MC = 6cm
Given SM = 8 cm
By Pythagoras theorem SC2 = SM2 + MC2
SC2 = 82 + 62
SC2 = 64 + 36
CS2 = 100
CS2 = 102
CS = 10 cm
Question 8.
Identify the centroid of ∆PQR.
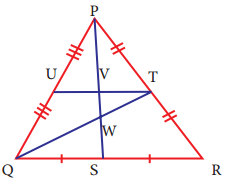
Answer:
In ∆PQR, PT = TR ⇒ QT is a median from vertex Q.
QS = SR ⇒ PS is a median from vertex P.
QT and PS meet at W and therefore W is the centroid of ∆PQR.
![]()
Question 9.
Name the orthocentre of ∆PQR.
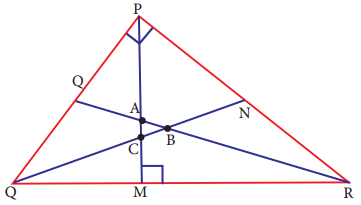
Answer:
This is a right triangle
∴ orthocentre = P [∵ In right triangle orthocentre is the vertex containing 90°]
Question 10.
In the given figure, A is the midpoint of YZ and G is the centroid of the triangle XYZ. If the length of GA is 3 cm, find XA.
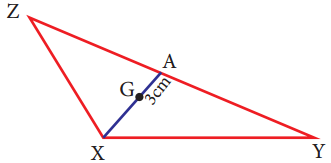
Answer:
Given A is the midpoint of YZ.
∴ ZA = AY
G is the centroid of XYZ centroid divides each median in a ratio 2 : 1 ⇒ XG : GA = 2:1
\(\frac{\mathrm{XG}}{\mathrm{GA}}=\frac{2}{1}\)
\(\frac{\mathrm{XG}}{3}=\frac{2}{1}\)
XG = 2 × 3
XG = 6 cm
XA = XG + GA = 6 + 3 ⇒ XA = 9cm
![]()
Question 11.
If I is the incentre of ∆XYZ, ∠IYZ = 30° and ∠IZY = 40°, find ∠YXZ.
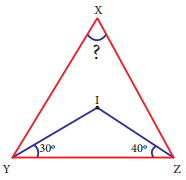
Answer:
Since I is the incentre of AXYZ
∠IYZ = 30° ⇒ ∠IYX = 30°
∠IZY = 40° ⇒ ∠IZX = 40°
∴ ∠XYZ = ∠XYI + ∠IYZ = 30° + 30°
∠XYZ = 60°
![]()
∠XYZ = 80°
By angle sum property of a triangle
∠XZY + ∠XYZ + ∠YXZ = 180°
80° + 60° + ∠YXZ = 180°
140° + ∠YXZ = 180°
∠YXZ = 180° – 140°
∠YXZ = 40°
![]()
Objective Type Questions
Question 12.
If ∆GUT is isosceles and right angled, then ∠TUG is ______ .
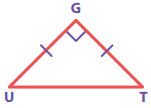
(A) 30°
(B) 40°
(C) 45°
(D) 55°
Answer:
(C) 45°
Hint:
∠U ∠T = 45° (∵ GUT is an isosceles given)
∴ ∠TUG = 45°
Question 13.
The hypotenuse of a right angled triangle of sides 12cm and 16cm is ______ .
(A) 28 cm
(B) 20 cm
(C) 24 cm
(D) 21 cm
Answer:
(B) 20 cm
Hint:
Side take a = 12 cm
b = 16cm
The hypotenuse c2 = a2 + b2
= 122 + 162
= 144 + 256
c2 = 400 ⇒ c = 20 cm
![]()
Question 14.
The area of a rectangle of length 21cm and diagonal 29 cm is ______ .
(A) 609 cm2
(B) 580 cm2
(C) 420 cm2
(D) 210 cm2
Answer:
(C) 420 cm2
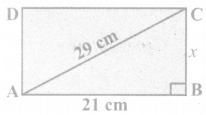
length = 21 cm
diagonal = 29 cm
By the converse of Pythagoras theorem,
AB2 + BC2 = AC2
212 + x2 = 292
x2 = 841 – 441 400 = 202
x = 20 cm
Now area of the rectangle = length × breadth.
ie AB × BC = 21 cm × 20 cm = 420 cm2
![]()
Question 15.
The sides of a right angled triangle are in the ratio 5:12:13 and its perimeter is 120 units then, the sides are .
(A) 25, 36, 59
(B) 10, 24, 26
(C) 36, 39, 45
(D) 20, 48, 52
Answer:
(D) 20,48,52
Hint:
The sides of a right angled triangle are in the ratio 5 : 12 : 13
Take the three sides as 5a, 12a, 13a
Its perimeter is 5a + 12a + 13a = 30a
It is given that 30a = 120 units
a = 4 units
∴ the sides 5a = 5 × 4 = 20 units
12a = 12 × 4 = 48 units
13a = 13 × 4 = 52 units