Samacheer Kalvi 9th Maths Guide Chapter 5 Coordinate Geometry Ex 5.5

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.5 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.5

Question 1.
Find the centroid of the triangle whose vertices are
(i) (2, -4), (-3, -7) and (7, 2)
Solution:
Let the vertices of a triangle be A (2, -4), B (-3, -7) and C (7, 2) Centroid

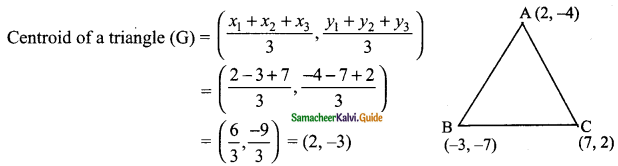
Centroid is (2, -3)

(ii) (-5, -5), (1, -4) and (-4, -2)
Solution:
Let the vertices of a triangle be A (-5, -5), B (1, -4) and C (-4, -2)

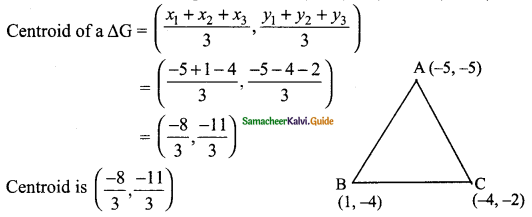
Question 2.
If the centroid of a triangle is at (4, -2) and two of its vertices are (3, -2) and (5, 2) then find the third vertex of the triangle.
Solution:
Let the vertices of a triangle be A (3, -2), B (5, 2) and C (x₃, y₃)
Centroid of a triangle is (4, -2)

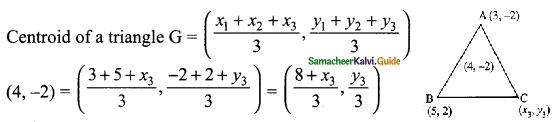
∴ \(\frac{8+x_{3}}{3}\) = 4
8 + x₃ = 12
x₃ = 12 – 8
= 4
and
\(\frac{y_{3}}{3}\) = -2
y₃ = -6
∴ The third vertex is (4, -6)

Question 3.
Find the length of median through A of a triangle whose vertices are A(-1, 3), B (1, -1) and C (5, 1).
Solution:
AD is the median of the ΔABC
D is the mid-point of BC

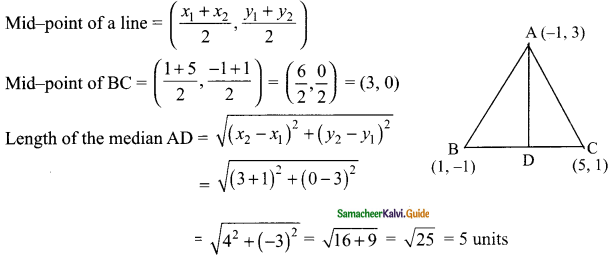
Length of the median AD is 5 units.

Question 4.
The vertices of a triangle are (1, 2), (h, -3) and (-4, k). If the centroid of the triangle is at the point (5, -1) then find the value of \(\sqrt{(h+k)^{2}+(h+3k)^{2}}\)
Solution:
Let the vertices A (1, 2), B (h, -3) and C (-4, k)


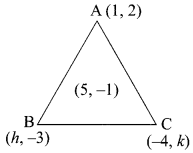
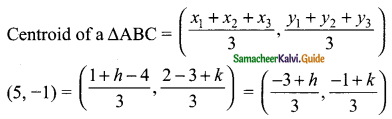
\(\frac{-3+h}{3}\) = 5
-3 + h = 15
h = 15 + 3 = 18
and
\(\frac{-1+k}{3}\) = -1
-1 + k = -3
k = -3 + 1
k = -2

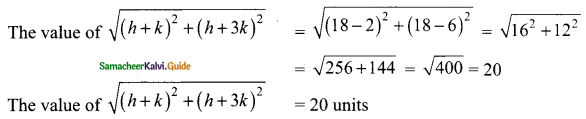
Question 5.
Orthocentre and centroid of a triangle are A(-3, 5) and B(3, 3) respectively. If C is the circumcentre and AC is the diameter of this circle, then find the radius of the circle.
Solution:
Let PQR be any triangle orthocentre, centroid and circumcentre.

A orthocentre is (-3, 5)
B centroid is (3, 3)
C orthocentre is (a, 6)
Also \(\frac{AB}{BC}\) = \(\frac{2}{1}\)
B divides AC in the ratio 2 : 1
A line divides internally in the ratio point P is (\(\frac{mx_{2}+nx_{1}}{m+n}\), \(\frac{my_{2}+ny_{1}}{m+n}\))
m = 2
x₁ = 3
y₁ = 5
amd
n = 1
x₂ = a
y₂ = b
∴ The point B (\(\frac{2a-3}{2+1}\), \(\frac{2b+5}{2+1}\))
(3, 3) = (\(\frac{2a-3}{3}\), \(\frac{2b+5}{3}\))
\(\frac{2a-3}{3}\) = 3
2a – 3 = 9
2a = 9 + 3
2a = 12
a = \(\frac{12}{2}\) = 6
and
\(\frac{2b+5}{3}\)
2b + 5 = 9
2b = 9 – 5
2b = 4
b = \(\frac{4}{2}\) = 2
∴ Orthocentre C is (6, 2)

Question 6.
ABC is a triangle whose vertices are A (3, 4), B (-2, -1) and C (5, 3). If G is the centroid and BDCG is a parallelogram then find the coordinates of the vertex D.
Solution:
The vertices of a triangle are A (3, 4), B (-2, -1) and C (5, 3)

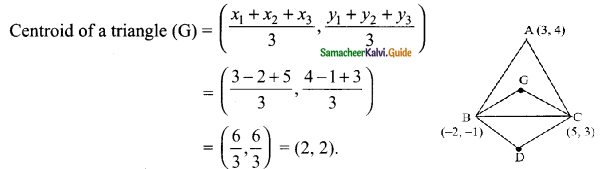
The point G is (2, 2)
Let the vertices D be (a, b)
Since BDCG is a parallelogram
Mid-point of BC = Mid-point of DG

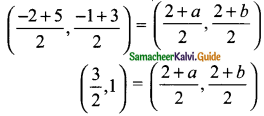
\(\frac{2+a}{2}\) = \(\frac{3}{2}\)
4 + 2a = 6
2a = 6 – 4
2a = 2
a = 1
and
\(\frac{2+b}{2}\) = 1
2 + b = 2
b = 2 – 2 = 0
The vertices D is (1, 0).

Question 7.

Solution:
In ΔABC, Let A (x₁, y₁), B (x₂, y₁) and C (x₃, y₃)

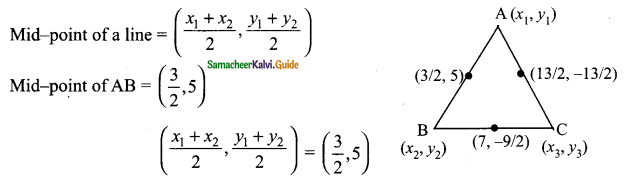
x₁ + x₂ = 3 → (1)
y₁ + y₂ = 10 → (2)

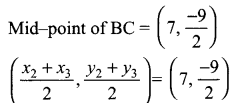
x₂ + x₃ = 14 → (3)
y₂ + y₃ = 10 → (4)

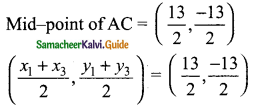
x₁ + x₃ = 3 → (5)
y₁ + y₃ = 10 → (6)
Add (1) + (3) + (5) We get
2x₁ + 2x₂ + 2x₃ = 30
2(x₁ + x₂ + x₃) = 30
x₁ + x₂ + x₃ = 15
From (1), x₁ + x₂ = 3
∴ x₃ = 12
From (3), x₂ + x₃ = 14
∴ x₁ = 1
From (5), x₁ + x₃ = 13
∴ x₂ = 2
Add (2), (4) and (6) we get
2y₁ + 2y₂ + 2y₃ = -12
2(y₁ + y₂ + y₃) = – 12
∴ y₁ + y₂ + y₃ = -6
From (2), y₁ + y₂ = 10
∴ y₃ = -16
From (4) y₂ + y₃ = -9
∴ y₁ = 3
From (6) y₁ + y₃ = -13
∴ y₂ = 7
The vertices of the A are A (1, 3), B (2, 7) and C (12, -16)

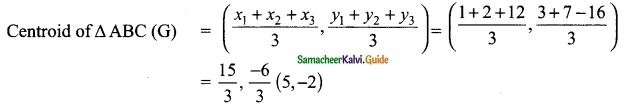
The Centroid of Δ is (5, -2)