Students can download Maths Chapter 5 Coordinate Geometry Ex 5.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.6
Question 1.
If the y-coordinate of a point is zero, then the point always lies ……..
(a) in the I quadrant
(b) in the II quadrant
(c) on x-axis
(d) on y-axis
Solution:
(c) on x-axis
Question 2.
The points (-5, 2) and (2, -5) lie in the ……….
(a) same quadrant
(b) II and III quadrant respectively
(c) II and IV quadrant respectively
(d) IV and II quadrant respectively
Solution:
(c) II and IV quadrant respectively
![]()
Question 3.
On plotting the points O (0, 0), A (3, -4), B (3, 4) and C (0, 4) and joining OA, AB, BC and CO, which of the following figure is obtained?
(a) Square
(b) Rectangle
(c) Trapezium
(d) Rhombus
Solution:
(c) Trapezium
Question 4.
If P (-1, 1), Q ( 3, -4), R (1, -1), S (-2, -3) and T (- 4, 4) are plotted on a graph paper, then the points in the fourth quadrant are ………
(a) P and T
(b) Q and R
(c) only S
(d) P and Q
Solution:
(b) Q and R
![]()
Question 5.
The point whose ordinate is 4 and which lies on the v-axis is ……….
(a) (4, 0)
(b) (0, 4)
(c) (1, 4)
(d) (4, 2)
Solution:
(b) (0, 4)
Question 6.
The distance between the two points (2, 3) and (1, 4) is ……..
(a) 2
(b) \(\sqrt{56}\)
(c) \(\sqrt{10}\)
(d) √2
Solution:
(d) √2
Hint:
\(\sqrt{(1-2)^{2}+(4+3)^{2}}\)
= \(\sqrt{(-1)^{2}+1^{2}}\)
= \(\sqrt{1+1}\)
= √2
![]()
Question 7.
If the points A (2, 0), B (-6, 0), C (3, a – 3) lie on the x-axis then the value of a is ……..
(a) 0
(b) 2
(c) 3
(d) -6
Solution:
(c) 3
Hint:
a – 3 = 0 ⇒ a = 3
Question 8.
If (x + 2, 4) = (5, y – 2), then the coordinates (x, y) are ………
(a) (7, 12)
(b) (6, 3)
(c) (3, 6)
(d) (2, 1)
Solution:
(c) (3, 6)
Hint:
x + 2 = 5
∴ x = 5 – 2 = 3
and
4 = y – 2
4 + 2 = y
∴ y = 6
![]()
Question 9.
If Q1, Q2, Q3, Q4 are the quadrants in a Cartesian plane then Q2 ∩ Q3 is ……..
(a) Q1 U Q2
(b) Q2 U Q3
(C) Null set
(d) Negative x-axis
Solution:
(c) Null set
Question 10.
The distance between the point (5, -1 ) and the origin is ………
(a) \(\sqrt{24}\)
(b) \(\sqrt{37}\)
(c) \(\sqrt{26}\)
(d) \(\sqrt{17}\)
Solution:
(c) \(\sqrt{26}\)
Hint:
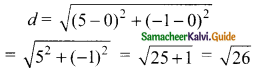
![]()
Question 11.
The coordinates of the point C dividing the line segment joining the points P (2, 4) and Q (5, 7) internally in the ratio 2 : 1 is ……..
(a) (\(\frac{7}{2}, \frac{11}{2}\))
(b) (3, 5)
(c) (4, 4)
(d) (4, 6)
Solution:
(d) (4, 6)
Hint:
A line divides internally in the ratio m : n
m = 2, n = 1
x1 = 2, x2 = 5
y1 = 4, y2 = 7
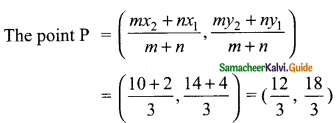
= (4, 6)
Question 12.
If p (\(\frac{a}{3}, \frac{b}{2}\)) is the mid-point of the line segment joining A (-4, 3) and B (-2, 4) then (a, b) is ………
(a) (-9, 7)
(b) (-3, \(\frac{7}{2}\))
(c) (9, -7)
(d) (3, –\(\frac{7}{2}\))
Solution:
(a) (-9, 7)
Hint:
Mid point of a line

\(\frac{a}{3}\) = -3 ⇒ a = -9
\(\frac{b}{2}\) = \(\frac{7}{2}\) ⇒ b = 7
(a, b) is (-9, 7)
![]()
Question 13.
In what ratio does the point Q (1, 6) divide the line segment joining the points P (2, 7) and R(-2, 3) ………
(a) 1 : 2
(6) 2 : 1
(c) 1 : 3
(d) 3 : 1
Solution:
(c) 1 : 3
Hint:
A line divides internally in the ratio m : n the point P =
(\(\frac{mx_{2}+nx_{1}}{m+n}\), \(\frac{my_{2}+ny_{1}}{m+n}\))
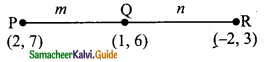
(1, 6) = (\(\frac{-2m+2n}{m+n}\), \(\frac{3m+7n}{m+n}\))
\(\frac{-2m+2n}{m+n}\) = 1
-2m + 2n = m + nx
-3m = n – 2n
3m = n
\(\frac{m}{n}\) = \(\frac{1}{3}\)
∴ m : n = 1 : 3
and
\(\frac{3m+7n}{m+n}\) = 6
3m + 7n = 6m + 6n
6m – 3n = 7n – 6n
3m = n
\(\frac{m}{n}\) = \(\frac{1}{3}\)
![]()
Question 14.
If the coordinates of one end of a diameter of a circle is (3, 4) and the coordinates of its centre is (-3, 2), then the coordinate of the other end of the diameter is ……..
(a) (0, -3)
(b) (0, 9)
(c) (3, 0)
(d) (-9, 0)
Solution:
(d) (-9, 0)
Hint:
Let the other end of the diameter be (a, b)
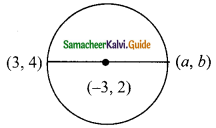
Mid point of a line =
(\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
(-3, 2) = \(\frac{3+a}{2}, \frac{4+b}{2}\)
\(\frac{3+a}{2}\) = -3
3 + a = -6
a = -6 – 3 = -9
and
\(\frac{4+b}{2}\) = 2
4 + b = 4
b = 4 – 4 = 0
The other end is (-9, 0)
Question 15.
The ratio in which the x-axis divides the line segment joining the points A (a1, b1) and B (a2, b2) is ……..
(a) b1 : b2
(b) -b1 : b2
(c) a1 : a2
(d) -a1 : a2
Solution:
(b) -b1 : b2
Hint:
A line divides internally in the ratio m : n the point P is,
(\(\frac{mx_{2}+nx_{1}}{m+n}, \frac{my_{2}+ny_{1}}{m+n}\))
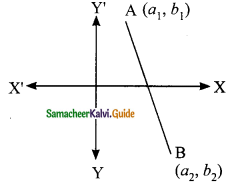
The point P is (a, 0) = (\(\frac{ma_{2}+na_{1}}{m+n}, \frac{mb_{2}+nb_{1}}{m+n}\))
∴ \(\frac{mb_{2}+nb_{1}}{m+n}\) = 0
mb2 + nb1 = 0 ⇒ mb2 = -nb1
\(\frac{m}{n}\) = \(\frac{b_{1}}{b_{2}}\)
∴ m : n = -b1 : b2
![]()
Question 16.
The ratio in which the x-axis divides the line segment joining the points (6, 4) and (1, -7) is ………
(a) 2 : 3
(b) 3 : 4
(c) 4 : 7
(d) 4 : 3
Solution:
(c) 4 : 7
Hint:
A line divides internally in the ratio m : n the point P
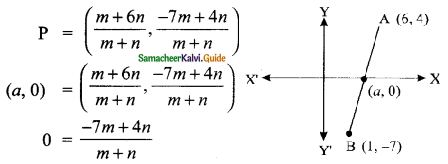
-7m + 4n = 0
4n = 7m
\(\frac{m}{n}\) = \(\frac{4}{7}\)
The ratio is 4 : 7
Question 17.
If the coordinates of the mid-points of the sides AB, BC and CA of a triangle are (3, 4), (1, 1) and (2, -3) respectively, then the vertices A and B of the triangle are ……….
(a) (3, 2), (2, 4)
(b) (4, 0), (2, 8)
(c) (3, 4), (2, 0)
(d) (4, 3), (2, 4)
Solution:
(b) (4, 0), (2, 8)
Hint:
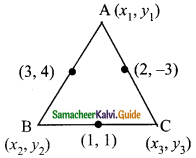
x1 + x2 = 6 → (1)
y1 + y2 = 8 → (2)
x2 + x3 = 2 → (3)
y2 + y3 = 2 → (4)
x1 + x3 = 4 → (5)
y1 + y3 = -6 → (6)
Adding (1) + (3) + (5) we get,
2(x1 + x2 + x3) = 3
x1 + x2 + x3 = 6
x1 + x3 = 4
∴ x2 = 6 – 4 = 2
x2 + x3 = 2
x1 = 6 – 2 = 4
Adding (2) + (4) + (6) we get,
2 (y1 + y2 + y3) = 4
y1 + y2 + y3 = 2
y2 + y3 = 2
∴ y1 = 2 – 2 = 0
y1 + y3 = -6
y2 = 2 + 6 = 8
∴ The vertices A is (4, 0) and B is (2, 8).
![]()
Question 18.
The mid-point of the line joining (-a, 2b) and (-3a, -4b) is ……..
(a) (2a, 3b)
(b) (-2a, -b)
(c) (2a, b)
(d) (-2a, -3b)
Solution:
(b) (-2a, -b)
Mid points of line
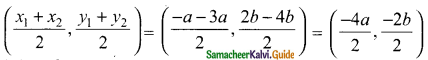
= (-2a, -b)
Question 19.
In what ratio does the y-axis divides the line joining the points (-5, 1) and (2, 3) internally ………
(a) 1 : 3
(b) 2 : 5
(c) 3 : 1
(d) 5 : 2
Solution:
(d) 5 : 2
Hint:
When it cut the y-axis the point P is (0, a)
A line divides internally in the ratio m : n the point
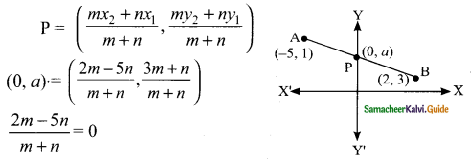
2m – 5n = 0 ⇒ 2m = 5n
\(\frac{m}{n}\) = \(\frac{5}{2}\) ⇒ m : n = 5 : 2
![]()
Question 20.
If (1, -2), (3, 6), (x, 10) and (3, 2) are the vertices of the parallelogram taken in order, then the value of x is ………
(a) 6
(b) 5
(c) 4
(d) 3
Solution:
(b) 5
Hint:
Since ABCD is a parallelogram
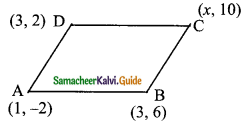
Mid-point of AC = Mid-point of BD
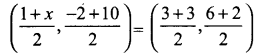
\(\frac{1+x}{2}\) = \(\frac{6}{2}\) ⇒ 1 + x = 6 ⇒ x = 6 – 1 = 5
The value of x = 5