Students can download Maths Chapter 7 Mensuration Ex 7.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 7 Mensuration Ex 7.1
Question 1.
Using Heron’s formula, find the area of a triangle whose sides are
(i) 10 cm, 24 cm, 26 cm
Solution:
Let a = 10 cm, b = 24 cm and c = 26 cm
s = \(\frac{a + b + c}{2}\)
= \(\frac{10 + 24 + 26}{2}\)
s = \(\frac{60}{2}\)
= 30 cm
s – a = 30 – 10 = 20 cm
s – b = 30 – 24 = 6 cm
s – c = 30 – 26 = 4 cm
Area of a triangle
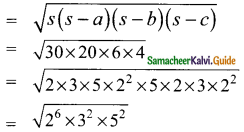
= 2³ × 3 × 5
= 8 × 3 × 5
= 120 cm²
Area of a triangle = 120 cm²
![]()
(ii) 1.8 m, 8 m, 8.2 m
Solution:
Here a = 1.8 m, b = 8 m, c = 8.2 m
s = \(\frac{a+b+c}{2}\)
= \(\frac{(1.8+8+8.2)m}{2}\)
= \(\frac{18}{2}\)
= 9 m
s – a = 9 – 1.8 = 7.2 m
s – b = 9 – 8 = 1 m
s – c = 9 – 8.2 m = 0.8 m
Area of triangle

= 3 × 2.4
= 7.2 m²
∴ Area of the triangle = 7.2 sq. m
![]()
Question 2.
The sides of the triangular ground are 22 m, 120 m and 122 m. Find the area and cost of levelling the ground at the rate of Rs 20 per m².
Solution:
The sides of the triangular ground are 22m, 120m and 122 m
a = 22 m, b = 120 m, c = 122 m
s = \(\frac{a+b+c}{2}\)
\(\frac{22+120+122}{2}\)m
= 132
s – a = 132 – 22 = 110 m
s – b = 132 – 120 = 12 m
s – c = 132 – 122 = 10 m
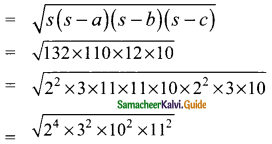
= 4 × 3 × 10 × 11
= 1320 sq.m
Cost of levelling for one sq.m = Rs 20
Cost of levelling the ground = Rs 1320 × 20
= Rs 26400
Area of the ground = Rs 1320 sq.m
Cost of levelling the ground = Rs 26400
![]()
Question 3.
The perimeter of a triangular plot is 600 m. If the sides are in the ratio 5 : 12 : 13, then find the area of the plot.
Solution:
Let the side of the triangle a, b and c be 5x, 12x and 13x
Perimeter of a triangular plot = 600 m
5x + 12x + 13x = 600
30x = 600 ⇒ x = \(\frac{600}{30}\)
x = 20
a = 5x = 5 × 20 = 100 m
b = 12x = 12 × 20 = 240 m
c = 13x = 13 × 20 = 260 m
s = \(\frac{600}{2}\)
= 300 m
s – a = 300 – 100 = 200 m
s – b = 300 – 240 = 60 m
s – c = 300 – 260 = 40 m
Area of triangle
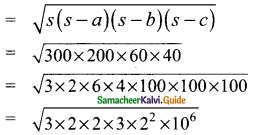
= 10³ × 3 × 2 × 2 m²
= 1000 × 12 m²
= 12000 m²
Area of the triangular Plot = 12000 sq.m
Question 4.
Find the area of an equilateral triangle whose perimeter is 180 cm.
Solution:
Perimeter of an equilateral triangle = 180 cm
3a = 180
a = \(\frac{180}{3}\)
= 60 m
Area of an equilateral triangle
= \(\frac{√3}{4}\) a² sq.unit
= \(\frac{√3}{4}\) × 60 × 60 sq.m
= √3 × 15 × 60 sq.m
= 1.732 × 15 × 60 sq.m
= 1558.8 sq.m
Area of an equilateral triangle = 1558.8 sq.m
![]()
Question 5.
An advertisement board is in the form of an isosceles triangle with perimeter 36 m and each of the equal sides are 13 m. Find the cost of painting it at Rs 17.50 per square metre.
Solution:
Equal sides of a triangle = 13m
Perimeter of an isosceles triangle = 36 m
Length of the third side = 36 – (13 + 13) m
= 36 – 26
= 10 m
Here a = 13m, b = 13m and c = 10m
s = \(\frac{a+b+c}{2}\)
= \(\frac{36}{2}\)
= 18 m
s – a = 18 – 13 = 5 m
s – b = 18 – 13 = 5 m
s – c = 18 – 10 = 8 m
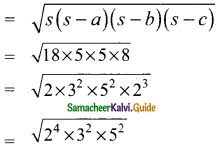
= 2² × 3 × 5
= 60 sq.m
Cost of painting for one sq. m = Rs 17.50
Cost of painting for 60 sq. m = Rs 60 × 17.50
= Rs 1050
Question 6.
Find the area of the unshaded region.
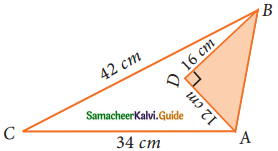
Solution:
Since ABD is a right angle triangle
AB² = AD² + BD²
= 12² + 16²
= 144 + 256
= 400
AB = \(\sqrt{400}\)
= 20 cm
Area of the right angle triangle = \(\frac{1}{2}\) bh sq.unit
= \(\frac{1}{2}\) × 12 × 16 cm²
= 6 × 16 cm²
= 96 cm²
To find the Area of the triangle ABC
Here a = 42 cm, b = 34 cm, c = 20 cm
s = \(\frac{a+b+c}{2}\)
= \(\frac{42+34+20}{2}\) cm
= \(\frac{96}{2}\)
= 48 cm
s – a = 48 – 42 = 6 cm
s – b = 48 – 34 = 14 m
s – c = 48 – 20 = 28 m
Area of triangle
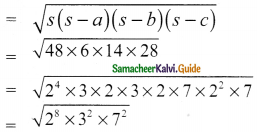
= 16 × 3 × 7 cm²
= 336 cm²
Area of the unshaded region = Area of the ΔABC – Area of the ΔABD
= (336 – 96) cm²
= 240 cm²
![]()
Question 7.
Find the area of a quadrilateral ABCD whose sides are AB = 13 cm, BC = 12 cm, CD = 9 cm, AD = 14 cm and diagonal BD = 15 cm.
Solution:
In the triangle ABD,
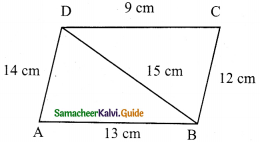
Let a = 15 cm, b = 14 cm c = 13 cm
s = \(\frac{a+b+c}{2}\)
= \(\frac{15+14+13}{2}\) cm
= \(\frac{42}{2}\)
= 21 cm
s – a = 21 – 15 = 6 cm
s – b = 21 – 14 = 7 cm
s – c = 21 – 13 = 8 cm
Area of ΔABD
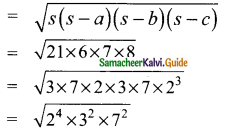
= 2² × 3 × 7 3
= 84 cm²
In the ΔBCD,
Let a = 15 cm, b = 9 cm, c = 12 cm
s = \(\frac{a+b+c}{2}\)
= \(\frac{15+9+12}{2}\) cm
= \(\frac{36}{2}\)
= 18 cm
s – a = 18 – 15 = 3 cm
s – b = 18 – 9 = 9 cm
s – c = 18 – 12 = 6 cm
Area of the ΔBCD
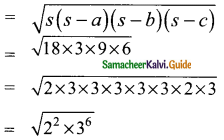
= 2 × 3³
= 2 × 27 sq.cm
= 54 sq. cm
Area of the quadrilateral ABCD = Area of ΔABD + Area of ΔBCD
= (84 + 54) sq.cm
= 138 sq.cm
![]()
Question 8.
A park is in the shape of a quadrilateral. The sides of the park are 15 m, 20 m, 26 m and 17 m and the angle between the first two sides is a right angle. Find the area of the park.
Solution:
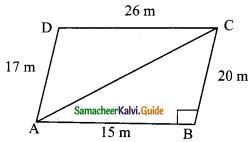
In the right angle triangle ABC (Given ⌊B= 90°)
AC² = AB² + BC²
= 15² + 20²
= 225 + 400
AC² = 625
AC = \(\sqrt{225}\)
= 25 m
Area of the right ΔABC = \(\frac{1}{2}\) × AB × BC
= \(\frac{1}{2}\) × 15 × 20 sq.m
= 150 sq.m
In the triangle ACD
a = 25 m b = 17 m, c = 26 m
s = \(\frac{a+b+c}{2}\)
= \(\frac{25+17+26}{2}\) cm
= \(\frac{62}{2}\)
= 34 m
s – a = 34 – 25 = 9 m
s – b = 34 – 17 = 17 m
s – c = 34 – 26 = 8 m
Area of the triangle ACD
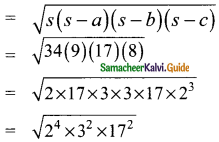
4 × 3 × 17
= 204 sq.m
Area of the quadrilateral = Area of the ΔABC + Area of the ΔACD
= (150 + 204) sq.m
= 354 sq.m
Area of the quadrilateral = 354 sq.m
![]()
Question 9.
A land is in the shape of rhombus. The perimeter of the land is 160 m and one of the diagonal is 48 m. Find the area of the land.
Solution:
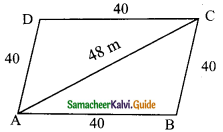
Perimeter of the rhombus = 160 m
4 × side = 160
Side of a rhombus = \(\frac{160}{4}\)
= 40 m
In ΔABC, a = 40 m, b = 40 m, c = 48 m
s = \(\frac{a+b+c}{2}\)
= \(\frac{40+40+48}{2}\) cm
= \(\frac{128}{2}\)
= 64 m
s – a = 64 – 40 = 24 m
s – b = 64 – 40 = 24 m
s – c = 64 – 48 = 16m
Area of the ΔABC = \(\sqrt{64×24×24×16}\)
= 8 × 24 × 4
= 768 sq.m
Since ABCD is a rhombus Area of two triangles are equal.
Area of the rhombus ABCD = (768 + 768) sq.m
= 1536 sq.m
∴ Area of the land = 1536 sq.m
![]()
Question 10.
The adjacent sides of a parallelogram measures 34 m, 20 m and the measure of the diagonal is 42 m. Find the area of parallelogram.
Solution:
Since ABCD is a parallelogram opposite sides are equal.
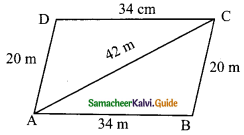
In the ΔABC
a = 20 m, b = 42 m and c = 34 m
s = \(\frac{a+b+c}{2}\)
= \(\frac{20+42+34}{2}\) cm
= \(\frac{96}{2}\)
= 48 m
s – a = 48 – 20 = 28 m
s – b = 48 – 42 = 6 m
s – c = 48 – 34 = 14 m
Area of the ΔABC
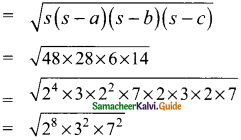
= 24 × 3 × 7 sq.m
= 16 × 3 × 7 sq.m
= 336 sq.m
Since ABCD is a parallelogram
Area of ΔABC and Area of ΔACD are equal
Area of the parallelogram ABCD = (336 + 336) sq.m
= 672 sq.m
∴ Area of the parallelogram = 672 sq.m