Bhagya

Students can download Maths Chapter 4 Geometry Ex 4.5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Ex 4.5

Question 1.
If in triangles ABC and EDF, \(\frac { AB }{ DE } \) = \(\frac { BC }{ FD } \) then they will be similar, when ……….
(1) ∠B = ∠E
(2) ∠A = ∠D
(3) ∠B = ∠D
(4) ∠A = ∠F
Answer:
(3) ∠B = ∠D
Hint:

Question 2.
In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is ……………
(1) 40°
(2) 70°
(3) 30°
(4) 110°
Answer:
(2) 70°
Hint:
Since ∆LMN ~ ∆PQR
∠N = ∠R
∠N = 180 – (60 + 50)
= 180 – 110°
∠N = 70° ∴ ∠R = 70°

Question 3.
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is ………
(1) 2.5 cm
(2) 5 cm
(3) 10 cm
(4) 5 \(\sqrt { 2 }\) cm
Answer:
(4) 5 \(\sqrt { 2 }\) cm
Hint:

AB² = AC² + BC²
AB² = 5² + 5²
(It is an isosceles triangle)
AB = \(\sqrt { 50 }\) = \(\sqrt{25 \times 2}\)
AB = 5 \(\sqrt { 2 }\)

Question 4.
In a given figure ST || QR, PS = 2 cm and SQ = 3 cm. Then the ratio of the area of ∆PQR to the area of ∆PST is …………….

(1) 25 : 4
(2) 25 : 7
(3) 25 : 11
(4) 25 : 13
Answer:
(1) 25 : 4
Hint. Area of ∆PQR : Area of ∆PST
\(\frac{\text { Area of } \Delta \mathrm{PQR}}{\text { Area of } \Delta \mathrm{PST}}=\frac{\mathrm{PQ}^{2}}{\mathrm{PS}^{2}}=\frac{5^{2}}{2^{2}}=\frac{25}{4}\)
Area of ∆PQR : Area of ∆PST = 25 : 4

Question 5.
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ =10 cm, then the length of AB is ………….
(1) 6 \(\frac { 2 }{ 3 } \) cm
(2) \(\frac{10 \sqrt{6}}{3}\)
(3) 66 \(\frac { 2 }{ 3 } \) cm
(4) 15 cm
Answer:
(4) 15 cm
Hint:

Question 6.
If in ∆ABC, DE || BC. AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm then the length of AE is ………..
(1) 1.4 cm
(2) 1.8 cm
(3) 1.2 cm
(4) 1.05 cm
Answer:
(1) 1.4 cm
Hint:

Question 7.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm.
The length of the side AC is ………….
(1) 6 cm
(2) 4 cm
(3) 3 cm
(4) 8 cm
Answer:
(2) 4 cm
Hint:

Question 8.
In the adjacent figure ∠BAC = 90° and AD ⊥ BC then ………..

(1) BD.CD = BC²
(2) AB.AC = BC²
(3) BD.CD = AD²
(4) AB.AC = AD²
Answer:
(3) BD CD = AD²
Hint:

Question 9.
Two poles of heights 6 m and 11m stand vertically on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?
(1) 13 m
(2) 14 m
(3) 15 m
(4) 12.8 m
Answer:
(1) 13 m
Hint:

AC² (Distance between the two tops)
= AE² + EC²
= 5² + 122
= 25 + 144= 169
AC = \(\sqrt { 169 }\) = 13 cm

Question 10.
In the given figure, PR = 26 cm, QR = 24 cm, ∠PAQ = 90°, PA = 6 cm and QA = 8 cm. Find ∠PQR.

(1) 80°
(2) 85°
(3) 75°
(4) 90°
Answer:
(4) 90°
Hint.
PR = 26 cm, QR = 24 cm, ∠PAQ = 90°
In the ∆PQR,

In the right ∆ APQ
PQ² = PA² + AQ²
= 6² + 8²
= 36 + 64 = 100
PQ = \(\sqrt { 100 }\) = 10
∆ PQR is a right angled triangle at Q. Since
PR² = PQ² + QR²
∠PQR = 90°

Question 11.
A tangent is perpendicular to the radius at the
(1) centre
(2) point of contact
(3) infinity
(4) chord
Solution:
(2) point of contact

Question 12.
How many tangents can be drawn to the circle from an exterior point?
(1) one
(2) two
(3) infinite
(4) zero
Answer:
(2) two

Question 13.
The two tangents from an external points P to a circle with centre at O are PA and PB.
If ∠APB = 70° then the value of ∠AOB is ……….
(1) 100°
(2) 110°
(3) 120°
(4) 130°
Answer:
(2) 110°
Hint.

∠OAP = 90°
∠APO = 35°
∠AOP = 180 – (90 + 35)
= 180 – 125 = 55
∠AOB = 2 × 55 = 110°

Question 14.
In figure CP and CQ are tangents to a circle with centre at 0. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm, then the length of BR is …….

(1) 6 cm
(2) 5 cm
(3) 8 cm
(4) 4 cm
Answer:
(4) 4 cm
Hint.
BQ = BR = 4 cm (tangent of the circle)
PC = QC = 11 cm (tangent of the circle)
QC = 11 cm
QB + BC = 11
QB + 7 = 11
QB = 11 – 7 = 4 cm
BR = BQ = 4 cm

Question 15.
In figure if PR is tangent to the circle at P and O is the centre of the circle, then ∠POQ is ………….

(1) 120°
(2) 100°
(3) 110°
(4) 90°
Answer:
(1) 120°
Hint.
Since PR is tangent of the circle.
∠QPR = 90°
∠OPQ = 90° – 60° = 30°
∠OQB = 30°
In ∆OPQ
∠P + ∠Q + ∠O = 180°
30 + 30° + ∠O = 180°
(OP and OQ are equal radius)
∠O = 180° – 60° = 120°

Students can download Maths Chapter 9 Probability Ex 9.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 9 Probability Ex 9.1

Question 1.
You are walking along a street. If you just choose a stranger crossing you, what is the probability that his next birthday will fall on a Sunday?
Solution:
Sample space = {M, T, W, Th, F, S, Sun}
n(S) = 7
Let E be the event of getting birthday on Sunday
n(E) = 1
p(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{1}{7}\)

Question 2.
What is the probability of drawing a King or a Queen or a Jack from a deck of cards?
Solution:
The outcomes n(S) = 52
Let E be the event of getting a king or a queen or a jack
= 4 + 4 + 4
n(E) = 12
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{12}{52}\)
= \(\frac{3}{13}\)

Question 3.
What is the probability of throwing an even number with a single standard dice of six faces?
Solution:
Sample space (S) = {1, 2, 3, 4, 5, 6}
n(S) = 6
Let E be the event of getting an even number
E = {2, 4, 6}
n(E) = 3
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{3}{6}\)
= \(\frac{1}{2}\)

Question 4.
There are 24 balls in a pot. If 3 of them are Red, 5 of them are Blue and the remaining are Green then, what is the probability of picking out (i) a Blue ball,
(ii) a Red ball and
(ii) a Green ball?
Solution:
Sample space n(S) = 24
Number of green ball = 24 – (3 + 5)
= 24 – 8
= 16

(i) Let E₁ be the event of getting a blue ball
n(E₁) = 5
p(E₁) = \(\frac{n(E_{1})}{n(S)}\)
= \(\frac{5}{24}\)

(ii) Let E₂ be the event of getting a red ball
n(E₂) = 3
p(E₂) = \(\frac{n(E_{2})}{n(S)}\)
= \(\frac{3}{24}\)
= \(\frac{1}{8}\)

(iii) Let E₃ be the event of getting a green ball
n(E₃) = 16
p(E₃) = \(\frac{n(E_{3})}{n(S)}\)
= \(\frac{16}{24}\)
= \(\frac{2}{3}\)

Question 5.
When two coins are tossed, what is the probability that two heads are obtained?
Solution:
Sample space (S) = {(H, H), (H, T), (T, H), (T, T)}
n(S) = 4
Let E be the event of getting two heads
n(E) = 1
p(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{1}{4}\)

Question 6.
Two dice are rolled, find the probability that the sum is

(i) equal to 1
(ii) equal to 4
(iii) less than 13
Solution:
Sample space (S) = {(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)}
n(S) = 36

(i) Let E₁ be the event of getting the sum is equal to 1
n(E₁) = 0
p(E₁) = \(\frac{n(E_{1})}{n(S)}\)
= \(\frac{0}{36}\)
= 0

(ii) Let E₂ be the event of getting the sum is equal to 4
E₂ = {(1,3), (2, 2) (3, 1)}
n(E₂) = 3
p(E₂) = \(\frac{n(E_{2})}{n(S)}\)
= \(\frac{3}{36}\)
= \(\frac{1}{12}\)

(iii) Let E₃ be the event of getting the sum is less than 13
n(E₃) = 36
p(E₃) = \(\frac{n(E_{3})}{n(S)}\)
= \(\frac{36}{36}\)
= 1

Question 7.
A manufacturer tested 7000 LED lights at random and found that 25 of them were defective. If a LED light is selected at random, what is the probability that the selected LED light is a defective one.
Solution:
Sample space n(S) = 7000
Let E₁ be the event of getting selected LED light is a defective one
n(E₁) = 25
p(E₁) = \(\frac{n(E_{1})}{n(S)}\)
= \(\frac{25}{7000}\)
= \(\frac{1}{280}\)

Question 8.
In a football match, a goalkeeper of a team can stop the goal, 32 times out of 40 attempts tried by a team. Find the probability that the opponent team can convert the attempt into a goal.
Solution:
Sample space n(S) = 40
Opponent team trying to attempt the goal = 40 – 32 = 8
Let E be the event of getting opponent team convert the attempt into a goal
n(E) = 8
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{8}{40}\)
= \(\frac{1}{5}\)

Question 9.
What is the probability that the spinner will not land on a multiple of 3?

Solution:
Sample space (S) = {1, 2, 3, 4, 5, 6, 7, 8}
n(S) = 8
Land in a multiple of 3 = {3, 6}
Land not a multiple of 3 = 8 – 2
= 6
Let E be the event of getting not a multiple of 6
n(E) = 6
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{6}{8}\)
= \(\frac{3}{4}\)

Question 10.
Frame two problems in calculating probability, based on the spinner shown here.

Solution:
(i) What is the probability that the spinner will get an odd number?
(ii) What is the probability that the spinner will not land on a multiple of 2?

Students can download Maths Chapter 8 Statistics Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Additional Questions

I. Choose the Best Answer

Question 1.
The Arithmetic mean of all the factors of 10 is ………
(a) 4.5
(b) 5.5
(c) 10
(d) 55
Solution:
(a) 4.5

Question 2.
The mean of five numbers is 27, if one number is excluded, then mean is 25. Then the excluded number is ……..
(a) 0
(b) 15
(c) 25
(d) 35
Solution:
(d) 35

Question 3.
The mean of 8 numbers is 15. If each number is multiplied by 2, then the new mean will be ……..
(a) 7.5
(b) 30
(c) 10
(d) 25
Solution:
(b) 30

Question 4.
The median of 11, 8, 4, 9, 7, 5, 2, 4, 10 is ……..
(a) 1
(b) 8
(c) 4
(d) 11
Solution:
(a) 1

Question 5.
Median is …….
(a) the most frequent value
(b) the least frequent value
(c) middle most value
(d) mean of first and last values
Solution:
(c) middle most value

Question 6.
The mode of the distribution is …….

(a) 3
(b) 4
(c) 6
(d) 14
Solution:
(b) 4

Question 7.
Mode is …….
(a) the middle value
(b) extreme value
(c) minimum value
(d) the most repeated value
Solution:
(d) the most repeated value

Question 8.
The mode of the data 72, 33, 44, 72, 81, 72, 15 is ……..
(a) 12
(b) 33
(c) 81
(d) 15
Solution:
(a) 12

Question 9.
The Arithmetic mean of 10 number is -7. If 5 is added to every number, then the new arithmetic mean is ……..
(a) 17
(b) 12
(c) -2
(d) -7
Solution:
(c) -2

Question 10.
The Arithmetic mean of integers from -5 to 5 is ……..
(a) 25
(b) 10
(c) 3
(d) 0
Solution:
(d) 0

II. Answer the Following Questions

Question 1.
Find the Arithmetic mean for the following data.

Solution:

Arithmetic mean (\(\bar { X }\)) = \(\frac{Σfx}{Σf}\)
= \(\frac{5540}{96}\)
= 57.7
∴ Arithmetic mean = 57.7

Question 2.
Calculate the Arithmetic mean of the following data using step deviation method.

Solution:
Assumed mean = 35

Arithmetic mean (\(\bar { X }\)) = A + \(\frac{Σfd}{Σf}\) × c
= 35 + \(\frac{(-20)}{100}\) × 10
= 35 – 2
= 33
∴ Arithmetic mean = 33

Question 3.
Find the median for the following data.

Solution:
The given class intervals is inclusive type we convert it into exclusive type.

\(\frac{N}{2}\) = \(\frac{70}{2}\)
= 35
Median class is 25.5 – 30.5
Here l = 25.5, f = 26, m = 30, c = 5
Median = l + \(\frac{\frac{N}{2}-m}{f}\) × c
= 25.5 + \(\frac{35-30}{26}\) × 5
= 25.5 + \(\frac{5×5}{26}\)
= 25.5 + 0.96
= 26.46
∴ Median = 26.46

Question 4.
Calculate the mode of the following data.

Solution:

The highest frequency is 30. Corresponding class interval is the modal class.
Here l = 25, f = 30, f₁ = 18, f₂ = 20 and c = 5
Mode

∴ Arithmetic mean = 25 + 2.727
= 25 + 2.73
= 27.73
mode = 27.73

Question 5.
Find the mean, median and mode of marks obtained by 20 students in an examination. The marks are given below.

Solution:

Arithmetic mean:
Here Σfx = 560, Σf = 20
\(\bar { X }\) = \(\frac{Σfx}{Σf}\)
= \(\frac{560}{20}\)

Median:
Median class is 20 – 30
Here l = 20, \(\frac{N}{2}\) = 10, m = 5, c = 10, f = 5
Median

= 20 + 10
= 30

Mode:
The highest frequency is 8
Modal class is 30 – 40
Here, l = 30, f = 8, f₁ = 5, f₂ = 2, c = 10
Mode

= 33.33
Mean = 28, median = 30, mode = 33.33

Students can download Maths Chapter 2 Introduction to Algebra Ex 2.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 2 Introduction to Algebra Ex 2.1

Question 1.
Fill in the blanks:
(i) The letters a, b, c, .., x, y, z are used to represent _____
(ii) A quantity that takes _____ values is called a variable.
(iii) If there are 5 students on a bench, then the number of students in ‘n’ benches is ‘5 × n’. Here _____ is a variable.
Solution:
(i) Variables
(ii) Different
(iii) n

Question 2.
Say True or False.

(iii) If there are 11 players in a team, then there will be ’11 + q’ players in ‘q’ teams.
Solution:
(i) False
(ii) True
(iii) False

Question 3.
Draw the next two patterns and complete the table

Solution:

Question 4.
Use a variable to write the rule, which gives the number of ice candy sticks required to make the following patterns.

Solution:
(a) No of ice candy sticks used = 3 × n = 3n
(b) No of ice candy sticks used = 4 × n = 4n

Question 5.
The teacher forms groups of five students in a class. How many students will be there in ‘p’ groups?
Solution:
No of students in a group = 5
No of students in ‘p’ groups = 5 × p = 5p

Question 6.
Arivazhagan is 30 years younger than his father. Write Arivazhagan’s age in terms of his father’s age.
Solution:
Let Arivazhagan’s father’s age be x years
According to the problem,
Arivazhagan’s age = (x – 30) years

Question 7.
If ‘u’ is an even number, how would you represent
(i) the next even number?
(ii) the previous even number?
Solution:
(i) Difference between two even numbers = 2
Given that ‘u’ is an even number.
Next, the even number is u + 2.
(ii) Previous even number is u – 2.

Objective Type Questions

Question 8.
Variable means that it
(a) can take only a few values
(b) has a fixed value
(c) can take different values
(d) can take only 8 values
Solution:
(c) can take different values

Question 9.
‘6y’ means
(a) 6 + y
(b) 6 – y
(c) 6 × y
(d) \(\frac{6}{7}\)
Solution:
(c) 6 × y

Question 10.
Radha is ‘x’ years of age now. 4 years ago, her age was
(a) x – 4
(b) 4 – x
(c) 4 + x
(d) 4x
Solution:
(a) x – 4

Question 11.
The number of days in ‘w’ weeks is
(a) 30 + w
(b) 30w
(c) 7 + w
(d) 7w
Solution:
(d) 7w

Question 12.
The value of ‘x’ in the circle is

(a) 6
(b) 8
(c) 21
(d) 22
Solution:
(d) 22

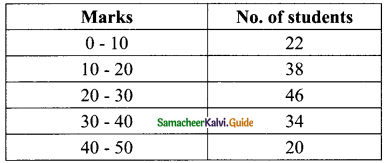
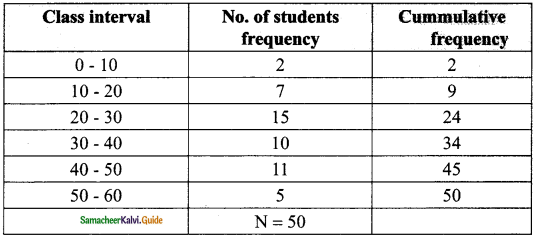
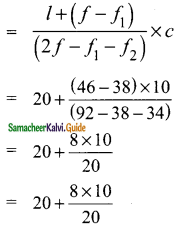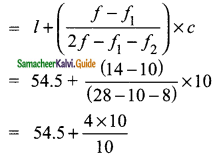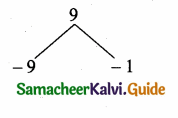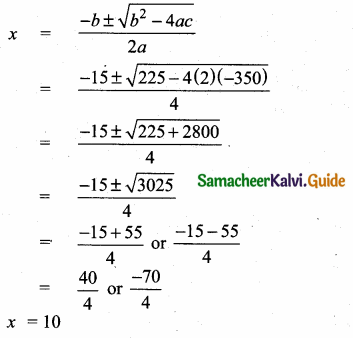Students can download Maths Chapter 8 Statistics Ex 8.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Ex 8.4

Question 1.
Let m be the mid point and b be the upper limit of a class in a continuous frequency distribution. The lower limit of the class is …….
(a) 2m – b
(b) 2m + b
(c) m – b
(d) m – 2b
Solution:
(a) 2m – b

Question 2.
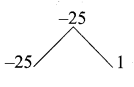
The mean of a set of seven numbers is 81. If one of the numbers is discarded, the mean of the remaining numbers is 78. The value of discarded number is ……..
(a) 101
(b) 100
(c) 99
(d) 98
Solution:
(c) 99
Hint:
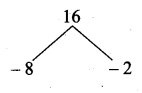
Total of 8 numbers = 81 × 7 = 567
Total of 7 numbers = 78 × 6 = 468
The number is = 567 – 468
= 99

Question 3.
A particular observation which occurs maximum number of times in a given data is called its ………
(a) frequency
(b) range
(c) mode
(d) median
Solution:
(c) mode

Question 4.
For which set of numbers do the mean, median and mode all have the same values?
(a) 2, 2, 2, 4
(b) 1, 3, 3, 3, 5
(c) 1, 1, 2, 5, 6
(d) 1, 1, 2, 1, 5
Solution:
(b) 1, 3, 3, 3, 5

Question 5.
The algebraic sum of the deviations of a set of n values from their mean is ……..
(a) 0
(b) n – 1
(c) n
(d) n + 1
Solution:
(a) 0

Question 6.
The mean of a, b, c, d and e is 28. If the mean of a, c and e is 24, then mean of b and d is ……..
(a) 24
(b) 36
(c) 26
(d) 34
Solution:
(d) 34
Hint:
Mean = 28
a + b + c + d + e = 28 × 5 = 140
= 140 …… (1)
But \(\frac{a+c+e}{3}\) = 24
a + c + e = 72
a + b + c + d + e = 140
b + d + 72 = 140
b + d = 140 – 72
= 68
Mean = \(\frac{68}{2}\)
= 34

Question 7.
If the mean of five observations x, x + 2, x + 4, x + 6, x + 8, is 11, then the mean of first three observations is …….
(a) 9
(b) 11
(c) 13
(d) 15
Solution:
(a) 9
Hint:
Mean = \(\frac{x+x+2+x+4+x+6+x+8}{5}\)
11 = \(\frac{5x+20}{5}\)
5x + 20 = 55
5x = 55 – 20
= 35
x = \(\frac{35}{5}\)
= 7
Mean of first 3 observation is = \(\frac{7+9+11}{3}\)
= 9

Question 8.
The mean of 5, 9, x, 17 and 21 is 13, then find the value of x.
(a) 9
(b) 13
(c) 17
(d) 21
Solution:
(b) 13
Hint:
Mean = \(\frac{5+9+x+17+21}{5}\)
13 = \(\frac{52+x}{5}\)
65 = 52 + x
x = 65 – 52
= 13

Question 9.
The mean of the square of first 11 natural numbers is
(a) 26
(b) 46
(c) 48
(d) 52
Solution:
(b) 46
Hint:

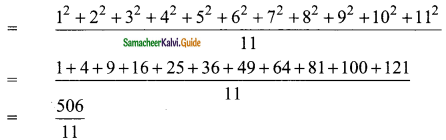
= 46

Question 10.
The mean of a set of numbers is \(\bar { X }\). If each number is multiplied by z, the mean is ……..
(a) \(\bar { X }\) + z
(b) \(\bar { X }\) – z
(c) z\(\bar { X }\)
(d) \(\bar { X }\)
Solution:
(c) z\(\bar { X }\)
Hint:
If each observation is multiplied by k, k ≠ 0 then the arithmetic mean is also multiplied by the same quantity.

Students can download Maths Chapter 4 Geometry Ex 4.4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Ex 4.4

Question 1.
The length of the tangent to a circle from a point P, which is 25 cm away from the centre is 24 cm. What is the radius of the circle?
Solution:
Let the radius AB be r. In the right ∆ ABO,
OB² = OA² + AB²
25² = 24² + r²

25² – 24² = r²
(25 + 24) (25 – 24) = r²
r = \(\sqrt { 49 }\) =7
Radius of the circle = 7 cm

Question 2.
∆ LMN is a right angled triangle with ∠L = 90°. A circle is inscribed in it. The lengths of the sides containing the right angle are 6 cm and 8 cm. Find the radius of the circle.
Solution:
LN = 6; ML = 8. In the right ∆ LMN,
MN² = LN² + LM²
= 6² + 8² = 36 + 64 = 100
MN = \(\sqrt { 100 }\) = 10

OA= OB = OC = r
AN = CN (Tangent of the circle)
LN – AL= CN
LN – r = CN
8 – r = CN ……(1)
MC = MB (tangent of the circle)
MC = ML – LB
MC = 6 – r …….(2)

Add (1) and (2)
MC + CN = (6 – r) + (8 – r)
MN = 14 – 2r
10 = 14 – 2r
2r = 14 – 10 = 4
r = \(\frac { 4 }{ 2 } \) = 2 cm
radius of the circle = 2 cm

Question 3.
A circle is inscribed in ∆ ABC having sides 8 cm, 10 cm and 12 cm as shown in figure, Find AD, BE and CF.

Solution:
AD = AF = x (tangent of the circle)
BD = BE = y (tangent of the circle)
CE = CF = z (tangent of the circle)
AB = AD + DB
x + y = 12 ……(1)
BC = BE + EC
y + z= 8 …….(2)
AC = AF + FC
x + z = 10 ……(3)
Add (1) (2) and (3)
2x + 2y + 2z = 12 + 8 + 10
x + y + z = \(\frac { 30 }{ 2 } \) = 15 …….(4)
By x + y = 12 in (4)
z = 3
y + z = 8 in (4)
x = 7
x + z = 10 in (4)
y = 5
AD = 7 cm; BE = 5 cm and CF = 3 cm

Question 4.
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120° . Find ∠OPQ.
Solution:
∠POQ = 180° – 120° = 60°
In ∆OPQ, we know

∠POQ + ∠OQP + ∠OPQ = 180°
(Sum of the angles of a ∆ is 180°)
60° + 90° + ∠OPQ = 180°
∠OPQ = 180° – 150° = 30°
∠OPQ = 30°

Question 5.
A tangent ST to a circle touches it at B. AB is a chord such that ∠ABT = 65°. Find ∠AOB, where “O” is the centre of the circle.
Solution:
Given ∠ABT = 65°
∠OBT = 90°(TB is the tangent of the circle)
∠ABO = 90° – 65° = 25°
∠ABO + ∠BOA + ∠OAB = 180°
25° + x + 25° = 180° (Sum of the angles of a ∆)

(OA and OB are the radius of the circle.
∴ ∠ABO = ∠BAO = 25°
x + 50 = 180°
x = 180° – 50° = 130°
∴ ∠BOA = 130°

Question 6.
In figure, O is the centre of the circle with radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle E, if AB is the tangent to the circle at E, find the length of AB.

Solution:
In the right ∆ OTP,
PT² = OT² – OP²
= 13² – 5²
= 169 – 25
= 144
PT = \(\sqrt { 144 }\) = 12 cm
Since lengths of tangent drawn from a point to circle are equal.
∴ AP = AE = x
AT = PT – AP
= (12 – x) cm
Since AB is the tangent to the circle E.
∴ OE ⊥ AB
∠OEA = 90°
∠AET = 90°
In ∆AET, AT² = AE² + ET²
In the right triangle AET,
AT² = AE² + ET²
(12 – x)² = x² + (13 – 5)²
144 – 24x + x² = x² + 64
24x = 80 ⇒ x = \(\frac { 80 }{ 24 } \) = \(\frac { 20 }{ 6 } \) = \(\frac { 10 }{ 3 } \)
BE = \(\frac { 10 }{ 3 } \) cm
AB = AE + BE
= \(\frac { 10 }{ 3 } \) + \(\frac { 10 }{ 3 } \) = \(\frac { 20 }{ 3 } \)
Lenght of AB = \(\frac { 20 }{ 3 } \) cm

Question 7.
In two concentric circles, a chord of length 16 cm of larger circle becomes a tangent to the smaller circle whose radius is 6 cm. Find the radius of the larger circle.
Solution:
Here AP = PB = 8 cm
In ∆OPA,
OA² = OP² + AP²

= 6² + 8²
= 36 + 64
= 100
OA = \(\sqrt { 100 }\) = 10 cm
Radius of the larger circle = 10 cm

Question 8.
Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q, such that OP and O’ P are tangents to the two circles. Find the length of the common chord PQ.
Solution:
In ∆ OO’P
(O’O)² = OP² + O’P²
= 3² + 4²

= 9 + 16
(OO’)² = 25
∴ OO’ = 5cm
Since the line joining the centres of two intersecting circles is perpendicular bisector of their common chord.
OR ⊥ PQ and PR = RQ
Let OR be x, then O’R = 5 – x again Let PR = RQ = y cm
In ∆ ORP, OP² = OR² + PR²
9 = x² + y² …(1)
In ∆ O’RP, O’P² = O’R² + PR²
16 = (5 – x)² + y²
16 = 25 + x² – 10x + y²
16 = x² + y² + 25 – 10x
16 = 9 + 25 – 10x (from 1)
16 = 34 – 10x
10x = 34 – 16 = 18
x = \(\frac { 18 }{ 10 } \) = 1.8 cm
Substitute the value of x = 1.8 in (1)
9 = (1.8)² + y²
y² = 9 – 3.24
y² = 5.76
y = \(\sqrt { 5.76 }\) = 2.4 cm
Hence PQ = 2 (2.4) = 4.8 cm
Length of the common chord PQ = 4.8 cm

Question 9.
Show that the angle bisectors of a triangle are concurrent.
Solution:
Given: ABC is a triangle. AD, BE and CF are the angle bisector of ∠A, ∠B, and ∠C.
To Prove: Bisector AD, BE and CF intersect
Proof: The angle bisectors AD and BE meet at O. Assume CF does not pass through O. By angle bisector theorem.
AD is the angle bisector of ∠A
\(\frac { BD }{ DC } \) = \(\frac { AB }{ AC } \) …..(1)
BE is the angle bisector of ∠B

\(\frac { CE }{ EA } \) = \(\frac { BC }{ AB } \) …….(2)
CF is the angle bisector ∠C
\(\frac { AF }{ FB } \) = \(\frac { AC }{ BC } \) …….(3)
Multiply (1) (2) and (3)
\(\frac { BD }{ DC } \) × \(\frac { CE }{ EA } \) × \(\frac { AF }{ FB } \) = \(\frac { AB }{ AC } \) × \(\frac { BC }{ AB } \) × \(\frac { AC }{ BC } \)
So by Ceva’s theorem.
The bisector AD, BE and CF are concurrent.

Question 10.
In ∆ABC , with ∠B = 90° , BC = 6 cm and AB = 8 cm, D is a point on AC such that AD = 2 cm and E is the midpoint of AB. Join D to E and extend it to meet at F. Find BF.
Solution:
Consider ∆ABC. Then D, E and F are respective points on the sides AC, AB and BC.
By construction D, E, F are collinear.
By Menelaus’ theorem \(\frac { AE }{ EB } \) × \(\frac { BF }{ FC } \) × \(\frac { CD }{ DA } \) = 1 ……(1)
AD = 2 cm; AE = EB = 4 cm; BC = 6 cm; FC = FB + BC = x + 6
In ∆ABC, By Pythagoras theorem.

AC²= AB² + BC²
AC² = 8² + 6² = 64 + 36 = 100
AC = \(\sqrt { 100 }\) = 10
CD = AC – AD
= 10 – 2 = 8 cm
Substituting the values in (1) we get
\(\frac { 4 }{ 4 } \) × \(\frac { x }{ x+6 } \) × \(\frac { 8 }{ 2 } \) = 1
\(\frac { x }{ x+6 } \) × 4 = 1
4x = x + 6
3x = 6 ⇒ x = \(\frac { 6 }{ 3 } \) = 2
The value of BF = 2 cm

Question 11.
An artist has created a triangular stained glass window and has one strip of small length left before completing the window. She needs to figure out the length of left out portion based on the lengths of the other sides as shown in the figure.

Solution:
Given that AE = 3 cm, EC = 4 cm, CD = 10 cm, DB = 3 cm, AF = 5 cm.
Let FB be x
Using Ceva’s theorem we have
\(\frac { AE }{ EC } \) × \(\frac { CD }{ DB } \) × \(\frac { BF }{ AF } \) = 1
\(\frac { 3 }{ 4 } \) × \(\frac { 10 }{ 3 } \) × \(\frac { x }{ 5 } \) = 1
\(\frac { 2x }{ 4 } \) = 1
2x = 4 ⇒ x = \(\frac { 4 }{ 2 } \) = 2
The value of BF = 2

Question 12.
Draw a tangent at any point R on the circle of radius 3.4 cm and centre at P ?
Answer:
Given Radius = 3.4 cm


Steps of construction:

1. Draw a circle with centre “O” of radius 3.4 cm.
2. Take a point P on the circle Join OP.
3. Draw a perpendicular line TT’ to OP which passes through P.
4. TT’ is the required tangent.

Question 13.
Draw a circle of radius 4.5 cm. Take a point on the circle. Draw the tangent at that point using the alternate segment theorem.
Answer:
Radius of the circle = 4.5 cm


Steps of construction:

1. With O as centre, draw a circle of radius 4.5 cm.
2. Take a point L on the circle. Through L draw any chord LM.
3. Take a point M distinct from L and N on the circle, so that L, M, N are in anti-clockwise direction. Join LN and NM.
4. Through “L” draw tangent TT’such that ∠TLM = ∠MNL
5. TT’ is the required tangent.

Question 14.
Draw the two tangents from a point which is 10 cm away from the centre of a circle of radius 5 cm. Also, measure the lengths of the tangents.
Answer:
Radius = 5 cm; Distance = 10 cm


Steps of construction:

1. With O as centre, draw a circle of radius 5 cm.
2. Draw a line OP =10 cm.
3. Draw a perpendicular bisector of OP, which cuts OP at M.
4. With M as centre and MO as radius draw a circle which cuts previous circle at A and B.
5. Join AP and BP. AP and BP are the required tangents.

Verification: In the right ∆ OAP
PA² = OP² – OA²
= 10² – 5² = \(\sqrt { 100-25 }\) = \(\sqrt { 75 }\) = 8.7 cm
Lenght of the tangent is = 8.7 cm

Question 15.
Take a point which is 11 cm away from the centre of a circle of radius 4 cm and draw the two tangents to the circle from that point.
Answer:
Radius = 4 cm; Distance = 11 cm


Steps of construction:

1. With O as centre, draw a circle of radius 4 cm.
2. Draw a line OP = 11 cm.
3. Draw a perpendicular bisector of OP, which cuts OP at M.
4. With M as centre and MO as radius, draw a circle which cuts previous circle A and B.
5. Join AP and BP. AP and BP are the required tangents.

This the length of the tangents PA = PB = 10.2 cm
Verification: In the right angle triangle OAP
PA² = OP² – OA²
= 11² – 4² = 121 – 16 = 105
PA = \(\sqrt { 105 }\) = 10.2 cm
Length of the tangents = 10.2 cm

Question 16.
Draw the two tangents from a point which is 5 cm away from the centre of a circle of diameter 6 cm. Also, measure the lengths of the tangents.
Answer:
Radius = 3cm; Distance = 5cm.


Steps of construction:

1. With O as centre, draw a circle of radius 3 cm.
2. Draw a line OP = 5 cm.
3. Draw a perpendicular bisector of OP, which cuts OP at M.
4. With M as centre and MO as radius draw a circle which cuts previous circles at A and B.
5. Join AP and BP, AP and BP are the required tangents.

The length of the tangent PA = PB = 4 cm
Verification: In the right angle triangle OAP
PA² = OP² – OA²
= 5² – 3²
= 25 – 9
= 16 PA
= \(\sqrt { 16 }\) = 4 cm
Length of the tangent = 4 cm

Question 17.
Draw a tangent to the circle from the point P having radius 3.6 cm, and centre at O. Point P is at a distance 7.2 cm from the centre.
Answer:
Radius = 3.6; Distance = 7.2 cm.


Steps of construction:

1. With O as centre, draw a circle of radius 3.6 cm.
2. Draw a line OP = 7.2 cm.
3. Draw a perpendicular bisector of OP which cuts OP at M.
4. With M as centre and MO as radius draw a circle which cuts the previous circle at A and B.
5. Join AP and BP, AP and BP are the required tangents.

Length of the tangents PA = PB = 6.26 cm
Verification: In the right triangle ∆OAP
PA² = OP² – OA²
= 7.22 – 3.62 =(7.2 + 3.6) (7.2 – 3.6)
PA² = 10.8 × 3.6 = \(\sqrt { 38.88 }\)
PA = 6.2 cm
Length of the tangent = 6.2 cm

Students can download Maths Chapter 8 Statistics Ex 8.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Ex 8.3

Question 1.
The monthly salary of 10 employees in a factory are given below:
Rs 5000, Rs 7000, Rs 5000, Rs 7000, Rs 8000, Rs 7000, Rs 7000, Rs 8000, Rs 7000, Rs 5000
Find the mean, median and mode.
Solution:

Mean = 6600
Median:
Arrange in ascending order we get.
5000, 5000, 5000, 7000, 7000, 7000, 7000, 7000, 8000, 8000
The number of values = 10
Median = Average of (\(\frac{10}{2})^{th}\) and (\(\frac{10}{2}+1)^{th}\)
= Average of 5^th value and 6^th value
= \(\frac{7000+7000}{2}\)
∴ Median = 7000
Mode: 7000 repeated 5 times
∴ Mode = 7000

Question 2.
Find the mode of the given data: 3.1, 3.2, 3.3, 2.1, 1.3, 3.3, 3.1
Solution:
3.1 occuring two times
3.3 occuring two times
∴ 3.1 and 3.3 are the mode (bimodal)

Question 3.
For the data 11, 15, 17, x + 1, 19, x – 2, 3 if the mean is 14, find the value of x. Also find the mode of the data.
Solution:
Arithmetic mean

∴ 2x + 64 = 14 × 7
2x = 98 – 64
2x = 34
x = \(\frac{34}{2}\)
= 17
The given numbers are 11, 15, 17, 18, 19, 15 and 3
15 occuring two times
∴ Mode = 15
The value of x = 17 and mode = 15

Question 4.
The demand of track suit of different sizes as obtained by a survey is given below:

Which size is demanded more?
Solution:
The highest frequency is 37
The corresponding value is the mode
∴ Mode = 40
Size 40 is demanded more.

Question 5.
Find the mode of the following data:

Solution:

The highest frequency is 46
20 – 30 is the modal class
Here l = 20, f = 46, f₁ = 38, f₂ = 34 and c = 10
Mode

= 20 + 4
= 24
∴ Mode = 24

Question 6.
Find the mode of the following distribution

Solution:
In the given table the class intervals are in inclusive form; convert them into exclusive form.

The highest frequency is 14
Modal class is 54.5 – 64.5
Here l = 54.5, f = 14, f₁ = 10, f₂ = 8 and c = 10
mode

= 58.5
∴ Mode = 58.5

Students can download Maths Chapter 8 Statistics Ex 8.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Ex 8.2

Question 1.
Find the median of the given values: 47, 53, 62, 71, 83, 21, 43, 47, 41
Solution:
Arrange the values in ascending order we get
21, 41, 43, 47, 47, 53, 62, 71, 83
The number of values = 9 which is odd
Median = (\(\frac{9+1}{2})^{th}\) variable
= 5^th variable
∴ Median = 47

Question 2.
Find the median of the given data: 36, 44, 86, 31, 37, 44, 86, 35, 60, 51
Solution:
Arrange the values in ascending order we get
31, 35, 36, 37, 44, 44, 51, 60, 86, 86
The number of values = 10 which is even
Median = Average of (\(\frac{10}{2})^{th}\) and (\(\frac{10}{2}+1)^{th}\) value
= Average of 5^th and 6^th value
= \(\frac{44+44}{2}\)
= \(\frac{88}{2}\)
= 44
∴ Median = 44

Question 3.
The median of observation 11, 12, 14, 18, x + 2, x + 4, 30, 32, 35, 41 arranged in ascending order is 24. Find the values of x.
Solution:
The given observation is 11, 12, 14, 18, x + 2, x + 4, 30, 32, 35, 41 (is ascending order)
The number of values =10
Median = Average of (\(\frac{10}{2})^{th}\) and (\(\frac{10}{2}+1)^{th}\) value
= Average of 5^th and 6^th value
24 = \(\frac{x+2.+x+4}{2}\)
24 = \(\frac{2x+6}{2}\)
2x + 6 = 48
2x = 48 – 6
2x = 42
x = \(\frac{42}{2}\)
= 21
The value of x = 21

Question 4.
A researcher studying the behavior of mice has recorded the time (in seconds) taken by each mouse to locate its food by considering 13 different mice as 31, 33, 63, 33, 28, 29, 33, 27, 27, 34, 35, 28, 32. Find the median time that mice spent in searching its food.
Solution:
Arrange the value in ascending order we get
27, 27, 28, 28, 29, 31, 32, 33, 33, 33, 34, 35, 63
The number of values = 13 which is odd
Median = (\(\frac{13+1}{2})^{th}\) value
= (\(\frac{14}{2})^{th}\)
= 7th value
7th value is = 32
∴ Median = 32

Question 5.
The following are the marks scored by the students in the Summative Assessment exam.

Calculate the median.
Solution:

\(\frac{N}{2}\) = \(\frac{50}{2}\)
= 25
Here l = 30, f = 10; m = 24 and c = 10
Median = l + \(\frac{(\frac{N}{2}-m)×c}{f}\)
= 30 + \(\frac{(25-24)10}{10}\)
= 30 + 1
= 31
∴ Median = 31

Question 6.
The mean of five positive integers is twice their median. If four of the integers are 3, 4, 6, 9 and median is 6, then find the fifth integer.
Solution:
Let the 5th positive integer be x
\(\bar { x }\) = \(\frac{3+4+6+9+x}{5}\)
= \(\frac{22+x}{5}\)
Median = 6
Mean = 2 × median
\(\frac{22+x}{5}\) = 2 × 6
22 + x = 60
x = 60 – 22
= 38
The fifth integer is 38.

Students can download Maths Chapter 4 Geometry Ex 4.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.2

Question 1.
The angles of a quadrilateral are in the ratio 2 : 4 : 5 : 7. Find all the angles.
Solution:
Let the angles of a quadrilateral be 2x, 4x, 5x, and 7x.
Total angle of a quadrilateral = 360°
2x + 4x + 5x + 7x = 360°
18° = 360°
x = \(\frac{360°}{18}\)
= 20°
2x = 2 × 20° = 40°; 4x = 4 × 20° = 80°;
5x = 5 × 20° = 100°; 7x = 7 × 20° = 140°
The angles of a quadrilateral are 40°, 80°, 100° and 140°.

Question 2.
In a quadrilateral ABCD, ∠A = 72° and ∠C is the supplementary of ∠A. The other two angles are 2x – 10 and x + 4. Find the value of x and the measure of all the angles.
Solution:

∠A = 72°
∠C = 180° – 12° (∠A and ∠C are supplementary)
= 108°
∠A + ∠B + ∠C + ∠D = 360° (Total angles of quadrilateral)
72° + 2x – 10 + 108° + x + 4 = 360°
3x + 174° = 360°
x = \(\frac{186°}{3}\)
= 62°
The value of x is 62°
∠B = 2x – 10
= 2(62°) – 10
= 124° – 10°
= 114°
∠D = x + 4
= 62° + 4
= 66°
The other angles are 114°, 62° and 66°.

Question 3.
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC.
Solution:
Since the diagonals of a rectangle AC and BD are equal and bisect each other

∴ OA = OB
∠OAB = ∠OBA = 46°
Each angle of a rectangle measures 90°
∠ABC = 90°
∠ABO + ∠OBC = 90°
46° + ∠OBC = 90°
∠OBC = 90°-46°
∴ ∠OBC = 44°

Question 4.
The lengths of the diagonals of a Rhombus are 12 cm and 16 cm. Find the side of the rhombus.
Solution:
Since the diagonals of a rhombus bisect each other at right angles

AO = \(\frac{1}{2}\)AC = \(\frac{1}{2}\) × 12 = 6 cm
BO = \(\frac{1}{2}\)BD = \(\frac{1}{2}\) × 16 = 8 cm
In the right triangle AOD
AD² = AO² + DO²
= 6² + 8²
= 36 + 64
= 100
∴ AD = \(\sqrt{100}\)
= 10
∴ AB = BC = CD = AD = 10 cm.

Question 5.
Show that the bisectors of angles of a parallelogram form a rectangle.
Solution:
Given: A parallelogram in which bisector of angle A, B, C, D intersect at P, Q, R, S to form a quadrilateral PQRS.
To prove: Quadrilateral PQRS is a rectangle.
Proof: Since ABCD is a parallelogram. Therefore, AB || DC.

Now, AB || DC, and transversal AD cuts them, so we have
∠A + ∠D = 180°
\(\frac{1}{2}\)∠A + \(\frac{1}{2}\)∠D = \(\frac{180°}{2}\)
∠DAS + ∠ADS = 90°
But in ΔASD, we have
∠ADS + ∠DAS + ∠ASD = 180°
90° + ∠ASD = 180°
∠ASD = 90°
∠RSP = ∠ASD (vertically opposite angle)
∠RSP = 90°
Similarly, we can prove that
∠SRQ = 90°, ∠RQP = 90° and ∠QPS = 90°
Thus, PQRS is a quadrilateral each of whose angle is 90°.
Hence, PQRS is a rectangle.

Question 6.
If a triangle and a parallelogram lie on the same base and between the same parallels then prove that the area of the triangle is equal to half of the area of parallelogram.
Solution:
Let ΔAPB and parallelogram ABCD lie on base AB and between parallels AB and PC.
To show area ΔAPB = \(\frac{1}{2}\) Area (ABCD)
Now, draw BQ || AP. Then ABQP is a parallelogram.
Now area ABQP = Area ABCD
(They are on same base AB and between same parallels AB and PC)

⇒ ΔPAB ≅ ΔBQP
Area PAB = Area BQP
= \(\frac{1}{2}\) Area ABQP
= \(\frac{1}{2}\) Area ABCD

Question 7.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure.

If a || b, c || d, e || f, find the marked angles between
(i) b and c
(ii) d and e
(iii) d and f
(iv) c and f
Solution:
(i) Angle between b and c = 30°
(vertically opposite angles)

(ii) Angle between d and e = 180° – 75° = 105°
(sum of the adjacent angles of a parallelogram is 180°)

(iii) Angle between d and f = 75°
(opposite angles of a parallelogram)

(iv) Angle between c and f = 180° – 75° = 105°
(Adjacent angles of a parallelogram)

Question 8.
In the given figure, ∠A = 64°, ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°.

Solution:
In the given ΔABC
∠A = 64° and ∠B = 58°
∠C = 180°- (64° + 58°)
= 180° – 122°
= 58°
Since OC is the bisector of ∠C
y = \(\frac{58°}{2}\)
= 29°
Given ΔOBC
∠OCB = \(\frac{58°}{2}\) = 29°
∠OCB = 29°
∴ ∠BOC = 180°- (29° + 29°)
x = 180° – 58°
x = 122°
∠x = 122° and ∠y = 29°.

Question 9.
In the given figure, if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7 and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ΔCDF.

Solution:
Given: AB = 2 cm, BC = 6 cm, AE = 6 cm, BF = 8 cm, CE = 7 cm and CF = 7 cm
Consider ΔAEC and ΔBCF.
In ΔAEC, AE = 6 cm, EC = 7 cm and AC = 8 cm (2 + 6 = 8)
In ΔBCF, BC = 6 cm, CF = 7 cm and BF = 8 cm
∴ ΔAEC s ΔBCF
∴ Area of ΔAEC = Area of ΔBCF (Two triangles are similar areas are equal)
Subtract area of ΔBDC on both sides we get,
Area of ΔAEC – Area of ΔBDC = Area of ΔBCF – Area of ΔBDC
Area of quadrilateral ABDE = Area of ΔCDF

Question 10.
In the given figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length ”d” of the segment that is perpendicular to \(\overline { HE }\) and \(\overline { FG }\)?

Solution:
In the given figure ABCD is a rectangle and EFGH is a parallelogram.
In the right triangle AEH
HE = \(\sqrt{AH^{2} + AE^{2}}\)
= \(\sqrt{3^{2} + 4^{2}}\)
= \(\sqrt{9 + 16}\)
= \(\sqrt{25}\)
HE = 5
∴ GF = 5 (HE and Gf are opposite sides of a parallelogram)
In the right triangle
GC = \(\sqrt{GF^{2} – FC^{2}}\)
= \(\sqrt{5^{2} – 3^{2}}\)
= \(\sqrt{25 – 9}\)
= \(\sqrt{16}\)
∴ DG = 10 – 6 = 4
Area of ΔAEH + Area of ΔBEF + Area of ΔFCG + Area of ΔHDG
= \(\frac{1}{2}\) × 3 × 4 + \(\frac{1}{2}\) × 6 × 5 + \(\frac{1}{2}\) × 3 × 4 + \(\frac{1}{2}\) × 5 × 6
= (6 + 15 + 6 + 15)
= 42
∴ Area of 4 triangles = 42
Area of the parallelogram = Area of the rectangle ABCD – Area of 4 triangles.
= 10 × 8 – 42
= 80 – 42
= 38
b × h = 38
5 × d = 38
d = \(\frac{38}{5}\)
= 7\(\frac{3}{5}\)
Length of d = 7\(\frac{3}{5}\) or 7.6

Question 11.
In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is \(\frac{9}{8}\) of the area of the parallelogram ABCD.

Solution:
Draw OX perpendicular to QP.
In ΔADP, MN = \(\frac{1}{2}\) AP,
In ΔBCQ, MN = \(\frac{1}{2}\) QB
So, AP = BQ (or) AB + BP = AB + QA
∴ PB = QA
∴ QA = AB = BP (or) QP = QA + AB + BP = 3 AB
Area of ΔOQP = \(\frac{1}{2}\) × QP × OX
= \(\frac{1}{2}\) × 3 AB × OX
= \(\frac{3}{2}\) × AB × OX
= \(\frac{3}{2}\) AB (OY + YX)
= \(\frac{3}{2}\) × AB × OY + \(\frac{3}{2}\) × AB × YX (AB = MN)
= \(\frac{3}{2}\) × MN × OY + \(\frac{3}{2}\) × AB × YX
= 3 Area ΔOMN + \(\frac{3}{2}\) + Area ΔBNM
= 3[\(\frac{1}{4}\) area of MNCD] + \(\frac{3}{2}\)[\(\frac{1}{2}\) area of ABCD]
= \(\frac{3}{4}\)[\(\frac{1}{2}\) area of ABCD] + \(\frac{3}{4}\)[area of ABCD]
= \(\frac{3}{8}\) area of ABCD + \(\frac{3}{4}\) area of ABCD
= area of ABCD [\(\frac{3}{8}\) + \(\frac{3}{4}\)]
= area of ABCD (\(\frac{3+6}{8}\))
= \(\frac{9}{8}\) area of ABCD.
Hence it is proved.

Students can download Maths Chapter 3 Algebra Ex 3.13 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.13

Question 1.
Determine the nature of the roots for the following quadratic equations
(i) 15x² + 11x + 2 = 0
Answer:
Here a = 15, b = 11, c = 2
∆ = b² – 4ac
∆ = 11² – 4(15) × 2
= 121 – 120
∆ = 1 > 0
So the equation will have real and unequal roots

(ii) x² – x – 1 = 0
Answer:
Here a = 1, b = -1, c = -1
∆ = b² – 4ac
= (-1)² – 4(1)(-1)
= 1 + 4 = 5
∆ = 1 > 0
So the equation will have real and unequal roots.

(iii) \(\sqrt { 2 }\) t² – 3t + 3\(\sqrt { 2 }\) = 0
Answer:
Here a = \(\sqrt { 2 }\) , b = -3, c = 3\(\sqrt { 2 }\)
∆ = b² – 4ac
= (-3)² – 4(\(\sqrt { 2 }\)) (3\(\sqrt { 2 }\))
= 9 – 24 = -15
∆ = -15 < 0
So the equation will have no real roots.

(iv) 9y² – 6\(\sqrt { 2y }\) + 2 = 0
Answer:
Here a = 9, b = -6\(\sqrt { 2 }\), c = 2
∆ = b² – 4ac
= (-6\(\sqrt { 2 }\))² – 4(9) (2)
= 72 – 72
= 0
So the equation will have real and equal roots.

(v) 9a²b²x² – 24abcdx + 16c²d² = 0, a ≠ 0, b ≠ 0
Answer:
Here a = 9a²b²; b = -24 abed, c = 16c²d²
∆ = b² – 4ac
= (-24abcd)² – 4(9a²b²) (16c²d²)
= 576a²b²c²d² – 576a²b²c²d²
∆ = 0
So the equation will have real and equal roots.

Question 2.
Find the value(s) of ‘k’ for which the roots of the following equations are real and equal.
(i) (5k – 6)² + 2kx + 1 = 0
(ii) kx² + (6k + 2)x + 16 = 0
Solution:
(5k – 6)x² + 2kx + 1 :
a = (5k – 6), b = 2, c = 1
Δ = b² – 4ac
⇒ (2k)² – 4 (5k – 6)(1)
⇒ 4k² – 20k + 24 = 0 [∵ Since the roots are real and equal)
⇒ k² – 5k + 6 = 0
⇒ (k – 3)(k – 2) = 0
k = 3, 2

(ii) kx² + (6k + 2)x + 16 = 0
a = k, b = (6k + 2), c = 16
Δ = b² – 4ac [∵ the roots are real and equal)
⇒ (6k + 2)² – 4 × k × 16 = 0
⇒ 36k² + 24k + 4 – 64k = 0
⇒ 36k² – 40k + 4 =0
⇒ 36k² – 36k – 4k + 4 =0
⇒ 36k (k – 1) – 4 (k – 1) = 0
⇒ 4 (k – 1) (9k – 1) =0
⇒ k = 1 or k = \(\frac{1}{9}\)

Question 3.
If the roots of (a – b)x² + (b – c)x + (c – a) = 0 are real and equal, then prove that b, a, c are in arithmetic progression.
Answer:
(a – b) x2 + (b – c) x + (c – a) = 0
Here a = (a – b);b = b – c ; c = c – a

Since the equation has real and equal roots ∆ = 0
∴ b² – 4ac = 0
(b – c)² – 4(a – b)(c – a) = 0
b² + c² – 2bc -4 (ac – a² – bc + ab) = 0
b² + c² – 2bc – 4ac + 4a² + 4bc – 4ab = 0
b² + c² + 2bc -4a (b + c) + 4a² = 0
(b + c)² – 4a (b + c) + 4a² = 0
[(b+c) – 2a]² = 0 [using a² – 2ab + b² = (a – b)²]
b + c – 2a = 0
b + c = 2a
b + c = a + a
c – a = a – b (t₂ – t₁ = t₃ – t₂)
b,a,c are in A.P.

Question 4.
If a, b are real then show that the roots of the equation (a – b)² – 6(a + b)x – 9(a – b) = 0 are real and unequal.
Solution:
(a – b)x² – 6(a + b)x – 9(a – b) = 0
Δ = b² – 4ac
= (-6(a + b)² – 4(a – b)(-9(a – b))
= 36(a + b)² + 36(a – b)²
= 36 (a² + 2ab + b²) + 36(a² – 2ab + b²)
= 72a² + 12b²
= 72(a² + b²) > 0
∴ The roots are real and unequal.

Question 5.
If the roots of the equation (c² – ab)x² – 2(a² – bc)x + b² – ac = 0 are real and equal prove that either a = 0 (or) a³ + b³ + c³ = 3abc
Answer:
(c² – ab)x² – 2(a² – bc)x + b² – ac = 0
Here a = c² – ab ; b = – 2 (a² – bc); c = b² – ac
Since the roots are real and equal
∆ = b² – 4ac
[-2 (a² – bc)]² – 4(c² – ab) (b² – ac) = 0
4(a² – bc)² – 4[c² b² – ac³ – ab³ + a²bc] = 0
Divided by 4 we get
(a² – bc)² – [c² b² – ac³ – ab³ + a²bc] = 0
a⁴ + b² c² – 2a² bc – c²b² + ac³ + ab³ – a²bc = 0
a⁴ + ab³ + ac³ – 3a²bc = 0
= a(a³ + b³ + c³) = 3a²bc
a³ + b³ + c³ = \(\frac{3 a^{2} b c}{a}\)
a³ + b³ + c³ = 3 abc
Hence it is proved