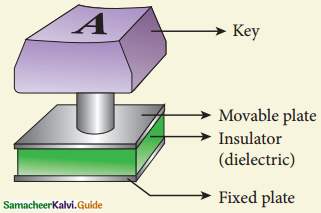
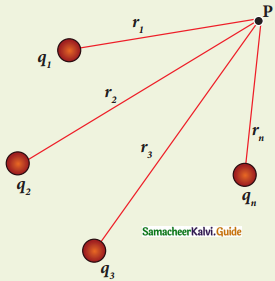
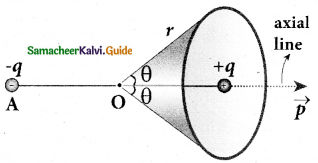
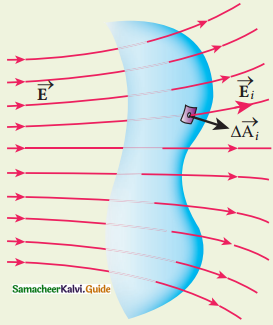
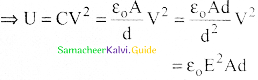Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Accountancy Guide Pdf Chapter 6 Retirement and Death of a Partner Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 12th Accountancy Solutions Chapter 6 Retirement and Death of a Partner
12th Accountancy Guide Retirement and Death of a Partner Text Book Back Questions and Answers
I Multiple Choice Questions
Choose the correct answer
Question 1.
A partner retires from the partnership firm on 30th June. He is liable for all the acts of the firm up to the
(a) End of the current accounting period
(b) End of the previous accounting period
(c) Date of his retirement
(d) Date of his final settlement
Answer:
(c) Date of his retirement
![]()
Question 2.
On the retirement of a partner from a partnership firm, accumulated profits and losses are distributed to the partners on the basis of
(a) New profit sharing ratio
(b) Old profit sharing ratio
(c) Gaming ratio
(d) Sacrificing ratio
Answer:
(b) Old profit sharing ratio
Question 3.
On the retirement of a partner, general reserve will be transferred to the
(a) Capital account of all the partners
(b) Revaluation account
(c) Capital account of the continuing partners
(d) Memorandum revaluation account
Answer:
(a) Capital account of all the partners
![]()
Question 4.
On revaluation, the increase in liabilities leads to ……………….
(a) Gain
(b) Loss
(c) Profit
(d) None of these
Answer:
(b) Loss
Question 5.
At the time of retirement of a partner, determination of gaining ratio is required
(a) To transfer revaluation profit or loss
(b) To distribute accumulated profits and losses .
(c) To adjust goodwill
(d) None of these
Answer:
(c) To adjust goodwill
Question 6.
The final amount due to a retiring partner is not paid immediately,it is transferred to
(a) BankA/c
(b) Retiring partners capital A/c
(c) Retiring partner s loan A/c
(d) Other partner s capital A/c
Answer:
(c) Retiring partner s loan A/c
![]()
Question 7.
‘A’was a partner in a partnership firm. He died on 31st March 2019. The final amount due to him is ? 24,000 which is not paid immediately. It will be.transferred to
(a) As capital account
(b) A’s loan account
(c) As Executors account
(d) As Executors loan account
Answer:
(d) As Executors loan account
Question 8.
A, B and C are partners sharingprofits in the ratio of 2:2:1. On retirement of B, goodwill of the firm was valued as ₹ 30,000. Find the contribution of A and C to compensate B:
(a) ₹ 20,000 and ₹ 10,000
(b) ₹ 8,000 and ₹ 4,000
(c) ₹ 10,000 and ₹ 20,000
(d) ₹ 15,000 and ₹ 15,000
Hint:
| Partners | Ratio | Retirement Partner |
| A, B, C | 2:2:1 | ‘B’ |
∴ Retire partner share will be compensate of‘A’ and ‘Copartners
’A’ Goodwill value = 30,000 x \(\frac{2}{5}\) = 5 12,000
‘B’ Goodwill Value = 30,000 x \(\frac{2}{5}\) = 5 12,000
‘C’ Goodwill Value = 30,000 x \(\frac{1}{5}\) = 5 6,000
Now Compensate A& C
‘B’ Share good will – 12,000 x \(\frac{2}{3}\) = 8,000
12,000 x \(\frac{1}{3}\) = 4,000
Answer:
(b) ₹ 8,000 and ₹ 4,000
![]()
Question 9.
A, B and C are partners sharing profits in the ratio of 4:2:3. C retires. The new profit sharing ratio between A and B will be
(a) 4:3
(b) 3:4
(c) 2:1
(d) 1:2
Hint:
OldPartnersABC

Answer:
(c) 2:1
Question 10.
X, Y and Z were partners sharing profits and losses equally. X died on 1st April 2019. Find out the share of X in the profit of 2019 based on the profit of 2018 which showed ₹ 36,000.
(a) ₹ 1,000
(b) ₹ 3,000
(c) ₹ 12,000
(d) ₹ 36,000
Hint:
Partner’s X: Y: Z
Sharing ratio = equally =\(\frac{1}{3}: \frac{1}{3}: \frac{1}{3}\)
Profit = ₹ 36,000
Share of ‘X’
36,000 x \(\frac{1}{3}\) = ₹ 12,000
Answer:
(c) ₹ 12,000
II Very Short Answer Questions
Question 1.
What is meant by the retirement of a partner?
Answer:
When a partner leaves from partnership firm it is known as retirement. The reasons for the retirement of a partner may be illness, old age, and disagreement with other partners, etc.
![]()
Question 2.
What is the gaining ratio?
Answer:
The continuing partners may gain a portion of the share of profit of the retiring partner. The gain may be shared by all the partners or some of the partners. The gaining ratio is the proportion of the profit which is gained by the continuing partners.
Question 3.
What is the purpose of calculating the gaining ratio?
Answer:
The purpose of finding the gaining ratio is to bear the goodwill to be paid to the retiring partner.
Question 4.
What Is the journal entry to be passed to transfer the amount due to the deceased partner to the executor of the deceased partner?
Answer:
To transfer the amount due to the deceased partner to the executor or legal representative of the deceased partner.

![]()
III. Short Answer Questions
Question 1.
List out the adjustments made at the time of retirement.
Answer:
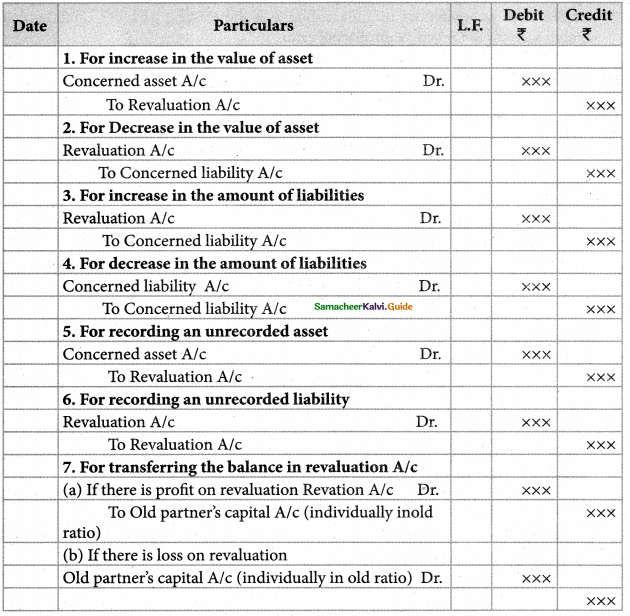
The Following adjustments are necessary at the time of retirement of a partner:
- Distribution of accumulated profits, reserves, and losses
- Revaluation of assets and liabilities
- Determination of new profit sharing ratio and gaining ratio
- Adjustment for goodwill
- Adjustment for current year’s profit or loss up to the date of retirement
- Settlement of the amount due to the retiring partner
Question 2.
Distinguish between sacrificing ratio and gaining ratio.
Answer:
| Basis | Sacrificing ratio | Gaining ratio |
| l.Meaning | it is the proportion of the profit which is sacrificed by the old partners in favor of new partners. | It is the proportion of the profit which is gained by the continuing partners from the retiring partner. |
| 2.purpose | It is calculated to determine the amount to be adjusted towards goodwill for the sacrificing partner. | It is calculated to determine the amount to be adjusted towards goodwill for the gaining partner. |
| 3.Time of Calculation | It is calculated at the time of admis¬sion of a new partner. | It is calculated at the time of retirement of a partner. |
| 4. Method of Calculation | It is the difference between the old ratio and the new ratio | It is the difference between the new ratio and the old ratio. |
| Sacrificing ratio = old profit sharing ratio – New profit sharing ratio | Gaining ratio = New profit sharing ratio – Old profit sharing ratio |
![]()
Question 3.
What are the ways in which the final amount to an outgoing partner can be settled?
Answer:
The amount due to the retiring partner may be settled one of the following ways:
- Paying the entire amount due immediately in cash
- Transfer the entire amount due to the loan account of the partner
- Paying part of the amount immediately in cash and transferring the balance to the loan account of the partner.
IV Exercise
Distribution of accumulated profits, reserves, and losses
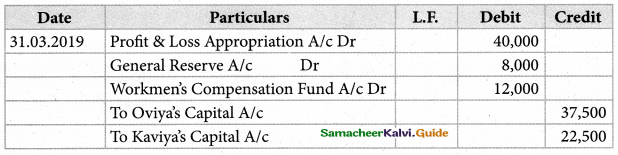
Question 1.
Dheena, Surya, and Jankai are partners sharing profits and losses in the ratio of 5:3:2. on 31.3.2018, Dheena retired. On the date of retirement, the books of the firm showed a reserve fund of ₹ 50,000. The pass journal entry to transfer the reserve fund.
Solution:

Answer:
Reserves fund: dheena: ? 25,000(Cr); Surya: ₹ 15,000(Cr.); Janaki: ₹ 10,000(Cr.);
Question 2.
Rosi, Rathi, and Rani are partners of firms sharing profits and losses equally. Rathi retired from the partnership on 1.1.2018. On the date, their balance sheet showed an accumulated loss of ₹ 45,000 on the asset side of the balance sheet. Give the journal [ entry to distribute the accumulated loss.
Solution:


Answer:
Rosi: ₹ 15,000(Dr.); Rathi: ₹ 15,000(Dr.);Rani: ₹ 15,000(Dr.);
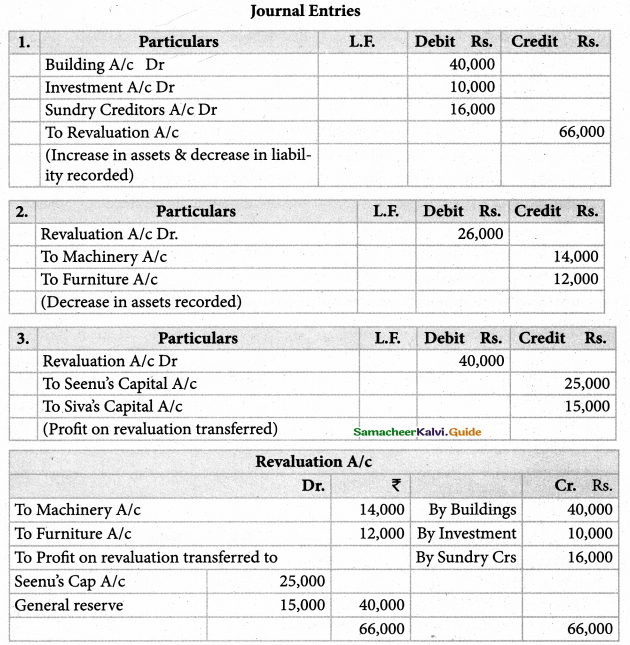
Question 3.
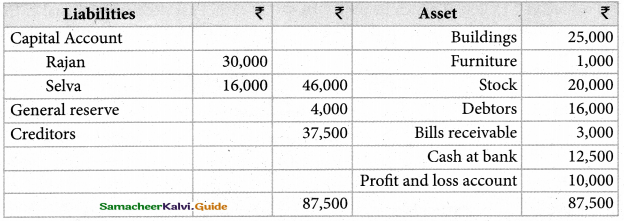
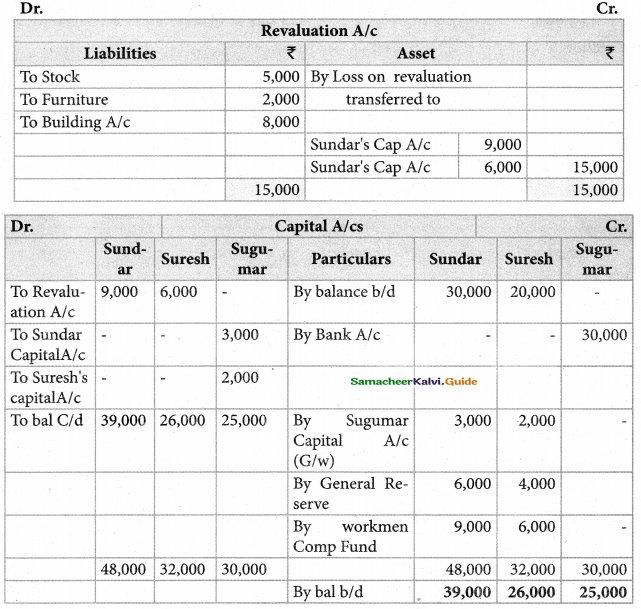
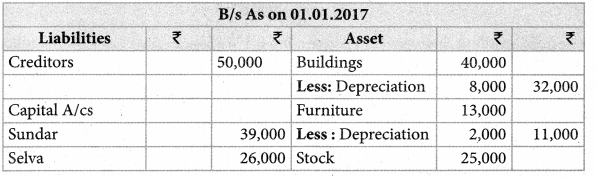
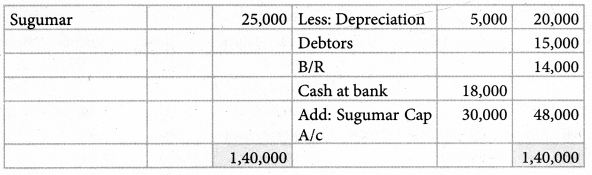
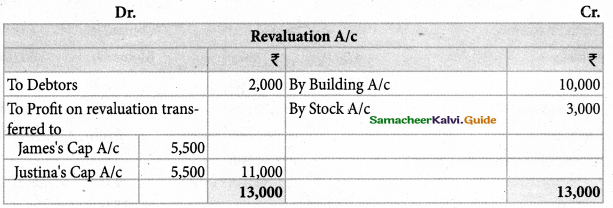
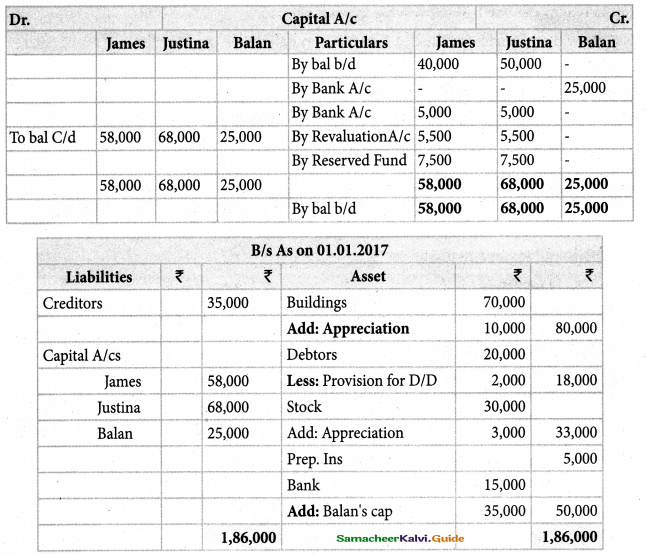
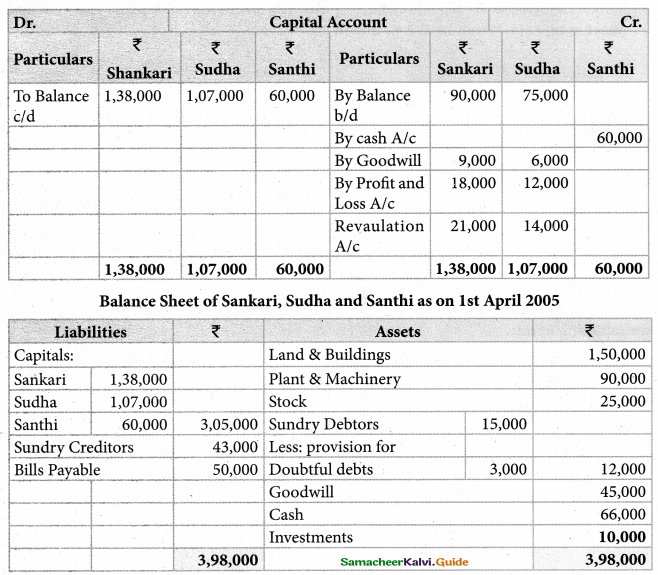
Akash, Mukesh, and Sanjay are partners in firm sharing profits and losses in the ratio of 3:2:1. Their balance sheet as on 31st March 2017 is as follows:
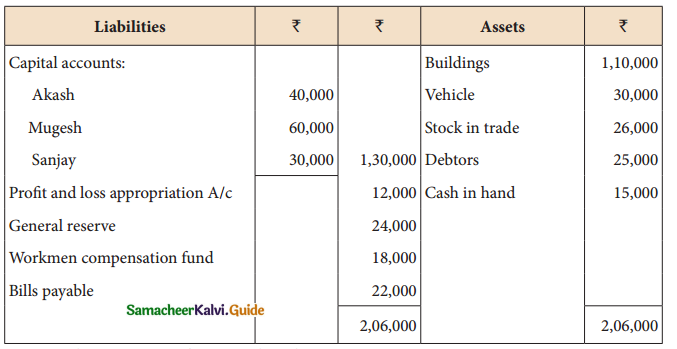
Pass journal entry to transfer the accumulated profit and prepare the capital account of the partners
Solution:
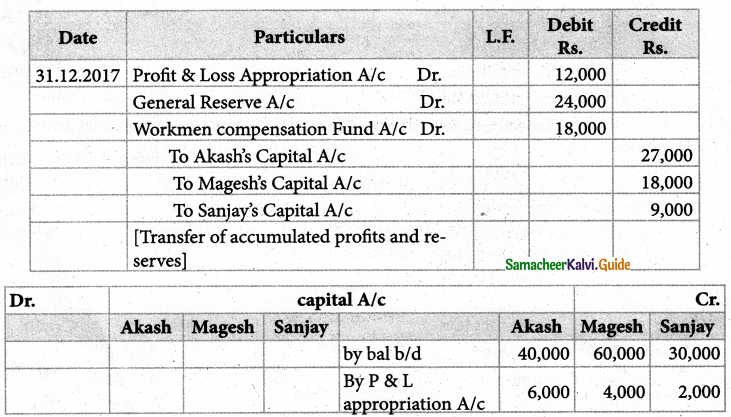
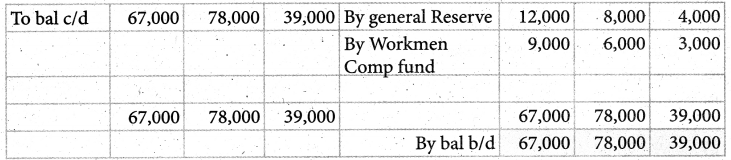
Answer:
Akash capital: ₹ 67,000(Cr.); Mugesh Capital: ₹ 78,000(Cr.); Sanjay’s Capital:₹ 39,000(Cr.);
![]()
Question 4.
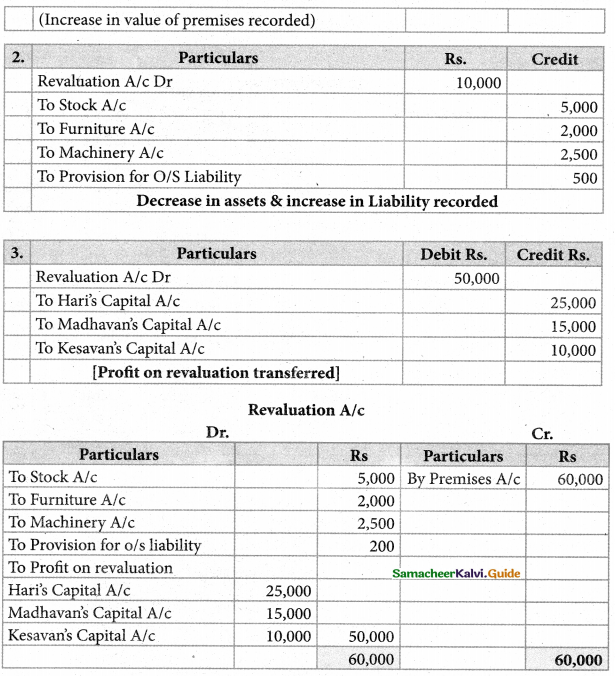
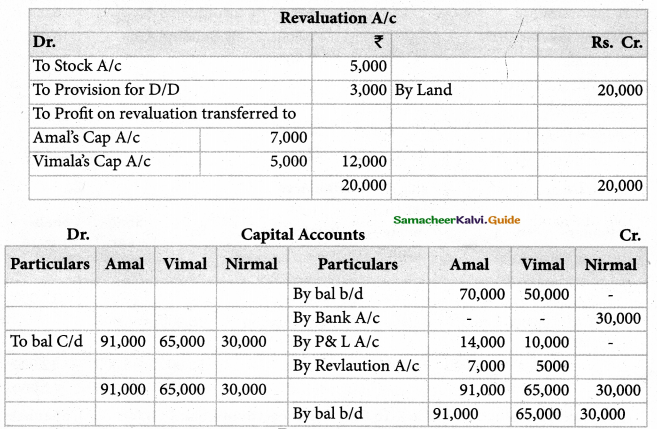
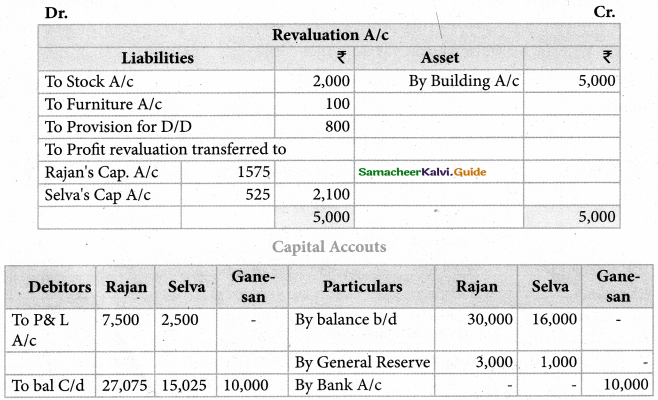
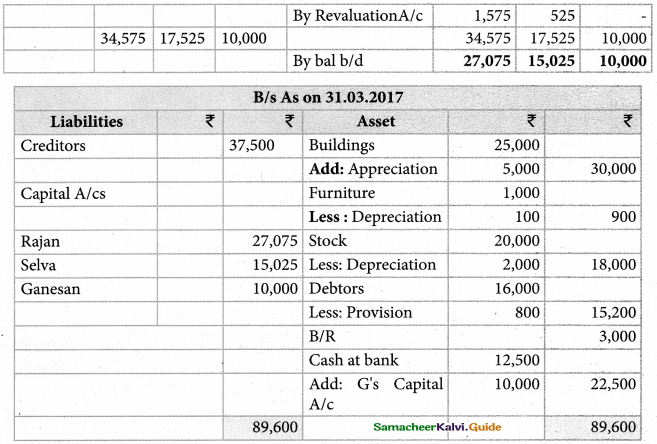
Roja, Neeia ‘and Kanaga are partners, sharing profit and losses in the ratio of 4:3:3. On 1st April 2017, Roja retires and on retirement, the following adjustments are agreed upon.
(i) Increase the value of the Building by ₹ 30,000.
(ii) Depreciate stock by ₹ 5,000, and furniture by ₹ 12,000.
(iii) Provide for an outstanding liability of ₹ 1,000.
Pass journal entries and prepare revaluation account.
Solution:
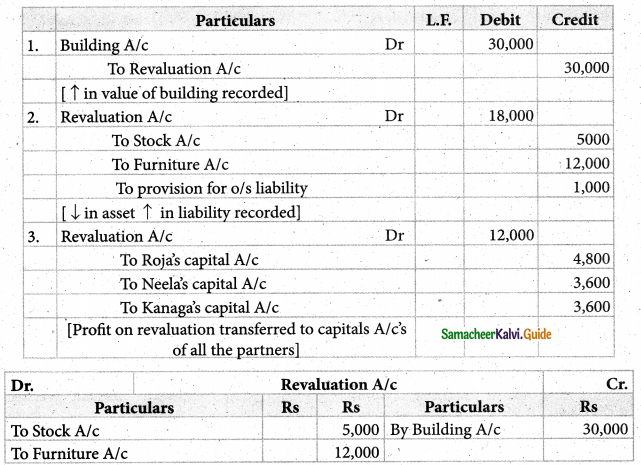
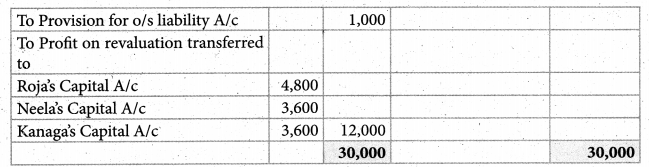
Answer:
Revaluation profit : ₹ 12,000
Question 5.
Vinoth, Karthi, and Pranav are partners sharing profits and. losses’ in the ratio of 2:2:1 Pranav retires from the partnership on 1st April 2018. The following adjustments are to be made.
(i) increase the value of the land building by ₹ 18,000.
(ii) Reduce the value of machinery by ₹ 15,000.
(iii) A provision would also be made for outstanding expenses for ₹ 8,000.
Give journal entries and prepare a revaluation account.
Solution:
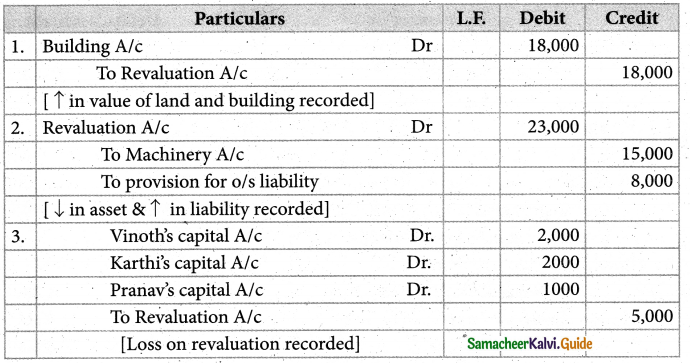


![]()
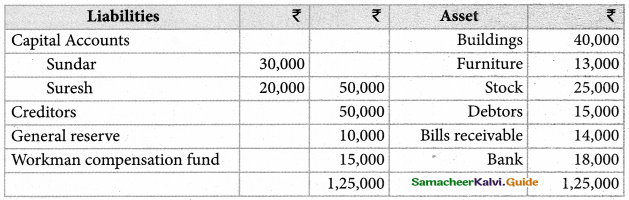
Question 6
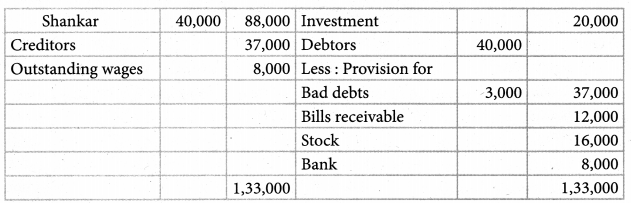
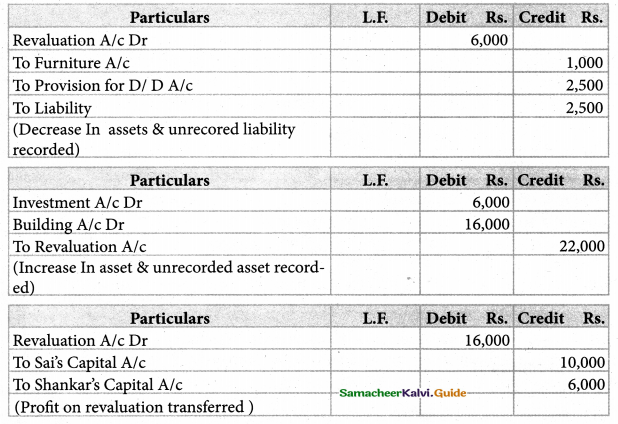
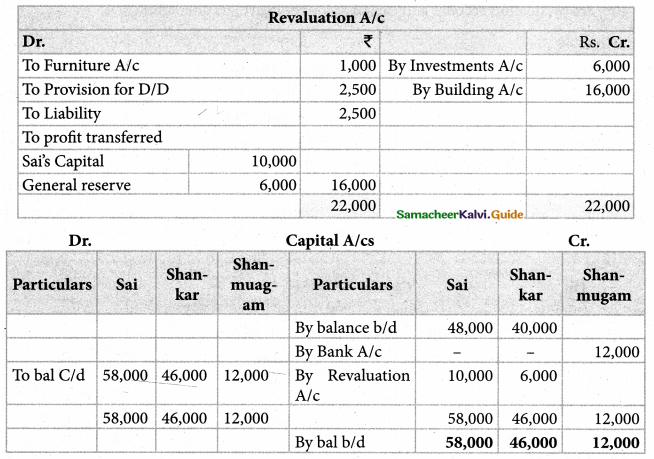
Chandru, Vishal, and Ramanan are partners in firms sharing profits and losses equally. Their balance sheet as of 31st March 2018 is as follows.
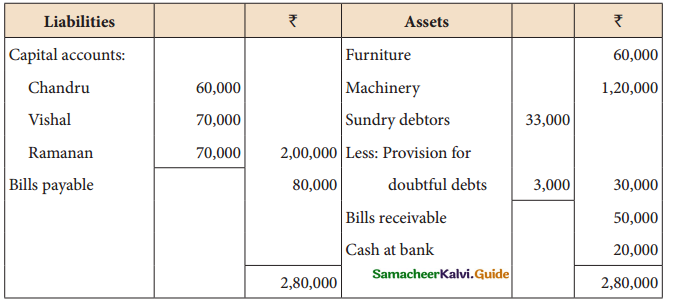
Ramanan retired on 31st March 2019 subject to the following conditions:
(i) Machinery is valued at ₹ 1,50,000
(ii) Value of furniture brought down by ₹ 10,000
(iii) Provision for doubtful debts should be increased to ₹ 5,000. ,
(iv) investment of ₹ 30,000 not recorded in the books is to be recorded now.
Pass necessary journal entries and prepare revaluation account and capital account of partners.
Solution:
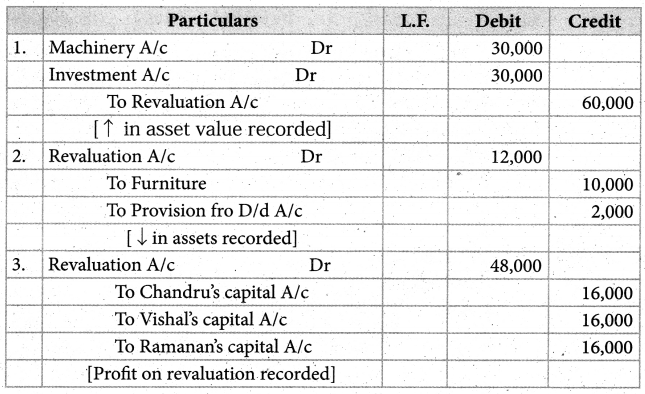
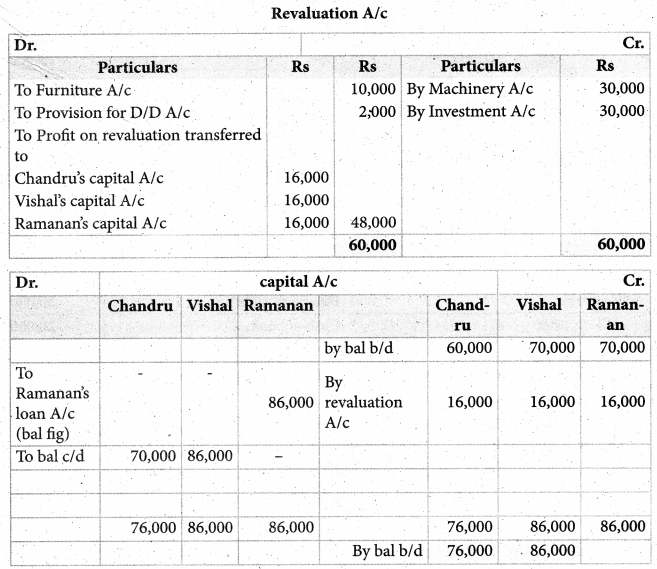
Answer:
Revaluation profit: ₹ 48,000;
Capital account:)
Chandru :₹ 76,000(Cr);
Vishal: ₹ 86,000(Cr);
Ramanan’s loan account: ₹ 86,000 (a))
Question 7.
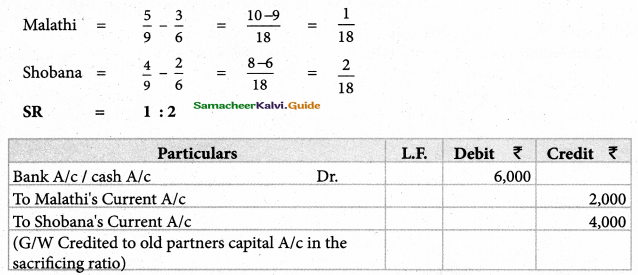
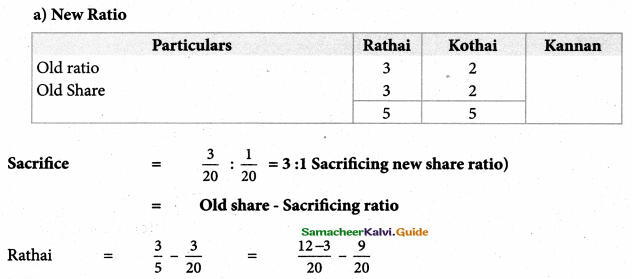
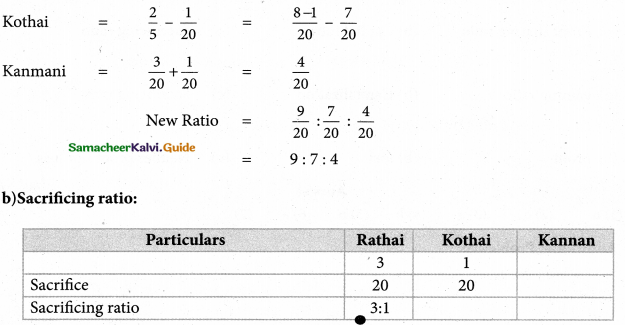
Kayal, Mala and Neela are partners sharing profits in the ratio of 2:2:1. kayal retires and the new profit sharing ratio between Mala and Neela is 3:2. Calculate the gaining ratio.
Solution:
New Profit Sharing Ratio and Gaining Ratio
Gain Ratio = New Ratio – Old Ratio
Kayal –
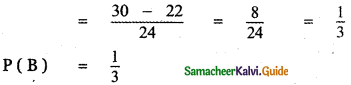
Mala = \(\frac { 3 }{ 2 }\) – \(\frac { 2 }{ 5 }\) – \(\frac { 1 }{ 5 }\)
Neela = \(\frac { 2 }{ 5 }\) – \(\frac { 1 }{ 5}\) = \(\frac { 1 }{ 5 }\)
Gaining Ratio = 1:1
![]()
Question 8.
Sunil, Sumathi and Sundari are partners sharing profits in the ratio of 3:3:4. Sundari retires and her share is taken up entirely by Sunil. Calculate the new profit sharing ratio and gaining ratio.
Solution:
old ratio = 3:3:4 (Sunil:sumathi:sundar)
New Ratio = old ratio + gaining ratio

Answer:
Gaining ratio:4:0;
New ratio:7:3
Question 9.
Ramu, Somu and Gopu are partners sharing profits in the ratio of 3:5:7. Gopu retires and the share is purchased by Ramu and Somu in the ratio of 3:1. Find the new profit sharing ratio and gaining ratio.
Solution:
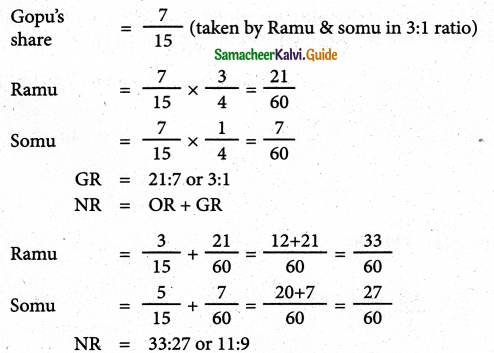
Question 10.
Navin, Ravi and Kumar are partners sharing profits in the ratio of 1/2, 1/4 and 1/4 respectively. Kumar retires and his share is taken up by Navin and Ravi equally. Calculate the new profit sharing ratio and gaining ratio.
Solution :
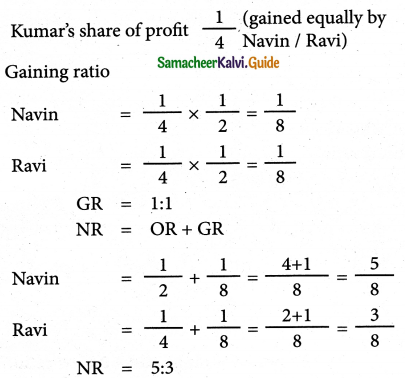
Answer:
New ratio:5:3;
Gaining ratio: 1:1
![]()
Question 11.
Mani, Gani and Soni are partners sharing the profits and losses in the ratio of 4:5:6. Mani retires from the firm. Calculate the new profit sharing ratio and gaining ratio.
Mani: Gani: Soni → 4:5:6
[If nothing is mentioned about the new ratio, old ratio of the continuing partners is equal to their new ratio.]
Solution:
Old ratio = 4:5:6
New ratio – 5:6

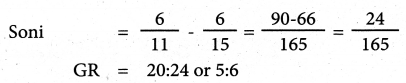
Answer:
New profit shaving ratio and gaining ratio is 5:6
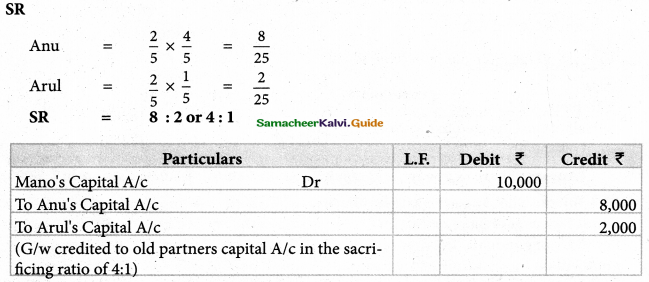
Question 12.
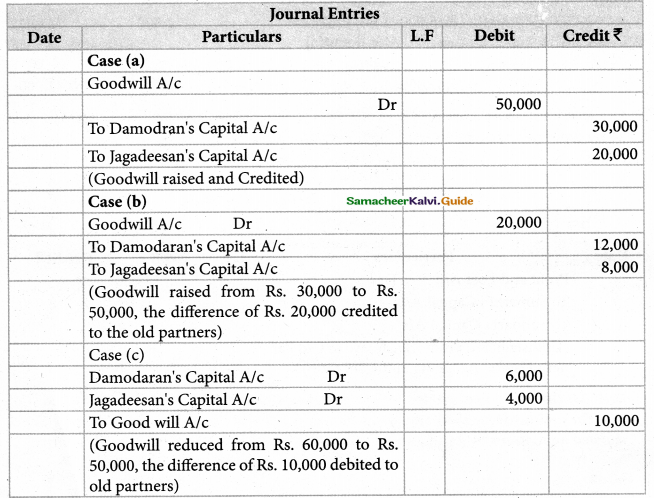
Rajan, Suman and jegan were partners in firm sharing profits and losses in the ratio of 4:3:2 Suman retired from partnership. The goodwill of the firm on the date of retirement was valued at ₹ 45,000. Pass necessary journal entries for goodwill on the assumption that the fluctuating capital method is followed.
Solution :
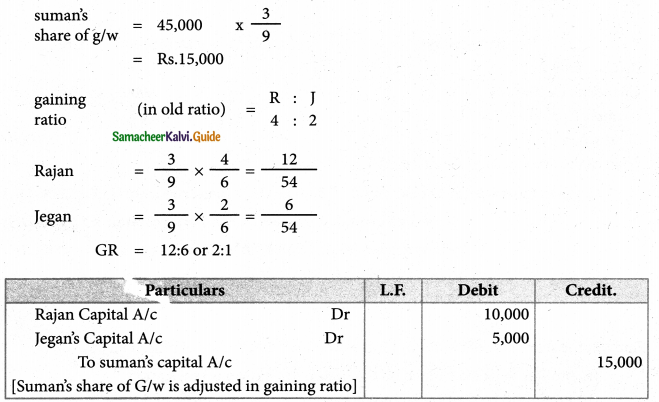
Answer:
Suman’s share of goodwill: ₹ 15,000;
Rajan’s capital: ₹ 10,000(Dr);Jegan’s capital: ₹ 5,000(Dr);
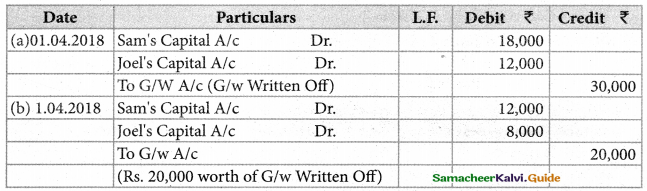
Question 13.
Balu, Chandru and Nirmal are partners in a firm sharing profits and losses in the ratio of 5:3:2 on 31st March 2018, Nirmal retires from the firm. On the date of Nirmal’s retirement, goodwill appeared in the books of the firm at ₹ 60,000 By assuming thuctuating capital account, pass the necessary journal entry if the partners decide to
(a) Write off the entire amount of existing goodwill
(b) Write off half of the existing goodwill.
Solution :
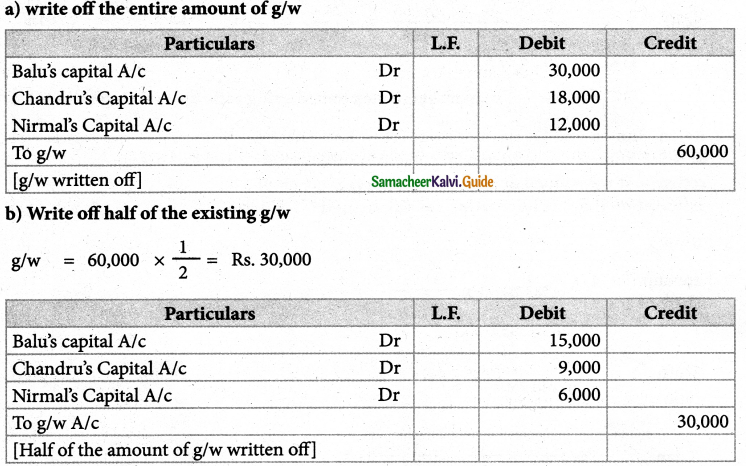
Answer:
(a) Balu’s capital: ₹ 30,000(Dr.); Chandru’s capital: ₹ 18,000(Dr.)
Nirmala’s capital: ₹ 12,000(Dr);(b)balu’s capital: ₹ 15,000(Dr);
Chandru’s capital: ₹ 9,000(Dr);Nirmala’s capital: ₹ 6,000(Dr);
![]()
Question 14.
Rani, Jaya and Rathi are partners sharing profits and losses in the ratio of 2:2:1. On 31.3.2018, Rathi retired from the partnership. Profit of the preceding years is as follows: 2014: ₹ 10,000; 2015; ₹ 20,000; 2016; ₹ 18,000 and 2017; ₹ 32,000
Find out the share of profit of Rathi for the year 2018 till the date of retirement if
(a) profit is to be distributed on the basis of the previous year’s profit
(b) Profit is to be distributed on the basis of the average profit of the past 4 years.
Also pass necessary journal entries by assuming partners’ capitals are fluctuating.
Solution:
(a) on the basis of previous years profit
Profit of 2017 = Rs.32,000
Date of retirement = 31.3.2018
share of profit of Rathi for 3 months = \(32,000 \times \frac{3}{12} \times \frac{1}{5}\)
= Rs. 1600
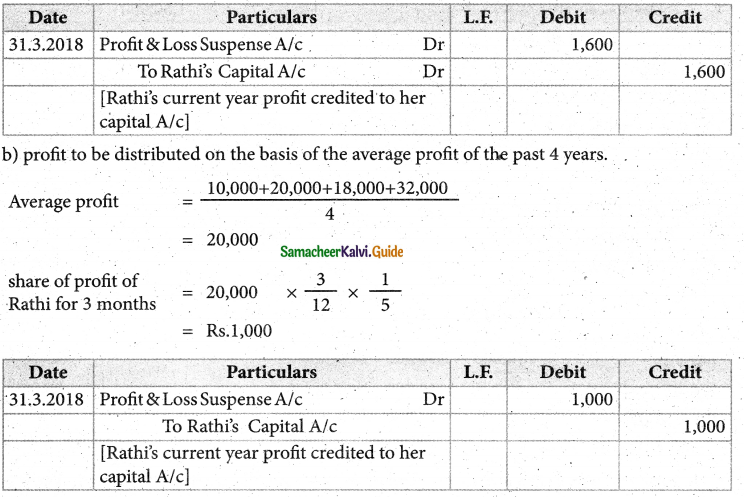
Answer:
(a) Rathi’s share of profit: ₹ 1,600; (b) Rathi’s share of profit: ₹ 1,000;
Settlement of amount due to the retiring partner.
Question 15.
Kavin, Madhan, and Ranjith are partners sharing profits and losses in the ratio of 4:3:3 respectively. Kavin retires from the firm on 31st December 2018. On the date of retirement, his capital account shows a credit balance of ₹ 1,50,000. Pass journal entries if:
(a) The amount due is paid off immediately.
(b) The amount due is not paid immediately.
(c) ₹ 1,00,000 is paid and the balance in the future.
Solution:


Answer:
(a) Kavin’s loan:Nil;
(b) Kavin’s loan: ₹ 1,50,000;
(c) Kavin’s loan: ₹ 50,000;
![]()
Question 16.
Manju, Chara’and Lavanya are partners in firm sharing profits and losses in the ratio of 5:3:2. The balance sheet as of 31st March, 2018 was as follows:
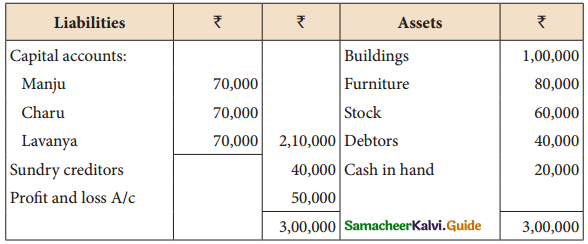
Manju retired from the partnership firm on 31.3.2018 subject to the following adjustments:
(i) Stock to be depreciated by ₹ 10,000
(ii) Provision for doubtful debts to be created for ₹ 3,000
(iii) Buildings to be appreciated by ₹ 28,000.
Prepare revaluation account and capital accounts of partners after retirement.
Solution:
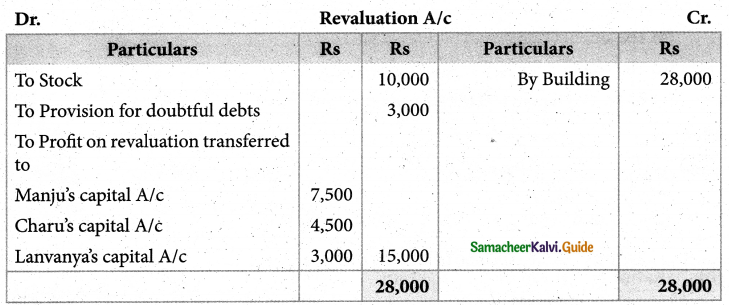
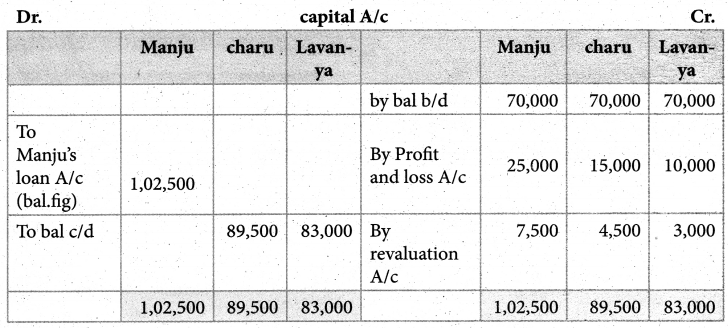
Answer:
Revaluation profit: ₹ 15,000; Manju’s loan account:
₹ 1,02,000(Cr).Capital account: Charu ₹ 89,OO0(Cr); Lavanya: ₹ 83,000(Cr))
Question 17.
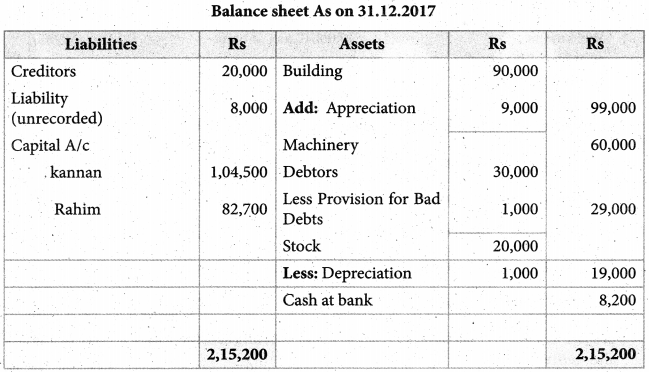
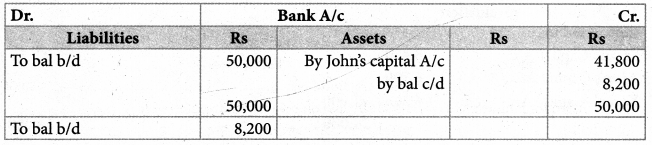
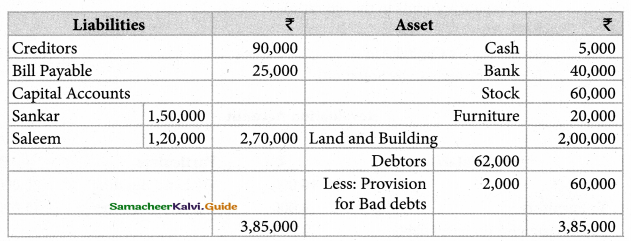
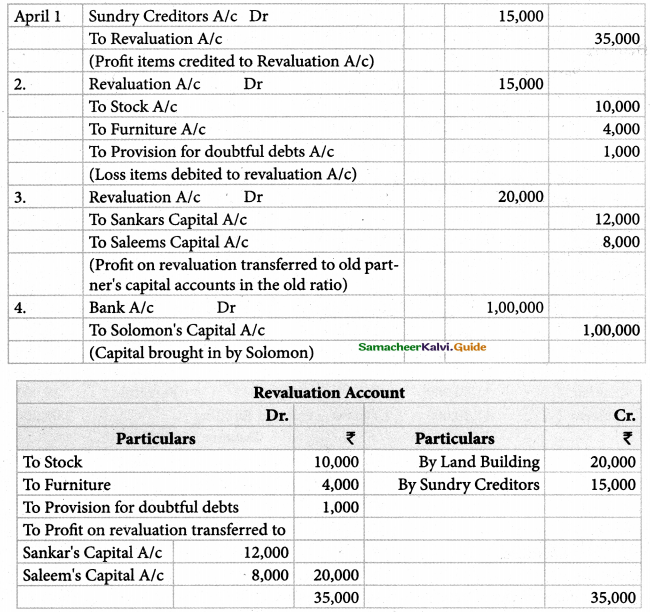
Kannan, Rahim, and John are partners in a firm sharing profits and losses in the ratio of 5:3:2. The balance sheet as of 31st December 2017 was as follows:
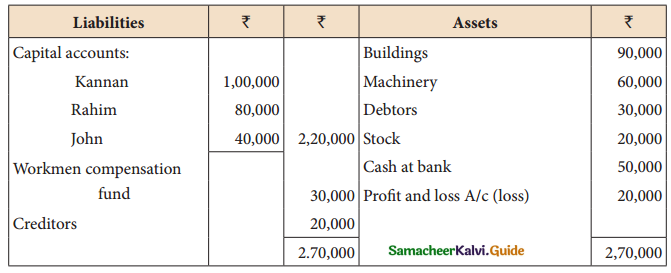
John retires on 1st January 2018, subject to the following conditions :
(i) To appreciate building by 10%
(ii) Stock to be depreciated by 5%
(iii) To provide ₹ 1,000 for bad debts
(iv) An unrecorded liability of ₹ 8,000 has been noticed.
(v) The retiring partner shall be paid immediately.
prepare revaluation account, partner’s capital account, and the balance sheet of the firm after retirement.
Solution :
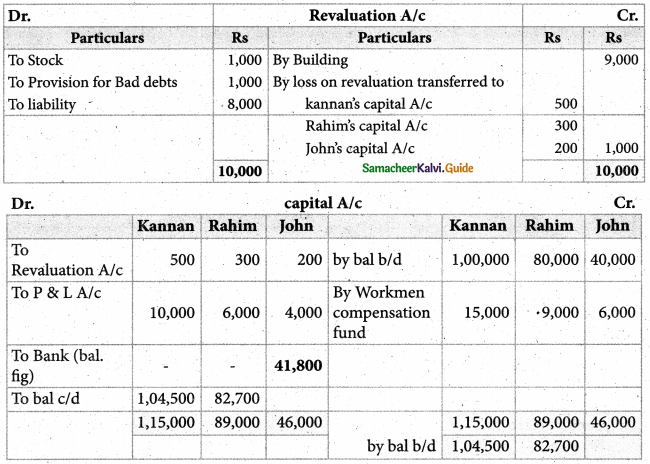
Answer:
Revaluation loss: ₹ 1,000; capital Account; Kannan: ₹ 1,04,500
Rahim: ₹ 82,700 Amount paid to John ₹ 41,800; Balance sheet total: ₹ 2,15,000
![]()
Question 18.
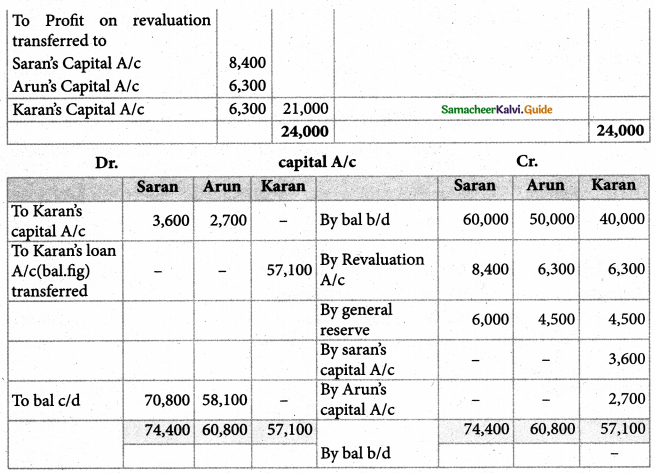
Saran, Arun, and Karan are partners in firms sharing profits and losses in the ratio of 4:3:3. The balance sheet as of 31.12.2016 was as follows:
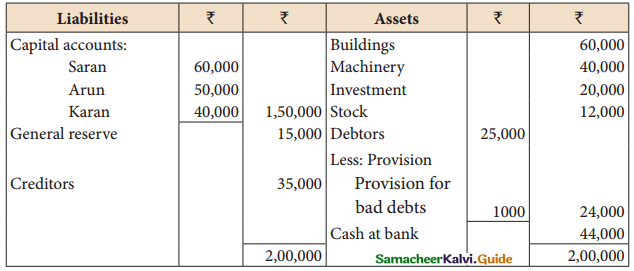
Karan retires on 1.1.2017, subject to the following conditions:
(i) Goodwill of the firm is valued at ₹ 21,000 %
(ii) Machinery to be appreciated by 10%
(iii) Building to be valued at ₹ 80,000
(iv) provision for bad debts to be raised to ₹ 2,000
(v) Stock to be depreciated by ₹ 2,000
(vi) The final amount due to Karan is not paid immediately.
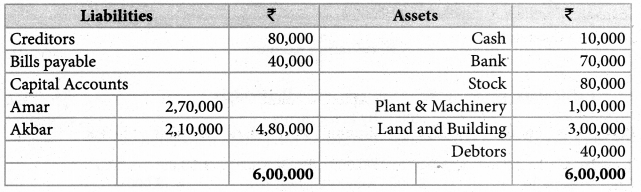
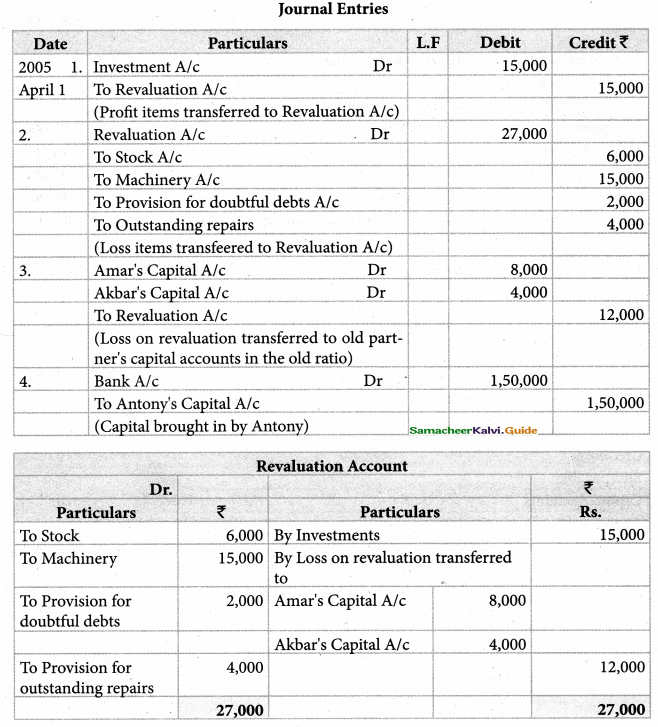
prepare the necessary ledger accounts and show the balance sheet of the firm after retirement. *
Solution:
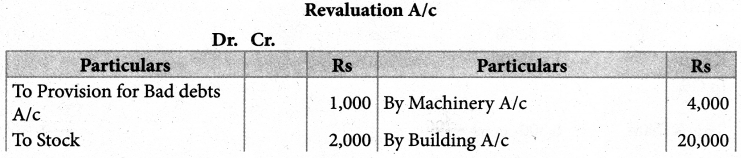
Gaining ratio
Old ratio = 4:3:3
New ratio = 4:3
Gaining ratio = Saran = New ratio – old ratio
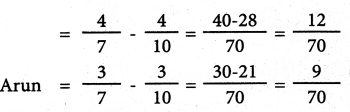
GR = 12:9 or 4:3
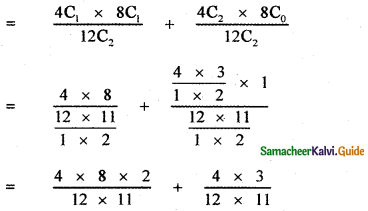
Karan’s share of G/w = 21,000 x \(\frac{3}{10}\) = Rs.6,300
K’s g/w In GR = Rs. 6,300
Saran’s share = 6300 x \(\frac{3}{10}\) = Rs.3,600
Aruns share = 6,300 x \(\frac{3}{7}\) = Rs.2,700
Answer:
Revaluation profit: ₹ 21,000; capital A/c: Saran: ₹ 70,800, Arun: ₹ 58,100
Karan’s loan Account ₹ 57,100; Balance sheet total: ₹ 2,21,000
![]()
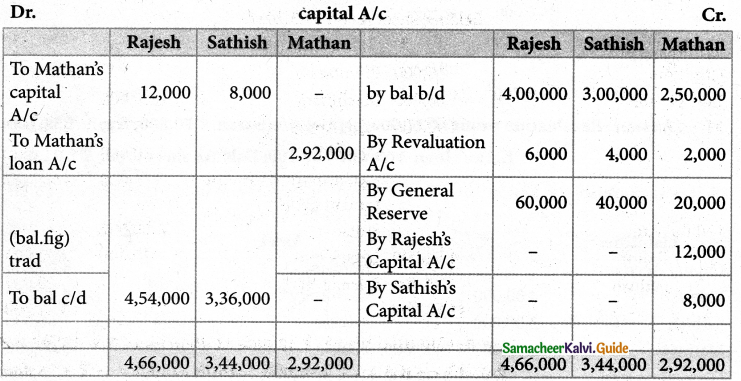
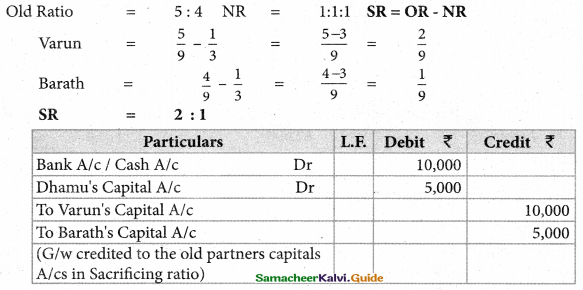
Question 19.
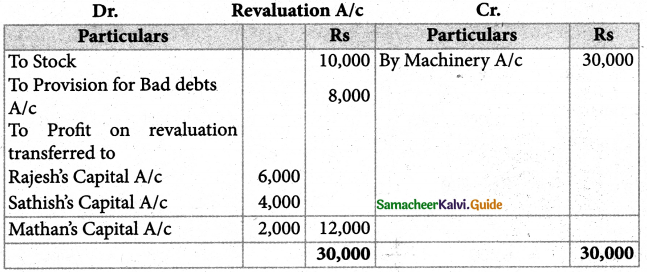
Rajesh, Sathish and Mathan are partners sharing profits and losses in the ratio of 3:2:1. respectively. Their balance sheet as on 31.3.2017 is given below:
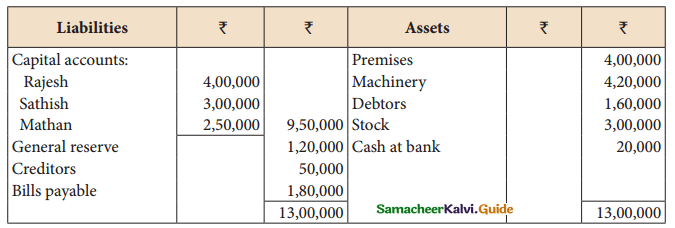
Mathan retires on 31st March, 2017 subject to the following conditions :
(i) Rajesh and Sathis will share profits and losses in the ratio of 3:2
(ii) Assets are to be revalued as follows;
Machinery ₹ 4,50,000, Stock ₹ 2,90,000 , Debtors ₹ 1,52,000
(iii) Goodwill of the firm is valued at ₹ 1,20,000
prepare the necessary ledger accounts and the balance sheet immediately after the retirement of Mathan.
Solution:
Gaining ratio = New ratio – old ratio
Rajesh = \(\frac{3}{5}-\frac{3}{6}=\frac{18-15}{30}=\frac{3}{30}\)
Sathish = \(\frac{2}{5}-\frac{2}{6}=\frac{12-10}{30}=\frac{2}{30}\)
GR = 3:2
Mathans share of G/w = 12,000 x \(\frac{1}{6}\) = Rs.20,000
In gaining ratio
Rajeshs share = 20,000 x \(\frac{3}{5}\) = Rs. 12,000
Sathishs share = 12,000 x \(\frac{2}{5}\) = Rs. 8,000
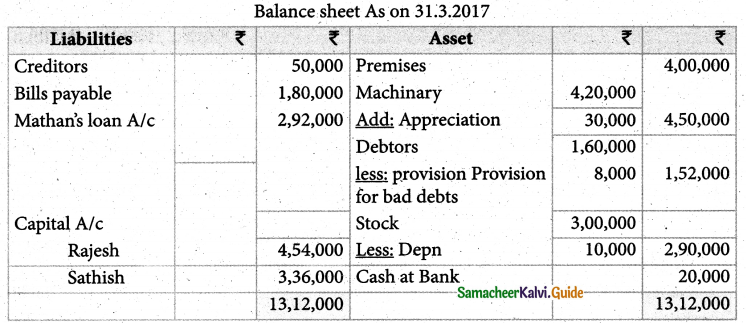
Answer:
Revaluation Profit: ₹ 12,000; Mathan loan: A/c: ₹ 2,92,000 Rajesh’s capital A/c ₹ 4,54,000; Sathish capital A/c: ₹ 3,36,000
Balance sheet total ₹ 13,10,000
Question 20.
Janani and Jamuna are partners sharing profits and losses in the ratio of 3:3:1. respectively. Janaki died on 31st December 2017. The final amount due to her showed a credit balance of ₹ 1,40,000. Pass Journal Entry if
(i) The amount due is paid off immediately.
(ii) The amount due is not paid immediately.
(iii) ₹ 75,000 is paid and the balance in the future.
Solution:


![]()
Question 21.
Varsha, Shanthi, and Madhuri are partners in a firm sharing profits in the ratio of 5:4:3. Their balance sheet as of 31st December 2017 is as under:
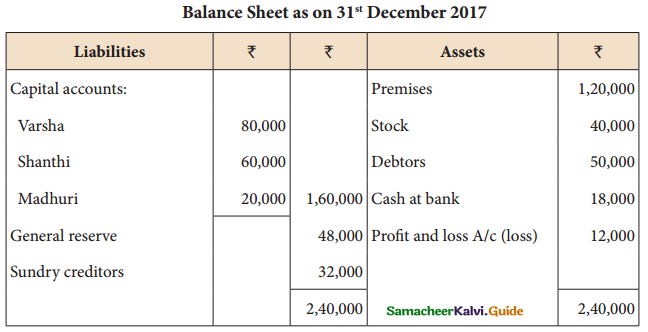
on 1st January 2018, Madhuri died and on her death, the following arrangements are made:
(i) Stock to be depreciated by ₹ 5,000
(ii) Premises is to be appreciated by 20%
(iii) To provide ₹ 4,000 for bad debts
(iv) The final amount due to Madhuri was not paid.
prepare revaluation account, partners capital account, and the balance sheet of the firm after death.
Solution:
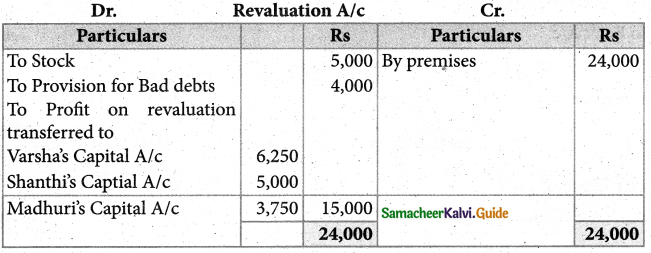
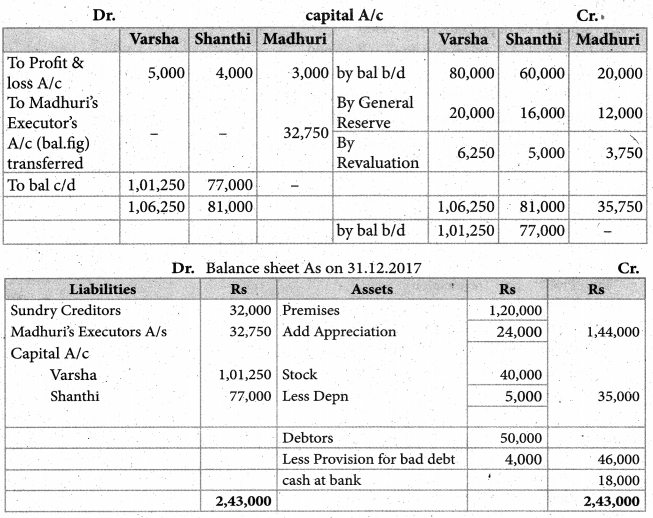
Answer: Revaluation Profit ₹ 15,000;
Varsha’s capital A/c ₹ 1,01,250; Sathish capital A/c: ₹ 77,000
Madhuri’s executors account ₹ 32,750; Balance sheet total: ₹ 2,43,000
Question 22.
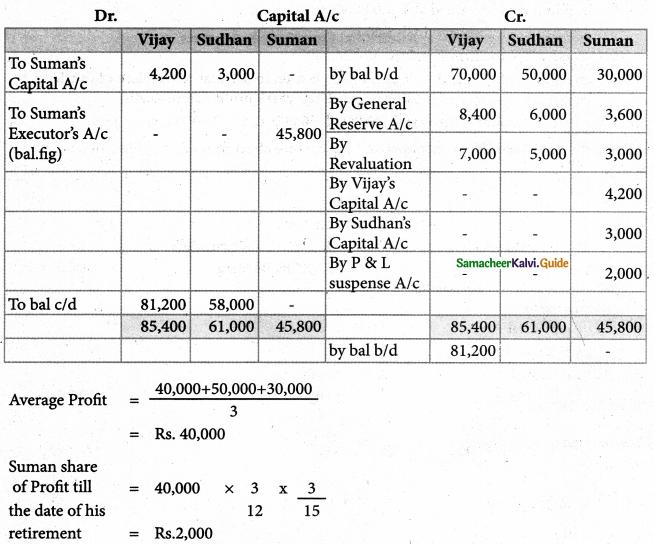
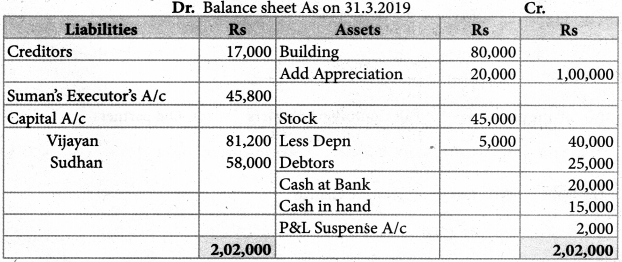
Vijayan, Sudhan, and Suman are partners who share profits and losses; in the capital ratio. Their balance sheet as of 31st December 2018 is as follows:
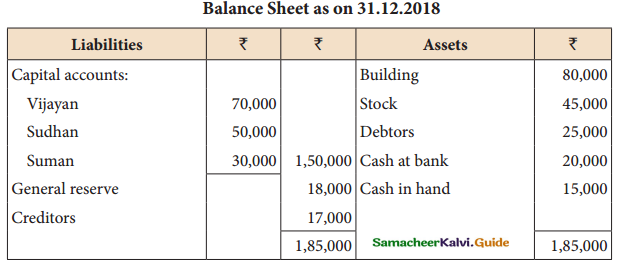
Suman died on 31.3.2019. On the death of Suman, the following adjustments are made:
(i) Building is to be valued at ₹ 1,00,000
(ii) Stock to be depreciated by ₹ 5,000
(iii) Goodwill of the firm is valued at ₹ 36,000
(iv) Share of profit from the closing of the last financial year to the date of death on the basis of the average of the three completed year’s profit before death.
profit for 2016, 2017 and 2018 were ₹ 40,000,₹ 50,000 and ₹ 30,000 respectively.
Prepare the necessary ledger accounts and the balance sheet immediately after the death of Suman.
Solution:
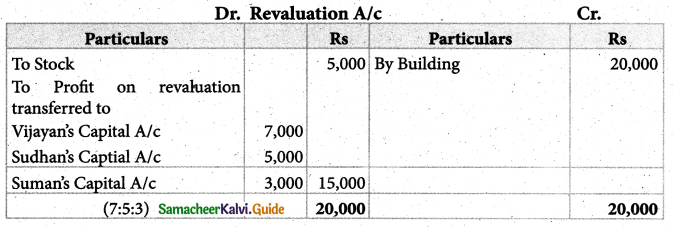
Suman share of G/w
Vijayan : Sudhan : suman
Old ratio = 7:5:3
New ratio = 7:5
Gaining ratio New ratio – old ratio
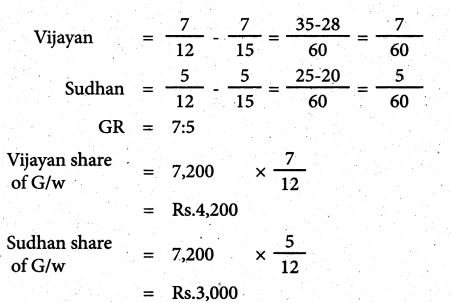
Answer:
Revaluation Profit: ₹ 15,000; Vijayan’s capital A/c: ₹ 81,200;
Sudhan’s capital A/c ₹ 58,000; Suman’s Executor’s A/c: ₹ 45,800
Balance sheet total: ₹ 2,02,000
12th Accountancy Guide Retirement and Death of a Partner Additional Important Questions and Answers
I. Choose the best answer
![]()
Question 1.
In the absence of any specific agreement, between the partners, partners loan to the firms will carry an inters at the rate of …………… %
(a) 5%
(b) 6%
(c) 4%
Answer:
(b) 6%
Question 2.
A,B & C shares profit as 1/2 to A, 1/3 to B, and 1/6 to C. If B retries, then the new profit sharing ratio ………..
(a) 3:1
(b) 3:2
(c) 1:3
Hint:
Old Partner’s A, B, C
Old ratio = \(\frac{1}{2}: \frac{1}{3}: \frac{1}{6}\)
‘B’ Retire Partner
In order to equalise the denomination
\(\frac{3}{6}: \frac{2}{3}: \frac{1}{6}\)
Now profit sharing ration = \(\frac{3}{4}: \frac{1}{4}\). or 3 :1
Answer:
(a) 3:1
Question 3.
At the time of retirement, the revelation profits of the business will be shared by ……………… partners.
(a) all the partners
(b) Continuing partners
(c) Old partners
Answer:
(a) all the partners
Question 4.
At the time of retirement, of partners, the existing partners stand to
(a) gain
(b) loss
(c) no change
Answer:
(a) gain
![]()
Question 5.
A,B & C are sharing profits in the ratio of \(\frac{2}{5}\) , \(\frac{2}{5}\) \(\frac{1}{5}\) C retired from business and his share was purchased equally by A and B, Then new profit sharing ratio shall be
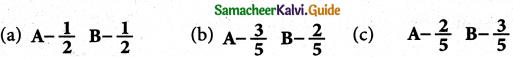
Hint:

Answer:
a
Question 6.
If the amount due to the outgoing partner is transferred to loan A/c then he is entitled to interest at ……………….. until it is paid out.
(a) 6%
(b) 5%
(c) 8%
Answer:
(a) 6%
Question 7.
At the time of retirement of a partner calculation of new profit, ratio is
(a) not necessary
(b) necessary
(c) optional
Answer:
(b) necessary
III Short Answer Questions
Question 1.
What are the journal entries to be passed to transfer the accumulated profits, losses & reserves?
Answer:


Question 2.
Write the format of Revaluation A/c.
Answer:
New profit sharing ratio is the agreed proportion in which future profit will be distributed to the continuing partners. If the new profit sharing ratio is not agreed, the continuing partners will share the profits and losses equally.
![]()
Question 3.
How will you adjust the share of profits loss of the retaining partner if he retires in between in an accounting year?
Answer:
When a partner retires in between in an accounting year, his share of the current year’s profit or loss upto the date of retirement has to be distributed to the retiring partner. It may be estimated based on the current year’s turnover. The previous year’s profit or the average of the past year’s profit may also be taken as the base to estimate the current year’s profit. The following journal entry is passed

Question 4.
What are the adjustments to be made on the death of a partner?
Answer:
The following adjustments are made on the death of a partner.
- Distribution of accumulated profits, reserves, and losses
- Revaluation of assets and liabilities
- Determination of new profit sharing ratio and gaining ratio
- Adjustment for goodwill
- Adjustment for current year’s profit or loss upto the date of death
- Settlement of the amount due to the deceased partner.
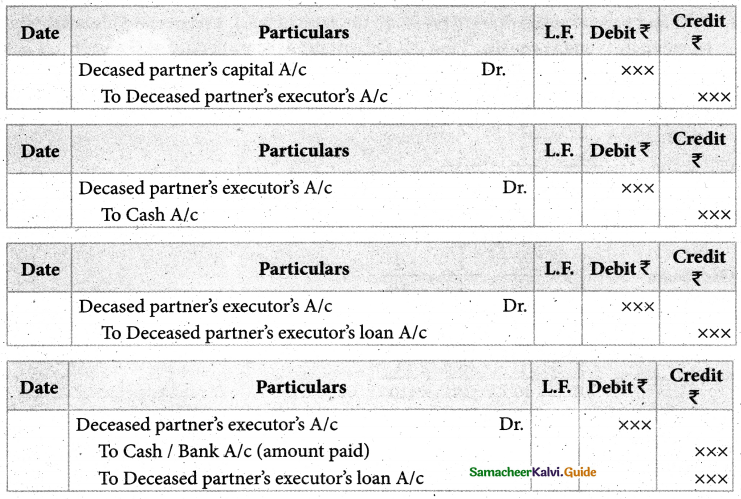
Question 5.
What are the journal entries to be passed for settlement of the amount due to the deceased partner
Answer:
To transfer the amount due to the deceased partner to the executor or legal representative of the deceased partner.
![]()
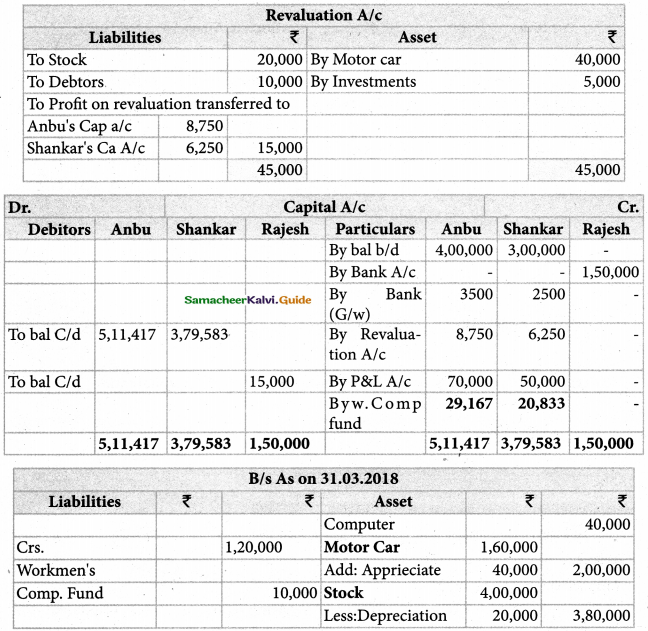
IV Additional Problems:
Question 1.
A, B, and C sharing profits in the ratio of 5:3:2. C retires. Find out the new profit sharing ratio and gaining ratio.
Solution:

Question 2.
G, H, and I are partners sharing profits in the ratio of 5:3:2.1 taken up by G and H equally. Find out the new profit sharing ratio of G and H.
Solution:

Question 3.
J, K and L are partners sharing profits in the ratio of 5:3:2. retires and his share was taken up entirely by K. Find out the new profit sharing ratio and gaining ratio of continuing partners
Solution:

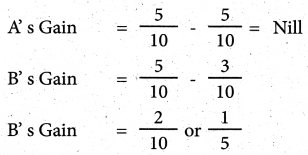
![]()
Question 4.
X,Y and Z are partners sharing profits in- the ratio of 5:3:2 Z retires and the ratio between X and Y is 3:2. Find out the gaining ratio
Solution :

Question 5.
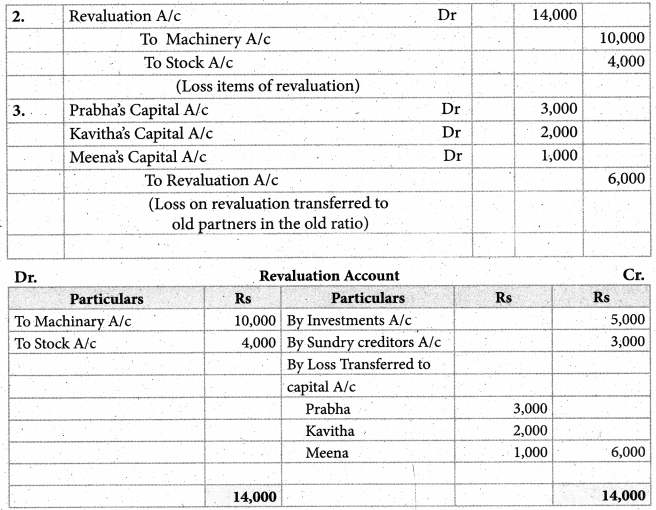
Prabha,Kavitha and Meena were partners of a firm sharing profit and loss in the ratio of 3:2:1 Meena Wanted to retire. They decided to revalue the assets and liabilities of the firm as indicated below:
To write down Machinery by Rs 10,000 and Stock by Rs. 4,000
To bring into books as unrecorded investments Rs. 5,000
To Write off Rs.3,000 from sundry creditors as it was no longer liable.
Pass entries to give effect to the above adjustments. Show also Revaluation account.
Solution:

Question 6.
Banumathi, Bharafhi and Shanthi are partners sharing, profits in the ratio of 5:3:2. On April 1, 2005 Shanthi decided to retire. On that date, there was a credit balance of Rs. 60,000 in their profit and loss account. Pass entry.
Solution:

Question 7.
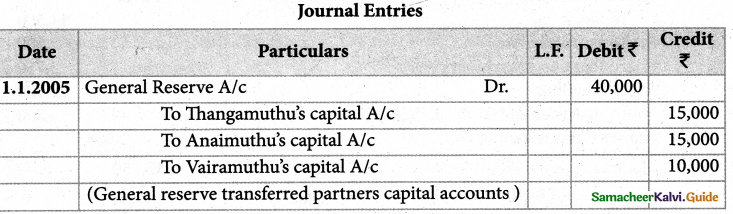
Thangamuthu, Anaimuthu and Vairamuthu are partners sharing profit and loss in the ratio of 3:3:2. Thangamuthu wanted to retire on 1st June 2005, the firms books showed a general reserve of Rs. 40,000. Pass entry.
Solution:
![]()
Question 8.
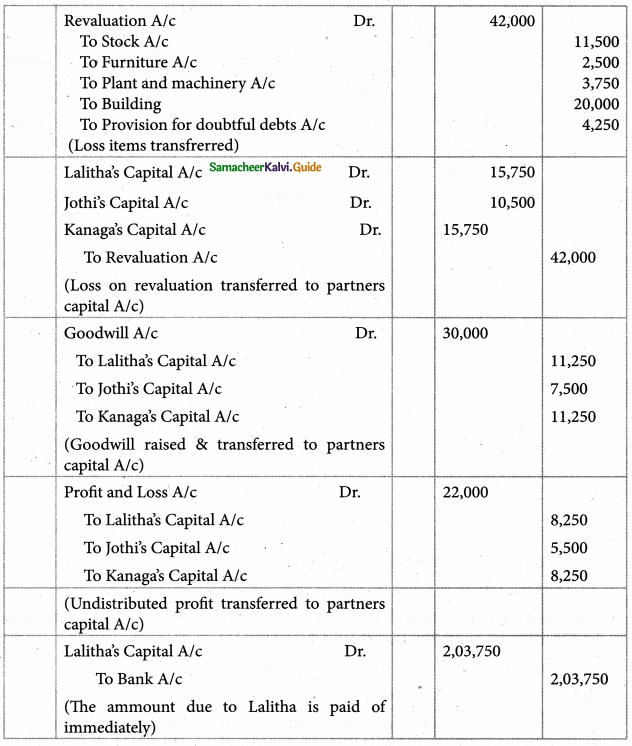
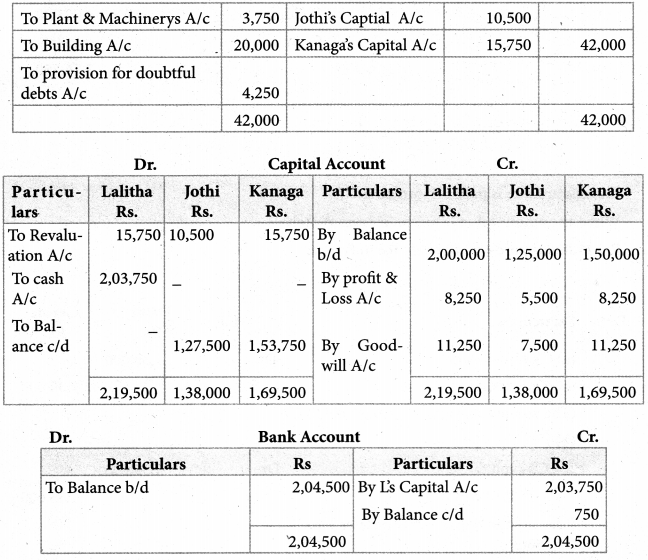
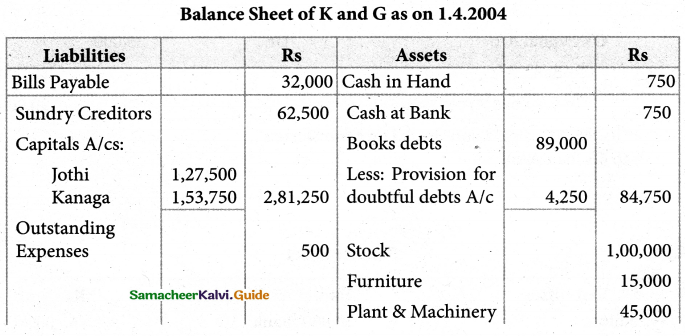
Lalitha, Jothi and Kanaga were partners of a sharing profit and losses in the ratio of 3:2:3, Set out below was their balance sheet as on 31st March 2003.
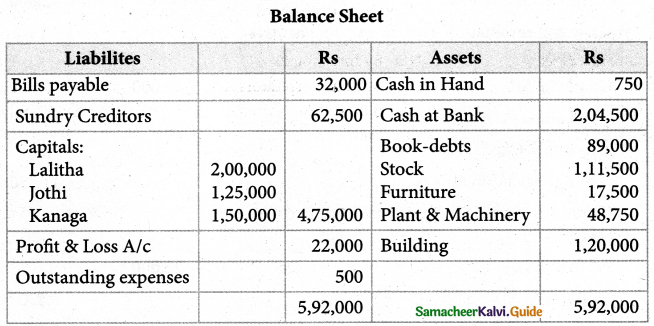
Lalitha retired from the partnership on 1st April 2004 on the following terms:
Goodwill of the firm was to be valued at Rs.30,000
The assets are to be valued as under Stock Rs. 1,00,000; Furniture Rs.15,000; Plant and Machinery Rs.45,000; Building Rs.1,00,000.
A provision for doubtful debts is created at Rs.4,250.
Lalitha was to be paid off immediately.
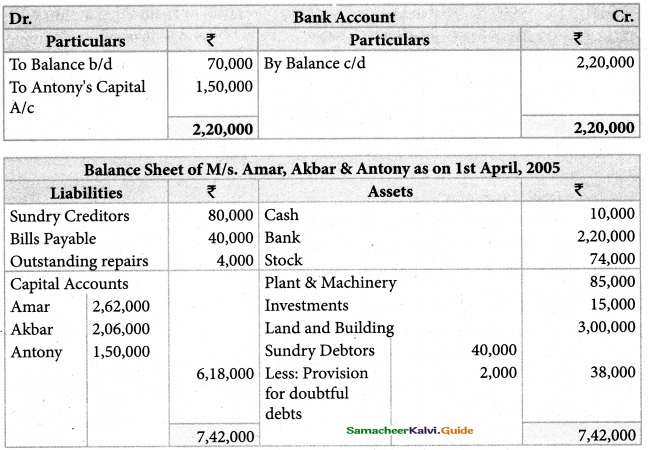
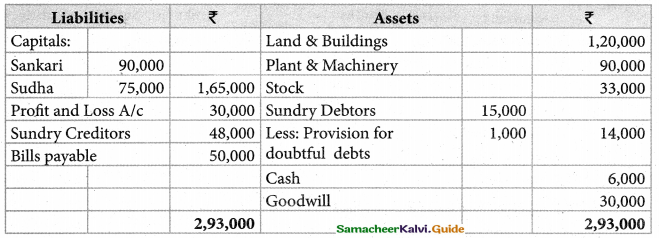
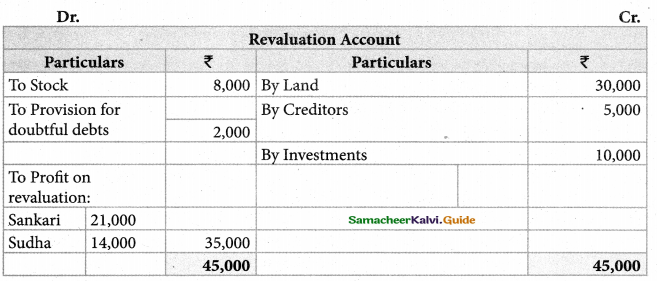
Show the journal entries, prepare a revaluation account, capital account, Bank account, and balance sheet of the reconstituted partnership.
Solution:



Question 9.
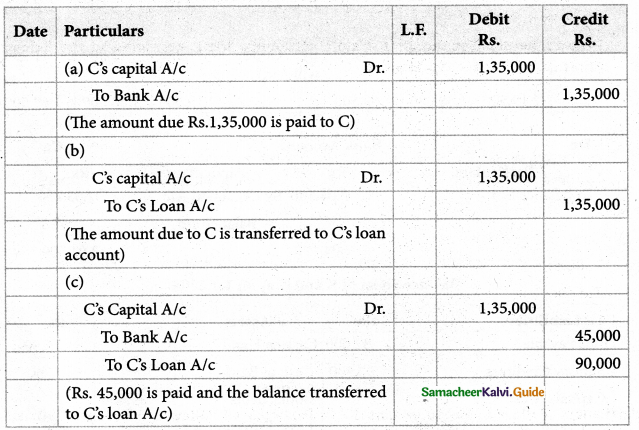
‘9. A, B and C are partners sharing profits and losses in the ration of 5:3:2 respectively. Retries from the firm on 1st April 2005. After his retirement, his capital account shows a credit balance of Rs.1,35,000 after the necessary adjustment made. Give journal entries, if.
the amount due is paid off immediately.
When the amount due is not paid immediately.
Rs. 45,000 is paid and the balance In the future.
Solution :
![]()
Question 10.
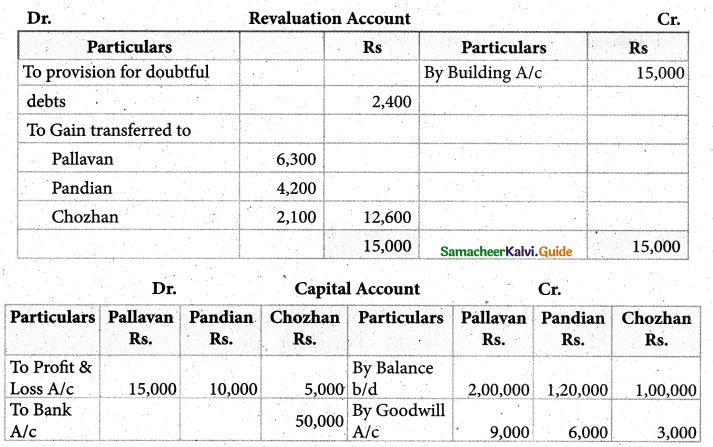
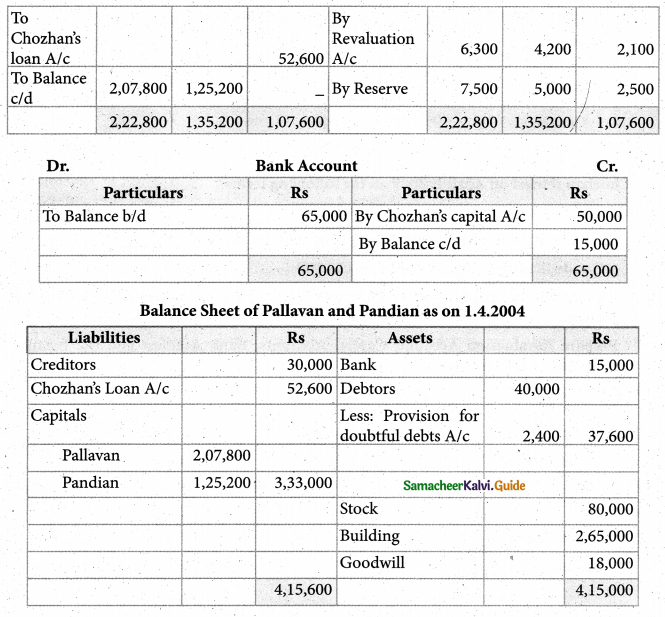
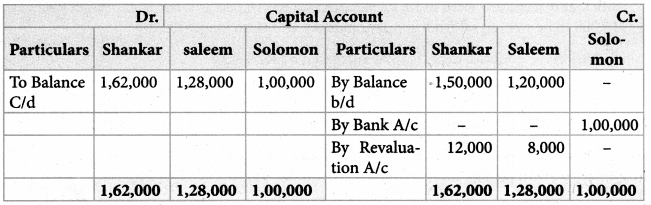
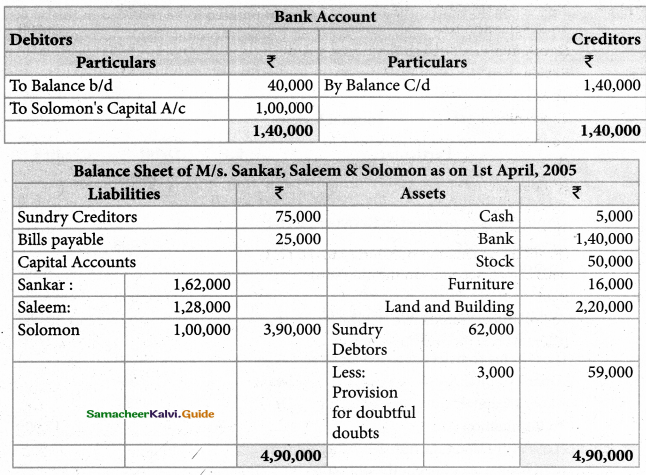
Pallavan, Pandian and Chozhan were carrying on partnership business sharing profits in the ratio of 3:2:1. On March 31, 2005, the balance sheet of the firm stood as follows:

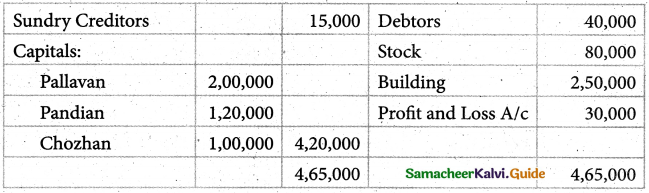
Chozhan retried on April 1, 2005 on the following terms:
Building to be appreciated by Rs. 15,000
Provision for doubtful debts to be made at 6% on debtors
Goodwill of the firm is valued at Rs. 18,000
Rs.50,000 to be paid to chozhan immediately and the balance transferred to his loan account.
Prepare Revaluation Account, Capital Accounts, Bank Account and the Balance Sheet after Chozhan’s retirement.
Solution :

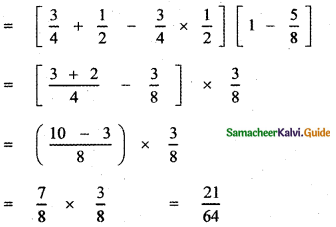

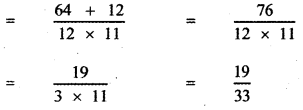




























































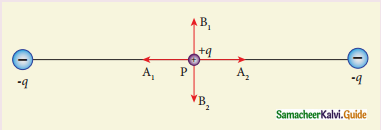
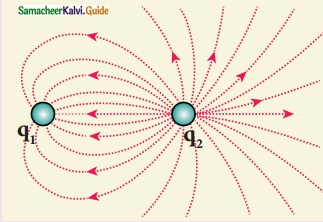
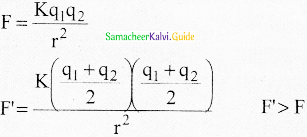
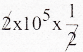 q = 8 × 10-2c
q = 8 × 10-2c
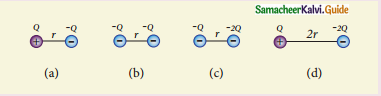

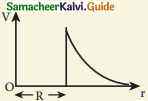
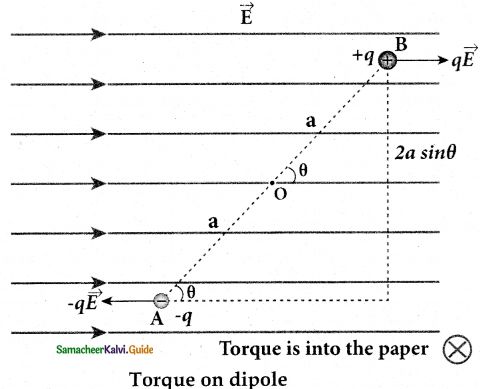
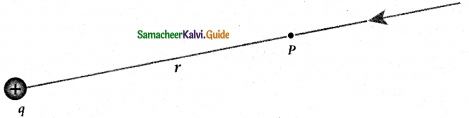
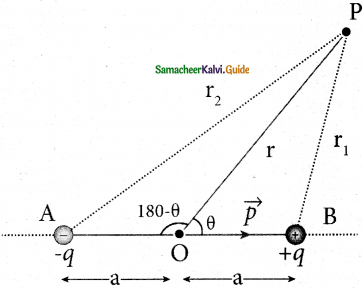

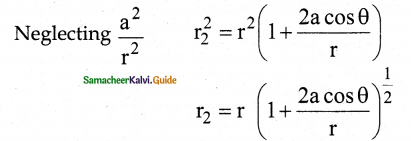

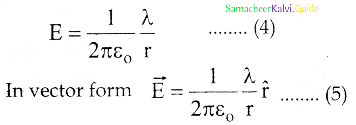
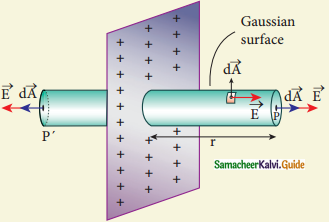

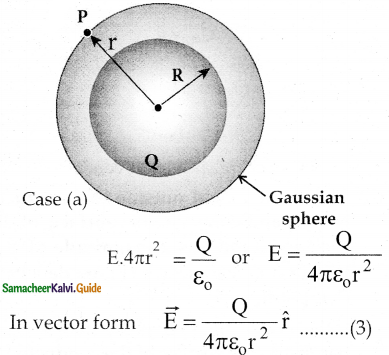
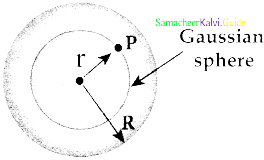
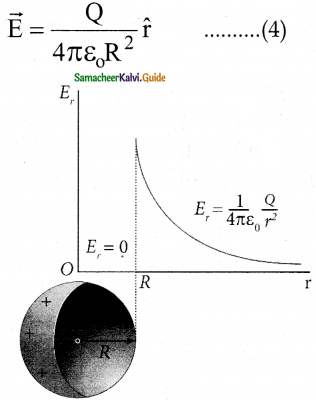
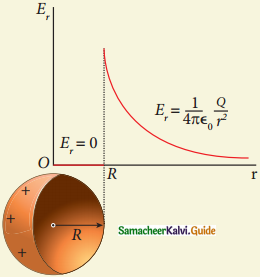 Electric field versus distance for a spherical shell of radius R
Electric field versus distance for a spherical shell of radius R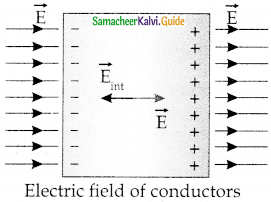
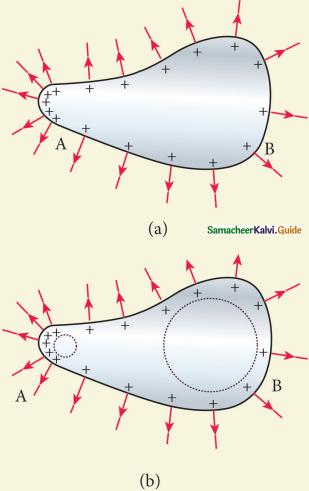
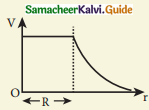
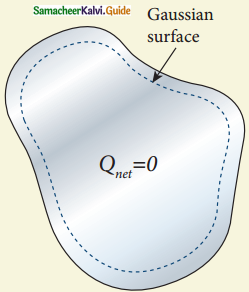 No net charge inside the conductor
No net charge inside the conductor