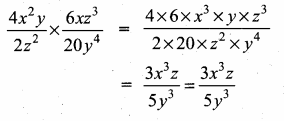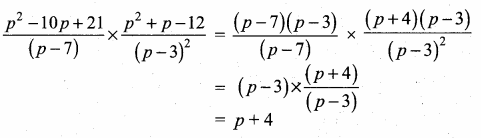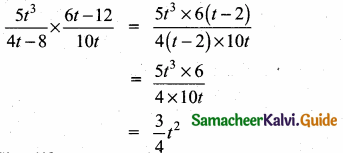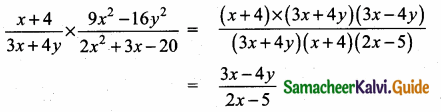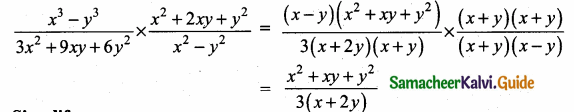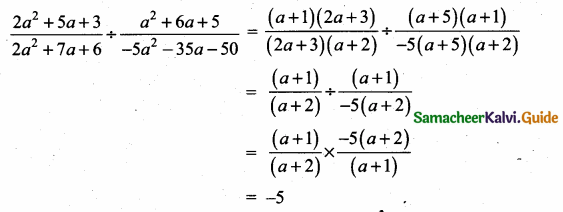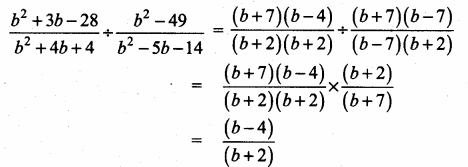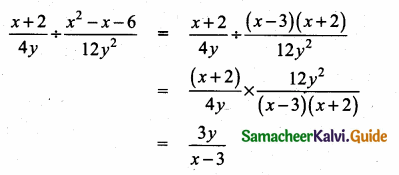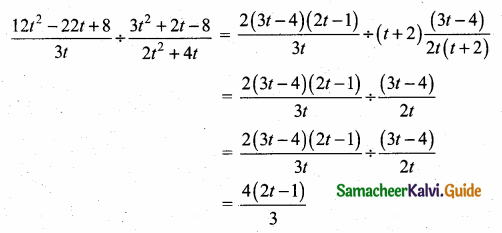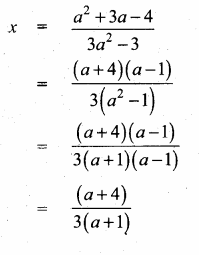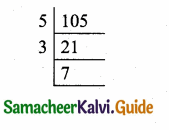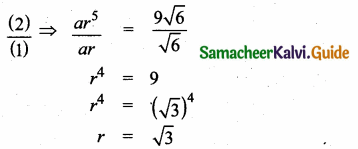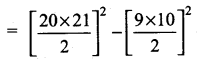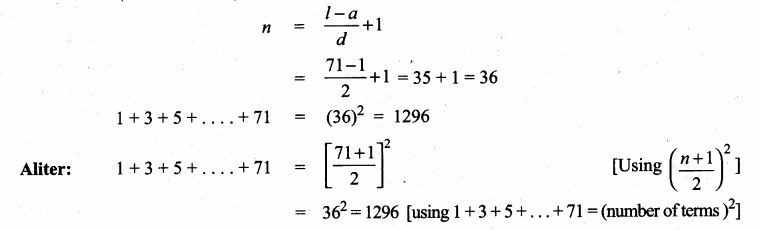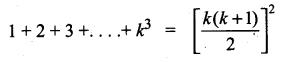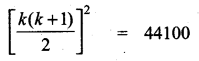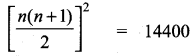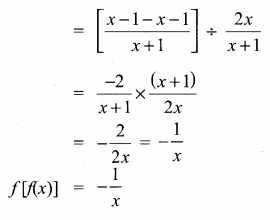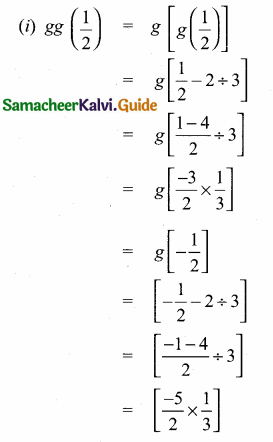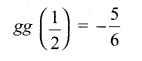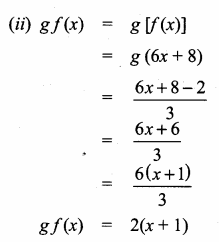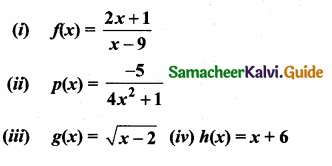Category: Class 10

Students can download Maths Chapter 3 Algebra Ex 3.14 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.14

Question 1.
Write each of the following expression in terms of α + β and αβ
(i) \(\frac{\alpha}{3 \beta}+\frac{\beta}{3 \alpha}\)
Answer:

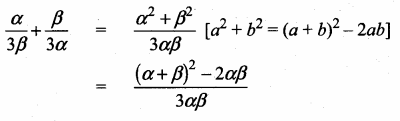
(ii) \(\frac{1}{\alpha^{2} \beta}+\frac{1}{\beta^{2} \alpha}\)
Answer:

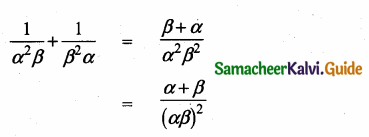
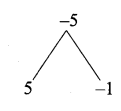
(iii) (3α – 1) (3β – 1)
Answer:
(3α – 1) (3β – 1) = 9αc – 3α – 3β + 1
= 9αβ – 3(α + β) + 1

(iv) \(\frac{\alpha+3}{\beta}+\frac{\beta+3}{\alpha}\)
Answer:

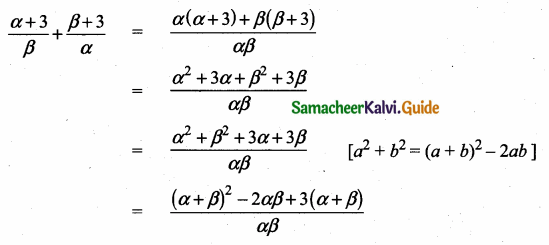
Question 2.
The roots of the equation 2x² – 7x + 5 = 0 are a and p. Find the value of [without solving the equation]
\(\text { (i) } \frac{1}{\alpha}+\frac{1}{\beta}\)
Answer:
α and α are the roots of the equation 2x² – 7x + 5 = 0
α + β = \(\frac { 7 }{ 2 } \) ; αβ = \(\frac { 5 }{ 2 } \)
(i) \(\frac{1}{\alpha}+\frac{1}{\beta}\) = \(\frac{\beta+\alpha}{\alpha \beta}\)
= \(\frac { 7 }{ 2 } \) + \(\frac { 5 }{ 2 } \) = \(\frac { 7 }{ 2 } \) × \(\frac { 2 }{ 5 } \) = \(\frac { 7 }{ 5 } \)

(ii) \(\frac{\alpha}{\beta}+\frac{\beta}{\alpha}\)
Answer

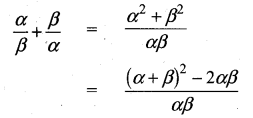
= (\(\frac { 7 }{ 2 } \))² – 2 × \(\frac { 5 }{ 2 } \) ÷ \(\frac { 5 }{ 2 } \)
= \(\frac { 49 }{ 4 } \) – 5 ÷ \(\frac { 5 }{ 2 } \) = \(\frac { 49-20 }{ 4 } \) ÷ \(\frac { 5 }{ 2 } \)
= \(\frac { 29 }{ 4 } \) × \(\frac { 2 }{ 5 } \) = \(\frac { 29 }{ 10 } \)

(iii) \(\frac{\alpha+2}{\beta+2}+\frac{\beta+2}{\alpha+2}\)
Answer:

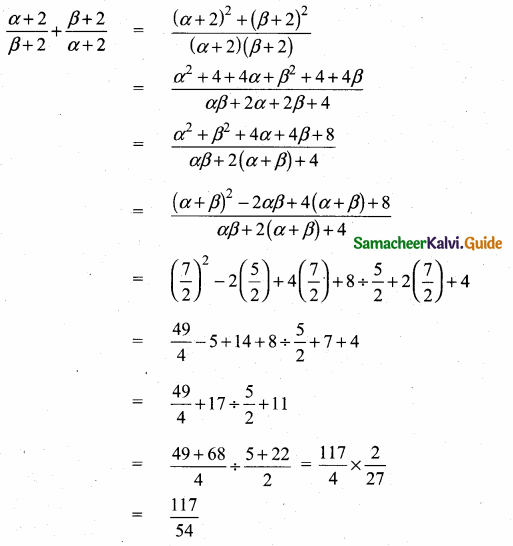
Question 3.
The roots of the equation x² + 6x – 4 = 0 are a, p. Find the quadratic equation whose roots are
(i) α² and β²
Answer:
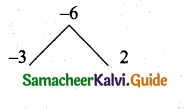
α and β are the roots of x² + 6x – 4 = 0
α + β = -6; αβ = -4

(i) Sum of the roots = α² + β²
= (α + β)² – 2αβ
= 36 – 2 – (4) = 36 + 8
= 44
Product of the roots = α² + β²
= (αβ)²
= (-4)²
= 16
The Quadratic equation is
x² – (sum of the roots) x + Product of the roots = 0
x² – (44)x + 16 = 0
x² – 44x + 16 = 0

(ii) \(\frac{2}{\alpha}\) and \(\frac{2}{\beta}\)
Answer:
Sum of the roots = \(\frac{2}{\alpha}\) + \(\frac{2}{\beta}\)
= \(\frac{2 \beta+2 \alpha}{\alpha \beta}=\frac{2(\alpha+\beta)}{\alpha \beta}\)
= \(\frac{2(-6)}{-4}=\frac{-12}{-4}=3\)
Product of the roots = \(\frac{2}{\alpha} \times \frac{2}{\beta}=\frac{4}{\alpha \beta}\)
= \(\frac { 4 }{ -4 } \) = -1
The Quadratic equation is
x² – (sum of the roots) x + Product of the roots = 0
x² – 3x – 1 = 0

(iii) α²β and β²α
Answer:
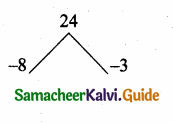
Sum of the roots = α²β + β²α
= αβ (α + β)
= -4 (-6) = 24
Product of the roots = α²β × β²α
= α²β³ = (αβ)³
= (-4)³ = -64
The Quadratic equation is
x² – (Sum of the roots) x + Product of the roots = 0
x² – 24x – 64 = 0

Question 4.
If α, β are the roots of 7x² + ax + 2 = 0 and if β – α = \(\frac { 13 }{ 7 } \) Find the values of a.
Answer:
α and β are the roots of 7x² + ax + 2 = 0
α + β = \(\frac { -a }{ 7 } \); αβ = \(\frac { 2 }{ 7 } \)
Given β – α = – \(\frac { 13 }{ 7 } \) ⇒ α – β = \(\frac { 13 }{ 7 } \)
Squaring on both sides
(α – β)² = (\(\frac { 13 }{ 7 } \))²
α² + β² = 2αβ = \(\frac { 169 }{ 49 } \)
(- \(\frac { a }{ 7 } \))² -4(\(\frac { 2 }{ 7 } \)) = \(\frac { 169 }{ 49 } \) ⇒ \(\frac{a^{2}}{49}-\frac{8}{7}=\frac{169}{49}\)
\(\frac{a^{2}}{49}\) = \(\frac { 225 }{ 49 } \) ⇒ a2 = \(\frac{225 \times 49}{49}\)
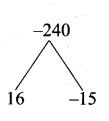
a² = 225 ⇒ a = ± \(\sqrt { 225 }\) = ± 15
The value of a = 15 or – 15

Question 5.
If one root of the equation 2y², – ay + 64 = 0 is twice the other then find the values of a.
Answer:
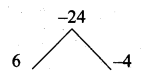
Let the roots be α and 2α
Here a = 2, b = – a, c = 64
Sum of the roots = – \(\frac { b }{ a } \)
α + 2α = \(\frac { a }{ 2 } \)
3α = \(\frac { a }{ 2 } \)
a = 6α …….(1)
Product of the roots = \(\frac { c }{ a } \)
α × 2α = \(\frac { 64 }{ 2 } \) = 2α² = 32
α² = \(\frac { 32 }{ 2 } \) = 16
α = \(\sqrt { 16 }\) = ± 4
Substitute the value of a in (1)
When α = 4
a = 6(4)
a = 24
The Value of a is 24 or -24
When α = -4
a = 6(-4)
a = -24

Question 6.
If one root of the equation 3x² + kx + 81 = 0 (having real roots) is the square of the other then find k.
Answer:
Let α and α² be the root of the equation 3x² + kx + 81
Here a = 3, b = k, c = 81
Sum of the roots = – \(\frac { b }{ a } \) = – \(\frac { k }{ 3 } \)
α + α² = –\(\frac { k }{ 3 } \)
3α + 3α² = -k ……..(1)
Product of the roots = \(\frac { c }{ a } \) = \(\frac { 81 }{ 3 } \) = 27
α × α² = 27
α³ = 27 ⇒ α³ = 3³
α = 3
Substitute the value of α = 3 in (1)
3(3) + 3(3)² = -k
9 + 27 = -k ⇒ 36 = – k
∴ k = -36
The value of k = -36

Students can download Maths Chapter 3 Algebra Ex 3.5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.5

Question 1.
Simplify
(i) \(\frac{4 x^{2} y}{2 z^{2}} \times \frac{6 x z^{3}}{20 y^{4}}\)
Answer:

(ii) \(\frac{p^{2}-10 p+21}{p-7} \times \frac{p^{2}+p-12}{(p-3)^{2}}\)
Answer:
P² – 10p + 21 = (p – 7) (p – 3)
p² + p – 12 = (p + 4) (p – 3)

(iii) \(\frac{5 t^{3}}{4 t-8} \times \frac{6 t-12}{10 t}\)
Answer:

Question 2.
Simplify
(i) \(\frac{x+4}{3 x+4 y} \times \frac{9 x^{2}-16 y^{2}}{2 x^{2}+3 x-20}\)
Answer:
9x² – 16y² = (3x)² – (4y)²
= (3x + 4y) (3x – 4y)
2x² + 3x – 20 = 2x² + 8x – 5x – 20
= 2x (x + 4) – 5 (x + 4)
= (x + 4) (2x – 5)

(ii) \(\frac{x^{3}-y^{3}}{3 x^{2}+9 x y+6 y^{2}} \times \frac{x^{2}+2 x y+y^{2}}{x^{2}-y^{2}}\)
Answer:
x³ – y³ = (x – y) (x² + xy + y²)
x² + 2xy + y² = (x + y) (x + y)

3x² + 9xy + 6y² = 3(x² + 3xy + 2y²)
= 3 (x + 2y) (x + y)
(x² – y²) = (x + y) (x – y)

Question 3.
Simplify
(i) \(\frac{2 a^{2}+5 a+3}{2 a^{2}+7 a+6} \div \frac{a^{2}+6 a+5}{-5 a^{2}-35 a-50}\)
Answer:

2 a² + 5a + 3a + 3 = 2a² + 2a + 3a + 3
= 2a(a + 1) + 3 (a + 1)
= (a + 1) (2a + 3)

2a² + 7a + 6 = 2a² + 3a + 4a + 6
= a(2a + 3) + 2 (2a + 3)
= (2a + 3) (a + 2)

a² + 6a + 5 = (a + 5) + (a + 1)
-5a² – 35a – 50 = -5(a² + 7a + 10)
= -5(a + 5)(a + 2)

(ii) \(\frac{b^{2}+3 b-28}{b^{2}+4 b+4}+\frac{b^{2}-49}{b^{2}-5 b-14}\)
Solution:

b² + 3b – 28 = (b + 7) (b – 4)
b² + 4b + 4 = (b + 2) (b + 2)
b² – 49 = b² – 7²
= (b + 7) (b – 7)
b² – 5b – 14 = (b – 7) (b + 2)

(iii) \(\frac{x+2}{4 y}+\frac{x^{2}-x-6}{12 y^{2}}\)
Answer:

x² – x – 6 = (x – 3) (x + 2)

(iv) \(\frac{12 t^{2}-22 t+8}{3 t} \div \frac{3 t^{2}+2 t-8}{2 t^{2}+4 t}\)
Answer:
12t² – 22t + 8 = 2(6t² – 11t + 4)
= 2[6t² – 8t – 3t + 4]

= 2[2t (3t – 4) – 1 (3t – 4)]
= 2(3t – 4) (2t – 1)
3t² + 2t – 8 = 3t² + 6t – 4t – 8
= 3t(t + 2) – 4 (t + 2)

= (t + 2) (3t – 4)
2t² + 4t = 2t(t + 2)

Question 4.
If x = \(\frac{a^{2}+3 a-4}{3 a^{2}-3}\) and y = \(\frac{a^{2}+2 a-8}{2 a^{2}-2 a-4}\) find the value of x²y^-2
Answer:


The value of x² y^-2 = \(\frac{x^{2}}{y^{2}}\) = (\(\frac { x }{ y } \))²

Question 5.
If a polynomial p(x) = x² – 5x – 14 when divided by another polynomial q(x) gets reduced to \(\frac { x-7 }{ x+2 } \) find q(x).
Answer:
p(x) = x² – 5x – 14
= (x – 7) (x + 2)

By the given data
\(\frac { p(x) }{ q(x) } \) = \(\frac { (x-7) }{ x+2 } \)
\(\frac{(x-7)(x+2)}{q(x)}\) = \(\frac { (x-7) }{ x+2 } \)
q(x) × (x – 7) = (x – 7) (x + 2) (x + 2)
q(x) = \(\frac{(x-7)(x+2)(x+2)}{(x-7)}\)
= (x + 2)²
q(x) = x² + 4x + 4

Students can download Maths Chapter 2 Relations and Functions Unit Exercise 2 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Unit Exercise 2

Question 1.
Prove that n² – n divisible by 2 for every positive integer n.
Answer:
We know that any positive integer is of the form 2q or 2q + 1 for some integer q.
Case 1: When n = 2 q
n² – n = (2q)² – 2q = 4q² – 2q
= 2q (2q – 1)
In n² – n = 2r
2r = 2q(2q – 1)
r = q(2q + 1)
n² – n is divisible by 2

Case 2: When n = 2q + 1
n² – n = (2q + 1)² – (2q + 1)
= 4q² + 1 + 4q – 2q – 1 = 4q² + 2q
= 2q (2q + 1)
If n² – n = 2r
r = q (2q + 1)
∴ n² – n is divisible by 2 for every positive integer “n”

Question 2.
A milk man has 175 litres of cow’s milk and 105 litres of buffalow’s milk. He wishes to sell the milk by filling the two types of milk in cans of equal capacity. Calculate the following
(i) Capacity of a can
(ii) Number of cans of cow’s milk
(iii) Number of cans of buffalow’s milk.
Answer:
175 litres of cow’s milk.
105 litres of goat’s milk.
H.C.F of 175 & 105 by using Euclid’s division algorithm.
175 = 105 × 1 + 70, the remainder 70 ≠ 0

Again using division algorithm,

105 = 70 × 1 + 35, the remainder 35 ≠ 0
Again using division algorithm.
70 = 35 × 2 + 0, the remainder is 0.
∴ 35 is the H.C.F of 175 & 105.
(i) ∴ The milk man’s milk can’s capacity is 35 litres.
(ii) No. of cow’s milk obtained = \(\frac { 175 }{ 35 } \) = 5 cans
(iii) No. of buffalow’s milk obtained = \(\frac { 105 }{ 35 } \) = 3 cans

Question 3.
When the positive integers a, b and c are divided by 13 the respective remainders are 9,7 and 10. Find the remainder when a + 2b + 3c is divided by 13.
Answer:
Given the positive integer are a, b and c
a = 13q + 9 (divided by 13 leaves remainder 9)
b = 13q + 7
c = 13q + 10
a + 2b + 3c = 13q + 9 + 2(13q + 7) + 3 (13q + 10)
= 13q + 9 + 26q + 14 + 39q + 30
= 78q + 53
When compare with a = 3q + r
= (13 × 6) q + 53
The remainder is 53

Question 4.
Show that 107 is of the form 4q +3 for any integer q.
Solution:
107 = 4 × 26 + 3. This is of the form a = bq + r.
Hence it is proved.

Question 5.
If (m + 1)^th term of an A.P. is twice the (n + 1)^th term, then prove that (3m + 1)^th term is twice the (m + n + 1)^th term.
Answer:
t_n = a + (n – 1)d
Given t_m+1 = 2 t_n+1
a + (m + 1 – 1)d = 2[a + (n + 1 – 1)d]
a + md = 2(a + nd) ⇒ a + md =2a + 2nd
md – 2nd = a
d(m – 2n) = a ….(1)
To Prove t_{(3m + 1)} = 2(t_m+n+1)
L.H.S. = t_3m+1
= a + (3m + 1 – 1)d
= a + 3md
= d(m – 2n) + 3md (from 1)
= md – 2nd + 3md
= 4md – 2nd
= 2d (2m – n)
R.H.S. = 2(t_m+n+1)
= 2 [a + (m + n + 1 – 1) d]
= 2 [a + (m + n)d]
= 2 [d (m – 2n) + md + nd)] (from 1)
= 2 [dm – 2nd + md + nd]
= 2 [2 md – nd]
= 2d (2m – n)
R.H.S = L.H.S
∴ t_(3m+1) = 2 t_(m+n+1)
Hence it is proved.

Question 6.
Find the 12^th term from the last term of the A.P -2, -4, -6,… -100.
Answer:
The given A.P is -2, -4, -6, …. 100
d = -4 – (-2) = -4 + 2 = – 2
Finding the 12 term from the last term
a = -100, d = 2 (taking from the last term)
n = 12
t_n = a + (n – 1)d
t₁₂ = – 100 + 11 (2)
= -100 + 22
= -78
∴ The 12^th term of the A.P from the last term is – 78

Question 7.
Two A.P’s have the same common difference. The first term of one A.P is 2 and that of the other is 7. Show that the difference between their 10th terms is the same as the difference between their 21st terms, which is the same as the difference between any two corresponding terms.
Solution:
Let the two A.Ps be
AP₁ = a₁, a₁ + d, a₁ + 2d,…
AP₂ = a₂, a₂ + d, a₂ + 2d,…
In AP₁ we have a₁ = 2
In AP₂ we have a₂ = 7
t₁₀ in AP₁ = a₁ + 9d = 2 + 9d ………….. (1)
t₁₀ in AP₂ = a₂ + 9d = 7 + 9d …………… (2)
The difference between their 10th terms
= (1) – (2) = 2 + 9d – 7 – 9d
= -5 ………….. (I)
t₂₁ m AP₁ = a₁ + 20d = 2 + 20d …………. (3)
t₂₁ in AP₂ = a₂ + 20d = 7 + 20d ………… (4)
The difference between their 21 st terms is
(3) – (4)
= 2 + 20d – 7 – 20d
= -5 ……………. (II)
I = II
Hence it is Proved.

Question 8.
A man saved ₹16500 in ten years. In each year after the first he saved ₹100 more than he did in the preceding year. How much did he save in the first year?
Answer:
Amount of saving in ten years = ₹ 16500
S₁₀ = 16500, d= 100
S_n = \(\frac { n }{ 2 } \) [2a + (n – 1)d]
S₁₀ = \(\frac { 10 }{ 2 } \) [2a + 9d]
16500 = \(\frac { 10 }{ 2 } \) [2a + 900] = 5(2a + 900)
16500 = 10a + 4500 ⇒ 16500 – 4500 = 10a
12000 = 10a
a = \(\frac { 12000 }{ 10 } \) = 1200
Amount saved in the first year = ₹ 1200

Question 9.
Find the G.P. in which the 2nd term is \(\sqrt { 6 }\) and the 6th term is 9 \(\sqrt { 6 }\).
Answer:
2^nd term of the G.P = \(\sqrt { 6 }\)
t₂ = \(\sqrt { 6 }\)
[t_n = a r^n-1]
a.r = \(\sqrt { 6 }\) ….(1)
6^th term of the G.P. = 9 \(\sqrt { 6 }\)
a. r⁵ = 9\(\sqrt { 6 }\) ……..(2)

Question 10.
The value of a motorcycle depreciates at a rate of 15% per year. What will be the value of the motorcycle 3 year hence, which is now purchased for ₹45,000?
Solution:
a = ₹45000
Depreciation = 15% for ₹45000
= 45000 × \(\frac { 15 }{ 100 } \)
d = ₹6750 since it is depreciation
d = -6750
At the end of 1^st year its value = ₹45000 – ₹6750
= ₹38250,
Again depreciation = 38250 × \(\frac { 15 }{ 100 } \) = 5737.50
At the end of 2^nd year its value
= ₹38250 – ₹5737.50 = 32512.50
Again depreciation = 32512.50 × \(\frac { 15 }{ 100 } \) = 4876.88
At the end of the 3^rd year its value
= 32512.50 – 4876.88 = 27635.63
∴ The value of the automobile at the 3^rd year
= ₹ 27636

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.10 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.10

Multiple choice questions:

Question 1.
Euclid’s division lemma states that for positive integers a and b, there exist unique integers q and r such that a = bq + r, where r must satisfy ………………….
(1) 1 < r < b
(2) 0 < r < b
(3) 0 < r < 6
(4) 0 < r < b
Ans.
(3) 0 < r < b

Question 2.
Using Euclid’s division lemma, if the cube of any positive integer is divided by 9 then the possible remainders are ………………….
(1) 0, 1, 8
(2) 1, 4, 8
(3) 0, 1, 3
(4) 1, 3, 5
Answer:
(1) 0, 1, 8
Hint: Let the +ve integer be 1, 2, 3, 4 …………
1³ = 1 when it is divided by 9 the remainder is 1.
2³ = 8 when it is divided by 9 the remainder is 8.
3³ = 27 when it is divided by 9 the remainder is 0.
4³ = 64 when it is divided by 9 the remainder is 1.
5³ = 125 when it is divided by 9 the remainder is 8.
The remainder 0, 1, 8 is repeated.

Question 3.
If the H.C.F of 65 and 117 is expressible in the form of 65m – 117 , then the value of m is
(1) 4
(2) 2
(3) 1
(4) 3
Answer:
(2) 2
Hint:
H.C.F. of 65 and 117
117 = 65 × 1 + 52
65 = 52 × 1 + 13
52 = 13 × 4 + 0
∴ 13 is the H.C.F. of 65 and 117.
65m – 117 = 65 × 2 – 117
130 – 117 = 13
∴ m = 2

Question 4.
The sum of the exponents of the prime factors in the prime factorization of 1729 is …………………….
(1) 1
(2) 2
(3) 3
(4) 4
Answer:
(3) 3
Hint: 1729 = 7 × 13 × 19
Sum of the exponents = 1 + 1 + 1
= 3

Question 5.
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is
(1) 2025
(2) 5220
(3) 5025
(4) 2520
Answer:
(4) 2520
Hint:

L.C.M. = 2³ × 3² × 5 × 7
= 8 × 9 × 5 × 7
= 2520

Question 6.
7^4k ≡ ______ (mod 100)
(1) 1
(2) 2
(3) 3
(4) 4
Answer:
(1) 1
Hint:
7^4k ≡______ (mod 100)
y^4k ≡ y^{4 × 1} = 1 (mod 100)

Question 7.
Given F₁ = 1 , F₂ = 3 and F_n = F_n-1 + F_n-2 then F₅ is ………….
(1) 3
(2) 5
(3) 8
(4) 11
Answer:
(4) 11
Hint:
F_n = F_n-1 + F_n-2
F₃ = F₂ + F₁ = 3 + 1 = 4
F₄ = F₃ + F₂ = 4 + 3 = 7
F₅ = F₄ + F₃ = 7 + 4 = 11

Question 8.
The first term of an arithmetic progression is unity and the common difference is 4. Which of the following will be a term of this A.P
(1) 4551
(2) 10091
(3) 7881
(4) 13531
Answer:
(3) 7881
Hint:
t₁ = 1
d = 4
t_n = a + (n – 1)d
= 1 + 4n – 4
4n – 3 = 4551
4n = 4554
n = will be a fraction
It is not possible.
4n – 3 = 10091
4n = 10091 + 3 = 10094
n = a fraction
4n – 3 = 7881
4n = 7881 + 3 = 7884
n = \(\frac{7884}{4}\), n is a whole number.
4n – 3 = 13531
4n = 13531 – 3 = 13534
n is a fraction.
∴ 7881 will be 1971st term of A.P.

Question 9.
If 6 times of 6^th term of an A.P is equal to 7 times the 7^th term, then the 13^th term of the A.P. is ………..
(1) 0
(2) 6
(3) 7
(4) 13
Answer:
(1) 0
Hint:
6 t₆ = 7 t₇
6(a + 5d) = 7 (a + 6d) ⇒ 6a + 30d = 7a + 42d
30 d – 42 d = 7a – 6a ⇒ -12d = a
t₁₃ = a + 12d (12d = -a)
= a – a = 0

Question 10.
An A.P consists of 31 terms. If its 16th term is m, then the sum of all the terms of this A.P. is
(1) 16 m
(2) 62 m
(3) 31 m
(4) \(\frac { 31 }{ 2 } \) m
Answer:
(3) 31 m
Hint:
t₁₆ = m
S₃₁ = \(\frac { 31 }{ 2 } \) (2a + 30d)
= \(\frac { 31 }{ 2 } \) (2(a + 15d))
(∵ t₁₆ = a + 15d)
= 31(t₁₆) = 31m

Question 11.
In an A.P., the first term is 1 and the common difference is 4. How many terms of the A.P must be taken for their sum to be equal to 120?
(1) 6
(2) 7
(3) 8
(4) 9
Answer:
(3) 8
Here a = 1, d = 4, S_n = 120
S_n = \(\frac { n }{ 2 } \)[2a + (n – 1)d]
120 = \(\frac { n }{ 2 } \) [2 + (n – 1)4] = \(\frac { n }{ 2 } \) [2 + 4n – 4)]
= \(\frac { n }{ 2 } \) [4n – 2)] = \(\frac { n }{ 2 } \) × 2 (2n – 1)
120 = 2n² – n
∴ 2n² – n – 120 = 0 ⇒ 2n² – 16n + 15n – 120 = 0
2n(n – 8) + 15 (n – 8) = 0 ⇒ (n – 8) (2n + 15) = 0
n = 8 or n = \(\frac { -15 }{ 2 } \) (omitted)
∴ n = 8

Question 12.
A = 2⁶⁵ and B = 2⁶⁴ + 2⁶³ + 2⁶² …. + 2⁰ which of the following is true?
(1) B is 2⁶⁴ more than A
(2) A and B are equal
(3) B is larger than A by 1
(4) A is larger than B by 1
Answer:
(4) A is larger than B by
A = 2⁶⁵
B = 2⁶⁴⁺⁶³ + 2⁶² + …….. + 2⁰
= 2
= 1 + 2² + 2² + ……. + 2⁶⁴
a = 1, r = 2, n = 65 it is in G.P.
S₆₅ = 1 (2⁶⁵ – 1) = 2⁶⁵ – 1
A = 2⁶⁵ is larger than B

Question 13.
The next term of the sequence \(\frac { 3 }{ 16 } \),\(\frac { 1 }{ 8 } \),\(\frac { 1 }{ 12 } \),\(\frac { 1 }{ 18 } \) is ………..
(1) \(\frac { 1 }{ 24 } \)
(2) \(\frac { 1 }{ 27 } \)
(3) \(\frac { 2 }{ 3 } \)
(4) \(\frac { 1 }{ 81 } \)
Answer:
(2) \(\frac { 1 }{ 27 } \)
Hint:
\(\frac { 3 }{ 16 } \),\(\frac { 1 }{ 8 } \),\(\frac { 1 }{ 12 } \),\(\frac { 1 }{ 18 } \)
a = \(\frac { 3 }{ 16 } \), r = \(\frac { 1 }{ 8 } \) ÷ \(\frac { 3 }{ 16 } \) = \(\frac { 1 }{ 8 } \) × \(\frac { 16 }{ 3 } \) = \(\frac { 2 }{ 3 } \)
The next term is = \(\frac { 1 }{ 18 } \) × \(\frac { 2 }{ 3 } \) = \(\frac { 1 }{ 27 } \)

Question 14.
If the sequence t₁,t₂,t₃ … are in A.P. then the sequence t₆,t₁₂,t₁₈ … is
(1) a Geometric Progression
(2) an Arithmetic Progression
(3) neither an Arithmetic Progression nor a Geometric Progression
(4) a constant sequence
Answer:
(2) an Arithmetic Progression
Hint:
If t₁, t₂, t₃, … is 1, 2, 3, …
If t₆ = 6, t₁₂ = 12, t₁₈ = 18 then 6, 12, 18 … is an arithmetic progression

Question 15.
The value of (1³ + 2³ + 3³ + ……. + 15³) – (1 + 2 + 3 + …….. + 15) is …………….
(1) 14400
(2) 14200
(3) 14280
(4) 14520
Answer:
(3) 14280
Hint:

1202 – 120 = 120(120 – 1)
120 × 119 = 14280

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.9 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.9

Question 1.
Find the sum of the following series
(i) 1 + 2 + 3 + …….. + 60
(ii) 3 + 6 + 9 + …….. +96
(iii) 51 + 52 + 53 + …….. + 92
(iv) 1 + 4 + 9 + 16 + …….. + 225
(v) 6² + 7² + 8² + …….. + 21²
(vi) 10³ + 11³ + 12³ + …….. + 20³
(vii) 1 + 3 + 5 + …… + 71
Solution:
(i) 1 + 2 + 3 + …….. + 60 = \(\frac{60 \times 61}{2}\)
[Using \(\frac{n(n+1)}{2}\) formula]
= 1830

(ii) 3 + 6 + 9 + …….. + 96 = 3(1 + 2 + 3 + ……… + 32)
= \(\frac{3 \times 32 \times 33}{2}\)
= 1584

(iii) 51 + 52 + 53 + …….. + 92 = (1 + 2 + 3 + ……. + 92) – (1 + 2 + 3 + …… + 50)

= 4278 – 1275
= 3003

(iv) 1 + 4 + 9 + 16 + …….. + 225 = 1² + 2² + 3² + 4² + ………… + 15²
\(\frac{15 \times 16 \times 31}{6}\)
[using \(\frac{n(n+1)(2 n+1)}{6}\)] formula
= 1240

(v) 6² + 7² + 8² + …….. + 21² = 1 + 2² + 3² + 4² + ………… + 21² – (1 + 2² + ………… + 5²)
= \(\frac{21 \times 22 \times 43}{6}\) – \(\frac{5 \times 6 \times 11}{6}\)
= 3311 – 55
= 3256

(vi) 10³ = 11³ + 12³ + …….. + 20³ = 1³ + 2³+ 3³ + ………… + 20³ – (1³ + 2³ + 3³ + …………. + 9³)

[Using (\(\frac{n(n+1)}{2}\))² formula]
= 210² – 45² = 44100 – 2025
= 42075

(vii) 1 + 3 + 5+ … + 71
Here a = 1; d = 3 – 1 = 2; l = 71

Question 2.
If 1 + 2 + 3 + …. + k = 325 , then find 1³ + 2³ + 3³ + …………. + k³
Answer:
1 + 2 + 3 + …. + k = 325
\(\frac{k(k+1)}{2}\) = 325 ……(1)

= 325² (From 1)
= 105625

Question 3.
If 1³ + 2³ + 3³ + ………… + K³ = 44100 then find 1 + 2 + 3 + ……. + k
Answer:
1³ + 2³ + 3³ + ………….. + k³ = 44100

\(\frac{k(k+1)}{2}\) = \(\sqrt { 44100 }\) = 210
1 + 2 + 3 + …… + k = \(\frac{k(k+1)}{2}\)
= 210

Question 4.
How many terms of the series 1³ + 2³ + 3³ + …………… should be taken to get the sum 14400?
Answer:
1³ + 2³ + 3³ + ……. + n³ = 14400

\(\frac{n(n+1)}{2}\) = \(\sqrt { 14400 }\)
\(\frac{n(n+1)}{2}\) = 120 ⇒ n² + n = 240

n² + n – 240 = 0
(n + 16) (n – 15) = 0
(n + 16) = 0 or (n – 15) = 0
n = -16 or n = 15 (Negative will be omitted)
∴ The number of terms taken is 15

Question 5.
The sum of the squares of the first n natural numbers is 285, while the sum of their cubes is 2025. Find the value of n.
Answer:
1² + 2² + 3² + …. + n² = 285

Question 6.
Rekha has 15 square colour papers of sizes 10 cm, 11 cm, 12 cm, …, 24 cm. How much area can be decorated with these colour papers?
Answer:
Area of 15 square colour papers
= 10² + 11² + 12² + …. + 24²
= (1² + 2² + 3² + …. + 24²) – (1² + 2² + 9²)
= \(\frac{24 \times 25 \times 49}{6}-\frac{9 \times 10 \times 19}{6}\)
= 4 × 25 × 49 – 3 × 5 × 19
= 4900 – 285
= 4615
Area can be decorated is 4615 cm²

Question 7.
Find the sum of the series (2³ – 1)+(4³ – 3³) + (6³ – 15³) + …….. to
(i) n terms
(ii) 8 terms
Answer:
Sum of the series = (2³ – 1) + (4³ – 3³) + (6³ – 15³) + …. n terms
= 2³ + 4³ + 6³ + …. n terms – (1³ + 3³ + 5³ + …. n terms) …….(1)
2³ + 4³ + 6³ + …. n = ∑(2³ + 4³ + 6³ + ….(2n)³]
∑ 2³ (1³ + 2³ + 3³ + …. n³)
= 8 (\(\frac{n(n+1)}{2}\))²
= 2[n (n + 1)]²
1³ + 3³ + 5³ + ……….(2n – 1)³ [sum of first 2n cubes – sum of first n even cubes]

Substituting (2) and (3) in (1)
Sum of the series = 2n² (n + 1)² – n² (2n + 1)² + 2n²(n + 1)²
= 4n² (n + 1)² – n² (2n + 1)²
= n² [(4(n + 1)² – (2n + 1)²]
= n² [4n² + 4 + 8n – 4n² – 1 – 4n]
= n² [4n + 3]
= 4n³ + 3n²

(ii) when n = 8 = 4(8)³ + 3(8)²
= 4(512) + 3(64)
= 2240

Students can download Maths Chapter 1 Relations and Functions Ex 1.5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.5

Question 1.
Using the functions f and g given below, find fog and gof Check whether fog = gof.

(i) f(x) = x – 6, g(x) = x²
Answer:
f(x) = x – 6, g(x) = x²
fog = fog (x)
= f(g(x))
fog = f(x)²
= x² – 6
gof = go f(x)
= g(x – 6)
= (x – 6)²
= x² – 12x + 36
fog ≠ gof

(ii) f(x) = \(\frac { 2 }{ x } \), g(x) = 2x² – 1
Answer:
f(x) – \(\frac { 2 }{ x } \); g(x) = 2x² – 1
fag = f[g (x)]
= f(2x² – 1)
= \(\frac{2}{2 x^{2}-1}\)
gof = g [f(x)]
= g (\(\frac { 2 }{ x } \))
= 2 (\(\frac { 2 }{ x } \))² – 1
\(=2 \times \frac{4}{x^{2}}-1\)
\(=\frac{8}{x^{2}}-1\)
fog ≠ gof

(iii) f(x) = \(\frac { x+6 }{ 3 } \), g(x) = 3 – x
Answer:
f(x) = \(\frac { x+6 }{ x } \), g(x) = 3 – x
fog = f[g(x)]
= f(3 – x)

(iv) f(x) = 3 + x, g(x) = x – 4
Answer:
f(x) = 3 + x ;g(x) = x – 4
fog = f[g(x)]
= f(x – 4)
= 3 + x – 4
= x – 1
gof = g[f(x)]
= g(3 + x)
= 3 + x – 4
= x – 1
fog = gof

(v) f(x) = 4x² – 1,g(x) = 1 + x
Answer:
f(x) = 4x² – 1 ; g(x) = 1 + x
fog = f[g(x)]
= 4(1 + x)
= 4(1 + x)² – 1
= 4[1 + x² + 2x] – 1
= 4 + 4x² + 8x – 1
= 4x² + 8x + 3
gof = g [f(x)]
= g (4x² – 1)
= 1 + 4x² – 1
= 4x²
fog ≠ gof

Question 2.
Find the value of k, such that fog = gof
(i) f(x) = 3x + 2, g(x) = 6x – k
(ii) f(x) = 2x – k, g(x) = 4x + 5
Solution:
(i) f(x) = 3x + 2, g(x) = 6x – k
fog(x) = f(g(x)) = f(6x – k) = 3(6x – k) + 2
= 18x – 3k + 2 …………… (1)
gof(x) = g(f(x)) = g(3x + 2) = 6(3x + 2) – k
= 18x + 12 – k ……………. (2)
(1) = (2)
⇒ 18x – 3k + 2 = 18x + 12 – k
2k = -10
k = -5

(ii) f(x) = 2x – k, g(x) = 4x + 5
fog(x) = f(g(x)) = f(4x + 5) = 2(4x + 5) – k
= 8x + 10 – k ……………… (1)
gof(x) = g(f(x)) = g(2x – k) = 4(2x – k) + 5
= 8x – 4k + 5 ……………. (2)
(1) = (2)
⇒ 8x + 10 – k = 8x – 4k + 5
3k = -5
k = \(\frac{-5}{3}\)

Question 3.
If f(x) = 2x – 1, g(x) = \(\frac { x+1 }{ 2 } \), show that f o g = g o f = x
Answer:
f(x) = 2x – 1 ; g(x) = \(\frac { x+1 }{ 2 } \)
fog = f[g(x)]

∴ fog = gof = x
Hence it is proved.

Question 4.
(i) If f (x) = x² – 1, g(x) = x – 2 find a, if gof(a) = 1.
(ii) Find k, if f(k) = 2k – 1 and fof (k) = 5.
Solution:
(i) f(x) = x² – 1, g(x) = x – 2
Given gof(a) = 1
gof(x) = g(f(x)
= g(x² – 1) = x² – 1 – 2
= x² – 3
gof(a) ⇒ a² – 3 = 1 =+ a² = 4
a = ± 2
(ii) f(k) = 2k – 1
fo f(k) = 5
f(f(k)m = f(2k – 1) = 5
⇒ 2(2k – 1) – 1 = 5
4 k – 2 – 1 = 5 ⇒ 4k = 8
k = 2

Question 5.
Let A,B,C ⊂ N and a function f: A → B be defined by f(x) = 2x + 1 and g: B → C be defined by g(x) = x² . Find the range of fog and gof.
Answer:
f(x) = 2x + 1 ; g(x) = x²
fog = f[g(x)]
= f(x²)
= 2x² + 1
2x² + 1 ∈ N
g o f = g [f(x)]
= g (2x + 1)
g o f = (2x + 1)²
(2x + 1)² ∈ N
Range = {y/y = 2x² + 1, x ∈ N};
{y/y = (2x + 1)², x ∈ N)

Question 6.
If f(x) = x² – 1. Find (i)f(x) = x² – 1, (ii)fofof
Solution:
(i) f(x) = x² – 1
fof(x) = f(fx)) = f(x² – 1)
= (x² – 1 )² – 1;
= x⁴ – 2x² + 1 – 1
= x⁴ – 2x²
(ii) fofof = f o f(f(x))
= f o f (x⁴ – 2x²)
= f(f(x⁴ – 2x²))
= (x⁴ – 2x²)² – 1
= x⁸ – 4x⁶ + 4x⁴ – 1

Question 7.
If f : R → R and g : R → R are defined by f(x) = x⁵ and g(x) = x⁴ then check if f, g are one – one and fog is one – one?
Answer:
f(x) = x⁵ – It is one – one function
g(x) = x⁴ – It is one – one function
fog = f[g(x)]
= f(x⁴)
= (x⁴)⁵
fag = x²⁰
It is also one-one function.

Question 8.
Consider the functions f(x), g(x), h(x) as given below. Show that (fog)oh = fo(goh) in each case.
(i) f(x) = x – 1, g(x) = 3x + 1 and h(x) = x²
(ii) f(x) = x², g(x) = 2x and h(x) = x + 4
(iii) f(x) = x – 4, g(x) = x² and h(x) = 3x – 5
Solution:
(i) f(x) = x – 1, g(x) = 3x + 1 and h(x) = x²
f(x) = x – 1
g(x) = 3x + 1
f(x) = x²
(fog)oh = fo(goh)
LHS = (fog)oh
fog = f(g(x)) = f(3x + 1) = 3x + 1 – 1 = 3x
(fog)oh = (fog)(h(x)) = (fog)(x² ) = 3²  ……………. (1)
RHS = fo(goh)
goh = g(h(x)) = g(x²) = 3x² + 1
fo(goh) = f(3x² + 1) = 3x² + 1 – 1= 3x² ………… (2)
LHS = RHS Hence it is verified.

(ii) f(x) = x², g(x) = 2x, h(x) = x + 4
(fog)oh = fo(goh)
LHS = (fog)oh
fog = f(g(x)) = f(2x) = (2x)² = 4x²
(fog)oh = (fog) h(x) = (fog) (x + 4)
= 4(x + 4)² = 4(x² + 8x+16)
= 4x² + 32x + 64 ………….. (1)
RHS = fo(goh) goh = g(h(x)) = g(x + 4)
= 2(x + 4) = (2x + 8)
fo(goh) = f(goh) = f(2x + 8) = (2x + 8)²
= 4x² + 32x + 64 ……………… (2)
(1) = (2)
LHS = RHS
∴ (fog)oh = fo(goh) It is proved.

(iii) f(x) = x – 4, g(x) = x², h(x) = 3x – 5
(fog)oh = fo(goh)
LHS = (fog)oh
fog = f(g(x)) = f(x²) = x² – 4
(fog)oh = (fog)(3x – 5) = (3x – 5)² – 4
= 9x² – 30x + 25 -4
= 9x² – 30x + 21 ………….. (1)
∴ RHS = fo(goh)
(goh) = g(h(x)) = g(3x – 5) = (3x – 5)²
= 9x² – 30x + 25
fo(goh) = f(9x² – 30 x + 25)
= 9x² – 30x + 25 – 4
= 9x² – 30x + 21 …………… (2)
(1) = (2)
LHS = RHS
∴ (fog)oh = fo(goh)
It is proved.

Question 9.
Let f = {(-1, 3), (0, -1), (2, -9)} be a linear function from Z into Z. Find f(x).
Answer:
The linear equation is f(x) = ax + b
f(-1) = 3
a(-1) + b = 3
-a + b = 3 ….(1)
f(0) = -1
a(0) + b = -1
0 + b = -1
b = -1
Substitute the value of b = -1 in (1)
-a – 1 = 3
-a = 3 + 1
-a = 4
a = -4
∴ The linear equation is -4(x) -1 = -4x – 1 (or) – (4x + 1)

Question 10.
In electrical circuit theory, a circuit C(t) is called a linear circuit if it satisfies the superposition principle given by C(at₁ + bt₂) = aC(t₁) + bC(t₂), where a,b are constants. Show that the circuit C(t) = 31 is linear.
Solution:
Given C(t) = 3t. To prove that the function is linear
C(at₁) = 3a(t₁)
C(bt₂) = 3 b(t₂)
C(at₁ + bt₂) = 3 [at₁ + bt₂] = 3at₁ + 3bt₂
= a(3t₁) + b(3t₂) = a[C(t₁) + b(Ct₂)]
∴ Superposition principle is satisfied.
Hence C(t) = 3t is linear function.

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.2 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.2

Question 1.
For what values of natural number n, 4th can end with the digit 6?
Answer:
4n = (2²)ⁿ = 2²ⁿ
= 2ⁿ × 2ⁿ
2 is a factor of 4ⁿ
∴ 4ⁿ is always even.

Question 2.
If m, n are natural numbers, for what values of m, does 2ⁿ × 5ⁿ ends in 5?
Solution:
2ⁿ × 5^m
2ⁿ is always even for all values of n.
5^m is always odd and ends with 5 for all values of m.
But 2ⁿ × 5^m is always even and ends in 0.
∴ 2ⁿ × 5^m cannot end with the digit 5 for any values of m. No value of m will satisfy 2ⁿ × 5^m ends in 5.

Question 3.
Find the H.C.F. of 252525 and 363636.
Answer:
To find the HCF of 252525 and 363636 by using Euclid’s Division algorithm.
363636 = 252525 × 1 + 111111
The remainder 111111 ≠ 0
By division of Euclid’s algorithm
252525 = 111111 × 2 + 30303
The remainder 30303 ≠ 0
Again by division of Euclid’s algorithm
111111 = 30303 × 3 + 20202
The remainder 20202 ≠ 0
Again by division of Euclid’s algorithm.
30303 = 20202 + 10101
The remainder 10101 ≠ 0
Again by division of Euclid’s algorithm.
20202 = 10101 × 2 + 0
The remainder is 0
∴ The H.C.F. is 10101

Question 4.
If 13824 = 2^a × 3^b then find a and b?
Answer:
Using factor tree method factorise 13824


13824 = 2⁹ × 3³
Given 13824 = 2a × 3b
Compare we get a = 9 and b = 3

Aliter:
13824 = 2⁹ × 3³
Compare with
13824 = 2^a × 3^b
The value of a = 9 b = 3

Question 5.
If p₁^x1 × p₂^x2 × p₃^x3 × p₄^x4 = 113400 where p₁ p₂, p₃, p₄ are primes in ascending order and x₁, x₂, x₃, x₄, are integers, find the value of p₁,p₂,p₃,p₄ and x₁,x₂,x₃,x₄.
Answer:
Given 113400 = p₁^x1 × p₂^x2 × p₃^x3 × p₄^x4
Using tree method factorize 113400

113400 = 23 × 34 × 52 × 7
compare with
113400 = p₁^x1 × p₂^x2 × p₃^x3 × p₄^x4
P₁ = 2, x₁ = 3
P₂ = 3, x₂ = 4
P₃ = 5, x₃ = 2
P₄ = 7, x₄ = 1

Question 6.
Find the L.C.M. and H.C.F. of 408 and 170 by applying the fundamental theorem of Arithmetic.
Answer:
Factorise 408 and 170 by factor tree method


408 = 2³ × 3 × 17
170 = 2 × 5 × 17
To find L.C.M. list all prime factors of 408 and 170 of their greatest exponents.
L.C.M. = 2³ × 3 × 5 × 17
= 2040
To find the H.C.F. list all common factors of 408 and 170.
H.C.F. = 2 × 17 = 34
L.C.M. = 2040 ; HCF = 34

Question 7.
Find the greatest number consisting of 6 digits which is exactly divisible by 24,15,36?
Answer:
The greatest number of 6 digits is 999999.
The greatest number must be divisible by L.C.M. of 24, 15 and 36

24 = 2³ × 3
15 = 3 × 5
36 = 2² × 3²
L.C.M = 2³ × 3² × 5
= 360
To find the greatest number 999999 must be subtracted by the remainder when 999999 is divided by 360
The greatest number in 6 digits = 999999 – 279
= 999720

Question 8.
What is the smallest number that when divided by three numbers such as 35, 56 and 91 leaves remainder 7 in each case?
Solution:
35 = 5 × 7
56 = 2 × 2 × 2 × 7
91 = 7 × 13
LCM of 35, 56, 91 = 5 × 7 × 2 × 2 × 2 × 13 = 3640
∴ Required number = 3647 which leaves remainder 7 in each case.

Question 9.
Find the least number that is divisible by the first ten natural numbers?
Answer:
Find the L.C.M of first 10 natural numbers

The least number is 2520

Modular Arithmetic
Two integers “a” and “b” are congruence modulo n if they differ by an integer multiple of n. That b – a = kn for some integer k. This can be written as a = b (mod n).

Euclid’s Division Lemma and Modular Arithmetic

Let m and n be integers, where m is positive. By Euclid’s division Lemma we can write n = mq + r where 0 < r < m and q is an integer.
This n = r (mod m)

Students can download Maths Chapter 1 Relations and Functions Unit Exercise 1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Unit Exercise 1

Question 1.
If the ordered pairs (x² – 3x, y² + 4y) and (-2, 5) are equal, then find x and y.
Answer:
(x² – 3x, y² + 4y) = (-2, 5)
x² – 3x = -2
x² – 3x + 2 = 0
(x – 2) (x – 1) = 0
x – 2 = 0 or x – 1 = 0
x = 2 or 1

y² + 4y = 5
y² + 4y – 5 = 0
(y + 5) (y – 1) = 0
y + 5 = 0 or y – 1 = 0
y = -5 or y = 1
The value of x = 2, 1
and 7 = -5, 1

Question 2.
The Cartesian product A × A has 9 elements among which (-1, 0) and (0, 1) are found. Find the set A and the remaining elements of A × A.
Solution:
A = {-1, 0, 1}, B = {1, 0, -1}
A × B = {(-1, 1), (-1, 0), (-1, -1), (0, 1), (0, 0), (0, -1), (1, 1), (1, 0), (1, -1)}

Question 3.
Given that f(x) = \(\left\{\begin{array}{rl}
{\sqrt{x-1}} & {x \geq 1} \\
{4} & {x<1}
\end{array}\right.\).
Find
(i) f(0) (ii)f (3) (iii) f(a + 1) in terms of a.(Given that a > 0)
Answer:
f(x) = \(\sqrt { x-1 }\) ; f(x) = 4
(i) f(0) = 4
(ii) f(3) = \(\sqrt { 3-1 }\) = \(\sqrt { 2 }\)
(iii) f(a + 1) = \(\sqrt { a+1-1 }\) = \(\sqrt { a }\)

Question 4.
Let A = {9, 10, 11, 12, 13, 14, 15, 16, 17} and let f: A → N be defined by f(n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f.
Solution:
A = {9, 10, 11, 12, 13, 14, 15, 16, 17}
f: A → N
f(n) = the highest prime factor of n ∈ A
f = {(9, 3), (10, 5), (11, 11), (12, 3), (13, 13), (14, 7), (15, 5), (16, 2), (17, 17)}
Range = {3, 5, 11, 13, 7, 2, 17}
= {2, 3, 5, 7, 11, 13, 17}

Question 5.
Find the domain of the function

Answer:

Domain of f(x) = {-1, 0, 1}

Question 6.
If f(x)= x², g(x) = 3x and h(x) = x – 2 Prove that (fog)oh = fo(goh).
Solution:
f(x) = x²
g(x) = 3x
h(x) = x – 2
(fog)oh = x – 2
LHS = fo(goh)
fog = f(g(x)) = f(3x) = (3x)² = 9x²
(fog)oh = (fog) h(x) = (fog) (x – 2)
= 9(x – 2)² = 9(x² – 4x + 4)
= 9x² – 36x + 36 ……………. (1)
RHS = fo(goh)
(goh) = g(h(x)) = g(x – 2)
= 3(x – 2) = 3x – 6
fo(goh) = f(3x – 6) = (3x – 6)²
= 9x² – 36x + 36 ………….. (2)
(1) = (2)
LHS = RHS
(fog)oh = fo(goh) is proved.

Question 7.
Let A= {1,2} and B = {1,2,3,4}, C = {5,6} and D = {5,6,7,8}. Verify whether A × C is a subset of B × D?
Answer:
Given A = {1, 2}
B = {1, 2, 3, 4}
C = {5,6}
D = {5,6, 7,8}
A × C = {1,2} × {5,6}
= {(1,5) (1,6) (2, 5) (2, 6)}
B × D = {1,2, 3, 4} × {5, 6, 7, 8}
= {(1,5) (1,6) (1,7) (1,8)
(2, 5) (2, 6) (2,7) (2, 8)
(3, 5) (3, 6) (3, 7) (3, 8)
(4, 5) (4, 6) (4, 7) (4, 8)}
∴ A × C ⊂ B × D
Hence it is verified

Question 8.
If f(x) = \(\frac{x-1}{x+1}, x \neq 1\) Show that
f(f(x)) = – \(\frac { 1 }{ x } \), Provided x ≠ 0.
Answer:

Question 9.
The functions f and g are defined by f{x) = 6x + 8; g(x) = \(\frac { x-2 }{ 3 } \)
(i) Calculate the value of gg [latex]\frac { 1 }{ 2 } [/latex]
(a) Write an expression for gf (x) in its simplest form.
Answer:
f(x) = 6x + 8 ; g(x) = \(\frac { x-2 }{ 3 } \)

Question 10.
Write the domain of the following real functions

Answer:
(i) f (x) = \(\frac { 2x+1 }{ x-9 } \)
If the denominator vanishes when x = 9
So f(x) is not defined at x = 9
∴ Domain is x ∈ [R – {9}]

(ii) if p(x) = \(=\frac{-5}{4 x^{2}+1}\)
p(x) is defined for all values of x. So domain is x ∈ R.

(iii) g(x) = \(\sqrt { x-2 }\)
When x < 2 g(x) becomes complex. But given “g” is real valued function.
So x > 2
Domain x ∈ (2, α)

(iv) h (x) = x + 6
For all values of x, h(x) is defined. Hence domain is x ∈ R.

Students can download Maths Chapter 1 Relations and Functions Ex 1.6 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.6

Multiple Choice Questions

Question 1.
If n(A × B) = 6 and A= {1, 3} then n (B) is ………….
(1) 1
(2) 2
(3) 3
(4) 6
Answer:
(3) 3
Hint: n(A × B) = 6
n(A) = 2
n(A × B) = n(A) × n(B)
6 = 2 × n(B)
n(B) = \(\frac { 6 }{ 2 } \) = 3

Question 2.
A = {a, b, p}, B = {2, 3}, C = {p, q, r, s} then n[(A ∪ C) × B] is
(1) 8
(2) 20
(3) 12
(4) 16
Answer:
(3) 12
Hint:
A = {a, b, p}, B = {2, 3}, C = {p, q, r, s}
n (A ∪ C) × B
A ∪ C = {a, b, p, q, r, s}
(A ∪ C) × B = {{a, 2), (a, 3), (b, 2), (b, 3), (p, 2), (p, 3), (q, 2), (q, 3), (r, 2), (r, 3), (s, 2), (s, 3)
n [(A ∪ C) × B] = 12

Question 3.
If A = {1,2}, B = {1,2, 3, 4}, C = {5,6} and D = {5, 6, 7, 8} then state which of the following statement is true ……………….
(1) (A × C) ⊂ (B × D)
(2) (B × D) ⊂ (A × C)
(3) (A × B) ⊂ (A × D)
(4) (D × A) ⊂ (B × A)
Answer:
(1) (A × C) ⊂ (B × D)
Hint: n(A × B) = 2 × 4 = 8
(A × C) = 2 × 2 = 4
n(B × C) = 4 × 2 = 8
n(C × D) = 2 × 4 = 8
n(A × C) = 2 × 2 = 4
n(A × D) = 2 × 4 = 8
n(B × D) = 4 × 4 = 16
∴ (A × C) ⊂ (B × D)

Question 4.
If there are 1024 relations from a set A = {1, 2, 3, 4, 5} to a set B, then the number of elements in B is
(1) 3
(2) 2
(3) 4
(4) 6
Answer:
(2) 2
Hint:
n(A) = 5
n(B) = x
n(A × B) = 1024 = 2¹⁰
2^5x = 2¹⁰
⇒ 5x = 10
⇒ x =2

Question 5.
The range of the relation R = {(x, x²) a prime number less than 13} is ……………………
(1) {2, 3, 5, 7}
(2) {2, 3, 5, 7, 11}
(3) {4, 9, 25, 49, 121}
(4) {1, 4, 9, 25, 49, 121}
Answer:
(3) {4, 9, 25, 49, 121}
Hint:
Prime number less than 13 = {2, 3, 5, 7, 11}
Range (R) = {(x, x²)}
Range = {4, 9, 25, 49, 121} (square of x)

Question 6.
If the ordered pairs (a + 2, 4) and (5, 2a + b)are equal then (a, b) is
(1) (2, -2)
(2) (5, 1)
(3) (2, 3)
(4) (3, -2)
Answer:
(4) (3, -2)
Hint:
(a + 2, 4), (5, 2a + b)
a + 2 = 5
a = 3
2a + b = 4
6 + b = 4
b = -2

Question 7.
Let n(A) = m and n(B) = n then the total number of non-empty relations that can be defined from A to B is ……………..
(1) mⁿ
(2) n^m
(3) 2^mn – 1
(4) 2^mn
Answer:
(4) 2^mn

Question 8.
If {(a, 8),(6, b)}represents an identity function, then the value of a and b are respectively
(1) (8, 6)
(2) (8, 8)
(3) (6, 8)
(4) (6, 6)
Answer:
(1) (8, 6)
Hint:
{{a, 8), (6, b)}
a = 8
b = 6

Question 9.
Let A = {1, 2, 3, 4} and B = {4, 8, 9, 10}.
A function f: A → B given by f = {(1, 4), (2, 8),(3,9),(4,10)} is a ……………
(1) Many-one function
(2) Identity function
(3) One-to-one function
(4) Into function
Answer:
(3) One-to-one function
Hint:

Different elements of A has different images in B.
∴ It is one-to-one function.

Question 10.
If f (x) = 2x² and g(x) = \(\frac { 1 }{ 3x } \), then fog is …………..
(1) \(\frac{3}{2 x^{2}}\)
(2) \(\frac{2}{3 x^{2}}\)
(3) \(\frac{2}{9 x^{2}}\)
(4) \(\frac{1}{6 x^{2}}\)
Answer:
(3) \(\frac{2}{9 x^{2}}\)
Hint:

Question 11.
If f: A → B is a bijective function and if n(B) = 7, then n(A) is equal to
(1) 7
(2) 49
(3) 1
(4) 14
Answer:
(1) 7
Hint:
In a bijective function, n(A) = n(B)
⇒ n(A) = 7

Question 12.
Let f and g be two functions given by
f = {(0,1),(2, 0),(3-4),(4,2),(5,7)}
g = {(0,2),(1,0),(2, 4),(-4,2),(7,0)}
then the range of f o g is …………………
(1) {0,2,3,4,5}
(2) {-4,1,0,2,7}
(3) {1,2,3,4,5}
(4) {0,1,2}
Answer:
(4) {0,1,2}
Hint: f = {(0, 1)(2, 0)(3, -4) (4, 2) (5, 7)}
g = {(0,2)(l,0)(2,4)(-4,2)(7,0)}

fog = f[g(x)]
f [g(0)] = f(2) = 0
f [g(1)] = f(0) = 1
f [g(2)] = f(4) = 2
f[g(-4)] = f(2) = 0
f[g(7)] = f(0) = 1
Range of fog = {0,1,2}

Question 13.
Let f(x) = \(\sqrt{1+x^{2}}\) then
(1) f(xy) = f(x),f(y)
(2) f(xy) ≥ f(x),f(y)
(3) f(xy) ≤ f(x).f(y)
(4) None of these
Answer:
(3) f(xy) ≤ f(x).f(y)
Hint:
\(\sqrt{1+x^{2} y^{2}} \leq \sqrt{\left(1+x^{2}\right)} \sqrt{\left(1+y^{2}\right)}\)
⇒ f(xy) ≤ f(x) . f(y)

Question 14.
If g= {(1,1),(2,3),(3,5),(4,7)} is a function given by g(x) = αx + β then the values of α and β are
(1) (-1,2)
(2) (2,-1)
(3) (-1,-2)
(4) (1,2)
Answer:
(2) (2, -1)
Hint: g (x) = αx + β
g(1) = α(1) + β
1 = α + β ….(1)
g (2) = α (2) + β
3 = 2α + β ….(2)
Solve the two equations we get
α = 2, β = -1

Question 15.
f(x) = (x + 1)³ – (x – 1)³ represents a function which is
(1) linear
(2) cubic
(3) reciprocal
(4) quadratic
Answer:
(4) quadratic
Hint:
f(x) = (x + 1)³ – (x – 1)³
= x³ + 3x² + 3x + 1 -[x³ – 3x² + 3x – 1]
= x³ + 3x² + 3x + 1 – x³ + 3x² – 3x + 1 = 6x² + 2
It is a quadratic function.

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.3 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.3

Question 1.
Find the least positive value of x such that

(i) 71 = x (mod 8)
Answer:
71 = 7 (mod 8)
∴ The value of x = 7

(ii) 78 + x = 3 (mod 5)
78 + x – 3 = 5n (n is any integer)
75 + x = 5n
(Let us take x = 5)
75 + 5 = 80 (80 is a multiple of 5)
∴ The least value of x is 5

(iii) 89 = (x + 3) (mod 4)
89 – (x + 3) = 4n
(n may be any integer)
89 – x – 3 = 4n
89 – x = 4n
86 – x is a multiple of 4
(84 is a multiple of 4)
86 – 2 = 4n
84 = 4n
The value of x is 2

(iv) 96 = \(\frac { x }{ 7 } \) (mod 5)
96 – \(\frac { x }{ 7 } \) = 5n (n may be any integer)
672 – x = 35n (multiple of 35 is 665)
672 – 7 = 665
∴ The value of x = 7

(v) 5x = 4 (mod 6)
5x – 4 = 6n (n may be any integer)
5x = 6n + 4
x = \(\frac { 6n+4 }{ 5 } \)
Substitute the value of n as 1, 6, 11, 16 …. as n values in x = \(\frac { 6n+4 }{ 5 } \) which is divisible by 5.
2, 8, 14, 20,…………
The least positive value is 2.

Question 2.
If x is congruent to 13 modulo 17 then 7x -3 is congruent to which number modulo 17?
Solution:
x ≡ 13 (mod 17)
Let p be the required number …………. (1)
7x – 3 ≡ p (mod 17) ………….. (2)
From (1),
x – 13 = 17n for some integer M.
x – 13 is a multiple of 17.
x must be 30.
∴ 30 – 13 = 17
which is a multiple of 17.
From (2),
7 × 30 – 3 ≡ p (mod 17)
210 – 3 ≡ p (mod 17)
207 ≡ p (mod 17)
207 ≡ 3 (mod 17)
∴ P ≡ 3

Question 3.
Solve 5x ≡ 4 (mod 6)
5x – 4 = 6n (n may be any integer)
5x = 6n + 4
x = \(\frac{6 n+4}{5}\)
The value of n 1, 6, 11, 16 ……..
∴ The value of x is 2, 8, 14, 20 …………..

Question 4.
Solve 3x – 2 = 0 (mod 11)
Answer:
Given 3x – 2 = 0(mod 11)
3x – 2 = 11n (n may be any integer)
3x = 2 + 11n
x = \(\frac { 11n+2 }{ 3 } \)
Substitute the value of n = 2, 5, 8, 11 ….
When n ≡ 2 ⇒ x = \(\frac { 22+2 }{ 3 } \) = \(\frac { 24 }{ 3 } \) = 8
When n = 5 ⇒ x = \(\frac { 55+2 }{ 3 } \) = \(\frac { 57 }{ 3 } \) = 19
When n = 8 ⇒ x = \(\frac { 88+2 }{ 3 } \) = \(\frac { 90 }{ 3 } \) = 30
When n = 11 ⇒ x = \(\frac { 121+2 }{ 3 } \) = \(\frac { 123 }{ 3 } \) = 41
∴ The value of x is 8, 19, 30,41

Question 5.
What is the time 100 hours after 7 a.m.?
Answer:
100 ≡ x (mod 12) Note: In a clock every 12 hours
100 ≡ 4 (mod 12) the numbers repeats.

The time repeat after 7 am is 7 + 4 = 11 o’ clock (or) 11 am.

Question 6.
What is time 15 hours before 11 p.m.?
Solution:
15 ≡ x (mod 12)
15 – x = 12n
15 – x is a multiple of 12 x must be 3.

∴ The time 15 hrs before 11 O’clock is 11 – 3 = 8 O’ clock i.e. 8 p.m

Question 7.
Today is Tuesday. My uncle will come after 45 days. In which day my uncle will be coming?
Answer:
Number of days in a week = 7
45 ≡ x (mod 7)
45 ≡ 3 (mod 7)

The value of x must be 3.
Three days after tuesday is friday uncle will come on friday.

Question 8.
Prove that 2ⁿ + 6 × 9ⁿ is always divisible by 7 for any positive integer n.
Solution:
2¹ + 6 × 9¹ = 2 + 54 = 56 is divisible by 7
When n = k,
2^k + 6 × 9^k = 7 m [where m is a scalar]
⇒ 6 × 9^k = 7 m – 2^k …………. (1)
Let us prove for n = k + 1
Consider 2^k+1 + 6 × 9^k+1 = 2^k+1 + 6 × 9^k × 9
= 2^k+1 + (7m – 2^k)9 (using (1))
= 2^k+1 + 63m – 9.2^k = 63m + 2^k.2¹ – 9.2^k
= 63m – 2^k (9 – 2) = 63m – 7.2^k
= 7 (9m – 2^k) which is divisible by 7
∴ 2ⁿ + 6 × 9ⁿ is divisible by 7 for any positive integer n

Question 9.
Find the remainder when 2⁸¹ is divided by 17?
Answer:
2⁸¹ ≡ x(mod 17)
2⁴⁰ × 2⁴⁰ × 2¹ ≡ x(mod 17)
(2⁴)¹⁰ × (2⁴)¹⁰ × 2¹ ≡ x(mod 17)
(16)¹⁰ × (16)¹⁰ × 2¹ ≡ x(mod 17)
(16²)⁵ × (16²)⁵ × 2¹ ≡ x(mod 17)
= 1 × 1 × 2 (mod 17)
[(16)² = 256 = 1 (mod 17)]
= 2 (mod 17)
2⁸¹ = 2(mod 17)
∴ x = 2
The remainder is 2

Question 10.
The duration of flight travel from Chennai to London through British Airlines is approximately 11 hours. The airplane begins its journey on Sunday at 23:30 hours. If the time at Chennai is four and half hours ahead to that of London’s time, then find the time at London, when will the flight lands at London Airport?
Answer:
Duration of the flight time = 11 hours
(Chennai to London)
Starting time on Sunday = 23 : 30 hour

Time difference is 4 \(\frac { 1 }{ 2 } \) horns ahead to london
The time to reach London airport = (10.30 – 4.30)
= 6 am
The first reach the london airport next day (monday) at 6 am