Category: Class 12

Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Accountancy Guide Pdf Chapter 8 Bank Reconciliation Statement Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 11th Accountancy Solutions Chapter 8 Bank Reconciliation Statement

11th Accountancy Guide Bank Reconciliation Statement Text Book Back Questions and Answers

I. Multiple Choice Questions

Choose the correct answer.

Question 1.
A bank reconciliation statement is prepared by ________.
a) Bank
b) Business
c) Debtor to the business
d) Creditor to the business
Answer:
b) Business

Question 2.
A bank reconciliation statement is prepared with the help of ________.
a) Bank statement
b) Cash book
c) Bank statement and bank column of the cash book
d) Petty cash book
Answer:
c) Bank statement and bank column of the cash book

Question 3.
Debit balance in the bank column of the cash book means ________.
a) Credit balance as per bank statement
b) Debit balance as per bank statement
c) Overdraft as per cash book
d) None of the above
Answer:
a) Credit balance as per bank statement

Question 4.
A bank statement is a copy of ________.
a) Cash column of the cash book
b) Bank column of the cash book
c) A customer’s account in the bank’s book
d) Cheques issued by the business
Answer:
c) A customer’s account in the bank’s book

Question 5.
A bank reconciliation statement is prepared to know the causes for the difference between:
a) The balance as per the cash column of the cash book and bank column of the cashbook
b) The balance as per the cash column of the cash book and bank statement
c) The balance as per the bank column of the cash book and the bank statement
d) The balance as per petty cash book and the cash book
Answer:
c) The balance as per the bank column of the cash book and the bank statement

Question 6.
When money is withdrawn from bank, the bank ________.
a) Credits customer’s account
b) Debits customer’s account
c) Debits and credits customer’s account
d) None of these
Answer:
b) Debits customer’s account

Question 7.
Which of the following is not the salient feature of bank reconciliation statement?
a) Any undue delay in the clearance of cheques will be shown up by the reconciliation
b) Reconciliation statement will discourage the accountant of the bank from embezzlement
c) It helps in finding the actual position of the bank balance
d) Reconciliation statement is prepared only at the end of the accounting period
Answer:
d) Reconciliation statement is prepared only at the end of the accounting period

Question 8.
Balance as per cash book is ₹ 2,000. Bank charge of ₹ 50 debited by the bank is not yet shown in the cash book. What is the bank statement balance now?
a) 1,950 credit balance
b) 1,950 debit balance
c) 2,050 debit balance
d) 2,050 credit balance
Answer:
a) 1,950 credit balance

Question 9.
Balance as per bank statement is 1, 000. Cheque deposited, but not yet credited by the bank is 2, 000. What is the balance as per bank column of the cash book?
a) 3,000 overdraft
b) 3,000 favourable
c) 1,000 overdraft
d) 1,000 favourable
Answer:
b) 3,000 favourable

Question 10.
Which one of the following is not a timing difference?
a) Cheque deposited but not yet credited
b) Cheque issued but not yet presented for payment
c) Amount directly paid into the bank
d) Wrong debit in the cash book
Answer:
d) Wrong debit in the cash book

II. Very Short Answer Questions

Question 1.
What is meant by bank overdraft?
Answer:
An amount of money that a customer with a bank account is temporarily allowed to owe to the bank. An overdraft occurs when money is withdrawn from a bank account and the available balance goes below zero.

Question 2.
What is bank reconciliation statement?
Answer:
The bank reconciliation statement is a statement that reconciles the balance as per the bank column of cash book with the balance as per the bank statement by giving the reasons for such difference along with the amount. The internal record of the business (bank column of cash) can be reconciled with the external record (bank statement).

Question 3.
State any two causes of disagreement between the balance as per bank column of cash book and bank statement.
Answer:

1. Cheques issued but not presented for payment.
2. Cheques paid into bank for collection but not yet collected.

Question 4.
Give any two expenses which may be paid by the banker as per standing instruction.
Answer:

1. Bank Charges
2. Interest

Question 5.
Substitute the following statements with one word/phrase.
Answer:

1. A copy of customer’s account issued by the bank – PASS BOOK
2. Debit balance as per bank statement – BANK OVERDRAFT
3. Statement showing the causes of disagreement between the balance as per cash book and balance as per bank statement – BANK RECONCILIATION STATEMENT

Question 6.
Do you agree on the following statements? Write “yes” if you agree, and write “no” if you Disagree
Answer:

1. Bank reconciliation statement is prepared by the banker. – Yes
2. Adjusting the cash book before preparing the bank reconciliation statement is compulsory. – No
3. Credit balance as per bank statement is an overdraft. – No
4. Bank charges debited by the bank increases the balance as per bank statement. – No
5. Bank reconciliation statement is prepared to identify the causes of differences between balance as per bank column of the cash book and balance as per cash column of the cash book. – Yes

III. Short Answer Questions

Question 1.
Give any three reasons for preparing bank reconciliation statement.
Answer:

1. To identify the reasons for the difference between the bank balance as per the cash book and bank balance as per bank statement.
2. To identify the delay in the clearance of cheques.
3. To ascertain the correct balance of bank column of cash book.
4. To discourage the accountants of the business as well as bank from misusing funds.

Question 2.
What is meant by the term “cheque not yet presented?”
Answer:

1. When the cheques are issued by the business, it is immediately entered on the credit side of the cash book by the business.
2. This may not be entered in the bank statement on the same day.
3. It will be entered in the bank statement only after it is presented with the bank.

Question 3.
Explain why does money deposited into bank appear on the debit side of the cash book, but on the credit side of the bank statement?
Answer:

1. The assets will be entered in the debit side. The balance of deposits held by bank is recorded.
2. It denotes a favourable balance as per cash boor unfavourable balance as per the pass book.
   On the debit side, receipts of cash and cheques are recorded.
3. Deposited cash in to bank decreases the amount of cash available and is, therefore, credited to cash account (cash column of the cash book).
4. But, it also increases the bank balance and is therefore, debited to bank account (bank column of the cash book).

Question 4.
What will be the effect of interest charged by the bank, if the balance is an overdraft?
Answer:

1. If the business has taken any loan or overdrawn, interest has to be paid by the business.
2. The entries for bank charges and interest are made in the bank statement.
3. The cash book shows more balance than the bank statement.

Question 5.
State the timing differences in BRS with examples.
Answer:
Cheques issues but not presented for payment for payment:
When the cheques are issued by the business, it is immediately entered on the credit side of the cash book by the business. But, this may not be entered in the bank statement on the same day.

lt will be entered in the bank statement only after it is presented with For example, the balances as per cash book and bank statement are ₹ 20,000 for X & Co. X & Co. issued a cheque in favour of Y & Co for ₹ 10,000, on 27th March 2017. So, X & Co’s cash book is credited with ₹ 10,000 on 27th March 2017. But, the cheque is presented to bank on 2nd April 2017.

In case, bank sends a statement to X & Co, upto 31st March 2017, it will not contain this transaction. As a result, there will be a difference of 10,000, between balance shown as per cash book and balance as per bank statement.

Cheques deposited into bank but not yet credited:
When the cheques are deposited into bank, the amount is debited in the cash book on the same day. But, these may not be shown in the bank pass book on the same day because these will be entered in the bank statement only after the collection of the cheques.

For example, the balances as per cash book and bank statement are ₹ 20,000 for X & Co. X & Co. receives a cheque on 25th March 2016, from ABC Limited for ₹ 5,000. On the same day, X & Co, debits its cash book with ₹ 5,000.

But bank credits X & Co’s account only when the cheque is collected from ABC Limited’s bank. This shows that is a time gap between depositing the cheque by the customer (X & Co) and collection of cheque by the bank.

Bank Charges and interest on loan and overdraft charged by the bank:
The bank has to cover the cost of running the customer’s account. So debit is given to the account of the business towards bank charges.

Also, if the business had taken any loan or over drawn, interest has to be paid by the business. These entries for bank charges and interest are made in the bank statement. But, the entry is made in the cash book only when the bank statement is received by the business.

Till then, the cash book shows more balance than bank statement. For example, the opening balance as per cash book and the bank statement as on 1st March 2017 is ₹ 7,000. Bank debits for bank charges ₹ 300 as on 27th March 2017. But there is no entry for the same in the cash book as on such date.

IV. Exercises

Question 1.
From the following particulars prepare a bank reconciliation statement of Jayakumar as on 31st December, 2016.
a) Balance as per cash book ₹ 7,130
b) Cheque deposited but not cleared ₹ 1,000
c) A customer has deposited ₹ 800 into the bank directly
Solution:
Bank reconciliation statement of Jayakumar as on 31st December, 2016.

Question 2.
From the following particulars of Kamakshi traders, prepare a bank reconciliation statement as on 31st March, 2018.
a) Debit balance as per cash book ₹ 10,500
b) Cheque deposited into bank amounting to ₹ 5,500 credited by bank, but entered twice in the cash book
c) Cheques issued and presented for payment amounting to ₹ 7,000 omitted in the cash book
d) Cheque book charges debited by the bank ₹ 200 not recorded in the cash book.
e) Cash of ₹ 1,000 deposited by a customer of the business in cash deposit machine not recorded in the cash book.
Solution:
Bank reconciliation statement of Kamakshi traders as on 31st March, 2018.

Question 3.
From the following information, prepare bank reconciliation statement to find out the bank statement balance as on 31st December, 2017.

Solution:
Bank reconciliation statement of Kamakshi traders as on 31st March, 2018.

Question 4.
On 31st March, 2017, Anand’s cash book showed a balance of ₹ 1,12,500, Prepare bank reconciliation statement,
a) He had issued cheques amounting to ₹ 23,000 on 28,3.2017, of which cheques amounting to ₹ 9,000 have so far been presented for payment.

b) A cheque for ₹ 6,300 deposited into bank on 27.3.2017, but the bank credited the same only on 5th Aprii 2017.

c) He had also received a cheque for ₹ 12,000 which, although entered by him in the cash book, was not deposited in the bank.

d) Wrong credit given by the bank on 30th March 2017 for ₹ 2,000.

e) On 30th March 2017, a bill already discounted with the bank for ₹ 3,000 was dishonoured, but no entry was made in the cash book.

f) Interest on debentures of ₹ 700 was received by the bank directly.

g) Cash sales of ₹ 4,000 wrongly entered in the bank column of the cash book.
Solution:
Bank reconciliation statement of Mr, Anand as on 31st March, 2017

Question 5.
From the following particulars of Siva and Company, prepare a bank reconciliation state- ment as on 31st December, 2017.
a) Credit balance as per cash book ₹ 12,000
b) A cheque of ₹ 1,200 Issued and presented for payment to the bank, wrongly credited in the cash book
c) Debit side of bank statement was under cast by ₹ 100
Solution:
Bank reconciliation statement as on 31st December, 2017.

Question 6.
From the following particulars of Raheem traders, prepare a bank reconciliation statement as on 31st March, 2018.
a) Overdraft as per cash book ₹ 2,500
b) Debit side of cash book was under cash by ₹ 700
c) Amount received by bank through RTGS amounting to ₹ 2,00,000, omitted in the cash book.
d) Two cheques issued for ₹ 1,800 and ₹ 2,000 on 29th March 2018. Only the second cheque is presented for payment.
e) Insurance premium on car for ₹ 1,000 paid by the bank as per standing instruction not recorded in the cash book
Solution:
Bank reconciliation statement as on 31st March, 2018.

Question 7.
From the following information, prepare bank reconciliation statement as on 31st December,

Solution:
Bank reconciliation statement as on 31st December, 2017

Question 8.
Prepare bank reconciliation statement from the following data.

Solution:
Bank reconciliation statement

Question 9.
From the following particulars of Veera traders, prepare a bank reconciliation statement as on 31st December, 2017.
a) Credit balance as per bank statement ₹ 6,000
b) Amount received by bank through NEFT for ₹ 3,500, entered twice in the cash book.
c) Cheque dishonoured amounting to ₹ 2,500, not entered in cash book.
Solution:
Bank reconciliation statement as on 31st December, 2017.

Question 10.
Prepare bank reconciliation statement from the following data and find out the balance as per cash book as on 31st March, 2018.

Solution:
Bank reconciliation statement as on 31st March, 2018.

Question 11.
Ascertain the cash book balance from the following particulars as on 31st December, 2017
i) Credit balance as per bank statement ₹ 2,500
ii) Bank charges of ?60 have not been entered in the cash book
iii) Cheque deposited on 28th December 2017 for ₹ 1,000 was not yet credited by the bank
iv) Cheque issued on 24th December 2017 for ₹ 700, not yet presented for payment
v) A dividend of ₹ 400 collected by the bank directly but not entered in the cash book
vi) Acheque of ₹ 600 had been dishonoured, but no entry was made in the cash book
vii) Interest on term loan ₹ 1,200 debited by bank but not accounted in cash book
viii) No entry had been made in the cash book for a trade subscription of ₹ 500 paid vide banker’s order on 23rd December 2014
Solution:
Bank reconciliation statement as on 31st December, 2017.

Question 12.
From the following particulars of Raja traders, prepare a bank reconciliation statement as on 31st January, 2018.
a) Balance as per bank statement ₹ 5,000

b) Cheques amounting to ₹ 800 had been recorded in the cash book as having been deposited into the bank on 25th January 2018, but were entered in the bank statement on 2nd February 2018.

c) Amount received by bank through NEFT amounting to ₹ 3,000, omitted in the cash book.

d) Two cheques issued for ₹ 3,000 and ₹ 2,000 on 29th March 2018. Only the first cheque is presented for payment.

e) Insurance premium on motor vehicles for ₹ 1,000 paid by the bank as per standing instruction not recorded in the cash book.

f) Credit side of cash book was undercast by ₹ 700

g) Subsidy received directly by the bank from the state government amounting to ? 10,000, not entered in cash book.
Solution:
Bank reconciliation statement of Mr. Raja traders as on 31st January, 2018.

Question 13.
From the following particulars of Simon traders, prepare a bank reconciliation statement as on 31st March, 2018.
a) Debit balance as per bank statement ₹ 2,500
b) Cheques deposited amounting to ₹ 10,000, not yet credited by bank.
c) Payment through net banking for ₹ 2,000, omitted in the cash book.
Solution:
Bank reconciliation statement as on 31st March, 2018.

Question 14.
From the following particulars, ascertain the cash book balance as on 31st December, 2016.
i) Overdraft balance as per bank statement ₹ 1,26,640
ii) Interest on overdraft entered in the bank statement, but not yet recorded in cash book ₹ 3,200
iii) Bank charges entered in bank statement, but not found in cash book ₹ 600
iv) Cheques issued, but not yet presented for payment ₹ 23,360
v) Cheques deposited into the bank but not yet credited ₹ 43,400
vi) Interest on investment collected by the bank ₹ 24,000
Solution:
Bank reconciliation statement as on 31st December, 2016.

Question 15.
From the following particulars of John traders, prepare a bank reconciliation statement as on 31st March, 2018.
a) Bank overdraft as per bank statement ₹ 4,000

b) Cheques amounting to ₹ 2,000 had been recorded in the cash book as having been deposited into the bank on 26th March 2018, but were entered in the bank statement on 4th April 2018.

c) Amount received by bank through cash deposit machine amounting to ₹ 5,000, omitted in the cash book.

d) Amount of ₹ 3,000 wrongly debited to John traders account by the bank, for which no details are available.

e) Bills for collection credited by the bank till 29th March 2017 amounting to ₹ 4,000, but no advice received by John traders.

f) Electricity charges made through net banking for ₹ 900 was wrongly entered in cash column of the cash book instead of bank column.
Solution:
Bank reconciliation statement as on 31st March, 2018.

Question 16.
Prepare bank reconciliation statement from the following data.

Solution:
Prepare bank reconciliation statement.

Question 17.
Prepare bank reconciliation statement as on 31st March, 2017 from the following extracts of cash book and bank statement.
Cash book (Bank column only)

Bank statement

Solution:
Bank reconciliation statement as on 31st March, 2017

Question 18.
A trader received his bank statement on 31st December, 2017 which showed an overdraft balance of ₹ 12,000. On the same day, his cash book showed a debit balance of ₹ 2,000.
Analyse the following transactions. Choose the possible causes and prepare a bank reconciliation statement to show the causes of differences.
a) Cheque deposited for ₹ 2,000 on 21st December, 2017. Bank credited the same on 26th December, 2017.

b) Cheque issued for payment on 26th December, 2017 amounting to ₹ 2,500, not yet presented until 31st, December, 2017.

c) Bank charges amounting to ₹ 200 not yet entered in the cash book.

d) Online payment for ₹ 1,500 entered twice in the cash book.

e) Cheque deposited amounting to ₹ 1,000, but omitted in the cash book. The same cheque was dishonoured by bank, but not yet entered in cash book.

f) Cheque deposited, not yet credited by bank amounting to ₹ 17,800.
Solution:
Bank reconciliation statement as on 31st December, 2017.

11th Accountancy Guide Bank Reconciliation Statement Additional Important Questions and Answers

I. Choose the correct answer.

Question 1.
A Bank Reconciliation Statement is prepared with the help of ________.
a) Bank statement and bank column of the cash book
b) Journal
c) Ledger
d) None of the above
Answer:
a) Bank statement and bank column of the cash book

Question 2.
Bank reconciliation statement is ______
a) Part of bank statement
b) Part of the cash book
c) A separate statement
d) A sub-division of journal
Answer:
a) Part of bank statement

Question 3.
Uncollected cheques are also known as ______.
a) Outstanding cheques
b) Uncleared cheques
c) Outstation cheques
d) Both a & c
Answer:
d) Both a & c

Question 4.
When cheque is not paid by the bank it is called as ______.
a) Honoured
b) Endorsed
c) Dishonoured
d) None of these
Answer:
c) Dishonoured

Question 5.
A bank reconciliation statement is prepared by ______.
a) Banker
b) Accountant of the business
c) Auditors₹
d) None of the above
Answer:
b) Accountant of the business

Question 6.
The cheque which is deposited into bank but not cleared at the end of a particular year is called ______.
a) Uncredited cheque
b) Unpresented cheque
c) Omitted cheque
d) Dishonoured cheque
Answer:
b) Unpresented cheque

Question 7.
In cash book bank charges recorded in the ______.
a) Credit side
b) Debit Side
c) Both a & b
d) None of the above
Answer:
a) Credit side

Question 8.
An amount of Rs,2G0Q is debited twice in the bank statement. What will the reflect when overdraft as per the cash book is the starting point ______.
a) ₹ 2000 will be deducted
b) ₹ 2000 will be added
c) ₹ 4000 will be deducted
d) ₹ 4000 will be deducted
Answer:
b) ₹ 2000 will be added

Question 9.
If any amount is directly deposited into the bank then ______.
a) Cash book will show less balance & bank book will show more
b) Cash book will show more balance & bank book will show less
c) Cash book will show double balance
d) Bank book will show double
Answer:
a) Cash book will show less balance & bank book will show more

Question 10.
Which of the following error results in unadjusted cash book balance?
a) Outstanding cheques
b) Unpresented Cheques
c) deposit in Transit
d) Omission of Bank charges
Answer:
d) Omission of Bank charges

Question 11.
Credit balance in the bank column of the cash book means ______.
a) Credit balance as per bank statement
b) Debit balance as per bank statement
c) Overdraft as per cash book
d) None of the above
Answer:
b) Debit balance as per bank statement

Question 12.
When balance as per Cash Book is the starting point, to ascertain balance as per bank statement interest allowed by Bank is ______.
a) Subtracted
b) added
c) not adjusted
d) None of the above
Answer:
b) added

Question 13.
When balance as per Cash Book is the starting point, to ascertain the balance as per bank statement interest charged by Bank is:
a) Added
b) subtracted
c) not adjusted
d) None of the above
Answer:
b) subtracted

Question 14.
When the balance as per Cash Book is the starting point to ascertain balance as per bank statement, direct deposits by customers are:
a) Added
b) subtracted
c) not adjusted
d) None of the above
Answer:
a) Added

Question 15.
When the balance as per Cash Book is the starting point to ascertain balance as per bank statement, direct payments by bank are:
a) Added
b) subtracted
c) not adjusted
d) None of the above
Answer:
b) subtracted

Question 16.
______ is not possible to have unfavourable cash balance in the cash book.
a) Bank statement
b) Bank overdraft
c) Cash overdraft
d) Cash book
Answer:
b) Bank overdraft

Question 17.
Bank overdraft is available only to the ______ holders.
a) Saving Account
b) Fixed Account
c) Joint Account
d) Current Account
Answer:
d) Current Account

Question 18.
______ is simply a copy of the customer’s account in the books of a bank.
a) Cash book
b) Bank statement
c) Bank Account
d) None of these
Answer:
b) Bank statement

Question 19.
A bank statement is a copy of ______ .
a) the cash column of a customer’s cash book
b) the bank column of a customer’s cash book
c) the customer’s account in the bank’s ledger
d) none of these
Answer:
c) the customer’s account in the bank’s ledger

Question 20.
Debit balance in the Cash Book means ______.
a) overdraft as per bank statement
b) credit balance as per bank statement
c) overdraft as per Cash Book
d) none of these
Answer:
b) credit balance as per bank statement

II. Additional Questions & Answers

Question 1.
Differences between bank column of cash book and bank statement.
Answer:
Bank column of cash book:

• It is prepared by business concern.
• Cash deposits are entered on the debit side.
• Cash withdrawals are entered on the credit side.
• Cheque deposits are debited on the day of deposit.
• Cheques issued are credited on the day of issue of cheque.
• Collections and payments as per standing instructions of the business are entered only after checking with the bank statement.
• It is balanced at the end of a specific period.

Bank statement:

• It is prepared by bank (banker).
• Cash deposits are entered in the credit column.
• Cash withdrawals are entered in the debit column.
• Cheque deposits are credited only at the time of realisation of cheque.
• Cheques issued by customers are debited by bank on the date on which the payment is made.
• Collections and payments as per standing instructions of the business are entered in the banker’s book on the date of realisation or payment.
• It is balanced after each transaction.

Question 2.
What are the items recorded on the debit side of the bank column of the cash book?
Answer:

1. Cheques deposited but not credited.
2. Credits in the pass book only.
   • Interest credited in bank statement
   • Dividend and other income
   • Direct deposit by a party
3. Any error in cash book/ bank statement which has the effect of increasing the balance as per bank statement.

Question 3.
What are the items recorded on the credit side of the bank column of the cash Book?
Answer:

1. Cheques deposited but not credited
2. Cheques dishonoured but not entered in cash book
3. Debits in bank statement only
   • Interest debited
   • Insurance premium, loan instalment, etc., paid as per standing instructions
   • Direct payment by banker
4. Any error in cash book/ bank statement which has the effect of decreasing the balance as per bank statement

Question 4.
What is meant by the term “Cheques deposited into bank but not yet credited?”
Answer:
When the cheques are deposited into bank, the amount is debited in the cash book on the same day. But, these may not be shown in the bank pass book on the same day because these will be entered in the bank statement only after the collection of the cheques.

For example, the balances as per cash book and bank statement are ₹ 20,000 for X & Co. X & Co. receives a cheque on 25th March 2016, from ABC Limited for ₹ 5,000. On the same day, X & Co, debits its cash book with ₹ 5,000.

But bank credits X & Co’s account only when the cheque is collected from ABC Limited’s bank. This shows that is a time gap between depositing the cheque by the customer (X & Co) and collection of cheque by the bank.

Question 5.
What will be the effect of Interest and dividends collected by the bank?
Answer:
The bank may collect dividends on its customer’s investment in shares and also interest on any investment. The entry for this will be made in the bank statement on the date of collection. But the entry is made in the cash book only when the bank statement is received by the customer. Till then, the cash book shows less balance than the bank statement.

Question 6.
What will be the effect of Dishonour of cheques and bills?
Answer:
When the cheque is received from outside parties, it is deposited with the bank and debited in the cash book. If the cheque is dishonoured, the bank cannot collect the amount of such cheque from outside parties’ bank. It is not credited in the bank statement. As a result of this, the two records would differ.

While discounting the bills receivables, in the cash book it is entered in the debit side and in the bank statement it is credited. When the bill is presented by the bank to the drawee of the bill and the payment is not received, the bank debits the same to cancel the credit.

But, credit is made in the cash book only when the customer gets the entries made in the bank statement is received. The bank may also charge some amount for such dishonour.

Question 7.
What will be the effect of Amount paid by parties directly into the bank?
Answer:
Sometimes, debtors or the customers of the business may directly deposit the money into bank account of the business. It may be done by directly visiting the branch of the bank by paying cash (including NEFT, RTGS) or swiping debit or credit or business card or depositing the money in cash deposit machine or transfer through online banking facility.

This will be credited in the banker’s book. But the entry is made in the cash book only when the bank statement is received by the customer. Until then, the cash book shows less balance than bank statement.

Question 8.
What will be the effect of Amount paid directly by the bank to others?
Answer:
Sometimes the bank may be instructed to make payments such as, insurance premium, instalment of loan, etc., as an agent of the customer on behalf of its customer. In all such cases, debit is made in bank statement. But, the entry is made in the cash book only when the bank statement is received by the customer. Till then, the cash book shows more balance than bank statement.

Question 9.
What will be the effect of Bills collected by the bank on behalf of its customers?
Answer:
When goods are sold by the business, the documents may be sent through the bank. When the bank collects the amount, it is credited in bank records. But, the entry is made in the cash book only when the bank statement is received by the business. Till then, the bank statement shows more balance than cash book.

Question 10.
Explain the differences arising due to errors in recording the entries.
Answer:
Errors committed in recording the transactions by the business in the cash book:
Sometimes, errors may be committed in the cash book. For example, omission or wrong recording of transaction relating to cheques deposited or issued, wrong balancing, etc. In these cases, obviously, there will be differences between bank balance as per bank statement and bank balance as per cash book.

Errors committed in recording the transactions by the bank:
Sometimes errors may be committed in the banker’s book. For example, omission or wrong recording of transaction relating to cheques deposited and wrong balancing. In these cases, obviously, there will be differences between bank balance as per bank statement and bank balance as per cash book.

Question 11.
What is the need for bank reconciliation statement?
Answer:

1. To identify the reasons for the difference between the bank balance as per the cash book and bank balance as per bank statement.
2. To identify the delay in the clearance of cheques.
3. To ascertain the correct balance of bank column of cash book.
4. To discourage the accountants of the business as well as bank from misusing funds.

Additional Sums:

Question 1.
Prepare bank reconciliation statement of Mr. Bala as on 31.03.2013.
a) Balance as per cash book ₹ 15,000
b) Cheques deposited but not cleared ₹ 1,000
c) Cheques issued but not yet present for payments ₹ 1500 d. Interest allowed by bank ₹ 200
Solution:
Prepare bank reconciliation statement

Question 2.
Prepare bank Reconciliation statement to find out balance as per bank statement on 31st March 2018,
1. Cheques deposited but not yet collected by the bank ₹ 1,000
2. Cheques issued but not yet presented for payment ₹ 2,000
3. Bank Interest Charged ₹ 200
4. Rent paid by bank as per standing Instruction ₹ 400
5. Cash book balances ₹ 600
Solution:
Prepare bank reconciliation statement

Question 3.
Form the following particulars of Ashok and company; prepare a bank reconciliation statement as on 31st March 2018.
a) Credit balance as per cash book ₹ 10,000
b) Cheques issued but not yet presented for payment ₹ 10,000
c) Cheques Deposited but not credited ₹ 9000
d) Rent collected by the bank as per standing Instruction ₹ 500
Solution:
Bank Reconciliation statement Mr. Ashok as on 31st March 2018

Question 4.
From the following information, Prepare bank Reconciliationstatement of Mr. Mohan as on 31st Dec. 2017 to find out the balance as per bank statement.
i) Overdraft as per cash book – 20000
ii) Cheques deposited but not yet credited – 10000
iii) Amount wrongly deposited by bank – 600
iv) Interest on overdraft debited by bank – 2000
v) Cheque issued but not yet present for payment – 2000
vi) Payment received from the customer directly by the bank – 1000
Solution:
Bank Reconciliation statement Mr. Mohan as on 31st Dec. 2018.

Question 5.
Prepare bank Reconciliation statement as on 31st December 2017. From the following in information.
a) Balance as perbank statement (pass book) is ₹ 50,000
b) Cheques deposited into bank amount into ₹ 7,000 were not yet collected.
c) Bank charges of ₹ 600 have not been entered in the cash book.
d) Cheques issued amount to ₹ 18,000 have not been presented by for payment.
Solution:
Bank Reconciliation statement as on 31st Dec. 2017.

Question 6.
From the following information, prepare bank Reconciliationstatement as of Mr. Pugazh as on 31st Dec. 2017.
i) Credit balance as per bank statement ₹ 12,000
ii) Cheques deposited on 28th December 2017 but not yet credited ₹ 4000
iii) Cheques issued for 20000 on 20th December 2017 but not yet presented for payment 6000.
iv) Interest on debentures directly in cash book ₹ 8000
v) Insurance premium on building directly paid by the bank ₹ 2000
vi) Amount wrongly credit by bank ₹ 1,000
Solution:
Bank Reconciliation statement of Mr. Pugazh as on 31st Dec. 2017.

Question 7.
From the following data, as certain the cash book balance as on 31st Dec. 2017.
1) Overdraft balance as per bank statement ₹ 13,000
2) Cheques deposited into the bank but not yet credited ₹ 21,000
3) Wrongly credit by the bank ₹ 1,000
4) Cheques issued, but not yet presented for payment₹ 6,000
5) Bank charges debited by bank ₹ 360
6) Insurance Premium on building directly paid by bank ₹ 200
Solution:
Bank Reconciliation statement on 31st Dec. 2017.

Question 8.
Prepare bank Reconciliation statement as on 31st Dec. 2017, From the following balance of cash book, and bank statement.
Cash book (Bank column)

Bank Statement

Solution:
Bank Reconciliation Statement on 31st Dec, 2017.

Question 9.
On 31st March 2017, the pass book of Mr, A showed a credit balance of Rs.92,500. A comparison of pass book and cash book revealed the following:

Solution:
Bank Reconciliation Statement of Mr. A as on 31st March 2017

Question 10.
The bank overdraft of Rajini on 31.12.2017 as per cash book is 90,000. From the following particulars, prepare bank reconciliation statement:

Solution:
Bank Reconciliation Statement as on 31,12.2017 3,000

Question 11.
Prepare a bank reconciliation statement from the following data as on 31.12.2017.
a) Balance as per cash book ₹ 1,25,500
b) Cheques issued but not presented for payment ₹ 9,000
c) Cheques deposited in bank but not collected ₹ 12,000
d) Bank paid insurance premium ₹ 5,000
e) Direct deposit by a customer ₹ 8,000
f) Interest on investment collected by bank ₹ 2,000
g) Bank charges ₹ 1,000
Solution:
Bank Reconciliation Statement as on 31.12.2017

Question 12.
The pass book of X with his bank shows a debit balance of Rs. 500 on 31.10.2017. On comparison of the pass book with the cash book, it is observed that:
i. Cheques issued by X in October 2017 amounted to ₹ 4, 535 of which cheques amounting to ₹ 3,535 were paid by the bank by 31st October 2017.

ii. X deposited cheques amounting to ₹ 5, 000 on 31st October 2017. These cheques were realised by the bank on 1st November, 2017.

iii. Y a customer of X had directly deposited a sum of ₹ 3, 000 on 24th October 2017 to the credit of X account with the bank. X recorded this receipt on 4th November, 2017.

iv. The bank had debited X’s account with ₹ 1, 520 on 31.1.2017 on account of a dishonoured bill. No entry for the same has been made in the account books.

v. On 31.10.1995 X’s account was credited with ₹ 130 being dividend collected by the bank. On the same day, his account was debited with ₹ 10 being bank charges. Both these entries were recorded by X only on 5th November, 2017.
Prepare the Bank Reconciliation Statement as at 31.10.2017.
Solution:
Bank Reconciliation Statement as on 31.10.2017

Question 13.
From the following particulars ascertain the bank balance as would appear in the pass‘book as on 31st December, 2016.
i. The bank overdraft (Credit balance) as per cash book on 31st December 2016 was ₹ 60,000
ii. Interest on overdraft, six months ending 31st December, amounting to ₹ 2,000 is debited in the pass book.
i. Bank charges for the above period also debited in the pass book which amounted to ₹ 500.
ii. Cheques issued but not presented for payment before 31st December amounted to ₹ 15,000.
iii. Cheques paid into the bank, but not cleared and credited before 31st December were ₹ 25,000.
iv. Interest on government securities collected by the bank and credited in the pass book amounted to ₹ 18,000.
Solution:
Bank Reconciliation Statement as on 31st March 2016

Question 14.
From the following information available from the books and records of X & Co., prepare BRS:

Solution:
Bank Reconciliation Statement for Bank A/c No. I

Bank Reconciliation Statement for Bank A/c No. II

Question 15.
From the following particulars ascertain the bank balance that would appear in the cash book of Son 31.12.2016.
i) The bank overdraft as per pass book on 31.12.2016 ₹ 6,340
ii) Interest on on for the year ending 31.12.2016 ₹ 160 is debited in the pass book
iii) Bank charges of ₹130 for the above period are also debited in the pass book.
iv) Cheques issued but not cashed prior to 31.12.2016 amounted to ₹ 11,168
v) Cheques paid into bank but not cleared before 31.12.2016 were ₹ 2170
vi) Interest on investments collected by the bankers and credited in the pass book, ₹ 1,200
Solution:
Bank Reconciliation Statement as on 31st December 2016

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 10 Operations Research Miscellaneous Problems Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 10 Operations Research Miscellaneous Problems

Question 1.
The following table summarizes the supply, demand and cost information for four factors S₁, S₂, S₃, S₄ Shipping goods to three warehouses D₁, D₂, D₃.

Find an initial solution by using north west corner rule. What is the total cost for this solution?
Solution:
The given transportation table is

Here total supply = 5 + 8 + 7+14 = 34
Total amount =7 + 9 + 18 = 34
(i.e) Total supply = Total demand.
∴ The given problem is balanced transformation problem.
We can find an initial basic feasible solution to the given problem.
First allocation:



Transportation schedule:
S₁ → D₁; S₂ → D₁; S₂ → D₂;
S₃ → D₂; S₃ → D₃; S₄ → D₃
The transportation cost:
= (5 × 2) + (2 × 3) + (6 × 3) + (3 × 4) + (4 × 7) + (14 × 2)
= 10 + 6 + 18 + 12 + 28 + 28
= 102

Question 2.
Consider the following transportation problem

Determine an initial basic feasible solution using (a) Least cost method (b) Vogel’s approximation method.
Solution:
(a) Least cost method
Given transportation table is

Total Availability = Total Requirement = 100
∴ The given problem is balanced transformation problem.
Hence there exists a feasible solution to the given problem
First allocation:



Here
x₁₂ = 10; x₁₃ = 20; x₂₁ = 30;
x₂₂ = 10; x₂₄ = 10; x₃₂ = 20
Transportation Scheme:
O₁ → D₂; O₁ → D₃; O₂ → D₁;
O₂ → D₂; O₂ → D₄; O₃ → D₂
The transportation cost:
=(10 × 8) + (20 × 3) + (30 × 4) + (10 × 5) + (10 × 4) + (20 × 2)
= 80 + 60 + 120 + 50 + 40 + 40
= 390

(ii) Vogel’s approximation method:
Here Σai = Σbj = 100
∴ The given problem is balanced transformation problem.
Hence there exists a feasible solution to the given problem
First allocation:



Here
x₁₁ = 30; x₁₃ = 20; x₂₂ = 20;
x₂₄ = 10; x₃₂ = 20
Transportation Scheme:
O₁ → D₁; O₂ → D₃; O₂ → D₂;
O₂ → D₄; O₃ → D₂;
Total transportation cost:
= (30 × 5) + (20 × 3) + (20 × 5) + (10 × 4) + (20 × 2)
= 150 + 60 + 100 + 40 + 40
= 390

Question 3.
Determine an initital basic feasible solution to the following transportation problem by using (i) North West Corner rule (ii) least cost method.

Solution:
(i) North West Corner rule:
The given transportation table is

Total supply = 25 + 35 + 40 = 100
Total Requirement = 30 + 25 + 45 + 100
(i.e) Total supply = Total requirement.
∴ The given problem is balanced transformation problem.
Hence there exists a feasible solution to the given problem
First allocation:


Transformation schedule:
S₁ → D₁; S₂ → D₁; S₂ → D₂;
S₃ → D₃; S₃ → D₃;
The transformation cost:
= (25 × 9) + (5 × 6) + (25 × 8) + (5 × 4) + (40 × 9)
= 225 + 30 + 200 + 20 + 360 = 835

(ii) Least cost method
The given transportation table is

(i.e) Total supply = Total requirement = 100
∴ The given problem is balanced transformation problem.
Hence there exists a feasible solution to the given problem
First allocation:


Transportation schedule:
S₁ → D₃; S₂ → D₃; S₃ → D₁
S₃ → D₂;
The transportation cost:
= (10 × 5) + (35 × 4) + (15 × 7) + (25 × 6) + (40 × 9)
= 50 + 140 + 105 + 150 + 360 = 805

Question 4.
Explain Vogel’s approximation method by obtaining initial basic feasible solution of the following transportation problem.

Solution:
The given transportation table is

Here Σai = Σbj =17
(i.e) Total supply = Total Demand
∴ The given problem is balanced transformation problem.
Hence there exists a feasible solution to the given problem
First allocation:



Here
x₁₁ = 1; x₁₂ = 5; x₂₄ = 1;
x₃₁ = 6; x₃₃ = 15;
Transportation schedule:
O₁ → D₁; O₁ → D₂; O₂ → D₄
O₃ → D₁; O₃ → D₃
The transportation cost:
=(1 × 2) + (5 × 3) + (1 × 1) + (6 × 5) + (3 × 15) + (1 × 9)
= 2 + 15 + 1 + 30 + 45 + 9
= 102

Question 5.
A car hire company has one car at each of five depots a,b,c,d and e. A customer in each of the fine towers A, B, C, D and E requires a car. The distance (in miles) between the depots (origins) and the towers (destinations) where the customers are given the following distance matrix.

How should the cars be assigned to the customers so as to minimize the distance travelled?
Solution:
Here the number of rows and columns are equal.
∴ The given assignment problem is balanced.
Step 1.
Select the smallest element in each row and subtract this from all the elements in its row.

Step 2.
Select the smallest element in each column and subtract this from all the elements in its column.

Step 3. (Assignment)
Examine the rows with exactly one zero, mark the zero by □ mark other zeros, in its column by X

Step 4.
Now Examine the rows with exactly one zero, mark the zero by □ mark other zeros, in its column by X

Step 5.
Cover all the zeros of table 4 with three lives. Since three assignments were made please note that check [✓] Row C and E which have no assignment.

Step 6.
Develop the new revised tableau. Examine those elements that are not covered by a line in Table 5. Take the smallest element in each row and subtract from the uncovered cells, depots

Step 7.
Go to step 3 and repeat the procedure until you arrive at an optimal assignments.
depots

Step 8.
Determine an assignment

Here all the five assignments have been made. The optimal assignment schedule and total distance is

∴ The optimum Distance (minimum) 575 kms

Question 6.
A natural truck – rental service has a surplus of one truck in each of the cities 1, 2, 3, 4, 5 and 6 and a deficit of one truck in each of the cities 7, 8, 9, 10, 11 and 12. The distance (in kilometers) between the cities with a surplus and the cities with

How should the truck be dispersed so as to minimize the total distance travelled?
Solution:
Here the number of rows and columns are equal.
∴ The given assignment problem is balanced.
Step 1.
Select the smallest element in each row and subtract this from all the elements in its row.

Step 2.
Select the smallest element in each column and subtract this from all the elements in its column.

Step 3.
Examine the rows with exactly one zero, mark the zero by □ mark other zeros, in its column by X

Step 4.
Examine the Columns with exactly one zero. If there is exactly one zero, mark that zero by □ mark other zeros in its rows by X

Step 5.
Cover all the zeros of table 4 with five lines. Since three assignments were made

Step 6.
Develop the new revised tableau. Examine those elements that are not covered by a line in Table 5. Take the smallest element. This is l(one) in our case. By subtracting 1 from the uncovered cells.

Step 7.
Go to step 3 and repeat the procedure until you arrive at an optimal assignments.

Step 8.
Determine an assignment

Here all the six assignments have been made. The optimal assignment schedule and total distance is

∴The optimum Distance (minimum) = 125 kms

Question 7.
A person wants to invest in one of three alternative investment plans: Stock, Bonds and Debentures. It is assumed that the person wishes to invest all of the funds in a plan. The pay – off matrix based on three potential economic conditions is given in the following table

Solution:

(i) Maximin
Max (3000, 1000, 6000) = 6000. Since the maximum pay of is 6000, the alternative ‘Debentures’, is selected.

(ii) Minimax
Min (10000, 8000, 6000) = 6000, Since the minimum pay-off is 6000. the alternative ‘Debentures’ is selected.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 10 Operations Research Ex 10.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 10 Operations Research Ex 10.4

Choose the correct answer

Question 1.
The transportation problem is said to be unbalanced if
(a) Total supply ≠ Total demand
(b) Total supply = Total demand
(c) m = n
(d) m + n – 1
Solution:
(a) Total supply ≠ Total demand

Question 2.
In a non – degenerate solution number of allocation is
(a) Equal to m + n – 1
(b) Equal to m + n + 1
(c) Not equal to m + n – 1
(d) Not equal to m + n + 1
Solution:
(a) Equal to m + n – 1

Question 3.
In a degenerate solution number of allocations is
(a) Equal to m + n – 1
(b) Not equal to m + n – 1
(c) Less then m + n – 1
(d) Greater then m + n – 1
Solution:
(c) Less then m + n – 1

Question 4.
The Penalty in VAM represents difference between the first
(a) Two largest costs
(b) Largest and Smallest costs
(c) smallest two costs
(d) None of these
Solution:
(c) smallest two costs

Question 5.
Number of basic allocation in any row or column in an assignment problem can be
(a) Exactly one
(b) At least one
(c) At most one
(d) None of these
Solution:
(a) Exactly one

Question 6.
North – West Corner refers to
(a) Top left corner
(b) Top right corner
(c) Bottom right corner
(d) Bottom left corner
Solution:
(a) Top left corner

Question 7.
Solution for transportation problem using method is nearer to an optimal
(a) NWCM
(b) LCM
(c) VAM
(d) Row Minima
Solution:
(c) VAM

Question 8.
In an assignment problem the value of iedsion variable x_ij is
(a) 1
(b) 0
(c) 1 or 0
(d) none of them
Solution:
(c) 1 or 0

Question 9.
If number of sources is not equal to number of destinations, the assignment problem is called
(a) balanced
(b) unsymmetric
(c) symmetric
(d) unbalanced
Solution:
(d) unbalanced

Question 10.
The purpose of a dummy row or column in an assignment problem is to
(a) prevent a solution from becoming degenerate
(b) balance between total activities and total resources
(c) provide a means of representing a dummy problem
(d) None of the above
Solution:
(b) balance between total activities and total resources

Question 11.
The solution for an assignment problem is optimal if
(a) each row and each column has no assignment
(b) each row and each column has atleast one assignment
(c) each row and each column has atmost one assignment
(d) each row and each column has exactly one assignment
Solution:
(d) each row and each column has exactly one assignment

Question 12.
In an assignment problem involving four workers and three jobs, total number of assignments possible are
(a) 4
(b) 3
(c) 7
(d) 12
Solution:
(b) 3

Question 13.
Decision theory is concerned with
(a) analysis of information that is available
(b) decision making under certainty
(c) selecting optimal decisions in sequential problem
(d) All of the above
Solution:
(d) All of the above

Question 14.
A type of decision – making environment is
(a) certainty
(b) uncertainty
(c) risk
(d) all of the above
Solution:
(d) all of the above

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 10 Operations Research Ex 10.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 10 Operations Research Ex 10.3

Question 1.
Given the following pay – off matrix (in rupees) for three strategies and two states for nature.

Select a strategy using each of the following rule (i) Maximin (ii) Minimax
Solution:

(i) Max min
Max ( 40, -20, -40) = 40. Since the maximum pay-off is 40, the alternative S, is selected.

(ii) Minimax
min (60, 10, 150) = 10, Since the minimum payoff is 10. the alternative S₂ is selected.

Question 2.
A farmer wants to decide which of three crops he should plant on his 100 – acre farm. The profit from each is dependent on the rainfall during the growing season. The farmer has categorized the amount of rainfall as high medium and low. His estimated profit for each is shown in the table.

In the farmer wishes to plant only crop, decide which should be his best crop using (i) Maximin (ii) Minimax
Solution:

(i) Maximin
Max ( 3500, 4500, 2000) = 4500. Since the maximum pay-off is 4500, the alternative ‘Medium’, is selected.

(ii) Minimax
min (8000, 5000, 5000) = 5000, Since the minimum pay-off is 5000. the alternatives both ‘Medium’ and ‘Low’ are selected.

Question 3.
The research department of Hindustan Ltd. has recommended to pay marketing department to launch a shampoo of three different types. The marketing types of shampoo to be launched under the following T estimated pay-offs for various level of sales.

What will be the marketing manager’s decision if (i) Maximin and (ii) Minimax principle applied?
Solution:

(i) Maximin
Max ( 10, 5, 3) = 10. Since the maximum pay of is 10, “Egg Shampoo”, is selected.

(ii) Minimax
min (30, 40, 55) = 30, Since the minimum pay-off is 30. the alternative “Egg Shampoo” is selected

Question 4.
Following pay – off matrix, which is the optimal decision under of the following rule (i) maximin (ii) minimax

Solution:

(i) Maximin
Max ( 5, 7, 9, 8) = 5. Since the maximum pay-off is 5, the alternative A₁ is selected.

(ii) Minimax
min (14, 11, 11, 13) = 11, Since the minimum pay-off is 11. the alternative alternatives A₂ and A₃ are selected.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 10 Operations Research Ex 10.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 10 Operations Research Ex 10.2

Question 1.
What is the Assignment problem?
Solution:
Suppose that we have ‘m1 jobs to be performed on ‘n’ machines. The cost of assigning each job to each machine is C_ij (i = 1, 2, … n and j = 1, 2, … , n). Our objective is to assign the different jobs to the different machines (one job per machine) to minimize the overall cost. This is known as assignment problem.

Question 2.
Give mathematical form of assignment problem.
Solution:
Consider the problem of assigning n jobs to n machines (one job to one machine). Let C_ij be the cost of assigning i^th job to the j^th machine and x_ij represents the assignment of i^th job to the j^th machine.

x_ij is missing in any cell means that no assignment is made between the pair of job and machine.(i.e) x_ij = 0.
x_ij is presents in any cell means that an assignment is made their. In such cases x_ij = 1
The assignment model can written in LPP as follows
Minimize Z = \(\sum_{i=1}^{m}\) \(\sum_{j=1}^{n}\) C_ij x_ij
Subject to the constrains
\(\sum_{i=1}^{n}\) x_ij = 1, j = 1, 2, …. n
\(\sum_{j=1}^{n}\) x_ij = 1, i = 1,2,….n and x_ij =0 (or) 1 for all i, j

Question 3.
What is the difference between Assignment Problem and Transportation Problem?
Solution:

Question 4.
Three jobs A, B and C one to be assigned to three machines U, V and W. The processing cost for each job machine combination is shown in the matrix given below. Determine the allocation that minimizes the overall processing cost.
(cost is in Rs per unit)

Solution:
Here the number of rows and columns are equal.
∴ The given assignment problem is balanced.
Step 1.
Select the smallest element in each row and subtract this from all the elements in its row.

Look for atleast one zero in each row and each column.
Here each and every row and columns having exactly one zero No need step 2 go to step 3.

Step 3.

Mark the zero by □ Mark other zeros in its column by X.
Since each row and each column contains exactly one assignment, all the three machine have been assigned a job.

The Optimal assignment (minimum) cost = 46

Question 5.
A computer centre has got three expert programmers. The centre needs three application programmes to be developed. The head of the computer centre, after studying carefully the programmes to be developed, estimates the computer time in minitues required by the experts to the application programme as follows.

Assign the programmers to the programme in such a way that the total computer time is least.
Solution:
Here the number of rows and columns are equal.
∴ The given assignment problem is balanced.
Step 1.
Select the smallest element in each row and subtract this from all the elements in its row.

Step 2.
Select the smallest element in each column and subtract this from all the elements in its column.

Step 3. (Assignment)
Examine the rows with exactly one zero, mark the zero by □. Mark other zeros in its column by X.

Step: 4
Now examine the columns with exactly one zero mark the zero by □. Mark other zeros in its row by X.

Thus all the three assignment have been made. The optimal assignment schedule and total cos is

The optimal assignment (minimum) cost = Rs 280

Question 6.
A departmental head has four subordinates and four tasks to be performed. The subordinates differ in efficiency and the tasks differ in their intrinsic difficulty. His estimates of the time man would take to perform each task is given below.

How should the tasks to allocated to subordinates so as to minimize the total man-hours?
Solution:
Here the number of rows and columns are equal.
∴ The given assignment problem is balanced.
Step 1.
Select the smallest element in each row and subtract this from all the elements in its row.

Step 2.
Select the smallest element in each column and subtract this from all the elements in its column.

Step 3. (Assignment)
Examine the rows with exactly one zero Mark the zero by □. Mark other zeros in its row by X.

Step 4.
Now examine the columns with exactly one zero. Mark the zero by □ Mark other zeros in its row by X.

Step 5.
Cover all the zeros of table 4 with three lines, since three assignments were made check (✓) row S since it has no assignment.

Step 6.
Develop the new revised tableau. Examine those elements that are not covered by a line in table 5. Take the smallest element. This is 1 (one) our case. By subtracting 1 from the uncovered cells.

[Adding 1 to elements (Q, S, R) that line at the intersection of two lines]

Step 7.
Go to step 3 and repeat the procedure until you arrive at an optimal assignment.

Step 8.
Determine an assignment.

Thus all the four assignment have been made. The optimal assignment schedule and total time is

The optimum time (minimum) = 41 Hrs.

Question 7.
Find the optimal solution for the assignment problem with the following cost matrix.

Solution:
Here the number of rows and columns are equal.
∴ The given assignment problem is balanced.
Step 1.
Select the smallest element in each row and subtract this from all the elements in its row.

Step 2.
Select the smallest element in each column and sub tract this from all the elements in its column.

Step 3. (Assignment)
Examine the rows with exactly one zero. Mark the zero by □ Mark other zeros in its column by X

Thus all the four assignments have been made. The optimal assignment schedule and total cost.

The Optimum cost (minimum) = Rs 37

Question 8.
Assign four trucks 1, 2, 3 and 4 to vacant spaces A, B, C, D, E and F so that distance travelled is minimized. The matrix below shows the distance.

Solution:
Since the number of columns is less than the number of rows, the given assignment problem is unbalanced one. To balance it, introduce two dummy columns with all the entries zeros.
The revised assignment problem is

Here only 4 tasks can be assigned to 4 vacant spaces.
Step 1.
It is not necessary, since each row contains zero entry. Go to step 2.

Step 2.
Select the smallest element in each column and subtract this from all the elements in its column.

Step 3. (Assignment)
Since each row contains more than one zeros. Go to step 4.

Step 4.
Examine the columns with exactly one zero, mark the zero by □ Mark other zeros in its rows by X.

Step 5.
Here all the four assignments have been made we can assign d₁ for D then we will get d₂ for E.

The optimal assignment schedule and total distance is

∴ The Optimum Distant (minimum) = 12 units

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 10 Operations Research Ex 10.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 10 Operations Research Ex 10.1

Question 1.
What is transportation problem?
Solution:
The objective of transportation problem is to determine the amount to be transported from each origin to each destinations such that the total transportation cost is minimized.

Question 2.
Write mathematical form of transportation problem.
Solution:
Let there be m origins and n destinations. Let the amount of supply at th i th origin is a_i. Let the demand at j th destination is b_j.
The cost of transporting one unit of an item from origin i to destination j is C_ij and is known for all combination (i,j). Quantity transported from origin i to destination j be x_ij.

The objective is to determine the quantity x_ij to be transported over all routes (i,j) so as to minimize the total transportation cost. The supply limits at the origins and the demand requirements at the destinations must be satisfied.
The above transportation problem can be written in the following tabular form:

Now the linear programming model representing the transportation problem is given by
The objective function is Minimize Z = \(\sum_{\mathbf{i}=\mathbf{1}}^{\mathbf{m}}\), \(\sum_{\mathbf{j}=\mathbf{1}}^{\mathbf{n}}\) c_ij x_ij
Subject to the constraints
\(\sum_{\mathbf{j}=\mathbf{1}}^{\mathbf{n}}\) = x_ij = a_i, i = 1, 2 …….. m (supply constraints)
\(\sum_{\mathbf{i}=\mathbf{1}}^{\mathbf{m}}\) = x_ij = b_j, i = 1, 2 …….. n (demand constraints)
x_ij ≥ 0 for all i, j (non- negative restrictions)

Question 3.
What is feasible solution and non degenerate solution in transportation problem?
Solution:
Feasible Solution:
A feasible solution to a transportation problem is a set of non-negative values x_ij (i = 1, 2, … m, j = 1, 2, … n) that satisfies the constraints.

Non degenerate basic feasible solution:
If a basic feasible solution to a transportation problem contains exactly m + n – 1 allocations in independent positions, it is called a Non degenerate basic feasible solution. Here m is the number of rows and n is the number of columns in a transportation problem.

Question 4.
What do you mean by balanced transportation problem?
Solution:
In a transportation problem if the total supply equals the total demand (Σa_i = Σb_j) then it is said to be balanced transportation problem.

Question 5.
Find an intial basic feasible solution of the following problem using north west corner rule.

Solution:
Here total Supply 19 + 37 + 34 = 90
Total demand = 16 + 18 + 31 + 25 = 90
(i.e) Total supply = Total demand
∴ The given problem is balanced transportation problem
∴ we can final an initial basic feasible solution to due given problem.

From the above table we can choose the cell in the North west corner. Here the cell is (Q₁, D₁). Allocate as much as possible in this cell so that either the capacity of first row is exhausted or the destination requirement of the first column’s exhausted.
(i.e) x₁₁ = min (19, 16) = 16

Now the cell in the north west corner is (O₁, D₂) Allocate as much as possible in the first cell so that either the capacity of second row is exhausted or the destination requirement of the first column is exhausted.
(i.e) x₁₂ = min (3, 18) = 3

Reduced transportation table is

Now the cell in the north west corner is (O₂, D₂)
x₂₂ = min (37, 15) = 15

Now the cell in the north west corner is (O₂, D₃)
x₂₃ = min (22, 31) = 9

Now the cell in the north west corner is (O₃, D₃)
x₃₃ = min (34, 9) = 9

Thus we have the following allocations

Transportation schedule:
O₁ → D₁, O₁, → D₂, O₂ → D₂; O₂ → D₃ O₃ → D₃; O₃ → D₄
= (16 × 5) + (3 × 3) + (15 × 7) + (22 × 9) + (9 × 7) + (25 × 5)
= 80 + 9 + 105 + 198 + 63 + 125
= 580

Question 6.
Determine an intial basic feasible solution of the following transportation problem by north west corner method.

Solution:
Here total capacity (a_i) = 30 + 40 + 50 = 120
Total demand (b_j) = 35 + 28 + 32 + 25 = 120
(i.e) Total capacity = Total demand
∴ The given problem is balanced transportation.
∴ We can find an initial basic feasible solution to the given problem.

From the above table we can choose the cell in the North west corner. Here the cell is (chennai, Bangalore)
x₁₁ = min (30, 35) = 30
Reduced transportation table is

Now the cell in the North west corner is (Madurai, Bangalore)
x₂₁ = min(40, 5) = 5

From the above table we can choose the cell in the North west corner. Here the cell is (Nasik, Madurai)
x₂₂ = min (35, 28) = 28

From the above table we can choose the cell in the North west corner. Here the cell is (Bhopal, Madurai)
x₂₂ = min (7, 32) = 7

From the above table we can choose the cell in the North west corner. Here the cell is (Trichy, Bhopal)
x₃₃ = min (50, 25) = 25
Reduced transportation table is

x₃₄ = min (25, 25) = 25
Thus we have the following allocations

Transportation Schedule:
Chennai → Bangalore; Madurai → Bangalore;
Madurai → Naisk; Madurai → Bhopal
Trichy → Bhopal; Trichy → Delhi
The total transportation cost =
(30 × 6) + (5 × 5) + (28 × 11) + (7 × 9) + (25 × 7) + (25 × 13)
= 180 + 25 + 308 + 63 + 175 + 325
= 1076

Question 7.
Obtain an initial basic feasible solution to the following transportation problem by using least-cost method.

Solution:
The given transportation table is

Total supply = 25 + 35 + 40 = 100
Total demand = 30 + 25 + 45 = 100
(i.e) Total supply = Total demand
∴ The given problem is a balanced transportation problem.
Hence there exists a feasible solution to the given problem.
The least cos is 4 corresponds to the cell (O₂, D₃)
Allocate min (35, 45) = 35 units to this cell

The least cost corresponds to the cell (O₁, D₃)
Allocate min (25, 10) = 10 units to this cell

The least cost is 6 corresponds to the cell (O₃, D₂)
Allocate min (40, 25) = 25 units to this cell

The least cost is 7 corresponds to the cell (O₃, D₁)
Allocate min (15, 30) = 15

Thus we have the following allocations

Transportation Schedule:
O₁ → D₁; O₁, → D₃; O₂ → D₃; O₃ → DI; O₃ → D₂
Total Transportation cost
= (15 × 9) + (10 × 5) + (35 × 4) + (15 × 7) + (25 × 6)
= 135 + 50 + 140 + 105 + 150
= 580

Question 8.
Explain vogel’s approximation method by obtaining initial feasible solution of the following transportation problem.

Solution:
Here Σ ai = 6 + 1 + 10 = 17
Σ bj = 7 + 5 + 3 + 2 = 17
Σ ai = Σ bj
(i.e) Total supply = Total Demand
∴ The given problem is balanced transportation problem
Hence there exists a feasible solution to the given problem.
First let us find the difference (penalty) between the first two smallest costs in each row and column and write them in brackets against the respective rows and columns.

Choose the largest difference. Here the largest difference is 6 which corresponds to column D₄
In this column choose the least cost. Here the least cost corresponds to (O₂, D₄)
Allocate min (1, 2) = 1 unit to this cell the reduced transportation table is

choose the largest difference 5 which corresponds to column D₂. Here the least cost corresponds to (O₁, D₂).
Allocate min (6, 5) = 5 units in this cell

Choose the largest difference 5 which corresponds to row O₁. Here the least cost corresponds to (O₁, D₁)
Allocate min (1, 7) = 1 unit in this cell

Choose the largest difference 4 which corresponds to row O₃. Here least cost corresponds to (10, 6) = 6 units in this cell.

Choose the largest difference 6 which corresponds to row O₃. Here the least cost corresponds to (O₃, D₄).
Allocate min (4, 1) = 1

Thus we have the following allocations

Transportation schedule
O₁ → D₁; O₁ → D₂; O₂ → D₄;
O₃ → D₁; O₃ → D₃; O₃ → D₄
Total transportation cost:
= (1 × 2) + (5 × 3) + (1 × 1) + (6 × 5) + (3 × 15) + (1 × 9)
= 2 + 15 + 1 + 30 + 45 + 9
= 102

Question 9.
Consider the following transportation problem.

Determine initital basic feasible solution by VAM
Solution:
Given Transportation problem is

Here Σ ai = Σ bj = 100
∴ The given problem is balanced transportation problem.
Hence there exists a feasible solution to the given problem.
First let us find the difference (penalty) between the first two smallest costs in each row and column and write them in brackets against the respective rows and columns

Choose the largest difference. Here the difference is 3 which corresponds to D₂
In this column choose the least cost. Here the least cos corresponds to (O₃, D₂)
Allocate min (20, 40) = 20 units to this cell

Choose the largest difference is 4 which corresponds to column D₃. In this column choose the least cost. Here the least cost corresponds to (O₁, D₃).
Allocate min (30, 20) = 20 units to this cell

Choose the largest different is 3 which corresponds to column D₂. In this column choose the least cost. Here the least cost corresponds to (O₂, D₂)
Allocate min (50, 20) = 20 units to this cell

Choose the largest difference is 2 which corresponds to column D₄. In this column choose the least cost. Here the least cost corresponds to (O₂, D₄).
Allocate min (30, 10) = 10 units to this cell

Allocate min (20, 30) = 20 units to this cell

Here
x₁₁ = 10
x₁₃ = 20
x₂₁ = 20
x₂₂ = 20
x₂₄ = 10
x₃₂ = 20
Transportation schedule
O₁ → D₁; O₁ → D₃; O₂ → D₁;
O₂ → D₂; O₂ → D₄; O₃ → D₂
The transportation cost
= (10 × 5) + (20 × 3) + (20 × 4) + (20 × 5) + (10 × 4) + (20 × 2)
= 50 + 60 + 80 + 100 + 40 + 40
= 370

Question 10.
Determine basic feasible solution to the following transportation problem using North west Corner rule.

Solution:
Here total supply = 4 + 8 + 9 = 21
Total demand = 3 + 3 + 4 + 5+ 6 = 21
(i.e) Total supply = Total demand
∴ The given problem is balanced transportation problem.
∴ we can find an initial basic feasible solution to the given problem.
From the above table we can choose the cell in the North west corner. Here the cell is (P, A)
Allocate as much as possible in this cell so that either the capacity of first row is exhausted or the destination requirement of the first column is exhausted.

Form the above table we can choose the cell in North west corner. Here the cell is (P,B)
x = min (1, 3) = 1

From the above table we can choose the cell in north west corner. Here the cell is (Q, B)
x = min (2, 8) = 2

From the above table, we can choose the cell in North west corner. Here the cell is (Q, C)

From the above table, we can choose the cell in North west corner. Here the cell is (Q, D)
x = min (2, 5) = 2

From the above table, we can choose the cell in North west corner. Here the cell is (R, D)
x = min (9, 3) = 3

Thus we have the following table

Transportation Schedule:
P → A; P → B; Q → B; Q → C; Q → D R → D; R → E
Total transportation cost:
= (3 × 2) + (1 × 11) + (2 × 4) + (4 × 7) + (2 × 2) + (3 × 8) + (6 × 2)
= 6 + 11 + 8 + 28 + 4 + 24 + 72
= 153

Question 11.
Find the initial basic feasible solution of the following transportation problem:

Using
(i) North West corner tule
(ii) Least Cost method
(iii) Vogel’s approximation method
Solution:
(i) North west corner rule:
Here the total supply = 10 + 10 + 10 = 30
Total demand = 7 + 12 + 11 = 30
(i.e) Total supply = Total demand
The given problem is balanced transportation problem.
∴ we can find an initial basic feasible solution to the given problem.
From the above table we can choose the cell in the North west corner. Here the cell is (A, I)
x₁₁ = min (7, 10) = 7

From the above table we can choose the cell in the north west corner. Here the cell is (B, I)
x = min (3, 12) = 3

From the above table we can choose the cell in the North west corner. Here the cell is (B, II)
x = min (9, 10) = 9

Here the cell in the North west corner is (C, II)
x = min (11, 1) = 1

Thus we have the following allocations

Transportation schedule:
A → I; B → I; B → II; C → II; C → III
Total transportation cost:
= (7 × 1) + (3 × 0) + (9 × 4) + (1 × 1) + (10 × 5)
= 7 + 0 + 36 + 1 + 50
= 94

(ii) Least cost method:
The given transportation table is

Here Total supply = Total demand = 30
∴ The given problem is a balanced transportation problem.
Hence there exists a feasible solution to the given problem.
The least cost is 0 corresponds to the cell (B, I)
Allocate min (12, 10) = 10 units to this cell

The least cost 1 corresponds to the cell (C, II)
Allocate min (11, 10) = 10 units to this cell

Here the least cost 2 corresponds to the cell (B, III)
Allocate min (2, 10) = 2 units to this cell.

Here the least cost is 5 corresponds to the cell (C, III)

Transportation schedule:
A → III; B → I; B → III; C → II; C → III
Total transportation cost:
= (7 × 6) + (10 × 10) + (2 × 2) + (10 × 1) + (1 × 5)
= 42 + 0 + 4 + 10 + 5
= 61

(iii) Vogel’s approximation method:
Here Σ ai = Σ bj = 30
(i.e) Total supply = Total demand
∴ This given problem is balanced transportation problem.
Hence there exists a feasible solution to the given problem.


A → I; B → I; B → III; C → I; C → II
Total transportation cost:
= (7 × 1) + (2 × 0) + (10 × 2) + (1 × 3) + (10 × 1)
= 7 + 0 + 20 + 3 + 10
= 40

Question 12.
Obtain an initial basic feasible solution to the following transportation problem by north west corner method.

Solution:
Here the total available = 250 + 300 + 400 = 950
Total Required = 200 + 225 + 275 + 250 = 950
(i.e) Total Available = total required
∴ The given problem is balanced transportation problem.
we can find an initial basic feasible solution to the given problem.
From the above table, we can choose the cell in the North west corner. Here the cell is (A, D).
x₁₁ = min (250, 200) = 200

From the above table we can choose the cell in North west corner. Here the cell is (A, E)
x = min (50, 225) = 50

From the above table, the north west corner cell is (B, E)
x = min (300, 175) = 175

From the above table, the north west corner cell is (B, F)
x = min (125, 275) = 125

Here the north west corner cell is (C, F)
x = min (400, 150) = 150

Transportation schedule:
A → D; A → E; B → E; B → F; C → G
Total Transportation cost:
= (200 × 11) + (50 × 13) + (175 × 18) + (125 × 14) + (150 × 13) + (250 × 10)
= 2200 + 650 + 3150 + 1750 + 1950 + 2500
= 12,200

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 9 Applied Statistics Miscellaneous Problems Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 9 Applied Statistics Miscellaneous Problems

Question 1.
Using three yearly moving averages, Determine the trend values from the following data.

Solution:

Question 2.
From the following data, calculate the trend values using fourly moving averages.

Solution:

Question 3.
Fit a straight line trend by the method of least squares to the following data.

Solution:

Therefore, the required equation of the straight line trend is given by
y = a + bx
y = 55.9875 + 0.830 x
⇒ y = 55.9875 + 0.83 (\(\frac { x-1983.5 }{0.5}\))
The trend values can be obtained by
When x = 1980
y = 55.9875 + 0.83 (\(\frac { 1980-1983.5 }{0.5}\))
= 55.9875 + 0.83 (-7)
= 55.9875 – 5.81
= 50.1775
When x = 1981
y = 55.9875 + 0.83 (\(\frac { 1981-1983.5 }{0.5}\))
= 55.9875 + 0.83 (-5)
= 55.9875 – 4.15
= 51.8375
When x = 1982
y = 55.9875 + 0.83 (\(\frac { 1981-1983.5 }{0.5}\))
= 55.9875 + 0.83 (-3)
= 55.9875 – 2.49
= 53.4975
When x = 1983
y = 55.9875 + 0.83 (\(\frac { 1983-1983.5 }{0.5}\))
= 55.9875 + 0.83 (-1)
= 55.9875 – 0.83
= 55.1575
When x = 1984
y = 55.9875 + 0.83 (\(\frac { 1984-1983.5 }{0.5}\))
55.9875 + 0.83 (1)
= 56.8175
when x = 1985
y = 55.9875 + 0.83 (\(\frac { 1985-1983.5 }{0.5}\))
= 55.9875 + 0.83 (3)
= 55.9875 + 2.49
= 58.4775
when x = 1986
y = 55.9875 + 0.83 (\(\frac { 1986-1983.5 }{0.5}\))
= 55.9875 + 0.83 (5)
= 55.9875 + 4.15
= 60.1375
when x = 1987
y = 55.9875 + 0.83 (\(\frac { 1987-1983.5 }{0.5}\))
= 55.9875 + 0.83 (7)
= 55.9875 + 5.81
= 61.7975

Question 4.
Fit a straight line trend by the method of least squares to the following data.

Solution:

Lasperyre’s price Index number


Hence Fisher’s Ideal Index satisfies Time reversal test

Question 5.
Using the following data, construct Fisher’s Ideal Index Number and Show that it satisfies Factor Reversal Test and Time Reversal Test?

Solution:

Factor reversal test

Hence Fisher’s Ideal Index satisfies Factor reversal test.

Question 6.
Compute the consumer price index for 2015 on the basis of 2014 from the following data.

Solution:

Question 7.
An Enquiry was made into the budgets of the middle class families in a city gave the following information.

What changes in the cost of living have taken place in the middle class families of a city?
Solution:

Conclusion:
The cost of living has increased up to 26.10% in 2011 as compared to 2010.

Question 8.
From the following data, calculate the control limits for the mean and range chart.

Solution:

UCL = \(\bar { \bar x}\) + A₂\(\bar { R}\)
= 51 + 0.577(6.5)
= 51 + 3.7505
= 54.7505
= 54.75
CL = \(\bar { \bar x}\) = 51
UCL = \(\bar { \bar x}\) – A₂\(\bar { R}\)
= 51 – 0.577(6.5)
= 51 – 3.7505
= 47.2495
= 47.25
The control limits for Range chart is
UCL = D₄\(\bar { R}\)
= 2.114(6.5)
= 13.741
CL = \(\bar { R}\) = 6.5
LCL = D₃\(\bar { R}\) = 0(6.5) = 0

Question 9.
The following data gives the average life(in hours) and range of 12 samples of 5 lamps each. The data are

Construct control charts for mean and range Comment on the control limits.
Solution:

UCL = \(\bar { \bar x}\) + A₂\(\bar { R}\)
= 1367.5 + 0.577(427.5)
= 1367.5 + 246.6675
= 1614.1675
= 1614.17
CL = \(\bar { \bar x}\) = 1367.5
LCL = \(\bar { \bar x}\) + A₂\(\bar { R}\)
= 1367.5 – 0.577(427.5)
= 1367.5 – 246.6675
= 1120.8325
= 1120.83
The control limits for Range chart is
UCL = D₄\(\bar { R}\)
= 2.115(427.5)
= 904.1625
= 904.16
CL = \(\bar { R}\) = 427.5
LCL = D₃\(\bar { R}\)
= 0(427.5)
= 0

Question 10.
The following are the sample means and I ranges for 10 samples, each of size 5. Calculate ; the control limits for the mean chart and range chart and state whether the process is in control or not.

Solution:

UCL = \(\bar { \bar x}\) + A₂\(\bar { R}\)
= 4.982 + 0.577(0.36)
= 4.982 + 0.20772
= 5.18972
= 5.19
CL = \(\bar { \bar x}\) = 4.982
LCL = \(\bar { \bar x}\) + A₂\(\bar { R}\)
= 4.982 – 0.577(0.36)
= 4.982 – 0.20772
= 4.77428
= 4.774
The control limits for range chart is
UCL = D₂\(\bar { R}\) = 2.115(3.6)
= 7.614
CL = \(\bar { R}\) = 3.6
LCL = D₃\(\bar { R}\)
= 0(0.36) = 0

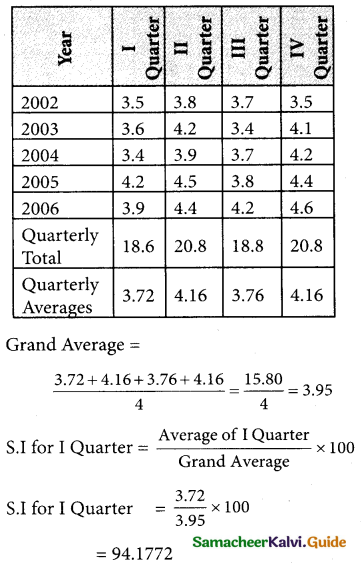
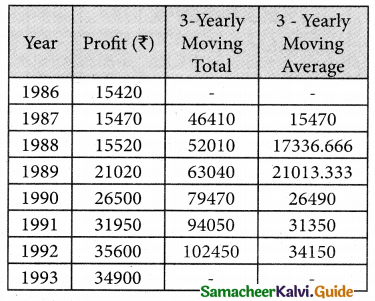
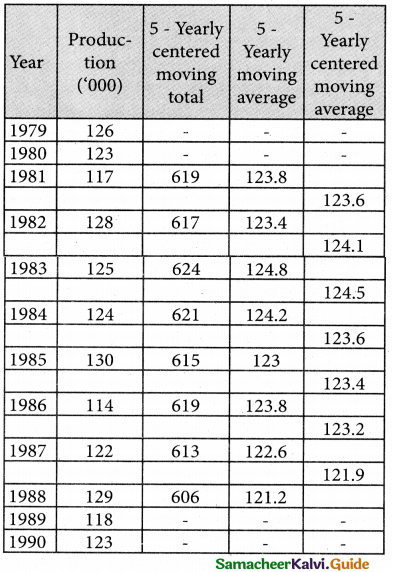
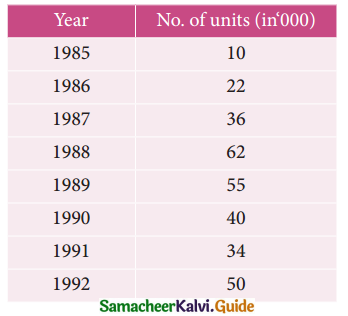
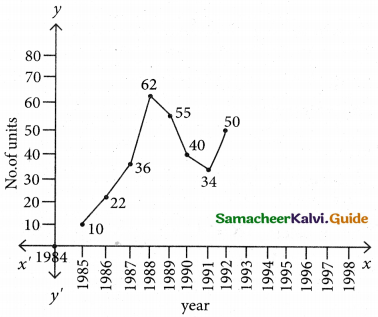
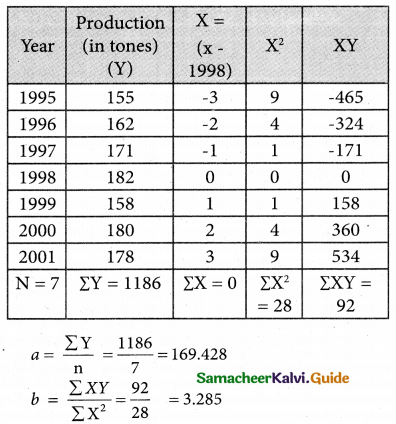
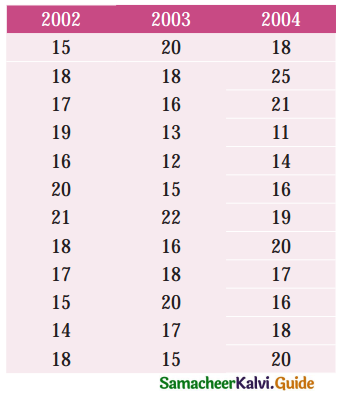
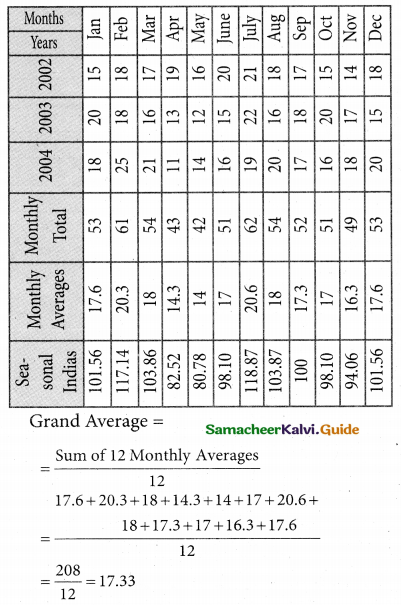
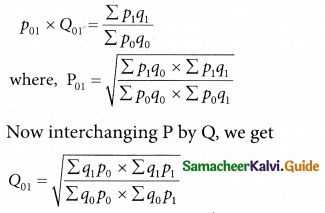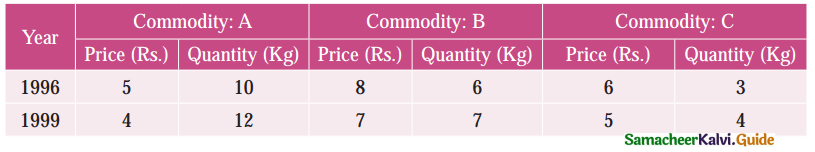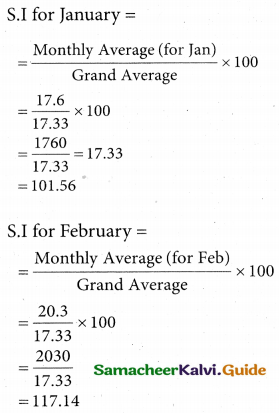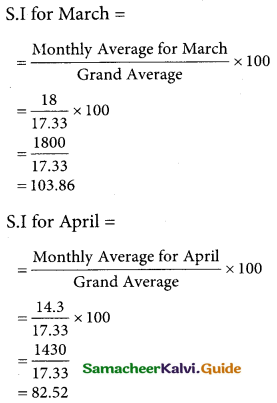Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 9 Applied Statistics Ex 9.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 9 Applied Statistics Ex 9.4

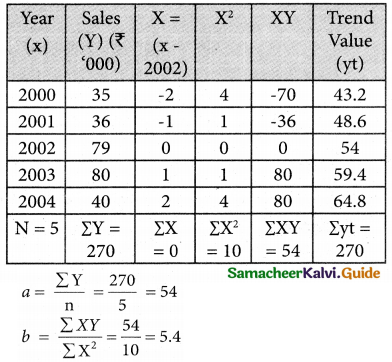
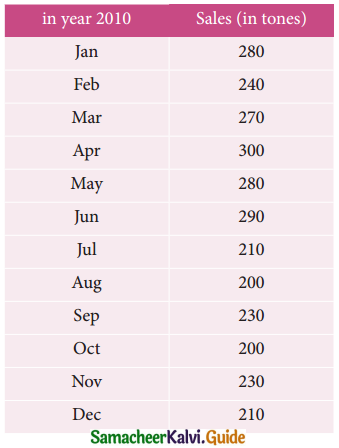
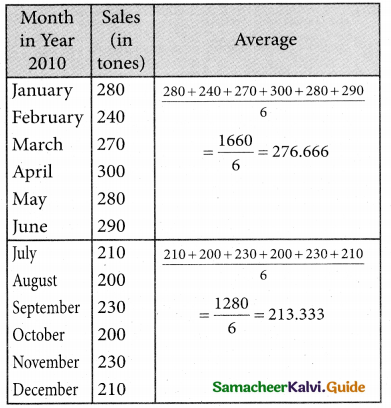
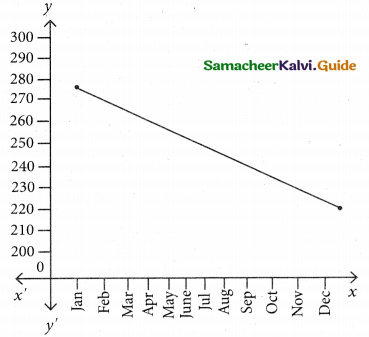
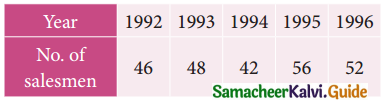
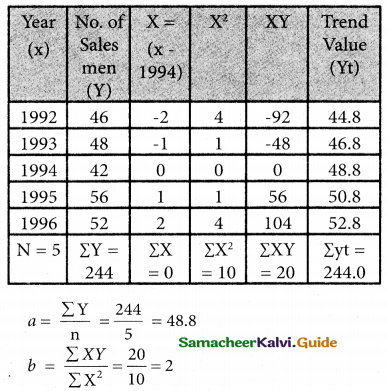
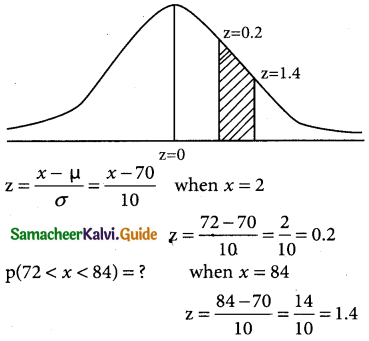
Question 1.
A time series is a set of data recorded
(a) Periodically
(b) Weekly
(c) successive points of time
(d) all the above
Solution:
(d) all the above

Question 2.
A time series consists of
(a) Five components
(b) Four components
(c) Three components
(d) Two components
Solution:
(b) Four components

Question 3.
The components of a time series which is attached to short term fluctuation is
(a) Secular trend
(b) Seasonal variations
(c) Cyclic variation
(d) Irregular variation
Solution:
(d) Irregular variation

Question 4.
Factors responsible for seasonal variations are
(a) Weather
(b) Festivals
(c) Social customs
(d) All the above
Solution:
(d) All the above

Question 5.
The additive model of the time series with the components T, S, C and I is
(a) y = T + S + C × I
(b) y = T + S × C × I
(c) y = T + S + C + I
(d) y = T + S × C + I
Solution:
(c) y = T + S + C + I

Question 6.
Least square method of fitting a trend is
(a) Most exact
(b) Least exact
(c) Full of subjectivity
(d) Mathematically unsolved
Solution:
(a) Most exact

Question 7.
The value of ‘b’ in the trend line y = a + bx is
(a) Always positive
(b) Always negative
(c) Either positive or negative
(d) Zero
Solution:
(c) Either positive or negative

Question 8.
The component of a time series attached to long term variation is trended as
(a) Cyclic variation
(b) Secular variations
(c) Irregular variation
(d) Seasonal variations
Solution:
(b) Secular variations

Question 9.
The seasonal variation means the variations occurring with in
(a) A number of years
(b) within a year
(c) within a month
(d) within a week
Solution:
(b) within a year

Question 10.
Another name of consumer’s price index number is:
(a) Whole-sale price index number
(b) Cost of living index
(c) Sensitive
(d) Composite
Solution:
(b) Cost of living index

Question 11.
Cost of living at two different cities can be compared with the help of
(a) Consumer price index
(b) Value index
(c) Volume index
(d) Un-weighted index
Solution:
(a) Consumer price index

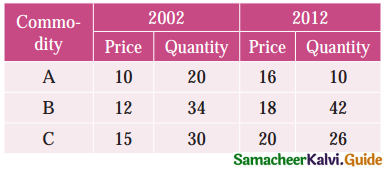
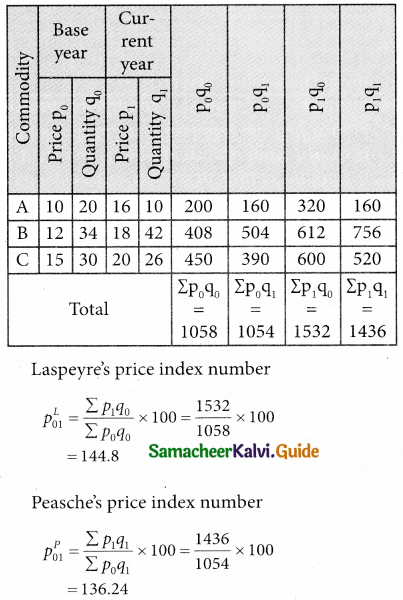
Question 12.
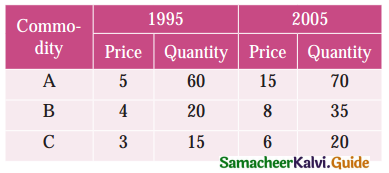
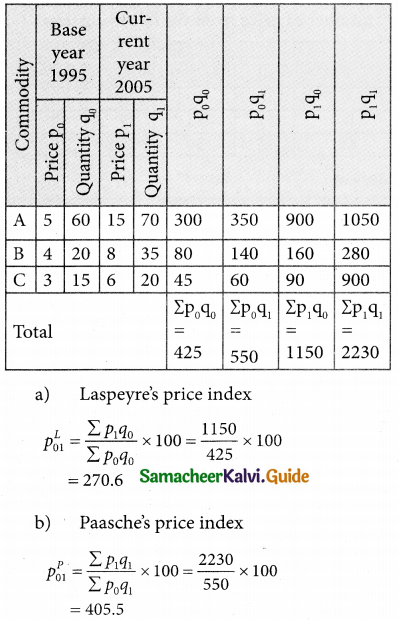
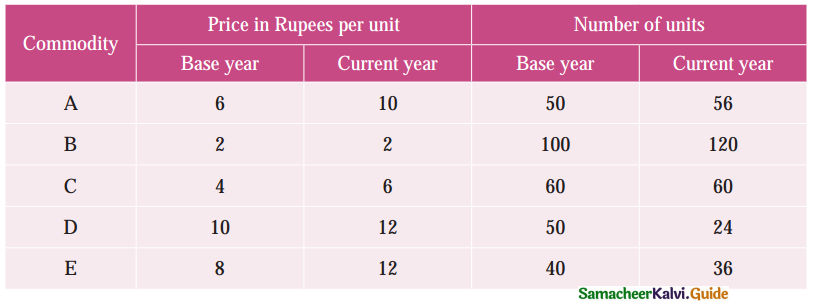
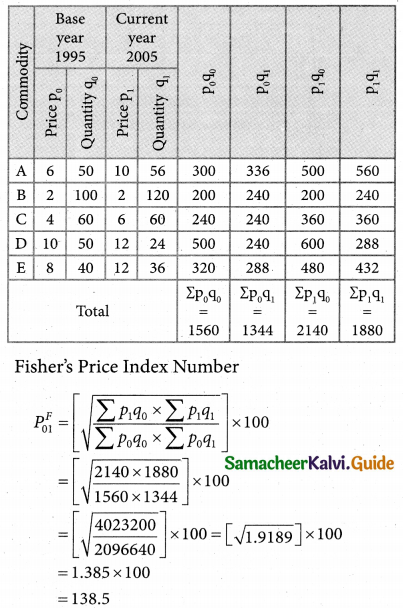
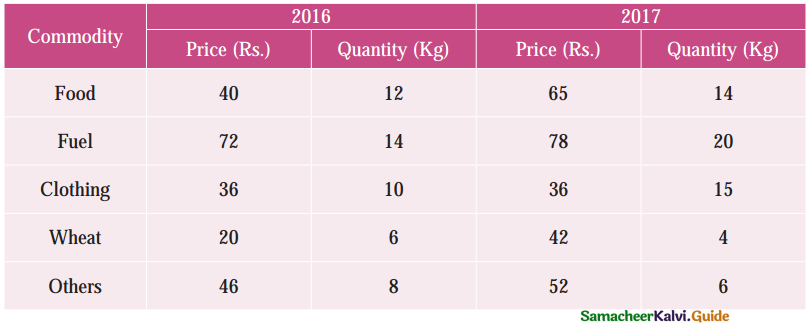
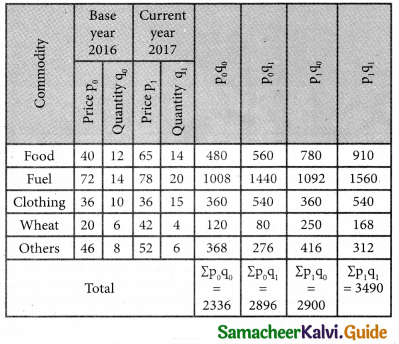
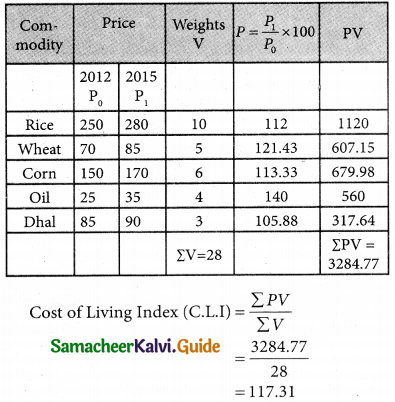
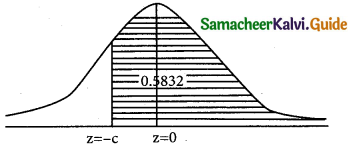
Laspeyre’s index = 110, Paasche’s index = 108, then Fisher’s Ideal index is equal to:
(a) 110
(b)108
(c) 100
(d) 109
Solution:
(d) 109
Hint:
p²₀₁ = 110; p^p₀₁ = 108
Fisher’s Ideal Index = \(\sqrt { 110×108 }\) = \(\sqrt { 11880 }\) = 108.99 = 109

Question 13.
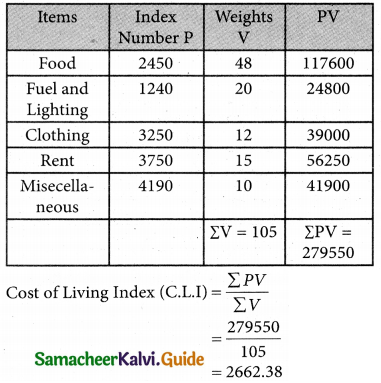
Most commonly used index number is:
(a) Volume index number
(b) Value index number
(c) Price index number
(d) Simple index number
Solution:
(c) Price index number

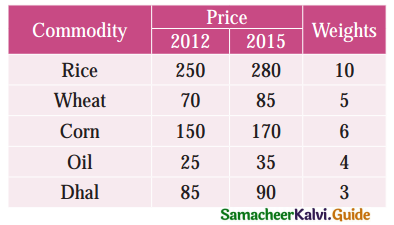
Question 14.
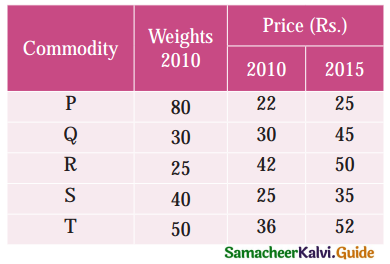
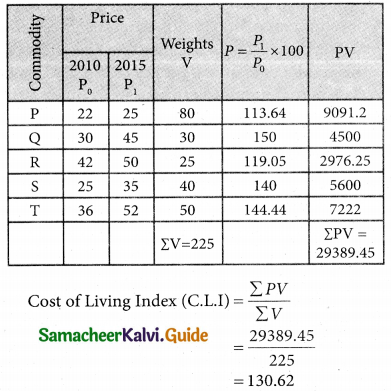
Consumer price index are obtained by:
(a) Paasche’s formula
(b) Fisher’s ideal formula
(c) Marshall Edgeworth formula
(d) Family budget method formula
Solution:
(d) Family budget method formula

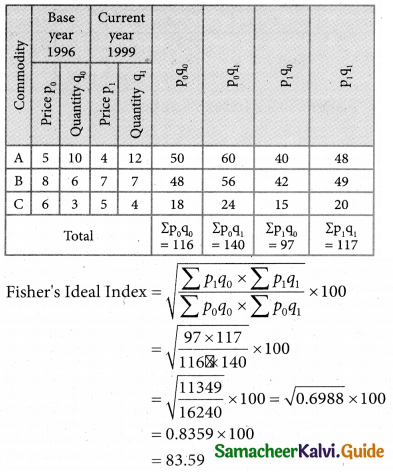
Question 15.
Which of the following Index number satisfy the time reversal test?
(a) Laspeyre’s Index number
(b) Paasche’s Index number
(c) Fisher Index number
(d) All of them.
Solution:
(c) Fisher Index number

Question 16.
While computing a weighted index, the current period quantities are used in the:
(a) Laspeyre’s method
(b) Paasche’s method
(c) Marshall Edgeworth method
(d) Fisher’s ideal method
Solution:
(b) Paasche’s method

Question 17.
The quantities that can be numerically measured can be plotted on a
(a) p – chart
(b) c – chart
(c) x bar chart
(d) np – chart
Solution:
(c) x bar chart

Question 18.
How many causes of variation will affect the quality of a product?
(a) 4
(b) 3
(c) 2
(d) 1
Solution:
(c) 2

Question 19.
Variations due to natural disorder is known as
(a) random cause
(b) non-random cause
(c) human cause
(d) all of them
Solution:
(a) random cause

Question 20.
The assignable causes can occur due to
(a) poor raw materials
(b) unskilled labour
(c) faulty machines
(d) all of them
Solution:
(d) all of them

Question 21.
A typical control charts consists of
(a) CL, UCL
(b) CL, LCL
(c) CL, LCL, UCL
(d) UCL, LCL
Solution:
(c) CL, LCL, UCL

Question 22.
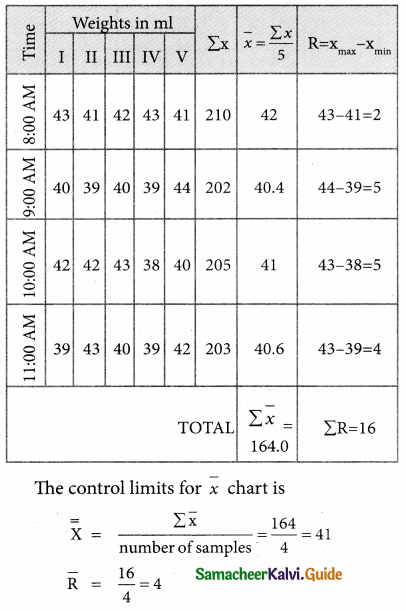
\(\bar { x}\) chart is a
(a) attribute control chart
(b) variable control chart
(c) neither Attribute nor variable control chart
(d) both Attribute and variable control chart
Solution:
(b) variable control chart

Question 23.
R is calculated using
(a) x_max – x_min
(b) x_min – x_max
(c) \(\bar { x}\)_max – \(\bar { x}\)_min
(d) \(\bar {\bar x}\)_max – \(\bar {\bar x}\)_min
Solution:
(a) x_max – x_min

Question 24.
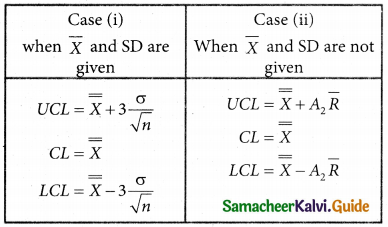
The upper control limit for x chart is given by
(a) \(\bar { x}\) + A₂\(\bar { R}\)
(b) \(\bar {\bar x}\) + A₂R
(c) \(\bar {\bar x}\) + A₂\(\bar { R}\)
(d) \(\bar { x}\) + A₂\(\bar {\bar R}\)
Solution:
(c) \(\bar {\bar x}\) + A₂\(\bar { R}\)

Question 25.
The LCL for R chart is given by
(a) D₂\(\bar { x}\)
(b) D₂\(\bar {\bar R}\)
(c) D₃\(\bar {\bar R}\)
(d) D₃\(\bar { x}\)
Solution:
(d) D₃\(\bar { x}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 9 Applied Statistics Ex 9.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 9 Applied Statistics Ex 9.3

Question 1.
Define Statistical Quality Control.
Solution:
The term Quality means a level or standard of a product which depends Material, Manpower, Machines, and Management (4M’s). Quality Control ensures the quality specifications all along them from the arrival of raw materials through each of their processing to the final delivery of goods. Quality Control is a powerful technique used to diagnose the lack of quality in any of the raw materials, processes, machines etc. It is essential that the end products should possess the qualities that the consumer expects from the manufacturer.

Question 2.
Mention the types of causes for variation in a production process.
Solution:
There are two causes of variation which affects the quality of a product, namely
1. Chance Causes (or) Random causes
2. Assignable Causes

Question 3.
Define Chance Cause.
Solution:
These are small variations which are natural and inherent in the manufacturing process. The variation occurring due to these causes is beyond the human control and cannot be prevented or eliminated under any circumstances, the minor causes which do not affect the quality of the products to an extent are called as Chance Causes (or) Random causes. For example Rain, floods, power cuts, etc.,

Question 4.
Define Assignable cause.
Solution:
The second type of variation which is present in any production process is due to non-random causes. The assignable causes may occur in at any stage of the process, right from the arrival of the raw materials to the final delivery of the product. Some of the important factors of assignable causes are defective raw materials, fault in machines, unskilled manpower, worn out tools, new operation, etc.

Question 5.
What do you mean by product control?
Solution:
Product Control means that controlling the quality of the product by critical examination through sampling inspection plans. Product Control aims at a certain quality level to be guaranteed to the customers. It attempts to ensure that the product sold does not contain a large number of defective items. Thus it is concerned with classification of raw materials, semi-finished goods or finished goods into acceptable on rejectable products.

Question 6.
What do you mean by process control?
Solution:
In Process Control the proportion of defective items in the production process is to be minimized and it is achieved through the technique of control charts.

Question 7.
Define a control chart.
Solution:
A control chart is essentially a graphic device for presenting data so as to directly reveal the frequency and extent of variations from established standards or goals. Control charts are simple to construct and easy to interpret and they tell the manager at a glance whether or not the process is in control, i.e within the tolerance limits.

Question 8.
Name the control charts for variables.
Solution:
(i) Charts for mean (\(\bar { X}\))
(ii) Charts for Range (R)

Question 9.
Define mean chart.
Solution:
The mean chart (\(\bar { X}\) chart) is used to show, the quality average of the samples taken from the given process. The \(\bar { X}\) charts are usually required for decision making to accept or reject the process.
Procedure for \(\bar { X}\)
i. Let X₁, X₂, X₃, etc. be the samples selected each containing “n” observations usually (n = 4.5 or 6)

ii. Calculate mean for each samples \(\bar { X}\)₁, \(\bar { X}\)₂, \(\bar { X}\)₃, ……… by using \(\bar { X}\)_i = \(\frac { ΣX_i }{n}\), i = 1, 2, 3, 4, ….
where Σx_i = total f “n” values included in the sample X₁.

iii. Find the mean (\(\bar { \bar X}\)) of the sample means
\(\bar { \bar X}\) = \(\frac { Σ \bar X }{number of samples}\)
where Σ\(\bar { X}\) = total of all the sample means.

Question 10.
Define R chart.
Solution:
The R chart is used to show the variability or dispersion of the samples taken from the given process. R charts are also required for decision making to accept of reject the process.
Procedure for R-Charts
Calculate R = Xmax – Xmin
Let R₁, R₂, R₃ ………….. be the ranges of the “n” samples. The average range is given by
\(\bar { X}\) = \(\frac { ΣR }{n}\)

Question 11.
What are the uses of statistical quality control?
Solution:
(i) The role of statistical quality control is to collect and analyse relevant data for the purpose of detecting whether the process is under control or not.
(ii) The value of quality control lies in the fact that assignable causes in a process can be quickly detected. Infact the variations are often discovered before the product becomes defective.
(iii) Statistical quality control is only diagnostic. It tells us whether the standard is being maintained or not.
(iv) This technique is used in almost all production industries such as automobile textile, electrical equipment, biscuits, both soaps, chemicals, Petroleum products, etc.
(v) The purpose for which SQC are used in two fold namely (a) process control (b) product control.
The main purpose of SQC is to device statistical techniques which would help in elimination of assignable causes and bring the production process under control.

Question 12.
Write the control limits for the mean chart.
Solution:
The calculation of control limits for x chart in two different cases is

Question 13.
Write the control limits for the R chart.
Solution:
The calculation of control limits for R chart in two different cases are

The values of A₂, D₂ and D₄ are given in the table.

Question 14.
A machine is set to deliver packets of a given j weight. Ten samples of size five each were recorded. Below are given relevant data:

Solution:
Calculate the control limits for mean chart and the range chart and then comment on the state of control, (conversion factors for n = 5, A₂ = 0.58, D₃ = 0 and D₄ = 2.115)

UCL = \(\bar { \bar X}\) + A₂ \(\bar { R}\)
= 16.2 + (0.58)(7.4)
= 16.2 + 4.292
= 20.492
= 20.49
CL = \(\bar { \bar X}\) = 16.2
LCL = \(\bar { \bar X}\) – A₂ \(\bar { R}\)
= 16.2 – (0.58) (7.4)
= 16.2 – 4.292
= 11.908
= 11.91
The control limits for Range chart is
UCL = D₄ \(\bar { R}\)
= (2.115)(7.4)
= 15.651
= 15.65
CL = \(\bar { R}\) = 7.4
LCL = D₃ \(\bar { R}\) = (0)(7.4) = 0

Question 15.
Ten samples each of size five are difawn at regular intervals from a manufacturing process. The sample means (X) and their ranges (R) are given below:

Calculate the control limits in respect of \(\bar { X}\) chart. (Given A₂ = 0.58, D₃ = 0 and D₄ = 2.115 ) Comment on the state of control.
Solution:

UCL = \(\bar { \bar X}\) + A₂ \(\bar { R}\)
= 46.2 + (0.58)(6.8)
= 46.2 + 3.944
= 50.144
= 50.14
CL = \(\bar { \bar X}\) = 46.2
LCL = \(\bar { \bar X}\) + A₂ \(\bar { R}\)
= 46.2 – (0.58)(6.8)
= 46.2 – 3.944
= 42.256
= 42.26
The control limits for Range chart is
UCL = D₄ \(\bar { R}\)
= (2.115)(6.8)
= 14.382
= 14.38
CL = \(\bar { R}\) = 6.8
LCL = D₃\(\bar { R}\) = (0)(6.8) = 0

Question 16.
Construct X and R charts for the following data:

Solution:


\(\bar { R}\) = \(\frac { 144 }{8}\) = 18
UCL = \(\bar { \bar x}\) + A₂ \(\bar { R}\)
= 37.71 + (0.58)(18)
= 37.71 + 10.44
= 48.15
CL = \(\bar { \bar x}\) = 37.71
LCL = \(\bar { \bar x}\) – A₂ \(\bar { R}\)
= 37.71 – (0.58)(18)
= 37.71 – 10.44
= 27.27
The control limits for Range chart is
UCL = D₄ \(\bar { R}\) = 2.115 (18) = 38.07
CL = \(\bar { R}\) = 18
LCL = D₃ \(\bar { R}\) = 0(18) = 0

Question 17.
The following data show the values of sample mean (\(\bar {x}\)) and its range (R) for the samples of size five each. Calculate the values for control limits for mean, range chart and determine whether the process is in control.

Solution:

UCL = \(\bar { \bar x}\) – A₂ \(\bar { R}\)
= 10.66 + (0.58)(6.3)
= 10.66 + 3.654 = 14.314
= 14.31
CL = \(\bar { \bar x}\) = 10.66
LCL = \(\bar { \bar x}\) – A₂ \(\bar { R}\)
= 10.66 – (0.58)(6.3)
= 10.66 – 3.654
= 7.006
The control limits for Range chart is
UCL = D₄ \(\bar { R}\) = 2.115 (6.3)
= 13.3245
= 13.32
CL = \(\bar { R}\) = 6.3
LCL = D₃ \(\bar { R}\) = 0(6.3) = 0
Conclusion: Since all the points of sample range is within UCL of R chart, the process is in control.

Question 18.
A quality control inspector has taken ten ” samples of size four packets each from a potato chips company. The contents of the sample are given below, Calculate the control limits for mean and range chart.

(Given for n = 5, A₂ = 0.58, D₃ = 0 and D₄ = 2.115)
Solution:

UCL = \(\bar { \bar X}\) – A₂ \(\bar { R}\)
= 12.5 + (0.58)(0.37)
= 12.5 + 0.2146 = 12.7146
= 12.71
CL = \(\bar { \bar X}\) = 12.5
LCL = \(\bar { \bar X}\) – A₂ \(\bar { R}\) = 12.5 – (0.58) (0.37)
= 12.5 – 0.2146 = 12.2854
= 12.29
The control limits for Range chart is
UCL = D₄ \(\bar { R}\) = (2.115)(0.37) = 0.78255
= 0.78
CL = \(\bar { R}\) = 0.37
LCL = D₃\(\bar { R}\) = (0)(0.37) = 0

Question 19.
The following data show the values of sample means and the ranges for ten samples of size 4 each. Construct the control chart for mean and range chart and determine whether the process is in control.

Solution:

UCL = \(\bar { \bar X}\) – A₂ \(\bar { R}\)
= 30.1 +(0.73)(20.1)
= 30.1 + 14.673 = 44.773
= 44.77
CL = \(\bar { \bar X}\) = 30.1
LCL = \(\bar { \bar X}\) – A₂ \(\bar { R}\)
= 30.1 – (0.73) (20.1)
= 30.1 – 14.673 = 15.427
= 15.43
The control limits for Range chart is
UCL = D₄ \(\bar { R}\)
= 2.28(20.1) = 45.828
= 45.83
CL = \(\bar { R}\) = 20.1
LCL = D₃ \(\bar { R}\) = 0(20.1) = 0

Question 20.
In a production process, eight samples of size 4 are collected and their means and ranges are given below. Construct mean chart and range chart with control limits.

Solution:

UCL = \(\bar { \bar X}\) – A₂ \(\bar { R}\)
= 13.25 + (0.73) (3.12)
= 13.25 + 2.2776 = 15.5276
= 15.53
CL = \(\bar { \bar X}\) = 13.25
LCL = \(\bar { \bar X}\) – A₂ \(\bar { R}\)
= 13.25 – (0.73)(3.12)
= 13.25 – 2.2776 = 10.972
= 10.97
The control limits for Range chart is
UCL = D₄ \(\bar { R}\)
= 2.28(3.12) = 7.11984
= 7.12
CL = \(\bar { R}\) = 3.12
LCL = D₃\(\bar { R}\) = 0(3.12) = 0

Question 21.
In a certain bottling industry the quality control inspector recorded the weight of each of the 5 bottles selected at random during each hour of four hours in the morning.

Solution:

UCL = \(\bar { \bar X}\) – A₂ \(\bar { R}\)
= 41 + (0.58)(4)
41 + 2.32 = 43.32
CL = \(\bar { \bar X}\) = 41
LCL = \(\bar { \bar X}\) – A₂ \(\bar { R}\)
= 41 – (0.58)(4)
= 41 – 2.32
= 38.68
The control limits for range chart is
UCL = D₄ \(\bar { R}\) = 2.115(4)
= 8.46
CL = \(\bar { R}\) = 4
LCL = D₂ \(\bar { R}\) = 0(4) = 0
Conclusion: Since all the points of sample mean and Range are within the control limits, the process is in control.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 9 Applied Statistics Ex 9.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 9 Applied Statistics Ex 9.2

Question 1.
Define Index Number.
Solution:
Index Numbers are the indicators which reflect the changes over a specified period of time in price of different commodities, production, sales, cost of living etc.

“An Index Number is a device which shows by its variations the change in a magnitude which is not capable of accurate measurements in it-self or of direct valuation in practice”. – Whel-don

“An Index number is a statistical measure of fluctuations in a variable arranged in the form of a series and using a base. Period for maxing H comparisons” – Lawrence J Kalpan.

Question 2.
State the uses of Index Number.
Solution:
(1) Index number is an important tool for formulating decision and management p policies.
(2) It helps in studying the trends and tendencies.
(3) It determines the inflation and deflation in an Economy.

Question 3.
Mention the classification of Index Number.
Solution:
Index number can be classified as follows,
(i) Price Index Number:
It measures the general changes in the retail or wholesale price level of a particular or group of commodities.

(ii) Quantity Index Number:
These are indices of measure the changes in the quantity of goods manufactured in a factory.

(iii) Cost of living Index Number:
These are intended to study the effect of change in the price level on the cost of living of different classes of people.

Question 4.
Define Laspeyre’s Price index number.
Solution:
Laspeyre’s Price index number
P\(_{ 01 }^{L}\) ⥪ \(\frac { Σp_1q_0 }{Σp_0q_0}\) × 100
where P₁ = Current year price
p₀ = base year price
q₀ = base year quantity

Question 5.
Explain Paasche’s price index number.
Solution:
Paasches price index number
P\(_{ 01 }^{L}\) = \(\frac { Σp_1q_1 }{Σp_0q_1}\) × 100
where P₁ = current year price
q₁ = current year quantity
p₀ = base year price
q₀ = base year quantity

Question 6.
Write note on Fisher’s price index number.
Solution:
Fishers price index number
P^F = \(\sqrt { P^L×P^P}\)
P\(_{ 01 }^{F}\) = \(\sqrt { \frac{Σp_1p_0×Σp_1q_1}{Σp_0q_0×Σp_0q_1}}\) × 100
where P₁ = current year price
q₁ = current year quantity
p₀ = base year price
q₀ = base year quantity

Question 7.
State the test of adequacy of index number.
Solution:
There are two tests which are used to test the adequacy for an index number. The two tests are as follows
(i) Time Reversal Test
(ii) Factory Reversal Test

Question 8.
Define Time Reversal Test.
Solution:
It is an important test for testing the consistency of a good index number. This test maintains time consistency by working both forward and backward with respect to time (here time refers to base year and current year). Symbolically the following relationship should be satisfied. P₀₁ × p₁₀ = 1

Fisher’s index number formula satisfies the above relationship
P\(_{ 01 }^{F}\) = \(\sqrt { \frac{Σp_1p_0×Σp_1q_1}{Σp_0q_0×Σp_0q_1}}\)

when the base year and current year are interchanged, we get
P\(_{ 10 }^{F}\) = \(\sqrt { \frac{Σp_0q_1×Σp_0q_0}{Σp_1q_1×Σp_1q_0}}\)
P\(_{ 01 }^{F}\) × P\(_{ 10 }^{F}\) = 1

Question 9.
Explain factor reversal test.
Solution:
This is another test for testing the consistency of a good index number. The product of price index number and quantity index number from the base year to the current year should be equal to the true value ratio. That is, the ratio between the total value of current period and total
value of the base period is known as true value ratio. Factor Reversal Test is given by,

where P₀₁ is the relative change in price
Q₀₁ is the relative change in quantity.

Question 10.
Define true value ratio.
Solution:
\(\frac { Σp_1q_1 }{Σp_0q_0}\) is the ratio of the total value in the current period to the total value in the base period and this ratio is called the true value ratio.

Question 11.
Discuss about cost of Living Index Number.
Solution:
Cost of living index numbers are generally designed to represent the average change over time in the prices paid by the ultimate consumer for a specified quantity of goods and services cost of living index number is also known as consumer price index number.

It is well known that a given change in the level of prices (retail) affects the cost of living of different classes of people in different manners. The general index number fails to reveal this. Therefore it is essential to construct a cost of living index number which helps us in determining the effect of rise and fall in prices on different classes of consumers living in different areas.

Question 12.
Define family budget method.
Solution:
In this method, the weights are calculated by multiplying prices and quantity of the base year.
(i.e.) V = Σp₀q₀. The formula is given by,
Cost of Living Index Number = \(\frac { Σpv }{Σv}\)
where P = \(\frac { p_1 }{p_0}\) × 100 is the price relative.
v = Σp₀q₀ is the value relative.

Question 13.
State the uses of cost of Living Index Number.
Solution:
(i) It indicates whether the real wages of workers are rising or falling for a given time.
(ii) It is used by the administrators for regulating dearness allowance or grant of bonus to the workers.

Question 14.
Calculate by a suitable method, the index number of price from the following data:

Solution:

Question 15.
Calculate price index number for 2005 by (a) Laspeyre’s (b) Paasche’s method

Solution:

Question 16.
Calculate price index number for 2005 by (a) Laspeyre’s (b) Paasche’s method

Solution:

Question 17.
Using the following data, construct Fisher’s Ideal index and show how it satisfies Factor Reversal Test and Time Reversal Test?

Solution:

Question 18.
Using the following data, construct Fisher’s Ideal index and show how it satisfies Factor Reversal Test and Time Reversal Test?

Solution:

Question 19.
Calculate Fisher’s index number to the following data. Also show that it satisfies Time Reversal Test.

Solution:

Question 20.
Th following are the group index numbers and the group weights of an average working class family’s budget. Construct the cost of living index number:

Solution:

Question 21.
Construct the cost of living Index number for 2015 on the basis of 2012 from the following data using family budget method.

Solution:

Question 22.
Calculate the cost of living index by aggregate expenditure method:

Solution: