Category: Class 8

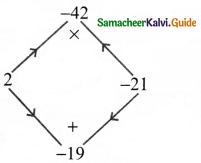
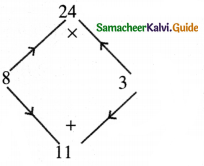
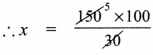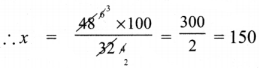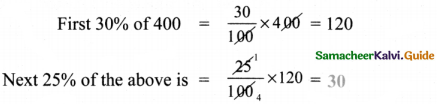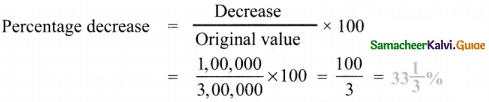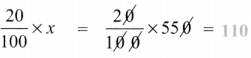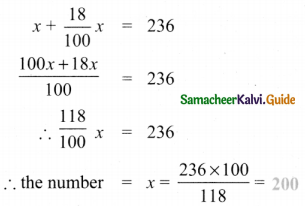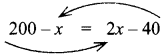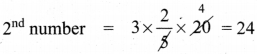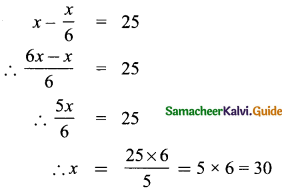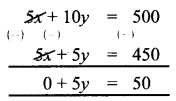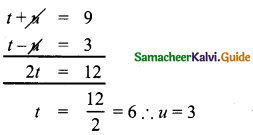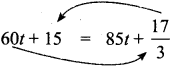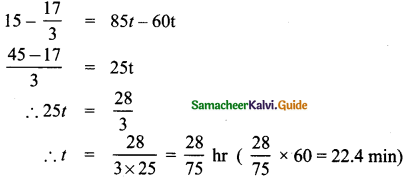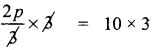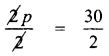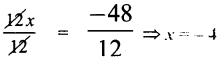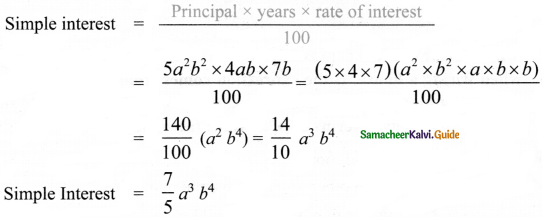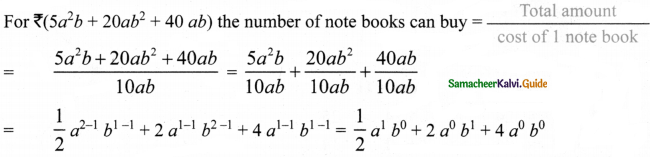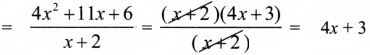Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 4 Life Mathematics Ex 4.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 4 Life Mathematics Ex 4.2

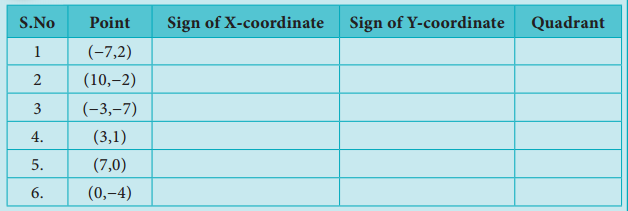
Question 1.
Fill in the blanks:
(i) Loss or gain percentage is always calculated on the ________ .
Answer:
Cost Price

(ii) A mobile phone is sold for ₹ 8400 at a gain of 20%. The cost price of the mobile phone is ________ .
Answer:
₹ 7000
Hint:
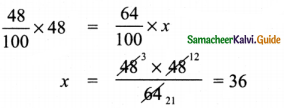
Let cost price of mobile be ₹ x
Given that selling price is ₹ 8400 and gain is 20%
As per formula,

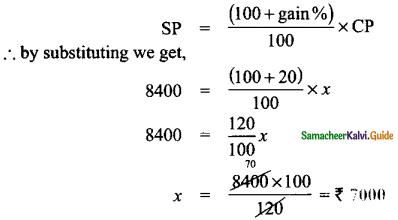
(iii) An article is sold for ₹ 555 at a loss of 7\(\frac { 1 }{ 2 }\)%. The cost price of the article is ________ .
Answer:
₹ 600
Hint:
Given selling price is ₹ 555 & loss 7\(\frac { 1 }{ 2 }\)%
as per formula

(iv) A mixer grinder marked at ₹ 4500 is sold for ₹ 4140 after discount. The rate of discount is ________ .
Answer:
8 %
Hint:
Marked price is ₹ 4500
Discounted price in ₹ 4140
∴ Discount = Marked price – Discounted priòe
= 4500 – 4140 = 360

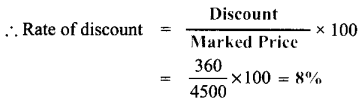
(v) The total bill amount of a shirt costing ₹ 575 and a T-shirt costing ₹ 325 with GST of 5% is ________ .
Answer:
Cost of price shirt = ₹ 575 (CP)
GST = 5%

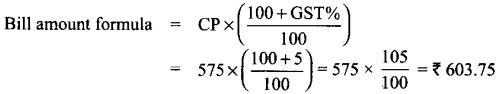
Cost of price shirt = ₹ 325 (CP)
GST = 5%

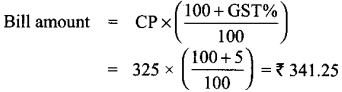
∴ Total bill amount = ₹ 603.75 + ₹ 341.25 = ₹ 945

Question 2.
If selling an article for ₹ 820 causes 10% loss on the selling price, then find its cost price.
Answer:
Given that selling price (SP) = ₹ 820
Loss % = 10 %

Question 3.
If the profit earned on selling an article for ₹ 810 is the same as loss on selling it for ₹ 530, then find the cost price of the article.
Answer:
Case 1: Profit = Selling price (SP) – Cost price (CP)
Case 2: Loss = Cost price (CP) – Selling price (SP)
Given that profit of case 1 = loss of case 2
∴ P = 810 – CP
L = CP – 530
Since profit (P) = loss (L)
810 – CP = CP – 530
∴ 2CP = 810 + 530 = 1340 ⇒ C.P = \(\frac{1340}{2}\)
∴ CP = 670

Question 4.
If the selling price of 10 rulers is the same as the cost price of 15 rulers, then find the profit percentage.
Answer:
Let cost price of one ruler be x
Given that selling price (SP) of 10 rulers.
i.e., same as cost price (CP) of 15 rulers
∴ SP of 10 rulers = 15 × x = 15x
∴ SP of 1 ruler = \(\frac{15 x}{10}\) = 1.5x
∴ Gain = SP of 1 ruler – CP of 1 ruler = 1.5x – x = 0.5x

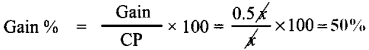
Question 5.
Some articles are bought at 2 for ₹ 15 and sold at 3 for ₹ 25. Find the gain percentage.
Answer:
Let cost price of one article be C.P
Given that 2 are bought for ₹ 15
∴ 2 × CP = 15 ⇒ CP = \(\frac{15}{2}\)
Let selling price of one article be SP
Given that 3 are sold for ₹ 25
∴ 3 × SP = 25 ⇒ SP = \(\frac{25}{3}\)
∴ Gain = SP – CP = \(\frac{25}{3}-\frac{15}{2}=\frac{50-45}{6}=\frac{5}{6}\)

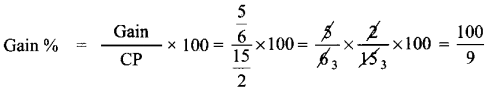
= \(11 \frac{1}{9}\)

Question 6.
By selling a speaker for ₹ 768, a man loses 20%. In order to gain 20%, how much should he sell the speaker?

Answer:
Selling price (SP) of speaker = ₹ 768
Loss % = 20 %
as per formula

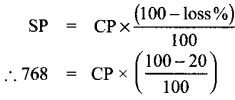
∴ CP = \(\frac{768 \times 100}{80}\) = 960
For gain of 20%, we should now calculate the selling price

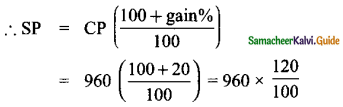
= 96 × 12 = ₹ 1152

Question 7.
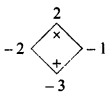
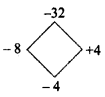
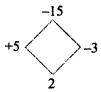
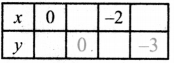
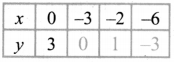
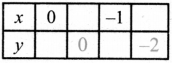
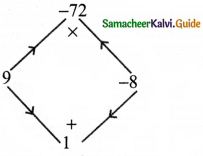
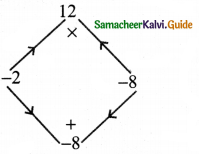
Find the unknowns x, y and z.

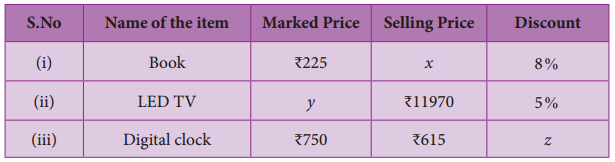
Answer:
(i) Book marked price = ₹ 225 discount 8%
∴ Selling price (x) = Marked price × \(\left(\frac{(100-d \%)}{100}\right)\)
= 225 × \(\frac{(100-8)}{100}\) = 225 × \(\frac{92}{100}\) = ₹ 207

(ii) LED TV selling price = 11970 discount = 5%, Marked price = y
∴ Selling price Marked price y × \(\left(\frac{(100-d \%)}{100}\right)\)
∴ 11970 = y × \(\frac{(100-5)}{100}\)
∴ y = \(\frac{11970 \times 100}{95}\) = 126 × 100 = ₹ 12,600

(iii) Digital clock marked price (MP) = ₹ 750, MP = ₹ 12.600
Selling price (SP) = ₹ 615, Discount = z

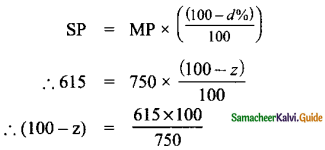
100 – z = 82
∴ z = 100 – 82, Discount = 18%

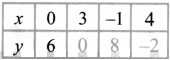
Question 8.
Find the total bill amount for the data given below:

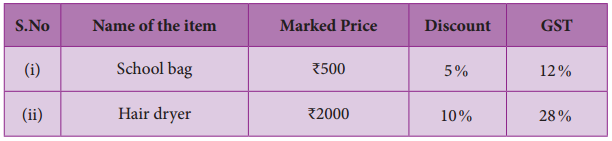
Answer:
Formula for discounted price LW = Marked price (MP) × \(\frac{(100-d \%)}{100}\)
When d is the discount %

For bill amount, we should apply GST on the discounted value of the items.
Formula: Bill amount = Discounted price × \(\left(\frac{(100+\mathrm{GST} \%)}{100}\right)\)
∴ For (i) School bag.
Bill amount 475 × \(\left(\frac{(100+12)}{100}\right)\) = 475 × 1.12 = %‘532
∴ For (ii) Hair drier,
Bill amount = 1800 × \(\left(\frac{(100+28)}{100}\right)\) = 1800 × 1.28 =
∴ Total bill amount Bill amount of School bag + Stationary + Cosmetics + Hair drier
= 532 + 252 + 1357 + 2304
= ₹ 4.445

Question 9.
A branded Air-Conditioner (AC) has a marked price of ₹ 38000. There are 2 options given for the customer.
(i) Selling Price is the same ₹ 38000 but with attractive gifts worth ₹ 3000
(or)
(ii) Discount of 8% on the marked price but no free gifts. Which offer is better?

Answer:
Marked price of AC = ₹ 38,000
Option 1:
Selling price = ₹ 38000 & gifts worth ₹ 3000
∴ Net gain for customer = ₹ 3000 as there is no discount on AC

Option 2:
Discount of 8%, but no gift
∴ Discounted value = MP × \(\left(\frac{(100-d \%)}{100}\right)\)
38000 × \(\frac{(100-8)}{100}\) = 38000 × 0.92 = 34960
∴ Savings for customer = 38000 – 34960 = 3040
Therefore, the customer gets 3000 gift in option I where as he is able to save only ₹ 3040 in option 2. Therefore, option 2 is better.

Question 10.
If a mattress is marked for ₹ 7500 and is available at two successive discount of 10% and 20%, find the amount to be paid by the customer.
Answer:
Marked price of mattress = ₹ 7500
Discount d₁ = 10%
Discount d₂ = 20%

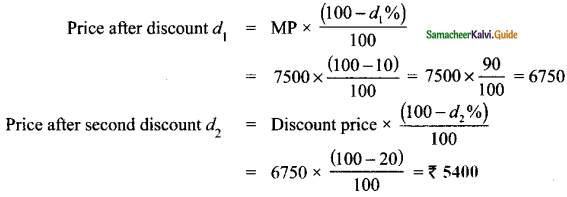
Objective Type Questions

Question 11.
A fruit vendor sells fruits for ₹ 200 gaining ₹ 40. His gain percentage is
(A) 20%
(B) 22%
(C) 25%
(D) 16
Answer:
(C) 25%
Hint:
Selling price ₹ 200
Gain = 40
∴ CP – Selling price – gain = 200 – 40 = 160

Question 12.
By selling a flower pot for Z528, a woman gains 20%. At what price should she sell it to gain 25%?
(A) ₹ 500
(B) ₹ 550
(C) ₹ 553
(D) ₹ 573
Answer:
(B) ₹ 550
Hint:
If selling price (sp) = ₹ 528
Gain % = 20 %
∴ CP = ?

Question 13.
A man buys an article for ₹ 150 and makes overhead expenses which are 12% of the cost price. At what price must he sell it to gain 5%?
(A) ₹ 180
(B) ₹ 168
(C) ₹ 176.40
(D) ₹ 88.20
Answer:
(C) ₹ 176.40
Hint:
Cost price of article = ₹ 150
Over head expenses = 12% of cost price
= \(\frac{12}{100}\) × 150 = ₹ 18
∴ Effective cost of article = 150 + 18 = ₹ 168
Now, to gain 5%, he has to sell at

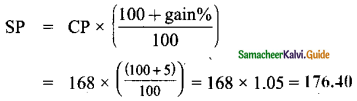
Question 14.
What is the marked price of a hat which is bought for Z210 at 16% discount?
(A) ₹ 243
(B) ₹ 176
(C) ₹ 230
(D) ₹ 250
Answer:
(D) ₹ 250
Hint:
Let marked price be MP
Discounted price = ₹ 210
Rate of discount = 16%
As per formula:

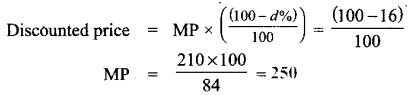
Question 15.
The single discount in % which is equivalent to two successive discounts of 20% and 25% is
(A) 40%
(B) 45%
(C) 5%
(D) 22.5%
Answer:
(A) 40%
Hint:
Let marked price be MP, after discount 1 of 20%,

Comparing with formula, we get
∴ This is equivalent to a single discount of 40%

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 4 Life Mathematics Ex 4.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 4 Life Mathematics Ex 4.1

Question 1.
Fill in the blanks:
(i) If 30 % of x is 150, then x is _______ .
Answer:
500
Hint:
Given 30% of x is 150
i.e \(\frac{30}{100}\) × x = 150

∴ x = 500

(ii) 2 minutes is _______ % to an hour.
Answer:
3\(\frac{1}{3}\)%
Hint:
Let 2 min be x% of an hour
and 1 hr = 60mm
x% = \(\frac{2}{60} \times 100=\frac{200}{60}=\frac{10}{3}=3 \frac{1}{3}\)
x = 3\(\frac{1}{3}\)%

(iii) If x% of x = 25, then x = _______ .
Answer:
50
Hint:
Given that x% of x is 25
∴ \(\frac{x}{100}\) × x = 25
∴ x² = 25 × 100 = 2500
∴ x = √2500 = 50

(iv) In a school of 1400 students, there are 420 girls. The percentage of boys in the school is _______ .
Answer:
70
Hint:
Given total number of students in school = 1400
Number of girls in school = 420
∴ Number of boys in school = 1400 – 420 = 980

= \(\frac{980}{14}\) = 70
% of boys = 70%

(v) 0.5252 is _______ %.
Answer:
52.52%
Hint:
Given a number, and to express as a percentage, we need to multiply by 100
∴ to express 0.5252 as percentage, we should multiply by 100
∴ 0.5252 × 100 = 52.52%

Question 2.
Rewrite each underlined part using percentage language.
(i) One half of the cake is distributed to the children.
Answer:
50% of the cake is distributed to the children
Hint:
One half is nothing but \(\frac { 1 }{ 2 }\)
as percentage, we need to multiply by 100
∴ \(\frac { 1 }{ 2 }\) × 100 = 50%

(ii) Aparna scored 7.5 points out of 10 in a competition.
Answer:
Aparna scored 75% in a competition
Hint:
7.5 points out of 10 is \(\frac{7.5}{10}\) = 0.75
For percentage, we need to multiply by 100
We get 0.75 × 100 = 75%

(iii) The statue was made of pure silver.
Answer:
The statue was made of 100% pure silver
Hint:
Pure silver means there are no other metals
so, 100 out of 100 parts is made of silver = \(\frac{100}{100}\)
∴ to express as percentage, \(\frac{100}{100}\) × 100% = 100%

(iv) 48 out of 50 students participated in sports.
Answer:
96% students participated in sports.
Hint:
48 out of 50 students in fraction form is \(\frac{48}{50}\)
As a percentage, we need to multiply by 100

(v) Only 2 persons out of 3 will be selected in the interview.
Answer:
Only 66\(\frac{2}{3}\)% will be selected in the interview.
Hint:
2 out of 3 in fraction form is \(\frac{2}{3}\)
to express as percentage, we need to multiply by 100
\(\frac{2}{3} \times 100=\frac{200}{3}=66 \frac{2}{3} \%\)

Question 3.
48 is 32% of which number?
Answer:
Let the number required to be found be ‘x’
Given that 32% of x is 48
i.e., \(\frac{32}{100}\) × x = 48

∴ x = 150

Question 4.
What is 25% of 30% of 400?
Answer:
Required to find 25% of 30% of 400

Question 5.
If a car is sold for ₹ 2,00,000 from its original price of ₹ 3,00,000, then find the percentage of decrease in the value of the car.

Answer:
original price of car = ₹ 3,00,000
actual selling price of car = ₹ 2,00,000
Decrease in amount from original = 3,00,000 – 2,00,000 = 1,00,000

Question 6.
If the difference between 75% of a number and 60% of the same number is 82.5, then find 20% of that number.
Answer:
Given that 75% of number less 60% of number is 82.5
Let the number be ‘x’
∴ \(\frac{75}{100}\) x x – \(\frac{60}{100}\) x x = 82.5
∴ 0.75 x – 0.60 x = 82.5
∴ 0.15 x = 82.5
∴ x = \(\frac{82.5}{0.15}=\frac{8250}{15}\) = 550
Required to find 20% of number ie 20% of x.

Question 7.
A number when increased by 18% gives 236. Find the number.
Answer:
Let the number be x. Given that when it is increased by 18%, we get 236.

Question 8.
A number when decreased by 20% gives 80. Find the number.
Answer:
Let the number be x. Given that when it is increased by 20% we get 80.

x = 100

Question 9.
A number is increased by 25% and then decreased by 20%. Find the percentage change in that number.
Answer:
Method 1.
Let the number be x.
First it is increased by 25%
∴ It becomes x + \(\frac{25}{100}\) × x = \(\frac{125}{100}\)
Secondary it is decreased by 20%
\(\frac{125 x}{100}-\frac{20}{100} \times \frac{125}{100} x=\frac{125}{100} x \times \frac{80}{100}=x\)
Now we get back x, therefore there is no change.
Hence percentage change in that number is 0%

Method 2.
[to understand, let us assume that number is 100]
So, first when we increase by 25%, we get

Now this 125 is decreased by 20%, we get
125 – \(\frac{25}{100}\) × 125 = 125 – 25 = 100
∴ We get back 100 ⇒ No change
Hence percentage change in that number is 0%

Question 10.
The ratio of boys and girls in a class is 5:3. If 16% of boys and 8% of girls failed in an examination, then find the percentage of passed students.
Answer:
Let number of boys be ‘b’ and number of girls be ‘g’
Ratio of boys and girls is given as 5:3
b:g = 5:3 ⇒ \(\frac{b}{g}=\frac{5}{3}\) …… (A)
Failure in boys = 16% = \(\frac{16}{100}\) × b = \(\frac{16b}{100}\)
Failure in girls = 8% = \(\frac{8}{100}\) × g = \(\frac{8g}{100}\)
Pass in boys = 100 – 16% = 84% = \(\frac{84}{100} b\) …… (1)
Pass in girls = 100 – 8% = 92% = \(\frac{92}{100} g\) ……. (2)
From A, we have \(\frac{b}{g}=\frac{5}{3}\) , adding I on both sides, we get
\(\frac{b}{g}\) + 1 = \(\frac{5}{3}\) + 1
\(\frac{b+g}{g}=\frac{5+3}{3}=\frac{8}{3}\)
∴ g = \(\frac{3}{8}\)(b + g) ……. (3)
Similarly b = \(\frac{5}{8}\) (b + g) ……. (4)
Total pass = pass in girls + pass in boys
= (1) + (2) = \(\frac{84}{100} b+\frac{92}{100} g\)

Objective Type Questions

Question 11.
12% of 250 litre is the same as ________ of 150 litre.
(A) 10%
(B) 15%
(C) 20%
(D) 30%
Answer:
(C) 20%
Hint:
12% of 250 = \(\frac{12}{100}\) × 250 = 30 lit.
Percentage: \(\frac{30}{150}\) × 100 = 20%

Question 12.
If three candidates A, B and C in a school election got 153,245 and 102 votes respectively, then the percentage of votes got by the winner is ________ .
(A) 48%
(B) 49%
(C) 50%
(D) 45%
Answer:
(B) 49%
Hint:
Candidate 1: 153
Candidate 2: 245 – winner [as maximum votes)
Candidate 3: 102
Total votes = 1 + 2 + 3 = 153 + 245 + 102 = 500

= \(\frac{245}{500}\) × 100 = 49%

Question 13.
15% of 25% of 10000 = ________ .
(A) 375
(B) 400
(C) 425
(D) 475
Answer:
(A) 375
Hint:
15% of 25% of 10000 is
First let us do 25% of 10,000, which is

Next 15% of the above is \(\frac{15}{100}\) × 2500 = 375

Question 14.
When 60 is subtracted from 60% of a number to give 60, the number is
(A) 60
(B) 100
(C) 150
(D) 200
Answer:
(D) 200
Hint:
Let the number be ‘X’
60% of the number is \(\frac{60}{100}\) × x = \(\frac{60x}{100}\)
Given that when 60 is subtracted from 60%, we get 60
i.e \(\frac{60}{100}\) x – 60 = 60
∴ \(\frac{60}{100}\) x 60 + 60 = 120
∴ x = \(\frac{120 \times 100}{60}\) = 200

Question 15.
If 48% of 48 = 64% of x, then x =
(A) 64
(B) 56
(C) 42
(D) 36
Answer:
(D) 36
Hint:
Given that 48% of 48 = 64% of x

x = 36

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra InText Questions Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra InText Questions

Recap (Text Book Page No. 74 & 75)

Question 1.
Write the number of terms in the following expressions
(i) x + y + z – xyz
Answer:
4 terms

(ii) m²n²c²
Answer:
1 term

(iii) a²b²c – ab²c² + a²bc² + 3abc
Answer:
4 terms

(iv) 8x² – 4xy + 7xy²
Answer:
3 terms

Question 2.
Identify the numerical co-efficient of each term in the following expressions.
(i) 2x² – 5xy + 6y² + 7x – 10y + 9
Answer:
Numerical co efficient in 2x² is 2
Numerical co efficient in -5xy is -5
Numerical co efficient in 6y² is 6
Numerical co efficient in 7x is 7
Numerical co efficient in -10y is -10
Numerical co-efficient in 9 is 9

(ii) \(\frac{x}{3}+\frac{2 y}{5}\) – xy + 7
Answer:
Numerical co efficient in \(\frac{x}{3}\) is \(\frac{1}{3}\)
Numerical co efficient in \(\frac{2 y}{5}\) is \(\frac{2}{5}\)
Numerical co efficient in – xy is – 1
Numerical co efficient in 7 is 7

Question 3.
Pick out the like terms from the following:

Like Terms
The variables of the terms along with their respective exponents must be same
Examples: x², 4x²
a²b², – 5a²b²
2m, – 7m

Answer:

Question 4.
Add: 2x, 6y, 9x – 2y
Answer:
2x + 6y + 9x – 2y
= 2x + 9x + 6y – 2y
= (2 + 9) x + (6 – 2)y
= 11 x + 4 y

Question 5.
Simplify: (5x³y³ – 3x²y² + xy + 7) + (2xy + x³y³ – 5 + 2x²y²)
Answer:
(5x³y³ – 3x²y² + xy + 7) + (2xy + x³y³ – 5 + 2x²y²)
= 5x³y³ + x³y³ – 3x²y² + 2x²y² + xy + 2xy + 7 – 5
= (5 + 1)x³y³ + (- 3 + 2)x²y² + (1 + 2)xy + 2
= 6x³y³ – x²y² + 3xy + 2

Question 6.
The sides of a triangle are 2x – 5y + 9, 3y + 6x – 7 and -4x + y + 10. Find the perimeter of the triangle.
Answer:
Perimeter of the triangle = Sum of three sides
= (2x – 5y + 9) + (3y + 6x – 7) + (-4x + y + 10)
= 2x – 5y + 9 + 3y + 6x – 7 – 4x + y + 10
= 2x + 6x – 4x – 5y + 3y + y + 9 – 7 + 10
= (2 + 6 – 4)x + (- 5 + 3 + 1)y + (9 – 7 + 10)
= 4x – y + 12
∴ Perimeter of the triangle = 4x – y + 12 units.

Question 7.
Subtract – 2mn from 6mn.
Answer:
6 mn – (-2mn) = 6mn + (+ 2mn)
= (6 + 2)mn
= 8mn

Question 8.
Subtract 6a² – 5ab + 3b² from 4a² – 3ab + b².
Answer:
(4a² – 3ab + b²) – (6a² – 5ab + 3b²)
= (4a² – 6a²) + (- 3ab – (-5 ab)] + (b² – 3b²)
= (4 – 6) a² + (-3ab + (+ 5ab)] + (1 – 3) b²
= [4+(-6)] a² + (-3 + 5)ab + [1 + (-3)]b²
= – 2a² + 2ab – 2b²

Question 9.
The length of a log is 3a + 4b – 2 and a piece (2a – b) is removed from it. What is the length of the remaining log?

Answer:
Length of the log = 3a + 4b – 2
Length of the piece removed = 2a – b
Remaining length of the log = (3a + 4b – 2) – (2a – b)
= (3a – 2a) + [4b – (-b)] – 2
= (3 – 2)a + (4 + 1)b – 2
= a + 5b – 2

Question 10.
A tin had ‘x’ litre oil. Another tin had (3x² + 6x – 5) litre of oil. The shopkeeper added (x + 7) litre more to the second tin. Later he sold (x² + 6) litres of oil from the second tin How much oil was left in the second tin?
Answer:
Quantity of oil in the second tin = 3x² + 6x – 5 litres.
Quantity of oil added = x + 7 litres
∴ Total quantity of oil in the second tin
= (3x² + 6x – 5) + (x + 7)litres
= 3x² + (6x + x) + (-5 + 7) = 3x⁴ + (6 + 1)x + 2
= 3x² + 7x + 2litres
Quantity of oil sold = x² + 6 litres
∴ Quantity of oil left in the second tin
= (3x² + 7x + 2) – (x² + 6) = (3x² – x²) + 7x + (2 – 6)
= (3 – 1)x² + 7x + (-4) = 2x² + 7x – 4
Quantity of oil left = 2x² + 7x – 4 litres

Think (Text Book Page No. 77)

Question 1.
Every algebraic expression is a polynomial. Is this statement true? Why?
Answer:
No, This statement is not true. Because Polynomials contain only whole numbers as the powers of their variables. But an algebraic expression may contains fractions and negative powers on their variables.
Eg. 2y² + 5y^-1 – 3 is a an algebraic expression. But not a polynomial.

Try These (Text Book Page No. 78)

Find the product of
(i) 3ab², – 2a²b³
Answer:
(3ab²) × (- 2a²b³) = (+) × (-) × (3 × 2) × (a × a²) × (b² × b³)
= – 6a³b⁵

(ii) 4xy, 5y²x, (-x²)
Answer:
(4xy) × (5y²x) × (-x²) = (+) × (+) × (-) × (4 × 5 × 1) × (x × x × x²) × (y × y²)
= -20x⁴y³

(iii) 2m, – 5n, – 3p
Answer:
(2m) × (-5n) × (-3p) = (+) × (-) × (-) × (2 × 5 × 3) × m × n × p
= + 30 mnp
= 30 mnp

Think (Text Book Page No. 79)

why 3 + (4x – 7y) ≠ 12 x – 21 y ?
Answer:
Addition and multiplication are different 3 + (4x – 7y) = 3 + 4x – 7y
We can add only like terms.

Try These (Text Book Page No. 79)

Question 1.
MuItipIy
(i) (5x² + 7x – 3) by -4x²
Answer:

= – 20x² – 28x² + 12x²

(ii) (10x – 7y + 5z) by 6xyz
Answer:

= 6xyz (10x) + 6xyz (- 7y) + 6xyz (5z)
= (6 × 10)(x × x × y × z) + (6 × – 7) + (x × y × y × z) + (6 × 5)(x × y × z × z)

(iii) (ab + 3bc – 5ca) by 3a²bc
Answer:
(ab + 3bc – 5ca) × (3a²bc ) = ab(3a²bc) + 3bc (3a²bc) – 5ca (3a²bc)
= 3a³b²c + 9a² b² c² – 15a³bc²

(iv) (4m² – 3m + 7) by – 5m³
Answer:
(4m² – 3m + 7) × (- 5m³) = 4m² (- 5m³) – (3m) (- 5m³) + 7(- 5m³)
= – 20m⁵ + 15m⁴ – 35m³

Try These (Text Book Page No. 81)

MuItipIy
(i) (a – 5) and (a + 4)
Answer:
(a – 5)(a + 4) = a(a + 4) – 5(a + 4)
= (a × a) + (a × 4) + (-5 × a) + (-5 × 4)
= a² + 4a – 5a – 20
= a² – a – 20

(ii) (a + b) and (a – b)
Answer:
(a + b)(a – b) = a(a – b) + b(a – b)
= (a × a) + (a × -b) + (b × a) + b(-b)
= a² – ab + ab – b = a² – b²

(iii) (m⁴ + n⁴) and (m – n)
Answer:
(m⁴ + n⁴)(m – n) = m⁴(m – n) + n⁴(m – n)
(m⁴ × m) + (m⁴ × (-n)) + (n⁴ × m) + (n⁴ × (-n))
= m⁵ – m⁴n + mn⁴ – n⁵

(iv) (2x + 3)(x + 4)
Answer:
(2x + 3)(x + 4) = 2x(x + 4) + 3(x + 4)
= (2x² × x) + (2x × 4) + (3 × x) + (3 × 4)
= 2x² + 8x + 3x + 12
= 2x² + 11x + 12

(v) x – 5)(3x + 7)
Answer:
(x – 5)(3x + 7) = x(3x + 7) – 5(3x + 7)
= (x × 3x) + (x × 7) + (-5 × 3x) + (-5 × 7)
= 3x² + 7x – 15x – 35
= 3x² – 8x – 35

(vi) (x – 2)(6x – 3)
Answer:
(x – 2)(6x-3) = x(6x – 3) – 2(6x – 3)
= (x × 6x) + (x × (-3) – (2 × 6x) – (2 × 3)
= 6x² – 3x – 12x + 6
= 6x² – 15x + 6

Think (Text Book Page No. 81)

(i) In 3x²(x⁴ – 7x³ + 2) what is the highest power in the expression?
Answer:
3x² (x⁴ – 7x³ + 2) = (3x²) (x⁴) + 3x² (-7x³) + (3x²)2
= 3x⁶ – 21x⁵ + 6x²

(ii) Is -5y² + 2y – 6 = -(5y² + 2y – 6)? If not, correct the mistake.
Answer:
No, -5y² + 2y – 6 = -(5y² + 2y – 6)

Think (Text Book Page No. 83)

Are the following correct?
(i) \(\frac{x^{3}}{x^{8}}\) = x^{8 – 3} = x⁵
Answer:
\(\frac{x^{3}}{x^{8}}\) = x^{8 – 3} = x⁵ (or) \(\frac{x^{3}}{x^{8}}=\frac{1}{x^{8-3}}=\frac{1}{x^{5}}\)
∴ The given answer is wrong

(ii) \(\frac{10 m^{4}}{10 m^{4}}=0\)
Answer:
\(\frac{10 m^{4}}{10 m^{4}}=\frac{10}{10} m^{4-4}=1\) m⁰ = 1
[∵ m⁰ = 1]
∴ The given answer is not correct.

(iii) When a monomial is divided by itself, we will get 1. ?
Answer:
When a monomial is divided by itself we get 1.
\(\frac{x}{x}\) = x^1-1 = x⁰ = 1
∴ The given statement is correct.

Try These (Text Book Page No. 83)

Divide
(i) 12x³y² by x²y
Answer:
\(\) = 12x^{3 – 2}y^{2 – 1} = 12x¹y¹ = 12xy

(ii) -20a⁵b² by 2a³b⁷
Answer:

(iii) 28a⁴c² by 21ca³
Answer:

(iv) (3x²y)³ √6x²y³
Answer:

(v) 64m⁴ (n²)³ by 4mn
Answer:

(vi) (8x²y²)³ by (8x²y²)²
Answer:

= 8x^{6 – 4} y^{6 – 4}
= 8x²y²

(vii) 81p²q⁴ by \(\sqrt{81 p^{2} q^{4}}\)
Answer:

= 9p^{2 – 1} q^{4 – 2}
= 9pq²

(vii) (4x²y³)⁰ by \(\frac{\left(x^{3}\right)^{2}}{x^{6}}\)
Answer:

Think (Text Book Page No. 84)

Are the following divisions correct?
(i) \(\frac{4 y+3}{4}\) = y + 3
Answer:
\(\frac{4 y+3}{4}=\frac{4 y}{4}+\frac{3}{4}=y+\frac{3}{4}\) is the correct answer.
∴ The given statement is not correct

(ii) \(\frac{5 m^{2}+9}{9}\) = 5m²
Answer:
\(\frac{5 m^{2}+9}{9}=\frac{5 m^{2}}{9}+\frac{9}{9}=\frac{5}{9} m^{2}+1\) is the correct answer.
∴ The given statement is not correct

(iii) \(\frac{2 x^{2}+8}{4}\) = 2x² + 2. If not , correct it.
Answer:
\(\frac{2 x^{2}+8}{4}=\frac{2 x^{2}}{4}+\frac{8}{4}=\frac{1}{2} x^{2}+2\) is the correct answer.
∴ The given statement is not correct

Try These (Text Book Page No. 84)

(i) (16y⁵ – 8y²) ÷ 4y
Answer:

(ii) (p⁵q² + 24p³q – 128q³) ÷ 6q
Answer:

(iii) (4m²n + 9n²m + 3mn) ÷ 4mn
Answer:

Try These (Text Book Page No. 86)

Expand the following
Question 1.
(p + 2)² = ………………….
Answer:
(p + 2)² = p² + 2(p)(2) + 2²
= p² + 4p + 4

Question 2.
(3 – a)² = ………………….
Answer:
(3 – a)² = 3² – 2(3)(a) + a²
= 9 – 6a + a²

Question 3.
(6² – x²) = ………………….
Answer:
(6² – x²) = (6 + x)(6 – x)

Question 4.
(a + b)² – (a – b)² = ………………….
Answer:
(a + b)² – (a – b)² = a² + 2ab + b² – (a² – 2ab + b²)
= a² + 2ab + b² – a² + 2ab – b²
= (1 – 1)a² + (2 + 2)ab + (+1 – 1)b² = 4ab

Question 5.
(a + b)² = (a + b) × ………………….
Answer:
(a + b)² = (a + b) × (a + b)

Question 6.
(m + n)(…..) = m² – n²
Answer:
(m + n)(m – n) = m² – n²

Question 7.
(m + ……)² = m² + 14m + 49
Answer:
(m + 7)² = m² + 14m + 49

Question 8.
(k² – 49) = (k + …)(k – …)
Answer:
k² – 49 = k² – 7² = (k + 7)(k – 7)

Question 9.
m² – 6m + 9 = ………………….
Answer:
m² – 6m + 9 = (m – 3)²

Question 10.
(m – 10)(m + 5) = ………………….
Answer:
(m – 10)(m + 5) = m² + (-10 + 5)m + (-10)(5) = m² – 5m – 50

Think (Text Book Page No. 87)

Which is correct? (3a)² is equal to
(i) 3a²
(ii) 3²a
(iii) 6a²
(iv) 9a²
Answer:
(iv) 9a²
Hint:
(3a)² = 3² a² = 9a²

Try These (Text Book Page No. 88)

Expand using appropriate identities.
Question 1.
(3p + 2q)²
Answer:
(3p + 2q)²
Comparing (3p + 2q)² with (a + b)², we get a = 3p and b = 2q.
(a + b)² = a² + 2ab + b²
(3p + 2q)² = (3p)² + 2(3p) (2q) + (2q)²
= 9p² + 12pq + 4q²

Question 2.
(105)²
Answer:
(105)² = (100 + 5)²
Comparing (100 + 5)² with (a + b)², we get a = 1oo and b = 5.
(a + b)² = a² + 2ab + b²
(100 + 5)² = (100)² + 2(100)(5) + 5²
= 10000 + 1000 + 25
105² = 11,025

Question 3.
(2x – 5d)²
Answer:
(2x – 5d)²
Comparing with (a – b)², we get
a = 2x, b = 5d.
(a – b)² = a² – 2ab + b²
(2x – 5d)² = (2x)² – 2 (2x) (5d) + (5d)²
= 2²x² – 20 xd + 5²d²
= 4x² – 20xd + 25d²

Question 4.
(98)²
Answer:
(98)² = (100 – 2)²
Comparing (100 – 2)² with (a – b)² we get
a = 100, b = 2
(a – b)² = a² – 2ab + b²
(100 – 2)² = 100² – 2(100)(2) + 2²
= 10000 – 400 + 4
= 9600 + 4
= 9604

Question 5.
(y – 5) (y + 5)
Answer:
(y – 5) (y + 5)
Comparing (y – 5) (y + 5) with (a – b) (a + b) we get
a = y; b = 5
(a – b) (a + b) = a² – b²
(y – 5)(y + 5) = y² – 5²
= y² – 25

Question 6.
(3x)² – 5²
Answer:
(3x)² – 5²
Comparing (3x)² – 5² with a² – b² we have
a = 3x; b = 5
(a² – b²) = (a + b)(a – b)
(3x)² – 5² = (3x + 5)(3x – 5)
= 3x(3x – 5) + 5(3x-5)
= (3x) (3x) – (3x) (5) + 5 (3x) – 5 (5)
= 9x² – 15x + 15x – 25
= 9x² – 25

Question 7.
(2m + n)(2m + p)
Answer:
(2m + n) (2m + p)
Comparing (2m + n) (2m + p) with (x + a) (x + b) we have
x = 2n; a = n;b = p
(x – a)(x + b) = x² + (a + b)x + ab
(2m + n) (2m +p) = (2m²) + (n + p)(2m) + (n) (p)
= 2²m² + n(2m) + p(2m) + np
= 4m² + 2mn + 2mp + np

Question 8.
203 × 197
Answer:
203 × 197 = (200 + 3)(200 – 3)
Comparing (a + b) (a – b) we have
a = 200, b = 3
(a + b)(a – b) = a² – b²
(200 + 3)(200 – 3) = 200² – 3²
203 × 197 = 40000 – 9
203 × 197 = 39991

Question 9.
Find the area of the square whose side is (x – 2) units.
Answer:
Side of a square = x – 2
∴ Area = Side × Side
= (x – 2)(x – 2) = x(x – 2) – 2 (x – 2)
= x(x) + (x) (-2) + (-2)(x) + (-2) (-2)
= x² – 2x – 2x + 4 .
= x² – 4x + 4 units square

Question 10.
Find the area of the rectangle whose length and breadth are (y + 4) units and (y – 3) units.
Answer:
Length of the rectangle = y + 4
breadth of the rectangle = y – 3
Area of the rectangle = length x breadth
= (y + 4)(y – 3) = y² + (4 + (-3))y + (4)(-3)
= y² + y – 12

Try These (Text Book Page No. 91)

Expand :
(i) (x + 5)³
Answer:
Comparing (x + 5)³ with (a + b)³, we have a = x and b = 4.
(a + b)³ = a³ + 3a²b + 3ab² + b³
(x + 5)³ = x³ + 3x²(5) + 3(x)(5)² + 5³
= x³ + 15x² + 75x + 125

(ii) (y – 2)³
Answer:
Comparing (y – 2)³ with (a – b)³ we have a = y b = z
(a – b)³ = a³ – 3a²b + 3ab² – b³
(y – 2)² = y³ – 3y²(2) + 3y(2)² + 2³
= y³ – 6y² + 12y + 8

(iii) (x + 1)(x + 4)(x + 6)
Answer:
Comparing (x + 1)(x + 4)(x + 6) with (x + a)(x + b)(x + c) we have
a = 1 b = 4 and c = 6
(x + a)(x + b)(x + c) = x³ + (a + b + c)x² + (ab + bc + ca)x + abc
= x³ + (1 + 4 + 6)x² + (1) (4) + (4) (6) + (6) (1)x + (1) (4) (6)
= x³ + 11x² + (4 + 24 + 6)x + 24
= x³ + 11x³ + 34x + 24

Try These (Text Book Page No. 94)

Find the factors

Answer:

Think (Text Book Page No. 94)

x² – 4(x – 2) = (x² – 4)(x – 2) Is this correct? If not correct it.
Answer:
(3a)² = 3²a² = 9a²
x² – 4 (x – 2) = x² – 4x + 8

Try These (Text Book Page No. 95)

Question 1.
3y + 6
Answer:
3y + 6
3y + 6 = 3 × y + 2 × 3
Taking out the common factor 3 from each term we get 3 (y + 2)
∴ 3y + 6 = 3(y + 2)

Question 2.
10x² + 15y²
Answer:
10x² + 15y²
10x² + 15y² = (2 × 5 × x × x) + (3 × 5 × y × y)
Taking out the common factor 5 we have
10x² + 15y² = 5(2x² + 3y²)

Question 3.
7m(m – 5) + 1(5 – m)
Answer:
7m(m – 5) + 1 (5 – m)
7m(m – 5) + 1(5 – m) = 7m(m – 5) + (-1)(-5 + m)
= 7m(m – 5) – 1 (m – 5)
Taking out the common binomial factor (m – 5) = (m – 5) (7m – 1)

Question 4.
64 – x²
Answer:
64 – x²
64 – x² = 82 – x²
This is of the form a² – b²
Comparing with a² – b² we have a = 8, b = x
a² – b² = (a + b)(a – b)
64 – x² = (8 + x)(8 – x)

Question 5.
x² – 3x + 2
Answer:

x² – 3x + 2 = x² – 2x – x + 2
= x(x – 2) – (x – 2)
= (x – 2)(x – 1)

Question 6.
y² – 4y – 32
Answer:

y² – 4y – 32 = y2 – 8y + 4y – 32
= y(y – 8) + 4(y – 8)
= (y – 8) (y + 4)

Question 7.
p² + 2p – 15
Answer:

p² + 2p – 15 = p² + 5p – 3p – 15
= p(p + 5) -3 (p + 5)
= (p + 5)(p – 3)

Question 8.
m² + 14m + 48
Answer:
m² + 14m + 48 = m² + 8m + 6m +48
= m(m + 8) + 6(m + 8)
= (m + 6)(m + 8)

Question 9.
x² – x – 90
Answer:
x² – x – 90 = x² – 10x + 9x – 90
= x(x – 10) + 9(x – 10)
= (x + 9)(x – 10)

Question 10.
9x² – 6x – 8
Answer:
9x² – 6x – 8 = 9x² – 12x + 6x – 8
= 3x(3x -4) + 2(3x -4)
= (3x + 2)(3x – 4)

Try These (Text Book Page No. 99)

Identify which among the following are linear equations.
(i) 2 + x = 19
Answer:
Linear as degree of the variable x is 1

(ii) 7x² – 5 = 3
Answer:
not linear as highest degree of x is 2

(iii) 4p³ = 12
Answer:
not linear as highest degree of p is 3

(iv) 6m + 2
Answer:
Linear, but not an equation

(v) n = 10
Answer:
Linear equation as degree of n is 1

(vi) 7k – 12 = 0
Answer:
Linear equation as degree of k is 1

(vii) \(\frac{6 x}{8}\) + y = 1
Answer:
Linear equation as degree of x & y is 1

(vii) 5 + y = 3x
Answer:
Linear equation as degree of y & x is 1

(ix) 10p + 2q = 3
Answer:
Linear equation as degree of p & q is 1

(x) x² – 2x – 4
Answer:
not linear equation as highest degree of x is 2

Think (Text Book Page No. 99)

(i) Is t(t – 5) = 10 a linear equation? Why?
Answer:
t(t – 5) = 10
= t × t – 5 × t = 10
= t² – 5t = 10
This is not a linear equations as the highest degree of the variable ‘t’ is 2

(ii) Is x² = 2x, a linear equation? Why?
Answer:
x² = 2x
= x² – 2x = 0
This is not a linear equations as the highest degree of the variable ‘x’ is 2

Try These (Text Book Page No. 100)

Convert the following statements into linear equations:

Question 1.
On subtracting 8 from the product of 5 and a number, I get 32.
Answer:
Convert to linear equations:
Given that on subtracting 8 from product of 5 and a, we get 32
∴ 5 × x – 8 = 32
∴ 5x – 8 = 32

Question 2.
The sum of three consecutive integers is 78.
Answer:
Sum of 3 consecutive integers is 78
Let integer be bx
∴ x + (x + 1) + (x + 2) = 78
∴ x + x + 1 + x + 2 = 78
∴ 3x + 3 = 78

Question 3.
Peter had a Two hundred rupee note. After buying 7 copies of a book he was left with 60.
Answer:
Let cost of one book be ‘x’
∴ Given that 200 – 7 × x = 60
∴ 200 – 7x = 60

Question 4.
The base angles of an isosceles triangle are equal and the vertex angle measures 80°.
Answer:
Let base angles each be equal to x & vertex bottom angle is 80°. Applying triangle property, sum of all angles is 180°
∴ x + x + 80 = 180°
∴ 2x + 80 = 180°

Question 5.
In a triangle ABC, ∠A is 100 more than ∠B. Also ∠C is three times ∠A. Express the equation in terms of angle B.
Answer:
Let ∠B = b
Given ∠A = 10° + ∠B = 10 + b
Also given that ∠C = 3 × ∠A = 3 × (10 + b) = 30 + 3b
Sum of the angles = 180°
∠A + ∠B + ∠C = 180°
10 + b + b + 30 + 3b = 180°
∴ 5b + 40 = 180°

Think (Text Book Page No. 101)

Can you get more than one solution for a linear equation?
Answer:
Yes, we can get. Consider the below line or equation.
x + y = 5
here,when x = 1, y = 4
when x = 2, y = 3
x = 3, y = 2
x = 4, y = 1
Hence, we get multiple solutions for the saine linear equation.

Try These (Text Book Page No. 101)

Identify which among the following are linear equations.

(i) 2 + x = 10
Answer:
2 + x = 10
⇒ x = \(\frac{10}{2}\) = 5

(ii) 3 + x = 5
Answer:
3 + x ⇒ 5
x = 5 – 3 = 2

(iii) x – 6 = 10
Answer:
x – 6 = 10
x = 10 + 6 = 16

(iv) 3x + 5 = 2
Answer:
⇒ 3x + 5 = 2
3x = 2 – 5 = -3

(v) \(\frac{2 x}{7}\) = 3
Answer:
⇒ 2x = 3 × 7 = 21
x = \(\frac{2 1}{2}\)

(vi) – 2 = 4m – 6
Answer:
⇒ -2x = 4m – 6
– 2 + 6 = 4m
4 = 4m
m = \(\frac{4}{4}\) = 1

(vii) 4(3x – 1) = 80
Answer:
⇒ 4(3x – 1) = 80
12x – 4 = 80
12x = 80 + 4 = 84
x = \(\frac{84}{12}\) = 7

(viii) 3x – 8 = 7 – 2x
Answer:
⇒ 3x – 8 = 7 – 2x
3x + 2x = 7 +8 = 15
5x = 15
x = \(\frac{15}{5}\) = 3

(ix) 7 – y = 3(5 – y)
Answer:
⇒ 7 – y = 3(5 – y)
7 – y = 15 – 3y
3y – y = 15 – 7
2y = 8
y = \(\frac{8}{2}\) = 4

(x) 4(1 – 2y) – 2(3 – y) = 0
Answer:
⇒ 4(1 – 2y) – 2(3 – y) = 0
4 – 8y – ó – 2y = 0
– 2 – 6y = 0
6y = -2
y = \(\frac{-2}{6}=\frac{-1}{3}\)

Think (Text Book Page No. 102)

Question 1.
“An equation is multiplied or divided by a non zero number on either side:’ Will there be any change in the solution?
Answer:
Not be any change in the solution

Question 2.
“An equation is multiplied or divided by two different numbers on either side. What will happen to the equation?
Answer:
When an equation is multiplied or divided by 2 different numbers on either side, there will be a change in the equation & accordingly, solution will also change.

Think (Text Book Page No. 104)

Suppose we take the second piece to be x and the first piece to be (200 – x), how will the steps vary ? Will the answer be different?
Answer:
Let 2^nd piece be ‘x’ & 1^st piece is 200 – x
Given that 1st piece is 40 cm smaller than hence the other piece
∴ 200 – x = 2 × x – 40

∴ 200 + 40 = 2x + x
240 = 3x
∴ x = \(\frac{240}{3}\) = 80
∴ 1^st piece = 200 – x = 200 – 80 = 120 cm
2^nd piece = x = 80 cm
The answer will not change

Think (Text Book Page No. 109)

If instead of (4,3), we write (3,4) and tn to mark it, will it represent ‘M’ again?
Answer:
Let 3, 4 be M. when we mark, we find that it is a different point and not ‘M’

Try These (Text Book Page No. 111)

Question 1.
Complete the table given below.

Answer:

Question 2.
Write the coordinates of the points marked in the following figure

Answer:
A – (-3, 2)
B – (5, 2)
C – (5, -3)
D – (-3, 3)
E – (-1, 4)
F – (1, 2)
G – (7, 4)
H – (0, 2)
I – (0, 3)
J – (-3, 0)
K – (5, 0)
L – (-1, 0)
M – (-2, 0)
N – (-2 ,-1)
O – (0, 0)
P – (-1, -1)
Q – (1, -1)
R – (2, -1)
S – (0, -3)
T – (7, 0)
U – (7, -2)

Think (Text Book Page No. 114)

Which of the points (5, -10) (0, 5) (5, 20) lie on the straight line x = 5?
Answer:
All points on the line X = 5 will have X-coordinate as 5. Therefore, any point with X – coordinate as 5 will lie on X = 5 line. Hence the points (5, — 10) & (5, 20) will lie on X = 5

Try These (Text Book Page No. 117)

Identify and correct the errors
(i)

Answer:

(ii)

Answer:

(iii)

Answer:

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.10 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.10

Question 1.
The sum of three numbers is 58. The second number is three times of two-fifth of the first number and the third number is 6 less than the first number. Find the three numbers.
Answer:
Here what we know
a + b + c = 58 (sum of three numbers is 58)
Let the first number be b ‘x’
b = a + 3 (the second number is three times of of the first \(\frac{2}{5}\) number)
b = 3 × \(\frac{2}{5}\)x \(\frac{6}{5}\)x
Third number = x – 6
Sum of the numbers is given as 58.
∴ x + \(\frac{6}{5}\)x + (x – 6) = 58
Multiplying by 5 throughout, we get
5 × x + 6x + 5 × (x – 6) = 58 × 5
5x + 6x + 5x – 30 = 290
∴ 16x = 290 + 30
∴ 16x = 320
∴ x = \(\frac{320}{16}\)
x = 20
1^st number = 20

3^rd number = 24 – 16 = 14

Question 2.
In triangle ABC, the measure of ∠B is two-third of the measure of ∠A. The measure of ∠C is 200 more than the measure of ∠A. Find the measures of the three angles.
Answer:
Let angle ∠A be a°
Given that ∠B = \(\frac{2}{3}\) × ∠A = \(\frac{2}{3}\)a
& given ∠C = ∠A + 20 = a + 20
Since A, B & C are angles of a triangle, they add up to 180° (∆ property)
∴∠A + ∠B + ∠C = 180°
⇒a + \(\frac{2}{3}\)a + a + 20 = 180°
\(\frac{3 a+2 a+3 a}{3}\) + 20 = 180°
\(\frac{8 a}{3}\) = 180 – 20 = 160
∴ a = \(\frac{160 \times 3}{8}\) = 60°

∠C = 80°

Question 3.
Two equal sides of an isosceles triangle are 5y – 2 and 4y + 9 units. The third side is 2y + 5 units. Find ‘y’ and the perimeter of the triangle.
Answer:
Given that 5y – 2 & 4y + 9 are the equal sides of an isosceles triangle.
∴ The 2 sides are equal

∴5y – 4y = 9 + 2 (by transposing)
∴ y = 11
∴ 1^st side = 5y – 2 = 5 × 11 – 2 = 55 – 2 = 53
2^ndside = 53 .
3^rdside = 2y + 5 = 2 × 11 + 5 = 22 + 5 = 27
Perimeter is the sum of all 3 sides
∴ P = 53 + 53 + 27 = 133 units

Question 4.
In the given figure, angle XOZ and angle ZOY form a linear pair. Find the value of x.

Answer:
Since ∠XOZ & ∠ZOY form a linear pair, by property, we have their sum to be 180°
∴ ∠XOZ + ∠ZOY 180°
∴ 3x – 2 + 5x + 6 = 180°
8x + 4 = 180 = 8x = 180 – 4
∴ 8x = 76 ⇒ x = \(\frac{176}{8}\) ⇒ x = 22°
XOZ = 3x – 2 = 3 × 22 – 2 = 66 – 2 = 64°
YOZ = 5x + 6 = 5 × 22 + 6
= 110 + 6 = 116

Question 5.
Draw a graph for the following data:

Answer:
Graph between side of square & area

When we plot the graph, we observe that it is not a linear relation.

Challenging problems

Question 6.
Three consecutive integers, when taken in increasing order and multiplied by 2, 3 and 4 respectIvely, total up to 74. Find the three numbers.
Answer:
Let the 3 consecutive integers be ‘x’, ‘x + 1’ & ‘x + 2’
Given that when multiplied by 2, 3 & 4 respectively & added up, we get 74

Simplifying the equation, we get
2x + 3x + 3 + 4x + 8 = 74
9x + 11 = 63
9x = 63 ⇒ x = \(\frac{63}{9}\) = 7
First number = 7
Second numbers = x + 1 ⇒ 7 + 1 = 8
Third numbers = x + 2 ⇒ 7 + 2 = 9
∴ The numbers are 7, 8 & 9

Question 7.
331 students went on a field trip. Six buses were filled to capacity and 7 students had to travel in a van. How many students were there in each bus?
Answer:
Let the number of students in each bus be ‘x’
∴ number of students in 6 buses = 6 × x = 6x
A part from 6 buses, 7 students went in van
A total number of students is 331
∴ 6x + 7 = 331
∴ 6x = 331 – 7 = 324
∴ x = \(\frac{324}{6}\) = 54
∴ There are 54 students in each bus.

Question 8.
A mobile vendor has 22 items, some which are pencils and others are ball pens. On a particular day, he is able to sell the pencils and ball pens. Pencils are sold for ₹ 15 each and ball pens are sold at ₹ 20 each. If the total sale amount with the vendor is ₹ 380,
how many pencils did he sell?
Answer:
Let vendor have ‘p’ number of pencils & ‘b’ number of ball pens
Given that total number of items is 22
∴ p + b = 22
Pencils are sold for ₹ 15 each & ball pens for ₹ 20 each
total sale amount = 15 × p + 20 × b
= 15p + 20b which is given to be 380.
∴ 15p + 20b = 380
Dividing by 5 throughout,
\(\frac{15 p}{5}+\frac{20 b}{5}\) = \(\frac{380}{5}\) ⇒ – 3p + 4b = 76
Multiplying equation (1) by 3 we get
3 × p + 3 × b = 22 × 3
⇒ 3p + 3b = 66
Equation (2) – (3) gives

∴ b = 10
∴ p = 12
He sold 12 pencils

Question 9.
Draw the graph of the lines y = x, y = 2x, y = 3x and y = 5x on the same graph sheet. Is there anything special that you find in these graphs?
Answer:
(i) y = x
(ii) y = 2x,
(iii) y = 3x
(iv) y = 5x

(i) y = x
When x = 1, y = 1
x = 2, y = 2
x = 3, y = 2

(ii) y = 2x
When x = 1, y = 2
x = 2, y = 4
x = 3, y = 6

(iii) y = 3x
When x = 1, y = 3
x = 2, y = 6
x = 3, y = 9

(i) y = 5x
When x = 1, y = 5
x = 2, y = 10
x = 3, y = 15
When we plot the above points & join the points to form line, we notice that the lines become progressively steeper. In other words, the slope keeps increasing.

Question 10.
Consider the number of angles of a convex polygon and the number of sides of that polygon. Tabulate as follows:

Use this to draw a graph illustrating the relationship between the number of angles and the number of sides of a polygon.
Answer:
Angles

Name of Polygon	No of angles	No. of Sides
Triangle	3	3
Rectangle	4	4
Pentagon	5	5
Hexagon	6	6
Deptagon	7	7
Octagon	8	8

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.9 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.9

Question 1.
Fill in the blanks:
(i) y = p x where p ∈ Z always passes through the _________ .
Answer:
Origin (0,0)
Hint:
[When we substitute x = 0 in equation, y also becomes zero. (0,0) is a solution]

(ii) The intersecting point of the line x = 4 and y = -4 is _________ .
Answer:
4, -4
Hint:
x = 4 is a line parallel to the y – axis and
y = -4 is a line parallel to the x – axis. The point of intersection is a point that lies on both lines & which should satisfy both the equations. Therefore, that point is (4, -4)

(iii) Scale for the given graph,
On the x-axis 1 cm = _________ units
y-axis 1 cm = _________ units

Answer:
3 units, 25 units
Hint:
With reference to given graph,
On the x – axis. 1 cm = 3 units
y axis, 1 cm = 25 units

Question 2.
Say True or False.
(i) The points (1,1) (2,2) (3,3) lie on a same straight line.
Answer:
True
Hint:
The points (1, 1), (2, 2), (3, 3) all satisfy the equation y = x which is straight line. Hence, it is true

(ii) y = -9x not passes through the origin.
Answer:
False
Hint:
y = -9x substituting for x as zero, we get y = -9 × 0 = 0
∴ for x = 0, y = 0. Which means line passes through (0, 0), hence statement is false.

Question 3.
Will a line pass through (2, 2) if it intersects the axes at (2, 0) and (0, 2).
Answer:
Given a line intersects the axis at (2, 0) & (0, 2)
Let line intercept form be expressed as
ax + by = 1 Where a & b are the x & y intercept respectively.
Since the intercept points are (2. 0) & (0, 2)
a = 2, b = 2
∴ 2x + 2y = 1
When the point (2. 2) is considered & substituted in the equation
2x + 2y = 1, we get
2 × 2 + 2 × 2 = 4 ≠ 1
∴ the point (2. 2) does not satisfy the equation. Therefore the line does not pass through (2, 2)
Alternatively graphical method

as we can see the line doesn’t pass through (2, 2)

Question 4.
A line passing through (4, – 2) and intersects the Y-axis at (0, 2). Find a point on the line in the second quadrant.
Answer:
Line passes through (4, – 2)
y – axis intercept point – (0, 2) using 2 point formula.



Any point in II quadrant will have x as negative & y as positive.
So let us take x value as – 2
∴ -2 + y = 2
∴ y = 2 + 2 = 4
∴ Point in II Quadrant is (-2, 4)

Question 5.
If the points P(5, 3) Q(-3, 3) R (-3, -4) and S form a rectangle then find the coordinate of S.
Answer:
Plotting the points on a graph (approximately)
Steps:

• Plot P, Q, R approximately on a graph.
• As it is a rectangle, RS should be parallel to PQ & QR should be paraHel to PS
• S should lie on the straight line from R parallel to x-axis & straight line from P parallel to y-axis
• Therefore, we get S to be (5, -4)

[Note: We don’t need graph sheet for approximate plotting. This is just for graphical understanding]

Question 6.
A line passes through (6, 0) and (0, 6) and an another line passes through (-3, 0) and (0, -3). What are the points to be joined to get a trapezium?
Answer:
In a trapezium. there are 2 opposite sides that are parallel. The other opposite sides are non-parallel.
Now, let us approximately plot the points for our understanding
[no need of graph sheet]

• Plot the points (0, 6), (6, 0), (-3, 0) & (0, -3)
• Join (0, 6) & (6, 0)
• Join (-3,0) & (0, – 3)
• We find that the lines formed by joining the points are parallel lines.
• So, for forming a trapezium, we should join (0, 6), (-3, 0) & (0, -3), (6, 0)

Question 7.
Find the point of intersection of the line joining points (- 3, 7) (2, – 4) and (4, 6) (- 5, – 7).Also find the point of intersection of these lines and also their intersection with the axis.
Answer:

Equation of line joining 2 points by 2 point formula is given by

Cross multiplying, we get

Transposing the variables, we get
11 x + 5 y = 35 – 33 = 2
11 x + 5y = 2 – Line 1
Similarly, we should find out equation of second line


∴ 9y – 54 = 13x – 52
∴ 9y – 13x = 2 – Line 2
For finding point of intersection, we need to solve the 2 line equation to find a point that will satisfy both the line equations.
∴ Solving for x & y from line 1 & line 2 as below
11x + 5y = 2 ⇒ multiply both sides by 13,
11 × 13x + 5 × 13y = 26 …….. (3)
Line 2: 9y – 13x = 2 ⇒ multiply both sides by 11
9 × 11y – 13 × 11x = 22 ……… (4)

∴ 164 y = 48
∴ y = \(\frac{48}{164}=\frac{12}{41}\)
Substituting this value ofy in line I we get
11 x + 5 y = 2
11 x + 5 × \(\frac{12}{41}\) = 2
11 x = 2 – \(\frac{60}{41}=\frac{82-60}{41}=\frac{22}{41}\)
∴ x = \(\frac{2}{41}\)
[∴ Point of intersection is \(\left(\frac{2}{41}, \frac{12}{41}\right)\)]
To find point of intersection of the lines with the axis, we should substitute values & check
Line 1: 11 x + 5 y = 2
Point of intersection of line with x – axis, i.e y coordinate is ‘0’
∴ put y = 0 in above equation
∴ 11 x – 5 × 0 = 2
∴ 11x + 0 = 2
∴ x = \(\frac{2}{11}\)
∴ [Point is \(\left(\frac{2}{11}, 0\right)\)]
Similarly, Point of intersection of line with y – axis is when x-coordinate becomes ‘0’
∴ put x = 0 in above equation
∴ 11 × 0 + 5y = 2
∴ 0 + 5y = 2
y = \(\frac{2}{5}\)
∴ [Point is \(\left(0, \frac{2}{5}\right)\)]
Similarly for line 2,
9y – 13x = 2
For finding x intercept, i.e point where line meets x axis, we know that y coordinate becomes ‘0’
∴ Substituting y = 0 in above eqn. we get
9 × 0 – 13x = 2
∴ 0 – 13x = 2
∴ x = \(\frac{-2}{13}\)
∴ [Point: \(\left(\frac{-2}{13}, 0\right)\)]
Similarly for y – intercept, x – coordinate becomes ‘0’,
∴ Substituting for x = 0 in above equation, we get
9 y – 13 × 0 = 2
9y – 0 = 2
9y = 2
y = \(\frac{2}{9}\)
[Point \(\left(0, \frac{2}{9}\right)\)]

Question 8.
Draw the graph of the following equations: (i) x = – 7 (ii) y = 6
Answer:

Question 9.
Draw the graph of
(i) y = – 3x
(ii ) y = x – 4
(ii) y = 2x + 5
Answer:
To draw graph, we need to find out some points.
(i) y = – 3x
for y = -3x, let us first substituting values & check
put x = 0
y = 3 × 0 = 0
∴ (0,0) is a point
put x = 1
y = -3 × 1 = – 3
∴ (1, – 3) is a point
If join these 2 points, we will get the line

(ii) y = x – 4
for y = x – 4
put x = 0
y = 0 – 4 = – 4
∴ (0, – 4) is a point
x = 4
y = 4 – 4 = 0
∴ (4, 0) is a point

(iii) y = 2x + 5
for y = 2x + 5
put x = – 1
y = 2(-1) + 5 = – 2 + 5 = 3
∴ (-1, 3) is a point
put x = – 2
y = 2(-2) + 5 = – 4 + 5 = 1
∴ (-2, 1) is a point
Now let us plot the points & join them on graph

Question 10.
Find the values
(a) y = x + 3

Answer:
Let y = x+3
(i) if x = 0, y = 0 + 3 = 3,
∴ y = 3
(ii) y = 0, 0 = x + 3,
∴ x = – 3
(iii) x = -2, y = -2 + 3,
∴ y = 1
(iv) y = – 3, – 3 = x + 3,
∴ x = – 6

y = x + 3

(b) 2x + y – 6 = 0

Answer:
Let 2x + y – 6 = 0
(i) x = 0 2 × 0 + y – 6 = 0 ∴ y = 6
(ii) y = 0, 2x + 0 – 6 = 0, ∴ 2x = 6
x = 3 ,
(iii) x = -1, 2 × (-1) + y – 6 = 0, 8 + y = 0
y = 8
(iv) y = -2, 2x – 2 – 6 = 0, 2x = 8
x = 4

2x + y – 6 = 0

(c) y = 3x + 1

Answer:
(i) x = -1, y = 3(-1) + 1 = 0
∴ y = -2
(ii) x = 0, y = 3(0) + 1 = 0
∴ y = 1
(iii) x = 1, y = 3(1) + 1 = 0
∴ y = 4
(iv) x = 2, y = 3(2) + 1 = 0
∴ y = 7

y = 3x + 1

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.8 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.8

Question 1.
Fill in the blanks:
(i) X- axis and Y-axis intersect at _________ .
Answer:
Origin (0,0)

(ii) The coordinates of the point in third quadrant are always _________ .
Answer:
negative

(iii) (0, -5) point lies on _________ axis.
Answer:
Y-axis

(iv) The x- coordinate is always ______ on the y-axis.
Answer:
Zero

(v) ___________ coordinates are the same for a line parallel to Y-axis.
Answer:
X

Question 2.
Say True or False:
(i) (-10,20) lies in the second quadrant.
Answer:
True
Hint:
(-10, 20)
x = -10, y = 20
∴ (-10, 20) lies in second quadrant – True

(ii) (-9, 0) lies on the x-axis.
Answer:
True
Hint:
(-9, 0) on x – axis. Y- coordinate is always zero.
∴ (-9, 0) lies on x axis – True

(iii) The coordinates of the origin are (1,1).
Answer:
False
Hint:
Coordinate of origin is (0, 0), not (1, 1). Hence – False

Question 3.
Find the quadrants without plotting the points on a graph sheet.
(3, -4), (5, 7), (2, 0), (-3, -5), (4, -3), (-7, 2), (-8, 0), (0, 10), (-9, 50).
Answer:

If X & y coordinate are positive – I quad
If x is positive,y is negative – IV quad
If x is negative, y is positive – II quad
If both are negative, then – III quad

Question 4.
Plot the following points in a graph sheet.
A(5, 2), B(-7, -3), C(-2, 4), D(-1, -1), E(0, -5), F(2, 0), G(7, -4), H(-4, 0), I(2, 3), J(8, -4), K(0, 7).
Answer:

Question 5.
Use the graph to determine the coordinates where each figure is located.

a) Star	____________
b) Bird	____________
c) Red circle	____________
d) Diamond	____________
e) Triangle	____________
f) Ant	____________
g) Mango	____________
h) Housefly	____________
i) Medal	____________
j) Spider	____________

Answer:

a) Star	(3, 2)
b) Bird	(-2, 0)
c) Red circle	(-2, -2)
d) Diamond	(-2, 2)
e) Triangle	(-1, 1)
f) Ant	(3, -1)
g) Mango	(0, 2)
h) Housefly	(2, 0)
i) Medal	(-3, 3)
j) Spider	(0, -2)

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.7 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.7

Question 1.
Fill in the blanks:
(i) The solution of the equation ax + b = 0 is _______ .
Answer:
\(-\frac{b}{a}\)
Hint:
ax + b = 0
ax = – b
∴ x = \(-\frac{b}{a}\)

(ii) If a and b are positive integers then the solution of the equation ax = b has to be always _______ .
Answer:
Positive
Hint:
Since a & b are positive integers, b
The solution to the equation ax = b is x = \(\frac{b}{a}\) is also positive.

(iii) One-sixth of a number when subtracted from the number itself gives 25. The number is _______ .
Answer:
30
Hint:
Let the number be x.
As per question, when one sixth of number is subtracted from itself it gives 25

(iv) If the angles of a triangle are in the ratio 2:3:4 then the difference between the greatest and the smallest angle is _______ .
Answer:
40°
Hint:
Given angles are in the ratio 2:3:4
Let the angles be 2x, 3x & 4x
Since sum of the angles of a triangle is 180°,
We get 2x + 3x + 4x = 180
∴ 9x = 180
∴ x = \(\frac{180}{9}\) = 20°
∴ The angles are 2x = 2 × 20 = 40°
3x = 3 × 20 = 60°
4x = 4 × 20 = 80°
∴ Difference between greatest & smallest angle is
80° – 40° = 40°

(v) In an equation a + b = 23. The value of a is 14 then the value of b is _______ .
Answer:
b = 9
Hint:
Given equation is a + b = 23, a = 14
14 + b = 23
∴ b = 23 – 14 = 9
b = 9

Question 2.
Say True or False
(i) “Sum of a number and two times that number is 48” can be written as y + 2y = 48
Answer:
True
Hint:
Let the number be ‘y’
∴ Sum of number & two times that number is 48
Can be written as y + 2y = 48 – True

(ii) 5(3x + 2) = 3(5x – 7) is a linear equation in one variable.
Answer:
True
Hint:
5 (3x + 2) = 3 (5x – 7) is a linear equation in one variable – ‘x’ – True

(iii) x = 25 is the solution of one third of a number is less than 10 the original number.
Answer:
False
Hint:
One third of number is 10 less than original number.
Let number be ‘x’. Therefore let us frame the equation
\(\frac{x}{3}\) = x – 10
∴ x = 3x – 30
3x – x = 30
2x = 30
x = 15 is the solution

Question 3.
One number is seven times another. If their difference is 18, find the numbers.
Answer:
Let the numbers be x & y
Given that one number is 7 times the other & that the difference is 18.
Let x = 7y
also, x – y = 18 (given)
Substituting for x in the above
We get 7y – y = 18
∴ 6y = 18
y = \(\frac{18}{6}\) = 3
∴ x = 7y = 7 × 3 = 21
The number are 3 & 21

Question 4.
The sum of three consecutive odd numbers is 75. Which is the largest among them?
Answer:
Given sum of three consecutive odd numbers is 75
Odd numbers are 1,3,5,7,9, 11, 13
∴ The difference between 2 consecutive odd numbers is always 2. or in other words, if one odd number is x, the next odd number would be x + 2 and the next number would be x + 2 + 2x + 4
i.e x + 4
Since sum of 3 consecutive odd nos is 75
∴ x + x + 2 + x + 4 = 75
∴ 3x + 6 = 75 ⇒ 3x = 75 – 6
∴ 3x = 69
x = \(\frac{69}{3}\) = 23
∴ The odd numbers are 23, 23 + 2, 23 + 4
i.e 23, 25, 27
∴ Largest number is 27.

Question 5.
The length of a rectangle is \(\frac{1}{3}\) rd of its breadth. If its perimeter is 64 m, then find the length and breadth of the rectangle.
Answer:
Let length & breadth of rectangle be ‘l’ and ‘b’ respectively
Given that length is \(\frac{1}{3}\) of breadth,
∴ l = \(\frac{1}{3}\) × b ⇒ l = \(\frac{b}{3}\) ⇒ b = 3l ……. (1)

Also given that perimeter is 64 m
Perimeter = 2 × (l + b)
2 × 1 + 2 × b = 64
Substituting for value of b from (1), we get
2l + 2(3l) = 64
∴ 2l + 6l = 64
8l = 64
∴ l = \(\frac{64}{8}\) = 8m
b = 3l = 3 × 8 = 24m
Ienglh l = 8 m in & breadth b = 24 m

Question 6.
A total of 90 currency notes, consisting only of ₹ 5 and ₹ 10 denominations, amount to ₹ 500. Find the number of notes in each denomination.
Answer:
Let the number of ₹ 5 notes be ‘x’
And number of ₹ 10 notes be ‘y’
Total numbers of notes is x + y = 90 (given)
The total value of the notes is 500 rupees.
Value of one ₹ 5 rupee note is 5
Value of x ₹ 5 rupee notes is 5 × x = 5x
∴ Value of y ₹ 10 rupee flotes is 10 × y = lOy
∴ The total value is 5x + 10y which is 500
∴ we have 2 equations:
x + y = 90 ….(1)
5x + 10y = 500 ….(2)
Multiplying both sides of(1) by 5, we get
5 × x + 5 × y = 90 × 5
5x + 5y = 450
Subtracting (3) from (2), we get

∴ y = \(\frac{50}{5}\) = 10
Substitute y = 10 in equation (1)
x + y = 90 ⇒ x + 10 = 90 ⇒ x = 90 – 10 ⇒ x = 80
There are ₹5 denominations are 80 numbers and ₹10 denominations are 10 numbers

Question 7.
At present, Thenmozhi’s age is 5 years more than that of Murali’s age. Five years ago, the ratio of Then mozhi’s age to Murali’s age was 3 : 2. Find their present ages.
Answer:
Let present ages of Thenmozhi & Murali be ‘t’ & ‘m’
Given that at present
Then mozhi’s age is 5 years more than Murali
∴ t = m + 5 …… (1)
5 years ago, Thenmozhi’s age would be t – 5
& Murali’s age would be m – 5
Ratio of their ages is given as 3 : 2

2(t – 5) = 3(m – 5)
2 × t – 2 × 5 = 3 × m – 3 × 5 ⇒ 2t – 10 = 3m – 15
Substituting for t from (1)
2(m + 5) – 10 = 3m – 15

2m = 3m – 15
3m – 2m = 15
m = 15
t = m + 5 = 15 + 5 = 20
∴ Present ages of Thenmozhi & Murali are 20 & 15

Question 8.
A number consists of two digits whose sum is 9. If 27 is subtracted from the original number, its djgit.s are interchanged. Find the original number.
Answer:
Let the units/digit of a number be ‘u’ & tens digit of the number be ‘t’
Given that sum of it’s digits is 9
∴ t + u = 9 ……. (1)
If 27 is subtracted from original number, the digits are interchanged
The number is written as 10t + u
[Understand: Suppose a 2 digit number is 21
it can be written as 2 × 10 + 1
∴ 32 = 3 × 10 + 2
45 = 4 × 10 + 5
tu = t × 10 + u = 1ot + u]
Given that when 27 is subtracted, digits interchange
10t + u – 27 = 10u + t (number with interchanged digits)
∴ By transposition & bringing like variables together
10t – t + u – 10u = 27
∴ 9t – 9u = 27
Dividing by ‘9’ throughout , we get
\(\frac{9 t}{9}-\frac{9 u}{9}=\frac{27}{9}\) ⇒ t – u = 3 ……. (2)
Solving (1) & (2):

t = 6 substitute in (1)
t + u = 9 ⇒ 6 + u = 9 ⇒ u = 9 – 6 = 3
Hence the number is 63.

Question 9.
The denominator of a fraction exceeds Its numerator by 8. If the numerator is increased by 17 and the denominator is decreased by 1, we get \(\frac{3}{2}\). Find the original fraction.
Answer:
Let the numerator & denominator be ‘n’ & ‘d’
Given that denominator exceeds numerator by 8
∴ d = n + 8 ……. (1)
If numerator increased by 17 & denominator decreased by 1,
it becomes (n + 17) & (d – 1), fraction is \(\frac{3}{2}\).

2(n + 17) = 3(d – 1)
2n + 2 × 17 = 3d – 3

∴ 34 + 3 = 3d – 2n
∴ 3d – 2n = 37 …….. (2)
Substituting eqn. (1) in (2), we get,
3 × (n + 8) – 2n = 37
3n + 3 × 8 – 2n = 37

∴ n = 37 – 24 = 13
d = n + 8 = 13 + 8 = 21
The fraction is \(\frac{n}{d}=\frac{13}{21}\)

Question 10.
If a train runs at 60 km/hr it reaches its destination late by 15 minutes. But, if it runs at 85 kmph it is late by only 4 minutes. Find the distance to be covered by the train.
Answer:
Let the distance to be covered by train be ‘d’

Case 1:
If speed = 60km/h
The time taken is 15 minutes more than usual (t + \(\frac{15}{60}\))
Let usual time taken be ‘t’ hrs.
Caution: Since speed is given in km/hr, we should take care to maintain all units such as time should be in hour and distance should be in kin.
Given that in case 1, it takes 15 min. more
15m = \(\frac{15}{60}\) hr = \(\frac{1}{4}\)hr.
∴ Substituting in formula,

Since usually it takes ‘t’ hr, but when running at 60 k, it kes 15 min (\(\frac{1}{4}\)hr) extra.
Multiplying by 60 on both sides
d = 60 × t + 60 × \(\frac{1}{4}\) = 6ot + 15 …… (1)

Case 2:
Speed is given as 85 km/h
Time taken is only 4 min (\(\frac{4}{60}\)hr) more than usual time
∴ time taken = (t + \(\frac{1}{15}\)) hr. \(\left(\frac{4}{60}=\frac{1}{15}\right)\)
Using the formula,

Multiplying by 85 on both sides
\(\frac{d}{85}\) × 85 = 85 × t + 85 × \(\frac{1}{15}\)
∴ d = 85t + \(\frac{17}{3}\) ….. (2)
From (1) & (2), we will solve for ‘r’
Equating & eliminating ‘d’ we get

∴ By transposing, we get

Substituting this value of ‘t’ in eqn. (1), we get
d = 60t + 15
= 60 × \(\frac{28}{75}\) + 15 = \(\frac{1680}{75}\) + 15 = 22.4 + 15
= 37.4 km

Question 11.
Sum of a number and its half is 30 then the number is ______
(a) 15
(b) 20
(c) 25
(d) 40
Answer:
(b) 20
Hint:
Let number be ‘x’
∴ half of number is \(\frac{x}{2}\)
Sum of number and it’s half is given by
x + \(\frac{x}{2}\) = 30 [Multiplying by 2 on both sides]
2x + x = 30 × 2
3x = 60
x = \(\frac{60}{3}\) = 20

Question 12.
The exterior angle of a triangle is 1200 and one of its interior opposite angle 58°, then the other opposite interior angle is _________
(a) 62°
(b) 72°
(c) 78°
(d) 68°
Answer:
(a) 62°
As per property of A. exterior angle is equals to sum of interior opposite angles
Let the other interior angle to be found be ‘x’
∴ x + 58 = 120°
∴ x = 120 – 58 = 62°

Question 13.
What sum of money will earn 500 as simple interest in 1 year at 5% per annum?
(a) 50000
(b) 30000
(c) 10000
(d) 5000
Answer:
(c) 10000
Hint:
Let sum of money be P’
Time period (n) is given as 1 yr.
Rate of simple interest (r) is given as 5% p.a
∴ As per formula for simple interest.
S.I = \(\frac{\mathrm{P} \times r \times n}{100}=\frac{\mathrm{P} \times 5 \times 1}{100}\) = 500
∴ P × 5 × n = 500 × 100
∴ p = \(\frac{500 \times 100}{5}\) = 100 × 100 = 10,000

Question 14.
The product of LCM and HCF of two numbers is 24. If one of the number is 6, then the other number is ________
(a) 6
(b) 2
(c) 4
(d) 8
Answer:
(C) 4
Hint:
Product of LCM & HCF of 2 numbers is always product of the numbers. [this is property]
Product of LCM & HCF is given as 24
∴ Product of the 2 nos. is 24
Given one number is 6. Let other number be ‘x’
∴ 6 × x = 24
x = \(\frac{24}{6}\) = 4

Question 15.
The largest number of the three consecutie numbers is x+ 1, then the smallest number is ________ .
(A) x
(B) x + 1
(C) x + 2
(D) x – 1
Answer:
(D) x – 1
Hint:
The 3 consecutive numbers are: x – 1, x, x + 1

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.6 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.6

Question 1.
Fill in the blanks:
(i) The value of x in the equation x + 5 = 12 is ________ .
Answer:
7
Hint:
Given, x + 5 = 12
x = 12 – 5 = 7 (by transposition method)
Value of x is 7

(ii) The value of y in the equation y – 9 = (-5) + 7 is ________ .
Answer:
11
Hint:
Given, y – 9 = (-5) + 7
y – 9 = 7 – 5 (re-arranging)
y – 9 = 2
∴ y = 2 + 9 = 11 (by transposition method)

(iii) The value of m in the equation 8m = 56 is ________ .
Answer:
7
Hint:
Given, 8m = 56
Divided by 8 on both sides
\(\frac{8 \times m}{8}=\frac{56}{8}\)
∴ m = 7

(iv) The value of p in the equation \(\frac{2 p}{3}\) = 10 is ________ .
Answer:
15
Hint:
Given, \(\frac{2 p}{3}\) = 10
Multiplying by 3 on both sides

Dividing by 2 on both sides

∴ p = 15

(v) The linear equation in one variable has ________ solution.
Answer:
one

Question 2.
Say True or False.
(i) The shifting of a number from one side of an equation to other is called transposition.
Answer:
True

(ii) Linear equation in one variable has only one variable with power 2.
Answer:
False
[Linear equation in one variable has only one variable with power one – correct statement]

Question 3.
Match the following

(A) (i),(ii), (iv) ,(iii),(v)
(B) (iii), (iv), (i) ,(ii), (v)
(C) (iii),(i) ,(iv), (v), (ii)
(D) (iii) , (i) , (v) ,(iv) ,(ii)
Answer:
(C) (iii),(i) ,(iv), (v), (ii)

a. \(\frac{x}{2}\) = 10, multiplying by 2 on both sides, we get
\(\frac{x}{2}\) × 2 = 10 × 2 ⇒ x = 20

b. 20 = 6x – 4 by transposition ⇒ 20 + 4 =6x
6x = 24 dividing by 6 on both sides,
\(\frac{6 x}{6}=\frac{24}{6}\) ⇒ x = 4

c. 2x – 5 = 3 – x
By transposing the variable ‘x’, we get
2x – 5 + x = 3
by transposing – 5 to other side,
2x + x = 3 + 5

∴ x = \(\frac{8}{3}\)

d. 7x – 4 – 8x = 20
by transposing – 4 to other side,
7x – 8x = 20 + 4
– x = 24
∴ x = – 24

e. \(\frac{4}{11}-x=\frac{-7}{11}\)
Transposing \(\frac{4}{11}\) to other side,
– x = \(\frac{-7}{11} \frac{-4}{11}=\frac{-7-4}{11}=\frac{-11}{11}\) = – 1
∴ – x = – 1 ⇒ x = 1

Question 4.
Find x:
(i) \(\frac{2 x}{3}-4=\frac{10}{3}\)
Answer:
Transposing – 4 to other side, it becomes + 4

(ii) \(y+\frac{1}{6}-3 y=\frac{2}{3}\)
Answer:
Transposing \(\) to the other side,

(iii) \(\frac{1}{3}-\frac{x}{3}=\frac{7 x}{12}+\frac{5}{4}\)
Answer:
Transposing \(\frac{-x}{3}\) to the other side, it becomes + \(\frac{x}{3}\)
∴ \(\frac{1}{3}=\frac{7 x}{12}+\frac{5}{4}+\frac{x}{3}\)
Transposing \(\frac{5}{4}\) to the other side, it becomes \(\frac{-5}{4}\)
\(\frac{1}{3}-\frac{5}{4}=\frac{7 x}{12}+\frac{x}{3}\)
Multiply by 12 throughout [we look at the denominators 3, 4, 12, 3 and take the LCM, which is 12]

4 – 15 = 7x + x × 4
– 11 = 7x + 4x
11x = – 11
x = -1

Question 5.
Find x
(i) -3(4x + 9) = 21
Answer:

Expanding the bracket,
-3 × 4 + (-3) × 9 = 21
∴ -12x + (-27) = 21
– 12x – 27 = 21
Transposing – 27 to other side, it becomes +27
– 12 x = 21 + 27 = 48
∴ – 12x = 48 ⇒ 12x = – 48
Dividing by 12 on both sides

(ii) 20 – 2 (5 – p) = 8
Answer:

Expanding the bracket,
20 – 2 × 5 – 2 × (-p) = 8
20 – 10 + 2p = 8
(- 2 × – p = 2p)
10 + 2p = 8 transposing lo to other side
2p = 8 – 10 = – 2
∴ 2p = – 2
∴ p = – 1

(iii) (7x – 5) – 4(2 + 5x) = 10(2 – x)
Answer:

Expanding the brackets,
7x – 5 – 4 × 2 – 4 × 5x = 10 × 2 + 10 × (-x)
7x – 5 – 8 – 20x = 20 – 10x
7x – 13 – 20x = 20 – 10x
Transposing 10x & – 13, we get
7x – 13 – 20x + 10x = 20
7x – 20x + 10x = 20 + 13, Simplifying,
– 3x = 33
3x = – 33
x = \(\frac{-33}{3}\) = – 11
x = – 11

Question 6.
Find x and m:
(i) \(\frac{3 x-2}{4}-\frac{(x-3)}{5}=-1\)
Answer:

(ii) \(\frac{m+9}{3 m+15}=\frac{5}{3}\)
Answer:
Cross multiplying, we get

∴ (m + 9) × 3 = 5 × (3m + 15)
m × 3 + 9 × 3 = 5 × 3m + 5 × 15

27 – 75 = 15m – 3m
– 48 = 12m

⇒ m = – 4

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.5

Question 1.
Subtract: -2(xy)² (y³ + 7x²y + 5) from 5y² (x²y³ – 2x⁴y + 10x²)
Answer:

Question 2.
Multiply (4x² + 9) and (3x – 2).
Answer:
(4x² + 9)(3x – 2) = 4x²(3x – 2) + 9(3x – 2)
= (4x²)(3x) – (4x²) (2) + 9(3x) – 9(2)
= (4 × 3 × x × x²) – (4 × 2 × x²) + (9 × 3 × x) – 18
= 12x³ – 8x² + 27x – 18(4x³ + 9)(3x – 2)
= 12x³ – 8x² + 27x – 18

Question 3.
Find the simple interest on Rs. 5a²b² for 4ab years at 7b% per annum.
Answer:

Question 4.
The cost of a note book is Rs. 10ab. If Babu has Rs. (5a²b + 20ab² + 40ab). Then how many note books can he buy?
Answer:
For ₹ 10 ab the number of note books can buy = 1.

Number of note book he can buy = \(\frac { 1 }{ 2 }\)a + 2b + 4

Question 5.
Factorise: (7y² – 19y – 6)
Answer:
7y² – 19y – 6 is of the form ax² + bx + c where a = 7; b = – 19; c = – 6

Product = – 42	Sum = -19
1 × – 42 = -42	1 + (-42) = – 41
2 × – 21 = – 42	2 + (-21) = – 19

The product a × c = 7 × – 6 = – 42
sum b = – 19

The middle term – 19 y can be written as – 21y + 2y
7y² – 19y – 6 = 7y² – 21y + 2y – 6
= 7y(y – 3) + 2(y – 3)
= (y – 3)(7y + 2)
7y² – 19y – 6 = (y – 3)(7y + 2)

Question 6.
A contractor uses the expression 4x² + 11x + 6 to determine the amount of wire to order when wiring a house. If the expression comes from multiplying the number of rooms times the number of outlets and he knows the number of rooms to be (x + 2), find the number of outlets in terms of ’x’. [Hint : factorise 4x² + 11x + 6]
Answer:
Given Number of rooms = x + 2
Number of rooms × Number of outlets = amount of wire.
(x + 2) × Number of outlets = 4x² + 11x + 6
Number of outlets = \(\frac{4 x^{2}+11 x+6}{x+2}\) … (1)
Now factorising 4x² + 11x + 6 which is of the form ax² + bx + c with a = 4 b = 11 c = 6.
The product a × c = 4 × 6 = 24
sum b = 11

Product = 24	Sum = 11
1 × 24 = 24	1 + 24 = 25
2 × 12 = 24	2 + 12 = 14
3 × 8 = 24	3 + 18 = 11

The middle term 11x can be written as 8x + 3x
∴ 4x² + 11 x + 6 = 4x² + 8x + 3x + 6
= 4x(x + 2) + 3 (x + 2)
4x² + 11x + 6 = (x + 2)(4x + 3)
Now from (1) the number of outlets

∴ Number of outlets = 4x + 3

Question 7.
A mason uses the expression x² + 6x + 8 to represent the area of the floor of a room. If the decides that the length of the room will be represented by (x + 4), what will the width of the room be in terms of x?
Answer:
Given length of the room = x + 4 .
Area of the room = x² + 6x + 8
Length × breadth = x² + 6x + 8
breadth = \(\frac{x^{2}+6 x+8}{x+4}\) ….. (1)
Factorizing x² + 6x + 8, it is in the form of ax² + bx + c
Where a =1 b = 6 c = 8.
The product a × c = 1 × 8 = 8
sum = b = 6

Product = 8	Sum = 6
1 × 8 = 8	1 + 8 = 9
2 × 4 = 8	2 + 4 = 6

The middle term 6x can be written as 2x + 4x
∴ x² + 6x + 8 = x² + 2x + 4x + 8
= x(x + 2) + 4(x + 2)
x² + 6x + 8 = (x + 2)(x + 4)
Now from (1)

∴ Width of the room = x + 2

Question 8.
Find the missing term: y² + (-)x + 56 = (y + 7)(y + -)
Answer:
We have (x + a)(x + b) = x² + (a + b)x + ab
56 = 7 × 8
∴ y² + (7 + 8)x + 56 = (y + 7) (y + 8)

Question 9.
Factorise : 16p⁴ – 1
Answer:
16p⁴ – 1 = 2⁴p⁴ – 1 =(2²)² (p²)² – 1²
= (2²p²)² – 1²
Comparing with a² – b² (a + b)(a – b) where a = 2²p² and b= 1
∴ (2²p²)² – 1² = (2²p² + 1)(2²p² – 1)
= (4p² + 1)(4p² – 1)
∴ 16p⁴ – 1 = (4p² + 1)(4p² – 1) = (4p² + 1)(2²p² – 1²)
= (4p² + 1) [(2p)² – 1²] = (4p² + 1) (2p + 1)(2p – 1) [∵ using a² – b² = (a + b)(a – b)]
∴ 16p⁴ – 1 = (4p² + 1)(2p + 1)(2p – 1)

Question 10.
Factorise : 3x³ – 45x²y + 225xy² – 375y³
Answer:
= 3x³ – 45x²y + 225xy² – 375y³
= 3(x³ – 15x²y + 75xy² – 125y³)
= 3(x³ – 3x²(5y) + 3x(5y)² – (5y)³)
= 3(x – 5y)³

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.4

Question 1.
Factorise the following by taking out the common factor
(i) 18xy – 12yz
Answer:
18xy – 12yz = (2 × 3 × 3 × y × x) – (2 × 2 × 3 × y × z)
Taking out the common factors 2, 3, y, we get
= 2 × 3 × y(3x – 2z) = 6y(3x – 2z)

(ii) 9x⁵y³ + 6x³y² – 18x²y
Answer:
9x⁵ + 6x³y² – 18x²y = (3 × 3 × x² × x³ × y × y) + (2 × 3 × x² × x × y × y) – (2 × 3 × 3 × x² × y)
Taking out the common factors 3, x², y, we get
= 3 × x² × y (3x³y² + 2xy – 6)
= 3x²y (3x³y² + 2xy – 6)

(iii) x(b – 2c) + y(b – 2c)
Answer:
Taking out the binomial factor (b – 2c) from each term, we have
= (b – 2c)(x + y)

(iv)(ax + ay) + (bx + by)
Answer:
Taking at ‘a’ from the first term and ‘b’ from the second term we have
(ax + ay )+ (bx + by) = a(x + y) + b(x + y)
Now taking out the binomial factor (x + y) from each term
= (x + y) (a + b)

(v) 2x²(4x – 1) – 4x + 1
Answer:
Taking out -1 from last two terms
2x² (4x – 1) – 4x + 1 = 2x² (4x – 1) – 1 (4x – 1)
Taking out the binomial factor 4x – 1, we get
= (4x – 1) (2x² – 1)

(vi) 3y(x – 2)² – 2(2 – x)
Answer:
3y(x – 2)² – 2(2 – x) = 3y(x – 2)(x – 2) – 2( -1)(x – 2)
[∵ Taking out – 1 from 2 – x]
= 3y(x – 2)(x – 2) + 2(x – 2)
Taking out the binomial factor x – 2 from each term, we get
= (x – 2) [3y(x – 2) + 2]

(vii) 6xy – 4y² + 12xy – 2yzx
Answer:
= 6xy + 12xy – 4y² – 2yzx [∵ Addition is commutative]
= (6 × x × y) + (2 × 6 × x × y) + (-1) (2) (2) y + y) + ((-1) (2) (y) (z) (x))
Taking out 6 x x x y from first two terms and (-1) × 2 × y from last two terms we get
= 6 × x × y(1 + 2) + (-1) (2) y [2y + zx]
= 6 × y(3) – 2y(2y + zx)
= (2 × 3 × 3 × x × y) – 2xy(2y + zx)
Taking out 2y from two terms
= 2y(9x – (2y + zx))
= 2y (9x – 2y – xz)

(viii) a³ – 3a² + a – 3
Answer:
a² – 3a² + a – 3 = a²(a – 3) + 1(a – 3) [:Groupingthetermssuitably]
= (a – 3) (a² + 1)

(ix) 3y³ – 48y
Answer:
3y² – 48y = 3 × y × y² – 3 × l6 × y
Taking out 3 × y
= 3y(y² – 16) = 3y(y² – 4²)
Comparing y² – 4² with a² – b²
a = y, b = 4
a² – b² = (a + b) (a – b)
y² – 4² = (y + 4) (y – 4)
∴ 3y(y² – 16) = 3y(y + 4)(y – 4)

(x) ab² – bc² – ab + c²
Answer:
ab² – bc² – ab + c²
Grouping suitably
ab² – bc² – ab + c² = b (ab – c²) – 1 (ab – c²)
Taking out the binomial factor ab – c² = (ab – c²) (b – 1)

Question 2.
Factorise the following expressions
(i) x² + 14x + 49
Answer:
x² + 14x + 49 = x² + 14x + 72
Comparing with a² + 2ab + b² = (a + b)² we have a = x and b = 7
⇒ x² + 2(x)(7) + 7² = (x + 7)²
∴ x² + 14x + 49 = (x + 7)²

(ii) y² – 10y + 25
Answer:
y² – 10y + 25 = y² – 10y + 5²
Comparing with a² – 2ab + b² = (a – b)² we get a = y; b = 5
⇒ y² – 2(y) (5) + 5² = (y – 5)²
∴ y² – 10y + 25 = (y – 5)²

(iii) c² – 4c – 12
Answer:
This is of the form ax² + bx + c
Where a = 1, b = -4 c = -12, x = c
Now the product ac = 1 × – 12 = -12 and the sum b = -4

Product = – 72	Sum = 1
1 × (-12) = -12	1 + (-12) = -11
2 × (-6) = – 12	2 + (-6)  = – 4

∴ The middle term – 4c can be written as 2c – 6c
∴ c² – 4c – 12 = c² + 2c – 6c – 12
= c(c + 2) -6 (c + 2)

Taking out (c + 2)
⇒ (c + 2)(c – 6)
∴ c² – 4c – 12 = (c + 2)(c – 6)

(iv) m² + m – 72
Answer:
m² + m – 72
This is of the form ax + bx + c
where a = 1, b = 1, c = -72

Product = – 72	Sum = 1
1 × -72 = – 72	1 + (-72) =  -71
2 × – 36 = – 72	2 + (-36) = – 34
3 × (-24) = – 72	3 + (-24) =  – 21
4 ×  (-18) = -72	4 + (-18) =  – 14
6 × (-12) = -72	6 + (-12) = – 6
8 × (-9) = -72	8 + (-9) = – 1
9 × (-8) = – 72	9 + (-8) = 1

Product a × c = 1 × -72 = -72
Sum b = 1
The middle term m can be written as 9m – 8m
m² + m – 72 = m² + 9m – 8m – 72
= m(m + 9) – 8(m + 9)

Taking out (m + 9)
= (m + 9)(m – 8)
∴ m² + m – 72 = (m + 9)(m – 8)

(v) 4x² – 8x + 3
Answer:
4x² – 8x + 3
This is of the form ax² + bx + c with a = 4 b = -8 c = 3
Product ac = 4 × 3 = 12
sum b = -8

Product = 12	Sum = -8
(-1) × (-12) = 12	(-1) + (-12) = – 13
(-2) × (-6) = 12	(-2) + (-6) = – 8

The middle term can be written as – 8x = – 2x – 6x
4x² – 8x + 3 = 4x² – 2x – 6x + 3
= 2x (2x – 1) – 3 (2x – 1)
= (2x – 1)(2x – 3)
4x² – 8x + 3 = (2x – 1) (2x – 3)

Question 3.
Factorise the following expressions using (a + b)³ = a³ + 3a²b + 3ab² + b³ identity
(i) 64x³ + 144x² + 108x + 27
(ii) 27p³ + 54p³q + 36pq² + 8q³
Answer:
(i) 64x³ + 144x² + 108x + 27
= (4x)³ + 3(4x)² (3) + 3(4) (3)² + 3³
= (4x + 3)³

(ii) 27p³ + 54p³q + 36pq² + 8q³
= (3p)³ + 3(3p)² (2q) + 3(3p) (2q)² + (2q)³
= (3p + 2q)³

Question 4.
Factorise the following expressions using (a – b)³ = a³ – 3a²b + 3ab² – b³ identity
(i) y³ – 18y² + 108y – 216
(ii) 8m³ – 60m²n + 150mn² – 125n³
Answer:
(i) y³ – 18y² + 108y – 216
= y³ – 3y²(6) + 3(6)²y – 6³
= (y – 6)³

(ii) 8m³ – 60m²n + 150mn² – 125n³
= (2m)³ – 3(2m)² (5) + 3(2m)(5n)² – (5n)³
= (2m – 5n)³