Category: Class 9

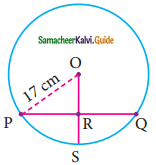
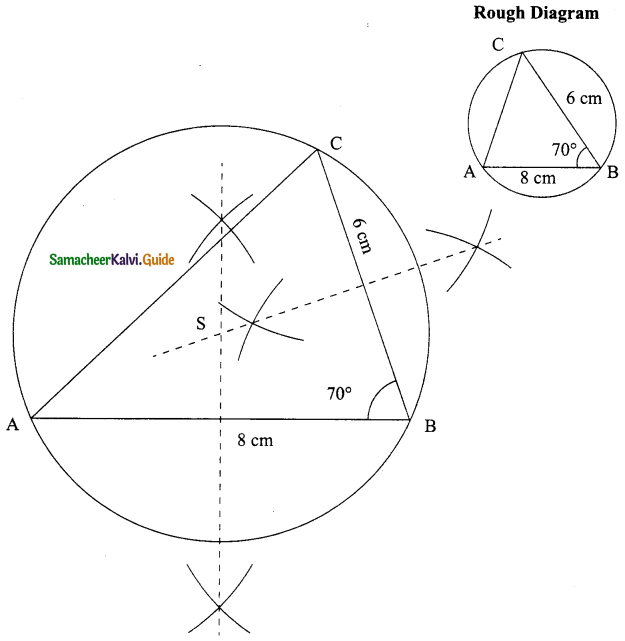
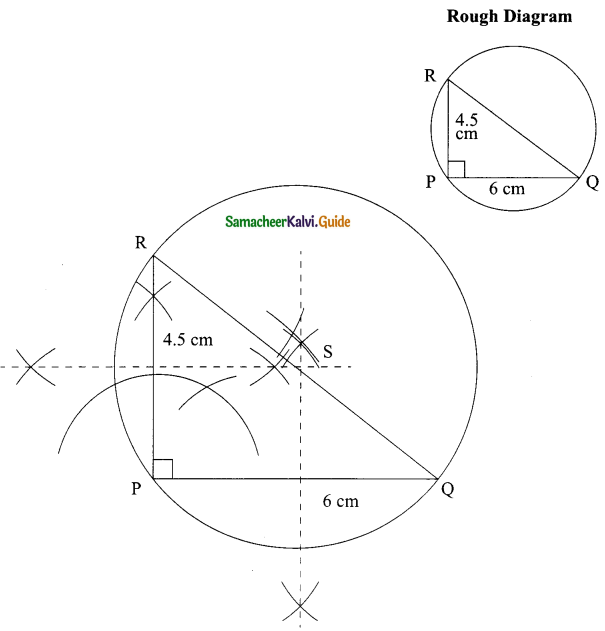
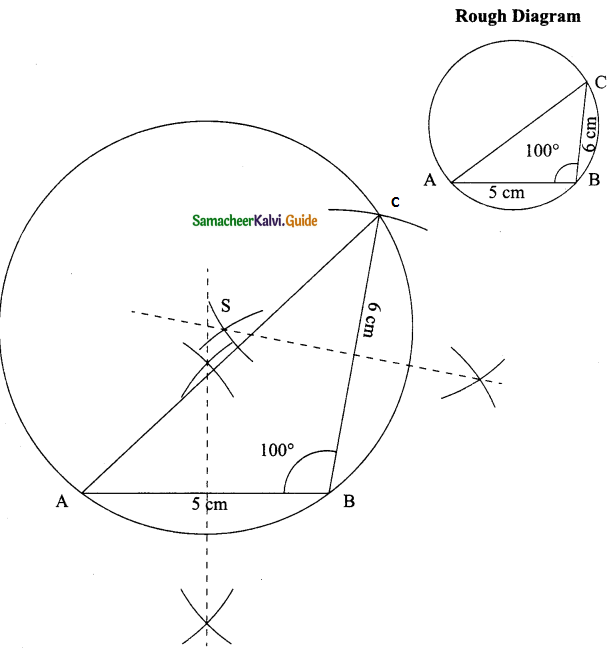
Students can download Maths Chapter 8 Statistics Ex 8.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Ex 8.3

Question 1.
The monthly salary of 10 employees in a factory are given below:
Rs 5000, Rs 7000, Rs 5000, Rs 7000, Rs 8000, Rs 7000, Rs 7000, Rs 8000, Rs 7000, Rs 5000
Find the mean, median and mode.
Solution:

Mean = 6600
Median:
Arrange in ascending order we get.
5000, 5000, 5000, 7000, 7000, 7000, 7000, 7000, 8000, 8000
The number of values = 10
Median = Average of (\(\frac{10}{2})^{th}\) and (\(\frac{10}{2}+1)^{th}\)
= Average of 5^th value and 6^th value
= \(\frac{7000+7000}{2}\)
∴ Median = 7000
Mode: 7000 repeated 5 times
∴ Mode = 7000

Question 2.
Find the mode of the given data: 3.1, 3.2, 3.3, 2.1, 1.3, 3.3, 3.1
Solution:
3.1 occuring two times
3.3 occuring two times
∴ 3.1 and 3.3 are the mode (bimodal)

Question 3.
For the data 11, 15, 17, x + 1, 19, x – 2, 3 if the mean is 14, find the value of x. Also find the mode of the data.
Solution:
Arithmetic mean

∴ 2x + 64 = 14 × 7
2x = 98 – 64
2x = 34
x = \(\frac{34}{2}\)
= 17
The given numbers are 11, 15, 17, 18, 19, 15 and 3
15 occuring two times
∴ Mode = 15
The value of x = 17 and mode = 15

Question 4.
The demand of track suit of different sizes as obtained by a survey is given below:

Which size is demanded more?
Solution:
The highest frequency is 37
The corresponding value is the mode
∴ Mode = 40
Size 40 is demanded more.

Question 5.
Find the mode of the following data:

Solution:

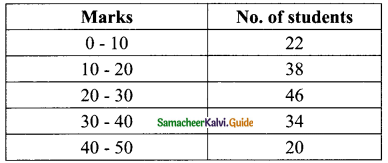
The highest frequency is 46
20 – 30 is the modal class
Here l = 20, f = 46, f₁ = 38, f₂ = 34 and c = 10
Mode

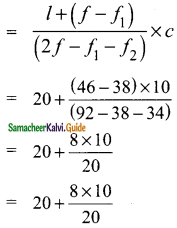
= 20 + 4
= 24
∴ Mode = 24

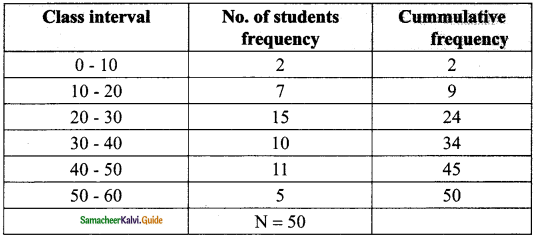
Question 6.
Find the mode of the following distribution

Solution:
In the given table the class intervals are in inclusive form; convert them into exclusive form.

The highest frequency is 14
Modal class is 54.5 – 64.5
Here l = 54.5, f = 14, f₁ = 10, f₂ = 8 and c = 10
mode

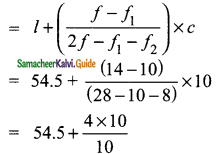
= 58.5
∴ Mode = 58.5

Students can download Maths Chapter 8 Statistics Ex 8.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Ex 8.2

Question 1.
Find the median of the given values: 47, 53, 62, 71, 83, 21, 43, 47, 41
Solution:
Arrange the values in ascending order we get
21, 41, 43, 47, 47, 53, 62, 71, 83
The number of values = 9 which is odd
Median = (\(\frac{9+1}{2})^{th}\) variable
= 5^th variable
∴ Median = 47

Question 2.
Find the median of the given data: 36, 44, 86, 31, 37, 44, 86, 35, 60, 51
Solution:
Arrange the values in ascending order we get
31, 35, 36, 37, 44, 44, 51, 60, 86, 86
The number of values = 10 which is even
Median = Average of (\(\frac{10}{2})^{th}\) and (\(\frac{10}{2}+1)^{th}\) value
= Average of 5^th and 6^th value
= \(\frac{44+44}{2}\)
= \(\frac{88}{2}\)
= 44
∴ Median = 44

Question 3.
The median of observation 11, 12, 14, 18, x + 2, x + 4, 30, 32, 35, 41 arranged in ascending order is 24. Find the values of x.
Solution:
The given observation is 11, 12, 14, 18, x + 2, x + 4, 30, 32, 35, 41 (is ascending order)
The number of values =10
Median = Average of (\(\frac{10}{2})^{th}\) and (\(\frac{10}{2}+1)^{th}\) value
= Average of 5^th and 6^th value
24 = \(\frac{x+2.+x+4}{2}\)
24 = \(\frac{2x+6}{2}\)
2x + 6 = 48
2x = 48 – 6
2x = 42
x = \(\frac{42}{2}\)
= 21
The value of x = 21

Question 4.
A researcher studying the behavior of mice has recorded the time (in seconds) taken by each mouse to locate its food by considering 13 different mice as 31, 33, 63, 33, 28, 29, 33, 27, 27, 34, 35, 28, 32. Find the median time that mice spent in searching its food.
Solution:
Arrange the value in ascending order we get
27, 27, 28, 28, 29, 31, 32, 33, 33, 33, 34, 35, 63
The number of values = 13 which is odd
Median = (\(\frac{13+1}{2})^{th}\) value
= (\(\frac{14}{2})^{th}\)
= 7th value
7th value is = 32
∴ Median = 32

Question 5.
The following are the marks scored by the students in the Summative Assessment exam.

Calculate the median.
Solution:

\(\frac{N}{2}\) = \(\frac{50}{2}\)
= 25
Here l = 30, f = 10; m = 24 and c = 10
Median = l + \(\frac{(\frac{N}{2}-m)×c}{f}\)
= 30 + \(\frac{(25-24)10}{10}\)
= 30 + 1
= 31
∴ Median = 31

Question 6.
The mean of five positive integers is twice their median. If four of the integers are 3, 4, 6, 9 and median is 6, then find the fifth integer.
Solution:
Let the 5th positive integer be x
\(\bar { x }\) = \(\frac{3+4+6+9+x}{5}\)
= \(\frac{22+x}{5}\)
Median = 6
Mean = 2 × median
\(\frac{22+x}{5}\) = 2 × 6
22 + x = 60
x = 60 – 22
= 38
The fifth integer is 38.

Students can download Maths Chapter 4 Geometry Ex 4.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.2

Question 1.
The angles of a quadrilateral are in the ratio 2 : 4 : 5 : 7. Find all the angles.
Solution:
Let the angles of a quadrilateral be 2x, 4x, 5x, and 7x.
Total angle of a quadrilateral = 360°
2x + 4x + 5x + 7x = 360°
18° = 360°
x = \(\frac{360°}{18}\)
= 20°
2x = 2 × 20° = 40°; 4x = 4 × 20° = 80°;
5x = 5 × 20° = 100°; 7x = 7 × 20° = 140°
The angles of a quadrilateral are 40°, 80°, 100° and 140°.

Question 2.
In a quadrilateral ABCD, ∠A = 72° and ∠C is the supplementary of ∠A. The other two angles are 2x – 10 and x + 4. Find the value of x and the measure of all the angles.
Solution:

∠A = 72°
∠C = 180° – 12° (∠A and ∠C are supplementary)
= 108°
∠A + ∠B + ∠C + ∠D = 360° (Total angles of quadrilateral)
72° + 2x – 10 + 108° + x + 4 = 360°
3x + 174° = 360°
x = \(\frac{186°}{3}\)
= 62°
The value of x is 62°
∠B = 2x – 10
= 2(62°) – 10
= 124° – 10°
= 114°
∠D = x + 4
= 62° + 4
= 66°
The other angles are 114°, 62° and 66°.

Question 3.
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC.
Solution:
Since the diagonals of a rectangle AC and BD are equal and bisect each other

∴ OA = OB
∠OAB = ∠OBA = 46°
Each angle of a rectangle measures 90°
∠ABC = 90°
∠ABO + ∠OBC = 90°
46° + ∠OBC = 90°
∠OBC = 90°-46°
∴ ∠OBC = 44°

Question 4.
The lengths of the diagonals of a Rhombus are 12 cm and 16 cm. Find the side of the rhombus.
Solution:
Since the diagonals of a rhombus bisect each other at right angles

AO = \(\frac{1}{2}\)AC = \(\frac{1}{2}\) × 12 = 6 cm
BO = \(\frac{1}{2}\)BD = \(\frac{1}{2}\) × 16 = 8 cm
In the right triangle AOD
AD² = AO² + DO²
= 6² + 8²
= 36 + 64
= 100
∴ AD = \(\sqrt{100}\)
= 10
∴ AB = BC = CD = AD = 10 cm.

Question 5.
Show that the bisectors of angles of a parallelogram form a rectangle.
Solution:
Given: A parallelogram in which bisector of angle A, B, C, D intersect at P, Q, R, S to form a quadrilateral PQRS.
To prove: Quadrilateral PQRS is a rectangle.
Proof: Since ABCD is a parallelogram. Therefore, AB || DC.

Now, AB || DC, and transversal AD cuts them, so we have
∠A + ∠D = 180°
\(\frac{1}{2}\)∠A + \(\frac{1}{2}\)∠D = \(\frac{180°}{2}\)
∠DAS + ∠ADS = 90°
But in ΔASD, we have
∠ADS + ∠DAS + ∠ASD = 180°
90° + ∠ASD = 180°
∠ASD = 90°
∠RSP = ∠ASD (vertically opposite angle)
∠RSP = 90°
Similarly, we can prove that
∠SRQ = 90°, ∠RQP = 90° and ∠QPS = 90°
Thus, PQRS is a quadrilateral each of whose angle is 90°.
Hence, PQRS is a rectangle.

Question 6.
If a triangle and a parallelogram lie on the same base and between the same parallels then prove that the area of the triangle is equal to half of the area of parallelogram.
Solution:
Let ΔAPB and parallelogram ABCD lie on base AB and between parallels AB and PC.
To show area ΔAPB = \(\frac{1}{2}\) Area (ABCD)
Now, draw BQ || AP. Then ABQP is a parallelogram.
Now area ABQP = Area ABCD
(They are on same base AB and between same parallels AB and PC)

⇒ ΔPAB ≅ ΔBQP
Area PAB = Area BQP
= \(\frac{1}{2}\) Area ABQP
= \(\frac{1}{2}\) Area ABCD

Question 7.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure.

If a || b, c || d, e || f, find the marked angles between
(i) b and c
(ii) d and e
(iii) d and f
(iv) c and f
Solution:
(i) Angle between b and c = 30°
(vertically opposite angles)

(ii) Angle between d and e = 180° – 75° = 105°
(sum of the adjacent angles of a parallelogram is 180°)

(iii) Angle between d and f = 75°
(opposite angles of a parallelogram)

(iv) Angle between c and f = 180° – 75° = 105°
(Adjacent angles of a parallelogram)

Question 8.
In the given figure, ∠A = 64°, ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°.

Solution:
In the given ΔABC
∠A = 64° and ∠B = 58°
∠C = 180°- (64° + 58°)
= 180° – 122°
= 58°
Since OC is the bisector of ∠C
y = \(\frac{58°}{2}\)
= 29°
Given ΔOBC
∠OCB = \(\frac{58°}{2}\) = 29°
∠OCB = 29°
∴ ∠BOC = 180°- (29° + 29°)
x = 180° – 58°
x = 122°
∠x = 122° and ∠y = 29°.

Question 9.
In the given figure, if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7 and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ΔCDF.

Solution:
Given: AB = 2 cm, BC = 6 cm, AE = 6 cm, BF = 8 cm, CE = 7 cm and CF = 7 cm
Consider ΔAEC and ΔBCF.
In ΔAEC, AE = 6 cm, EC = 7 cm and AC = 8 cm (2 + 6 = 8)
In ΔBCF, BC = 6 cm, CF = 7 cm and BF = 8 cm
∴ ΔAEC s ΔBCF
∴ Area of ΔAEC = Area of ΔBCF (Two triangles are similar areas are equal)
Subtract area of ΔBDC on both sides we get,
Area of ΔAEC – Area of ΔBDC = Area of ΔBCF – Area of ΔBDC
Area of quadrilateral ABDE = Area of ΔCDF

Question 10.
In the given figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length ”d” of the segment that is perpendicular to \(\overline { HE }\) and \(\overline { FG }\)?

Solution:
In the given figure ABCD is a rectangle and EFGH is a parallelogram.
In the right triangle AEH
HE = \(\sqrt{AH^{2} + AE^{2}}\)
= \(\sqrt{3^{2} + 4^{2}}\)
= \(\sqrt{9 + 16}\)
= \(\sqrt{25}\)
HE = 5
∴ GF = 5 (HE and Gf are opposite sides of a parallelogram)
In the right triangle
GC = \(\sqrt{GF^{2} – FC^{2}}\)
= \(\sqrt{5^{2} – 3^{2}}\)
= \(\sqrt{25 – 9}\)
= \(\sqrt{16}\)
∴ DG = 10 – 6 = 4
Area of ΔAEH + Area of ΔBEF + Area of ΔFCG + Area of ΔHDG
= \(\frac{1}{2}\) × 3 × 4 + \(\frac{1}{2}\) × 6 × 5 + \(\frac{1}{2}\) × 3 × 4 + \(\frac{1}{2}\) × 5 × 6
= (6 + 15 + 6 + 15)
= 42
∴ Area of 4 triangles = 42
Area of the parallelogram = Area of the rectangle ABCD – Area of 4 triangles.
= 10 × 8 – 42
= 80 – 42
= 38
b × h = 38
5 × d = 38
d = \(\frac{38}{5}\)
= 7\(\frac{3}{5}\)
Length of d = 7\(\frac{3}{5}\) or 7.6

Question 11.
In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is \(\frac{9}{8}\) of the area of the parallelogram ABCD.

Solution:
Draw OX perpendicular to QP.
In ΔADP, MN = \(\frac{1}{2}\) AP,
In ΔBCQ, MN = \(\frac{1}{2}\) QB
So, AP = BQ (or) AB + BP = AB + QA
∴ PB = QA
∴ QA = AB = BP (or) QP = QA + AB + BP = 3 AB
Area of ΔOQP = \(\frac{1}{2}\) × QP × OX
= \(\frac{1}{2}\) × 3 AB × OX
= \(\frac{3}{2}\) × AB × OX
= \(\frac{3}{2}\) AB (OY + YX)
= \(\frac{3}{2}\) × AB × OY + \(\frac{3}{2}\) × AB × YX (AB = MN)
= \(\frac{3}{2}\) × MN × OY + \(\frac{3}{2}\) × AB × YX
= 3 Area ΔOMN + \(\frac{3}{2}\) + Area ΔBNM
= 3[\(\frac{1}{4}\) area of MNCD] + \(\frac{3}{2}\)[\(\frac{1}{2}\) area of ABCD]
= \(\frac{3}{4}\)[\(\frac{1}{2}\) area of ABCD] + \(\frac{3}{4}\)[area of ABCD]
= \(\frac{3}{8}\) area of ABCD + \(\frac{3}{4}\) area of ABCD
= area of ABCD [\(\frac{3}{8}\) + \(\frac{3}{4}\)]
= area of ABCD (\(\frac{3+6}{8}\))
= \(\frac{9}{8}\) area of ABCD.
Hence it is proved.

Students can download Maths Chapter 4 Geometry Ex 4.7 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.7

Multiple Choice Questions

Question 1.
The exterior angle of a triangle is equal to the sum of two ……….
(a) Exterior angles
(b) Interior opposite angles
(c) Alternate angles
(d) Interior angles
Solution:
(b) Interior opposite angles

Question 2.
In the quadrilateral ABCD, AB = BC and AD = DC Measure of ∠BCD is …………..

(a) 150°
(b) 30°
(c) 105°
(d) 72°
Solution:
(c) 105°
Hint:
Join BD
∠DBC = 54°; ∠BDC = 21°
∴ ∠BCD = 180° – (54° + 21°)
= 180° – 75°
= 105°

Question 3.
ABCD is a square, diagonals AC and BD meet at O. The number of pairs of congruent triangles with vertex O are ……….

(a) 6
(b) 8
(c) 4
(d) 12
Solution:
(a) 6

Question 4.
In the given figure CE || DB then the value of x° is ………

(a) 45°
(b) 30°
(c) 75°
(d) 85°
∠B = 360° – (∠A + ∠D + ∠BCD)
= 360° – (110° + 75° + 60°)
= 360° – 245°
= 115°
∠DBC = 115° – 30°
= 85°
∴ ∠x = 85° (BD || CE) Alternate angles are equal

Question 5.
The correct statement out of the following is ……..

(a) ΔABC ≅ ΔDEF
(b) ΔABC ≅ ΔEDF
(c) ΔABC ≅ ΔFDE
(d) ΔABC ≅ ΔFED
Solution:
(d) ΔABC ≅ ΔFED

Question 6.
If the diagonal of a rhombus are equal, then the rhombus is a ……..
(a) Parallelogram but not a rectangle
(b) Rectangle but not a square
(c) Square
(d) Parallelogram but not a square
Solution:
(c) Square

Question 7.
If bisectors of ∠A and ∠B of a quadrilateral ABCD meet at O, then ∠AOB is ……..
(a) ∠C + ∠D
(b) \(\frac{1}{2}\) (∠C + ∠D)
(c) \(\frac{1}{2}\) ∠C + \(\frac{1}{3}\) ∠D
(d) \(\frac{1}{3}\) ∠C + \(\frac{1}{2}\) ∠D
Solution:
(b) \(\frac{1}{2}\) (∠C + ∠D)

Question 8.
The interior angle made by the side in a parallelogram is 90° then the parallelogram is a …….
(a) rhombus
(b) rectangle
(c) trapezium
(d) kite
Solution:
(b) rectangle
Hint:
Opposite sides are equal and each angle is 90° then it is a rectangle.

Question 9.
Which of the following statement is correct?
(a) Opposite angles of a parallelogram are not equal
(b) Adjacent angles of a parallelogram are complementary.
(c) Diagonals of a parallelogram are always equal.
(d) Both pairs of opposite sides of a parallelogram are always equal.
Solution:
(d) Both pairs of opposite sides of a parallelogram are always equal.

Question 10.
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is ………
(a) 40°
(b) 35°
(c) 50°
(d) 45°
Solution:
(b) 35°
Hint:
3x – 40 + x + 20 + 2x – 10 = 180° (Sum of the angles of a triangle is 180°)
6x – 30 = 180°
6x = 180°+ 30°
x = \(\frac{210°}{6°}\)
= 35°

Question 11.
PQ and RS are two equal chords of a circle with centre O such that ∠POQ = 70°, then ∠ORS = ……….
(a) 60°
(b) 70°
(c) 55°
(d) 80°
Solution:
(c) 55°
Hint:

∠POQ = 70° (Vertically opposite Angle)
∠ORS and ∠OSR are equal. (OR = OS radius of the circle)
∠ORS + ∠OSR + ∠ROS = 180°
x° + x° + 70° = 180°
2x + 70° = 180°
2x = 180° – 70° = 110°
x = \(\frac{110°}{2}\) = 55°
∴ ∠ORS = 55°

Question 12.
A chord is at a distance of 15cm from the centre of the circle of radius 25cm. The length of the chord is ……….
(a) 25cm
(b) 20cm
(c) 40cm
(d) 18cm
Solution:
(c) 40cm
Hint:

In the right triangle OAC,
AC² = OA² – OC²
= 25² – 15²
= (25 + 15) (25 – 15)
= 40 × 10
AC² = 400
AC = \(\sqrt{400}\)
= 20
Length of the chord AB = 20 + 20 = 40 cm.

Question 13.
In the figure, O is the centre of the circle and ∠ACB = 40° then ∠AOB = ………

(a) 80°
(b) 85°
(c) 70°
(d) 65°
Solution:
(a) 80°
Hint:
∠AOB = 2∠ACB (The angle subtended by an arc of the circle at the centre is double the angle subtended at the remaining part of the circle.)
= 2 × 40° = 80°

Question 14.
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is ……..
(a) 30°
(b) 20°
(c) 15°
(d) 25
Solution:
(a) 30°
Hint:

∠A + ∠C = 180° (Sum of the opposite angle of cyclic quadrilateral is 180°)
4x + 2x = 180°
x = \(\frac{180°}{6}\)
= 30°

Question 15.
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4cm. The radius of the circle is ………

(a) 8cm
(b) 4cm
(c) 6cm
(d) 10cm
Solution:
(i) 10cm
Hint:

Let the radius OD be x.
OE = OB – BE
= x – 4 (OB radius of the circle)
In the ΔOED,
OD² = OE² + ED²
x² = (x – 4)² + 8²
x² = x² + 16 – 8x + 64
8x = 80
x = \(\frac{80}{8}\)
= 10 cm
Radius of the circle = 10 cm.

Question 16.
In the figure, PQRS and PTVS are two cyclic quadrilaterals, If ∠QRS = 80°, then ∠TVS = ………

(a) 80°
(b) 100°
(c) 70°
(d) 90°
Solution:
(a) 80°
Hint:
∠SPQ = 180° – 80° (Opposite angles of a cyclic quadrilateral PQRS)
= 100°
In the cyclic quadrilateral PVTS,
∠V = 180° – 100° = 80° (Opposite angles of a cyclic quadrilateral)

Question 17.
If one angle of a cyclic quadrilateral is 75°, then the opposite angle is ………
(a) 100°
(b) 105°
(c) 85°
(d) 90°
Solution:
(b) 105°
Hint:
Opposite angles = 180° – 75°
= 105° (Sum of the opposite angle is 180°)

Question 18.
In the figure, ABCD is a cyclic quadrilateral in which DC produced to E and CF is drawn parallel to AB such that ∠ADC = 80° and ∠ECF = 20°, then BAD = ?

(a) 100°
(b) 20°
(c) 120°
(d) 110°
Solution:
(c) 120°
Hint:
∠BAD = ∠ABC + ∠ECF (By exterior angle property)
= 100° + 20°
= 120°

Question 19.
AD is a diameter of a circle and AB is a chord If AD = 30cm and AB = 24cm then the distance of AB from the centre of the circle is ………
(a) 10cm
(b) 9cm
(c) 8cm
(d) 6cm
Solution:
(b) 9cm
Hint:

In ΔAOC,
AO = 15 cm
AC = \(\frac{1}{2}\) AB
= \(\frac{1}{2}\) × 24
= 12 cm
In ΔAOC,
OC² = AO² – AC²
= 15² – 12²
= 225 – 144
= 81
OC = \(\sqrt{81}\)
= 9 cm

Question 20.
In the given figure, If OP = 17cm, PQ = 30cm and OS is perpendicular to PQ, then RS is ……….

(a) 10cm
(b) 6cm
(c) 7cm
(d) 9cm
Solution:
(d) 9cm
Hint:
In ΔOPR, OP = 17cm, PR = 30/2 = 15 cm.
OR² = OP² – PR²
= 17² – 15²
= (17 + 15) (17 – 15)
= 32 × 2
OR² = \(\sqrt{64}\)
= 8 cm
RS = OS – OR
= 17 – 8
= 9 cm

Students can download Maths Chapter 4 Geometry Ex 4.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.6

Question 1.
Draw a triangle ABC, where AB = 8 cm, BC = 6 cm and ∠B = 70° and locate its circumcentre and draw the circumcircle.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with the given measures.
Step 2: Construct the perpendicular bisector of (AB and BC) any two sides and let them, meet at S which is the circumcenter.
Step 3: With S as centre and SA = SB = SC as radius draw the circumcircle to passes through A, B and C.
Circum radius = 4.3 cm.

Question 2.
Construct the right triangle PQR whose perpendicular sides are 4.5 cm and 6 cm. Also locate its circumcentre and draw circumcircle.
Solution:

Steps for construction:
Step 1: Draw the ΔPQR with the given measures.
Step 2: Construct the perpendicular bisector of (PQ and PR) any two sides and let them meet at S which is the circumcenter.
Step 3: With S as centre and SP = SQ = SR as radius draw the circumcircle to passes through P, Q and R.
Circum radius = 3.8 cm.

Question 3.
Construct ΔABC with AB = 5 cm ∠B = 100° and BC = 6 cm. Also locate its circumcentre draw circumcircle.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with the given measures.
Step 2: Construct the perpendicular bisector of any two sides (AB and BC) and let them meet at S which is the circumcenter.
Step 3: With S as centre and SA = SB = SC as radius draw the circumcircle to passes through A, B and C.
Circum radius = 4.3 cm.

Question 4.
Construct an isosceles triangle PQR where PQ = PR and ∠Q = 50°, QR = 7cm. Also draw its circumcircle.
Solution:

Given PQ = PR
∴ ∠R = 50° (opposite angles are equal)
Steps for construction:
Step 1: Draw the ΔABC with the given measures.
Step 2: Construct the perpendicular bisector of any two sides (QR and PR) and let them meet at S. S is the circumcenter of ΔPQR.
Step 3: With S as centre SP = SQ = SR as radius. Draw the circumcircle.
Circum radius = 3.5 cm.

Question 5.
Draw an equilateral triangle of side 6.5 cm and locate its incentre. Also draw the incircle.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with the each side measure 6.5 cm.
Step 2: Construct the angles bisectors of any two angles (A and B) and let them meet at I. Then I is the incentre of ΔABC.
Step 3: Draw perpendicular from I to any one of the side (AB) to meet AB at D.
Step 4: With I as centre and ID as radius draw the circle. This circle touches all the sides of the triangle internally.
Step 5: Measure of In-radius = 1.5 cm.

Question 6.
Draw a right triangle whose hypotenuse is 10 cm and one of the legs is 8 cm. Locate its incentre and also draw the incircle
Solution:

Steps for construction:
Step 1: Draw the ΔABC with AB = 8cm, BC = 10 cm and ∠A = 90°.
Step 2: Construct the angle bisectors of any two angles (∠B and ∠C) and let them meet at I. Then I is the incentre of ΔABC.
Step 3: Draw perpendicular from I to any one of the side to meet AB at D.
Step 4: With I as centre and ID as radius draw the circle. This circle touches all the sides of the triangle internally.
Step 5: Measure of In-radius = 1.8 cm.

Question 7.
Draw ΔABC given AB = 9 cm, ∠CAB = 115° and ∠ABC = 40°. Locate its incentre and also draw the incircle. (Note: You can check from the above examples that the incentre of any triangle is always in its interior).
Solution:

Step 1: Draw the ΔABC with AB = 9cm, ∠B = 40° and ∠A = 115°.
Step 2: Construct the angle bisectors of any two angles (A and B) and let them meet at I. Then I is the incentre of ΔABC.
Step 3: Draw perpendicular from I to any one of the side (AB) to meet AB at D.
Step 4: With I as centre and ID as radius draw the circle. This circle touches all the sides of the triangle internally.
Step 5: Measure of In-radius = 2.7 cm.

Question 8.
Construct ΔABC in which AB = BC = 6cm and ∠B = 80°. Locate its incentre and draw the incircle.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with AB = 6 cm, ∠B = 80° and BC = 6 cm.
Step 2: Construct the angle bisectors of any two angles (A and B) and let them meet at I. Then I is the incentre of ΔABC.
Step 3: Draw perpendicular from I to any one of the side (AB) to meet AB at D.
Step 4: With I as centre and ID as radius draw the circle. This circle touches all the sides of the triangle internally.
Step 5: Measure of In-radius = 1.9 cm.

Students can download Maths Chapter 4 Geometry Ex 4.5 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.5

Question 1.
Construct the ΔLMN such that LM = 7.5 cm, MN = 5cm and LN = 8cm. Locate its centroid.
Solution:

Steps for construction:
Step 1: Draw the ΔLMN using the given measurement LM = 7.5 cm, MN = 5cm and LN = 8cm.
Step 2: Construct the perpendicular bisectors of any two sides LM and MN intersect LM at P and MN at Q respectively.
Step 3: Draw the median LQ and PN meet at G.
The point G is the centroid of the given ΔLMN.

Question 2.
Draw and locate the centroid of the triangle ABC where right angle at A, AB = 4cm and AC = 3 cm.
Solution:

Steps for construction:
Step 1: Draw the ΔABC using the given measurement AB = 4cm and AC = 3 cm and ZA = 90°.
Step 2: Construct the perpendicular bisectors of any two sides AB and AC to find the mid-points P and Q of AB and AC.
Step 3: Draw the medians PC and BQ intersect at G.
The point G is the centroid of the given ΔABC.

Question 3.
Draw the ΔABC, where AB = 6cm, ∠B = 110° and AC = 9cm and construct the centroid.
Solution:

Steps for construction:
Step 1: Draw the ΔABC using the given measurement AB = 6cm, AC = 9cm and ∠B =110°.
Step 2: Construct the perpendicular bisectors of any two sides AB and BC to find the mid-points P and Q of AB and BC.
Step 3: Draw the medians PC and AQ intersect at G.
The point G is the centroid of the given ΔABC.

Question 4.
Construct the ΔPQR such that PQ = 5cm, PR = 6cm and ∠QPR = 60° and locate its centroid.
Solution:

Steps for construction:
Step 1 : Draw ΔPQR using the given measurements PQ = 5cm, PR = 6cm and ∠P = 60°.
Step 2 : Construct the perpendicular bisectors of any two sides PQ and QR to find the mid-points of M and N respectively.
Step 3 : Draw the median PN and MR and let them meet at G.
The point G is the centroid of the given ΔPQR.

Question 5.
Draw ΔPQR with sides PQ = 7 cm, QR = 8 cm and PR = 5 cm and construct its Orthocentre.
Solution:

Steps for construction:
Step 1: Draw the ΔPQR with the given measurements.
Step 2: Construct altitudes from any two vertices P and Q to their opposite sides QR and PR respectively.
Step 3: The point of intersection of the altitude H is the orthocentre of the given ΔPQR.

Question 6.
Draw an equilateral triangle of sides 6.5 cm and locate its Orthocentre.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with the given measurements.
Step 2: Construct altitudes from any two vertices A and C to their opposite sides BC and AB respectively.
Step 3: The point of intersection of the altitude H is the orthocentre of the given ΔABC.

Question 7.
Draw ΔABC, where AB = 6 cm, ∠B = 110° and BC = 5 cm and construct its Orthocentre.
Solution:

Steps for construction:
Step 1: Draw the ΔABC with the given measurements.
Step 2: Construct altitudes from any two vertices B and C to their opposite sides AC and BC respectively.
Step 3: The point of intersection of the altitude H is the orthocentre of the given ΔABC.

Question 8.
Draw and locate the Orthocentre of a right triangle PQR where PQ = 4.5 cm, QR = 6 cm and PR = 7.5 cm.
Solution:

Steps for construction:
Step 1: Draw the ΔPQR with the given measures.
Step 2: Construct altitude from any two vertices Q and R to their opposite side PR and PQ respectively.
Step 3: The point of intersection of the altitude H is the orthocentre of the given ΔPQR.

Students can download Maths Chapter 4 Geometry Ex 4.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.4

Question 1.
Find the value of x in the given figure.

Solution:
∠B = 180° – 120°
(Sum of the opposite angles of a quadrilateral are supplementary)
∠B = 60°
∠BCA = 90° (Angle in a semicircle)
∠BAC + ∠B + ∠BCA = 180°
x + 60° + 90° = 180°
x + 150° = 180°
x = 180° – 150°
= 30°
The value of x = 30°

Question 2.
In the given figure, AC is the diameter of the circle with centre O.

If ∠ADE = 30°; ∠DAC = 35° and ∠CAB = 40°.
Find (i) ∠ACD
(ii) ∠ACB
(iii) ∠DAE
Solution:
(i) ∠ADC = 90° (Angle in a semi-circle)
∠ADC + ∠ACD + ∠DAC = 180° (Sum of the angles of a triangle is 180°)
90° + ∠ACD + 35° = 180°
∠ACD = 180° – 125°
∠ACD = 55°

(ii) ∠ABC = 90° (Angle in a semi-circle)
∠ACB + ∠CBA + ∠BAC = 180° (Sum of the angles of a triangle is 180°)
∠ACB + 90 °+ 40° = 180°
∠ACB = 180° – 130°
= 50°

(iii) In the cyclic quadrilateral ACDE,
∠AED = 180° – 55°
= 125°
In ΔAED,
∠DAE + ∠AED + ∠EDA = 180° (Sum of the angles of a triangle is 180°)
∠DAE + 125° + 30° = 180°
∠DAE = 180°- 155°
= 25°
∴ ∠DAE = 25°

Question 3.
Find all the angles of the given cyclic quadrilateral ABCD in the figure.

Solution:
In a cyclic quadrilateral ABCD,
∠B + ∠D = 180° (Sum of the opposite angles of a cyclic quadrilateral is 180°)
6x – 4° + 7x + 2° = 180°
13x – 2° = 180°
13x = 182°
x = 182°
x = \(\frac{182°}{13}\)
x = 14°
∠B = 6x – 4°
= 6(14) – 4°
= 84 – 4
= 80°
∠D = 7x + 2°
7(14) + 2°
98 + 2
= 100°
180°
2y + 4° + 4y – 4° = (Sum of the opposite angles of a cyclic quadrilateral is 180°)
6y = 180°
y = \(\frac{180°}{6}\)
= 30°
∠A = 2y + 4°
= 2(30) + 4°
= 64°
∠C = 4y – 4°
= 4(30) – 4°
= 120° – 4°
= 116°
∴ ∠A = 64°, ∠B = 80°, ∠C = 116°, ∠D = 100°.

Question 4.
In the given figure, ABCD is a cyclic quadrilateral where diagonals intersect at P such that ∠DBC = 40° and ∠BAC = 60° find

(i) ∠CAD
(ii) ∠BCD
Solution:
(i) ∠CAD = ∠DBC = 40° [Angles at the circumference to the same segment]
(ii) ∠BAC – ∠BDC = 60° [Angles at the circumference to the same segment]
∠BCD + ∠BDC + ∠CBD = 180° (Sum of the three angles of A is 180°)
∠BCD + 60° + 40° = 180°
∠BCD = 180° – 100°
= 80°

Question 5.
In the given figure, AB and CD are the parallel chords of a circle with centre O. Such that AB = 8 cm and CD = 6 cm. If OM ⊥ AB and OL ⊥ CD distance between LM is 7cm. Find the radius of the circle?

Solution:
Let OM be x.
∴ OL = 7 – x
In the right ΔAOM,
OA² = AM² + OM²
= 4² + x²
OA² = 16 + x²
r² = 16 + x² ……… (1) [r is the radius]
In the right ΔOCL,
OC² = OL² + CL²
r² = (7 – x)² + 3²
= 49 + x² – 14x + 9
= 58 + x² – 14x …….. (2)
From (1) and (2) we get,
16 + x² = 58 + x² – 14x
14x = 58 – 16
14x = 42
x = \(\frac{42}{14}\)
x = 3 cm
r² = 16 + x²
= 16 + 9
= 25
∴ r = \(\sqrt{25}\)
= 5
∴ radius of the circle = 5 cm.

Question 6.
The arch of a bridge has dimensions as shown, where the arch measure 2 m at its highest point and its width is 6 cm. What is the radius of the circle that contains the arch?

Solution:
AD = \(\frac{6}{2}\)
= 3 m
In the right ΔADC,

AC² = AD² + DC²
= 32 + 22
= 9 + 4
= 13
AC = \(\sqrt{13}\)
= 3.6m
radius = 3.6 m

Question 7.
In figure ∠ABC = 120°, where A, B and C are points on the circle with centre O. Find ∠OAC?

Solution:
Reflex ∠AOC = 2∠ABC
= 20 × 120°
= 240°
∴ ∠AOC = 360° – 240°
= 120°
∠OCA + ∠OAC = 180° – 120°
= 60°
∴ ∠OAC = \(\frac{60}{2}\)
= 30° (Since OA = OC)

Question 8.
A school wants to conduct tree plantation programme. For this a teacher allotted a circle of radius 6m ground to nineth standard students for planting sapplings. Four students plant trees at the points A, B, C and D as shown in figure. Here AB = 8m, CD = 10m and AB ⊥ CD. If another student places a flower pot at the point P, the intersection of AB and CD, then find the distance from the centre to P.

Solution:
OA = OD = 6 m
AB = 8 m (chord)
CD = 10 m (chord)
In Δ AOM, OM = \(\sqrt{6² – 4²}\) (∴ OM bisects the chord and ⊥ to the chord)
= \(\sqrt{36 – 16}\)
= \(\sqrt{20}\)m
In Δ CON, ON = \(\sqrt{6² – 5²}\)
= \(\sqrt{36 – 25}\)
= \(\sqrt{11}\)m (ON bisects the chord and ⊥ to the chord)
ONPM is a rectangle with all the angles 90° and with length \(\sqrt{20}\) m, breadth \(\sqrt{11}\)l m.
We need to find OP which is the diagonal of the rectangle ONPM.
∴ OP = \(\sqrt{ON² + NP²}\) = \(\sqrt{(\sqrt{11})² + (\sqrt{20})²}\)
(∴ OM = NP, opposite sides of the rectangle)
= \(\sqrt{11 + 20}\)
= \(\sqrt{31}\)
= 5.56 m

Question 9.
In the given figure, ∠POQ = 100° and ∠PQR° = 30°, then find ∠RPO.

Solution:
∠PRQ = \(\frac{1}{2}\) ∠POQ (Angles at the circumference)
= \(\frac{1}{2}\) × 100°
= 50°
∠OPQ + ∠OQP = 180° – 100° (Total angles of A is 180°)
= 80°
∴ ∠OPQ = \(\frac{80}{2}\)
= 40° (Since OP = OQ, radius of the circle)
∠RPQ = 180°- (30 + 50)°
= 100°
∴ ∠RPO = ∠RPQ – ∠OPQ
= 100° – 40°
= 60°

Students can download Maths Chapter 4 Geometry Ex 4.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.3

Question 1.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre.
Radius of a circle = \(\frac{56}{2}\) = 26 cm
Solution:

Length of the chord = 20 cm
AC = \(\frac{20}{2}\)
= 10 cm
In ΔOAC, OC² = OA² – AC²
= 26² – 10²
= (26 + 10) (26 – 10)
= 36 × 16
OC = \(\sqrt{30×16}\)
= 6 × 4 cm
= 24 cm
Distance of the chord from the centre = 24 cm.

Question 2.
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle.
Solution:

Distance AC = \(\frac{1}{2}\) × Length of chord
= \(\frac{1}{2}\) × 30
= 15 cm
Distance from the centre = 8 cm
In ΔOAC Radius (OA) = \(\sqrt{AC² + OC²}\)
= \(\sqrt{15² + 8²}\)
= \(\sqrt{224 + 64}\)
= \(\sqrt{289}\)
= 17
Radius of the circle = 17 cm.

Question 3.
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius 4√2 cm and also find ∠OAC and ∠OCA.
Solution:
Radius of a circle = 4√2 cm
In the right ΔAOC,

AC² = OA² + OC²
AC² = (4√2)² + (4√2)²
= 32 + 32 = 64
AC = \(\sqrt{64}\)
= 8
Length of the chord = 8 cm,
∠OAC = ∠OCA = 45°
Since OAC is an isosceles right angle triangle.

Question 4.
A chord is 12 cm away from the centre of the circle of radius 15cm. Find the length of the chord.
Solution:
Radius of a circle (OA) = 15 cm
Distance from centre to the chord (OC) = 12 cm
In the right ΔOAC,

AC² = OA² – OC²
= 15² – 12²
= 225 – 144
= 81
AC = \(\sqrt{81}\)
= 9
Length of the chord (AB) = AC + CB
= 9 + 9 = 18 cm.

Question 5.
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
Solution:
Length of the chord (AB) = 16 cm
∴ AF = \(\frac{1}{2}\) × 16
= 8 cm
Length of the chord (CD) = 12 cm
∴ CE = \(\frac{1}{2}\) × 12
= 6 cm

In the right ΔOCE,
OE² = OC² – CE²
= 10² – 6²
= 100 – 36
= 64
OE = \(\sqrt{64}\)
= 8 cm
In the right ΔOAF,
OF² = OA² – AF²
= 10² – 8²
= 100 – 64
= 36
OE = \(\sqrt{36}\)
= 6 cm
Distance between the two chords = OE + OF
= 8 + 6
= 14 cm.

Question 6.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Ans

Two circules intersect at C and D
CD is the common chord.
CD = AC + AD
= 3 + 3
= 6 cm
Length of the common chord = 6 cm.

Question 7.
Find the value of x° in the following figures:

Solution:
(i) ∠BOC = 30° + 60°
= 90°
∠BAC (x) = \(\frac{1}{2}\) ∠BOC (By theorem)
= \(\frac{1}{2}\) × 90°
x = 45°

(ii) Join OP
∠QPR = \(\frac{80}{2}\) = 40° (Angle of the circumference is \(\frac{1}{2}\) the angle at the centre)
∠RPO = 30° (OP and OR are equal sides)
∠OPQ = 40° – 30°
= 10°
∠OQP = 10° (OQ and OP are equal sides)
∴ x = 10°

(iii) ∠OPN = ∠ONP (ON and OP are the radius of the circle)
= 90°
In ΔOPN
∠PON + ∠ONP + ∠NPO = 180° (Sum of the angles of a triangle)
70° + x° + x° = 180°
2x° + 70° = 180°
2x = 180° – 70°
2x = 110°
X = \(\frac{110°}{2}\)
= 55°
The value of x = 55°

(iv) Reflex ∠YOZ = 2∠YXZ
= 2(120°)
= 240°
∠YOZ = 360° – reflex ∠YOZ
= 360° – 240°
= 120°
∴ x = 120°

(v) ∠OAC + ∠OCA = 180° – 100°
= 80°
∠OAC = \(\frac{1}{2}\) × 80° [Since OA = OC, (∴ ∠OAC = ∠OCA)]
= 40°
∠OBA + ∠OAB = 180° – 140°
= 40° [Since ∠OBA = ∠OAB, since OB = OA]
∴∠OAB = \(\frac{40°}{2}\)
= 20°
∠BAC = ∠OAB + ∠OAC
= 20° + 40°
x = 60°

Question 8.
In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB.

Solution:
In ΔACP,
∠ACP = 180° – (25° + 90°)
= 180° – 115°
= 65°
∠CBA = ∠CAB = 25° [Both the angles are standing in the same base]
∠DBA = 65° [∠DBA and ∠BCA standing in the same base]
∠COB = 50°

Students can download Maths Chapter 5 Coordinate Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Additional Questions

I. Multiple Choice Questions.

Question 1.
On which quadrant does the point (- 4, 3) lie?
(a) I
(b) II
(c) III
(d) IV
Solution:
(b) II

Question 2.
The point whose abscissa is 5 and lies on the x-axis is …….
(a) (-5, 0)
(b) (5, 5)
(c) (0, 5)
(d) (5, 0)
Solution:
(d) (5, 0)

Question 3.
A point which lies in the III quadrant is ……..
(a) (5, 4)
(b) (5, -4)
(c) (-5, -4)
(d) (-5, 4)
Solution:
(c) (-5, -4)

Question 4.
A point on the y-axis is ……..
(a) (1, 1)
(b) (6, 0)
(c) (0, 6)
(d) (-1, -1)
Solution:
(c) (0, 6)

Question 5.
The distance between the points (4, -1) and the origin is ……..
(a) \(\sqrt{24}\)
(b) \(\sqrt{37}\)
(c) \(\sqrt{26}\)
(d) \(\sqrt{17}\)
Solution:
(d) \(\sqrt{17}\)

Question 6.
The distance between the points (-1, 2) and (3, 2) is ……..
(a) \(\sqrt{14}\)
(b) \(\sqrt{15}\)
(c) 4
(d) 0
Solution:
(c) 4

Question 7.
The centre of a circle is (0, 0). One end point of a diameter is (5, -1), then the radius is …….
(a) \(\sqrt{24}\)
(b) \(\sqrt{37}\)
(c) \(\sqrt{26}\)
(d) \(\sqrt{17}\)
Solution:
(c) \(\sqrt{26}\)

Question 8.
The point (0, -3) lies on
(a) + ve x-axis
(b) + ve y-axis
(c) – ve x-axis
(d) – ve y-axis
Solution:
(d) – ve y-axis

Question 9.
The point which is on y-axis with ordinate -5 is ……..
(a) (0, -5)
(b) (-5, 0)
(c) (5, 0)
(d) (0, 5)
Solution:
(a) (0, -5)

Question 10.
The diagonal of a square formed by the points (1, 0), (0, 1), (-1, 0) and (0, -1) is …….
(a) 2
(b) 4
(c) √2
(d) 8
Solution:
(a) 2

Question 11.
The distance between the points (-2, 2) and (3, 2) is ……..
(a) 10 units
(b) 5 units
(c) 5√3 units
(d) 20 units
Solution:
(b) 5 units

Question 12.
The midpoint of the line joining the points (1, -1) and (-5, 3) is ……..
(a) (2, 1)
(b) (2, -1)
(c) (-2, -1)
(d) (-2, 1)
Solution:
(d) (-2, 1)

Question 13.
If the centroid of a triangle is at (1, 3) and two of its vertices are (-7, 6) and (8, 5) then the third vertex is ……..
(a) (-2, 2)
(b) (2, -2)
(c) (-2, -2)
(d) (2, 2)
Solution:
(b) (2, -2)

Question 14.
The ratio in which the X-axis divides the line segment joining the points (6, 4) and (1, -7) is ……..
(a) 1 : 2
(b) 2 : 3
(c) 4 : 7
(d) 7 : 4
Solution:
(c) 4 : 7

Question 15.
The centroid of a triangle (3, -5), (-7, 4) and (10, -2) is …….
(a) (2, -1)
(b) (2, 1)
(c) (-2, 1)
(d) (1, -2)
Solution:
(a) (2, -1)

II. Answer the Following Questions.

Question 1.
Show that the given points (1, 1), (5, 4), (-2, 5) are the vertices of an isosceles right angled triangle.
Solution:
Let A (1, 1), B (5, 4) and G (-2, 5)

AB = 5, AC = 5
∴ ABC is an isosceles triangle …….. (1)
BC² = AB² + AC²
50 = 25 + 25 ⇒ 50 = 50
∴ ∠A = 90° ……… (2)
From (1) and (2) we get ABC is an isosceles right angle triangle.

Question 2.
Show that the point (3, -2), (3, 2), (-1, 2) and (-1, -2) taken in order are the vertices of a square.
Solution:

= \(\sqrt{16}\)
= 4
AB = BC = CD = DA = 4. All the four sides are equal.
∴ ABCD is a Rhombus ……..(1)

Diagonal AC = Diagonal BD = \(\sqrt{32}\) ……..(2)
From (1) and (2) we get ABCD is a square.

Question 3.
Show that the point A (3, 7) B (6, 5) and C (15, -1) are collinear.
Solution:

AB + BC = AC ⇒ \(\sqrt{13}\) + 3\(\sqrt{13}\) = 4\(\sqrt{13}\)
∴ The points A, B, C are collinear.

Question 4.
Find the type of triangle formed by (-1, -1), (1, 1) and (-√, √3)
Solution:
Let the point A (-1, -1), B (1, 1) and C (-√3, √3)

AB = BC = AC = √8
∴ ABC is an equilateral triangle.

Question 5.
Find x such that PQ = QR where P(6, -1) Q(1, 3) and R(x, 8) respectively.
Solution:

But PQ = QR
\(\sqrt{(x-1)^{2}+25}\) = \(\sqrt{41}\)
Squaring on both sides
(x – 1)² + 25 = 41
(x – 1)² = 41 – 25 = 16
x – 1 = \(\sqrt{16}\) = ± 4
x – 1 = 4 (or) x – 1 = – 4
x = 5 (or) x = -4 + 1 = -3
The value of x = 5 or – 3

Question 6.
Find the coordinate of the point of trisection of the line segment joining (4, -1) and
Solution:
Let A (4, -1) and B (-2, -3) are the given points
Let P (a, b) and Q (c, d) be the points of trisection of AB.
∴ AP = PQ = QB

The required coordinate P is (2, –\(\frac{5}{3}\)) and Q is (0, –\(\frac{7}{3}\))

Question 7.
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
Solution:
Given points are A(-3, 10), B(6, -8) and P(-1, 6)
divides AB internally in the ratio m : n
By section formula.
A line divides internally in the ratio m : n the point P =

∴ \(\frac{6m-3n}{m+n}\) = -1
6m – 3n = -m – n
6m + m = 3n – n
7m = 2n ⇒ \(\frac{m}{n}\) = \(\frac{2}{7}\)
∴ m : n = 2 : 7
and
\(\frac{-8m+10n}{m+n}\) = 6
-8m + 10n = 6m + 6n
-8m – 6m = 6n – 10n
14m = 4n
∴ \(\frac{m}{n}\) = \(\frac{14}{4}\) = \(\frac{2}{7}\)
Hence P divides AB internally in the ratio 2 : 7

Question 8.
If (1, 2) (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find “x” and “y”.
Solution:
Let A(1, 2), B(4, y), C(x, 6) and D(3, 5)

Since ABCD is a parallelogram the diagonal bisect each other
Mid point of AC = Mid point of BD
(\(\frac{1+x}{2}\), 4) = (\(\frac{7}{2}\), \(\frac{y+5}{2}\))
\(\frac{1+x}{2}\) = \(\frac{7}{2}\)
1 + x = 7
x = 7 – 1
= 6
and
\(\frac{y+5}{2}\) = 4
y + 5 = 8
y = 8 – 5
= 3
∴ The value of x = 6 and y = 3

Students can download Maths Chapter 6 Trigonometry Ex 6.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.3

Question 1.
Find the value of the following:

(iii) tan 15° tan 30° tan 45° tan 60° tan 75°

Solution:
(i) cos 45° = \(\frac{1}{√2}\)

= 1² + 1² – 2(\(\frac{1}{√2}\))²
= 1 + 1 – 2(\(\frac{1}{2}\))
= 2 – 1
= 1

(ii) cos 60° = \(\frac{1}{2}\)

= 1 + 1 + 1 – 8(\(\frac{1}{2}\))²
= 3 – 8 × \(\frac{1}{4}\)
= 3 – 2
= 1

(iii) tan 30° = \(\frac{1}{√3}\), tan 45° = 1, tan 60° = √3
tan 15° . tan 30°. tan 45° . tan 60°. tan 75° = tan 15° . \(\frac{1}{√3}\) . 1 . √3 tan 75°
= tan 15° × tan 75° × \(\frac{1}{√3}\) × 1 × √3
= tan(90° – 75°) × \(\frac{1}{cot 75°}\) × 1 [tan 90° – θ = cot θ]
= cot 75° × \(\frac{1}{cot 75°}\) × 1
= 1

= 1 + 1
= 2