Category: Class 10

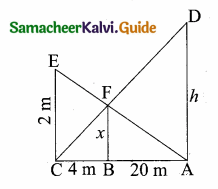
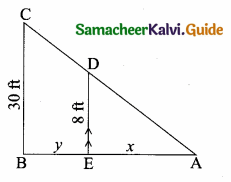
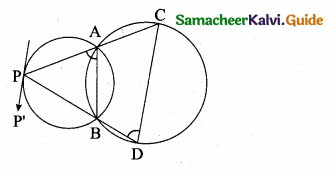
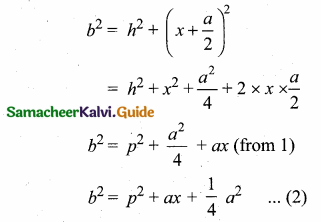Students can download Maths Chapter 5 Coordinate Geometry Ex 5.5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.5

Multiple Choice Questions

Question 1.
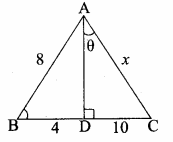
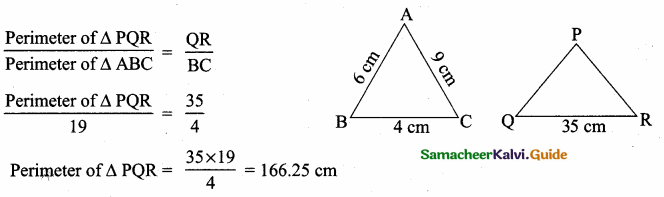
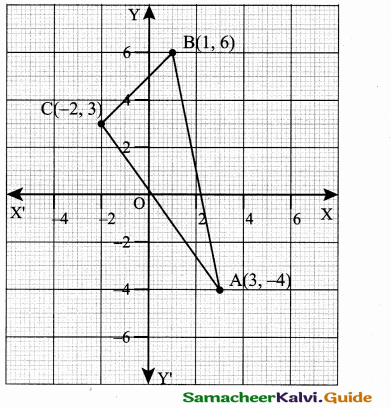
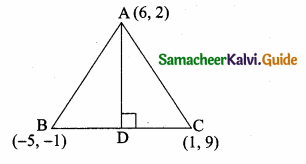
The area of triangle formed by the points (-5, 0), (0, – 5) and (5, 0) is …………..
(1) 0 sq.units
(2) 25 sq.units
(3) 5 sq.units
(4) none of these
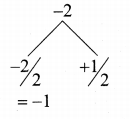
Answer:
(2) 25 sq.units Hint.
Hint:
Area of the ∆

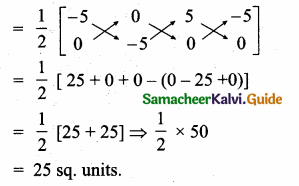
Question 2.
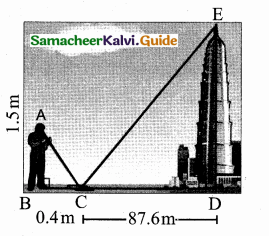
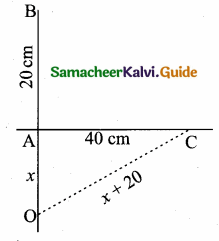
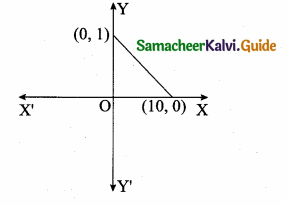
A man walks near a wall, such that the distance between him and the wall is 10 units. Consider the wall to be the Y axis. The path travelled by the man is …………
(1) x = 10
(2) y = 10
(3) x = 0
(4) y = 0
Answer:
(1) x = 10
Hint:

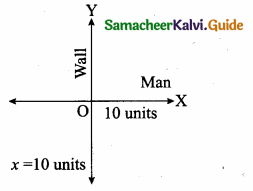
Question 3.
The straight line given by the equation x = 11 is …………….
(1) parallel to X axis
(2) parallel to Y axis
(3) passing through the origin
(4) passing through the point (0,11)
Answer:
(2) parallel to Y axis

Question 4.
If (5,7), (3,p) and (6,6) are collinear, then the value of p is ……………
(1) 3
(2) 6
(3) 9
(4) 12
Answer:
(3) 9
Hint:
Since the three points are collinear. Area of a triangle is 0

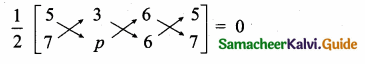
5p + 18 + 42 – (21 + 6p + 30) = 0
5p + 60 – (51 + 6p) = 0
5p + 60 – 51 – 6p = 0
-p + 9 = 0
-p = -9
p = 9

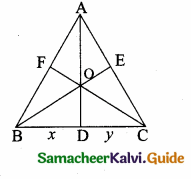
Question 5.
The point of intersection of 3x – y = 4 and x + 7 = 8 is ……………
(1) (5,3)
(2) (2,4)
(3) (3,5)
(4) (4, 4)
Answer:
(3) (3, 5)

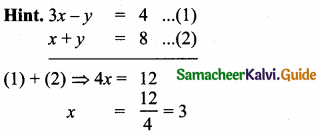
Substitute the value of x = 3 in (2)
3 + 7 = 8
y = 8 – 3 = 5
The point of intersection is (3, 5)

Question 6.
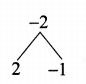
The slope of the line joining (12, 3), (4, a) is \(\frac { 1 }{ 8 } \). The value of ‘a’ is …………….
(1) 1
(2) 4
(3) -5
(4) 2
Answer:
(4) 2
Hint:
Slope of a line = \(\frac { 1 }{ 8 } \)

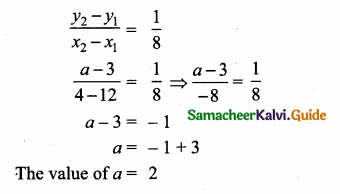
Question 7.
The slope of the line which is perpendicular to a line joining the points (0, 0) and (- 8, 8) is ………..
(1) -1
(2) 1
(3) \(\frac { 1 }{ 3 } \)
(4) -8
Answer:
(2) 1
Hint:
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac { 8-0 }{ -8-0 } \) = \(\frac { 8 }{ -8 } \) = -1
Slope of the Perpendicular = 1

Question 8.
If slope of the line PQ is \(\frac{1}{\sqrt{3}}\) then slope of the perpendicular bisector of PQ is …………..
(1) \(\sqrt { 3 }\)
(2) –\(\sqrt { 3 }\)
(3) \(\frac{1}{\sqrt{3}}\)
(4) 0
Answer:
(2) –\(\sqrt { 3 }\)
Hint:
Slope of a line = \(\frac{1}{\sqrt{3}}\)
Slope of the ⊥r bisector = –\(\sqrt { 3 }\)

Question 9.
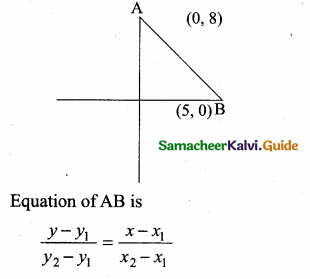
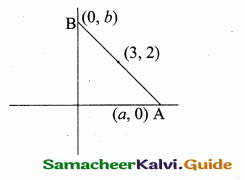
If A is a point on the Y axis whose ordinate is 8 and B is a point on the X axis whose abscissae is 5 then the equation of the line AB is ……………
(1) 8x + 5y = 40
(2) 8x – 5y = 40
(3) x = 8
(4) y = 5
Answer:
(1) 8x + 5y = 40
Hint:
Let the point A be (0, 8) and B (5, 0)

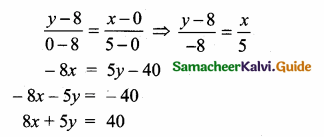
Question 10.
The equation of a line passing through the origin and perpendicular to the line lx -3y + 4 = 0 is
(1) 7x – 3y + 4 = 0
(2) 3x – 7y + 4 = 0
(3) 3x + 7y = 0
(4) 7x – 3y = 0
Answer:
(3) 3x + 7y = 0
Hint:
Slope of the line of 7x – 3y + 4 = 0
= \(\frac { -7 }{ -3 } \) = \(\frac { 7 }{ 3 } \)
Slope of its ⊥^r = \(\frac { -3 }{ 7 } \)
The line passes through (0,0)
Equation of a line is
y – y₁ = m(x – x₁)
y – 0 = \(\frac { -3 }{ 7 } \) (x – 0)
y = \(\frac { -3 }{ 7 } \) x ⇒ 7y = -3x
3x + 7y = 0

Question 11.
Consider four straight lines
(i) l₁ : 3y = 4x + 5
(ii) l₂ : 4y = 3x – 1
(iii) l₃ : 4y + 3x = 7
(iv) l₄ : 4x + 3y = 2
Which of the following statement is true?
(1) l₁ and l₂ are perpendicular
(2) l₂ and l₄ are parallel
(3) l₂ and l₄ are perpendicular
(4) l₂ and l₃ are parallel
Answer:
(3) l₂ and l₄ are perpendicular
Hint:
Slope of l₁ = \(\frac { 4 }{ 3 } \); Slope of l₂ = \(\frac { 3 }{ 4 } \)
Slope of l₃ = – \(\frac { 3 }{ 4 } \); Slope of l₄ = –\(\frac { 4 }{ 3 } \)
(1) l₁ × l₂ = \(\frac { 4 }{ 3 } \) × \(\frac { 3 }{ 4 } \) = 1 …….False
(2) l₁ = \(\frac { 4 }{ 3 } \); l₄ = – \(\frac { 4 }{ 3 } \) not parallel ………False
(3) l₂ × l₄ = \(\frac { 3 }{ 4 } \) × – \(\frac { 4 }{ 3 } \) = -1 …….True
(4) l₂ = \(\frac { 3 }{ 4 } \); l₃ = – \(\frac { 3 }{ 4 } \) not parallel ………False

Question 12.
A straight line has equation 87 = 4x + 21. Which of the following is true …………………….
(1) The slope is 0.5 and the y intercept is 2.6
(2) The slope is 5 and the y intercept is 1.6
(3) The slope is 0.5 and they intercept is 1.6
(4) The slope is 5 and the y intercept is 2.6
Answer:
(1) The slope is 0.5 and they intercept is 2.6
Hint:
8y = 4x + 21
y = \(\frac { 4 }{ 8 } \) x + \(\frac { 21 }{ 8 } \)
= \(\frac { 1 }{ 2 } \) x + \(\frac { 21 }{ 8 } \)
\(\frac { 1 }{ 2 } \) = 0.5
\(\frac { 21 }{ 8 } \) = 2.625
Slope = \(\frac { 1 }{ 2 } \) = 0.5
y intercept = \(\frac { 21 }{ 8 } \) = 2.6

Question 13.
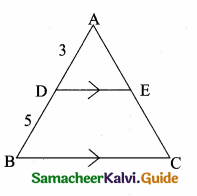
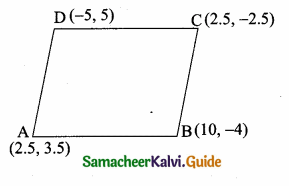
When proving that a quadrilateral is a trapezium, it is necessary to show
(1) Two sides are parallel.
(2) Two parallel and two non-parallel sides.
(3) Opposite sides are parallel.
(4) All sides are of equal length.
Solution:
(2) Two parallel and two non-parallel sides.

Question 14.
When proving that a quadrilateral is a parallelogram by using slopes you must find …………………
(1) The slopes of two sides
(2) The slopes of two pair of opposite sides
(3) The lengths of all sides
(4) Both the lengths and slopes of two sides
Answer:
(2) The slopes of two pair of opposite sides

Question 15.
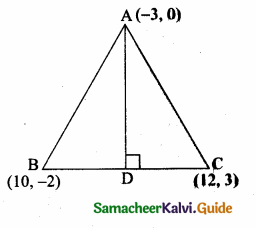
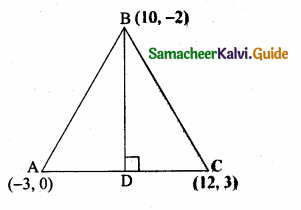
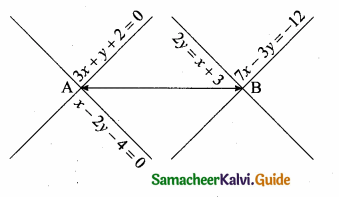
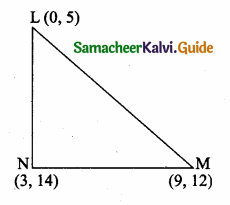
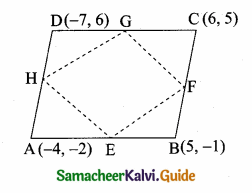
(2,1) is the point of intersection of two lines.
(1) x – y – 3 = 0; 3x – y – 7 = 0
(2) x + y = 3; 3x + y = 7
(3) 3x + y = 3; x + y = 7
(4) x + 3y – 3 = 0; x – y – 7 = 0
Solution:
(2) x + y = 3; 3x + y = 7

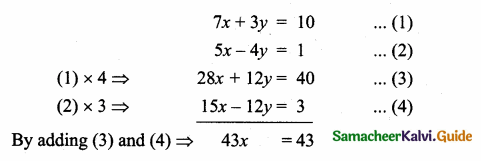
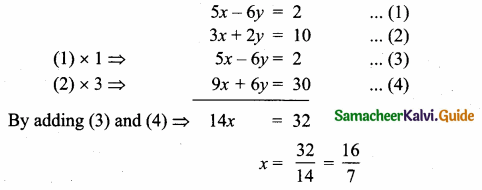
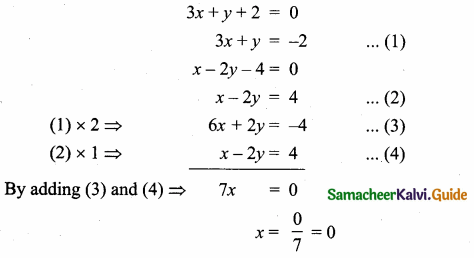
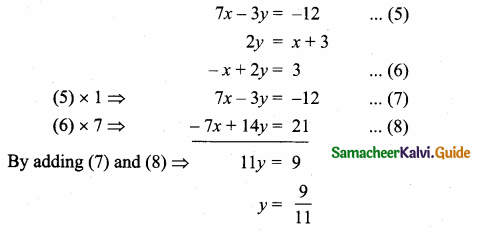
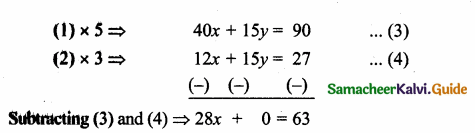
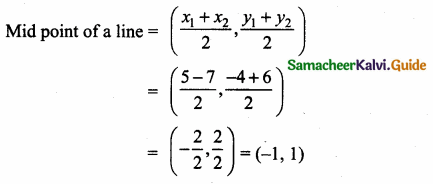
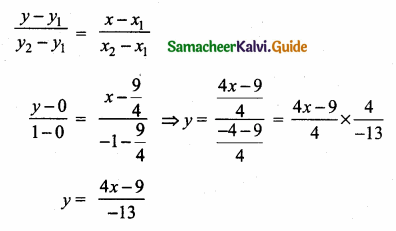
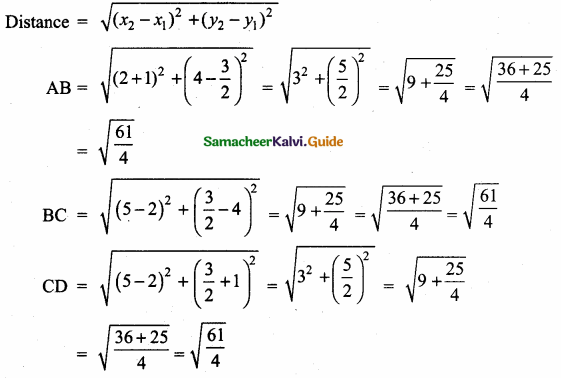
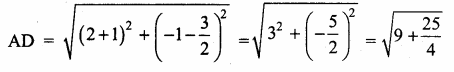
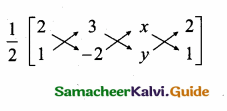
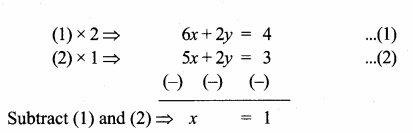
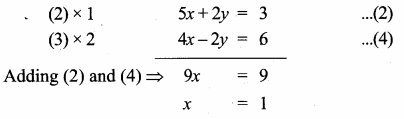
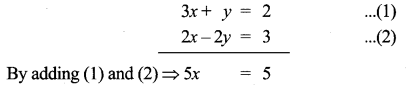
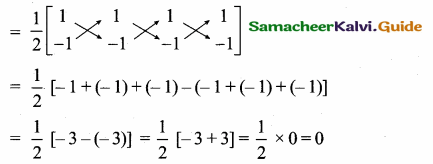
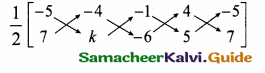
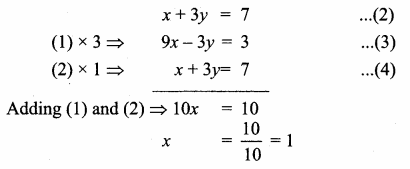
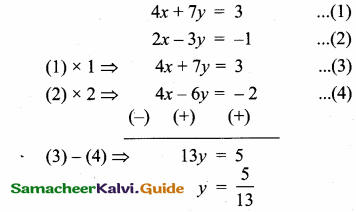
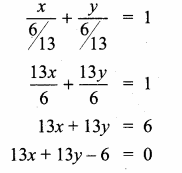
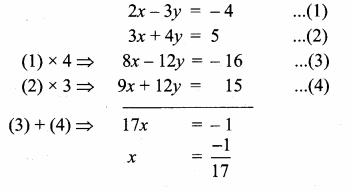
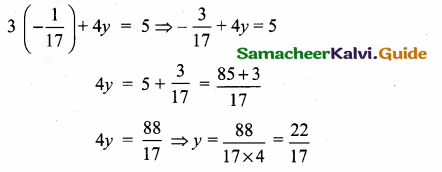
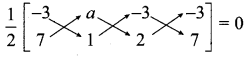
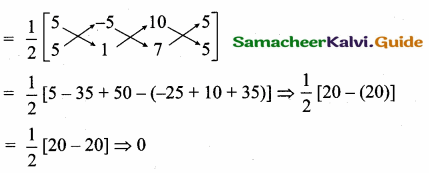
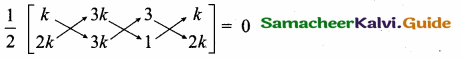
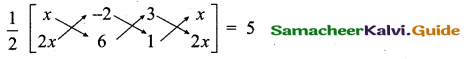
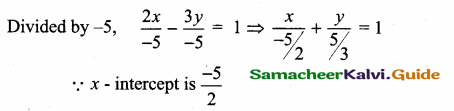
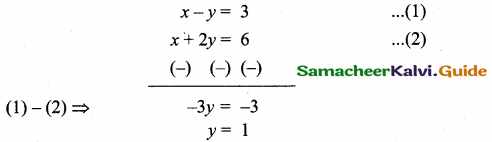
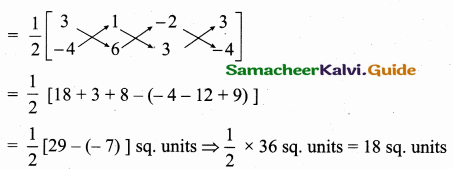
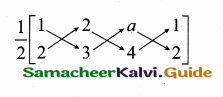
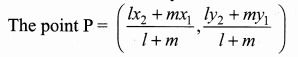
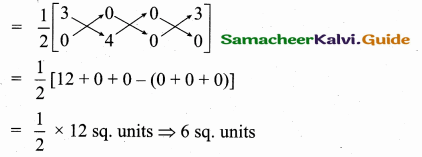
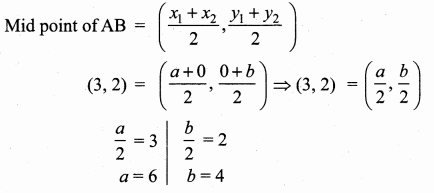
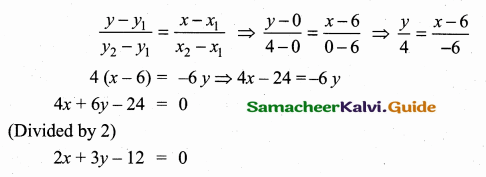
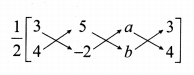
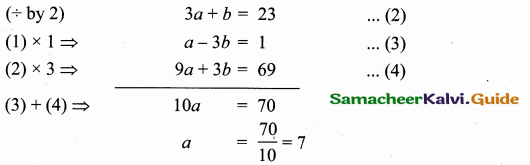
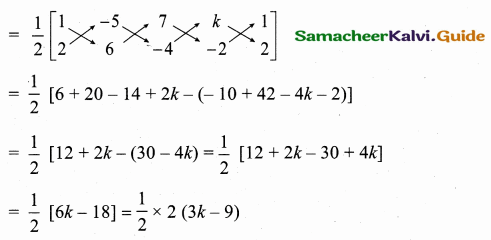
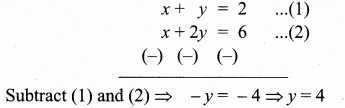
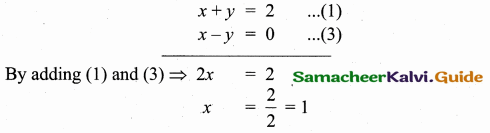
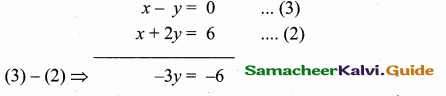
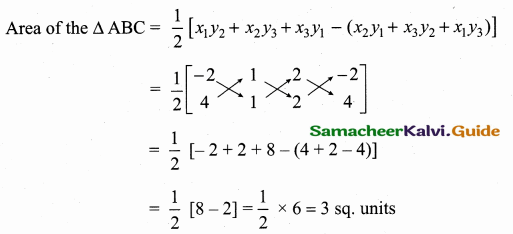
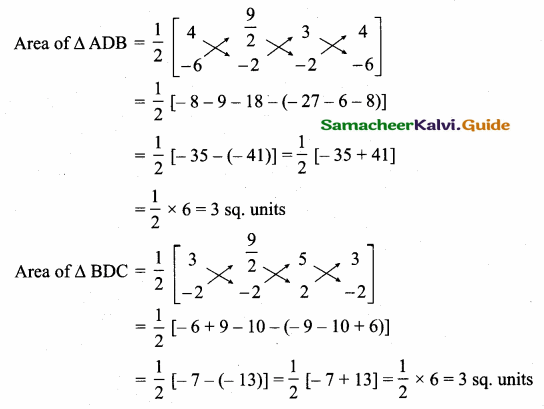
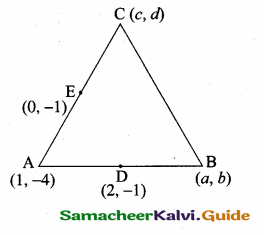
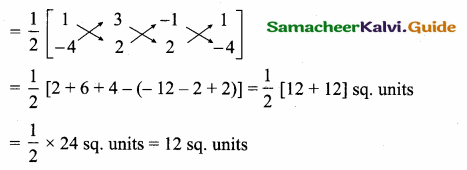
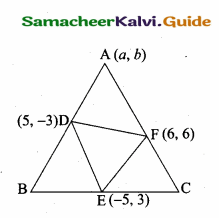
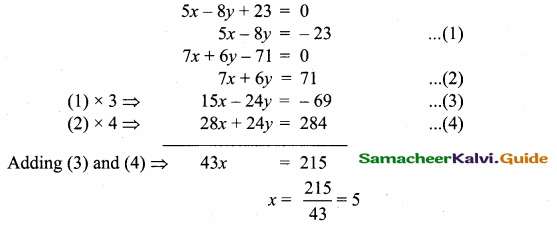
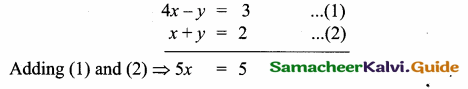
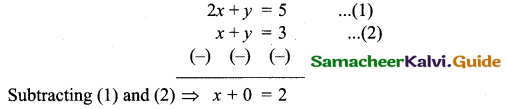
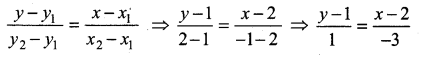
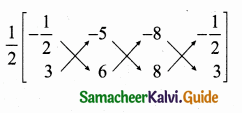
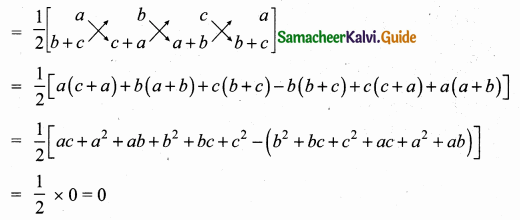
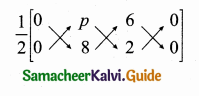
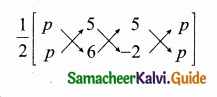
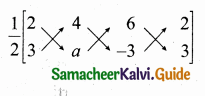
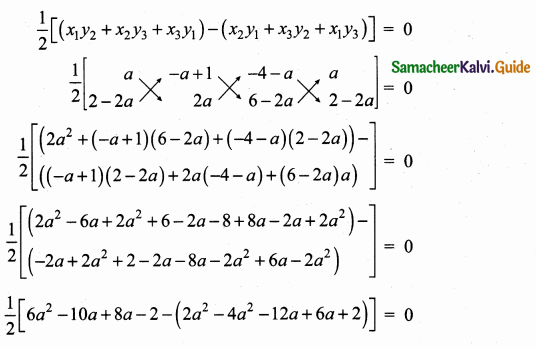
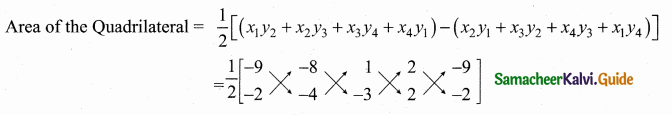
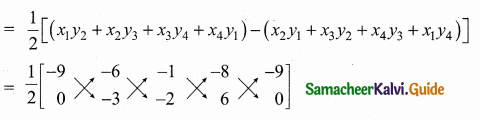
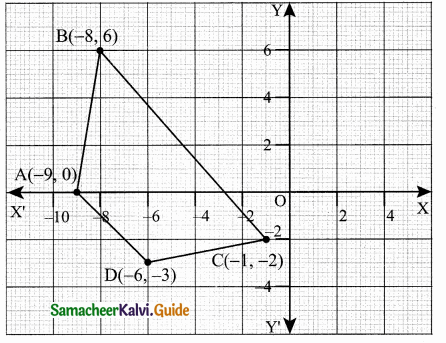
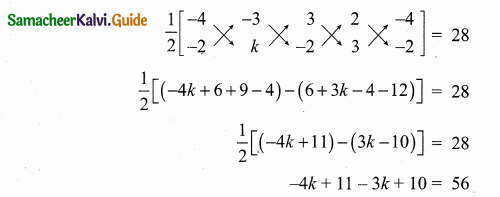
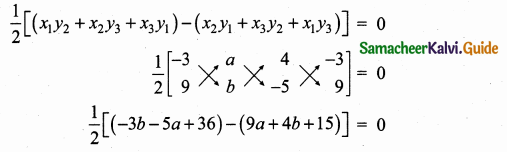
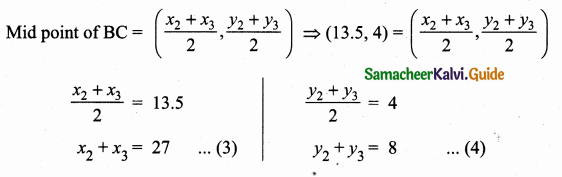
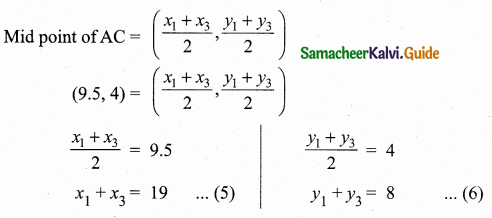
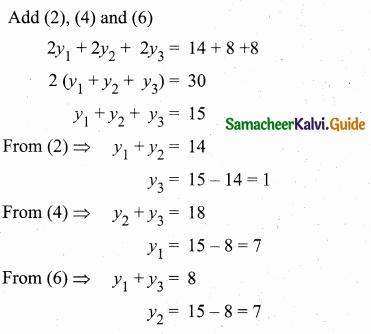
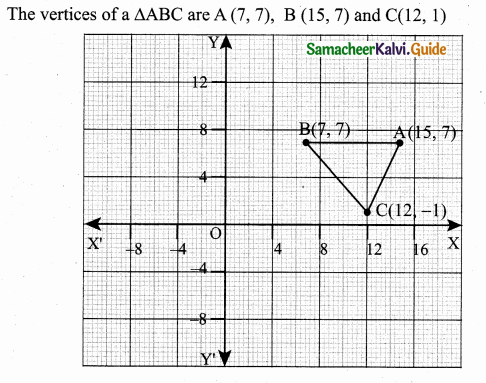
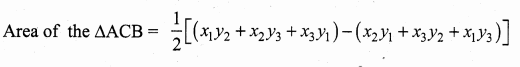
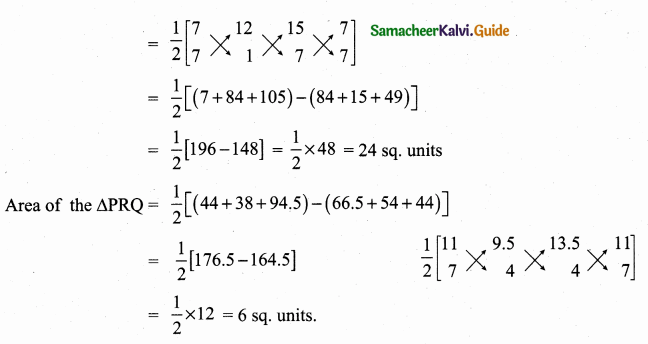
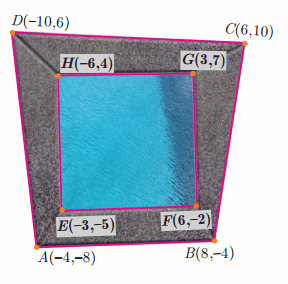
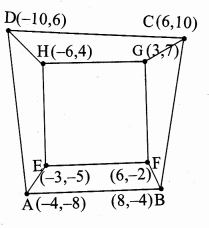
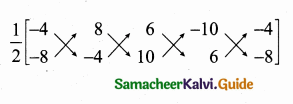
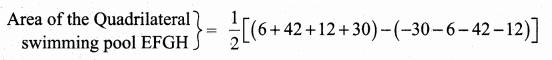
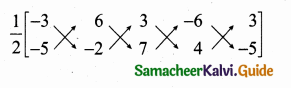
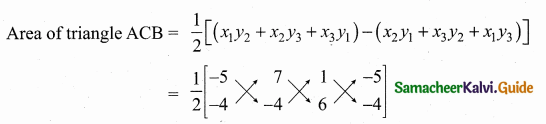
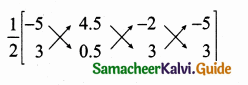
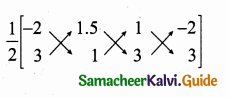
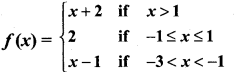
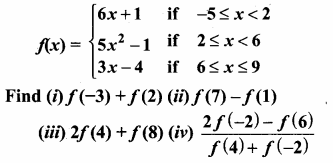
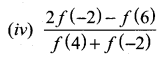
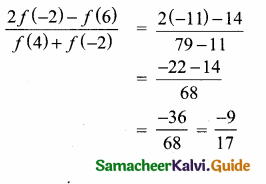
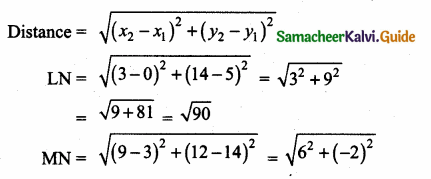
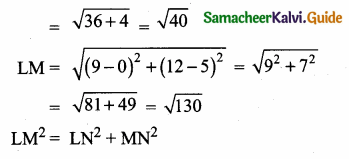
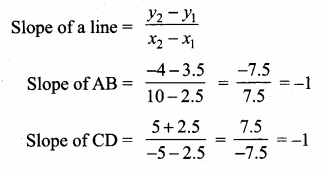
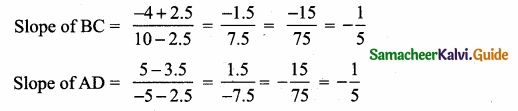
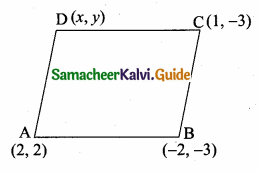
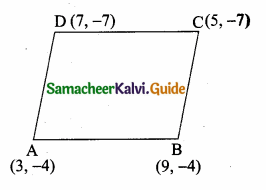
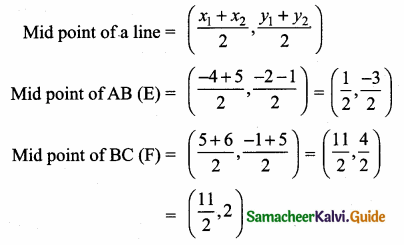
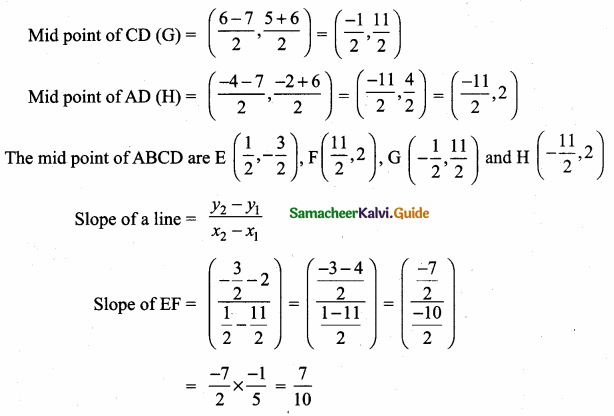
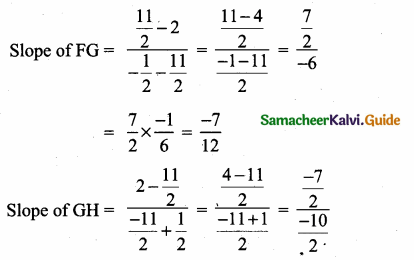
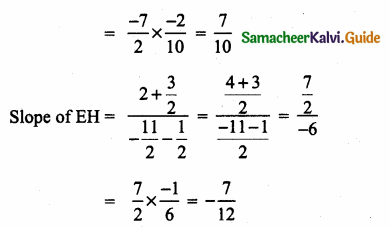
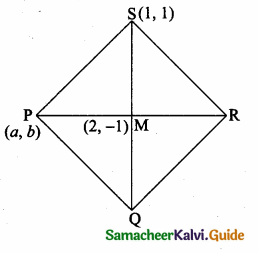
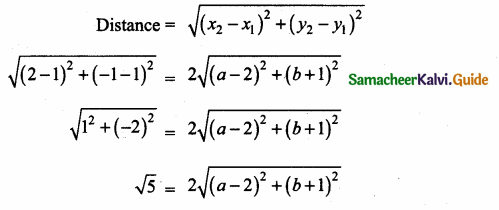
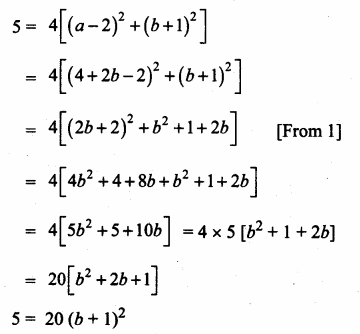
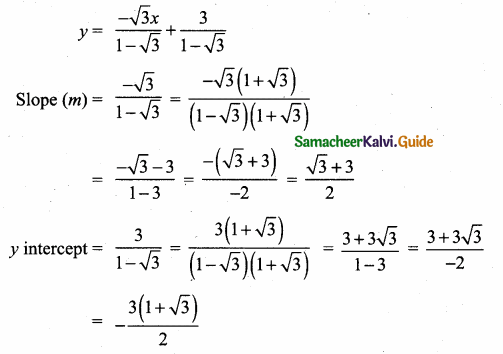
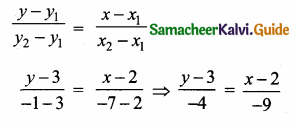
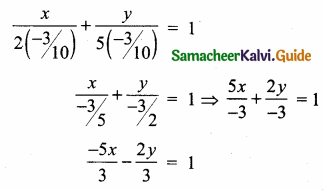
Students can download Maths Chapter 5 Coordinate Geometry Ex 5.4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.4

Question 1.
Find the slope of the following straight lines.
(i) 5y – 3 = 0
(ii) 7x – \(\frac { 3 }{ 17 } \) = 0
Solution:
(i) 5y – 3 = 0
5y = 3 ⇒ y = \(\frac { 3 }{ 5 } \)
Slope = 0

(ii) 7x – \(\frac { 3 }{ 17 } \) = 0 (Comparing with y = mx + c)
7x = \(\frac { 3 }{ 17 } \)
Slope is undefined

Question 2.
Find the slope of the line which is
(i) parallel to y = 0.7x – 11
(ii) perpendicular to the line x = -11
Solution:
(i) y = 0.7x – 11
Slope = 0.7 (Comparing with y = mx + c)
(ii) Perpendicular to the line x = – 11
Slope is undefined (Since the line is intersecting the X-axis)

Question 3.
Check whether the given lines are parallel or perpendicular
(i) \(\frac { x }{ 3 } \) + \(\frac { y }{ 4 } \) + \(\frac { 1 }{ 7 } \) = 0 and \(\frac { 2x }{ 3 } \) + \(\frac { y }{ 2 } \) + \(\frac { 1 }{ 10 } \) = 0
(ii) 5x + 23y + 14 = 0 and 23x – 5x + 9 = 0
Solution:
(i) \(\frac { x }{ 3 } \) + \(\frac { y }{ 4 } \) + \(\frac { 1 }{ 7 } \) = 0 ; \(\frac { 2x }{ 3 } \) + \(\frac { y }{ 2 } \) + \(\frac { 1 }{ 10 } \) = 0
Slope of the line (m₁) = \(\frac { -a }{ b } \)
= – \(\frac { 1 }{ 3 } \) ÷ \(\frac { 1 }{ 4 } \) = –\(\frac { 1 }{ 3 } \) × \(\frac { 4 }{ 1 } \) = – \(\frac { 4 }{ 3 } \)
Slope of the line (m₂) = – \(\frac { 2 }{ 3 } \) ÷ \(\frac { 1 }{ 2 } \) = –\(\frac { 2 }{ 3 } \) × \(\frac { 2 }{ 1 } \) = – \(\frac { 4 }{ 3 } \)
m₁ = m₂ = – \(\frac { 4 }{ 3 } \)
∴ The two lines are parallel.

(ii) 5x + 23y + 14 = 0 and 23x – 5x + 9 = 0
Slope of the line (m₁) = \(\frac { -5 }{ 23 } \)
Slope of the line (m₂) = \(\frac { -23 }{ -5 } \) = \(\frac { 23 }{ 5 } \)
m₁ × m₂ = \(\frac { -5 }{ 23 } \) × \(\frac { 23 }{ 5 } \) = -1
∴ The two lines are perpendicular

Question 4.
If the straight lines 12y = -(p + 3)x + 12, 12x – 7y = 16 are perpendicular then find ‘p’
Solution:
Slope of the first line 12y = -(p + 3)x +12
y = \(-\frac{(p+3) x}{12}+1\) (Comparing with y = mx + c)
Slope of the second line (m₁) = \(\frac { -(p+3) }{ 12 } \)
Slope of the second line 12x – 7y = 16
(m₂) = \(\frac { -a }{ b } \) = \(\frac { -12 }{ -7 } \) = \(\frac { 12 }{ 7 } \)
Since the two lines are perpendicular
m₁ × m₂ = -1
\(\frac { -(p+3) }{ 12 } \) × \(\frac { 12 }{ 7 } \) = -1 ⇒ \(\frac { -(p+3) }{ 7 } \) = -1
-(p + 3) = -7
– p – 3 = -7 ⇒ -p = -7 + 3
-p = -4 ⇒ p = 4
The value of p = 4

Question 5.
Find the equation of a straight line passing through the point P(-5,2) and parallel to the line joining the points Q(3, -2) and R(-5,4).
Solution:
Slope of the line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of the line QR = \(\frac { 4+2 }{ -5-3 } \) = \(\frac { 6 }{ -8 } \) = \(\frac { 3 }{ -4 } \) ⇒ – \(\frac { 3 }{ 4 } \)
Slope of its parallel = – \(\frac { 3 }{ 4 } \)
The given point is p(-5, 2)
Equation of the line is y – y₁ = m(x – x₁)
y – 2 = – \(\frac { 3 }{ 4 } \) (x + 5)
4y – 8 = -3x – 15
3x + 4y – 8 + 15 = 0
3x + 4y + 7 = 0
The equation of the line is 3x + 4y + 7 = 0

Question 6.
Find the equation of a line passing through (6, -2) and perpendicular to the line joining the points (6, 7) and (2, -3).
Solution:
Let the vertices A (6, 7), B (2, -3), D (6, -2)

Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = \(\frac { -3-7 }{ 2-6 } \) = \(\frac { -10 }{ -4 } \) = \(\frac { 5 }{ 2 } \)
Slope of its perpendicular (CD) = – \(\frac { 2 }{ 5 } \)
Equation of the line CD is y – y₁ = m(x – x₁)
y + 2 = –\(\frac { 2 }{ 5 } \) (x – 6)
5(y + 2) = -2 (x – 6)
5y + 10 = -2x + 12
2x + 5y + 10 – 12 = 0
2x + 5y – 2 = 0
The equation of the line is 2x + 5y – 2 = 0

Question 7.
A(-3,0) B(10, -2) and C(12,3) are the vertices of ∆ABC. Find the equation of the altitude through A and B.
Solution:
To find the equation of the altitude from A.
The vertices of ∆ABC are A(-3, 0), B(10, -2) and C(12, 3)

Slope of BC = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac { 3+2 }{ 12-10 } \) = \(\frac { 5 }{ 2 } \)
Slope of the altitude AD is – \(\frac { 2 }{ 5 } \)
Equation of the altitude AD is
y – y₁ = m (x – x₁)
y – 0 = – \(\frac { 2 }{ 5 } \) (x + 3)
5y = -2x -6
2x + 5y + 6 = 0
Equation of the altitude AD is 2x + 5y + 6 = 0
Equation of the altitude from B

Slope of AC = \(\frac { 3-0 }{ 12+3 } \) = \(\frac { 3 }{ 15 } \) = \(\frac { 1 }{ 5 } \)
Slope of the altitude AD is -5
Equation of the altitude BD is y – y₁= m (x – x₁)
7 + 2 = -5 (x – 10)
y + 2 = -5x + 50
5x + 7 + 2 – 50 = 0 ⇒ 5x + 7 – 48 = 0
Equation of the altitude from B is 5x + y – 48 = 0

Question 8.
Find the equation of the perpendicular bisector of the line joining the points A(-4,2) and B(6, -4).
Solution:
“C” is the mid point of AB also CD ⊥ AB.

Slope of AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac { -4-2 }{ 6+4 } \) = \(\frac { -6 }{ 10 } \) = – \(\frac { 3 }{ 5 } \)
Slope of the ⊥^r AB is \(\frac { 5 }{ 3 } \)
Mid point of AB = (\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
= (\(\frac { -4+6 }{ 2 } \),\(\frac { 2-4 }{ 2 } \)) = (\(\frac { 2 }{ 2 } \),\(\frac { -2 }{ 2 } \)) = (1,-1)
Equation of the perpendicular bisector of CD is
y – y₁ = m(x – x₁)
y + 1 = \(\frac { 5 }{ 3 } \) (x – 1)
5(x – 1) = 3(y + 1)
5x – 5 = 3y + 3
5x – 3y – 5 – 3 = 0
5x – 3y – 8 = 0
Equation of the perpendicular bisector is 5x – 3y – 8 = 0

Question 9.
Find the equation of a straight line through the intersection of lines 7x + 3y = 10, 5x – 4y = 1 and parallel to the line 13x + 5y + 12 = 0.
Solution:
Given lines are.

x = \(\frac { 43 }{ 43 } \) = 1
Substitute the value of x = 1 in (1)
7(1) + 3y = 10 ⇒ 3y = 10 – 7
y = \(\frac { 3 }{ 3 } \) = 1
The point of intersection is (1,1)
Equation of the line parallel to 13x + 5y + 12 = 0 is 13x + 5y + k = 0
This line passes through (1,1)
13 (1) + 5 (1) + k = 0
13 + 5 + k = 0 ⇒ 18 + k = 0
k = -18
∴ The equation of the line is 13x + 5y – 18 = 0

Question 10.
Find the equation of a straight line through the intersection of lines 5x – 6y = 2, 3x + 2y = 10 and perpendicular to the line 4x – 7y + 13 = 0.
Solution:
Given lines are.

Substitute the value of x = \(\frac { 16 }{ 7 } \) in (2)
3 × \(\frac { 16 }{ 7 } \) + 2y = 10 ⇒ 2y = 10 – \(\frac { 48 }{ 7 } \)
2y = \(\frac { 70-48 }{ 7 } \) ⇒ 2y = \(\frac { 22 }{ 7 } \)
y = \(\frac{22}{2 \times 7}\) = \(\frac { 11 }{ 7 } \)
The point of intersect is (\(\frac { 16 }{ 7 } \),\(\frac { 11 }{ 7 } \))
Equation of the line perpendicular to 4x – 7y + 13 = 0 is 7x + 4y + k = 0
This line passes through (\(\frac { 16 }{ 7 } \),\(\frac { 11 }{ 7 } \))
7 (\(\frac { 16 }{ 7 } \)) + 4 (\(\frac { 11 }{ 7 } \)) + k = 0 ⇒ 16 + \(\frac { 44 }{ 7 } \) + k = 0
\(\frac { 112+44 }{ 7 } \) + k = 0 ⇒ \(\frac { 156 }{ 7 } \) + k = 0
k = – \(\frac { 156 }{ 7 } \)
Equation of the line is 7x + 4y – \(\frac { 156 }{ 7 } \) = 0
49x + 28y – 156 = 0

Question 11.
Find the equation of a straight line joining the point of intersection of 3x + y + 2 = 0 and x – 2y -4 = 0 to the point of intersection of 7x – 3y = -12 and 2y = x + 3.
Solution:
The given lines are.


Substitute the value of x = 0 in (1)
3 (0) + y = -2
y = -2
The point of intersection is (0, -2).
The given equation is

Substitute the value of y = \(\frac { 9 }{ 11 } \) in (6)
– x + 2 (\(\frac { 9 }{ 11 } \)) = 3 ⇒ -x + \(\frac { 18 }{ 11 } \) = 3
-x = 3 – \(\frac { 18 }{ 11 } \) = \(\frac { 33-18 }{ 11 } \) = \(\frac { 15 }{ 11 } \)
x = – \(\frac { 15 }{ 11 } \)
The point of intersection is (-\(\frac { 15 }{ 11 } \),\(\frac { 9 }{ 11 } \))
Equation of the line joining the points (0, -2) and (-\(\frac { 15 }{ 11 } \),\(\frac { 9 }{ 11 } \)) is


31 × (- 11x) = 11 × 15 (y + 2) = 165 (y + 2)
– 341 x = 165 y + 330
– 341 x – 165 y – 330 = 0
341 x + 165 y + 330 = 0
(÷ by 11) ⇒ 31 x + 15 y + 30 = 0
The required equation is 31 x + 15 y + 30 = 0

Question 12.
Find the equation of a straight line through the point of intersection of the lines 8JC + 3j> = 18, 4JC + 5y = 9 and bisecting the line segment joining the points (5, -4) and (-7,6).
Solution:
Given lines are.
8x + 3y = 18 …..(1)
4x + 5y = 9 …..(2)

x = \(\frac { 63 }{ 28 } \) = \(\frac { 9 }{ 4 } \)
Substitute the value of x = \(\frac { 9 }{ 4 } \) in (2)
4 (\(\frac { 9 }{ 4 } \)) + 5y = 9
9 + 5y = 9 ⇒ 5y = 9 – 9
5y = 0 ⇒ y = 0
The point of intersection is (\(\frac { 9 }{ 4 } \),0)
Mid point of the points (5, -4) and (-7, 6)

Equation of the line joining the points (\(\frac { 9 }{ 4 } \),0) and (-1,1)

-13y = 4x – 9
-4x – 13y + 9 = 0 ⇒ 4x + 13y – 9 = 0
The equation of the line is 4x + 13y – 9 = 0

Students can download Maths Chapter 5 Coordinate Geometry Unit Exercise 5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Unit Exercise 5

Question 1.
PQRS is a rectangle formed by joining the points P(- 1, – 1), Q(- 1, 4) , R(5, 4) and S (5, – 1). A, B, C and D are the mid-points of PQ, QR, RS and SP respectively. Is the quadrilateral ABCD a square, a rectangle or a rhombus? Justify your answer.
Answer:

Mid point of a line = (\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
Mid point of PQ (A) = (\(\frac { -1-1 }{ 2 } \),\(\frac { -1+4 }{ 2 } \))
= (\(\frac { -2 }{ 2 } \),\(\frac { 3 }{ 2 } \)) = (-1,\(\frac { 3 }{ 2 } \))
Mid point of QR (B) = (\(\frac { -1+5 }{ 2 } \),\(\frac { 4+4 }{ 2 } \)) = (\(\frac { 4 }{ 2 } \),\(\frac { 8 }{ 2 } \)) = (2,4)
Mid point of RS (C) = (\(\frac { 5+5 }{ 2 } \),\(\frac { 4-1 }{ 2 } \)) = (\(\frac { 10 }{ 2 } \),\(\frac { 3 }{ 2 } \)) = (5,\(\frac { 3 }{ 2 } \))
Mid point of PS (D) = (\(\frac { 5-1 }{ 2 } \),\(\frac { -1-1 }{ 2 } \)) = (\(\frac { 4 }{ 2 } \),\(\frac { -2 }{ 2 } \)) = (2,-1)


img 355
AB = BC = CD = AD = \(\sqrt{\frac{61}{4}}\)
Since all the four sides are equal,
∴ ABCD is a rhombus.

Question 2.
The area of a triangle is 5 sq. units. Two of its vertices are (2,1) and (3, -2). The third vertex is (x, y) where y = x + 3 . Find the coordinates of the third vertex.
Answer:
Let the vertices A(2,1), B(3, – 2) and C(x, y)
Area of a triangle = 5 sq. unit

\(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)] = 5
\(\frac { 1 }{ 2 } \) [-4 + 3y + x – (3 – 2x + 2y)] = 5
-4 + 3y + x – 3 + 2x – 2y = 10
3x + y – 7 = 10
3x + y = 17 ……(1)
Given y = x + 3
Substitute the value ofy = x + 3 in (1)
3x + x + 3 = 17
4x = 17 – 3
4x = 14
x = \(\frac { 14 }{ 4 } \) = \(\frac { 7 }{ 2 } \)
Substitute the value of x in y = x + 3
y = \(\frac { 7 }{ 2 } \) + 3 ⇒ y = \(\frac { 7+6 }{ 2 } \) = \(\frac { 13 }{ 2 } \)
∴ The coordinates of the third vertex is (\(\frac { 7 }{ 2 } \),\(\frac { 13 }{ 2 } \))

Question 3.
Find the area of a triangle formed by the lines 3x + y – 2 = 0, 5x + 2y – 3 = 0 and 2x – y – 3 = 0
Answer:
3x + y = 2 ……..(1)
5x + 2y = 3 ………(2)
2x – y = 3 ……….(3)
Solve (1) and (2) to get the vertices B


Substitute the value of x = 1 in (1)
3(1) + y = 2
y = 2 – 3 = – 1
The point B is (1, – 1)
Solve (2) and (3) to get the vertices C

Substitute the value of x = 1 in (3)
2(1) – y = 3 ⇒ -y = 3 – 2
– y = 1 ⇒ y = – 1
The point C is (1, – 1)
Solve (1) and (3) to get the vertices A

Substitute the value of x = 1 in (1)
3(1) + y = 2
y = 2 – 3 = -1
The point A is (1, – 1)
The points A (1, – 1), B (1, -1), C(1, -1)
Area of ∆ABC = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)]

Area of the triangle = 0 sq. units.
Note: All the three vertices are equal, all the point lies in a same points.

Question 4.
If vertices of a quadrilateral are at A(- 5, 7), B(- 4, k), C(- 1, – 6) and D(4, 5) and its area is 72 sq.units. Find the value of k.
Answer:

Area of the quadrilateral ABCD = 72 sq. units.
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) – (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)] = 72

-5k + 24 – 5 + 28 – (- 28 – K – 24 – 25) = 144
– 5k + 47 – k – 77 = 144
– 5k + 47 + k + 77 = 144
– 4k + 124 = 144
-4k = 144 – 124
– 4k = 20
k = -5
The value of k = – 5

Question 5.
Without using distance formula, show that the points (-2,-1), (4,0), (3,3) and (-3,2) are vertices of a parallelogram.
Answer:
The vertices A(-2, -1), B(4, 0), C(3, 3) and D(- 3, 2)

Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = \(\frac { 0+1 }{ 4+2 } \) = \(\frac { 1 }{ 6 } \)
Slope of BC = \(\frac { 3-0 }{ 3-4 } \) = \(\frac { 3 }{ -1 } \) = -3
Slope of CD = \(\frac { 2-3 }{ -3-3 } \) = \(\frac { -1 }{ -6 } \) = \(\frac { 1 }{ 6 } \)
Slope of AD = \(\frac { 2+1 }{ -3+2 } \) = \(\frac { 3 }{ -1 } \) = -3
Slope of AB = Slope of CD = \(\frac { 1 }{ 6 } \)
∴ AB || CD ……(1)
Slope of BC = Slope of AD = -3
∴ BC || AD …..(2)
From (1) and (2) we get ABCD is a parallelogram.

Question 6.
Find the equations of the lines, whose sum and product of intercepts are 1 and – 6 respectively.
Answer:
Let the “x” intercept be “a”
y intercept = 1 – a (sum of the intercept is 1)
Product of the intercept = – 6
a (1 – a) = – 6 ⇒ a – a² = – 6
– a² + a + 6 = 0 ⇒ a² – a – 6 = 0
(a – 3) (a + 2) = 0 ⇒ a – 3 = 0 (or) a + 2 = 0
a = 3 (or) a = -2
When a = 3
x – intercept = 3
y – intercept = 1 – 3 = – 2
Equation of a line is
\(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
\(\frac { x }{ 3 } \) + \(\frac { y }{ -2 } \) = 1
\(\frac { x }{ 3 } \) – \(\frac { y }{ 2 } \) = 1
2x – 3y = 6
2x – 3y – 6 = 0

When a =-2
x – intercept = -2
y – intercept = 1 – (- 2) = 1 + 2 = 3
Equation of a line is
\(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
\(\frac { x }{ -2 } \) + \(\frac { y }{ 3 } \) = 1
– \(\frac { x }{ 2 } \) + \(\frac { y }{ 3 } \) = 1
– 3x + 2y = 6
3x – 2y + 6 = 0

Question 7.
The owner of a milk store finds that, he can sell 980 litres of milk each week at ₹ 14/litre and 1220 litres of milk each week at ₹ 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at ₹ 17/litre?
Answer:
Let the selling price of a milk be “x”
Let the demand be “y”
We have to find the linear equation connecting them
Two points on the line are (14, 980) and (16,1220)
Slope of the line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac { 1220-980 }{ 16-14 } \) = \(\frac { 240 }{ 2 } \) = 120
Equation of the line is y – y₁ = m (x – x₁)
y – 980 = 120 (x – 14) ⇒ y – 980 = 120 x – 1680
-120 x + y = -1680 + 980 ⇒ -120 x + y = -700 ⇒ 120 x – y = 700
Given the value of x = 17
120(17) – y = 700
-y = 700 – 2040 ⇒ – y = – 1340
y = 1340
The demand is 1340 liters

Question 8.
Find the image of the point (3,8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Answer:
Let the image of P(3, 8) and P’ (a, b)
Let the point of intersection be O

Slope of x + 3y = 7 is – \(\frac { 1 }{ 3 } \)
Slope of PP’ = 3 (perpendicular)
Equation of PP’ is
y – y₁ = m(x – x₁)
y – 8 = 3 (x – 3)
y – 8 = 3x – 9
-8 + 9 = 3x – y
∴ 3x – y = 1 ………(1)
The two line meet at 0

Substitute the value of x = 1 in (1)
3 – y = 1
3 – 1 = y
2 = y
The point O is (1,2)
Mid point of pp’ = (\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
(1,2) = (\(\frac { 3+a }{ 2 } \),\(\frac { 8+b }{ 2 } \))
∴ \(\frac { 3+a }{ 2 } \) = 1 ⇒ 3 + a = 2
a = 2 – 3 = -1
\(\frac { 8+b }{ 2 } \) = 2
8 + b = 4
b = 4 – 8 = – 4
The point P’ is (-1, -4)

Question 9.
Find the equation of a line passing through the point of intersection of the lines 4x + 7y – 3 = O and 2x – 3y + 1 = 0 that has equal intercepts on the axes.
Answer:
Given lines

Substitute the value of y = \(\frac { 5 }{ 13 } \) in (2)
2x – 3 × \(\frac { 5 }{ 13 } \) = -1
2x – \(\frac { 15 }{ 13 } \) = -1
26x – 15 = -13
26x = -13 + 15
26x = 2
x = \(\frac { 2 }{ 26 } \) = \(\frac { 1 }{ 13 } \)
The point of intersection is (\(\frac { 1 }{ 13 } \),\(\frac { 5 }{ 13 } \))

Let the x – intercept and y intercept be “a”
Equation of a line is
\(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
\(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1 (equal intercepts)
It passes through (\(\frac { 1 }{ 13 } \),\(\frac { 5 }{ 13 } \))
\(\frac { 1 }{ 13a } \) + \(\frac { 5 }{ 13a } \) = 1
\(\frac { 1+5 }{ 13a } \) = 1
13a = 6
a = \(\frac { 6 }{ 13 } \)
The equation of the line is

Question 10.
A person standing at a junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 seek to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find the equation of the path that he should follow.
Answer:
Two straight path will intersect at one point.
Solving this equations

2x – 3y + 4 = 0

Substitute the value of x = \(\frac { -1 }{ 17 } \) in (2)

The point of intersection is (-\(\frac { 1 }{ 17 } \),\(\frac { 22 }{ 17 } \))
Any equation perpendicular to 6x – 7y + 8 = 0 is 7x + 6y + k = 0
It passes through (-\(\frac { 1 }{ 17 } \),\(\frac { 22 }{ 17 } \))
7(-\(\frac { 1 }{ 17 } \)) + 6 (\(\frac { 22 }{ 17 } \)) + k = 0
Multiply by 17
-7 + 6 (22) + 17k = 0
-7 + 132 + 17k = 0
17k = -125 ⇒ k = – \(\frac { 125 }{ 17 } \)
The equation of a line is 7x + 6y – \(\frac { 125 }{ 17 } \) = 0
119x + 102y – 125 = 0
∴ Equation of the path is 119x + 102y – 125 = 0

Students can download Maths Chapter 5 Coordinate Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Additional Questions

I. Multiple Choice Questions

Question 1.
If the three points (-3, 7), (a, 1), (-3, 2) are collinear then the value of “a” is
(1) 0
(2) -1
(3) -3
(4) 1
Answer:
(3) -3
Hint:
Since the three points are collinear
Area of a ∆ = 0

-3 + 2a – 21 – (7a – 3 – 6) = 0 ⇒ 2a – 24 – 7a + 9 = 0
– 5a – 15 = 0 ⇒ – 5(a + 3) = 0
a + 3 = 0 ⇒ a = -3

Question 2.
If A (5, 5), B (-5, 1), C (10, 7) lie in a straight line, then the area of ∆ ABC is …………….
(1) \(\frac { 13 }{ 2 } \) sq.units
(2) 9 sq.units
(3) 25 sq.units
(4) 0
Answer:
(4) 0
Hint:
Area of the ∆^le

Question 3.
In a rectangle ABCD, area of ∆ ABC is \(\frac { 31 }{ 2 } \) sq. units. Then the area of rectangle is ……………
(1) 62 sq. units
(2) 31 sq. units
(3) 60 sq. units
(4) 30 sq. units
Answer:
(2) 31 sq. units
Hint:
In a rectangle area of ∆ ABC and area of ∆ ACD are equal.
Area of rectangle ABCD = 2 × \(\frac { 31 }{ 2 } \) = 31 sq.units

Question 4.
If the points (k, 2k), (3k, 3k) and (3,1) are collinear, then k is ……………..
(1) \(\frac { 1 }{ 3 } \)
(2) – \(\frac { 1 }{ 3 } \)
(3) \(\frac { 2 }{ 3 } \)
(4) – \(\frac { 2 }{ 3 } \)
Answer:
(2) – \(\frac { 1 }{ 3 } \)
Hint:
Since the three points are collinear. Area of a ∆ = 0

3k² + 3k + 6k – (6k² + 9k + k) = 0 ⇒ 3k² + 9k – 6k² – 10k = 0
-3 k² – k = 0 ⇒ -k(3k + 1) = 0
3k + 1 = 0 ⇒ 3 k = -1 ⇒ k = – \(\frac { 1 }{ 3 } \)

Question 5.
If the area of the triangle formed by the points (x, 2x), (-2, 6) and (3, 1) is 5 square units then x = ………….
(1) 2
(2) \(\frac { 3 }{ 5 } \)
(3) 3
(4) 5
Answer:
(1) 2
Hint:
Area of the triangle = 5 sq. units

6x – 2 + 6x – (-4x + 18 + x) = 10 ⇒ 12x – 2 – (-3x + 18) = 10
12x – 2 + 3x – 18 = 10
15x – 20 = 10 ⇒ 15x = 10 + 20 = 30
x = \(\frac { 30 }{ 15 } \) = 2

Question 6.
The slope of a line parallel to y-axis is equal to …………..
(1) 0
(2) -1
(3) 1
(4) not defined
Answer:
(4) not defined

Question 7.
In a rectangle PQRS, the slope of PQ = \(\frac { 5 }{ 6 } \) then the slope of RS is ………..
(1) \(\frac { -5 }{ 6 } \)
(2) \(\frac { 6 }{ 5 } \)
(3) \(\frac { -6 }{ 5 } \)
(4) \(\frac { 5 }{ 6 } \)
Answer:
\(\frac { 5 }{ 6 } \)
Hint:
In a rectangle opposite sides are parallel.
∴ Slope of the line RS is \(\frac { 5 }{ 6 } \).

Question 8.
The y – intercept of the line y = 2x is ………
(1) 1
(2) 2
(3) \(\frac { 1 }{ 2 } \)
(4) 0
Answer:
(4) 0

Question 9.
The straight line given by the equation y = 5 is …………..
(1) Parallel to x – axis
(2) Parallel to y – axis
(3) Passes through the origin
(4) None of these
Answer:
(1) Parallel to x – axis

Question 10.
The x – intercept of the line 2x – 3y + 5 = 0 is ………….
(1) \(\frac { 5 }{ 2 } \)
(2) \(\frac { -5 }{ 2 } \)
(3) \(\frac { 2 }{ 5 } \)
(4) \(\frac { -2 }{ 5 } \)
Answer:
(2) \(\frac { -5 }{ 2 } \)
Hint:
2x – 3y + 5 = 0 ⇒ 2x – 3y = – 5

Question 11.
The lines 3x – 5y + 1 = 0 and 5x + ky + 2 = 0 are perpendicular if the value of k is ………..
(1) -5
(2) 3
(3) -3
(4) 5
Answer:
(2) 3
Hint:
Slope of the first line (m₁) = \(\frac { -3 }{ -5 } \) = \(\frac { 3 }{ 5 } \)
Slope of the second line (m₂) = \(\frac { -5 }{ k } \)
Since the two lines are perpendicular.
m₁ × m₂ = -1
\(\frac { 3 }{ 5 } \) × \(\frac { -5 }{ k } \) = -1 ⇒ \(\frac { -3 }{ k } \) = -1
-k = -3 ⇒ The value of k = 3

Question 12.
If x – y = 3 and x + 2y = 6 are the diameters of a circle then the centre is at the point ………..
(1) (0, 0)
(2) (1, 2)
(3) (1, -1)
(4) (4, 1)
Answer:
(4) (4, 1)
Hint:
Centre of the circle is the intersection of the two diameters.

Centre of the circle is (4, 1)

Question 13.
The line 4x + 3y – 12 = 0 meets the x-axis at the point ……….
(1) (4, 0)
(2) (3, 0)
(3) (-3, 0)
Answer:
(2) (3,0)
Hint:
4x + 3y – 12 = 0 meet the x-axis the value of y = 0
4x- 12 = 0 ⇒ 4x = 12
x = \(\frac { 12 }{ 4 } \) = 3 ⇒ The point is (3, 0)

Question 14.
The equation of a straight line passing through the point (2, -7) and parallel to x-axis is ……………….
(1) x = 2
(2) x = -7
(3) y = -7
(4) y = 2
Answer:
(3) y = -7
Hint:
Equation of a line parallel to x-axis is y = -7

Question 15.
The equation of a straight line having slope 3 and y intercept – 4 is ………………
(1) 3x – y – 4 = 0
(2) 3x + y – 4 = 0
(3) 3x – y + 4 = 0
(4) 3x – y + 4 = 0
Answer:
(1) 3x – y – 4 = 0
Hint. The equation of a line is y = mx + c
y = 3 (x) + (-4) ⇒ y = 3x – 4
3x – y – 4 = 0

II. Answer the following questions:

Question 1.
If the points (3, – 4) (1, 6) and (- 2, 3) are the vertices of a triangle, find its area.
Answer:
Let the vertices A (3, – 4), B (1, 6) and C (- 2, 3)

Area of ∆ ABC = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁, – (x₂y₁ + x₃y₂ + x₁y₃)]

Area of a ∆ = 18 sq. units

Question 2.
If the area of the triangle formed by the points (1,2) (2,3) and (a, 4) is 8 sq. units, find a.
Answer:
Area of a triangle = 8 sq. units.

\(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)] = 8.
\(\frac { 1 }{ 2 } \) [3 + 8 + 2a – (4 + 3a + 4)] = 8
11 + 2a – 8 – 3a= 16 ⇒ – a + 3 = 16
– a = 16 – 3 ⇒ a = -13
The value of a = -13

Question 3.
If the points A (2, 5), B (4, 6) and C (8, a) are collinear find the value of “a” using slope concept.
Answer:
Since the three points are collineal
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = Slope of BC
\(\frac { 6-5 }{ 4-2 } \) = \(\frac { a-6 }{ 8-4 } \) ⇒ \(\frac { 1 }{ 2 } \) = \(\frac { a-6 }{ 4 } \) ⇒ 2a – 12 = 4 ⇒ 2a = 16
a = \(\frac { 16 }{ 2 } \) = 8 ⇒ The value of a = 8

Question 4.
If the points (x,y) is collinear with the points (a, 0) and (0, b) then prove that \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
Answer:
Let A (x, y), B (a, 0), C(0, b)
Since the three points are collinear
Slope of AB = Slope of BC
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
\(\frac { 0-y }{ a-x } \) = \(\frac { b-0 }{ 0-a } \)
\(\frac { -y }{ a-x } \) = \(\frac { b }{ -a } \)
ay = b (a – x)
ay = ba – bx
ay + bx = ab
Divided by ab
\(\frac { ay }{ ab } \) + \(\frac { bx }{ ab } \) = \(\frac { ab }{ ab } \)
\(\frac { y }{ b } \) + \(\frac { x }{ a } \) = 1 ⇒ \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1

Question 5.
A straight line passes through (1, 2) and has the equation y – 2x – k = 0. Find k.
Answer:
The given line is y – 2x – k = 0
It passes through (1,2)
(2) -2 (1) -k = 0 ⇒ 2 – 2 – k = 0
0 – k = 0 ⇒ k = 0
The value of k = 0

Question 6.
If a line passes through the mid point of AB where A is (3, 0) and B is (5, 4) and makes an angle 60° with x – axis find its equation.
Answer:

Slope of a line = tan 60°
= \(\sqrt { 3 }\)
Equation of a line is y – y₁ = m (x – x₁)
y – 2 = \(\sqrt { 3 }\) (x – 4)
y – 2 = \(\sqrt { 3 }\) x – 4 \(\sqrt { 3 }\)
\(\sqrt { 3x }\) – y + 2 – 4\(\sqrt { 3 }\) = 0

Question 7.
Find the equation of the line through (3, 2) and perpendicular to the line joining (4, 5) and (1,2)
Answer:
Slope of a line = \(\frac { 2-5 }{ 1-4 } \) ⇒ \(\frac { -3 }{ -3 } \) = 1
Slope of the line perpendicular to it is – 1
Equation of the line joining -1 and (3, 2) is
y – y₁ = m (x – x₁) ⇒ y – 2 = -1(x – 3)
y – 2 = -x + 3 ⇒ x + y – 5 = 0

Question 8.
P and Q trisect the line segment joining the points (2, 1) and (5, – 8). If the point P lies on 2x – y + k = 0, then find the value of k.
Answer:

A line divides internally in the ratio 1 : 2
A line divide internally in the ratio l : m

The point P = (\(\frac { 5+4 }{ 3 } \),\(\frac { -8+2 }{ 3 } \))
= (\(\frac { 9 }{ 3 } \),\(\frac { -6 }{ 3 } \)) = (3, -2)
The given line 2x – y + k = 0 passes through the point (3,-2)
2 (3) – (- 2) + k = 0
6 + 2 + k = 0
8 + k = 0
k = – 8
The value of k = – 8

Question 9.
The line 4x + 3y – 12 = 0 intersect the X, Y – axis at A and B respectively. Fine the area of ∆AOB.
Answer:
The equation of the line AB is 4x + 3y – 12 = 0

4x + 3y = 12
\(\frac { 4x }{ 12 } \) + \(\frac { 3y }{ 12 } \) = 1 ⇒ \(\frac { x }{ 3 } \) + \(\frac { y }{ 4 } \) = 1
The point A is (3, 0) (it intersect the X – axis)
and B is (0, 4) (it intersect the Y – axis)
Area of ∆ AOB = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ (x₂y₁ + x₃y₂ + x₁y₃)]

Question 10.
Find the equation of the line passing through (4, 5) and making equal intercept in the axes.
Answer:
Let the equal intercept on the axes be a, a.
Equation of the line is \(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1 (Given equal intercepts)
The line passes through (4, 5)
\(\frac { 4 }{ a } \) + \(\frac { 5 }{ a } \) = 1 ⇒ \(\frac { 9 }{ a } \) = 1 ⇒ a = 9
The equation of the line is \(\frac { x }{ 9 } \) + \(\frac { y }{ 9 } \) = 1
Multiply by 9
x + y – 9 = 0

Question 11.
Find the equation of the line passing through (2, – 1) and whose intercepts on the axes are equal in magnitude but opposite in sign.
Answer:
Let the x – intercept be “a” and y intercept be = “-a”
The equation of the line is
\(\frac { x }{ a } \) + \(\frac { y }{ -a } \) = 1 (y – intercept is – a)
\(\frac { x }{ a } \) – \(\frac { y }{ a } \) = 1
It passes through (2, -1)
\(\frac { 2 }{ a } \) – \(\frac { (-1) }{ a } \) = 1
\(\frac { 2 }{ a } \) + \(\frac { 1 }{ a } \) = 1 ⇒ \(\frac { 3 }{ a } \) = 1
a = 3
The equation of the line is
\(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
\(\frac { x }{ 3 } \) + \(\frac { y }{ -3 } \) = 1 ⇒ \(\frac { x }{ 3 } \) – \(\frac { y }{ 3 } \) = 1
x – y = 3
The equation is x – y – 3 = 0

Question 12.
The straight line cuts the coordinate axes at A and B. If the mid point of AB is (3,2) then find the equation of AB.
Answer:
Let the point A be (a, 0) and B be (0, b)


The point A (6, 0) and B (0, 4)
Equation of the line AB is

III. Answer the following questions

Question 1.
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the ‘ coordinates of any point “c”, if AC = BC and Area of triangle ABC = 10 sq. units.
Answer:
Let the coordinates C be (a, 6) then AC = BC
AC² = BC²
(a – 3)² + (b – 4)² = (a – 5)² + (b + 2)²
a² + 9 – 6a + b² + 16 – 8b = a² + 25 – 10a + b² + 4 – 4b
a² + b² + 25 – 6a – 86 = a² + b² + 29 – 10a + 4b

25 – 6a – 8b = 29 – 10a + 46
4a – 12b = 4 ⇒ a – 3b = 1 ………… (1)
Area of ∆ ABC = 10 sq. units
\(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)] = 10

-6 + 5b + 4a – (20 – 2a + 3b) = 20
-6 + 5b + 4a – 20 + 2a – 3b = 20
6a + 2b – 26 = 20 ⇒ 6a + 2b = 46

Substitute the value of a = 7 in (2)
3 (7) + b = 23 ⇒ b = 23 – 21 = 2
The coordinate C is (7, 2)

Question 2.
The four vertices of a Quadrilateral are (1,2) (- 5,6) (7, – 4) and (k, – 2) taken in order. If the area of the Quadrilateral is 9 sq. units, find the value of k.
Answer:
Let A (1, 2) B (- 5, 6) C (7, – 4) and D (k, – 2)
Area of the
Quadrilateral ABCD = \(\frac { 1 }{ 2 } \)[(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) – (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)]

Area of the Quadrilateral ABCD = 3k – 9
Given area of a Quadrilateral is 9 sq. units.
3k – 9 = 9 ⇒ 3k = 18 ⇒ k = \(\frac { 18 }{ 3 } \) = 6
The value of k = 6

Question 3.
Find the area of a triangles whose three sides are having the equations x + y = 2, x – y = 0 and x + 2y – 6 = 0.
Answer:
Find the three vertices of the triangles by solving their equation.
To find vertices A


Substitute the value of y = 4 in (1)
x + 4 = 2 ⇒ x = 2 – 4 = -2
The vertices A is (- 2, 4)
To find vertices B

Substitute the value of x = 1 in (1)
1 + y = 2 ⇒ y = 2 – 1 = 1
The vertices B is (1, 1)
To find vertices C

y = \(\frac { 6 }{ 3 } \) = 2
Substitute the value y = 2 in (3)
x – 2 = 0 ⇒ x = 2
The vertices C is (2, 2)

Area of the ∆ BC = 3 sq. units

Question 4.
Verify the Median of a triangle divides into two triangles of equal areas whose vertices are A (4, – 6), B (3, – 2) and C (5, 2)
Answer:

Let D be the mid point of AC .
Mid point of AC = (\(\frac { 5+4 }{ 2 } \),\(\frac { 2-6 }{ 2 } \)) = (\(\frac { 9 }{ 2 } \),-2)
Area of the triangle = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)]

Area of ∆ ADB = Area of ∆ BDC
A median divides the triangle of equal areas.

Question 5.
Find the area of the ∆ ABC with A (1, – 4) and the mid points of sides through A being (2,-1) and (0,-1)
Answer:
Let the coordinates of B and C are (a, b) and (c, d) respectively.
Sides through A are AB and AC

Mid point of AB = (\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
(2, -1) = (\(\frac { 1+a }{ 2 } \),\(\frac { -4+b }{ 2 } \))
\(\frac { 1+a }{ 2 } \) = 2
1 + a = 4
a = 4 – 1
= 3
The point B is (3,2)
\(\frac { -4+b }{ 2 } \) = -1
-4 + b = -2
b = -2 + 4
= 2
Mid point of AC = (\(\frac { 1+c }{ 2 } \),\(\frac { -4+d }{ 2 } \))
(0,-1) = (\(\frac { 1+c }{ 2 } \),\(\frac { -4+d }{ 2 } \))
\(\frac { 1+c }{ 2 } \) = 0
1 + c = 0
c = 0 – 1
= – 1
The point C is (-1,2)
\(\frac { -4+d }{ 2 } \) = -1
– 4 + d = -2
d = – 2 + 4
= 2
Thus the coordinates of the vertices of ∆ ABC are A (1, – 4) B (3, 2) and C (- 1, 2)
Area of ∆ ABC = \(\frac { 1 }{ 2 } \) [x₁y₂ + x₂y₃ + x₃y₁ – (x₂y₁ + x₃y₂ + x₁y₃)]

Area of ∆ ABC = 12 sq. units

Question 6.
Find the equation of the straight lines passing through (- 3, 10) whose sum of the intercepts is 8.
Answer:
Let the “x” intercept be “a” and y intercept be “b”
Sum of the intercepts = 8
a + b = 8 ⇒ b = 8 – a
Equation of a line is \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1 ⇒ \(\frac { x }{ a } \) + \(\frac { y }{ 8-a } \) = 1
It passes through (-3,10)
\(\frac { -3 }{ a } \) + \(\frac { 10 }{ 8-a } \) = 1
\(\frac { -3(8-a)+10a }{ a(8-a) } \) = 1
-24 + 3a + 10a = 8a – a²
-24 + 13a = 8a – a²
a² + 5a – 24 = 0 ⇒ (a + 8) (a – 3) = 0
a + 8 = 0 (or) a – 3 = 0 ⇒ a = -8 (or) a = 3
The equation of a line is a
a = -8
\(\frac { x }{ -8 } \) + \(\frac { y }{ 8+8 } \) = 1
\(\frac { x }{ -8 } \) + \(\frac { y }{ 16 } \) = 1
-2x + y = 16
2x – y + 16 = 0
a = 3
\(\frac { x }{ 3 } \) + \(\frac { y }{ 5 } \) = 1
5x + 3y = 15
5x + 3y – 15 = 0
The equation of the lines are 2x – y + 16 = 0 (or) 5x + 3y – 15 = 0.

Question 7.
If (5, – 3), (- 5, 3), (6, 6) are the mid points of the sides of a triangle, find the equation of the sides.
Answer:
Since D, E, F are the mid points of ∆ ABC
EF || AB, FD || BC and DE || AC
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of EF = \(\frac { 6-3 }{ 6+5 } \) = \(\frac { 3 }{ 11 } \)
Since EF || AB; Slope of AB = \(\frac { 3 }{ 11 } \)
Equation of AB is
y – y₁ = m (x – x₁)
y + 3 = \(\frac { 3 }{ 11 } \) (x – 5)
3x – 15 = 11y + 33
3x – 11y – 15 – 33 = 0
3x – 11y – 48 = 0
Slope of DE = Slope of AC
Slope of DE = \(\frac { 3+3 }{ -5-5 } \) = \(\frac { 6 }{ -10 } \) = –\(\frac { 6 }{ 10 } \) = –\(\frac { 3 }{ 5 } \)
Slope of AC = – \(\frac { 3 }{ 5 } \)
Equation of AC is
y – y₁ = m (x – x₁)

y – 6 = – \(\frac { 3 }{ 5 } \) (x – 6) ⇒ 5y – 30 = -3x + 18
3x + 5y – 30 – 18 = 0 ⇒ 3x + 5y – 48 = 0
Slope of DF = Slope of BC
Slope of DF = \(\frac { 6+3 }{ 6-5 } \) = \(\frac { 9 }{ 1 } \) = 9
Slope of BC = 9
Equation of the line BC is
y – y₁ = m(x – x₁)
y – 3 = 9 (x + 5) ⇒ 9x + 45 = y – 3
9x – y + 45 + 3 = 0 ⇒ 9x – y + 48 = 0
Equation of the sides are
3x – 11y – 48 = 0 ; 9x – y + 48 = 0 and 3x + 5y – 48 = 0

Question 8.
Find the equation of the straight line passing through the point of intersection of the lines 5x – 8y + 23 = 0 and 7x + 6y – 71 = 0 and is perpendicular to the line joining the points (5,1) and (-2, 2)
Answer:

Substitute the value of x in (1)
5 (5) – 8y = – 23 ⇒ 25 – 8y = – 23
-8y = – 23 – 25 ⇒ -8y = – 48
y = \(\frac { 48 }{ 8 } \) = 6
The point of intersection is (5,6)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of the line joining the points (5,1) and (-2,2) = \(\frac { 2-1 }{ -2-5 } \)
= \(\frac { 1 }{ -7 } \) = – \(\frac { 1 }{ 7 } \)
Slope of the perpendicular line is = 7
Equation of a line is
y – y₁ = m(x – x₁) ⇒ y – 6 = 7 (x – 5)
y – 6 = 7x – 35 ⇒ -7x + y – 6 + 35 = 0
7x – y – 29 = 0

Question 9.
Find the equation of the line passing through the point of intersection of 4x – y – 3 = 0 and x + y – 2 = 0 and perpendicular to 2x – 5y + 3 = 0.
Answer:

x = \(\frac { 5 }{ 5 } \) = 1
Substitute the value of x = 1 in (2)
1 + y = 2
y = 2 – 1 = 1
The point of intersection is (1, 1)
Any line perpendicular to 2x – 5y + 3 = 0 is
5x + 2y + k = 0
It passes through (1,1)
5(1) + 2(1) + k = 0 ⇒ 5 + 2 + k = 0
7 + k = 0 ⇒ k = -7
The line is 5x + 2y – 7 = 0

Question 10.
Find the equation of the line through the point of intersection of the lines 2x + y – 5 = 0 and x + y – 3 = 0 and bisecting the line segment joining the points (3, – 2) and (- 5, 6).
Answer:

x = 2
Substitute the value of x = 2 in (2)
2 + y = 3
y = 3 – 2 = 1
The point of intersection is (2, 1)
Mid point of the line joining the points (3,-2) and (-5,6)

Mid point of the line
Equation of the line joining the points (2, 1) and (-1,2) is

x – 2 = -3 (y – 1)
x – 2 = -3y + 3
x + 3y – 5 = 0
The equation of the line is x + 3y – 5 = 0

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.1

Question 1.
Find the area of the triangle formed by the points
(i) (1,-1), (-4, 6) and (-3, -5)
(ii) (-10, -4), (-8, -1) and (-3, -5)
Solution:
(i) Let the vertices A (1, -1), B (-4, 6) and C (-3, -5)


= \(\frac { 1 }{ 2 } \) [(6 + 20 + 3) – (4 – 18 – 5)] = \(\frac { 1 }{ 2 } \) [29 – (-19)] = \(\frac { 1 }{ 2 } \) [29 + 19]
= \(\frac { 1 }{ 2 } \) × 48 = 24 sq. units.
Area of ∆ABC = 24 sq. units

(ii) Let the vertices be A(-10, -4), B(-8 -1) and C(-3, -5)

Area of ∆ABC = \(\frac { 1 }{ 2 } \)[(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)]
= \(\frac { 1 }{ 2 } \) [(50 + 3 + 32) – (12 + 40 + 10)]

= \(\frac { 1 }{ 2 } \) [85 – (62)] = \(\frac { 1 }{ 2 } \) [23] = 11.5
Area of ∆ACB = 11.5 sq.units

Question 2.
Determine whether the sets of points are collinear?
(i) (-\(\frac { 1 }{ 2 } \),3)
(ii) (a,b + c), (b,c + a) and (c,a + b)
Solution:
(i) Let the points be A (-\(\frac { 1 }{ 2 } \),3), B (-5, 6) and C(-8, 8)
Area of ∆ABC = \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₃ + x₁y₃)]
= \(\frac { 1 }{ 2 } \) [(- 3 – 40 – 24) – (-15 – 48 – 4)]

= \(\frac { 1 }{ 2 } \) [-67 + 67] = \(\frac { 1 }{ 2 } \) × 0 = 0
Area of a ∆ is 0.
∴ The three points are collinear.

(ii) Let the points be A (a, b + c), B (b, c + a) and C (c, a + b)
Area of the triangle = \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)]

Since the area of a triangle is 0.
∴ The given points are collinear.

Question 3.
Vertices of given triangles are taken in order and their areas are provided aside. In each case, find the value of ‘p’

Solution:
(i) Let the vertices be A (0,0) B (p, 8), c (6, 2)
Area of a triangle = 20 sq. units
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)] = 20

\(\frac { 1 }{ 2 } \) [(0 + 2p + 0) – (0 + 48 + 0)] = 20
\(\frac { 1 }{ 2 } \) [2p – 48] = 20
2p – 48 = 40 ⇒ 2p = 40 + 48
p = \(\frac { 88 }{ 2 } \) = 44
The value of p = 44

(ii) Let the vertices be A (p, p), B (5, 6) and C (5, -2)
Area of a triangle = 32 sq. units
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)] = 32

\(\frac { 1 }{ 2 } \) [6p – 10 + 5p) – (5p + 30 – 2p)] = 32
\(\frac { 1 }{ 2 } \) [11 p – 10 – 3p – 30] = 32
11p – 10 – 3p – 30 = 64
8p – 40 = 64
8p = 64 + 40 ⇒ 8p = 104
p = \(\frac { 104 }{ 8 } \) = 13
The value of p = 13

Question 4.
In each of the following, find the value of ‘a’ for which the given points are collinear.
(i) (2,3), (4, a) and (6, -3)
(ii) (a, 2 – 2a), (-a + 1, 2a) and (-4 -a, 6 – 2a).
Solution:
(i) Let the points be A (2, 3), B(4, a) and C(6, -3).
Since the given points are collinear.
Area of a triangle = 0
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)] = 0)

\(\frac { 1 }{ 2 } \) [(2a – 12 + 18) – (12 + 6a – 6)] = 0
2a + 6 – (6 + 6a) = 0
2a + 6 – 6 – 6a = 0
-4a = 0 ⇒ a = \(\frac { 0 }{ 4 } \) = 0
The value of a = 0

(ii) Let the points be A (a, 2 – 2a), B (-a + 1, 2a) C (-4 -a, 6 – 2a).
Since the given points are collinear.
Area of a ∆ = 0

6a² – 2a – 2 – (-2a² – 6a + 2) = 0
6a² – 2a – 2 + 2a² + 6a – 2 = 0
8a² + 4a – 4 = 0 (Divided by 4)
2a² + a – 1 = 0
2a² + 2a – a – 1 = 0
2a (a + 1) – 1 (a + 1) = 0

(a + 1) (2a – 1) = 0
a + 1 = 0 (or) 2a – 1 = 0
a = -1 (or) 2a = 1 ⇒ a = \(\frac { 1 }{ 2 } \)
The value of a = -1 (or) \(\frac { 1 }{ 2 } \)

Question 5.
Find the area of the quadrilateral whose vertices are at
(i) (-9, -2), (-8, -4), (2, 2) and (1, -3)
(ii) (-9, 0), (-8,6), (-1, -2) and (-6, -3)
Solution:
(i) Let the vertices A (-9, -2), B(-8, -4), C(2, 2) and D(1, -3).
Plot the vertices in a graph.

[Note: Consider the points in counter clock wise order]

Area of the Quadrilateral ABDC = \(\frac { 1 }{ 2 } \) [36 + 24 + 2 – 4 – (16 – 4 – 6 – 18)]
= \(\frac { 1 }{ 2 } \) [58 – (-12)] – \(\frac { 1 }{ 2 } \)[58 + 12]
= \(\frac { 1 }{ 2 } \) × 70 = 35 sq. units 2
Area of the Quadrilateral = 35 sq. units

(ii) Let the vertices A(-9, 0), B(-8, 6), C(-1, -2) and D(-6, -3)
Plot the vertices in a graph and take them in counter – clock wise order.
Area of the Quadrilateral DCB

= \(\frac { 1 }{ 2 } \) [33 + 35] = \(\frac { 1 }{ 2 } \) × 68 = 34 sq. units
Area of the Quadrilateral = 34 sq. units

Question 6.
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (-4, -2), (-3, k), (3, -2) and (2, 3)
Solution:
Let the vertices A (-A, -2), B (-3, k), C (3, -2) and D (2, 3)
Area of the Quadrilateral = 28 sq. units
\(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) – (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)] = 28

-7k + 21 = 56
-7k = 56 – 21
-7k = 35 ⇒ 7k = – 35
k = – \(\frac { 35 }{ 7 } \) = -5
The value of k = -5

Question 7.
If the points A(-3, 9), B(a, b) and C(4, -5) are collinear and if a + b = 1, then find a and b.
Solution:
Since the three points are collinear
Area of a ∆ = 0

-3b – 5a + 36 – 9a – 4b – 15 = 0
-7b – 14a + 21 = 0
(÷ by 7) – b – 2a + 3 = 0
2a + b – 3 = 0

Substitute the value of a = 2 in (2) ⇒ 2 + b = 1
b = 1 – 2 = -1
The value of a = 2 and b = -1

Question 8.
Let P(11, 7), Q(13.5, 4) and R(9.5, 4) be the midpoints of the sides AB, BC and AC respectively of ∆ABC . Find the coordinates of the vertices A, B and C. Hence find the area of ∆ABC and compare this with area of ∆PQR.
Solution:
Let the vertices of the ∆ABC be A(x₁,y₁), B(x₂,y₂), C(x₃,y₃)

Question 9.
In the figure, the quadrilateral swimming pool shown is surrounded by concrete patio. Find the area of the patio.

Solution:

= \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) – (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)]
= \(\frac { 1 }{ 2 } \) [(16 + 80 + 36 + 80) – (-64 – 24 – 100 – 24)]
= \(\frac { 1 }{ 2 } \) [212 – (-212)]

= \(\frac { 1 }{ 2 } \) [212 + 212] = \(\frac { 1 }{ 2 } \) [424] = 212 sq. units

= \(\frac { 1 }{ 2 } \) [90 – (-90)]

= \(\frac { 1 }{ 2 } \) [90 + 90]
= \(\frac { 1 }{ 2 } \) × 180 = 90 sq. units
Area of the patio = Area of the Quadrilateral ABCD – Area of the Quadrilateral EFGH
= (212 – 90) sq. units
Area of the patio = 122 sq. units

Question 10.
A triangular shaped glass with vertices at A(-5, -4), B(l, 6) and C(7, -4) has to be painted. If one bucket of paint covers 6 square feet, how many buckets of paint will be required to paint the whole glass, if only one coat of paint is applied.
Solution:
Given the vertices of the triangular glass is A (-5, -4), B (1, 6), and C (7, -4)


= \(\frac { 1 }{ 2 } \) [(20 + 42 – 4) – (-28 – 4 – 30)]
= \(\frac { 1 }{ 2 } \) [58 – (-62)]
= \(\frac { 1 }{ 2 } \) [58 + 62]
= \(\frac { 1 }{ 2 } \) × 120 = 60 sq. feet
Number of cans to paint 6 square feet = 1
∴ Number of cans = \(\frac { 60 }{ 6 } \) = 10 ⇒ Number of cans = 10

Question 11.
In the figure, find the area of
(i) triangle AGF
(ii) triangle FED
(iii) quadrilateral BCEG.

Solution:
Area of a triangle = \(\frac { 1 }{ 2 } \) [(x₁y₂ + x₂y₃ + x₃y₁) – (x₂y₁ + x₃y₂ + x₁y₃)]
(i) Area of ∆AGF = \(\frac { 1 }{ 2 } \) [(-2.5 – 13.5 – 6) – (-13.5 – 1 – 15)]
= \(\frac { 1 }{ 2 } \) [-22 – (-29.5)]

= \(\frac { 1 }{ 2 } \) [-22 + 29.5]
= \(\frac { 1 }{ 2 } \) × 7.5 = 3.75 sq.units

(ii) Area of ∆FED = \(\frac { 1 }{ 2 } \) [(-2 + 4.5 + 3) – (4.5 + 1 – 6)]
= \(\frac { 1 }{ 2 } \) [5.5 – (-0.5)]

= \(\frac { 1 }{ 2 } \) [5.5 + 0.5] = \(\frac { 1 }{ 2 } \) × 6 = 3 sq.units

(iii)

= \(\frac { 1 }{ 2 } \) [(4 + 2 + 0.75 + 9) – (-4 -1.5 – 4.5 -2)]
= \(\frac { 1 }{ 2 } \) [15.75 + 12]
= \(\frac { 1 }{ 2 } \) [27.75] = 13.875
= 13.88 sq. units

Students can download Maths Chapter 1 Relations and Functions Ex 1.4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.4

Question 1.
Determine whether the graph given below represent functions. Give reason for your answers concerning each graph.




Answer:

The vertical line cuts the graph at A and B. The given graph does not represent a function.

The vertical line cuts the graph at most one point P. The given graph represent a function.

The vertical line cuts the graph at three points S,T and U. The given graph does not represent a function.

The vertical line cuts the graph at most one point D. The given graph represents a function.

Question 2.
Let f: A → B be a function defined by
f(x) = \(\frac { x }{ 2 } \) – 1, where A = {2, 4,6,10,12},
B = {0,1,2,4,5,9}. Represent f by
(i) set of ordered pairs
(ii) a table
(iii) an arrow diagram
(iv) a graph
Answer:
A = {2,4,6, 10, 12}
B = {0,1, 2, 4, 5, 9}
f(x) = \(\frac { x }{ 2 } \) – 1
f(2) = \(\frac { 2 }{ 2 } \) – 1 = 1 – 1 = 0
f(4) = \(\frac { 4 }{ 2 } \) – 1 = 2 – 1 = 1
f(6) = \(\frac { 6 }{ 2 } \) – 1 = 3 – 1 = 2
f(10) = \(\frac { 10 }{ 2 } \) – 1 = 5 – 1 = 4
f(12) = \(\frac { 12 }{ 2 } \) – 1 = 6 – 1 = 5

(i) Set of ordered pairs
f = {(2, 0) (4, 1) (6, 2) (10, 4) (12, 5}

(ii) Table

X	2	4	6	10	12
f(x)	0	1	2	4	5

(iii) Arrow diagram

(iv) Graph

Question 3.
Represent the function f = {(1,2), (2,2), (3,2), (4,3),(5,4)} through (i) an arrow diagram (it) a table form (iii) a graph.
Answer:
f = {(1, 2) (2, 2) (3, 2) (4, 3) (5,4)}
Let A = {1,2, 3, 4, 5}
B = {2, 3, 4}

(i) Arrow diagram

(ii) Table form

X	1	2	3	4	5
f(x)	2	2	2	3	4

(iii) Graph

Question 4.
Show that the function f : N → N defined by f(x) = 2x – 1 is one-one but not onto.
Answer:
f: N → N
N = {1,2,3,4,5,… }
f(x) = 2x – 1
f(1) = 2(1) – 1 = 2 – 1 = 1
f(2) = 2(2) – 1 = 4 – 1 = 3
f(3) = 2(3) – 1 = 6 – 1 = 5
f(4) = 2(4) – 1 = 8 – 1 = 7
f(5) = 2(5) – 1 = 10 – 1 = 9
f = {(1,1) (2, 3) (3, 5) (4, 7) (5,9) …..}

(i) Different elements has different images. This function is one to one function.
(ii) Here Range is not equal to co-domain. This function not an onto function.
∴ The given function is one-one but not an onto.

Question 5.
Show that the function f: N ⇒ N defined by f(m) = m² + m + 3 is one-one function.
Answer:
N = {1,2,3, 4,5, ….. }
f(m) = m² + m + 3
f(1) = 1² + 1 + 3 = 5
f(2) = 2² + 2 + 3 = 9
f(3) = 3² + 3 + 3 = 15
f(4) = 4² + 4 + 3 = 23
f = {(1,5) (2, 9) (3, 15) (4, 23)}

From the diagram we can understand different elements in (N) in the domain, there are different images in (N) co-domain.
∴ The function is a one-one function.

Question 6.
Let A = {1, 2, 3, 4) and B = N. Letf: A → B be
defined by f(x) = x³ then,
(i) find the range off
(ii) identify the tpe of function
Solution:
A = {1, 2, 3, 4}
B = N
f: A → B,f(x) = x³
(i) f(1) = 1³ = 1
f(2) = 2³ = 8
f(3) = 3³ = 27
f(4) = 4³ = 64
(ii) Therange of f = {1, 8, 27, 64 )
(iii) It is one-one and into function.

Question 7.
In each of the following cases state whether the function is bijective or not. Justify your answer.
(i) f: R → R defined by f (x) = 2x + 1
(ii) f: R → R defined by f(x) = 3 – 4x²
Answer:
(i) f(x) = 2x + 1
f(0) = 2(0) + 1 = 0 + 1 = 1
f(1) = 2(1) + 1 = 2 + 1 = 3
f(2) = 2(2) + 1 = 4 + 1 = 5
f(3) = 2(3) + 1 = 6 + 1 = 7
Different elements has different images
∴ It is an one-one function.
It is also an onto function. The function is one-one and onto function.
∴ It is a bijective function.

(ii) f(x) = 3 – 4x²
f(1) = 3 – 4(1)²
= 3 – 4 = -1
f(2) = 3 – 4(2)² = 3 – 16 = – 13
f(3) = 3 – 4(3)² = 3 – 36 = – 33
f(4) = 3 – 4(4²) = 3 – 64 = – 61
It is not a bijective function. The positive numbers “R” do not have negative pre – image in X in R.

Question 8.
Let A= {-1,1}and B = {0,2}.
If the function f: A → B defined by
f(x) = ax + b is an onto function? Find a and b.
Answer:
A = {-1, 1}; B = {0,2}
f(x) = ax + b
f(-1) = a(-1) + b
0 = -a + b
a – b = 0 ….(1)
f(1) = a(1) + b
2 = a + b
a + b = 2 ….(2)
Solving (1) and (2) we get

Substitute a = 1 in (1)
The value of a = 1 and b = 1

Question 9.
If the function f is defined by

find the value of
(i) f(3)
(ii) f(0)
(iii) f(1. 5)
(iv) f(2) + f(-2)
Answer:
f(x) = x + 2 when x = {2,3,4,……}
f(x) = 2
f(x) = x – 1 when x = {-2}
(i) f(x) = x + 2
f(3) = 3 + 2 = 5

(ii) f(x) = 2
f(0) = 2

(iii) f(x) = x – 1
f(-1.5) = -1.5 – 1 = -2.5

(iv) f(x) = x + 2
f(2) = 2 + 2 = 4
f(x) = x – 1
f(-2) = – 2 – 1 = – 3
f(2) + f(-2) = 4 – 3
= 1

Question 10.
A function f: [-5, 9] → R is defined as follows:

Answer:
f(x) = 6x + 1 ; x = {-5,-4,-3,-2,-1,0,1}
f(x) = 5x² – 1 ; x = {2, 3, 4, 5}
f(x) = 3x – 4 ; x = {6, 7, 8, 9}

(i) f(-3) + f(2)
f(x) = 6x + 1
f(-3) = 6(-3) + 1 = -18 + 1 = -17
f(x) = 5x² – 1
f(2) = 5(2)² – 1 = 20 – 1 = + 19
f(-3) + f(2) = – 17 + 19
= 2

(ii) f(7) – f(1)
f(x) = 3x – 4
f(7) = 3(7) – 4 = 21 – 4 = 17
f(x) = 6x + 1
f(1) = 6(1) + 1 = 6 + 1 = 7
f(7) – f(1) = 17 – 7
= 10

(iii) 2f(4) + f(8)
f(x) = 5x² – 1
f(4) = 5(4)2 – 1 = 5(16) – 1
= 80 – 1 = 79
f(x) = 3x – 4
f(8) = 3(8) – 4 = 24 – 4 = 20
2f(4) + f(8) = 2(79) + 20
= 158 + 20
= 178

f(x) = 6x + 1
f(-2) = 6(-2) + 1 = -12 + 1 = -11
f(x) = 3x – 4
f(6) = 3(6) – 4 = 18 – 4 = 14
f(x) = 5x² – 1
f(4) = 5(4)² – 1 = 5(16) – 1
= 80 – 1 = 79
f(x) = 6x + 1
f(-2) = 6(-2) + 1 = -12 + 1 = -11

Question 11.
The distance S an object travels under the influence of gravity in time t seconds is given by S(t) = \(\frac{1}{2}\) gt² + at + b where, (g is the acceleration due to gravity), a, b are constants. Check if the function S (t)is one-one.
Solution:
S(t) = \(\frac{1}{2}\) gt² + at + b
Let t be 1, 2, 3, ………, seconds
S(1) = \(\frac{1}{2}\) g(1²) + a(1) + b = \(\frac{1}{2}\) g + a + b
S(2) = \(\frac{1}{2}\) g(2²) + a(2) + b = 2g + 2a + b
Yes, for every different values of t, there will be different values as images. And there will be different preimages for the different values of the range. Therefore it is one-one function.

Question 12.
The function ‘t’ which maps temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by
t(C) = F where F = \(\frac { 9 }{ 5 } \) C + 32. Find,
(i) t(0)
(ii) t(28)
(iii) t(-10)
(iv) the value of C when t(C) = 212
(v) the temperature when the Celsius value is equal to the Fahrenheit value.
Answer:
Given t(C) = \(\frac { 9C }{ 5 } \) + 32

(i) t(0) = \(\frac { 9(0) }{ 5 } \) + 32
= 32° F

(ii) t(28) = \(\frac { 9(28) }{ 5 } \) + 32
= \(\frac { 252 }{ 5 } \) + 32
= 50.4 + 32
= 82.4° F

(iii) t(-10) = \(\frac { 9(-10) }{ 5 } \) + 32
= -18 + 32
= 14° F

(iv) t(C) = 212
\(\frac { 9C }{ 5 } \) + 32 = 212
\(\frac { 9C }{ 5 } \) = 212 – 32
= 180
9C = 180 × 5
C = \(\frac{180 \times 5}{9}\)
= 100° C

(v) consider the value of C be “x”
t(C) = \(\frac { 9C }{ 5 } \) + 32
x = \(\frac { 9x }{ 5 } \) + 32
5x = 9x + 160
-160 = 9x – 5x
-160 = 4x
x = \(\frac { -160 }{ 4 } \) = -40
The temperature when the Celsius value is equal to the fahrenheit value is -40°

Composition of two Functions

Let f: A → B and g: B → C be two functions. Then the composition of f and g denoted by gof is defined as the function gof (x) = g[f(x)] for all x ∈ A.

Composition of three Functions

Let A, B, C, D be four sets and let f: A → B; g : B → C and h : C → D be three functions, using composite functions fog and goh, we get two new functions like (fog) oh and fo (goh).
Note: Composition of three function is always associative.

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.2 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.2

Question 1.
What is the slope of a line whose inclination with positive direction of x -axis is
(i) 90°
(ii) 0°
Solution:
Here θ = 90°
Slope (m) = tan θ
Slope = tan 90°
= undefined.

(ii) Here θ = 0°
Slope (m) = tan θ
Slope = tan 0°
= 0

Question 2.
What is the inclination of a line whose slope is
(i) 0
(ii) 1
Solution:
(i) m = 0
tan θ = 0 ⇒ θ = 0°
(ii) m = 1 ⇒ tan θ = tan 45° ⇒ 0 = 45°

Question 3.
Find the slope of a line joining the points
(i) (5,\(\sqrt { 5 }\)) with the origin
(ii) (sin θ, -cos θ) and (-sin θ, cos θ)
Solution:
(i) The given points is (5,\(\sqrt { 5 }\)) and (0, 0)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) = \(\frac{0-\sqrt{5}}{0-5}\)
= \(\frac{\sqrt{5}}{5}=\frac{1}{\sqrt{5}}\)

(ii) The given points is (sin θ, -cos θ) and (-sin θ, cos θ)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{\cos \theta+\cos \theta}{-\sin \theta-\sin \theta}\)
= \(\frac{2 \cos \theta}{-2 \sin \theta}\) = – cot θ

Question 4.
What is the slope of a line perpendicular to the line joining A(5,1) and P where P is the mid-point of the segment joining (4,2) and (-6,4).
Solution:
Mid point of XY = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\) = (\(\frac { 4-6 }{ 2 } \),\(\frac { 2+4 }{ 2 } \))
= (\(\frac { -2 }{ 2 } \),\(\frac { 6 }{ 2 } \)) = (-1, 3)

Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) = (\(\frac { 3-1 }{ -1-5 } \))
= \(\frac { 2 }{ -6 } \) = – \(\frac { 1 }{ 3 } \)

Question 5.
Show that the given points are collinear: (-3, -4), (7,2) and (12, 5)
Solution:
The vertices are A(-3, -4), B(7, 2) and C(12, 5)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = \(\frac { 2+4 }{ 7+3 } \) = \(\frac { 6 }{ 10 } \) = \(\frac { 3 }{ 5 } \)
Slope of BC = \(\frac { 5-2 }{ 12-7 } \) = \(\frac { 3 }{ 5 } \)
Slope of AB = Slope of BC = \(\frac { 3 }{ 5 } \)
∴ The three points A,B,C are collinear.

Question 6.
If the three points (3, -1), (a, 3) and (1, -3) are collinear, find the value of a.
Solution:
The vertices are A(3, -1), B(a, 3) and C(1, -3)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = \(\frac { 3+1 }{ a-3 } \) = \(\frac { 4 }{ a-3 } \)
Slope of BC = \(\frac { 3+3 }{ a-1 } \) = \(\frac { 6 }{ a-1 } \)
Since the three points are collinear.
Slope of AB = Slope BC
\(\frac { 4 }{ a-3 } \) = \(\frac { 6 }{ a-1 } \)
6 (a – 3) = 4 (a – 1)
6a – 18 = 4a – 4
6a – 4a = -4 + 18
2a = 14 ⇒ a = \(\frac { 14 }{ 2 } \) = 7
The value of a = 7

Question 7.
The line through the points (-2, a) and (9,3) has slope –\(\frac { 1 }{ 2 } \) Find the value of a.
Solution:
The given points are (-2, a) and (9, 3)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
– \(\frac { 1 }{ 2 } \) = \(\frac { 3-a }{ 9+2 } \) ⇒ – \(\frac { 1 }{ 2 } \) = \(\frac { 3-a }{ 11 } \)
2(3 – a) = -11 ⇒ 6 – 2a = -11
-2a = -11 – 6 ⇒ -2a = -17 ⇒ a = – \(\frac { 17 }{ 2 } \)
∴ The value of a = \(\frac { 17 }{ 2 } \)

Question 8.
The line through the points (-2, 6) and (4, 8) is perpendicular to the line through the points (8,12) and (x, 24). Find the value of x.
Solution:
Find the slope of the line joining the point (-2, 6) and (4, 8)
Slope of line (m1) = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac { 8-6 }{ 4+2 } \) = \(\frac { 2 }{ 6 } \) = \(\frac { 1 }{ 3 } \)
Find the slope of the line joining the points (8, 12) and (x, 24)
Slope of a line (m2) = \(\frac { 24-12 }{ x-8 } \) = \(\frac { 12 }{ x-8 } \)
Since the two lines are perpendicular.
m₁ × m₂ = -1
\(\frac { 1 }{ 3 } \) × \(\frac { 12 }{ x-8 } \) = -1 ⇒ \(\frac{12}{3(x-8)}=-1\)
-1 × 3 (x – 8) = 12
-3x + 24 = 12 ⇒ – 3x = 12 -24
-3x = -12 ⇒ x = \(\frac { 12 }{ 3 } \) = 4
∴ The value of x = 4

Question 9.
Show that the given points form a right angled triangle and check whether they satisfies Pythagoras theorem.
(i) A(1, -4) , B(2, -3) and C(4, -7)
(ii) L(0, 5), M(9,12) and N(3,14)
Solution:
(i) The vertices are A(1, -4), B(2, -3) and C(4, -7)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = \(\frac { -3+4 }{ 2-1 } \) = \(\frac { 1 }{ 1 } \) = 1
Slope of BC = \(\frac { -7+3 }{ 4-2 } \) = \(\frac { -4 }{ 2 } \) = -2
Slope of AC = \(\frac { -7+4 }{ 4-1 } \) = – \(\frac { 3 }{ 3 } \) = -1
Slope of AB × Slope of AC = 1 × -1 = -1

∴ AB is ⊥^r to AC
∠A = 90°
∴ ABC is a right angle triangle
Verification:

20 = 2 + 18
20 = 20 ⇒ Pythagoras theorem verified

(ii) The vertices are L(0, 5), M(9, 12) and N(3, 14)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of LM = \(\frac { 12-5 }{ 9-0 } \) = \(\frac { 7 }{ 9 } \)

Slope of MN = \(\frac { 14-12 }{ 3-9 } \) = \(\frac { 2 }{ -6 } \) = – \(\frac { 1 }{ 3 } \)
Slope of LN = \(\frac { 14-5 }{ 3-0 } \) = \(\frac { 9 }{ 3 } \) = 3
Slope of MN × Slope of LN = – \(\frac { 1 }{ 3 } \) × 3 = -1
∴ MN ⊥ LN
∠N = 90°
∴ LMN is a right angle triangle
Verification:


130 = 90 + 40
130 = 130 ⇒ Pythagoras theorem is verified

Question 10.
Show that the given points form a parallelogram:
A (2.5,3.5), B(10, -4), C(2.5, -2.5) and D(-5, 5).
Solution:
Let A(2.5, 3.5), B(10, -4), C(2.5, -2.5) and D(-5, 5) are the vertices of a parallelogram.


Slope of AB = Slope of CD = -1
∴ AB is Parallel to CD ……(1)

Slope of BC = Slope of AD
∴ BC is parallel to AD
From (1) and (2) we get ABCD is a parallelogram.

Question 11.
If the points A(2, 2), B(-2, -3), C(1, -3) and D(x, y) form a parallelogram then find the value of x and y.
Solution:
Let A(2, 2), B(-2, -3), C(1, -3) and D(x, y) are the vertices of a parallelogram.

Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = \(\frac { -3-2 }{ -2-2 } \) = \(\frac { -5 }{ -4 } \) = \(\frac { 5 }{ 4 } \)
Slope of BC = \(\frac { -3+3 }{ -2-1 } \) = \(\frac { 0 }{ -3 } \) = 0
Slope of CD = \(\frac { y+3 }{ x-1 } \)
Slope of AD = \(\frac { y-2 }{ x-2 } \)
Since ABCD is a parallelogram
Slope of AB = Slope of CD
\(\frac { 5 }{ 4 } \) = \(\frac { y+3 }{ x-1 } \)
5(x – 1) = 4 (y + 3)
5x – 5 = 4y + 12
5x – 4y = 12 + 5
5x – 4y = 17 ……(1)
Slope of BC = Slope of AD
0 = \(\frac { y-2 }{ x-2 } \)
y – 2 = 0
y = 2
Substitute the value of y = 2 in (1)
5x – 4(2) = 17
5x -8 = 17 ⇒ 5x = 17 + 18
5x = 25 ⇒ x = \(\frac { 25 }{ 5 } \) = 5
The value of x = 5 and y = 2.

Question 12.
Let A(3, -4), B(9, -4) , C(5, -7) and D(7, -7). Show that ABCD is a trapezium.
Solution:
Let A(3, -4), B(9, -4), C(5, -7) and D(7, -7) are the vertices of a quadrilateral.

Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of AB = \(\frac { -4+4 }{ 9-3 } \) = \(\frac { 0 }{ 6 } \) = 0
Slope of BC = \(\frac { -7+4 }{ 5-9 } \) = \(\frac { -3 }{ -4 } \) = \(\frac { 3 }{ 4 } \)
Slope of CD = \(\frac { -7+7 }{ 7-5 } \) = \(\frac { 0 }{ 2 } \) = 0
Slope of AD = \(\frac { -7+4 }{ 7-3 } \) = \(\frac { -3 }{ 4 } \) = – \(\frac { 3 }{ 4 } \)
The slope of AB and CD are equal.
∴ AB is parallel to CD. Similarly the slope of AD and BC are not equal.
∴ AD and BC are not parallel.
∴ The Quadrilateral ABCD is a trapezium.

Question 13.
A quadrilateral has vertices at A(-4, -2), B(5, -1) , C(6, 5) and D(-7, 6). Show that the mid-points of its sides form a parallelogram.
Solution:
Let A(-4, -2), B(5, -1), C(6, 5) and D(-7, 6) are the vertices of a quadrilateral.





Slope of EF = Slope of GH = \(\frac { 7 }{ 10 } \)
∴ EF || GH …….(1)
Slope of FG= Slope of EH = – \(\frac { 7 }{ 12 } \)
∴ FG || EH ……(2)
From (1) and (2) we get EFGH is a parallelogram.
The mid point of the sides of the Quadrilateral ABCD is a Parallelogram.

Question 14.
PQRS is a rhombus. Its diagonals PR and QS intersect at the point M and satisfy QS = 2PR. If the coordinates of S and M are (1, 1) and (2, -1) respectively, find the coordinates of P.
Solution:
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Slope of SM = \(\frac { 1+1 }{ 1-2 } \) = \(\frac { 2 }{ -1 } \) = -2
Slope of PM = \(\frac { 1 }{ 2 } \) (Since SM and PM are ⊥^r)
Let the point p be (a,b)
Slope of PM = \(\frac { 1 }{ 2 } \)
\(\frac { b+1 }{ a-2 } \) = \(\frac { 1 }{ 2 } \) ⇒ a – 2 = 2b + 2

a – 2b = 4
a = 4 + 2b ……(1)
Given QS = 2PR
\(\frac { QS }{ 2 } \) = PR
∴ SM = PR
SM = 2PM (PR = 2PM)

Squaring on both sides

∴ (b + 1)² = \(\frac { 1 }{ 4 } \) ⇒ b + 1 = ± \(\frac { 1 }{ 2 } \)
b = \(\frac { 1 }{ 2 } \) – 1 (or) b = – \(\frac { 1 }{ 2 } \) – 1
= – \(\frac { 1 }{ 2 } \) – 1 (or) b = –\(\frac { 1 }{ 2 } \) – 1
= – \(\frac { 1 }{ 2 } \) (or) – \(\frac { 3 }{ 2 } \)
a = 4 + 2b
a = 4 + 2 (\(\frac { -1 }{ 2 } \))
a = 3
a = 4 + 2 (\(\frac { -3 }{ 2 } \))
a = 4 – 3
a = 1
The point of p is (3,\(\frac { -1 }{ 2 } \)) (or) (1,\(\frac { -3 }{ 2 } \))

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.3 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.3

Question 1.
Find the equation of a straight line passing through the mid-point of a line segment joining the points (1, -5), (4, 2) and parallel to (i) X axis (ii) Y axis
Solution:
Mid point of the line joining to points (1, -5), (4, 2)
Mid point of the line = (\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
= (\(\frac { 1+4 }{ 2 } \),\(\frac { -5+2 }{ 2 } \)) = (\(\frac { 5 }{ 2 } \),\(\frac { -3 }{ 2 } \))

(i) Any line parallel to X-axis. Slope of a line is 0.
Equation of a line is y – y₁ = m (x – x₁)
y + \(\frac { 3 }{ 2 } \) = 0 (x – \(\frac { 5 }{ 2 } \))
y + \(\frac { 3 }{ 2 } \) = 0 ⇒ \(\frac { 2y+3 }{ 2 } \) = 0
2y + 3 = 0

(ii) Equation of a line parallel to Y-axis is
x = \(\frac { 5 }{ 2 } \) ⇒ 2x = 5
2x – 5 = 0

Question 2.
The equation of a straight line is 2(x – y) + 5 = 0. Find its slope, inclination and intercept on the Y axis.
Solution:
Equation of a line is
2 (x – y) + 5 = 0
2 x – 2y + 5 = 0
-2y = -2x – 5
2y = 2x + 5
y = \(\frac { 2x }{ 2 } \) + \(\frac { 5 }{ 2 } \)
y = x + \(\frac { 5 }{ 2 } \)
Slope of line = 1
Y intercept = \(\frac { 5 }{ 2 } \)
tan θ = 1
tan θ = tan 45°
∴ angle of inclination = 45°

Question 3.
Find the equation of a line whose inclination is 30° and making an intercept -3 on the Y axis.
Solution:
Angle of inclination = 30°
Slope of a line = tan 30°
(m) = \(\frac{1}{\sqrt{3}}\)
y intercept (c) = -3
Equation of a line is y = mx + c
y = \(\frac{1}{\sqrt{3}}\) x – 3
\(\sqrt { 3 }\) y = x – 3 \(\sqrt { 3 }\)
∴ x – \(\sqrt { 3 }\) y – 3 \(\sqrt { 3 }\) = 0

Question 4.
Find the slope and y intercept of \(\sqrt { 3x }\) + (1 – \(\sqrt { 3 }\))y = 3.
Solution:
The equation of a line is \(\sqrt { 3 }\)x + (1 – \(\sqrt { 3 }\))y = 3
(1 – \(\sqrt { 3 }\))y = \(\sqrt { 3 }\) x + 3

Question 5.
Find the value of ‘a’, if the line through (-2,3) and (8,5) is perpendicular to y = ax + 2
Solution:
Given points are (-2, 3) and (8, 5)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac { 5-3 }{ 8+2 } \) = \(\frac { 2 }{ 10 } \) = \(\frac { 1 }{ 5 } \)
Slope of a line y = ax + 2 is “a”
Since two lines are ⊥^r
m₁ × m₂ = -1
\(\frac { 1 }{ 5 } \) × a = -1 ⇒ \(\frac { a }{ 5 } \) = -1 ⇒ a = -5
∴ The value of a = -5

Question 6.
The hill in the form of a right triangle has its foot at (19,3). The inclination of the hill to the ground is 45°. Find the equation of the hill joining the foot and top.
Solution:
Slope of AB (m) = tan 45°
= 1
Equation of the hill joining the foot and the top is
y – y₁ = m(x – x₁)
y – 3 = 1 (x – 19)

y – 3 = x – 19
– x + y – 3 + 19 = 0
– x + y + 16 = 0
x – y – 16 = 0
The required equation is x – y – 16 = 0

Question 7.
Find the equation of a line through the given pair of points.
(i) (2,\(\frac { 2 }{ 3 } \)) and (\(\frac { -1 }{ 2 } \),-2)
(ii) (2,3) and (-7,-1)
Solution:
(i) Equation of the line passing through the point (2,\(\frac { 2 }{ 3 } \)) and (\(\frac { -1 }{ 2 } \),-2)


-5(3y – 2) = -8 × 2 (x – 2)
-15y + 10= -16 (x – 2)
-15y + 10= -16x + 32
16x – 15y + 10 – 32 = 0
16x – 15y – 22 = 0
The required equation is 16x – 15y – 22 = 0

(ii) Equation of the line joining the point (2, 3) and (-7, -1) is

-9 (y – 3) = -4 (x – 2)
-9y + 27 = – 4x + 8
4x – 9y + 27 – 8 = 0
4x – 9y + 19 = 0
The required equation is 4x – 9y + 19 = 0

Question 8.
A cat is located at the point(-6, -4) in xy plane. A bottle of milk is kept at (5,11). The cat wish to consume the milk travelling through shortest possible distance. Find the equation of the path it needs to take its milk.
Solution:

Equation of the line joining the point is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
\(\frac { y+4 }{ 11+4 } \) = \(\frac { x+6 }{ 5+6 } \)
\(\frac { y+4 }{ 15 } \) = \(\frac { x+6 }{ 11 } \)
15(x + 6) = 11(y + 4)
15x + 90 = 11y + 44
15x – 11y + 90 – 44 = 0
15x – 11y + 46 = 0
The equation of the path is 15x – 11y + 46 = 0

Question 9.
Find the equation of the median and altitude of AABC through A where the vertices are A(6,2), B(-5, -1) and C(1,9).
Solution:
(i) To find median


Equation of the median AD is

2(x – 6) = -8 (y – 2)
2x – 12= -8y + 16
2x + 8y – 28 = 0
(÷ by 2) x + 4y – 14 = 0
∴ Equation of the median is x + 4y – 14 = 0
Equation of the altitude is 3x + 5y – 28 = 0

(ii) To find the equation of the altitude

Slope of BC = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac { 9+1 }{ 1+5 } \)
= \(\frac { 10 }{ 6 } \) = \(\frac { 5 }{ 3 } \)
Slope of the altitude = – \(\frac { 3 }{ 5 } \)
Equation of the altitude AD is
y – y1 = m (x – x₁)
y – 2 = – \(\frac { 3 }{ 5 } \) (x – 6)
-3 (x – 6) = 5 (y – 2)
-3x + 18 = 5y – 10
-3x – 5y + 18 + 10 = 0
-3x – 5y + 28 = 0
3x + 5y – 28 = 0

Question 10.
Find the equation of a straight line which has slope \(\frac { -5 }{ 4 } \) and passing through the point (-1,2).
Solution:
Slope of a line (m) = \(\frac { -5 }{ 4 } \)
The given point (x₁, y₁) = (-1, 2)
Equation of a line is y – y₁ = m (x – x₁)
y – 2= \(\frac { -5 }{ 4 } \) (x + 1)
5(x + 1) = -4(y – 2)
5x +5 = -4y + 8
5x + 4y + 5 – 8 = 0
5x + 4y – 3 = 0
The equation of a line is 5x + 4y – 3 = 0

Question 11.
You are downloading a song. The percenty (in decimal form) of mega bytes remaining to get downloaded in x seconds is given by y = -0.1x + 1.
(i) graph the equation.
(ii) find the total MB of the song.
(iii) after how many seconds will 75% of the song gets downloaded?
(iv) after how many seconds the song will be downloaded completely?
Solution:
(i) y = – 0. 1x + 1

(ii) y = -0.1x + 1
x → seconds
y → Mega byte of the song.
The total mega byte of the song is at the beginning that is when x = 0
y = 1 mega byte

(iii) When 75% of song gets downloaded 25% remains.
In other words y = 25%
y = 0.25
By using the equation we get
0.25 = -0.1x + 1
0.1 x = 0.75
x = \(\frac { 0.75 }{ 0.1 } \) = 7.5 seconds

(iv) When song is downloaded completely the remaining percent is zero.
i.e y = 0
0 = -0.1 x + 1
0.1 x = 1 second
x = \(\frac { 1 }{ 0.1 } \) = \(\frac { 1 }{ 1 } \) × 10
x = 10 seconds

Question 12.
Find the equation of a line whose intercepts on the x and y axes are given below.
(i) 4, -6
(ii) -5, – 4
Solution:
(i) x intercept (a) = 4; y intercept (b) = – 6
Equation of a line is \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
\(\frac { x }{ 4 } \) + \(\frac { y }{ -6 } \) = 1 ⇒ \(\frac { x }{ 4 } \) – \(\frac { y }{ 6 } \) = 1
(LCM of 4 and 6 is 12)
3x – 2y = 12
3x – 2y – 12 = 0
The equation of a line is 3x – 2y – 12 = 0

(ii) x intercept (a) = -5; y intercept (b) = \(\frac { 3 }{ 4 } \)
Equation of a line is \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1 ⇒ \(\frac{x}{-5}+\frac{y}{\frac{3}{4}}=1\)
\(\frac { x }{ -5 } \) + \(\frac { 4y }{ 3 } \) = 1
(LCM of 5 and 3 is 15)
– 3x + 20y = 15
– 3x + 20y – 15 = 0
3x – 20y + 15 = 0
∴ Equation of a line is 3x – 20y + 15 = 0

Question 13.
Find the intercepts made by the following lines on the coordinate axes.
(i) 3x – 2y – 6 = 0
(ii) 4x + 3y + 12 = 0
Solution:
(i) 3x – 2y – 6 =0.
x intercept when y = 0
⇒ 3x – 6 = 0
⇒ x = 2
y intercept when x = 0
⇒ 0 – 2y – 6 = 0
⇒ y = -3
(ii) 4x + 3y + 12 = 0. x intercept when y = 0
⇒ 4x + 0 + 12 = 0
⇒ x = -3
y intercept when x = 0
⇒ 0 + 3y + 12 = 0
⇒ y = -4

Question 14.
Find the equation of a straight line.
(i) passing through (1,-4) and has intercepts which are in the ratio 2 : 5
(ii) passing through (-8, 4) and making equal intercepts on the coordinate axes.
Solution:
(i) Let the x-intercept be 2a and the y intercept 5 a
The equation of a line is
\(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1 ⇒ \(\frac { x }{ 2a } \) + \(\frac { y }{ 5a } \) = 1
The line passes through the point (1, -4)
\(\frac { 1 }{ 2a } \) + \(\frac { (-4) }{ 5a } \) = 1 ⇒ \(\frac { 1 }{ 2a } \) – \(\frac { 4 }{ 5a } \) = 1
Multiply by 10a
(L.C.M of 2a and 5a is 10a)
5 – 8 = 10a ⇒ -3 = 10a
a = \(\frac { -3 }{ 10 } \)
The equation of the line is

Multiply by 3
-5x – 2y = 3 ⇒ -5x – 2y – 3 = 0
5x + 2y + 3 = 0
The equation of a line is 5x + 2y + 3 = 0

(ii) Let the x-intercept andy intercept “a”
The equation of a line is
\(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1
The line passes through the point (-8, 4)
\(\frac { -8 }{ a } \) + \(\frac { 4 }{ a } \) = 1
\(\frac { -8+4 }{ a } \) = 1
-4 = a
The equation of a line is
\(\frac { x }{ -4 } \) + \(\frac { y }{ -4 } \) = 1
Multiply by -4
x + y = -4
x + y + 4 = 0
The equation of the line is x + y + 4 = 0

Students can download Maths Chapter 4 Geometry Unit Exercise 4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Unit Exercise 4

Question 1.
In the figure, if BD ⊥ AC and CE ⊥ AB , prove that
(i) ∆ AEC ~ ∆ADB
(ii) \(\frac { CA }{ AB } \) = \(\frac { CE }{ DB } \)

Solution:
(i) ∠AEC = ∠ADB = 90° ∠A is common By AA – Similarity.
∴ ∆AEC ~ ∆ADB
Since the two triangles are similar

(ii) \(\frac { AE }{ AD } \) = \(\frac { AC }{ AB } \) = \(\frac { EC }{ DB } \)
\(\frac { AC }{ AB } \) = \(\frac { CE }{ DB } \)

Question 2.
In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.

Solution:
In the given diagram ∆AEF and ∆ACD
∠AEF = ∠ACD = 90°
∠A is common
By AA – Similarity.
∴ ∆AEF ~ ∆ACD
\(\frac { AE }{ AC } \) = \(\frac { AF }{ AD } \) = \(\frac { EF }{ CD } \)
\(\frac { AE }{ AC } \) = \(\frac { EF }{ CD } \)
\(\frac { AE }{ AC } \) = \(\frac { 4 }{ x } \)
AC = \(\frac{\mathrm{AE} \times x}{4}\) …..(1)
In ∆EAB and ∆ECD,
∠EAB = ∠ECD = 90°
∠E is common
∆ ECD ~ ∆EAB
\(\frac { EC }{ EA } \) = \(\frac { ED }{ EB } \) = \(\frac { CD }{ AB } \)
\(\frac { EC }{ EA } \) = \(\frac { x }{ 6 } \)
EC = \(\frac{\mathrm{EA} \times x}{6}\) …….(2)
In ∆AEB; CD || AB
By Basic Proportionality Theorem
\(\frac { AB }{ CD } \) = \(\frac { EB }{ ED } \)
\(\frac { 6 }{ x } \) = \(\frac { 5+y }{ y } \)
x = \(\frac { 6y }{ y+5 } \) (EC = x) …….(3)
Add (1) and (2) we get
AC + EC = \(\frac{A E \times x}{4}+\frac{x \times E A}{6}\)
>
Substitute the value of x = 2.4 in (3)
2.4 = \(\frac { 6y }{ y+5 } \)
6y = 2.4y + 12
6y – 2.4y = 12 ⇒ 3.6 y = 12
y = \(\frac { 12 }{ 3.6 } \) = \(\frac { 120 }{ 36 } \) = \(\frac { 10 }{ 3 } \) = 3.3 cm
The value of x = \(\frac { 12 }{ 5 } \) (or) 2.4 cm and y = \(\frac { 10 }{ 3 } \) (or) 3.3 cm

Question 3.
O is any point inside a triangle ABC. The bisector of ∠AOB, ∠BOC and ∠COA meet the sides AB, BC and CA in point D, E and F respectively. Show that AD × BE × CF = DB × EC × FA.
Solution:
In ∆ABC the bisector meets AB at D, BC at E and AC at F.

The angle bisector AO, BO and CO intersect at “O”.
By Cevas Theorem
\(\frac { AD }{ DB } \) × \(\frac { BE }{ EC } \) × \(\frac { CF }{ AF } \) = 1
AD × BE × CF = DB × EC × AF
Hence it is proved

Question 4.
In the figure, ABC is a triangle in which AB = AC. Points D and E are points on the side AB and AC respectively such that AD = AE. Show that the points B, C, E and D lie on a same circle.

Solution:
∠B = ∠C (Given AB = AC)
AD + DB = AE + EC
BD = EC (Given AD = AE)
DE parallel BC Since AEC is a straight line.
∠AED + ∠CED = 180°
∠CBD + ∠CED = 180°
Similarly of the opposite angles = 180°
∴ BCED is a cyclic quadrilateral

Question 5.
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of 20 km/hr and the second train travels at 30 km/hr. After 2 hours, what is the distance between them?
Solution:
A is the position of the 1^st train.
B is the position of the 2^nd train.

Distance Covered in 2 hours
OA = 2 × 20 = 40 km
OB = 2 × 30 = 60 km
Distance between the train after 2 hours

Distance between
the two train = 72.11 km (or) 20\(\sqrt { 13 }\) km

Question 6.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that
(i) b² = p² + ax + \(\frac{a^{2}}{4}\)
(ii) c² = p² – ax + \(\frac{a^{2}}{4}\)
(iii) a² + c² = 2 p² + \(\frac{a^{2}}{2}\)
Solution:
(i) Given ∠AED = 90°

ED = x; DC = \(\frac { a }{ 2 } \)
(D is the mid point of BC)
∴ EC = x + \(\frac { a }{ 2 } \), BE = \(\frac { a }{ 2 } \) – x
∴ In the right ∆ AED
AD² = AE² + ED²
p² = h² + x²
In the right ∆ AEC,
AC² = AE² + EC²

(ii) In the right triangle ABE,
AB² = AE² + BE²
c² = h² + (\(\frac { a }{ 2 } \) – x)²
c² = h² + \(\frac{a^{2}}{4}\) + x² – ax
c² = h² + x² + \(\frac { 1 }{ 4 } \) a² – ax
c² = p² – ax + \(\frac{a^{2}}{4}\) (from 1)

(iii) By adding (2) and (3)
b² + c² = p² + ax + \(\frac{a^{2}}{4}\) + p² – ax + \(\frac{a^{2}}{4}\)
= 2p² + \(\frac{2a^{2}}{4}\)
= 2p² + \(\frac{a^{2}}{2}\)

Question 7.
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
Solution:
Let the height of the tree AD be “h”.

In ∆ ACD and ∆ BCF,
∠A = ∠B = 90°
∠C is common
∆ ACD ~ ∆ BCF by AA similarity
\(\frac { AD }{ BF } \) = \(\frac { AC }{ BC } \)
\(\frac { h }{ x } \) = \(\frac { 24 }{ 2 } \) = 6
h = 6x ………(1)
In ∆ ACE and ∆ ABF,
∠C = ∠B = 90°
∠A is common
∴ ∆ ACE ~ ∆ ABF
\(\frac { CE }{ BF } \) = \(\frac { AC }{ AB } \)
\(\frac { 2 }{ x } \) = \(\frac { 24 }{ 20 } \)
24x = 20 × 2
x = \(\frac{20 \times 2}{24}=\frac{5 \times 2}{6}=\frac{10}{6}\)
x = \(\frac { 5 }{ 3 } \)
Substitute the value of x in (1)
h = 6 × \(\frac { 5 }{ 3 } \) = 10 m
∴ Height of the tree is 10 m

Question 8.
An emu which is 8 ft tail is standing at the foot of a pillar which is 30 ft high. It walks away from the pillar. The shadow of the emu falls beyond emu. What is the relation between the length of the shadow and the distance from the emu to the pillar?
Solution:
Let the shadow of the emu AE be “x” and BE be “y” ED || BC

By basic proportionality theorem
\(\frac { AE }{ AB } \) = \(\frac { ED }{ BC } \)
\(\frac { x }{ x+y } \) = \(\frac { 8 }{ 30 } \)
30x = 8x + 8y
22x – 8y = 0
(÷ by 2) 11x – 4y = 0
11x = 4y
x = \(\frac { 4 }{ 11 } \) × y
x = \(\frac { 4 }{ 11 } \) × distance from the pillar to emu
Length of = \(\frac { 4 }{ 11 } \) × distance from the shadow the pillar to emu

Question 9.
Two circles intersect at A and B. From a point P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
Solution:
Proof:

A and B are the points intersecting the circles. Join AB.
∠P’PB = ∠PAB (alternate segment theorem)
∠PAB + ∠BAC = 180° …(1)
(PAC is a straight line)
∠BAC + ∠BDC = 180° …(2)
ABDC is a cyclic quadrilateral.
From (1) and (2) we get
∠P’PB = ∠PAB = ∠BDC
P’P and DC are straight lines.
PD is a transversal alternate angles are equal.
∴ P’P || DC.

Question 10.
Let ABC be a triangle and D, E, F are points on the respective sides AB, BC, AC (or their extensions).
Let AD : DB = 5 : 3, BE : EC = 3 : 2 and AC = 21. Find the length of the line segment CF.
Solution:

\(\frac { AD }{ DB } \) = \(\frac { 5 }{ 3 } \); \(\frac { BE }{ EC } \) = \(\frac { 3 }{ 2 } \); AC = 21
By Ceva’s theorem

Length of the line segment CF = 6 units

Students can download Maths Chapter 4 Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Additional Questions

I. Multiple choice questions

Question 1.
If a straight line intersects the sides AB and AC of a ∆ABC at D and E respectively and is parallel to BC, then \(\frac { AE }{ AC } \) = …………
(1) \(\frac { AD }{ DB } \)
(2) \(\frac { AD }{ DB } \)
(3) \(\frac { DE }{ BC } \)
(4) \(\frac { AD }{ EC } \)
Answer:
(2) \(\frac { AD }{ DB } \)

Hint:
By BPT theorem,
\(\frac { AE }{ AC } \) = \(\frac { AD }{ AB } \)

Question 2.
In ∆ABC, DE is || to BC, meeting AB and AC at D and E. If AD = 3 cm, DB = 2 cm and AE = 2.7 cm, then AC is equal to ……..
(1) 6.5 cm
(2) 4.5 cm
(3) 3.5 cm
(4) 3.5 cm
Answer:
(2) 4.5 cm
Hint:
By BPT theorem,

\(\frac { AD }{ DB } \) = \(\frac { AE }{ EC } \)
\(\frac { 3 }{ 2 } \) = \(\frac { 2.7 }{ EC } \)
∴ EC = \(\frac{2.7 \times 2}{3}\) = 1.8 CM
AC = AE + EC
= 2.7 + 1.8 = 4.5 cm

Question 3.
In ∆PQR, RS is the bisector of ∠R. If PQ = 6 cm, QR = 8 cm, RP = 4 cm then PS is equal to …………..
(1) 2 cm
(2) 4 cm
(3) 3 cm
(4) 6 cm
Answer:
(2) 2 cm
Hint:

By ABT theorem,
\(\frac { PS }{ SQ } \) = \(\frac { PR }{ QR } \) ⇒ \(\frac { x }{ 6-x } \) = \(\frac { 4 }{ 8 } \)
24 – 4x = 8x ⇒ 24 = 12x
x = 2
PS = 2 cm

Question 4.
In figure, if \(\frac { AB }{ AC } \) = \(\frac { BD }{ DC } \), ∠B = 40° and ∠C = 60°, then ∠BAD = ……………
(1) 30°
(2) 50°
(3) 80°
(4) 40°
Answer:
(4) 40°
Hint:
\(\frac { AB }{ AC } \) = \(\frac { BD }{ DC } \)

AD is the internal bisector of ∠BAC
∠A + ∠B + ∠C = 180°
∠A + 40° + 60° = 180° ⇒ ∠A = 80°
∴ ∠BAC = \(\frac { 80 }{ 2 } \) = 40°

Question 5.
In the figure, the value x is equal to …………
(1) 4.2
(2) 3.2
(3) 0.8
(4) 0.4

Answer:
(2) 3.2
Hint:
By Thales theorem
(DE || BC)
\(\frac { AD }{ BD } \) = \(\frac { AE }{ EC } \)
\(\frac { x }{ 8 } \) = \(\frac { 4 }{ 10 } \) ⇒ x = \(\frac{8 \times 4}{10}\) = 3.2

Question 6.
In triangles ABC and DEF, ∠B = ∠E, ∠C = ∠F, then ………….
(1) \(\frac { AB }{ DE } \) = \(\frac { CA }{ EF } \)
(2) \(\frac { BC }{ EF } \) = \(\frac { AB }{ FD } \)
(3) \(\frac { AB }{ DE } \) = \(\frac { BC }{ EF } \)
(4) \(\frac { CA }{ FD } \) = \(\frac { AB }{ EF } \)
Answer:
(3) \(\frac { AB }{ DE } \) = \(\frac { BC }{ EF } \)
Hint:

Question 7.
From the given figure, identify the wrong statement.

(1) ∆ADB ~ ∆ABC
(2) ∆ABD ~ ∆ABC
(3) ∆BDC ~ ∆ABC
(4) ∆ADB ~ ∆BDC
Answer:
(2) ∆ ABD ~ ∆ ABC

Question 8.
If a vertical stick 12 m long casts a shadow 8 m long on the ground and at the same time a tower casts a shadow 40 m long on the ground, then the height of the tower is …………..
(1) 40 m
(2) 50 m
(3) 75 m
(4) 60 m
Answer:
(4) 60 m
Hint:

\(\frac { AB }{ DE } \) = \(\frac { BC }{ EF } \)
\(\frac { 12 }{ h } \) = \(\frac { 8 }{ 40 } \); h = \(\frac{40 \times 12}{8}\) = 60

Question 9.
The sides of two similar triangles are in the ratio 2:3, then their areas are in the ratio ………….
(1) 9 : 4
(2) 4 : 9
(3) 2 : 3
(4) 3 : 2
Answer:
(2) 4 : 9
Hint:
Ratio of the Area of two similar triangle
= 2² : 3² = 4 : 9
[squares of their corresponding sides]

Question 10.
Triangles ABC and DEF are similar. If their areas are 100 cm² and 49 cm² respectively and BC is 8.2 cm then EF = …………….
(1) 5.47 cm
(2) 5.74 cm
(3) 6.47 cm
(4) 6.74 cm
Answer:
(2) 5.74 cm
Hint:

Question 11.
The perimeters of two similar triangles are 24 cm and 18 cm respectively.
If one side of the first triangle is 8 cm, then the corresponding side of the other triangle is ………
(1) 4 cm
(2) 3 cm
(3) 9 cm
(4) 6 cm
Answer:
(4) 6 cm
Hint:

Question 12.
A point P is 26 cm away from the centre O of a circle and PT is the tangent drawn from P to the circle 10 cm, then OT is equal to …………
(1) 36 cm
(2) 20 cm
(3) 18 cm
(4) 24 cm
Answer:
(4) 24 cm
Hint:

OT² = OP² – PT²
= 26² – 10²
= (26 + 10) (26 – 10)
OT² = 36 × 16
OT = 6 × 4 = 24 cm

Question 13.
In the figure, if ∠PAB = 120° then ∠BPT = ……….

(1) 120°
(2) 30°
(3) 40°
(4) 60°
Answer:
(4) 60°
Hint:
∠BCP + ∠PAB = 180°
(sum of the opposite angles of a cyclic quadrilateral)
∠BCP = 180° – 120° = 60°
∠BPT = 60°
(By tangent chord theorem)

Question 14.
If the tangents PA and PB from an external point P to circle with centre O are inclined to each other at an angle of 40°, then ∠POA = ………………
(1) 70°
(2) 80°
(3) 50°
(4) 60°
Answer:
(1) 70°
Hint:
∠OPA = \(\frac { 40 }{ 2 } \) = 20°
In ∆OAP.
∠POA + ∠OAP + ∠APO = 180°
(sum of the angles of a triangle)

∠POA + 90° + 20° = 180°
∠POA = 180° – 110° = 70°

Question 15.
In the figure, PA and PB are tangents to the circle drawn from an external point P. Also CD is a tangent to the circle at Q. If PA = 8 cm and CQ = 3 cm, then PC is equal to ……….

(1) 11 cm
(2) 5 cm
(3) 24 cm
(4) 38 cm
Answer:
(2) 5 cm
Hint:
PA = PB (tangent of a circle)
PB = 8 cm
PC + BC = 8
PA + QC = (BC = QC tangent)
PC + 3 = 8
∴ PC = 8 cm – 3 cm = 5 cm

Question 16.
∆ABC is a right angled triangle where ∠B = 90° and BD ⊥ AC. If BD = 8 cm, AD = 4 cm, then CD is …………
(1) 24 cm
(2) 16 cm
(3) 32 cm
(4) 8 cm
Answer:
(2) 16 cm
Hint:
∆DCB ~ ∆DBA
\(\frac { DC }{ DB } \) = \(\frac { DB }{ DA } \)

DB² = DC × DA
8² = DC × 4
DC = \(\frac { 64 }{ 4 } \) = 16 cm

Question 17.
The areas of two similar triangles are 16 cm2 and 36 cm2 respectively. If the altitude of the first triangle is 3 cm, then the corresponding altitude of the other triangle is
(1) 6.5 cm
(2) 6 cm
(3) 4 cm
(4) 4.5 cm
Answer:
(4) 4.5 cm
Hint:

Question 18.
The perimeter of two similar triangles ∆ABC and ∆DEF are 36 cm and 24 cm respectively. If DE =10 cm, then AB is …………
(1) 12 cm
(2) 20 cm
(3) 15 cm
(4) 18 cm
Answer:
(3) 15 cm
Hint:
Perimeter of

Question 19.
In the given diagram θ is ………….
(1) 15°
(2) 30°
(3) 45°
(4) 60°

Answer:
(2) 30°
Hint:
∠BAD = 180° – 150° = 30°
= 180° – 150° = 30°
∠DAC = θ = 30°

Question 20.
If AD is the bisector of ∠A then AC is …………

(1) 12
(2) 16
(3) 18
(4) 20
Answer:
(4) 20
Hint. In ∆ABC, AD is the internal bisector of ∠A
\(\frac { BD }{ DC } \) = \(\frac { AB }{ AC } \)
\(\frac { 4 }{ 10 } \) = \(\frac { 8 }{ x } \)
4x = 10 × 8
x = \(\frac{10 \times 8}{4}\) = 20 cm

Question 21.
In ∆ABC and ∆DEF, ∠A = ∠E and ∠B = ∠F. Then AB : AC is ………….
(1) DE : DF
(2) DE : EF
(3) EF : ED
(4) DF : EF
Answer:
(3) EF : ED
Hint:

\(\frac { AB }{ EF } \) = \(\frac { BC }{ FD } \) = \(\frac { AC }{ ED } \)

Question 22.
Two circles of radius 8.2 cm and 3.6 cm touch each other externally, the distance between their centres is ………….
(1) 1.8 cm
(2) 4.1 cm
(3) 4.6 cm
(4) 11.8 cm
Answer:
(4) 11.8 cm
Hint:
Distance between the two centres

= r₁ + r₂
= 8.2 + 3.6
= 11.8 cm

Question 23.
In the given diagram PA and PB are tangents drawn from P to a circle with centre O. ∠OPA = 35° then a and b is …………

(1) a = 30°, b = 60°
(2) a = 35°, b = 55°
(3) a = 40°, b = 50°
(4) a = 45°, b = 45°
Answer:
(2) a = 35°, b = 55°
Hint:
∠OAP = 90° (tangent of the circle)
∠AOP + ∠OPA + ∠PAO = 180°
b + 35° + 90° = 180°
b = 180° – 125°
= 55°
OP is the angle bisector of ∠P
∴ a = 35°

II. Answer the following questions

Question 1.
The image of a man of height 1.8 m, is of length 1.5 cm on the film of a camera. If the film is 3 cm from the lens of the camera, how far is the man from the camera?
Solution:
Let AB be the height of the man, CD be the height of the image of the man of height 1.8 m (180 cm). LM be the distance between man and lens. LN be the distance between Lens and the film.

Given, AB = 1.8 m (180 cm)
CD = 1.5 cm and LN = 3 cm
Consider ∆ LAB and ∆ LCD
∠ALB = ∠DLC (vertically opposite angles)
∠LAB = ∠LDC (alternate angles) (AB || CD)
∴ ∆ LAB ~ ∆ LDC (AA similarity)
∴ \(\frac { AB }{ CD } \) = \(\frac { LM }{ LN } \) ⇒ \(\frac { 180 }{ 1.5 } \) = \(\frac { x }{ 3 } \) ⇒ 1.5x = 180 × 3
x = \(\frac{180 \times 3}{1.5}\) = \(\frac{180 \times 3 \times 10}{15}\)
x = 360 cm (or) 3.6 m
∴ The distance between the man and the camera = 3.6 cm

Question 2.
A girl of height 120 cm is walking away from the base of a lamp-post at a speed of 0. 6 m/sec. If the lamp is 3.6 m above the ground level, then find the length of her shadow after 4 seconds.
Solution:
Let AB be the height of the lamp-post above the ground level.
AB = 3.6 m = 360 cm
Let CD be the height of the girl.
CD = 1.2 m = 120 cm
The distance travelled by the girl in 4 seconds (AC)
= 4 × 0.6 = 2.4m = 240 cm
Consider ∆ECD and ∆EAB
Given (CD || AB)
∠EAB = ∠ECD = 90°
∠E is common

∴ ∆ EAB = ∆ ECD = 90°
\(\frac { AB }{ CD } \) = \(\frac { AE }{ CE } \)
= \(\frac { x+240 }{ x } \) ⇒ 3 = \(\frac { x+240 }{ x } \)
3x = x + 240
2x = 240 ⇒ x = \(\frac { 240 }{ 2 } \) = 120 cm
∴ Lenght of girls shadow after 4 seconds = 120 cm

Question 3.
In ∆ ABC, AB = AC and BC = 6 cm. D is a point on the side AC such that AD = 5 cm and CD = 4 cm. Show that ∆BCD ~ ∆ACB and hence find BD.
Solution:
Given, In ∆ ABC, AB = AC = 9 cm and BC = 6 cm, AD = 5 cm and CD = 4 cm
\(\frac { BC }{ AC } \) = \(\frac { 6 }{ 9 } \) = \(\frac { 2 }{ 3 } \) …..(1)
\(\frac { CD }{ CB } \) = \(\frac { 4 }{ 6 } \) = \(\frac { 2 }{ 3 } \) ……..(2)

From (1) and (2) we get,
\(\frac { BC }{ AC } \) = \(\frac { CD }{ CB } \)
In ∆ BCD and ∆ ACB
∠C = ∠C (common angle)
\(\frac { BC }{ AC } \) = \(\frac { CD }{ CB } \)
∴ ∆ BCD ~ ∆ ACB
\(\frac { BD }{ AB } \) = \(\frac { BC }{ AC } \) ⇒ \(\frac { BD }{ 9 } \) = \(\frac { 6 }{ 9 } \) ⇒ ∴ BD = 6 cm

Question 4.
The lengths of three sides of a triangle ABC are 6 cm, 4 cm and 9 cm. ∆PQR ~ ∆ABC. One of the lengths of sides of APQR is 35 cm. What is the greatest perimeter possible for ∆PQR?
Solution:
Given, ∆ PQR ~ ∆ ABC

Perimeter of ∆ ABC = 6 + 4 + 9 = 19 cm
When the perimeter of ∆ PQR is the greatest only the corresponding side QR must be equal to 35 cm

Question 5.
A man sees the top of a tower in a mirror which is at a distance of 87.6 m from the tower. The mirror is on the ground, facing upward. The man is 0.4 m away from the mirror, and the distance of his eye level from the ground is 1.5 m. How tall is the tower? (The foot of man, the mirror and the foot of the tower lie along a straight line).
Solution:
Let AB and ED be the heights of the man and the tower respectively. Let C be the point of incidence of the tower in the mirror.
In ∆ ABC and ∆ EDC, we have

∠ABC = ∠EDC = 90°
∠BCA = ∠DCE
(angular elevation is same at the same instant, i.e., the angle of incidence and the angle of reflection are same.)
∴ ∆ ABC ~ ∆ EDC (AA similarity criterion)
Thus,
\(\frac { ED }{ AB } \) = \(\frac { DC }{ BC } \) (corresponding sides are proportional)
ED = \(\frac { DC }{ BC } \) × AB = \(\frac { 87.6 }{ 0.4 } \) × 1.5 = 328.5
Hence, the height of the tower is 328.5 m.

Question 6.
In ∆ PQR, given that S is a point on PQ such that ST || QR and \(\frac { PS }{ SQ } \) = \(\frac { 3 }{ 5 } \). If PR = 5.6 cm, then find PT.
Solution:
In ∆ PQR, we have ST || QR and by Thales theorem,
\(\frac { PS }{ SQ } \) = \(\frac { PT }{ TR } \) …….(1)
Let PT = x
Thus, TR = PR – PT = 5.6 – x

From (1), we get PT = TR (\(\frac { PS }{ SQ } \))
x = (5.6 – x) (\(\frac { 3 }{ 5 } \))
5x = 16.8 – 3x
8x = 16.8
x = \(\frac { 16.8 }{ 8 } \) = 2.1
That is PT = 2.1 cm

Question 7.
In a ∆ ABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = 4x – 3, BD = 3x – 1, AE = 8x – 7 and EC = 5x – 3, then find the value of x.
Solution:
In ∆ ABC, DE || BC. By BPT theorem. (Thales theorem)
We get \(\frac { AD }{ DB } \) = \(\frac { AE }{ EC } \) ⇒ \(\frac { 4x-3 }{ 3x-1 } \) = \(\frac { 8x-7 }{ 5x-3 } \)

(8x – 7) (3x – 1) = (4x – 3) (5x – 3)
24x² – 8x – 21x + 7 = 20x² – 12x – 15x + 9
24x² – 8x – 21x + 7 = 20x² – 27x + 9
24x² – 29x + 7 – 20x² + 27x – 9 = 0
∴ 4x² – 2x – 2 = 0
÷ 2 ⇒ 2x² – x – 1 = 0
(x – 1) (2x + 1) = 0

x – 1 = 0 (or) 2x + 1 = 0
x = 1 (or) 2x = – 1
x = – \(\frac { 1 }{ 2 } \) ⇒ since, x ≠ – \(\frac { 1 }{ 2 } \)
∴ The value of x = 1

Question 8.
In the figure AC || BD and CE || DF. if OA = 12 cm, AB = 9cm, OC = 8 cm and EF = 4.5 cm, then find FO.
Solution:

In OBD, AC || BD
∴ \(\frac { OA }{ AB } \) = \(\frac { OC }{ CD } \) (By Thales theorem)
\(\frac { 12 }{ 9 } \) = \(\frac { 8 }{ CD } \)
∴ CD = \(\frac{9 \times 8}{12}\) = 6 CM
In ODF, CE || DF
\(\frac { OC }{ CD } \) = \(\frac { OE }{ EF } \) (By Thales theorem)
\(\frac { 8 }{ 6 } \) = \(\frac { OE }{ 4.5 } \) ⇒ OE = \(=\frac{8 \times 4.5}{6}\) = 6 cm
FO = FE + EO = 4.5 + 6 = 10.5 cm
∴ The value of FO = 10.5 cm

Question 9.
Check whether AD is the bisector of ∠A of ∆ABC in each of the following.
(i) AB = 4 cm, AC = 6 cm, BD 1.6 cm, and CD = 2.4 cm.
Solution:
\(\frac { BD }{ DC } \) = \(\frac { 1.6 }{ 2.4 } \) = \(\frac { 16 }{ 24 } \) = \(\frac { 2 }{ 3 } \) …..(1)
\(\frac { AB }{ AC } \) = \(\frac { 4 }{ 6 } \) = \(\frac { 2 }{ 3 } \) ……..(2)
From (1) and (2) we get,

\(\frac { BD }{ DC } \) = \(\frac { AB }{ AC } \)
By the converse of angle bisector theorem we have,
∴ AD is the internal bisector of ∠A

(ii) AB = 6 cm, AC = 8 cm, BD = 1.5 cm and CD = 3 cm
Solution:
\(\frac { BD }{ DC } \) = \(\frac { 1.5 }{ 3 } \) = 0.5 …….(1)
\(\frac { AB }{ AC } \) = \(\frac { 6 }{ 8 } \) = \(\frac { 3 }{ 4 } \) …….(2)

From (1) and (2) we get,
\(\frac { BD }{ DC } \) ≠ \(\frac { AB }{ AC } \)
Hence AD is not the bisector of ∠A.

Question 10.
In a ∆ABC, AD is the internal bisector of ∠A, meeting BC at D. If AB 5.6 cm, AC = 6 cm and DC = 3 cm, find BC.
Solution:
Given, AB = 5.6 cm, AC = 6 cm, DC = 3 cm
Let BD be x
In ∆ ABC, AD is the internal bisector of ∠A.
By Angle bisector theorem, we have,

\(\frac { BD }{ DC } \) = \(\frac { AB }{ AC } \) ⇒ \(\frac { x }{ 3 } \) = \(\frac { 5.6 }{ 6 } \)
x = \(\frac{3 \times 5.6}{6}\) = 2.8 cm
∴ BC = BD + DC = 2.8 + 3 = 5.8 cm
Length of BC = 5.8 cm

Question 11.
In the figure, tangents PA and PB are drawn to a circle with centre O from an external point P. If CD is a tangent to the circle at E and AP = 15 cm, find the perimeter of ∆PCD.
Solution:
We know that the lengths of the two tangents from an exterior point to a circle are equal.
∴ CA = CE, DB = DE and PA = PB
Now, the perimeter of ∆PCD

= PC + CD + DP
= PC + CE + ED + DP
= PC + CA + DB + DP
= PA + PB = 2 PA (PB = PA)
Thus, the perimeter of APCD = 2 × 15 = 30 cm

Question 12.
ABCD is a quadrilateral such that all of its sides touch a circle. If AB = 6 cm, BC = 6.5 cm and CD = 7 cm, then find the length of AD.
Solution:
Let P, Q, R and S be the points where the circle touches the quadrilateral.
We know that the lengths of the two tangents drawn from an exterior point to a circle are equal. Thus, we have,

AP = AS, BP = BQ, CR = CQ and DR = DS
Hence, AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ AB + CD = AD + BC
⇒ AD = AB + CD – BC
= 6 + 7 – 6.5 = 6.5
Thus, AD = 6.5 cm

Question 13.
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point.
Solution:
Let the initial position of the man be “O” and the final position be B.
In the ∆AOB,

OB² = OA² + AB²
OB² = 10² + 24²
= 100 + 576 = 676
OB = \(\sqrt { 676 }\) = 26 m
The man is at a distance of 26 m from the starting point.

Question 14.
Suppose AB, AC and BC have lengths 13, 16 and 20 respectively. If \(\frac { AF }{ FB } \) = \(\frac { 4 }{ 5 } \) and \(\frac { CE }{ EA } \) = \(\frac { 5 }{ 12 } \) Find BD and DC.
Solution:
Given that AB = 13, AC = 16 and BC = 20. Let BD = JC and DC = y.
Using Ceva’s theorem we have

\(\frac { BD }{ DC } \) × \(\frac { CE }{ EA } \) × \(\frac { AF }{ FB } \) = 1 ………(1)
Substitute the given values
\(\frac { x }{ y } \) × \(\frac { 5 }{ 12 } \) × \(\frac { 4 }{ 5 } \) = 1 ⇒ \(\frac { x }{ y } \) × \(\frac { 1 }{ 3 } \) = 1
\(\frac { x }{ y } \) = 3 ⇒ x = 3y
x – 3y = 0 ……(2)
Given BC = 20
x + y = 20 …..(3)
Subtract (2) and (3)

Question 15.
ABC is a right – angled triangle at B. Let D and E be any two points on AB and BC respectively. prove that AE² + CD² = AC² + DE².
Solution:
In the right ∆ ABE right- angled at B.
AE² = AB² + BE² …..(1)
In the right ∆ DBC,CD² = BD² + BC² ………(2)
Adding (1) and (2) we get
AE² + CD² = AB² + BE² + BD² + BC²
= (AB² + BC²) + (BC² + BD²)
AE² + CD² = AC² + DE²
Hence it is proved

[AC² = AB² + BC²]
[DE² = BE² + BD²]

III. Answer the following questions

Question 1.
A point O in the interior of a rectangle ABCD is joined to each of the vertices A, B, C and D. Prove that OA² + OC² = OB² + OD².
Solution:
Given: O is any point inside the rectangle ABCD.
To prove: OA² + OC² = OB² + OD²
Construction: Through “O” draw EF || AB.
Proof: Using Pythagoras theorem

In the right ∆OEA,
∴ OA²= OE² + AE² …(1)
(By Pythagoras theorem)
In the right ∆OFC,
OC² = OF² + FC² …(2)
(By Pythagoras theorem)
OB² = OF² + FB² … (3)
(By Pythagoras theorem)
In the right ∆OED,
OD² = OE² + ED² … (4)
(By Pythagoras theorem)
By adding (3) and (4) we get
OB² + OD² = OF² + FB² + OE² + ED²
= (OE² + FB²) + (OF² + ED²)
= (OE² + EA²) + (OF² + FC²)
[FB = EA and ED = FC]
OB² + OD² = OA² + OC² using (1) and (2)

Question 2.
A lotus is 20 cm above the water surface in a pond and its stem is partly below the water surface. As the wind blew, the stem is pushed aside so that the lotus touched the water 40 cm away from the original position of the stem. How much of the stem was below the water surface originally?
Solution:
Let O be the bottom of the stem immersed in water.
Let B be the lotus, AB be the length of the stem above the water surface
AB = 20 cm
Let OA be the length of the stem below the water surface
Let OA = x cm
Let C be the point where the lotus touches the water surface when the wind blow.
OC = OA + AB
OC = x + 20 cm
In ∆ AOC, OC² = OA² + AC²
(x + 20)² = x² + 40²
x² + 400 + 40x = x² + 1600

40x = 1600 – 400
40x = 1200
x = \(\frac { 1200 }{ 40 } \) = 30 cm
The stem is 30 cm below the water surface.

Question 3.
In the figure, DE || BC and \(\frac { AD }{ BD } \) = \(\frac { 3 }{ 5 } \), calculate the value of

Solution:
(i) Given, DE || BC and \(\frac { AD }{ BD } \) = \(\frac { 3 }{ 5 } \)
Let AD = 3k and BD = 5k; AB = 3k + 5k = 8k
In ∆^le ABC and ∆ADE
∠A = ∠A (common angle)
∠ABC = ∠ADE (corresponding angle)
Since DE || BC
∴ ∆ ABC ~ ∆ ADE

(ii) Let Area of ∆ ADE be 9k and Area of ∆ ABC be 64 k
Area of ∆ BCED = Area of ∆ ABC – Area of ∆ ADE
= 64 k – 9 k
= 55 k

Question 4.
A boy is designing a diamond shaped kite, as shown in the figure where AE = 16 cm, EC = 81 cm. He wants to use a straight cross bar BD. How long should it be?
Solution:
Let in AB be “x”, BE be “z” and BC be “y”
In the right ∆ AEB,
AB² = AE² + BE²
x² = 16² + Z² …….(1)
In the right ∆ BEC,
BC² = EC² + BE²
y² = 81² + z² ……(2)

In the right ∆ ACD,
AC² = AD² + DC²
97² = x² + y² ….(3)
Add (1) and (2) ⇒ x² + y² = 162 + z² + 81² + z²
x² + y² = 2z² + 16² + 81²
97² = 2z² + 16² + 81² (from 3)
9409 = 2z² + 256 + 6561
= 2z² + 6817
2z² = 9409 – 6817 = 2592
z² = \(\frac { 2592 }{ 2 } \) = 1296
z = \(\sqrt { 1296 }\) = 36
∴ Length of cross bar BD = 2 × BE = 2 × 36 = 72 cm

Question 5.
Find the unknown values in each of the following figures. All lengths are given in centimetres (All measures are not in scale)

Solution:
(i) In ∆ ABC and ∆ ADE,
∠A = ∠A (common angle)
∠ABC = ∠ADE (corresponding angle) [BC || DE]
∆ ABC ~ ∆ ADE (By AAA similarity)

In ∆ EAG and ∆ ECF,
∠E || ∠E (common angle)
∠ECF = ∠EAG (corresponding angle)
Given CF || AG
∆ EAG ~ ∆ ECF
\(\frac { EC }{ EA } \) = \(\frac { CF }{ AG } \) ⇒ \(\frac { 8 }{ x+8 } \) = \(\frac { 6 }{ y } \) ⇒ \(\frac { 8 }{ 12 } \) = \(\frac { 6 }{ y } \) (x = 4)
8y = 6 × 12
y = \(\frac{12 \times 6}{8}\) = 9 cm
∴ The value of x = 4 cm and y = 9 cm.

(ii) In ∆ HBC and ∆ HFG,
∠H = ∠H (common angle)
∠HFG = ∠HBC (corresponding angle)
Given FG || BC
\(\frac { HF }{ HB } \) = \(\frac { FG }{ BC } \) ⇒ \(\frac { 4 }{ 10 } \) = \(\frac { x }{ 9 } \) ⇒ 10x = 36
x = 3.6 cm
In ∆ FBD and ∆ FHD,
∠BFD = ∠HFG (vertically opposite angle)
∠FBD = ∠FHG (Alternate angles)
By AA similarity
∆ FBD ~ ∆ FHG
\(\frac { FG }{ FD } \) = \(\frac { FH }{ FB } \) ⇒ \(\frac { x }{ 3+y } \) = \(\frac { 4 }{ 6 } \)
4 (3 + y) = 3.6 × 6
3 + y = \(\frac{3.6 \times 6}{4}\) = 5.4 ⇒ y = 5.4 – 3 = 2.4 cm
In ∆ AEG and ∆ ABC,
∠A = ∠A (common angle)
∠AEG = ∠ABC (corresponding angles)
Given EG || BC
\(\frac { AE }{ AB } \) = \(\frac { EG }{ BC } \)
\(\frac { z }{ z+5 } \) = \(\frac { x+y }{ 9 } \) ⇒ \(\frac { z }{ z+5 } \) = \(\frac { 3.6+2.4 }{ 9 } \)
\(\frac { z }{ z+5 } \) = \(\frac { 6 }{ 9 } \) ⇒ \(\frac { z }{ z+5 } \) = \(\frac { 2 }{ 3 } \)
3z = 2z + 10 ⇒ 3z – 2z = 10 ⇒ z = 10
∴ The values of x = 3.6 cm, y = 2.4 cm and z = 10 cm.

Question 6.
The internal bisector of ∠A of AABC meets BC at D and the external bisector of ∠A meets BC produced at E. Prove that \(\frac { BD }{ BE } \) = \(\frac { CD}{ CE } \)
Solution:
Given: In ∆ ABC, AD is the internal bisector of ∠A meets BC at D. AE is the external bisector of ∠A meets BC produced to E.
To Proof: \(\frac { BD }{ BE } \) = \(\frac { CD }{ CE } \)

Proof: In ∆ ABC, AD is the internal bisector of ∠A.
By ABT theorem we have,
∴ \(\frac { BE }{ CD } \) = \(\frac { AB }{ AC } \) ……….(1)
In ∆ABC, AE is the external bisector of ∠A.
By ABT theorem we have,
∴ \(\frac { BE }{ CE } \) = \(\frac { AB }{ AC } \) ……….(2)
From (1) and (2) we get
\(\frac { BD }{ CD } \) = \(\frac { BE }{ CE } \) ⇒ ∴ \(\frac { BD }{ BE } \) = \(\frac { CD }{ CE } \)

Question 7.
In a quadrilateral ABCD, the bisectors of ∠B and ∠D intersect on AC at E. Prove that \(\frac { AB }{ BC } \) = \(\frac { AD }{ DC } \)
Solution:
Given: ABCD is a quadrilateral. BE is the bisector of ∠B intersecting AC at E, DE is the bisector of ∠D intersecting AC at E.
To proove: \(\frac { AB }{ BC } \) = \(\frac { AD }{ DC } \)
Proof: In ∆ABC, BE is the internal bisector of ∠D.
By Angle bisector theorem we have,
\(\frac { AE }{ EC } \) = \(\frac { AB }{ BC } \) ……..(1)

In ∆ ACD, DE is the internal bisector of ∠C.
By Angle bisector theorem we have,
∴ \(\frac { AE }{ EC } \) = \(\frac { AD }{ DC } \) ……….(2)
From (1) and (2) we get,
\(\frac { AB }{ BC } \) = \(\frac { AD }{ DC } \)

Question 8.
ABCD is a quadrilateral with AB parallel to DC. A line drawn parallel to AB meets AD at P and BC at Q. Prove that \(\frac { AP }{ PD } \) = \(\frac { BQ }{ QC } \)
Solution:
Given: ABCD is a quadrilateral. AB || DC.
The line PQ intersect AD at P and BC at Q

To prove: \(\frac { AP }{ PD } \) = \(\frac { BQ }{ QC } \)
Proof: In the ∆ABC, OQ || AB
By BPT, theorem we have, \(\frac { AO }{ OC } \) = \(\frac { BQ}{ QC } \) ……………(1)
In the ∆ACD, PO || DC
By BPT, theorem we have, \(\frac { AO }{ OC } \) = \(\frac { AP }{ PD } \) ……..(2)
From (1) and (2) we get, \(\frac { AP }{ PD } \) = \(\frac { BQ }{ QC } \)

Question 9.
D is the midpoint of the side BC of AABC. If P and Q are points on AB and on AC such that DP bisects ∠BDA and DQ bisects ∠ADC, then prove that PQ || BC.
Solution:
In ∆ABD,DP is the angle bisector of ∠BDA.
∴ \(\frac { AP }{ PB } \) = \(\frac { AD }{ BD } \) (angle bisector theorem) ……..(1)
In ∆ADC, DQ is the bisector of ∠ADC
∴ \(\frac { AQ }{ QC } \) = \(\frac { AD }{ DC } \) (angle bisector theorem) ……….(2)

But, BD = DC (D is the midpoint of BC)
Now (2) ⇒ ∴ \(\frac { AQ }{ QC } \) = \(\frac { AD }{ BD } \)
From (1) and (3) We get,
∴ \(\frac { AP }{ PB } \) = \(\frac { AQ }{ QC } \)
Thus PQ || BC (converse of thales theorem)

Question 10.
ABCD is a trapezium with AB || DC. The diagonal AC and BD intersect at E. If ∆AED ~ ∆BEC. Prove that AD = BC.
Solution:
By given data ABCD is a trapezium with AB || DC.
In ∆ ECD and ∆ ABE

∠EDC = ∠EBA
∠ECD = ∠EAB
∴ ∆ DEC ~ ∆ BEA by AA – similarity
\(\frac { DE }{ BE } \) = \(\frac { EC }{ EA } \) = \(\frac { DC }{ BA } \)
\(\frac { DE }{ BE } \) = \(\frac { EC }{ EA } \)
\(\frac { DE }{ EC } \) = \(\frac { BE }{ EA } \) ……….(1)

Also given ∆ DEA ~ ∆ CEB
\(\frac { DE }{ CE } \) = \(\frac { EA }{ EB } \) = \(\frac { DA }{ CB } \)
\(\frac { DE }{ CE } \) = \(\frac { EA }{ EB } \) …………(2)
From (1) and (2) we get
\(\frac { BE }{ EA } \) = \(\frac { EA }{ EB } \) ⇒ EB² = EA²
∴ EB = EA
Substitute in (2) we get
\(\frac { EA }{ EA } \) = \(\frac { DA }{ CB } \)
1 = \(\frac { DA }{ CB } \) ⇒ ∴ AD = DC Hence it is proved