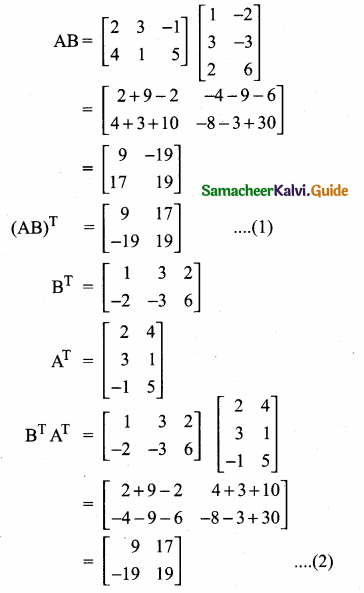
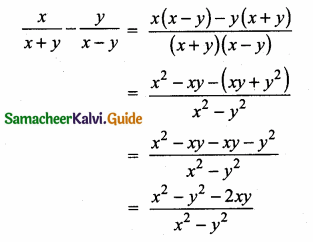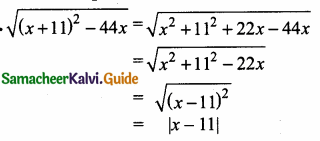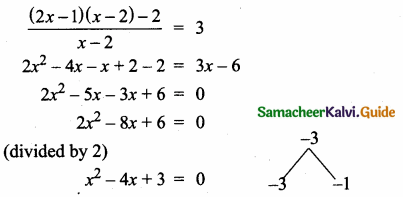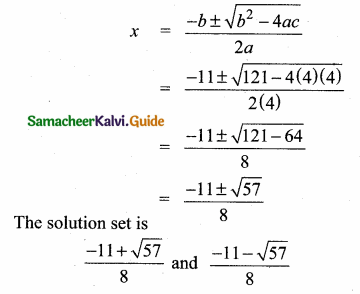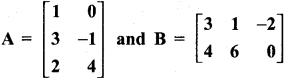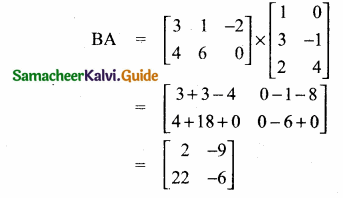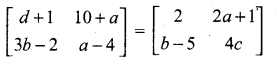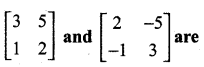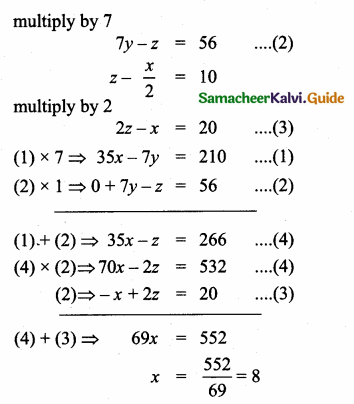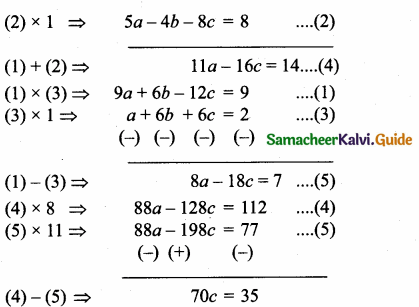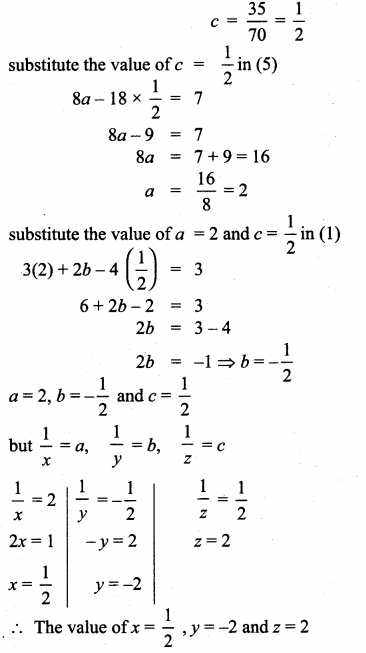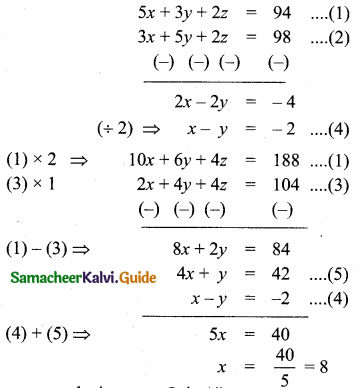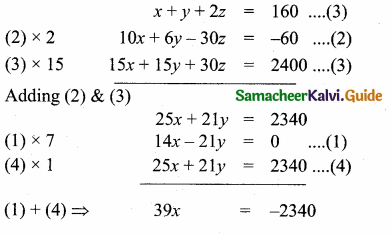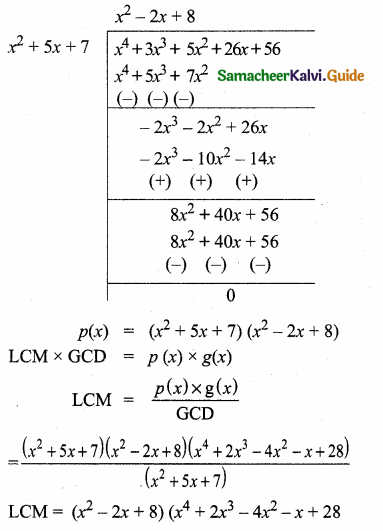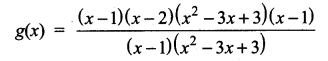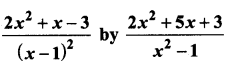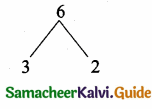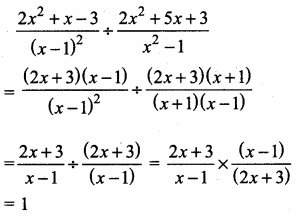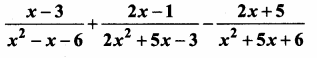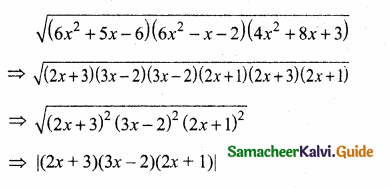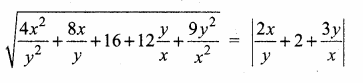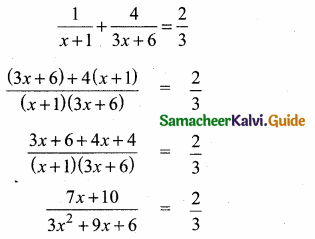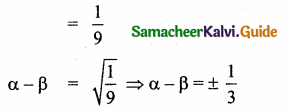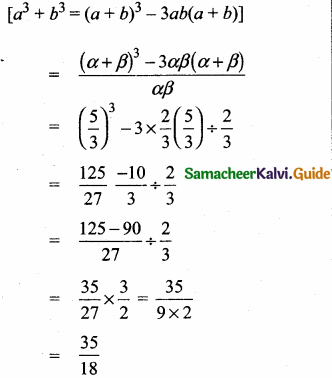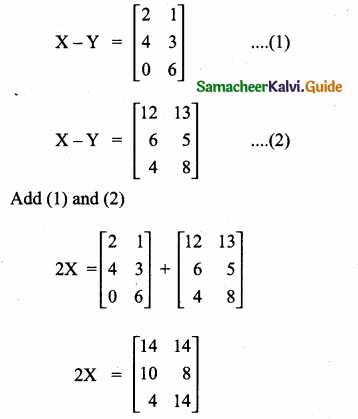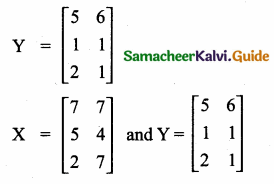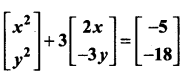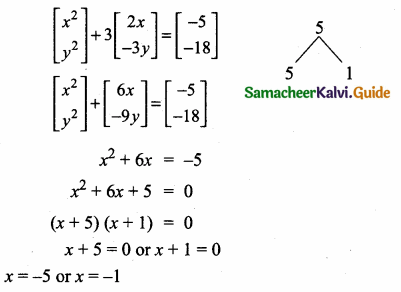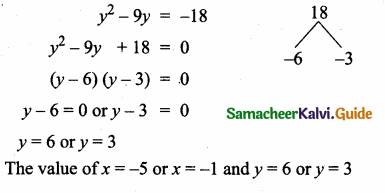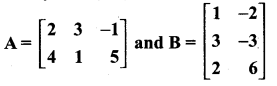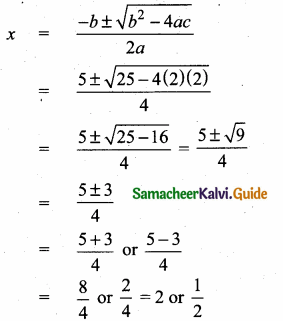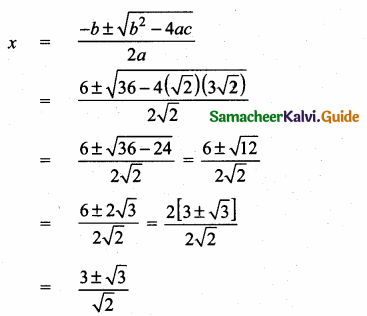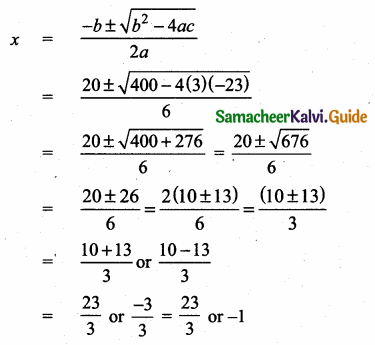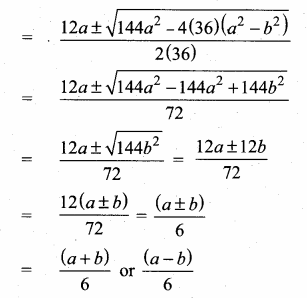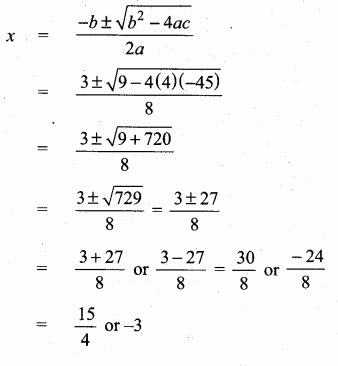Students can download Maths Chapter 4 Geometry Ex 4.1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Ex 4.1
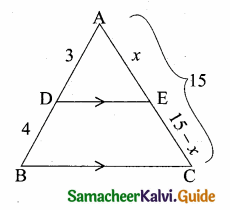
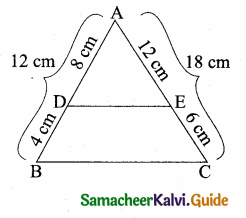
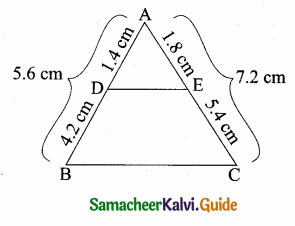
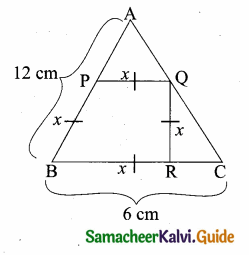
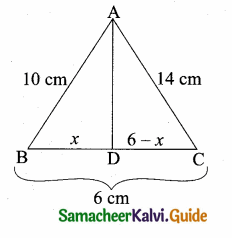
Question 1.
Check whether the which triangles are similar and find the value of x.
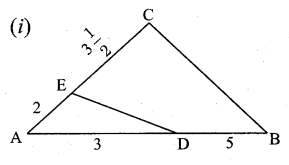
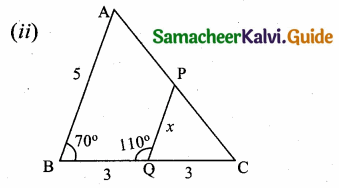
Solution:
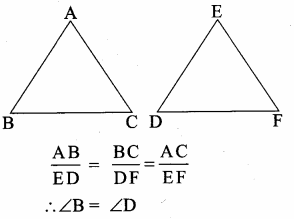
(i) In ∆ABC and ∆AED
\(\frac { AB }{ AD } \) = \(\frac { AC }{ AE } \)
\(\frac { 8 }{ 3 } \) = \(\frac{11}{\frac{2}{2}}\)
\(\frac { 8 }{ 3 } \) = \(\frac { 11 }{ 4 } \) ⇒ 32 ≠ 33
∴ The two triangles are not similar.
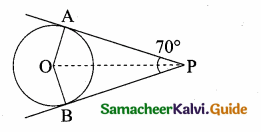
(ii) In ∆ABC and ∆PQC
∠PQC = 70°
∠ABC = ∠PQC = 70°
∠ACB = ∠PCQ (common)
∆ABC ~ ∆PQC
\(\frac { 5 }{ X } \) = \(\frac { 6 }{ 3 } \)
6x = 15
x = \(\frac { 15 }{ 6 } \) = \(\frac { 5 }{ 2 } \)
∴ x = 2.5
∆ ABC and ∆PQC are similar. The value of x = 2.5
![]()
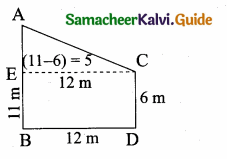
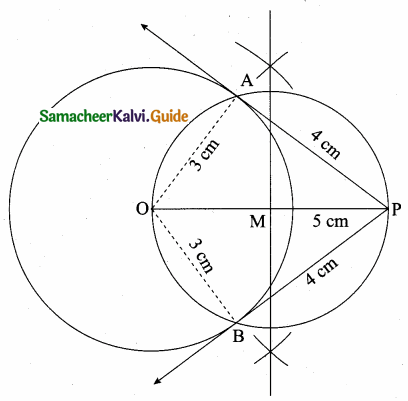
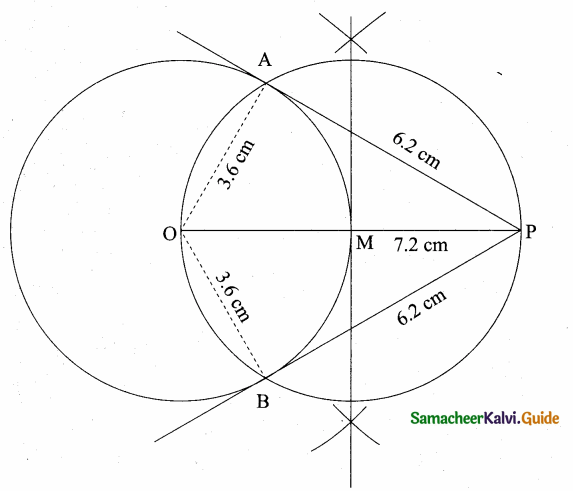
Question 2.
A girl looks the reflection of the top of the lamp post on the mirror which is 66 m away from the foot of the lamppost. The girl whose height is 12.5 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in a same line, find the height of the lamp post.
Solution:
Let the height of the tower ED be “x” m. In ∆ABC and ∆EDC.
∠ABC = ∠CED = 90° (vertical Pole)
∠ACB = ∠ECD (Laws of reflection)
∆ ABC ~ ∆DEC
\(\frac { AB }{ DE } \) = \(\frac { BC }{ EC } \)
\(\frac { 1.5 }{ x } \) = \(\frac { 0.4 }{ 87.6 } \)
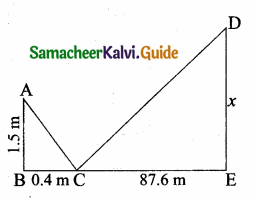
x = \(\frac{1.5 \times 87.6}{0.4}\) = \(\frac{1.5 \times 876}{4}\)
= 1.5 × 219 = 328.5
The height of the Lamp Post = 328.5 m
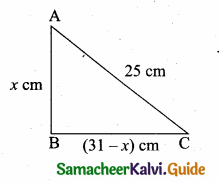
Question 3.
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower.
Solution:
In ∆ABC and ∆PQR,
∠ABC = ∠PQR = 90° (Vertical Stick)
∠ACB = ∠PRQ (Same time casts shadow)
∆BCA ~ ∆QRP
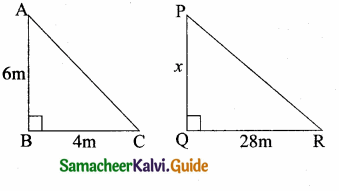
\(\frac { AB }{ PQ } \) = \(\frac { BC }{ QR } \)
\(\frac { 6 }{ x } \) = \(\frac { 4 }{ 28 } \)
4x = 6 × 28 ⇒ x = \(\frac{6 \times 28}{4}\) = 42
Length of the lamp post = 42m
![]()
Question 4.
Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT × TR = ST × TQ.
Solution:
In ∆PQT and ∆STR we have
∠P = ∠S = 90° (Given)
∠PTQ = ∠STR (Vertically opposite angle)
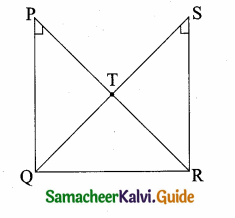
By AA similarity
∆PTQ ~ ∆STR we get
\(\frac { PT }{ ST } \) = \(\frac { TQ }{ TR } \)
PT × TR = ST × TQ
Hence it is proved.
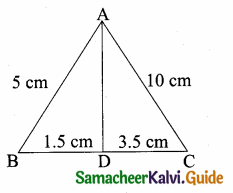
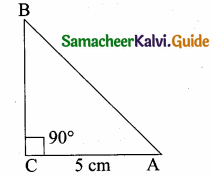
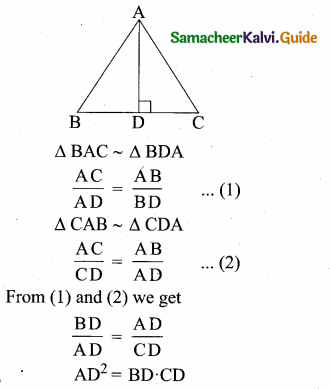
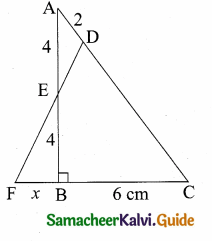
Question 5.
In the adjacent figure, ∆ABC is right angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE.
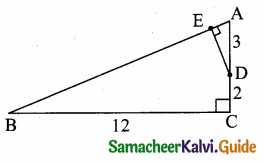
Solution:
In ∆ABC and ∆ADE
∠ACB = ∠AED = 90°
∠A = ∠A (common)
∴ ∆ABC ~ ∆ADE (By AA similarity)
\(\frac { BC }{ DE } \) = \(\frac { AB }{ AD } \) = \(\frac { AC }{ AE } \)
\(\frac { 12 }{ DE } \) = \(\frac { 13 }{ 3 } \) = \(\frac { 5 }{ AE } \)
In ∆ABC, AB2 = BC2 + AC2
= 122 + 52 = 144 + 25 = 169
AB = \(\sqrt { 169 }\) = 13
Consider, \(\frac { 13 }{ 3 } \) = \(\frac { 5 }{ AE } \)
∴ AE = \(\frac{5 \times 3}{13}\) = \(\frac { 15 }{ 13 } \)
AE = \(\frac { 15 }{ 13 } \) and DE = \(\frac { 36 }{ 13 } \)
Consider, \(\frac { 12 }{ DE } \) = \(\frac { 13 }{ 3 } \)
DE = \(\frac{12 \times 3}{13}\) = \(\frac { 36 }{ 13 } \)
![]()
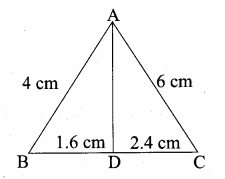
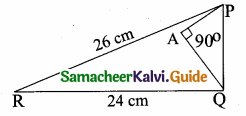
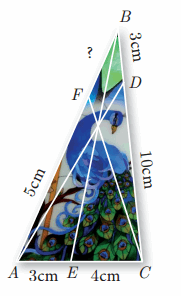
Question 6.
In the adjacent figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ.
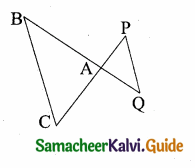
Solution:
Given ∆ACB ~ ∆APQ
\(\frac { AC }{ AP } \) = \(\frac { BC }{ PQ } \) = \(\frac { AB }{ AQ } \)
\(\frac { AC }{ 2.8 } \) = \(\frac { 8 }{ 4 } \) = \(\frac { 6.5 }{ AQ } \)
Consider \(\frac { AC }{ 2.8 } \) = \(\frac { 8 }{ 4 } \)
4 AC = 8 × 2.8
AC = \(\frac{8 \times 2.8}{4}\) = 5.6 cm
Consider \(\frac { 8 }{ 4 } \) = \(\frac { 6.5 }{ AQ } \)
8 AQ = 4 × 6.5
AQ = \(\frac{4 \times 6.5}{8}\) = 3.25 cm
Length of AC = 5.6 cm; Length of AQ = 3.25 cm
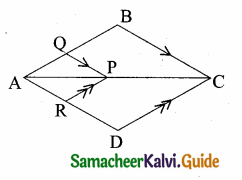
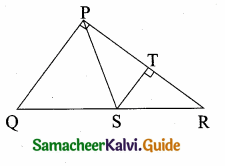
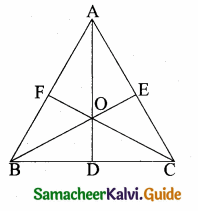
Question 7.
If figure OPRQ is a square and ∠MLN = 90°. Prove that
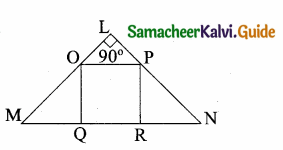
(i) ∆LOP ~ ∆QMO
(ii) ∆LOP ~ ∆RPN
(iii) ∆QMO ~ ∆RPN
(iv) QR2 = MQ × RN.
Solution:
(i) In ∆LOP and ∆QMO
∠OLP = ∠OQM = 90°
∠LOP = ∠OMQ (Since OQRP is a square OP || MN)
∴ ∆LOP~ ∆QMO (By AA similarity)
![]()
(ii) In ∆LOP and ∆RPN
∠OLP = ∠PRN = 90°
∠LPO = ∠PNR (OP || MN) .
∴ ∆LOP ~ ∆RPN (By AA similarity)
(iii) In ∆QMO and ∆RPN
∠MQO = ∠NRP = 90°
∠RPN = ∠QOM (OP || MN)
∴ ∆QMO ~ ∆RPN (By AA similarity)
(iv) We have ∆QMO ~ ∆RPN
\(\frac { MQ }{ PR } \) = \(\frac { QO }{ RN } \)
\(\frac { MQ }{ QR } \) = \(\frac { QR }{ RN } \)
QR2 = MQ × RN
Hence it is proved.
Question 8.
If ∆ABC ~ ∆DEF such that area of ∆ABC is 9cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
Solution:
Given ∆ABC ~ ∆DEF
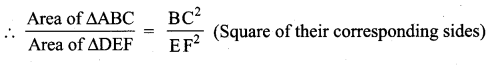
\(\frac { 9 }{ 16 } \) = \(\frac{(2.1)^{2}}{\mathrm{E} \mathrm{F}^{2}}\)
(\(\frac { 3 }{ 4 } \))2 = (\(\frac { 2.1 }{ EF } \))2
\(\frac { 3 }{ 4 } \) = \(\frac { 2.1 }{ EF } \)
EF = \(\frac{4 \times 2.1}{3}\) = 2.8 cm
Legth of EF = 2.8 cm
Question 9.
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y.
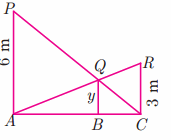
Solution:
In the ∆PAC and ∆BQC
∠PAC = ∠QBC = 90°
∠C is common
∆PAC ~ QBC
\(\frac { AP }{ BQ } \) = \(\frac { AC }{ BC } \)
\(\frac { 6 }{ y } \) = \(\frac { AC }{ BC } \)
∴ \(\frac { BC }{ AC } \) = \(\frac { y }{ 6 } \) …..(1)
In the ∆ACR and ∆QBC
∠ACR = ∠QBC = 90°
∠A is common
∆ACR ~ ABQ
\(\frac { RC }{ QB } \) = \(\frac { AC }{ AB } \)
\(\frac { 3 }{ y } \) = \(\frac { AC }{ AB } \)
\(\frac { AB }{ AC } \) = \(\frac { y }{ 3 } \) ……..(2)
By adding (1) and (2)
\(\frac { BC }{ AC } \) + \(\frac { AB }{ AC } \) = \(\frac { y }{ 6 } \) + \(\frac { y }{ 3 } \)
1 = \(\frac{3 y+6 y}{18}\)
9y = 18 ⇒ y = \(\frac { 18 }{ 9 } \) = 2
The Value of y = 2m
![]()
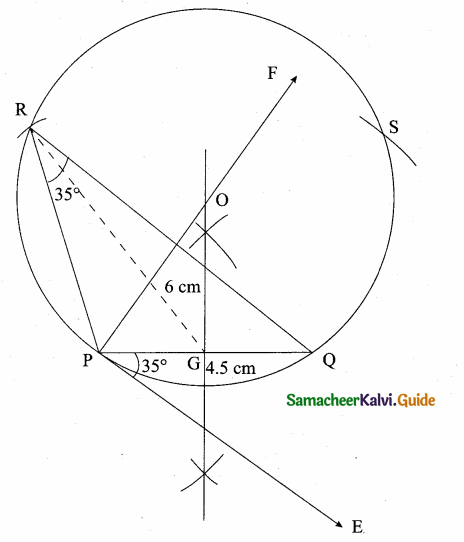
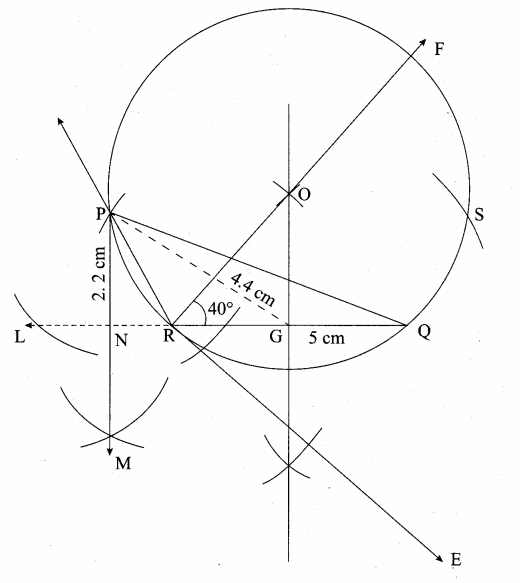
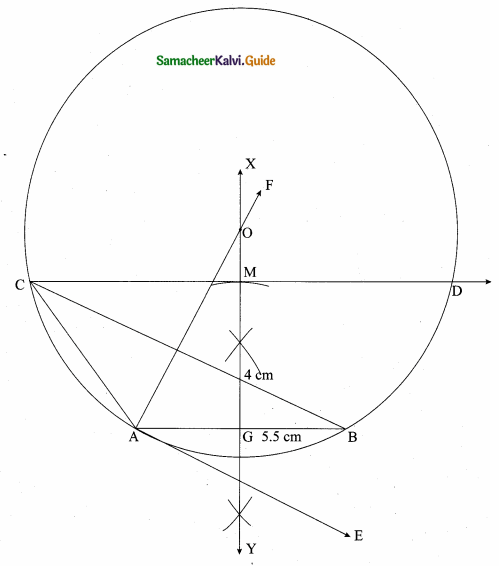
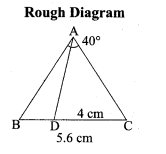
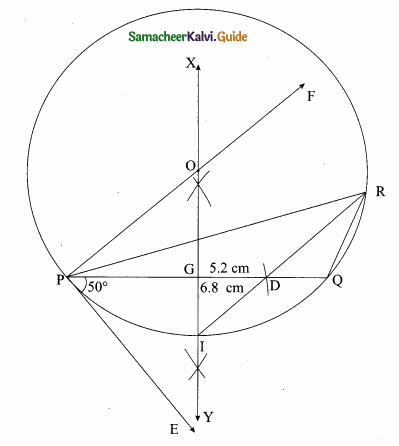
Question 10.
Construct a triangle similar to a given triangle PQR with its sides equal to \(\frac { 2 }{ 3 } \) of the corresponding sides of the triangle PQR (scale factor \(\frac { 2 }{ 3 } \) ).
Solution:
Given ∆PQR, we are required to construct another triangle whose sides are \(\frac { 2 }{ 3 } \) of the corresponding sides of the ∆PQR
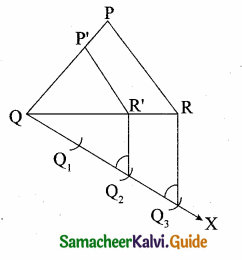
Steps of construction:
(i) Construct a ∆PQR with any measurement.
(ii) Draw a ray QX making an acute angle with QR on the side opposite to the vertex P.
(iii) Locate 3 points Q1, Q2 and Q3 on QX.
So that QQ1 = Q1Q2 = Q2Q3
(iv) Join Q3 R and draw a line through Q2 parallel to Q3 R to intersect QR at R’.
(v) Draw a line through R’ parallel to the line RP to intersect QP at P’. Then ∆ P’QR’ is the required triangle.
![]()
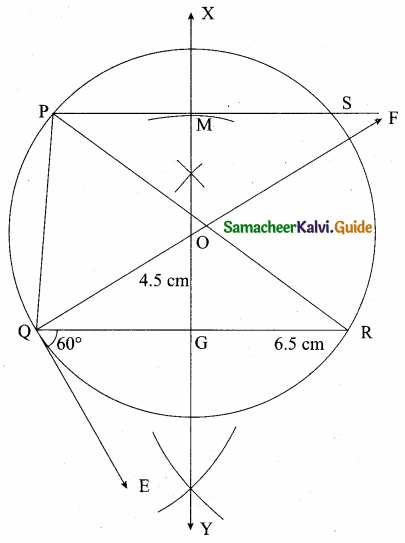
Question 11.
Construct a triangle similar to a given triangle LMN with its sides equal to \(\frac { 4 }{ 5 } \) of the corresponding sides of the triangle LMN (scale factor \(\frac { 4 }{ 5 } \) ).
Solution:
Given a triangle LMN, we are required to construct another ∆ whose sides are \(\frac { 4 }{ 5 } \) of the corresponding sides of the ∆LMN.
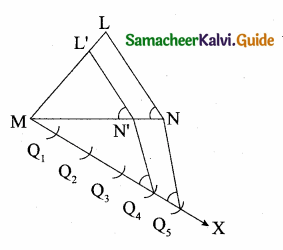
Steps of Construction:
- Construct a ∆LMN with any measurement.
- Draw a ray MX making an acute angle with MN on the side opposite to the vertex L.
- Locate 5 Points Q1, Q2, Q3, Q4, Q5 on MX.
So that MQ1 = Q1Q2 = Q2Q3 = Q3Q4 = Q4Q5 - Join Q5 N and draw a line through Q4. Parallel to Q5N to intersect MN at N’.
- Draw a line through N’ parallel to the line LN to intersect ML at L’.
∴ ∆L’ MN’ is the required triangle.
![]()
Question 12.
Construct a triangle similar to a given triangle ABC with its sides equal to \(\frac { 6 }{ 5 } \) of the corresponding sides of the triangle ABC (scale factor \(\frac { 6 }{ 4 } \)).
Solution:
Given triangle ∆ABC, we are required to construct another triangle whose sides are \(\frac { 6 }{ 5 } \) of the corresponding sides of the ∆ABC.
Steps of construction
(i) Construct an ∆ABC with any measurement.
(ii) Draw a ray BX making an acute angle with BC.
(iii) Locate 6 points Q1, Q2, Q3, Q4, Q5, Q6 on BX such that
BQ1 = Q1Q2 = Q2Q3 = Q3Q4 = Q5Q6
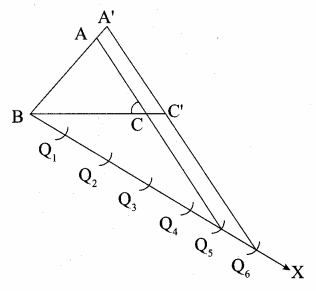
(iv) Join Q5 to C and draw a line through Q6 parallel to Q5 C intersecting the extended line BC at C’.
(v) Draw a line through C’ parallel to AC intersecting the extended line segment AB at A’.
∆A’BC’ is the required triangle.
![]()
Question 13.
Construct a triangle similar to a given triangle PQR with its sides equal to \(\frac { 7 }{ 3 } \) of the corresponding sides of the triangle PQR (scale factor \(\frac { 7 }{ 3 } \)).
Solution:
Given triangle ABC, we are required to construct another triangle whose sides are \(\frac { 7 }{ 3 } \) of the corresponding sides of the ∆ABC.
Steps of construction
(i) Construct a ∆PQR with any measurement.
(ii) Draw a ray QX making an acute angle with QR on the side opposite to the vertex P.
(iii) Locate 7 points Q1, Q2, Q3, Q4, Q5, Q6, Q7 on QX.
So that
QQ1 = Q1Q2 = Q2Q3 = Q3Q4 = Q5Q6 = Q6Q7
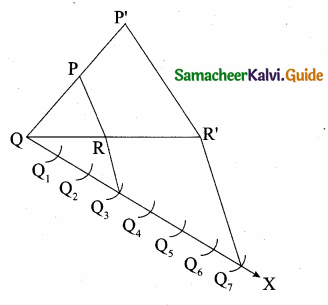
(iv) Join Q3 to R and draw a line through Q7 parallel to Q3R intersecting the extended line segment QR at R’.
(v) Draw a line through parallel to RP.
Intersecting the extended line segment QP at P’.
∴ ∆P’QR’ is the required triangle.
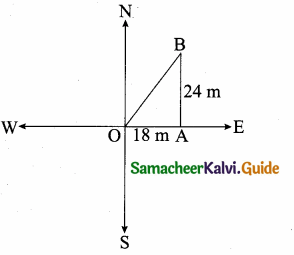


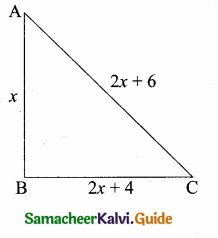
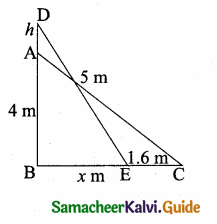
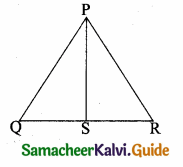
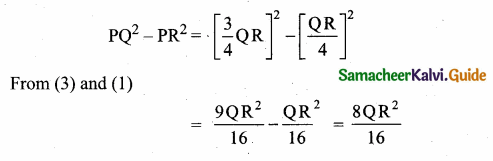
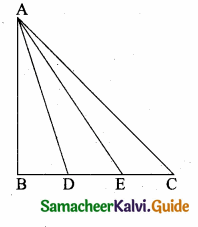
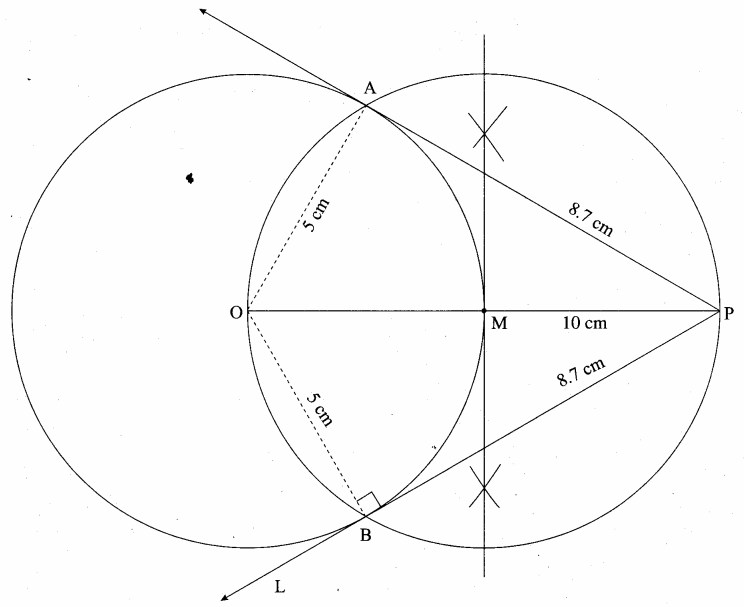
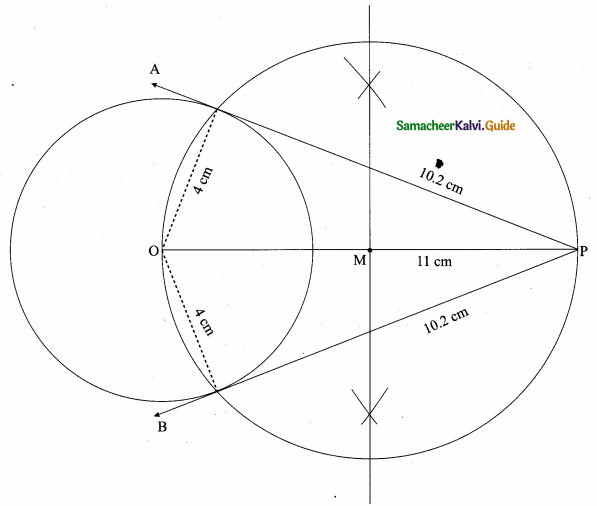
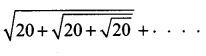 is ……….
is ……….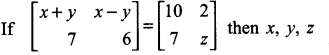
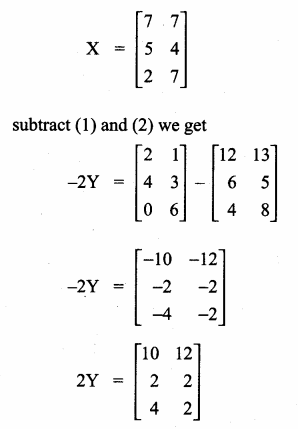
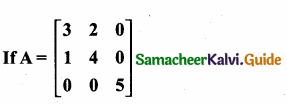
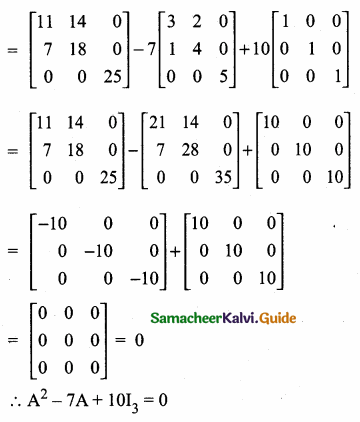
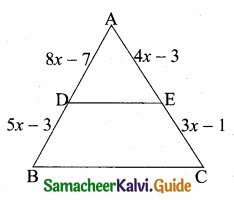
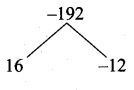
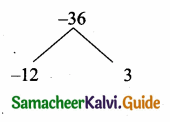
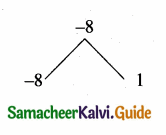
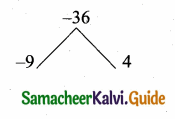
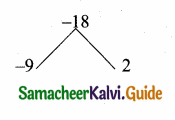
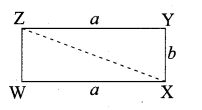
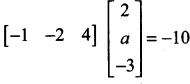 then the value of “a” is ………….
then the value of “a” is ………….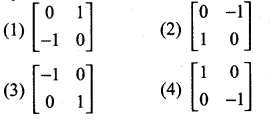

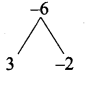
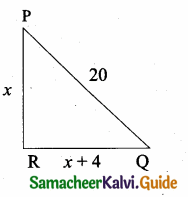
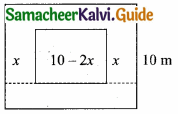
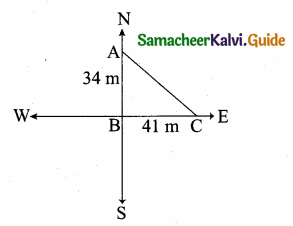
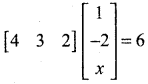 then “x” is ……………..
then “x” is ……………..