Category: Class 9

Students can download Maths Chapter 3 Algebra Ex 3.8 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.8

Question 1.
Factorise each of the following polynomials using synthetic division:
(i) x³ – 3x² – 10x + 24
Solution:
p(x) – x³ – 3x² – 10x + 24
p(1) = 1³ – 3(1)² – 10(1) + 24
= 1 – 3 – 10 + 24
= 25 – 13
≠ 0
x – 1 is not a factor

p(-1) = (-1)³ – 3(-1)² – 10(-1) + 24
= – 1 – 3(1) + 10 + 24
= -1 – 3 + 10 + 24
= 34 – 4
= 30
≠ 0
x + 1 is not a factor

p(2) = 2³ – 3(2)² – 10(2) + 24
= 8 – 3(4) – 20 + 24
= 8 – 12 – 20 + 24
= 32 – 32
= 0
∴ x – 2 is a factor

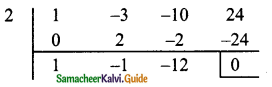
x² – x – 12 = x² – 4x + 3x – 12

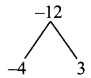
= x(x – 4) + 3 (x – 4)
= (x – 4) (x + 3)
∴ The factors of x³ – 3x² – 10x + 24 = (x – 2) (x – 4) (x + 3)

(ii) 2x³ – 3x² – 3x + 2
Solution:
p(x) = 2x³ – 3x² – 3x + 2
P(1) = 2(1)³ – 3(1)² – 3(1) + 2
= 2 – 3 – 3 + 2
= 2 – 6
= -4
≠ 0
x – 1 is not a factor

P(-1) = 2(-1)³ – 3(-1)² – 3(-1) + 2
= -2 – 3 + 3 + 2
= 5 – 5
= 0
∴ x + 1 is a factor

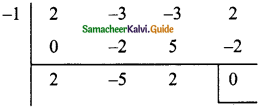
2x² – 5x + 2 = 2x² – 4x – x + 2

= 2x(x – 2) – 1 (x – 2)
= (x – 2) (2x – 1)
∴ The factors of 2x³ – 3x² – 3x + 2 = (x + 1) (x – 2) (2x – 1)

(iii) – 7x + 3 + 4x³
Solution:
p(x) = – 7x + 3 + 4x³
= 4x³ – 7x + 3
P(1) = 4(1)³ – 7(1) + 3
4 – 7 + 3
= 7 – 7
= 0
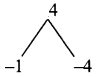
∴ x – 1 is a factor

4x² + 4x – 3 = 4x² + 6x – 2x – 3

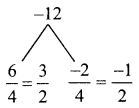
= 2x(2x + 3) – 1 (2x + 3)
= (2x + 3) (2x – 1)
∴ The factors of – 7x + 3 + 4x³ = (x – 1) (2x + 3) (2x – 1)

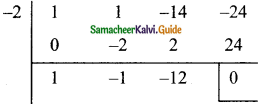
(iv) x³ + x² – 14x – 24
Solution:
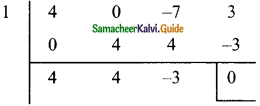
p(x) = x³ + x² – 14x – 24
p(1) = (1)³ + (1)² – 14 (1) – 24
= 1 + 1 – 14 – 24
= -36
≠ 0
x + 1 is not a factor.

p(-1) = (-1)³ + (-1)² – 14(-1) – 24
= -1 + 1 + 14 – 24
= 15 – 25
≠ 0
x – 1 is not a factor.

p(2) = (-2)³ + (-2)² – 14 (-2) – 24
= -8 + 4 + 28 – 24
= 32 – 32
= 0
∴ x + 2 is a factor

x² – x – 12 = x² – 4x + 3x – 12

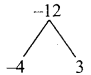
= x(x – 4) + 3 (x – 4)
= (x – 4) (x + 3)
This (x + 2) (x + 3) (x – 4) are the factors.
x³ + x² – 14x – 24 = (x + 2) (x + 3) (x – 4)

(v) x³ – 7x + 6
Solution:
p(x) = x³ – 7x + 6
P( 1) = 1³ – 7(1) + 6
= 1 – 7 + 6
= 7 – 7
= 0
∴ x – 1 is a factor

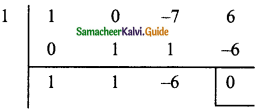
x² + x – 6 = x² + 3x – 2x – 6

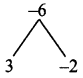
= x(x + 3) – 2 (x + 3)
= (x + 3) (x – 2)
This (x – 1) (x – 2) (x + 3) are factors.
∴ x³ – 7x + 6 = (x – 1) (x – 2) (x + 3)

(vi) x³ – 10x² – x + 10
p(x) = x³ – 10x² – x + 10
= 1 – 10 – 1 + 10
= 11 – 11
= 0
∴ x – 1 is a factor

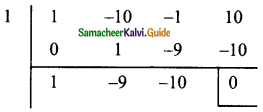
x² – 9x – 10 = x² – 10x + x – 10

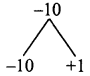
= x(x – 10) + 1 (x – 10)
= (x – 10) (x + 1)
This (x – 1) (x + 1) (x – 10) are the factors.
∴ x³ – 10x² – x + 10 = (x – 1) (x – 10) (x + 1)

Students can download Maths Chapter 2 Real Numbers Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Additional Questions

I. Multiple choice question

Question 1.
The decimal form of –\(\frac{3}{4}\) is ………
(a) – 0.75
(b) – 0.50
(c) – 0.25
(d) – 0.125
Solution:
(a) – 0.75

Question 2.
If a number has a non-terminating and non-recurring decimal expansion, then it is……….
(a) a rational number
(b) a natural number
(c) an irrational number
(d) an integer
Solution:
(c) an irrational number

Question 3.
Which one of the following has terminating decimal expansion?
(a) \(\frac{7}{9}\)
(b) \(\frac{8}{15}\)
(c) \(\frac{1}{12}\)
(d) \(\frac{5}{32}\)
Solution:
(d) \(\frac{5}{32}\)

Question 4.
Which of the following are irrational numbers?
(i) \(\sqrt{2+\sqrt3}\)
(ii) \(\sqrt{4+\sqrt25}\)
(iii) \(\sqrt[3]{5+\sqrt7}\)
(iv) \(\sqrt{8-\sqrt[3]8}\)
(a) (ii), (iii) and (iv)
(b) (i), (iii) and (iv)
(c) (i), (ii) and (iii)
(d) (i), (iii) and (iv)
Solution:
(d) (i), (iii) and (iv)

Question 5.
Irrational number has a
(a) terminating decimal
(b) no decimal part
(c) non-terminating and recurring decimal
(d) non-terminating and non-recurring decimal
Solution:
(d) non-terminating and non-recurring decimal

Question 6.
If \(\frac{1}{7}\) = 0.142857, then the value of \(\frac{3}{7}\) is……..
(a) 0.285741
(b) 0.428571
(c) 0.285714
(d) 0.574128
Solution:
(b) 0.428571

Question 7.
Which of the following are not rational numbers?
(a) 7√5
(b) \(\frac{7}{\sqrt{5}}\)
(c) \(\sqrt{36}\) – 9
(d) π + 2
Solution:
(c) \(\sqrt{36}\) – 9

Question 8.
The product of 2√5 and 6√5 is……….
(a) 12√5
(b) 60
(c) 40
(d) 8√5
Solution:
(b) 60

Question 9.
The rational number lying between \(\frac{1}{5}\) and \(\frac{1}{2}\)
(a) \(\frac{7}{20}\)
(b) \(\frac{2}{10}\)
(c) \(\frac{2}{7}\)
(d) \(\frac{3}{10}\)
Solution:
(a) \(\frac{7}{20}\)

Question 10.
The value of 0.03 + 0.03 is ……….
(a) 0.\(\overline { 09 }\)
(b) 0.\(\overline { 0303 }\)
(c) 0.\(\overline { 06 }\)
(d) 0
Solution:
(c) 0.06

Question 11.
The sum of \(\sqrt{343}\) + \(\sqrt{567}\) is
(a) 18√3
(b) 16√7
(c) 15√3
(d) 14√7
Solution:
(b) 16√7

Question 12.
If \(\sqrt{363}\) = x√3 then x = ………
(a) 8
(b) 9
(c) 10
(d) 11
Solution:
(d) 11

Question 13.
The rationalising factor of \(\frac{1}{\sqrt{7}}\) is ……….
(i) 7
(b) √7
(c) \(\frac{1}{7}\)
(d) \(\frac{1}{\sqrt{7}}\)
Solution:
(b) √7

Question 14.
The value of \((\frac{1}{3^5})^4\) is ……..
(a) 3²⁰
(b) 3^-20
(c) \(\frac{1}{3^{-20}}\)
(d) \(\frac{1}{3^{9}}\)
Solution:
(b) 3^-20

Question 15.
What is 3.976 × 10^-4 written in decimal form?
(a) 0.003976
(b) 0.0003976
(c) 39760
(d) 0.03976
Solution:
(b) 0.0003976

II. Answer the following Questions.

Question 1.
Find any seven rational numbers between \(\frac{5}{8}\) and –\(\frac{5}{6}\)
Solution:
Let us convert the given rational numbers having the same denominators.
L.C.M of 8 and 6 is 24.

Now the rational numbers between

We can take any seven of them.

Question 2.
Find any three rational numbers between \(\frac{1}{2}\) and \(\frac{1}{5}\)
Solution:

Thus the three rational numbers are \(\frac{7}{20}\), \(\frac{17}{40}\) and \(\frac{37}{80}\)

Question 3.
Represent \(-\frac{2}{11}\), \(-\frac{5}{11}\) and \(-\frac{9}{11}\) on the number lines.
Solution:

To Represent \(-\frac{2}{11}\), \(-\frac{5}{11}\) and \(-\frac{9}{11}\) on the number line we make 11 markings each being equal distence \(\frac{1}{11}\) on the left of 0.
The point A represent \((-\frac{2}{11})\), the point B represents \((-\frac{5}{11})\) and the point C represents \((-\frac{9}{11})\)

Question 4.
Express the following in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0.
(i) 0.\(\overline { 47 }\)
Solution:
Let x = 0.474747…….. →(1)
100 x = 47.4747…….. →(2)
(2) – (1) ⇒ 100x – x = 47.4747……..
(-) 0.4747……..
99 x = 47.0000
x = \(\frac{47}{99}\)
∴ 0.\(\overline { 47 }\) = \(\frac{47}{99}\)

(ii) 0.\(\overline { 57 }\)
Solution:
Let x = 0.57777…….. →(1)
10 x = 5.77777…….. →(2)
100 x = 57.7777…….. →(3)
(3) – (2) ⇒ 100 x – 10 x = 57.7777……..
(-) 5.7777……..
99 x = 52.0000
x = \(\frac{52}{90}\) = \(\frac{26}{45}\)
∴ 0.\(\overline { 57 }\) = \(\frac{26}{45}\)

(iii) 0.\(\overline { 245 }\)
Solution:
Let x = 0.2454545…….. →(1)
10 x = 2.454545…….. →(2)
1000 x = 245.4545…….. →(3)
(3) – (2) ⇒ 1000 x – 10 x = 245.4545
(-) 2.4545………
990 x = 243.00000
x = \(\frac{243}{990}\) (or) \(\frac{27}{110}\)
∴ 0.\(\overline { 245 }\) = \(\frac{27}{110}\)

Question 5.
Without actual division classify the decimal expansion of the following numbers as terminating or non-terminating and recurring.
(i) \(\frac{7}{16}\)
(ii) \(\frac{13}{150}\)
(ii) –\(\frac{11}{75}\)
(iv) \(\frac{17}{200}\)
Solution:
(i) \(\frac{7}{16}\) = \(\frac{7}{2^4}\) = \(\frac{7}{2^{4} \times 5^{0}}\)
∴ \(\frac{7}{16}\) has a terminating decimal expansion.

(ii) \(\frac{13}{150}=\frac{13}{2 \times 3 \times 5^{2}}\)
Since it is not in the form of \(\frac{P}{2^{m} \times 5^{n}}\)
∴ \(\frac{13}{150}\) as non-terminating and recurring decimal expansion.

(iii) \(-\frac{11}{75}=-\frac{11}{3 \times 5^{2}}\)
Since it is not in the form of \(\frac{P}{2^{m} \times 5^{n}}\)
∴ –\(\frac{11}{75}\) as non-terminating and recurring decimal expansion.

(iv) \(\frac{17}{200}=\frac{17}{2^{3} \times 5^{2}}\)
∴ \(\frac{17}{200}\) has a terminating decimal expansion.

Question 6.
Find the value of \(\sqrt{27}\) + \(\sqrt{75}\) – \(\sqrt{108}\) + \(\sqrt{48}\)
Solution:

= 3√3 + 5√3 – 6√3 + 4√3
= 12√3 – 6√3
= 6√3
= 6 × 1.732
= 10.392

Question 7.
Evaluate \(\frac{\sqrt{2}+1}{\sqrt{2-1}}\)
Solution:

= 2√2 + 3
= 2 × 1.414 + 3
= 2.828 + 3
= 5.828

Question 8.

Solution:

= 69984 × 1021^-21-20+9
= 69984 × 10^-32
= 6.9984 × 10⁴ × 10^-32
= 6.9984 × 10^-32+4
= 6.9984 × 10^-28

Question 9.
Write
(a) 9.87 × 10⁹
(b) 4.134 × 10^-4 and
(c) 1.432 × 10^-9 in decimal form.
Solution:
(a) 9.87 × 10⁹ = 9870000000
(b) 4.134 × 10^-4 = 0.0004134
(c) 1.432 × 10^-9 = 0.000000001432

Students can download Maths Chapter 2 Real Numbers Ex 2.8 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.8

Question 1.
Represent the following numbers in the scientific notation:
(i) 569430000000
(ii) 2000.57
(iii) 0.0000006000
(iv) 0.0009000002
Solution:
(i) 569430000000 = 5.6943 × 10¹¹
(ii) 2000.57 = 2.00057 × 10³
(iii) 0.0000006000 = 6.0 × 10^-7
(iv) 0.0009000002 = 9.000002 × 10^-4

Question 2.
Write the following numbers in decimal form:
(i) 3.459 × 10⁶
(ii) 5.678 × 10⁴
(iii) 1.00005 × 10^-5
(iv) 2.530009 × 10^-7
Solution:
(i) 3.459 × 10⁶
= 3459000
(ii) 5.678 × 10⁴
= 56780
(iii) 1.00005 × 10^-5
= 0.0000100005
(iv) 2.530009 × 10^-7
= 0.0000002530009

Question 3.
Represent the following numbers in scientific notation:
(i) (300000)² × (20000)⁴
(ii) (0.000001)¹¹ ÷ (0.005)³
(iii) {(0.00003)⁶ × (0.00005)⁴} ÷ {(0.009)³ × (0.05)²}
Solution:
(i) (300000)² × (20000)⁴ = (3 × 10⁵)² × (2 × 10⁴)⁴
= 3² × (10⁵)² × 2⁴ × (10⁴)⁴
= 9 × 10¹⁰ × 16 × 10¹⁶
= 9 × 16 × 10^10-16
= 144 × 10²⁶
= 1.44 × 10²⁸

(ii) (0.000001)¹¹ ÷ (0.005)³

0.008 × 10^-66+9
= 8.0 × 10^-3 × 10^-57
= 8.0 × 10^-3-57
= 8.0 × 10^-60

(iii) {(0.00003)⁶ × (0.00005)⁴} ÷ {(0.009)³ × (0.05)²}

= 2.5 × 10^-49+13
= 2.5 × 10^-36

Question 4.
Represent the following information in scientific notation:
(i) The world population is nearly 7000,000,000.
(ii) One light year means the distance 9460528400000000 km.
(iii) Mass of an electron is 0.000 000 000 000 000 000 000 000 000 00091093822 kg.
Solution:
(i) World population = 7.0 × 10⁹
(ii) Distance = 9.4605 × 10¹⁵ km.
(iii) Mass of an electron = 9.1093822 × 10^-31 kg

Question 5.
Simplify:
(2.75 × 10⁷) + (1.23 × 10⁸)
(ii) (1.598 × 10¹⁷) – (4.58 × 10¹⁵)
(iii) (1.02 × 10¹⁰) × (1.20 × 10^-3)
(iv) (8.41 × 10⁴) ÷ (4.3 × 10⁵)
Solution:
(i) (2.75 × 10⁷) + (1.23 × 10⁸) = 27500000 + 123000000

= 150500000
= 1.505 × 10⁸

(ii) (1.598 × 10¹⁷) – (4.58 × 10¹⁵) = 1552,20000000000000

= 1.5522 × 10¹⁷

(iii) (1.02 × 10¹⁰) × (1.20 × 10^-3) = 1.02 × 1.20 × 10¹⁰ × 10^-3
=1.224 × 10⁷

(iv) (8.41 × 10⁴) ÷ (4.3 × 10⁵) = \(\frac{8.41×10^{4}}{4.3×10^{5}}\)
= \(\frac{8.41}{4.3}\) × 10^4-5
= \(\frac{8.41}{4.3}\) × 10^-1
= 1.9558139 × 10^-1

Students can download Maths Chapter 2 Real Numbers Ex 2.7 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.7

Question 1.
Rationalise the denominator:
(i) \( \frac{1}{\sqrt{50}}\)
(ii) \( \frac{5}{3\sqrt{5}}\)
(iii) \( \frac{\sqrt{75}}{\sqrt{18}}\)
(iv) \( \frac{3\sqrt{5}}{\sqrt{6}}\)
Solution:
(i) \( \frac{1}{\sqrt{50}}\) = \(\frac{1}{\sqrt{25 \times 2}}=\frac{1}{5 \sqrt{2}}=\frac{1}{5 \sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{5 \times 2}=\frac{\sqrt{2}}{10}\)

(ii) \( \frac{5}{3\sqrt{5}}\) = \(\frac{5}{3 \sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}}=\frac{5 \sqrt{5}}{3 \times 5}=\frac{\sqrt{5}}{3}\)

(iii) \( \frac{\sqrt{75}}{\sqrt{18}}\) = \(\frac{\sqrt{3 \times 25}}{\sqrt{2 \times 9}}=\frac{5 \sqrt{3}}{3 \sqrt{2}}=\frac{5 \sqrt{3}}{3 \sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{5 \sqrt{6}}{3 \times 2}=\frac{5 \sqrt{6}}{6}\)

(iv) \( \frac{3\sqrt{5}}{\sqrt{6}}\) = \( \frac{3 \sqrt{5}}{\sqrt{6}} \times \frac{\sqrt{6}}{\sqrt{6}}=\frac{3 \sqrt{30}}{6}=\frac{\sqrt{30}}{2} \)

Question 2.
Rationalise the denominator and simplify:
(i) \(\frac{\sqrt{48}+\sqrt{32}}{\sqrt{27}-\sqrt{18}}\)
Solution:

(ii) \(\frac{5\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}\)
Solution:

(iii) \(\frac{2\sqrt{6}-\sqrt{5}}{3\sqrt{5}-2\sqrt{6}}\)
Solution:

(iv) \(\frac{\sqrt{5}}{\sqrt{6}+2} – \frac{\sqrt{5}}{\sqrt{6}-2}\)
Solution:

Question 3.
Find the value of a and b if \(\frac{\sqrt{7}-2}{\sqrt{7}+2} = a\sqrt{7} + b\).
Solution:

Question 4.
If x = \(\sqrt{7}\) + 2, then find the value of x² + \(\frac{1}{x^2}\)
Solution:
\(\sqrt{7}\) + 2 ⇒ x² = \((\sqrt{5}+2)^{2}\)
= \((\sqrt{5})^{2}\) + 2 × 2 × \(\sqrt{5}\) + 2² = 5 + 4 \(\sqrt{5}\) + 4 = 9 + 4\(\sqrt{5}\)
\(\frac{1}{x}=\frac{1}{\sqrt{5}+2}=\frac{\sqrt{5}-2}{(\sqrt{5}+2)(\sqrt{5}-2)}=\frac{\sqrt{5}-2}{(\sqrt{5})^{2}-2^{2}}=\frac{\sqrt{5}-2}{5-4}=\sqrt{5}-2\)
\(\frac{1}{x^{2}}\) = (\(\sqrt{5} – 2)^{2}\)
= \((\sqrt{5})^{2}\) – 2 × \(\sqrt{5}\) × 2 + 2² = 5 – 4 \(\sqrt{5}\) + 4 = 9 – 4 \(\sqrt{5}\)
∴ x² + \(\frac{1}{x^{2}}\) = 9 + \(4\sqrt{5}\) + 9 – \(4\sqrt{5}\) = 18
The value of x² + \(\frac{1}{x^{2}}\) = 18

Question 5.
Given \(\sqrt{2}\) = 1.414, find the value of \(\frac{8 – 5\sqrt{2}}{3 – 2\sqrt{2}}\) (to 3 places of decimals).
Solution:

= 4 + \(\sqrt{2}\) = 4 + 1.414 = 5.414

Students can download Maths Chapter 2 Real Numbers Ex 2.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.6

Question 1.
Simplify the following using addition and subtraction properties of surds:
(i) 5\(\sqrt{3}\) + 18\(\sqrt{3}\) – 2\(\sqrt{3}\)
(ii) 4\(\sqrt[3]{5}\) + 2\(\sqrt[3]{5}\) – 3\(\sqrt[3]{5}\)
(iii) 3\(\sqrt{75}\) + 5\(\sqrt{48}\) – \(\sqrt{243}\)
(iv) 5\(\sqrt[3]{40}\) + 2\(\sqrt[3]{625}\) – 3\(\sqrt[3]{320}\)
Solution:
(i) 5\(\sqrt{3}\) + 18\(\sqrt{3}\) – 2\(\sqrt{3}\) = (5 + 18 – 2)\(\sqrt{3}\)
= (23 – 2) \(\sqrt{3}\) = 21\(\sqrt{3}\)

(ii) 4\(\sqrt[3]{5}\) + 2\(\sqrt[3]{5}\) – 3\(\sqrt[3]{5}\) = (4 + 2 – 3) \(\sqrt[3]{5}\)
= (6 – 3) \(\sqrt[3]{5}\) = 3\(\sqrt[3]{5}\)

(iii) 3\(\sqrt{75}\) + 5\(\sqrt{48}\) – \(\sqrt{243}\) = \(3\sqrt{5^{2}×3} + 5\sqrt{2^{4}×3} – \sqrt{3^{5}}\)

= 3 × 5\(\sqrt{3}\) + 5 × 2²\(\sqrt{3}\) – 3²\(\sqrt{3}\) = 15\(\sqrt{3}\) + 20\(\sqrt{3}\) – 9\(\sqrt{3}\)
= (15 + 20 – 9)\(\sqrt{3}\)
= (35 – 9)\(\sqrt{3}\)
= 26 \(\sqrt{3}\)

(iv) 5\(\sqrt[3]{40}\) + 2\(\sqrt[3]{625}\) – 3\(\sqrt[3]{320}\)

= 5\(\sqrt[3]{2^{3}×5} + 2\sqrt[3]{5^{3}×5} – 3\sqrt[3]{2^{3}×2^{3}×5}\)
5 × 2\(\sqrt[3]{5} + 2 × 5\sqrt[3]{5} – 3 × 2 × 2\sqrt[3]{5} \)
= 10\(\sqrt[3]{5} + 10\sqrt[3]{5} – 12\sqrt[3]{5} \)
= 20\(\sqrt[3]{5} – 12\sqrt[3]{5}\)
= 8\(\sqrt[3]{5}\)

Question 2.
Simplify the following using multiplication and division properties of surds:
(i) \(\sqrt{3}\) × \(\sqrt{5}\) × \(\sqrt{2}\)
(ii) \(\sqrt{35}\) ÷ \(\sqrt{7}\)
(iii) \(\sqrt[3]{27}\) × \(\sqrt[3]{8}\) × \(\sqrt[3]{125}\)
(iv) (7\(\sqrt{a}\) – 5\(\sqrt{b}\)) (7\(\sqrt{a}\) + 5\(\sqrt{b}\))
(v) (\(\sqrt{\frac{225}{729}} – \sqrt{\frac{25}{144}}\)) ÷ \(\sqrt{\frac{16}{81}}\)
Solution:
(i) \(\sqrt{3}\) × \(\sqrt{5}\) × \(\sqrt{2}\) = \(\sqrt{3×5×2} = \sqrt{30}\)

(ii) \(\sqrt{37} ÷ \sqrt{7} = \frac{\sqrt{35}}{\sqrt{7}} = \sqrt{\frac{35}{7}} = \sqrt{5}\)

(iii) \(\sqrt[3]{27}\) × \(\sqrt[3]{8}\) × \(\sqrt[3]{125}\) = \(\sqrt[3]{27×8×125}\)
= \(\sqrt[3]{3^{3}×2^{3}×5^{3}}\) = 3 × 2 × 5 = 30

(iv) (7\(\sqrt{a}\) – 5\(\sqrt{b}\)) (7\(\sqrt{a}\) + 5\(\sqrt{b}\))
[using a2 – b2 = (a + b) (a – b)]
(7\(\sqrt{a}\) – 5\(\sqrt{b}\)) (7\(\sqrt{a}\) + 5\(\sqrt{b}\)) = \((7\sqrt{a})^{2} – (5\sqrt{b})^{2}\) = 49a – 25b

(v) (\(\sqrt{\frac{225}{729}} – \sqrt{\frac{25}{144}}\)) ÷ \(\sqrt{\frac{16}{81}}\)


= \(\frac{5}{36}\) × \(\frac{9}{4}\)
= \(\frac{5×1}{4×4}\)
= \(\frac{5}{16}\)

Question 3.
If \(\sqrt{2}\) = 1.414, \(\sqrt{3}\) = 1.732, \(\sqrt{5}\) = 2.236, \(\sqrt{10}\) = 3.162, then find the values of the following correct to 3 places of decimals.
(i) \(\sqrt{40}\) – \(\sqrt{20}\)
(ii) \(\sqrt{300}\) + \(\sqrt{90}\) – \(\sqrt{8}\)
Solution:
(i) \(\sqrt{40}\) – \(\sqrt{20}\) = \(\sqrt{4×10} – \sqrt{4×5} = 2\sqrt{10} – 2\sqrt{5}\)
= 2 × 3.162 – 2 × 2.236 = 6.324 – 4.472 = 1.852

(ii) \(\sqrt{300}\) + \(\sqrt{90}\) – \(\sqrt{8}\) = \(\sqrt{3×100} + \sqrt{9×10} – \sqrt{4×2}\)
= 10\(\sqrt{3}\) + 3\(\sqrt{10}\) – 2\(\sqrt{2}\)
= 10 × 1.732 + 3 × 3.162 – 2 × 1.414
= 17.32 + 9.486 – 2.828
= 26.806 – 2.828
= 23.978

Question 4.
Arrange surds in descending order
(i) \(\sqrt[3]{5}\), \(\sqrt[9]{4}\), \(\sqrt[6]{3}\)
Solution:
LCM of 3, 9 and 6 is 18

\(\sqrt[3]{5}\) = \(\sqrt[3×6]{5^{6}}\) = \(\sqrt[18]{15625}\)
\(\sqrt[9]{4}\) = \(\sqrt[2×9]{4^{2}}\) = \(\sqrt[18]{16}\)
\(\sqrt[6]{3}\) = \(\sqrt[3×6]{3^{3}}\) = \(\sqrt[18]{27}\)
\(\sqrt[18]{15625}\) > \(\sqrt[18]{27}\) > \(\sqrt[18]{16}\)
\(\sqrt[3]{5}\) > \(\sqrt[6]{3}\) > \(\sqrt[9]{4}\)

(ii) \(\sqrt[2]{\sqrt[3]{5}}\), \(\sqrt[3]{\sqrt[4]{7}}\), \(\sqrt{\sqrt{3}}\)
Solution:
\(\sqrt[2]{\sqrt[3]{5}}\) = \(\sqrt[6]{5}\); \(\sqrt[3]{\sqrt[4]{7}}\) = \(\sqrt[12]{7}\); \(\sqrt{\sqrt{3}}\) = \(\sqrt[4]{3}\)
LCM of 6, 12 and 4 is 12

\(\sqrt[2]{\sqrt[3]{5}}\) = \(\sqrt[6]{5}\) = \(\sqrt[12]{5^{2}}\) = \(\sqrt[12]{25}\)
\(\sqrt[3]{\sqrt[4]{7}}\) = \(\sqrt[12]{7}\) = \(\sqrt[12]{7}\)
\(\sqrt{\sqrt{3}}\) = \(\sqrt[4]{3}\) = \(\sqrt[12]{3^{3}}\) = \(\sqrt[12]{27}\)
\(\sqrt[12]{27}\) > \(\sqrt[12]{25}\) > \(\sqrt[12]{7}\)
\(\sqrt{\sqrt{3}}\) > \(\sqrt[2]{\sqrt[3]{5}}\) > \(\sqrt[3]{\sqrt[4]{7}}\)

Question 5.
Can you get a pure surd when you find:
(i) the sum of two surds
(ii) the difference of two surds
(iii) the product of two surds
(iv) the quotient of two surds
Justify each answer with an example.
Solution:
(i) Yes we can get a surd.
Example:
(a) 3\(\sqrt{2}\) + 5\(\sqrt{2}\) = (3 + 5)\(\sqrt{2}\) = 8\(\sqrt{2}\)
(b) 3\(\sqrt{6}\) + 2\(\sqrt{6}\) = (3 + 2)\(\sqrt{6}\) = 5\(\sqrt{6}\)

(ii) Yes we can get a surd.
Example:
(a) \(\sqrt{75}\) – \(\sqrt{48}\) = \(\sqrt{25×3}\) – \(\sqrt{16×3}\) = (5 – 4) \(\sqrt{3}\) = \(\sqrt{3}\)
(b) \(\sqrt{98}\) – \(\sqrt{72}\) = \(\sqrt{49×2}\) – \(\sqrt{36×2}\) = (7 – 6) \(\sqrt{2}\) = \(\sqrt{2}\)

(iii) Yes we can get a surd.
Example:
(a) \(\sqrt{8}\) × \(\sqrt{6}\) = \(\sqrt{8×6}\) = \(\sqrt{48}\)
(b) \(\sqrt{11}\) × \(\sqrt{3}\) = \(\sqrt{11×3}\) = \(\sqrt{33}\)

(iv) Yes we can get a surd.
Example:
(a) \(\sqrt{55}\) ÷ \(\sqrt{5}\) = \(\frac{\sqrt{11×5}}{\sqrt{5}} = \sqrt{11}\)
(b) \(\sqrt{65}\) ÷ \(\sqrt{5}\) = \(\frac{\sqrt{13×5}}{\sqrt{13}} = \sqrt{5}\)

Question 6.
Can you get a rational number when you compute:
(i) the sum of two surds
(ii) the difference of two surds
(iii) the product of two surds
(iv) the quotient of two surds
Justify each answer with an example.
Solution:
(i) Yes, the sum of two surds will give a rational number.
Example:
(a) (2 + \(\sqrt{3}\)) + (2 – \(\sqrt{3}\)) = 4
(b) (\(\sqrt{5}\) + 4) + (7 – \(\sqrt{5}\)) = 11

(ii) Yes, the difference of two surds will give a rational number.
Example:
(a) (5 + \(\sqrt{7}\)) – (- 5 + \(\sqrt{7}\)) = 10
(b) (\(\sqrt{11}\) + 5) – (-3 + \(\sqrt{11}\)) = 8

(iii) Yes, the product of two surds will give a rational number.
Example:
(a) \(\sqrt{125}\) × \(\sqrt{45}\) = \(\sqrt{25×5}\) × \(\sqrt{9×5}\) = 5\(\sqrt{5}\) × 3\(\sqrt{5}\) = 15 × 5 = 75
(b) \(\sqrt{150}\) × \(\sqrt{6}\) = \(\sqrt{25×6}\) × \(\sqrt{6}\) = 5\(\sqrt{6}\) × \(\sqrt{6}\) = 5 × 6 = 30

(iv) Yes. The quotient of two surds will give a rational number.
Example:
(a) \(\sqrt{32}\) ÷ \(\sqrt{8}\) = \(\frac{\sqrt{8×4}}{\sqrt{8}} = \sqrt{4}\) = 2
(b) \(\sqrt{50}\) ÷ \(\sqrt{2}\) = \(\frac{\sqrt{25×2}}{\sqrt{2}} = \sqrt{25}\) = 5

Students can download Maths Chapter 2 Real Numbers Ex 2.9 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.9

Question 1.
If n is a natural number then √n is……….
(a) always a natural number
(b) always an irrational number
(c) always a rational number
(d) may be rational or irrational
Solution:
(d) may be rational or irrational

Question 2.
Which of the following is not true?
(a) Every rational number is a real number
(b) Every integer is a rational number
(c) Every real number is an irrational number
(d) Every natural number is a whole number
Solution:
(c) Every real number is an irrational number

Question 3.
Which one of the following, regarding sum of two irrational numbers, is true?
(a) always an irrational number
(b) may be a rational or irrational number
(c) always a rational number
(d) always an integer
Solution:
(b) may be a rational or irrational number

Question 4.
Which one of the following has a terminating decimal expansion?
(a) \(\frac{5}{64}\)
(b) \(\frac{8}{9}\)
(c) \(\frac{14}{15}\)
(d) \(\frac{1}{12}\)
Solution:
(a) \(\frac{5}{64}\)
Hint:
\(\frac{5}{64}\) = \(\frac{5}{2^{6}}\)

Question 5.
Which one of the following is an irrational number?
(a) \(\sqrt{25}\)
(b) \(\sqrt{\frac{9}{4}}\)
(c) \(\frac{7}{11}\)
(d) π
Solution:
(d) π
Hint:
We take frequently π as \(\frac{22}{7}\) (which gives the value of 3.1428571428571…….) to be its correct value, but in reality these are only approximations

Question 6.
An irrational number between 2 and 2.5 is………
(a) \(\sqrt{11}\)
(b) √5
(c) \(\sqrt{2.5}\)
(d) √8
Solution:
(b) √5
Hint:
√5 = 2.236, it lies between 2 and 2.5

Question 7.
The smallest rational number by which \(\frac{1}{3}\) should be multiplied so that its decimal expansion terminates with one place of decimal is ………
(a) \(\frac{1}{10}\)
(b) \(\frac{3}{10}\)
(c) 3
(d) 30
Solution:
(b) \(\frac{3}{10}\)
Hint:
\(\frac{1}{3}\) × \(\frac{3}{10}\) = \(\frac{1}{10}\) = \(\frac{1}{2×5}\) it has terminating decimal expansion.

Question 8.
If \(\frac{1}{7}\) = 0.\(\overline { 142857 }\) then the value of \(\frac{5}{7}\) is ………..
(a) 0.\(\overline { 142857 }\)
(b) 0.\(\overline { 714285 }\)
(c) 0.\(\overline { 571428 }\)
(d) 0.714285
Solution:
(b) 0.\(\overline { 714285 }\)

Question 9.
Find the odd one out of the following.
(a) \(\sqrt{32}×\sqrt{2}\)
(b) \(\frac{\sqrt{27}}{\sqrt{3}}\)
(c) \(\sqrt{72}×\sqrt{8}\)
(d) \(\frac{\sqrt{54}}{\sqrt{18}}\)
Solution:
(b) \(\frac{\sqrt{27}}{\sqrt{3}}\)
Hint:
\(\frac{\sqrt{27}}{\sqrt{3}}\) = \(\frac{\sqrt{27}}{\sqrt{3}}\) = √9 = 3. It is an odd number

Question 10.
0.\(\overline { 34 }\) + 0.3\(\overline { 4 }\) = ……….
(a) 0.6\(\overline { 87 }\)
(b) 0.\(\overline { 68 }\)
(c) 0.6\(\overline { 8 }\)
(d) 0.68\(\overline { 7 }\)
Solution:
(a) 0.6\(\overline { 87 }\)
Hint:
0.34343434
0.34444444
0.68787878

Question 11.
Which of the following statement is false?
(a) The square root of 25 is 5 or -5
(b) \(-\sqrt{25}\) = -5
(c) \(\sqrt{25}\) = 5
(d) \(\sqrt{25}\) = ±5
Solution:
(d) \(\sqrt{25}\) = ±5

Question 12.
Which one of the following is not a rational number?
(a) \(\sqrt{\frac{8}{18}}\)
(b) \(\frac{7}{3}\)
(c) \(\sqrt{0.01}\)
(d) \(\sqrt{13}\)
Solution:
(d) \(\sqrt{13}\)

Question 13.
\(\sqrt{27}\) + \(\sqrt{12}\) = ……….
(a) \(\sqrt{39}\)
(b) 5√6
(c) 5√3
(d) 3√5
Solution:
(d) 3√5
Hint:
\(\sqrt{27}\) + \(\sqrt{12}\) = \(\sqrt{9×3}\) + \(\sqrt{3×4}\) = 3√3 + 2√3 = 5√3

Question 14.
If \(\sqrt{80}\) = k√5, then k = ………
(a) 2
(b) 4
(c) 8
(d) 16
Solution:
(b) 4
Hint:
\(\sqrt{80}\) = k√5
\(\sqrt{16×5}\) = k√5
4√5 = k√5
∴ k = 4

Question 15.
4√7 × 2√3 = ……….
(a) 6\(\sqrt{10}\)
(b) 8\(\sqrt{21}\)
(c) 8\(\sqrt{10}\)
(d) 6\(\sqrt{21}\)
Solution:
(b) 8\(\sqrt{21}\)
Hint:
4√7 × 2√3 = 4 × 2\(\sqrt{7×3}\) = 8\(\sqrt{21}\)

Question 16.
When written with a rational denominator, the expression \(\frac {2\sqrt{3}}{3\sqrt{2}}\) can be simplified as……..
(a) \(\frac {\sqrt{2}}{3}\)
(b) \(\frac {\sqrt{3}}{2}\)
(c) \(\frac {\sqrt{6}}{3}\)
(d) \(\frac {2}{3}\)
Solution:
(c) \(\frac {\sqrt{6}}{3}\)

Question 17.
When (2√5 – √2)² is simplified, we get………
(a) 4√5 + 2√2
(b) 22 – 4\(\sqrt{10}\)
(c) 8 – 4\(\sqrt{10}\)
(d) 2\(\sqrt{10}\) – 2
Solution:
(b) 22 – 4\(\sqrt{10}\)
Hint:
(2√5 – √2)² = (2√5)² + (√2)² – 2 × 2√5 × √2
= 20 – 4\(\sqrt{10}\) + 2
= 22 – 4\(\sqrt{10}\)

Question 18.
\((0.000729)^\frac{-3}{4}\) × \((0.09)^\frac{-3}{4}\) = ……..
(a) \(\frac {10^3}{3^3}\)
(b) \(\frac {10^5}{3^5}\)
(c) \(\frac {10^2}{3^2}\)
(d) \(\frac {10^6}{3^6}\)
Solution:
(d) \(\frac {10^6}{3^6}\)
Hint:

Question 19.
If √9^x = \(\sqrt[3]{9^2}\), then x = …….
(a) \(\frac {2}{3}\)
(b) \(\frac {4}{3}\)
(c) \(\frac {1}{3}\)
(d) \(\frac {5}{3}\)
Solution:
(b) \(\frac {4}{3}\)
Hint:

Question 20.
The length and breadth of a rectangular plot are 5 × 10⁵ and 4 × 10⁴ metres respectively. Its area is ……….
(a) 9 × 10¹ m²
(b) 9 × 10⁹ m²
(c) 2 × 10¹⁰ m²
(d) 20 × 10²⁰ m²
Solution:
(c) 2 × 10¹⁰ m²
Hint:
Area of a rectangle = l × b = 5 × 10⁵ × 4 × 10⁴
= 5 × 4 × 10⁵⁺⁴
= 20 × 10⁹
= 2.0 × 10 × 10⁹
= 2 × 10¹⁰ m²

Students can download Maths Chapter 4 Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Additional Questions

I. Multiple Choice Questions.

Question 1.
The angle sum of a convex polygon with number of sides 7 is ………
(a) 900°
(b) 1080°
(c) 1444°
(d) 720°
Solution:
(a) 900°

Question 2.
What is the name of a regular polygon of six sides?
(a) Square
(b) Equilateral triangle
(c) Regular hexagon
(d) Regular octagon
Solution:
(c) Regular hexagon

Question 3.
One angle of a parallelogram is a right angle. The name of the quadrilateral is ………
(a) square
(b) rectangle
(c) rhombus
(d) kite
Solution:
(b) rectangle

Question 4.
If all the four sides of a parallelogram are equal and the adjacent angles are of 120° and 60°, then the name of the quadrilateral is ………
(a) rectangle
(b) square
(c) rhombus
(d) kite
Solution:
(c) rhombus

Question 5.
In a parallelogram ∠A : ∠B = 1 : 2. Then ∠A ………
(a) 30°
(b) 60°
(c) 45°
(d) 90°
Solution:
(b) 60°

Question 6.
Which of the following is a formula to find the sum of interior angles of a quadrilateral of w-sides?
(a) \(\frac{n}{2}\) × 180°
(b) (\(\frac{n+1}{2}\)) 180°
(c) (\(\frac{n-1}{2}\)) 180°
(d) (n – 2) 180°
Solution:
(d) (n – 2) 180°

Question 7.
Diagonal of which of the following quadrilaterals do not bisect it into two congruent triangles?
(a) rhombus
(b) trapezium
(c) square
(d) rectangle
Solution:
(b) trapezium

Question 8.
The point of concurrency of the medians of a triangle is known as ………
(a) circumcentre
(b) incentre
(c) orthocentre
(d) centroid
Solution:
(d) centroid

Question 9.
Orthocentre of a triangle is the point of concurrency of ………
(a) medians
(b) altitudes
(c) angle bisectors
(d) perpendicular bisectors of side
Solution:
(b) altitudes

Question 10.
ABCD is a parallelogram as shown. Find x and y.

(a) 1, 7
(b) 2, 6
(c) 3, 5
(d) 4, 4
Solution:
(c) 3, 5

Question 11.
A circle divides the plane into part ………
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(c) 3

Question 12.
The longest chord of a circle is a of the circle……….
(a) radius
(b) diameter
(c) chord
(d) secant
Solution:
(b) diameter

Question 13.
Opposite angles of a cyclic quadrilateral are ………
(a) supplementary
(b) complementary
(c) equal
(d) none of these
Solution:
(a) supplementary

Question 14.
The value of x from figure is if ‘O’ is the centre of the circle ………

(a) 20 cm
(b) 15 cm
(c) 12 cm
(d) 5 cm
Solution:
(d) 5 cm

Question 15.
If PQ = x and ‘O’ is the centre of the circle, then x= ………

(a) 7 cm
(b) 14 cm
(c) 8 cm
(d) 13 cm
Solution:
(b) 14 cm

Question 16.
In figure OM = ON = 8cm and AB = 30 cm, then CD = ………

(a) 15 cm
(b) 30 cm
(c) 40 cm
(d) 10 cm
Solution:
(b) 30 cm

Question 17.
O is the centre of a circle, ∠AOB = 100°. Then angle ∠ ACB = ………

(a) 80°
(b) 40°
(c) 50°
(d) 60°
Solution:
(c) 50°

Question 18.
In,a circle, with center O, ∠AOB = 20°, ∠BOC = 40°, arc BC = 4 Then length of arc AB will be ………

(a) 8 cm
(b) 6 cm
(c) 2 cm
(d) 1 cm
Solution:
(c) 2 cm

Question 19.
In the figure , OC = 3cm and radius of circle is 5 cm. Then AB = ………

(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 8 cm
Solution:
(d) 8 cm

Question 20.
O is the centre of the circle. The value of x in the given diagram is ………

(a) 100°
(b) 160°
(c) 200°
(d) 80°
Solution:
(d) 80°

II. Answer the following questions.

Question 1.
In the figure find x° and y°.
Solution:
∠ACD = ∠A + ∠B
(An exterior angle of a triangle is sum of its interior opposite angles)
120° = 50° + x°
x° = 120° – 50°
= 70°
In the triangle ABC

∠A + ∠B + ∠ACB = 180° (Sum of the angles of a Δ)
50° + x + ∠ACB = 180°
50° + 70° + ∠ACB = 180°
∠ACB = 180° – 120°
y = 60°
(OR)
∠ACD + ∠ACB = 180° (Angles of a linear pair)
∠ACB = 180° – 120°
= 60°
The value of x = 70° and y = 60°.

Question 2.
The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution:
Let the angles of the quadrilateral be 3x, 5x, 9x and 13x.
Sum of all the angles of quadrilateral = 360°.
3x + 5x + 9x + 13x = 360°
30x = 360°
x = \(\frac{360°}{30}\)
= 12°
3x = 3 × 12 = 36°
5x = 5 × 12 = 60°
9x = 9 × 12 = 108°
13x = 13 × 12 = 156°
The required angles of quadrilateral are 36°, 60°, 108° and 156°.

Question 3.
Diagonal AC of a parallelogram ABCD bisects ∠A. Show that

(i) it bisects ∠C also
(ii) ABCD is a rhombus.
Solution:
We have a parallelogram ABCD in which diagonals AC bisect ∠A.
∠DAC = ∠BAC
(i) To prove that AC bisects ∠C
∴ ABCD is a parallelogram

∴ AB || DC and AC is a transversal
∴ ∠1 = ∠3 (Alternate interior angle) …….(1)
Also BC || AD and AC is a transversal
∴ ∠2 = ∠4 (Alternate interior angle) …….(2)
But AC bisects ∠A
∴ ∠1 = ∠2 ……… (3)
From (1), (2) and (3) we get
∠3 = ∠4
∴ AC bisects ∠C.

(ii) To prove that ABCD is a rhombus.
In ΔABC, we have ∠1 = ∠4 [∴ ∠ 1 = ∠2 = ∠4]
∴ BC = AB (side opposite to equal angles are equal) ……..(4)
Similarly AD = DC …….. (5)
But ABCD is a parallelogram AB = DC (Opposite sides of a parallelogram) ………(6)
From (4), (5) and (6) we have AB = BC = CD = DA.
Thus ABCD is a rhombus.

Question 4.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertex A and C on diagonal BD.
Show that

(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ.
Solution:
(i) In ΔAPB and ΔCQD we have
∠APB = ∠CQD (90° each)
AB = CD (opposite sides of parallelogram ABCD)
∠ABP = ∠CDQ (AB || CD and AD is a transversal)
Using ASA congruency we have,
ΔAPB ≅ ΔCQD

(ii) Since ΔAPB ≅ ΔCQD
∴ Their corresponding parts are equal.
∴ AP = CQ.

Question 5.
ABCD is a rectangle and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

Solution:
In rectangle ABCD, P is the mid-point of AB.
Q is the mid-point of BC. R is the mid-point of CD.
S is the mid-point of DA. AC is the diagonal.
Now in ΔABC,
PQ = \(\frac{1}{2}\) AC and PQ || AC ……. (1)
Similarly in ΔACD,
SR = \(\frac{1}{2}\) AC and SR || AC ……. (2)
From (1) and (2) we get,
PQ = SR and PQ || SR
Similarly by joining BD, we have
PS = QR and PS || QR
i.e. Both pairs of opposite sides of quadrilateral PQRS are equal and parallel.
∴ PQRS is a parallelogram.

Question 6.
In the figure A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
Solution:

O is the centre of the circle. ∠AOB = 60° and ∠BOC = 30°
Sum of all the angles of quadrilateral = 360°.
∠AOB + ∠BOC = ∠AOC
∴ ∠AOC = 30° + 60°
= 90°
∠ADC = \(\frac{1}{2}\) × 90°
= 45°

Question 7.
In the given figure A, B, C and D are four points on a circle, AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
Solution:
In ΔCDE,

Exterior ∠BEC = Sum of interior opposite angle
130° = ∠EDC + ∠ECD
130° = ∠EDC + 20°
130° – 20° = ∠EDC
110° = ∠EDC
∴ ∠BAC = ∠BDC = 110° (Both the triangles are standing on the same base)
∠BAC = 110°

Question 8.
In the given figure KLMN is a cyclic quadrilateral. KD is the tangent at K. If ∠N is a diameter ∠NLK = 40° and ∠LNM = 50°. Find ∠MLN and ∠DKL.

Solution:
LN is a diameter
∠LMN = ∠LKN = 90° (Angle in a semi-circle)
∴ ∠MLN = 90° – 50°
= 40°
∠LNK = 90° – 40°
= 50°
∠DKL = ∠LKN = 50° (angles in the alternate segment)
∴ ∠DKL = 50°
∠MLN = 40° and ∠DKL = 50°

Question 9.
In the given figure ∠PQR = 100°, where P, Q and R are points on a circle with centre ‘O’. Find ∠OPR.

Solution:
∠PQR is the angle subtended by the chord PR in the minor segment.
reflex ∠POR = 2∠PQR
= 2 × 100°
= 200°
Now ∠POR + reflex ∠POR = 360°
∠POR + 200° = 360°
∠POR = 360° – 200°
= 160°
From the given diagram, POR is an isosceles triangle (∴ PO = OR = radii)
∴ ∠OPR = ∠ORP (angles opposite to equal sides)
In ΔOPR,
∠OPR + ∠ORP + ∠POR = 180°
∠OPR + ∠OPR + 160° = 180°
2∠OPR = 180° – 160°
2∠OPR = 20°
∠OPR = \(\frac{20°}{2}\)
= 10°
∴ ∠OPR = 10°

Question 10.
AB and CD are two parallel chords of a circle which are on either sides of the centre such that AB = 10 cm and CD = 24 cm. Find the radius if the distance between AB and CD is 17 cm.
Solution:

Given AB = 10 cm, CD = 24 cm and PQ = 17 cm.
PC = PD = \(\frac{24}{2}\)
= 12 cm
AQ = QB = \(\frac{10}{2}\)
= 5 cm
Let OP be x; OQ = (17 – x)
In the ΔOPC,
OC² = OP² + PC²
= x² + 12²
In the ΔOAQ,
OA² = AQ² + QO²
= 5² + (17 – x)²
= 25 + 289 + x² – 34x
= 314 + x² – 34x
But OA² = OC²
314 + x² – 34x = x² + 144
-34x = 144 – 314
-34x = -170
34x = 170
x = \(\frac{170}{34}\)
= \(\frac{10}{2}\)
= 5
We know,
OC² = x²+ 144
= 5² + 144
= 25 + 144
OC² = 169
But OC = \(\sqrt{169}\)
= 13
Radius of the circle = 13 cm
= x² + 144

Students can download Maths Chapter 4 Geometry Ex 4.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.1

Question 1.
In the figure, AB is parallel to CD, find x.

Solution:
(i) Through T draw TE || AB.

∴ ∠BAT + ∠ATE = 180° (AB || TE)
140° + ∠ATE = 180°
∠ATE = 180°- 140° = 40°
Similarly ∠ETC + ∠TCD = 180° (TE || CD)
∠ETC+150° = 180°
∠ETC = 180°- 150° = 30°
x = ∠ATE + ∠ETC
= 40°+ 30° = 70°
x = 70°

(ii) Draw TE || AB.

∠ABT + ∠ETB = 180° (AB || TE)
48° + ∠ETB = 180°
∠ETB = 180° – 48° = 132°
Similarly ∠CDT + ∠DTE = 180°
24° + ∠DTE = 180°
∴ ∠DTE = 180° – 24°
= 156°
∴ ∠BTE + ∠ETD = 132° + 156°
= 288°
x = 288°

(iii) In the given figure AB || CD, AD is the transversal.
∠CDA = ∠BAD
= 53° (alternate angles are equal)
In ΔECD, ∠D = ∠A = 53° (Alternate angles are equal)
∠E + ∠C + ∠D = 180° (sum of the angles of a triangle)
x° + 38° + 53° = 180°
x° = 180°- 91°
= 89°
x = 89°

Question 2.
The angles of a triangle are in the ratio 1 : 2 : 3, find the measure of each angle of the triangle.
Solution:
The ratio of the angles of a triangle = 1 : 2 : 3.
Let the angles of a triangle be x, 2x and 3x.
x + 2x + 3x = 180° (Total angle of a triangle is 180°)
6x = 180°
x = \(\frac{180°}{6}\)
= 30°
x = 30°; 2x = 2 × 30° = 60°; 3x = 3 × 30° = 90°
Measures of the angles of a triangle = 30°, 60° and 90°.

Question 3.
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent:

(i) In ΔPQR and ΔABC
PQ = AB (Given)
RQ = BC (Given)
ΔABC is not congruent to ΔPQR.
If PR = AC then ΔABC ≅ ΔPQR

(ii) In ΔABD and ΔCDB
AB = CD (Given)
AD = BC (Given)
BD is common
By SSS congruency
ΔABD ≅ ΔCDB

(iii) In ΔPXY and ΔPXZ
PX is common.
XY = XZ (Given)
PY = PZ (Given)
By SSS congruency
ΔPXY ≅ ΔPXZ

(iv) In the given figure BD bisect AC
In ΔAOB and ΔOCD
OA = OC (Given)
∠AOB = ∠DOC (vertically opposite angles)
∠B = ∠D (Given)
By ASA congruency ΔAOB ≅ ΔOCD

(v) In the given figure AC and BD bisect each other at O.
∴ OA = OC (Given); OB = OD (Given)
∠AOB = ∠COD (vertically opposite angles)
By SAS congruency
ΔAOB ≅ ΔOCD

(vi) In the given figure
AB = AC (Given)
BM = MC (AM is the median of the ΔABC)
AM is common (By SSS congruency)
∴ ΔABM ≅ ΔACM

Question 4.
ΔABC and ΔDEF are two triangles in which AB = DF, ∠ACB = 70°, ∠ABC = 60°; ∠DEF = 70° and ∠EDF = 60°. Prove that the triangles are congruent.
Solution:

In ΔABC ∠B = 60° and ∠C = 70°
∴ ∠A = 180° – (60° + 70°)
= 180° – 130°
= 50°
In ΔDEF ∠E = 70° and ∠D = 60°
∠F = 180° – (70° + 60°)
= 180° – 130°
= 50°
∠A = ∠F = 50°
∠B = ∠D = 60°
∠C = ∠E = 70°
By AAA congruency
ΔABC ≅ ΔFDE
(or)
∠B = ∠D = 60°
∠C = ∠E = 70°
AB = FE
By ASA congruency
ΔABC ≅ ΔFDE

Question 5.
Find all the three angles of the ΔABC.

Solution:
∠A + ∠B = ∠ACD (An exterior angle of a triangle is sum of its interior opposite angles)
x + 35 + 2x – 5 = 4x – 15
3x + 30 = 4x – 15
30 + 15 = 4x – 3x
45° = x
∠A = x + 35°
= 45° + 35°
= 80°
∠B = 2x – 5
= 2(45°) – 5°
= 90° – 5°
= 85°
∠ACD = 4x – 15
= 4 (45°) – 15°
= 180° – 15°
= 165°
∠ACB = 180° – ∠ACD
= 180° – 165°
= 15°
∠A = 80°, ∠B = 85° and ∠C = 15°.

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.3

Question 1.
Find the mid-points of the line segment joining the points.
(i) (-2, 3) and (-6, -5)
(ii) (8, -2) and (-8, 0)
(iii) (a, b) and (a + 2b, 2a – b)
(iv) (\(\frac{1}{2},\frac{-3}{7}\)) and (\(\frac{3}{2},\frac{-11}{7}\))
Solution:

Question 2.
The centre of a circle is (-4, 2). If one end of the diameter of the circle is (-3, 7) then find the other end.
Solution:
Let the other end of the diameter B be (a, b)

∴ \(\frac{-3+a}{2}\) = -4
-3 + a = -8
a = -8 + 3
a = -5
\(\frac{7+b}{2}\)
7 + b = 4
b = 4 – 7 ⇒ b = -3
The other end of the diameter is (-5, -3).

Question 3.
If the mid-point (x, y) of the line joining (3, 4) and (p, 7) lies on 2x + 2y + 1 = 0, then what will be the value of p?
Solution:

3 + p + 11 + 1 = 0 ⇒ p + 15 = 0 ⇒ p = -15
The value of p is -15.

Question 4.
The mid-point of the sides of a triangle are (2, 4), (-2, 3) and (5, 2). Find the coordinates of the vertices of the triangle.
Solution:
Let the vertices of the ΔABC be A (x₁ y₁), B (x₂, y₂) and C (x₃, y₃)

\(\frac{x_{2}+x_{3}}{2}\) = -2 ⇒ x₂ + x₃ = -4 → (3)
\(\frac{y_{2}+y_{3}}{2}\) = 3 ⇒ y₂ + y₃ = 6 → (4)

\(\frac{x_{1}+x_{3}}{2}\) = 5 ⇒ x₁ + x₃ = 10 → (5)
\(\frac{y_{1}+y_{3}}{2}\) = 2 ⇒ y₁ + y₃ = 4 → (6)
By adding (1) + (3) + (5) we get
2x₁ + 2x₂ + 2x₃ = 4 – 4 + 10
2(x₁ + x₂ + x₃) = 10 ⇒ x₁ + x₂ + x₃ = 5
From (1) x₁ + x₂ = 4 ⇒ 4 + x₃ = 5
x₃ = 5 – 4 = 1
∴ The vertices of the ΔABC are
A (9, 3)
B (-5, 5), C (1, 1)
From (3) x₂ + x₃ = -4 ⇒ x₁ + (-4) = 5
x₁ = 5 + 4 = 9
From (5) ⇒ x₁ + x₃ = 8
x₂ + 10 = 5
x₂ = 5 – 10 = -5
∴ x₁ = 9, x₂ = -5, x₃ = 1
By adding (2) + (4) + (6) we get
2y₃ + 2y₂ + 2y₃ = 8 + 6 + 4
2(y₁ +y₂ + y₃) = 18 ⇒ y₁ + y₂ + y₃ = 9
From (2) ⇒ y₁ + y₂ = 8
8 + y₃ = 9 ⇒ y₃ = 9 – 8 = 1
From (4)
y₂ + y₃ = 6 ⇒ y₁ + 6 = 9
y₁ = 9 – 6 = 3
From (6)
y₁ + y₃ = 4 ⇒ y₂ + 4 = 9
y₂ = 9 – 4 = 5
∴ y₁ = 3, y₂ = 5, y₃ = 1

Question 5.
O (0, 0) is the centre of a circle whose one chord is AB, where the points A and B (8, 6) and (10, 0) respectively. OD is the perpendicular from the centre to the chord AB. Find the coordinates of the mid-point of OD.
Solution:
Note: Since OD is perpendicular to AB, OD bisect the chord
D is the mid-point of AB

Question 6.
The points A(-5, 4) , B(-1, -2) and C(5, 2) are the vertices of an isosceles right-angled triangle where the right angle is at B. Find the coordinates of D so that ABCD is a square.
Solution:
Since ABCD is a square
Mid-point of AC = mid-point of BD
Let the point D be (a, b)

But mid-point of BD = Mid-point of AC
(\(\frac{-1+a}{2}, \frac{-2+b}{2}\)) = (0, 3)
\(\frac{-1+a}{2}\) = 0
-1 + a = 0
a = 1
(\(\frac{-2+b}{2}\))
-2 + b = 6
b = 6 + 2 = 8
∴ The vertices D is (1, 8).

Question 7.
The points A (-3, 6), B (0, 7) and C (1, 9) are the mid points of the sides DE, EF and FD of a triangle DEF. Show that the quadrilateral ABCD is a parallellogram.
Solution:
Let D be (x₁ y₁), E (x₂, y₂) and F (x₃, y₃)


x₁ + x₂ = -6 → (1)
y₁ + y₂ = 12 → (2)

x₁ + x₃ = 2 → (5)
y₁ + y₃ = 18 → (6)
Add (1) + (3) + (5)
2x₁ + 2x₂ + 2x₃ = -6 + 0 + 2
2 (x₁ + x₂ + x₃) = -4
x₁ + x₂ + x₃ = -2
From (1) x₁ + x₂ = -6
x3 = -2 + 6 = 4
From (3) x₂ + x₃ = 0
x₁ = -2 + 0
x₁ = -2
From (5) x₁ + x₃ = 2
x₂ + 2 = -2
x₂ = -2 -2 = -4
∴ x₁ = -2, x₂ = -4, x₃= 4
Add (2) + (4) + 6
2y₁ + 2y₂ + 2y₃ = 12 + 14 + 18
2(y₁ + y₂ + y₃) = 44
y₁ + y₂+ y₃ = 44/2 = 22
From (2) y₁ + y₂ = 12
12 + y₃ = 22 ⇒ y₃ = 22 – 12 = 11
From (4) y₂ + y₃ = 14
y₁ + 14 = 22 ⇒ y₁ = 22 – 14
y₁ = 8
From (6)
y₁ +y₃ = 18
y2 + 18 = 22 ⇒ = 22 – 18
= 4
∴ y₁ = 8, y₂ = 4, y₃ = 11
The vertices D is (-2, 8)

Mid-point of diagonal AC = Mid-point of diagonal BD
The quadrilateral ABCD is a parallelogram

Question 8.
A(-3, 2) , B(3, 2) and C(-3, -2) are the vertices of the right triangle, right angled at A. Show that the mid point of the hypotenuse is equidistant from the vertices.
Solution:

AD = CD = BD = \(\sqrt{13}\)
Mid-point of BC is equidistance from the centre.

Students can download Maths Chapter 3 Algebra Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Additional Questions

I. Multiple choice questions

Question 1.
Which of the following is a monomial?
(a) 4x²
(b) a + b
(c) a + b + c
(d) a + b + c + d
Solution:
(a) 4x²

Question 2.
Which of the following is trinomial?
(a) -7z
(b) z² – 4y²
(c) x²y – xy² + y
(d) 12a – 9ab + 5b – 3
Solution:
(c) x²y – xy² + y

Question 3.
The sum of 5x²; -7x²; 8x²; 11x² and -9x² is ………
(a) 2x²
(b) 4x²
(c) 6x²
(d) 8x²
Solution:
(d) 8x²

Question 4.
The area of a rectangle with length 2l²m and breadth 3lm² is ………
(a) 6l³m³
(b) l³m³
(c) 2l³m³
(d) 4l³m³
Solution:
(a) 6l³m³

Question 5.
The coefficient of x² and x in 2x³ – 5x² + 6x – 3 are respectively ………
(a) 2, -5
(b) 2, 6
(c) – 5, 6
(d) -5, -3
Solution:
(c) – 5, 6

Question 6.
In the system 6x -2y = 3; kx – y = 2 has a unique solution then ………
(a) k = 3
(b) k ≠ 3
(c) k = 4
(d) k ≠ 4
Solution:
(b) k ≠ 3

Question 7.
A system of two linear equation in two variables is inconsistent. If their graphs ………
(a) coincide
(b) intersect only at a point
(c) do not intersect at any point
(d) cut the x-axis
Solution:
(c) do not intersect at any point

Question 8.
The system of equation x – 4y = 8; 3x – 12y = 24 ……….
(a) has infinitely many solution
(b) has no solution
(c) has a unique solution
(d) may or may not have a solution
Solution:
(a) has infinitely many solution

Question 9.
The solution set of x – ay = 4 and x + y = 0 is (1, -1) the value of a is ………
(a) -1
(b) 1
(c) -3
(d) 3
Solution:
(d) 3

Question 10.
The solution set of x + y = 7; x – y = 3 is ………
(a) (-5, -2)
(b) (-5, 2)
(c) (5, 2)
(d) (2, 5)
Solution:
(c) (5, 2)

II. Answer following Questions

Question 1.
What must be added to x⁴ – 3x² + 2x + 6 to get x⁴ – 2x³ – x + 8?
Solution:
Let A be the required number to be added.
(x⁴ – 3x² + 2x + 6) + A = x⁴ – 2x³ – x + 8
A = x⁴ – 2x³ – x + 8 – (x⁴ – 3x² + 2x + 6)
= x⁴ – 2x³ – x + 8 – x⁴ + 3x² – 2x – 6
= -2x³ + 3x² – 3x + 2
Hence -2x³ + 3x² – 3x + 2 must be added.

Question 2.
What must be subtracted to y⁴ + 2y³ – 3y + 8 to get y⁴ – 2y³ + 6?
Solution:
Let A be the required number to be subtracted.
(y⁴ + 2y³ – 3y² + 8) – A = y⁴ – 2y³ + 6
y⁴ + 2y³ – 3y² + 8 – (y⁴ – 2y³ + 6) = A
y⁴ + 2y³ – 3y² + 8 – y⁴ + 2y³ – 6 = A
4y³ – 3y² + 2 = A
Hence 4y³ – 3y² + 2 must be subtracted.

Question 3.
The area of a rectangle is x⁴ + 9x² + 20 sq.units and its length is x² + 4 units. Find its breadth in term of x.
Solution:
Let the breadth of a rectangle be “b”
Length of the rectangle = x² + 4
Area of the rectangle = x⁴ + 9x² + 20
Length × Breadth = x⁴ + 9x² + 20
(x² + 4) × b = x⁴ + 9x² + 20
b = \(\frac{x^{4}+9x^{2}+20}{x^{2}+4}\)
= x² + 5
breadth of a rectangle = x² + 5

Question 4.
Solve 3x + 4y = 24; 20x – 11y = 47 using cross multiplication method.
Solution:
3x + 4y – 24 = 0 → (1)
20x – 11y – 47 = 0 → (2)

\(\frac{x}{-452}\) = \(\frac{1}{-113}\)
-113 = -452
x = \(\frac{452}{113}\)
= 4
But \(\frac{y}{-339}\) = \(\frac{1}{-113}\)
-113y = -339
y = \(\frac{339}{113}\)
= 3
∴ The solution set is (4, 3)

Question 5.
A fraction such that if the numerator is multiplied by 3 and the denominator is reduced by 3, we get \(\frac{18}{11}\), but if the numerator is increased by 8 and the denominator is doubled, we get \(\frac{2}{5}\). Find the fraction.
Solution:
Let the numerator be x and the denominator be y
∴ The fraction is \(\frac{x}{y}\)
According to the given condition
\(\frac{3x}{y-3}\) = \(\frac{18}{11}\)
33x = 18(y – 3)
33x = 18y – 54
33x – 18y – 54 = 0
11x – 6y – 18 = 0 ……. (1)
According to the second condition
\(\frac{x+8}{2y}\) = \(\frac{2}{5}\)
5x + 40 = 4y
5x – 4y + 40 = 0 ……..(2)

∴ The fraction is = \(\frac{12}{25}\)

Question 6.
One number is greater than the thrice the other number by 2. If 4 times the smaller number exceeds the greater by 5, find the number.
Solution:
Let the greater number be x and the smaller number be “y” By the given first condition
x = 3y + 2
x – 3y = 2 ……(1)
Again by the given second condition
4y = x + 5
-x + 4y = 5 …….(2)
Add (1), (2) ⇒ y = 7
Substitute the value of y = 7 in (1)
x – 3(7) = 2
x = 2 + 21
= 23
The greater number is 23 and the smaller number is 7.

Question 7.
The cost of 11 pencils and 3 erasers is Rs 50 and the cost of 8 pencils and 3 erasers is Rs 38. Find the cost of 5 pencils and 5 erasers.
Solution:
Let the cost of a pencil be Rs x and the cost of an eraser be Rs y. According to the first condition.
11x + 3y = 50 …….(1)
According to the second condition
8x + 3y = 38 ……..(2)
(1) – (2) ⇒ 3x = 12
x = \(\frac{12}{3}\)
= 4
Substitute the value of x = 4 in (1)
11 (4) + 3y = 50
3y = 50 – 44
3y = 6
y = \(\frac{6}{3}\)
= 2
Cost of 5 pencils + 5 erasers = 5(4) + 5(2)
= 20 + 10
= 30
The required cost is Rs 30