Students can download Maths Chapter 9 Probability Ex 9.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 9 Probability Ex 9.1
Question 1.
You are walking along a street. If you just choose a stranger crossing you, what is the probability that his next birthday will fall on a Sunday?
Solution:
Sample space = {M, T, W, Th, F, S, Sun}
n(S) = 7
Let E be the event of getting birthday on Sunday
n(E) = 1
p(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{1}{7}\)
![]()
Question 2.
What is the probability of drawing a King or a Queen or a Jack from a deck of cards?
Solution:
The outcomes n(S) = 52
Let E be the event of getting a king or a queen or a jack
= 4 + 4 + 4
n(E) = 12
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{12}{52}\)
= \(\frac{3}{13}\)
Question 3.
What is the probability of throwing an even number with a single standard dice of six faces?
Solution:
Sample space (S) = {1, 2, 3, 4, 5, 6}
n(S) = 6
Let E be the event of getting an even number
E = {2, 4, 6}
n(E) = 3
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{3}{6}\)
= \(\frac{1}{2}\)
![]()
Question 4.
There are 24 balls in a pot. If 3 of them are Red, 5 of them are Blue and the remaining are Green then, what is the probability of picking out (i) a Blue ball,
(ii) a Red ball and
(ii) a Green ball?
Solution:
Sample space n(S) = 24
Number of green ball = 24 – (3 + 5)
= 24 – 8
= 16
(i) Let E1 be the event of getting a blue ball
n(E1) = 5
p(E1) = \(\frac{n(E_{1})}{n(S)}\)
= \(\frac{5}{24}\)
(ii) Let E2 be the event of getting a red ball
n(E2) = 3
p(E2) = \(\frac{n(E_{2})}{n(S)}\)
= \(\frac{3}{24}\)
= \(\frac{1}{8}\)
(iii) Let E3 be the event of getting a green ball
n(E3) = 16
p(E3) = \(\frac{n(E_{3})}{n(S)}\)
= \(\frac{16}{24}\)
= \(\frac{2}{3}\)
![]()
Question 5.
When two coins are tossed, what is the probability that two heads are obtained?
Solution:
Sample space (S) = {(H, H), (H, T), (T, H), (T, T)}
n(S) = 4
Let E be the event of getting two heads
n(E) = 1
p(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{1}{4}\)
![]()
Question 6.
Two dice are rolled, find the probability that the sum is

(i) equal to 1
(ii) equal to 4
(iii) less than 13
Solution:
Sample space (S) = {(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)}
n(S) = 36
(i) Let E1 be the event of getting the sum is equal to 1
n(E1) = 0
p(E1) = \(\frac{n(E_{1})}{n(S)}\)
= \(\frac{0}{36}\)
= 0
(ii) Let E2 be the event of getting the sum is equal to 4
E2 = {(1,3), (2, 2) (3, 1)}
n(E2) = 3
p(E2) = \(\frac{n(E_{2})}{n(S)}\)
= \(\frac{3}{36}\)
= \(\frac{1}{12}\)
(iii) Let E3 be the event of getting the sum is less than 13
n(E3) = 36
p(E3) = \(\frac{n(E_{3})}{n(S)}\)
= \(\frac{36}{36}\)
= 1
![]()
Question 7.
A manufacturer tested 7000 LED lights at random and found that 25 of them were defective. If a LED light is selected at random, what is the probability that the selected LED light is a defective one.
Solution:
Sample space n(S) = 7000
Let E1 be the event of getting selected LED light is a defective one
n(E1) = 25
p(E1) = \(\frac{n(E_{1})}{n(S)}\)
= \(\frac{25}{7000}\)
= \(\frac{1}{280}\)
![]()
Question 8.
In a football match, a goalkeeper of a team can stop the goal, 32 times out of 40 attempts tried by a team. Find the probability that the opponent team can convert the attempt into a goal.
Solution:
Sample space n(S) = 40
Opponent team trying to attempt the goal = 40 – 32 = 8
Let E be the event of getting opponent team convert the attempt into a goal
n(E) = 8
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{8}{40}\)
= \(\frac{1}{5}\)
Question 9.
What is the probability that the spinner will not land on a multiple of 3?
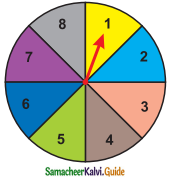
Solution:
Sample space (S) = {1, 2, 3, 4, 5, 6, 7, 8}
n(S) = 8
Land in a multiple of 3 = {3, 6}
Land not a multiple of 3 = 8 – 2
= 6
Let E be the event of getting not a multiple of 6
n(E) = 6
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{6}{8}\)
= \(\frac{3}{4}\)
![]()
Question 10.
Frame two problems in calculating probability, based on the spinner shown here.
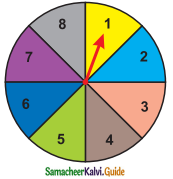
Solution:
(i) What is the probability that the spinner will get an odd number?
(ii) What is the probability that the spinner will not land on a multiple of 2?