TN State Board 11th Computer Science Important Questions Chapter 3 Computer Organization
Question 1.
Define computer organisation.
Answer:
Computer organization deals with the hardware components of a computer system. It includes input/output devices, the central processing unit, storage and primary memory. It is concerned with how the various components of computer hardware operate. It also deals with how they are interconnected to implement an architectural specification.
Question 2.
Define instruction set.
Answer:
A command which is given to a computer to perform an operation on data is called an instruction. Basic set of machine level instructions that a microprocessor is designed to execute is called as an instruction set.
![]()
Question 3.
What do you mean by word size?
Answer:
The number of bits that can be processed by a processor in a single instruction is called its word size. Word size determines the amount of RAM that can be accessed by a microprocessor. Total number of input and output pins in turn determines the architecture of the microprocessor.
Question 4.
Define bus.
Answer:
A bus is a collection of wires used for communication between the internal components of a computer.
Question 5.
What is decoder?
Answer:
A decoder is a digital circuit that is used to point to the specific memory location where the word can be located.
![]()
Question 6.
What is read operation?
Answer:
The read operation transfers the data (bits) from memory word to memory data register.
Question 7.
What is write operation?
Answer:
The write operation transfers the data (bits) from memory data register to word.
Question 8.
What criteria microprocessors are classified?
Answer:
Microprocessors are classified based on the following criteria:
(i) The width of data that can be processed.
(ii) The instruction set.
![]()
Question 9.
What is USB 3.0?
Answer:
USB 3.0 is the third major version of the Universal Serial Bus (USB) standard to connect computers with other electronic gadgets. It can transfer data up to 5 Giga byte/second. USB 3.1 and USB 3.2 are also released.
Question 10.
What are the two basic types of RAM?
Answer:
There are two basic types of RAM. They are
(i) Dynamic RAM (DRAM)
(ii) Static RAM (SRAM)
Question 11.
What is Access time?
Answer:
Access time is the time delay or latency between a request to an electronic system, and the access being completed or the requested data returned.
![]()
Question 12.
What is a computer memory?
Answer:
Computer memory is the storage space in the computer, where data and instructions are stored. Sequential access and random access are the two types of accessing methods to access (store or retrieve) the memory. In sequential access, the memory is accessed in an orderly manner from starting to end. In random access, any byte of memory can be accessed directly without navigating through previous bytes.
Question 13.
What is a system bus?
Answer:
The system bus is a bunch of wires which is the collection of address bus, data bus and control bus.
Question 14.
What do you understand by the word microprocessor?
Answer:
The microprocessor is a programmable multipurpose silicon chip. It is driven by clock pulses. It accepts input as a binary data and after processing, it provides the output data as per the instructions stored in the memory.
![]()
Question 15.
What is meant by Hertz?
Answer:
Hertz (Hz) is the standard unit of measurement used for measuring frequency. Frequency is measured in cycles per second, one hertz equals one cycle per second.
Question 16.
What is called clock speed?
Answer:
The speed at which the microprocessor executes instructions is called the clock speed. Clock speed is measured in MHz (Mega Hertz) or in GHz (Giga Hertz).
Question 17.
How the word size is determined?
Answer:
It determines the amount of RAM that can be accessed by a microprocessor at one time and the total number of pins on the microprocessor. Total number of input and output pins in turn determines the architecture of the microprocessor.
![]()
Question 18.
Why is top surface of the EPROM chip is covered by stickers?
Answer:
EPROM chips have a transparent area at the top surface which is covered by stickers. If it gets removed, the ultraviolet light in the sunlight may erase the contents.
Question 19.
What do you understand about cache memory?
Answer:
It is a very high speed and expensive memory, which is used to speed up the memory retrieval process.
Question 20.
What do you understand by backup storage?
Answer:
Secondary storage devices serve as a supportive storage to main memory and they are non-volatile in nature,
secondary storage is also called as backup storage.
![]()
Question 21.
What are the areas that can use flash memories?
Answer:
Flash memories can be used in personal computers, personal digital assistants (PDA), digital audio players, digital cameras and mobile phones.
Question 22.
What are the uses of Blu-ray disc?
Answer:
It enables recording, rewriting and playback of high-definition video and storing large amount of data.
Question 23.
What is the use of MDR?
Answer:
The memory Data Register (MDR) keeps the data which is transferee! between the memory and the CPU.
![]()
Question 24.
What is microprocessor? Draw the block diagram of microprocessor.
Answer:
The microprocessor is a programmable multipurpose silicon chip that is based on a register. It is driven by clock pulses. It accepts input as a binary data and after processing, it provides the output data as per the instructions stored in the memory.
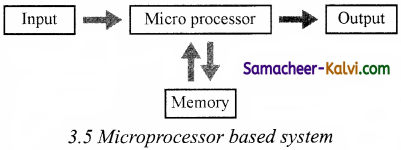
Question 25.
Write short notes on DVD.
Answer:
A DVD (Digital Versatile Disc or Digital Video Disc) is an optical disc capable of storing up to 4.7 GB of data, more than six times what a CD can hold. They are often used to store movies at a better quality. Like CDs, DVDs are read with a laser.
The disc can have one or two sides, and one or two layers of data per side; the number of sides and layers determines how much it can hold. A 12 cm diameter disc with single sided, single layer has 4.7 GB capacity, whereas the single sided, double layer has 8.5 GB capacity. The 8 cm DVD has 1.5 GB capacity.
The capacity of a DVD-ROM can be visually determined by noting the number of data sides of the disc. Double-layered sides are usually gold- coloured, while single-layered sides are usually silver-coloured, like a CD.
![]()
Question 26.
Write short notes on Blu-ray Disc.
Answer:
Blu-Ray Disc is a high-density optical disc similar to DVD. It is used for PlayStation games and for playing high-definition (HD) movies. A double-layer BIu-Ray disc can store up to 50GB (gigabytes) of data. This is more than 5 times the capacity of a DVD, and above 70 times of a CD.
The format was developed to enable recording, rewriting and playback of high-definition video, as well as storing large amount of data. DVD uses a red laser to read and write data. Blu-ray uses a blue-violet laser to write. Hence, it is called as Blu-Ray.
Question 27.
What are the methods to access the memory? Draw the Memory Hierarchy.
Answer:
There are two types of accessing methods to access (read or write) the memory. They are sequential access and random access. In sequential access, the memory is accessed in an orderly manner from starting to end. But, in random access, any byte of memory can be accessed directly without navigating through previous bytes.
→ refer figure no. 3.4.
![]()
Question 28.
Differentiate static RAM and Dynamic RAM.
Answer:
|
Static RAM |
Dynamic RAM |
| It needs to be refreshed less often. | It needs to be refreshed frequently. |
| It is more expensive. | It is less expensive. |
| It uses transistor to store a single bit of data. | It uses a separate capacitor to store each bit of data. |
| It is used in cache memory. | It is used in main memory. |
Question 29.
What are the three main units of microprocessor?
Answer:
The microprocessor is made up of 3 main units. They are-
(i) Arithmetic and Logic unit (ALU):
To perform arithmetic and logical instructions based on computer instructions.
(ii) Control unit:
To control the overall operations of the computer through signals.
(iii) Registers (Internal Memory):
They are used to hold the instruction and data for the execution of the processor.
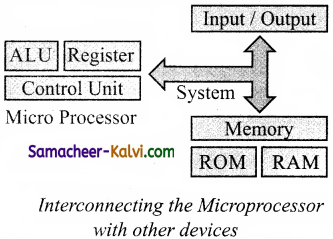
![]()
Question 30.
List down the types of operations that carried out by the instruction set.
Answer:
- Data transfer
- Arithmetic operations
- Logical operations
- Control flow
- Input / output
Question 31.
Explain in detail the various types of storage devices.
Answer:
Secondary Storage Devices:
The secondary storage devices are used to store data that is of larger size which can be accessed later. Since the main memory is costly, the size is generally very limited in a computer. A portion of a secondary storage which can serve as an extension of the main memory and can perform its job is called as virtual memory.
Hard Disks:
Hard disk is a magnetic disk on which you can store computer data. Hard disks can store more data and are faster than floppy disks. A hard disk cqtn store from 10 megabytes to several gigabytes, whereas most floppies have a maximum storage capacity of 1.4 megabytes. Hard disks are less portable than floppies, although it is possible to port by removable hard disks. There are two types of removable hard disks: disk packs and removable cartridges.
Compact Disc (CD):
A CD or CD-ROM is made from 1.2 millimeters thick, polycarbonate plastic material. A thin layer of aluminum or gold is applied to the surface. CD data is represented as tiny indentations known as “pits”, encoded in a spiral track moulded into the top of the polycarbonate layer. The areas between pits are known as “lands”. A motor within the CD player rotates the disk. The capacity of an ordinary CD-ROM is 700MB.
Digital Versatile Disc (DVD):
A DVD (Digital Versatile Disc or Digital Video Disc) is an optical disc capable of storing up to 4.7 GB of data, more than six times what a CD can hold. DVDs are often used to store movies at a better quality than with a VHS. They can also have interactive menus and bonus features such as deleted scenes and commentaries. Like CDs, DVDs are read with a laser.
The disc can have one or two sides, and one or two layers of data per side; the number of sides and layers determines how much it can hold. A 12 cm diameter disc with single sided, single layer has 4.7 GB capacity, whereas the single sided, double layer has 8.5 GB capacity. The 8 cm DVD has 1.5 GB capacity.
The capacity of a DVD-ROM can be visually determined by noting the number of data sides of the disc. Double-layered sides are usually gold- coloured, while single-layered sides are usually silver-coloured, like a CD.
Flash Memory Devices:
It is an electronic (solid-state) non-volatile computer storage medium that can be electrically erased and
reprogrammed. They are either EEPROM or EPROM. Eg: Pendrives, memory cards etc. Flash memories can be used in personal computers, Personal Digital Assistants (PDA), digital audio players, digital cameras and mobile phones. Flash memory offers fast access times. The time taken to read or write a character in memory is called access time. The capacity of the flash memories vary from 1 Gigabytes (GB) to 2 Terabytes (TB).
Blu-Ray Disc:
It is a high-density optical disc format similar to DVD. Blu-ray is used for Play station games and for playing high-definition (HD) movies. A double¬layer Blu-Ray disc can store up to 50GB (gigabytes) of data. This is more than 5 times the capacity of a DVD, and above 70 times of a CD.
The format was developed to enable recording, rewriting and playback of high-definition video (HD), as well as storing large amounts of data. DVD uses a red laser to read and write data. Blu-ray uses a blue-violet laser to write. Hence, it is called as Blu-Ray.
![]()
Question 32.
What are the parameters which influence the characteristics of a microprocessor?
Answer:
A Microprocessor’s performance depends on the following characteristics:
- Clock speed
- Instruction set
- Word size.
Question 33.
What is an instruction?
Answer:
A command which is given to a computer to perform an operation on a piece of data is called an instruction.
Question 34.
What is a program counter?
Answer:
The Program Counter (PC) is a special register in the CPU which always keeps the address of the next instruction to be executed.
Question 35.
What is HDMI?
Answer:
High-Definition Multimedia Interface is an audio/video interface which transfers the uncompressed video and audio data from a video controller, to a compatible computer monitor, LCD projector, digital television etc.
![]()
Question 36.
Which source is used to erase the content of a EPROM?
Answer:
Erasable Programmable Read Only Memory is a special type of memory which serves as a PROM, but the content can be erased using ultraviolet rays. EPROM retains its contents until it is exposed to ultraviolet light. The ultraviolet light clears its contents, making it possible to reprogram the memory.
Question 37.
Differentiate Computer Organisation from Computer Architecture.
Answer:
| Computer Organisation |
Computer Architecture |
| Computer organisation deals with the hardware components of a computer system. It includes input / output devices, the central processing unit, storage and primarv memory. | Computer architecture deals with the engineering considerations involved in designing a computer. |
Question 38.
Classify the microprocessor based on the size of the data.
Answer:
Depending on the data width, microprocessors can process instructions. The microprocessors can be classified as follows:
- 8-bit microprocessor
- 16-bit microprocessor
- 32-bit microprocessor
- 64-bit microprocessor.
![]()
Question 39.
Write down the classifications of microprocessors based on the instruction set.
Answer:
Reduced Instruction Set Computers (RISC):
They have a small set of highly optimized instructions. Complex instructions are also implemented using simpler instructions, thus reducing the size of the instruction set. Eg: RISC processors are Intel P6, Pentium IV, AMD K6 and K7.
Complex Instruction Set Computers (CISC):
They support hundreds of instructions. Computers supporting CISC can accomplish a wide variety of tasks, making them ideal for personal computers.
Eg: CISC processors are Intel 386 & 486, Pentium, Pentium II and III, and Motorola 68000.
Question 40.
Differentiate PROM and EPROM.
Answer:
|
PROM |
EPROM |
| PROM is a memory on which data can be written only once. | EPROM is a memory on which ultra violet rays are used to clear its contents and making it possible to reprogram the memory. |
![]()
Question 41.
Write down the interfaces and ports available in a computer.
Answer:
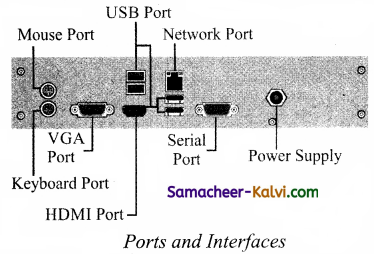
Serial Port:
To connect the external devices, found in old computers.
Parallel Port:
To connect the printers, found in old computers.
USB Ports:
To connect external devices like cameras, scanners, mobile phones, external hard disks and printers to the computer. USB 3.0 is the third major version of the Universal Serial Bus (USB) standard to connect computers with other electronic gadgets. USB 3.0 can transfer data up to 5 Giga byte/second. USB 3.1 and USB 3.2 are also released.
VGA Connector:
To connect a monitor or any display device like LCD projector.
Audio Plugs:
To connect sound speakers, microphone and headphones.
PS/2 Port:
To connect mouse and keyboard to PC.
SCSI Port:
To connect the jtard disk drives and network connectors.
High Definition Multimedia Interface (HDMI):
It is an audio/video interface which transfers the uncompressed video and audio data from a video controller, to a compatible computer monitor, LCD projector, digital television etc.
![]()
Question 42.
Differentiate CD and DVD.
Answer:
| CD |
DVD |
| CD stands for Compact Disk. | DVD stands for Digital Versatile Disc. |
| CDs are made with the purpose of holding audio files as well as program files. | DVDs are made with the purpose of holding video files, movies, substantial amount of programs etc. |
| A standard CD can store about 700 MB of data. | A standard DVD can hold 4.7 GB of data. |
Question 43.
How will you differentiate a flash memory and an EEPROM?
Answer:
|
Flash Memory |
EEPROM |
| The flash memory allows data to be written or erased in blocks. | The EEPROM requires data to be written or erased one bvte at a time. |
| Flash memory is faster in performance. | EEPROM is slower in performance. |
| It uses NAND type memory. | It uses NOR type memory. |
![]()
Question 44.
Explain the characteristics of a micro processor.
Answer:
A Microprocessor’s performance depends on the following characteristics:
(i) Clock speed
(ii) Instruction set
(iii) Word size.
(i) Clock Speed:
Every microprocessor has an internal clock that regulates the speed at which it executes instructions. The speed at which the microprocessor executes instructions is called the clock speed. Clock speed is measured in MHz (Mega Hertz) or in GHz (Giga Hertz).
Instruction Set:
A command which is given to a computer to perform an operation on data is called an instruction. Basic set of machine level instructions that a microprocessor is designed to execute is called as an instruction set This instruction set carries Data transfer, Arithmetic operations, Logical operations, Control flow, Input/output operations.
(iii) Word Size:
The number of bits that can be processed by a processor in a single instruction is called its word size. Word size determines the amount of RAM that can be accessed by a microprocessor at one time and the total number of pins on the microprocessor. Total number of input and output pins in turn determines the architecture of the microprocessor.
![]()
Question 45.
How the read and write operations are performed by a processor? Explain.
Answer:
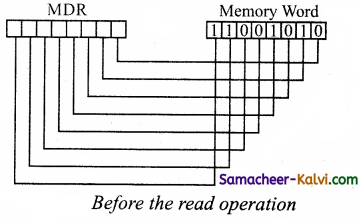
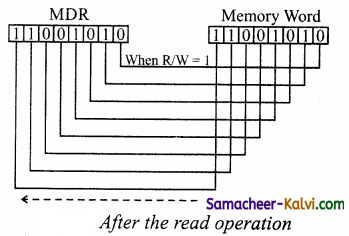
The read operation fetches data from memory and transfers to MDR. A single control line performs two operations like Read / Write using 1 or 0. The write operation transfers data from the MDR to memory. This organisation is shown below in figure.
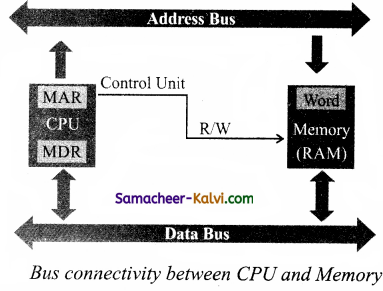
The word in the RAM has the same size (no. of bits) as the Memory Data Register (MDR). If the processor is an 8-bit processor like Intel 8085, its MDR and the word in the RAM both have 8 bits. If the size of the MDR is eight bits, which can be connected with a word of eight bits where the data can be stored or retrieved, the data bus has eight wires in parallel to transfer the data in any one direction which depends on whether the control is read or write.
This control line is labeled as R/W, which becomes 1 means READ operation and 0 means WRITE operation. Figure shows the content of MDR and the Memory Word before the READ operation. Also Figure shows the content of MDR and the Memory Word after the READ operation.read operation transfers the data (bits) from word to memory data register. The write operation transfers the data (bits) from memory data register to word.
![]()
Question 46.
Arrange the memory devices in ascending order based on the access time.
Answer:
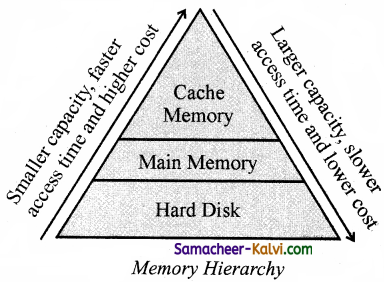
Cache memory:
The cache is a very hi§h speed, expensive piece of memory, which is used to speed up the memory retrieval process. The idea of introducing a cache is that, this extremely fast memory would store data that is frequently accessed and if possible, the data that is spatially closer to it. This helps to achieve the fast response time.
Random-access memory / main memory:
RAM is a volatile memory, which means that the information stored in it is not permanent. When the power is turned off, whatever data that resided in a RAM is lost. It allows both read and write operations.
Hard Disk:
Hard disk a ma§netic disk on which we can store computer data. Hard disks are less portable than floppies, although it is possible to port by removable hard disks. Disk packs and removable cartridges are the two types of removable hard disks.
Compact disk:
A CD or CD-ROM is made from 1.2 millimeters thick, polycarbonate plastic material. A thin layer of aluminium or gold is applied to the surface. CD data is represented as tiny indentations known as “pits”, encoded in a spiral track moulded into the top of the polycarbonate layer. The areas between pits are known as “lands”. A motor within the CD player rotates the disk. The capacity of an ordinary CD-ROM is 700MB.
Digital Versatile Disc (DVD):
A DVD (Digital Versatile Disc or Digital Video Disc) is an optical disc capable of storing up to 4.7 GB of data, more than six times what a CD can hold. DVDs are often used to store movies at a better quality. Like CDs, DVDs are read with a laser.
![]()
Question 47.
Explain the types of ROM.
Answer:
Read-Only memory (ROM):
It refers to special memory in a computer with pre-recorded data at manufacturing time which cannot be modified. The stored programs that start the computer and perform diagnostics are available in ROMs. ROM stores critical programs such as the program that boots the computer. Once the data has been written onto a ROM chip, it cannot be modified or removed and can only be read. ROM retains its contents even when the computer is turned off. So, ROM is called as a non¬volatile memory.
Programmable Read-Only Memory (PROM):
It is also a non-volatile memory on which data can be written only once. Once a program has been written onto a PROM, it remains there forever. Unlike the main memory, PROMs retain their contents even when the computer is turned off.
The PROM differs from ROM. PROM is manufactured as a blank memory, whereas a ROM is programmed during the manufacturing process itself. PROM programmer or a PROM burner is used to write data to a PROM chip. The process of programming a PROM is called burning the PROM.
Erasable Programmable Read-Only Memory (EPROM):
It is a special type of memory which serves as a PROM, out the content can be erased using ultraviolet rays. EPROM retains its contents until it is exposed to ultraviolet light. The ultraviolet light clears its contents, making it possible to reprogram the memory.
An EPROM differs from a PROM, PROM can be written only once and cannot be erased. EPROMs are used widely in personal computers because they enable the manufacturer to change the contents of the PROM to replace with updated versions or erase the contents before the computer is delivered.
Electrically Erasable Programmable Read Only Memory is a special type of PROM that can be erased by exposing it to an electrical charge. Like other types of PROM, EEPROM retains its contents even when the power is turned off. Comparing with all other types of ROM, EEPROM is slower in performance.
![]()
Choose the correct answer:
Question 1.
Which type of integrated circuit were introduced in early 1970s?
(a) Microprocessor
(b) Pentium
(c) Intel
(d) AMD
Answer:
(a) Microprocessor
Question 2.
Which is the first microprocessor developed by Intel Inc?
(a) 8008
(b) 4004
(c) 8086
(d) 8085
Answer:
(b) 4004
Question 3.
What is the standard unit of speed measurement used for measuring frequency?
(a) Watt
(b) Speed
(c) Hertz
(d) Meter
Answer:
(c) Hertz
![]()
Question 4.
One hertz equals:
(a) one cycle per second
(b) one cycle per minute
(c) one cycle per hour
(d) one cycle per year
Answer:
(a) one cycle per second
Question 5.
Which regulates the speed and executes instructions in every microprocessor?
(a) Instruction set
(b) Internal clock
(c) Clock speed
(d) Control flow
Answer:
(b) Internal clock
Question 6.
What is the unit of measuring clock speed?
(a) MHz (Mega Hertz)
(b) GHz (Giga Hertz)
(c) Speed
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)
![]()
Question 7.
Which command is given to a computer to perform an operation on data?
(a) Instruction
(b) Data
(c) Program
(d) Operation
Answer:
(a) Instruction
Question 8.
What is called a basic set of machine level instructions that a microprocessor is designed to execute?
(a) Instruction set
(b) Internal clock
(c) Internal memory
(d) Frequency
Answer:
(a) Instruction set
Question 9.
Which keeps the data that is transferred between the memory and the CPU?
(a) RAM
(b) Data transfer
(c) Instruction
(d) Memory Data Register
Answer:
(d) Memory Data Register
![]()
Question 10.
What is the special register which always keeps the address of next instruction to be executed?
(a) Program counter
(b) Data transfer
(c) Memory Register
(d) Memory Data Register
Answer:
(a) Program counter
Question 11.
What is called a collection of wires used for communication between internal components of the computer?
(a) Memory
(b) Data
(c) Bus
(d) Processor
Answer:
(c) Bus
Question 12.
Which digital circuit is used to point to the specific memory location where the word can be located?
(a) Instruction
(b) Decoder
(c) Compiler
(d) Interpreter
Answer:
(b) Decoder
![]()
Question 13.
Which operation is transfers the data from word to Memory Data Register?
(a) Read
(b) Write
(c) Copy
(d) Move
Answer:
(a) Read
Question 14.
Which operation transfers the data from Memory Data Register to word?
(a) Read
(b) Write
(c) Copy
(d) Move
Answer:
(b) Write
Question 15.
RISC stands for:
(a) Reduced Instruction Set Computers
(b) Replaced Instruction Set Computers
(c) Resolved Instruction Set Computers
(d) Recalled Instruction Set Computers
Answer:
(a) Reduced Instruction Set Computers
![]()
Question 16.
Which of the following is RISC processor?
(a) Pentium IV
(b) Intel P6
(c) AMD K7
(d) All the above
Answer:
(d) All the above
Question 17.
CISC stands for:
(a) Completed Instruction Set Computers
(b) Complex Instruction Set Computers
(c) Compiled Instruction Set Computers
(d) Copied Instruction Set Computers
Answer:
(b) Complex Instruction Set Computers
Question 18.
Which of the following is CISC processor?
(a) Intel 386
(b) Pentium
(c) Motorola 68000
(d) All the above
Answer:
(d) All the above
![]()
Question 19.
How many types of accessing methods are used to access the memory?
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(a) 2
Question 20.
The memory is accessed in an orderly manner from starting to end in:
(a) Sequential access
(b) Random access
(c) Directly access
(d) All the above
Answer:
(a) Sequential access
Question 21.
The memory is accessed directly without navigating through previous bytes is:
(a) Sequential access
(b) Random access
(c) Ascending access
(d) All the above
Answer:
(b) Random access
![]()
Question 22.
The Random access memory (RAM) is also called:
(a) Primary memory
(b) Main memory
(c) Volatile memory
(d) All the above
Answer:
(d) All the above
Question 23.
What is the smallest unit of information that can be stored in the memory?
(a) Bit
(b) Byte
(c) Kilo byte
(d) Mega byte
Answer:
(a) Bit
Question 24.
The bytes are referred by:
(a) Be
(b) B
(c) Bi
(d) By
Answer:
(b) B
![]()
Question 25.
Which of the following memory is more expensive than other memories?
(a) Static RAM (SRAM)
(b) Dynamic RAM (DRAM)
(c) PROM
(d) ROM
Answer:
(a) Static RAM (SRAM)
Question 26.
Which of the memory can store critical programs such as that boots the computer?
(a) RAM
(b) ROM
(c) Memory
(d) All the above
Answer:
(b) ROM
Question 27.
Which memory is programmed during the manufacturing process itself?
(a) ROM
(b) RAM
(c) PROM
(d) EPROM
Answer:
(a) ROM
![]()
Question 28.
Which memory retains its contents until it is exposed to ultraviolet light?
(a) ROM
(b) RAM
(c) PROM
(d) EPROM
Answer:
(d) EPROM
Question 29.
Which memory is used widely in personal computers?
(a) ROM
(b) RAM
(c) PROM
(d) EPROM
Answer:
(d) EPROM
Question 30.
Which memory is used to speedup the memory retrieval process?
(a) RAM
(b) ROM
(c) Cache memory
(d) EPROM
Answer:
(c) Cache memory
![]()
Question 31.
Which refers to how quickly the memory can respond to a read / write request?
(a) Response time
(b) Memory time
(c) Read time
(d) Both (a) and (b)
Answer:
(a) Response time
Question 32.
Secondary storage is also called as:
(a) Main storage
(b) Backup storage
(c) Temporary storage
(d) None of these
Answer:
(b) Backup storage
Question 33.
The CD data is represented as tiny indentations is:
(a) pits
(b) track
(c) layer
(d) disk
Answer:
(a) pits
![]()
Question 34.
The areas between pits are:
(a) lands
(b) tracks
(c) layers
(d) disks
Answer:
(a) lands
Question 35.
DVD stands for:
(a) Digital Versatile Disc
(b) Digital Video Disc
(c) Digital Volatile Disc
(d) Either (a) or (b)
Answer:
(d) Either (a) or (b)
Question 36.
CDs and DVDs are read with:
(a) layer
(b) laser
(c) pins
(d) rays
Answer:
(b) laser
![]()
Question 37.
What is the colour of double-layered CD sides?
(a) Silver
(b) Yellow
(c) White
(d) Gold
Answer:
(d) Gold
Question 38.
What is the colour of single-coloured CD sides?
(a) Silver
(b) Yellow
(c) White
(d) Gold
Answer:
(a) Silver
Question 39.
Which memory is an electronic non-volatile computer storage medium?
(a) RAM
(b) ROM
(c) Flash
(d) Blu-ray disc
Answer:
(c) Flash
![]()
Question 40.
Which of the following is known as flash memory?
(a) ROM
(b) Pen drives
(c) Memory cards
(d) Both (b) and (c)
Answer:
(d) Both (b) and (c)
Question 41.
Which is a high-density optical disc similar to DVD?
(a) HD
(b) RAM
(c) ROM
(d) Blu-ray
Answer:
(d) Blu-ray
Question 42.
How much gigabytes (GB) of data can be stored in double-layer Blu-ray disc?
(a) 20
(b) 30
(c) 40
(d) 50
Answer:
(d) 50
![]()
Question 43.
Which type of laser is used to read and write the data in blu-ray disc?
(a) Violet
(b) Blue-violet
(c) Red-violet
(d) Silver-violet
Answer:
(b) Blue-violet
Question 44.
Which type of laser is used to read and write the data in DVD?
(a) Red
(b) Blue
(c) Blue-violet
(d) Red-violet
Answer:
(a) Red
Question 45.
USB stands for:
(a) Universal Serial Bus
(b) United Serial Bus
(c) Union Serial Bus
(d) Uniform Serial Bus
Answer:
(a) Universal Serial Bus
![]()
Question 46.
Which port is used to connect external devices?
(a) USB
(b) VGA
(c) PS/2
(d) SCSI
Answer:
(a) USB
Question 47.
Which port is used to connect input devices?
(a) USB
(b) VGA
(c) PS/2
(d) SCSI
Answer:
(c) PS/2
Question 48.
Which port is used to connect sound devices and head phones?
(a) Audio plugs
(b) USB
(c) VGA
(d) PS/2
Answer:
(a) Audio plugs
![]()
Question 49.
Which port is used to connect hard disk and network connectors?
(a) USB
(b) VGA
(c) PS/2
(d) SCSI
Answer:
(d) SCSI
Question 50.
HDMI stands for:
(a) High Definition Multimedia Interface
(b) High Deallocation Multimedia Interface
(c) High Deblocking Multimedia Interface
(d) High Debugging Multimedia Interface
Answer:
(a) High Definition Multimedia Interface
Question 51.
HDMI is a/an:
(a) locator
(b) encoder
(c) audio / video interface
(d) multiplexer
Answer:
(c) audio / video interface
![]()
Question 52.
Match the following:
| (a) The speed which micro processor executes instructions | (i) Word size |
| (b) Determined by the processor | (ii) Write operation |
| (c) Address of the next instruction to be executed | (iii) Clock speed |
| (d) Transfers data from memory data register to word. | (iv) Program counter |
(a) (ii), (iii), (i), (iv)
(b) (iii), (i), (iv), (ii)
(c) (iv), (ii), (iii), (i)
(d) (iii), (iv), (ii), (i)
Answer:
(b) (iii), (i), (iv), (ii)
Question 53.
________ deals with the engineering considerations involved in designing a computer.
(a) Computer organisation
(b) Computer architecture
(c) Microprocessor
(d) Registers
Answer:
(b) Computer architecture
Question 54.
Microprocessor is made up of ______ units.
(a) 3
(b) 2
(c) 4
(d) 5
Answer:
(a) 3
![]()
Question 55.
The speed at which the microprocessor executes instructions is called:
(a) clock speed
(b) instruction set
(c) word size
(d) control flow
Answer:
(a) clock speed
Question 56.
The number of bits that can be processed by a processor in a single instruction is called its:
(a) clock speed
(b) instruction set
(c) word size
(d) control flow
Answer:
(c) word size
Question 57.
_________ is unidirectional.
(a) Data bus
(b) Control bus
(c) Register
(d) Address bus
Answer:
(d) Address bus
![]()
Question 58.
________ is bidirectional.
(a) Data bus
(b) Control bus
(c) Register
(d) Address bus
Answer:
(a) Data bus
Question 59.
_________ is a volatile memory.
(a) ROM
(b) EPROM
(c) PROM
(d) RAM
Answer:
(d) RAM
Question 60.
The areas between pits are known as:
(a) sector
(b) track
(c) layer
(d) lands
Answer:
(d) lands
![]()
Question 61.
The capacity of an ordinary CD-ROM is:
(a) 800 MB
(b) 700 MB
(c) 900 MB
(d) 600 MB
Answer:
(b) 700 MB
Question 62
________ is the type of disc used for play station games and for playing high-definition (HD) movies.
(a) Hard disks
(b) CD
(c) DVD
(d) Blu-ray disc
Answer:
(d) Blu-ray disc
Question 63.
Match the following:
| (i) ALU | (a) Perform an operation on data |
| (ii) Clock speed | (b) The number of bits that can be processed. |
| (iii) Instruction set | (c) Perform Arithmetic and Logical instructions |
| (iv) Word size | (d) Regulates the speed at which the microprocessor executes instruction |
(a) (i) – (c); (ii) – (d); (iii) – (a); (iv) – (b)
(b) (i) – (c); (ii) – (b); (iii) – (a); (iv) – (d)
(c) (i) – (b); (ii) – (a); (iii) – (d); (iv) – (c)
(d) (i) – (d); (ii) – (c); (iii) – (a); (iv) – (b)
Answer:
(a) (i) – (c); (ii) – (d); (iii) – (a); (iv) – (b)
![]()
Question 64.
Find the odd man out:
(a) Serial
(b) USB
(c) Keyboard
(d) SCSI
Answer:
(c) Keyboard
Question 65.
Find the odd man out:
(a) Intel 386
(b) Pentium II
(c) Motorola 68000
(d) AMD K6
Answer:
(d) AMD K6
Question 66.
Match the following:
| (i) Parallel port | (a) To connect sound speakers, microphones |
| (ii) Audio plugs | (b) To connect the printers |
| (iii) Ps/2 port | (c) To connect the hard disk drives and network connectors |
| (iv) SCSI port | (d) To connect mouse and keyboard to PC |
(a) (i) – (a); (ii) – (c); (iii) – (d); (iv) – (b)
(b) (i) – (b); (ii) – (a): (iii) – (c); (iv) – (d)
(c) (i) – (a); (ii) – (d); (iii) – (c); (iv) – (b)
(d) (i) – (b); (ii) – (a); (iii) – (d); (iv) – (c)
Answer:
(d) (i) – (b); (ii) – (a); (iii) – (d); (iv) – (c)
![]()
Question 67.
Match the incorrect pair:
|
Column I |
Column II |
| (a) CPU | Central Processing Unit |
| (b)MDR | Memory Digital Register |
| (c) MAR | Memory Address Register |
| (d) ALU | Arithmetic and Logic Unit |
Answer:
(b)
Question 68.
Assertion (A):
Computer organization deals with the hardware components of a computer system.
Reason (R):
It includes Input/Output devices, the central processing unit, storage devices and primary memory.
(a) Both A and R are true, and R is the correct explanation for A.
(b) Both A and R are true, but R is not the correct explanation for A.
(c) A is true, but R is false.
(d) A is false, but R is true.
Answer:
(a) Both A and R are true, and R is the correct explanation for A.
Question 69.
Assertion (A):
RISC have big set of highly optimized instructions.
Reason (R):
It reduces the size of the instruction set.
(a) Both A and R are true, and R is the correct explanation for A.
(b) Both A and R are true, but R is not the correct explanation for A.
(c) A is true, but R is false.
(d) A is false, but R is true.
Answer:
(d) A is false, but R is true.
![]()
Question 70.
Which Of the following is said to be the brain of a computer?
(a) Input devices
(b) Output devices
(c) Memory device
(d) Microprocessor
Answer:
(d) Microprocessor
Question 71.
Which of the following is not the part of a microprocessor unit?
(a) ALU
(b) Control unit
(c) Cache memory
(d) Register
Answer:
(c) Cache memory
Question 72.
How many bits constitute a word?
(a) 8
(b) 16
(c) 32
(d) Determined by the processor used.
Answer:
(d) Determined by the processor used.
![]()
Question 73.
Which of the following device identifies the location when address is placed in the memory address register?
(a) Locator
(b) Encoder
(c) Decoder
(d) Multiplexer
Answer:
(c) Decoder
Question 74.
Which of the following is a CISC processor?
(a) Intel P6
(b) AMD K6
(c) Pentium III
(d) Pentium IV
Answer:
(c) Pentium III
Question 75.
Which is the fastest memory?
(a) Hard disk
(b) Main memory
(c) Cache memory
(d) Blue-Ray disc
Answer:
(c) Cache memory
![]()
Question 76.
How many memory locations are identified by a processor with 8 bits address bus at a time?
(a) 28
(b) 1024
(c) 256
(d) 8000
Answer:
(c) 256
Question 77.
What is the capacity of 12cm diameter DVD with single sided and single layer?
(a) 4.7 GB
(b) 5.5 GB
(c) 7.8GB
(d) 2.2 GB
Answer:
(a) 4.7 GB
Question 78.
What is the smallest size of data represented in a CD?
(a) Blocks
(b) Sectors
(c) Pits
(d) Tracks
Answer:
(c) Pits
![]()
Question 79.
Display devices are connected to the computer through:
(a) USB port
(b) PS/2 port
(c) SCSI port
(d) VGA connector
Answer:
(d) VGA connector