TN State Board 11th Chemistry Important Questions Chapter 7 Thermodynamics
Question 1.
Explain the terms
(i) isolated system
(ii) closed system
(iii) open system.
Answer:
(i)Isolated system:
This type of system has no interactions with matter. The boundary is sealed and insulated. Neither matter nor energy can be exchanged with the surroundings.
(ii) Closed system:
This type of system can exchange energy in the form of heat, work or radiations but not matter with surroundings. The boundary between the system and surroundings is sealed but not insulated.
(iii) Open system:
This type of system can exchange matter as well as energy with surroundings. The boundary is not sealed and not insulated.
![]()
Question 2.
Give examples for extensive and intensive properties.
Answer:
| Extensive properties | Intensive properties |
| volume, mass, amount of substance (mole), energy, enthalpy, entropy, free energy, heat capacity. | molar volume, density, molar mass, molarity, mole fraction, molality, specific heat capacity. |
Question 3.
Mention the condition for Adiabatic, isothermal, isobaric, isochoric arid cyclic process.
Answer:
| Process | Condition |
| Adiabatic | q = 0 |
| Isothermal | dT = 0 |
| Isobaric | dP = 0 |
| Isochoric | dV = 0 |
| Cyclic | dE = 0, dH = 0, dP = 0, dV = 0 |
![]()
Question 4.
State zeroth law of thermodynamics.
Answer:
The law states that ‘If two systems are separately in thermal equilibrium with a third one, then they tend to be in thermal equilibrium with themselves’.
Question 5.
Explain Zeroth law of thermodynamics.
Answer:
According to this law, if systems B and C separately are in thermal equilibrium with another system A, thenb systems B and C will also be in thermal equilibrium with each other. This is also the principle by which thermometers are used.
Question 6.
What are informations do you get from the thermo chemical equations?
Answer:
A thermo chemical equation gives,
(i) The number of mol of the reactants and the number of mol of the products.
(ii) The amount of heat liberated or absorbed (as the case may) i.e., magnitude of enthalpy change (∆H).
(iii) The physical state of the reactants or products i.e., if the species are solid or liquid or gas.
eg: H2 (g) + 2 O2 (g) → H2O (g) ∆H = – 268 kJ mol-1
![]()
Question 7.
Define molar heat capacity at constant volume and molar heat capacity at constant pressure.
Answer:
(i) The heat capacity at constant volume (CV) is defined as the rate of change of internal energy with respect to temperature at constant volume.
CV = \(\left(\frac{\partial \mathrm{H}}{\partial \mathrm{T}}\right)_{\mathrm{V}}\)
(ii) The molar heat capacity at constant pressure (CP) can be defined as the rate of change of enthalpy with respect to temperature at constant.pressure.
CP = \(\left(\frac{\partial H}{\partial T}\right)_{P}\)
Question 8.
Define the relationship CP – CV = nR for an ideal gas.
Answer:
The enthalpy of a system is given by
H = U + PV ……….(1)
for 1 mole of an ideal gas
PV = nRT …………(2)
By substituting (2) in (1) i.e., PV in equation (1) by nRT
H = U + nRT ………….(3)
Differentiating the above equation with respect to T,
\(\frac{\partial \mathrm{H}}{\partial \mathrm{T}}=\frac{\partial \mathrm{U}}{\partial \mathrm{T}}+n \mathrm{R} \frac{\partial \mathrm{T}}{\partial \mathrm{T}}\)
CP = CV + nR …………(4)
∵ [\(\left(\frac{\partial H}{\partial T}\right)_{P}\) = CP and \(\left(\frac{\partial U}{\partial T}\right)_{V}\) = CV]
CP – CV = nR
![]()
Question 9.
Explain why CP is always greater than CV?
Answer:
At constant pressure processes, a system has to do work against the surroundings. Hence, the system would require more heat to effect a given temperature rise than at constant volume, so CP is always greater than CV.
Question 10.
Show that ∆U = nCV (T2 – T1) and ∆H = CP(T2 – T1).
Answer:
For one mole of an ideal gas, we have
CV = \(\frac{d \mathrm{U}}{d \mathrm{~T}}\)
dU = CV dT
For a finite change, we have
∆U = CV ∆T
∆U = CV (T2 – T1)
and for n moles of an ideal gas we get
∆U = nCV(T2 – T1) ……….(1)
Similarly for n moles of an ideal gas we get
∆H = nCP (T2 – T1) ………….(2)
Question 11.
Describe the application of heat of combustion.
Answer:
- The heat of formation of compounds can be calculated from heat of combustion values.
- The calorific value of food and fuels can be calculated from heat of combustion.
![]()
Question 12.
Explain application of Hess’s law of constant heat summation with an example.
Answer:
(i) Hess’s law can be applied to calculate enthalpies of reactions that are difficult to measure. For example, it is very difficult to measure the heat of combustion of graphite to give pure CO.
(ii) However, enthalpy for the oxidation of graphite to CO2 and CO to CO2 can easily be measured. For these conversions, the heat of combustion values are – 393.5 kJ and – 283.5 kJ respectively.
(iii) From these data the enthalpy of combustion of graphite to CO can be calculated by applying Hess’s law.
The reactions involved in this process can be expressed as follows
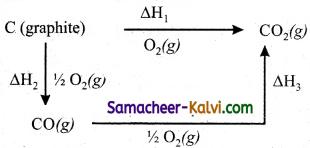
∆H1 = ∆H2 + ∆H3
– 393.5 kJ = X – 283.5 kJ
X = – 110.5 kJ
![]()
Question 13.
Derive an expression for the efficiency of a heat engine.
Answer:
Efficiency = \(\frac{\text { work performed }}{\text { heat absorbed }}\)
η = \(\frac{\left|q_{h}\right|-\left|q_{c}\right|}{\left|q_{h}\right|}\)
qh – heat absorbed fropi the hot reservoir
qc – heat transferred to cold reservoir
η = 1 – \(\frac{\left|q_{c}\right|}{\left|q_{h}\right|}\) …………(1)
For a reversible cyclic process
∆S(universe)= ∆S(system) + ∆S(surroundings) = 0
∆S(system) = – ∆S(surroundings)
\(\frac{\mathrm{T}_{c}}{\mathrm{~T}_{h}}=\frac{\left|q_{c}\right|}{\left|q_{h}\right|}\) …………..(2)
Substituting (2) in (1)
⇒ η = 1 – \(\frac{\mathrm{T}_{c}}{\mathrm{~T}_{h}}\) …………(3)
Hence, η < 1
Question 14.
Give expressions for the entropy change a phase change.
Answer:
∆S = \(\frac{q_{\mathrm{rev}}}{\mathrm{T}}=\frac{\Delta \mathrm{H}_{\mathrm{rev}}}{\mathrm{T}}\)
Where ∆Hrev is the enthalpy change at Temperature (T).
![]()
Question 15.
Define (i) molar heat of fusion (ii) molar heat of vaporisation (iii) enthalpy of transition.
Answer:
(i) Molar heat of fusion:
The molar heat of fusion is defined as “the change in enthalpy when one mole of a solid substance is converted into the liquid state at its melting point”.
(ii) Molar heat of vaporisation:
The molar heat of vaporisation is defined as “the change in enthalpy when one mole of liquid is converted into vapour state at its boiling point”.
(iii) Enthalpy of transition:
The heat of transition is defined as “The change in enthalpy when one mole of an element changes from one of its allotropic form to another.
Question 16.
Give examples for spontaneous processes.
Answer:
(i) A waterfall runs downhill, but never uphill, spontaneously.
(ii) A lump of sugar dissolves spontaneously in a cup of coffee, but never reappears in its original form spontaneously.
(iii) Heat flows from hotter object to a colder one; but never flows from colder to hotter object spontaneously.
(iv) The expansion of a gas into an evacuated bulb is a spontaneous process, the reverse process that is gathering of all molecules into one bulb is not spontaneous.
![]()
Question 17.
Explain how ∆G is related to spontaneity of a process.
Answer:
Let us consider a system which undergoes a change of state from state (1) to state (2) at constant temperature.
G2 – G1 = (H2 – H1) – T(S2 – S1)
∆G = ∆H – T ∆S ……….(1)
Now let us consider how ∆G is related to reaction spontaneity.
We know that
∆Stotal = ∆Ssys – ∆Ssurr
For a reversible process (equilibrium), the change in entropy of universe is zero.
∆Stotal = 0
[∵ ∆Ssys = – ∆Ssurr]
Similarly, for an equilibrium process ∆G = 0
For spontaneous process, ∆Stotal > 0, so ∆Stotal > 0
∆S(system) + ∆S(surroundings) > 0
\(\frac{\Delta \mathrm{H}_{\text {sys }}}{\mathrm{T}}\) – ∆S(system) > 0
∆Hsys – T∆Ssys > 0
T∆Ssys – ∆Hsys < 0
– (∆Hsys – T∆Ssys) > 0
– (∆G) > 0
Hence for a spontaneous process, ∆G < 0
i.e. ∆H – T ∆S < 0 …(1)
∆Hsys is the enthalpy change of a reaction, T∆Ssys is the energy which is not available to do useful work. So, ∆G is the net energy available to do usefuf work and is thus a measure of the ‘free energy’. For this reason, it is also known as the free energy of the reaction. For non spontaneous process, ∆G > 0.
![]()
Question 18.
How is Gibb’s free energy and network done by the system related?
Answer:
For any system at constant pressure and temperature.
∆G = ∆H – T∆S …(1)
We know that, ∆H = ∆U + P∆V
∴ ∆G = ∆U + P∆V – T∆S
from first law of thermodynamics if work is done by the system
∆U = q – w
from second law of thermodynamics
∆S = \(\frac{q}{\mathrm{~T}}\) ∆G = q – w + P∆V – T(\(\frac{q}{\mathrm{~T}}\))
∆G = -.w + P∆V
– ∆G = – w – P∆V …………… (3)
But – P∆V represents the work done due to expansion against a constant external pressure. Therefore, it is clear that the decrease, in free energy (- ∆G) accompanying a process taking place at constant temperature and pressure is equal to the maximum work obtainable from the system other than the work of expansion.
Question 19.
How is standard energy charge related to equilibrium constant?
Answer:
The standard free energy-change for a reversible reaction is related to its equilibrium constant (Keq) by means of the relationship
∆G° = ∆H° – T∆S°
where, ∆G° – Standard free energy change
∆H° = Standard enthalpy of formation
∆S° = Standard entropy of formation
![]()
Question 20.
Derive an expression for the standard free energy change for the reaction A + B ⇌ C + D in terms of the equilibrium constant.
Answer:
Lets consider a general equilibrium reaction A + B ⇌ C + D
The free energy change of the above reaction in any state (∆G) is related to the standard free energy change of the reaction (∆G° ) according to the following equation.
∆G = ∆G° + RT ln Q
where Q is reaction quotient and is defined as the ratio of concentration of the products to the concentrations of the reactants under non equilibrium condition.
When equilibrium is attained, there is no further free energy change i.e., ∆G = 0 and Q becomes equal to equilibrium constant. Hence the above equation becomes,
∆G° = – RT ln Keq
This equation is known as Van’t Hoff equation,
∆G° = – 2.303 RT log Keq
We also know that
∆G° = ∆H° – T∆S° = -RT ln Keq
Question 21.
Explain third law of thermodynamics.
Answer:
The entropy of pure crystalline substance s at absolute zero is zero. Alternatively it can be stated as, it is impossible to lower the temperature of an object to absolute zero in a finite number of steps. Mathematically,
\(\begin{gathered}
\text { lim } \\
\mathrm{T} \rightarrow 0
\end{gathered}\) S = 0 for a perfectly ordered crystalline state.
Crystals with defects (imperfection) at absolute zero, have entropy greater than zero. Absolute entropy of a substance can never be negative.
![]()
Question 22.
Two litres of an ideal gas at a pressure of 10 atm expands isothermally into vacuum until its total volume is 10 litres. How much heat is absorbed and how much work is done in the expansion.
Answer:
Work done in free expansion or work done against zero pressure is also zero.
wexp = -Pext(∆U)
0 = wexp = -Pext(V2 – V1)
0 = 0 (10 – 2) = 0
Hence heat change, and work done is zero.
Question 23.
Calculate the work done in reversible isothermal expansion when 2L of an ideal gas at a pressure of 10 atm expands isothermally against 1 atm to a final volume of 10 L.
Answer:
w = 2.303 nRT log\(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\) ………(1)
PV = nRT ……….(2)
From equations (1) and (2)
w = 2.303 PV log\(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\)
= 2.303 × 1 × 10 log \(\frac{10}{2}\)
= 2.303 × 1 × 10 × log 5
= 16.1 litre-atm
= 16.1 × 101.3 J = 1630.93 J
wexp = – 1630.93 J
q = -wexp = 1630.93 J
![]()
Question 24.
5 moles of an ideal gas expand isothermally and reversibly from a pressure of 10 atm to 2 atm at 300K. Calculate the work done by the system.
Answer:
w = – 2.303 nRT log\(\frac{P_{1}}{P_{2}}\)
= – 2.303 × 5 × 8.314 × 300 log \(\frac{10}{2}\)
= – 20.075 × 103 J
Question 25.
Liquid benzene is oxidised at constant pressure according to following equation.
C6H6 (l) + \(\frac{15}{2}\) O2(s) → 6 CO2(g) + 3 H2O (l) Enthalpy change (∆H) for the reaction at 300K is -3728 kJ.
Calculate the internal energy charge.
Answer:
The reaction is
C6H6 (l) + \(\frac{15}{2}\) O2(s) → 6 CO2(g) + 3 H2O (l)
∆n = number of mol of gaseous products – number of mol of gaseous reactants
∆n = 6 – \(\frac{15}{2}\) = – \(\frac{3}{2}\)
∆H = ∆U + RT (∆n)
-3728 = ∆U+ (-\(\frac{3}{2}\)) × 8.314 × 10-3 × 300
∆U = -3724.25 kJ mol-1
![]()
Question 26.
1 g of graphite is burnt in a bomb calorimeter in excess of oxygen at 298K and 1 atm pressure according to the equation.
C(graphite) + O2(g) → CO2 (g)
During the reaction, temperature rises from 298K ‘to 299K. If the heat capacity of the bomb calorimeter is 20.7 kJ mol-1. What is the enthalpy change for the above reaction at 298K and 1 atm?
Answer:
Heat evolved in the reaction (∆U) = – CV∆T
= -20.7 × 1 = -20.7 kJ mol-1
Heat evolved in the combustion of 1 mol of carbon i.e., 12g of graphite
= – 20.7 × 12 kJ mol-1
= – 2.48 × 102 kJ mol-1
In the given reactions ∆n = 0
∆H = ∆U = – 2.48 × 102 kJ mol-1
Question 27.
Enthalpies of formation of CO (g), CO2 (g), N2O (g) and N2O4 (g) are -110, -393, + 81 and + 9.7 kJ mol-1 respectively. Find the value of ∆H for the reaction.
Answer:
N2O4 (g) + 3 CO (g) → N2O (g) + 3 CO2 (g).
Given:

![]()
Question 28.
Given N2 (g) + 3H2 (g) → 2NH3 (g); ∆H° = – 92.4 kJ mol-1. What is the standard enthalpy of formation of NH3 (g)?
Answer:
The given reaction is .
N2 (g) + 3 H2 (g) → 2NH3 (g);
∆H° = – 92.4 kJ mol-1
∆H°= 2 ∆Hf° (NH3) – [∆Hf° (N2) + 3 ∆Hf° (H2)]
By definition, the standard enthalpy of formation of elements is equal to zero.
– 92.4 = 2 ∆Hf° (NH3) – (0 + 3 × 0)
i.e., for 2 mol of NH3 2∆Hf° (NH3) = – 92.4
for 1 mol of NH3 ∆Hf° (NH3) = – \(\frac{92.4}{2}\)
= 46.2 kJ mol-1
Question 29.
The enthalpy of combustion of carbon to carbondioxide is -393.5 kJ mol-1. Calculate the heat released upon the formation of 35.2g of CO2 from carbon and oxygen gas.
Answer:
The combustion of carbon is given by
C(s) + O2 (g) → CO2 (g)
∆H = – 393.5 kJ mol-1
Number of mol of CO2 = \(\frac{35.2}{44}\) = 0.8
Amount of heat evolved in the formation of 0.8 mol of CO2 is = 393.5 × 0.8 = 314.8 kJ
![]()
Question 30.
Calculate the enthalpy of formation of CH3OH(l) from the following data:
CH3OH (l) + \(\frac{3}{2}\) O2 (g) → CO2(g) + 2 H2O (l) ∆H° = – 726 kJ mol-1
C (s) + O2 (g) → CO2 (g) ∆H° = – 393 kJ mol-1
H2 (g) + \(\frac{1}{2}\) O2 (g) → H2O (l) ∆H° = – 286 kJ mol-1
Answer:
The required equation is
C (s) + 2 H2 (g) + \(\frac{1}{2}\) O2 (g) → CH3OH (l)
∆H = ? The given equations can be rearranged as
(i) CO2 (g) + 2H2O (l) → CH3OH (l).+ \(\frac{3}{2}\) O2 (g) + 726 kJmol-1
(ii) C (s) + O2 (g) → CO2 (g) -393 kJ mol-1
(iii) 2H2 (g) + O2 (g) → 2H2O (l) 2 x -286 kJ mol
On adding C (s) + 2H2 (g) + \(\frac{1}{2}\) O2 (g) → CH3OH – 239.0 kJ
AH°(CH3OH) = – 239.0 kJ mol-1
Question 31.
The heats of combustion of CH4 and C4H10 are – 890.3 and – 2878.7 kJ mol-1 respectively. Which of the two has greater efficiency as fuel per gram?
Answer:
Molar mass of methane = 16
Heat produced per gram of methane = –\(\frac{890}{16}\) = – 55.63 kJ
Molar mass of butane = 58
Heat produced per gram of butane = –\(\frac{2878.7}{58}\) = -49.62 kJ
Thus, methane has greater fuel efficiency than butane.
![]()
Question 32.
Whenever an acid is neutralised by a base, the net reaction is
H+ (aq) + OH– (aq) → H2O (l); ∆H = – 57.1 kJ
Calculate the heat evolved for the following experiments:
Answer:
According to the reaction
H+ (aq) + OH– (aq) → H2O (l); ∆H = – 57.1 kJ
i.e., when one mole of H+ ions reacts with one mole of OH– ions, one mole of water is formed and 57.1 kJ of energy is released.
(i) 6.50 mole of HCl solution is neutralised by 0.50 mole of NaOH solution.
0.50 mole of HCl = 0.50 mole of H+ ions
0.50 mole of NaOH = 0.50 mole of OH– ions
On mixing, 0.50 mole of H2O is formed.
Heat evolved for the formation of 0.50 mole of water = 57.1 × 0.5 = 28.55 kJ
(ii) 0.50 mole of HNO3 solution is neutralised
by 0.30 mole of NaOH solution.
0.50 mole of HNO3 = 0.50 mole of H+ ions
0.30 mole of KOH = 0.30 mole of OH– ions
i.e., 0.30 mole of H+ ions react with 0.30 mole of OH– ions and forms 0.30 mole of water.
Heat evolved in the formation of 0.30 mole of H2O = 57.1 × 0.3 = 17.13 kJ
(iii) 100 ml of 0.2 M HCl is mixed with 100 ml of 0.3M NaOH solution.
100 ml of 0.2 M HCl will give (\(\frac{0.2 \times 100}{1000}\)) mole of = 0.02 mole of H+ ions.
100 ml of 0.3 M NaOH will give (\(\frac{0.3 \times 100}{1000}\)) mole of = 0.03 mole of OH– ions.
i.e., 0.02 mole of H+ Ions will react 0.03 mole of OH– ions and produce 0.02 mole of H2O molecules.
Heat evolved in the formation of 0.02 mole of H2O = 0.02 × 57.1 = 1.142 kJ
(iv) 400 ml of 0.2 M H2SO4 is mixed with 600ml of 0.1M KOH solution.
400 ml of 0.2 M H2SO4 will give \(\left(\frac{2 \times 0.2}{1000}\right)\) × 400 = 0.16 mole of H+ ions.
600 ml of 0.1 M KOH will give \(\left(\frac{0.1 \times 600}{1000}\right)\) = 0 06 mole of OH– ion
Heat evolved in the formation of 0.06 mole of H2O = 0.06 × 57.1 = 3.426 kJ
![]()
Question 33.
Calculate the standard heat of formation of carbon di sulphide (l). Given that the standard heats of combustion of carbon (s), sulphur (s) and carbon di sulphide (l) are – 393.3, – 293.72, and – 1108.76 kJ mol-1 respectively.
Answer:
The required equation is
C (s) + 2 S (s) → CS2(l); ∆H = ?
Given:
C(s) + O2 (g) → CO2(g); ∆H = – 393.3 kJ …………(1)
S(s) + O2 (g) → SO2 (g); ∆H = -293.7 kJ ………….(2)
CS2 (l) + O2 (g) → CO2 (g) + SO2 (g);
∆H = – 1108.76 kJ ………….(3)
First method:
Multiply equation (2) by 2
2 S (s) + 2 O2 (g) → 2 SO2 (g); ∆H = – 587.44 ………….(4)
Adding equations (1) and (4) and subtracting (3),
C (s) + 2 S (s) + 3O2 (g) – CS2 (l) – 3O2 (g) → CO2 (g) + 2SO2 (g) – CO2 (g) – 2SO2 (g)
C (s) + 2S (s) → CS2(l)
Thus, ∆Hf = – 393.3 – 587.44 + 1108.76 = 128.02 kJ
i.e., standard heat of formation of CS2 is 128.02 kJ.
Second method:
Standard enthalpy of formation of
CO2 = – 393.3 kJ
SO2 = – 293.72 kJ
CS2 = ?
From the first law of thermodynamics, the standard enthalpy of a compound is equal to the standard enthalpy of formation of the compound and the standard enthalpies of elements is equal to zero.
The equation is
CS2 (l) + 3 SO2 (g) → CO2 (g) + 2 SO2 (g); ∆H° = -1108.76 kJ
∆H° = ΣH° (products) – ΣH° (reactants)
= {∆H°f(CO2) + 2H°fSO2)} – {∆H°f(CS2) + 3 H°f(O2)}
-1108.76 = {- 393.3 + 2 × (-296.72)} – ∆H°f(CS2)
∆H°f(CS2) = + 1108.76 – 393.3 – 2 × (297.72)
= 1108.76 – 980.74= 128.02 kJ
∴ ∆H°f(CS2) = 128.02 kJ mol-1
Bond energies or Bond enthalpies:
- The bond dissociation energy of a diatomic molecule is also called bond energy.
- When a molecule or a compound contains more than one bond of the same kind, the average value of the dissociation energies of a given bond is taken. This average bond dissociation energy required to break each bond in a compound is called bond energy.
- Using bond energy data, heat of reaction is (∆H) can be calculated by using the equation.
∆H – ΣB.E of (reactants) – ΣB.E of (products) - Alternating, of enthalpy change for the reaction and bond energies of all the bonds except one, the bond energy of that bond can be calculated.
![]()
Question 34.
Calculate ∆H, for the reaction,
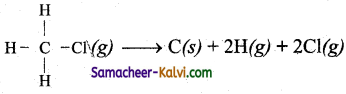
Bond energies of C – H bond, C – Cl bond are 415 kJ and 326 kJ respectively.
Answer:
∆H – Σ B.E of (Reactants) – ΣB.E of (products)
= 2 × (C – H) + 2[(Cl) – 0)] (B.E of all free atoms = 0)
= 2 × 415 + 2 × 326
= 830+ 652 = 1482 kJ
Question 35.
Calculate the enthalpy change for the following reactions.
H2C = CH3 (g) + H2 (g) → CH3 – CH3 (g)
The bond energies of C – H, C – C, C = C, H – H are 99, 83, 147, 104 kCal respectively.
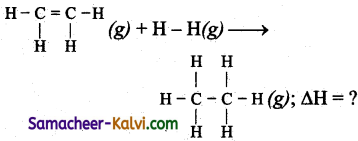
Answer:
∆H = Σ B.E (Reactants) – Σ B.E (products)
= [1 × (C = C) + 4 × (C – H)+ 1 × (H -H)] -1 × (C – C) + 6 × (C – H)
= (147 + 4 × 99 + 104) – (83 + 6 × 99) = – 30 k.cal
![]()
Question 36.
The bond dissociation energies of gaseous chlorine, hydrogen and hydrogen chloride are 104, 58 and 103 kcal mol-1 respectively. Calculate the enthalpy of foimation of HCl(g). Predict in which of the following, entropy increases / decreases.
(i) A liquid crystallises into a solid.
Answer:
When a liquid crystallises into a solid its entropy decreases because of randomness is less in a solid as compared to that in a liquid (∆s = negative)
(ii) Temperature of crystalline solid is raised from 0 K to 115 K.
Answer:
When a crystalline solid is heated from 0 K to 115 K, the entropy increases (∆S = positive) because at higher temperature, the constituent units starts vibrating around their mean position.
(iii) 2NaHCO3 (s) → Na2CO3 (s) + CO2 (g) + H2O (s)
Answer:
In the reaction
2NaHCO3 (s) → Na2CO3 (s) + CO2 (g) + H2O (g) the number of gaseous components increase aid hence entropy of the system will increase.
(iv) H2(g) → 2 H (g)
Answer:
In this reaction, the number of gaseous particles increase and hence entropy will also increase.
![]()
Question 37.
For the oxidation of iron:
4 Fe (s) + 3O2 (g) → 2Fe2O3 (s)
Answer:
The entropy change is – 549.4 Jk-1mol-1 at 298K. Inspite of negative entropy change of this reaction, why this reaction is spontaneous?
Answer:
∆H° for this reaction is – 1648 × 103 J mol-1
∆S° (system) = – 549.4 J k-1 mol-1
∆H°(reaction) = – 1648 × 103 J mol-1
T = 298 K (as standard state)
∆S(total) – ∆S(system) + ∆S(surrounding)
∆S(total) > 0 for spontaneous process
∆S(surrounding) = \(\frac{\Delta H(\text { surrounding) }}{\mathbf{T}}\)
= \(\frac{+1648 \times 10^{3}}{298}\)
= 5530 J k-1 mol-1
∆S(total) = – 549.4 + 5530 = 4960.6 J k-1 mol-1 = Positive
Hence, the reaction is spontaneous,
Question 38.
Calculate the enthalpy of Vaporisation per , mole Of ethanol, given ∆S = 109.8 J k-1 mol-1 and boiling point of ethanol is 78.5°C.
Answer:
∆S(vaporisation) = \(\frac{\Delta H \text { (Vaporisation) }}{T \text { (Boiling point) }}\)
Given,
∆S(vaporisation) = 109.8 J k-1 mol-1
T(Boiling point) = 78.5 + 273 = 351.5 K .
Substituting these values in the above equation
109.8 = \(\frac{\Delta \mathrm{H} \text { (vaporisation) }}{351.5}\)
∆H(vaporisation) = 38594.7 J mol-1 = 38.594 kJ mol-1
![]()
Question 39.
At 0°C, ice and water are in equilibrium and the enthalpy change for the process, HO (S) ⇌ HO (l) is 6 kJ mol-1. Calculate the entropy change for the conversion of ice into water.
Answer:
For the process,
H2O (S) ⇌ H2O (l)
∆S(fusion) = \(\frac{\Delta \mathrm{H}(\text { fusion })}{\text { Freezing temperature }}\)
= \(\frac{6 \times 1000}{273}\)
= 21.98 J k-1 mol-1
Question 40.
For the reaction, at 298K 2 A + B → C ∆H = 400 kJ mol-1, ∆S = 2 kJ mol-1
At what temperature will the reaction become spontaneous, considering ∆H and ∆S to be constant over the temperature range?
Answer:
For the reaction to be spontaneous
∆G = Negative (∆G < 0)
i.e., ∆H – T∆S < 0 (or) T >\(\frac{\Delta \mathrm{H}}{\Delta \mathrm{S}}\)
i.e., T > \(\frac{400 \times 1000}{2000}\) = T > 200 K
The reaction will be spontaneous above 200 K.
![]()
Question 41.
For the reaction,
2A (g) + B (g) → 2D (g) ∆U° = – 10.5 kJ and ∆S° = – 44.1 Jk-1
Calculate ∆G° for the reaction and predict whether the reaction is spontaneous or not.
Answer:
∆H° = ∆U° + RT(∆n)
= – 10.5 + 8.314 × 10-3 × 298 × (-1) = – 12.978 kJ
We know,
∆G° = ∆H° – T∆S°
= -12.978 -298 (-44.1 × 10-3) = 0.164 kJ
Hence, the reaction is non-spontaneous.
Question 42.
Will the reaction,
I2 (s) + H2S (g) → 2 HI (g) + S (s) proceed spontaneously in the forward direction at 298 K? ∆G°f (HI) = 1.8 kJ mol-1, ∆G°f(H2S) = 33.8 kJ mol-1.
Answer:
∆G° = 2G°f (product) – ∆G°f (reactants)
The standard free energies of elements are equal to zero = Standard free energy of formation of the compound
∆G° = {2 × ∆G°f (HI) + ∆G°f (S)} – {∆G°f (I2) – ∆G°f (H2S)}
= (2 × 1.8 + 0) – (0 + 33.8) = 30.2 kJ
Since, ∆G° is negative, the process is. spontaneous.
![]()
Question 43.
Compute the standard free energy of the reaction at 27°C for the combustion of methane using the given data:
CH4(g) + 2 O2 (g) → CO2 (g) + 2H2O (l)

Answer:
∆H° = ∆H°f (CO2) + 2 ∆H°f (H2O) – ∆H°f (CH4)
= – 393.5 + 2 × (- 285.8) – (-74.8)
= – 890 kJ mol-1
∆S° = S°(CO2) + 2 S°(H2O) – S°(CH4) – 2S°(O2)
= 214 × 2 × 70 – 186 – 2 × 205
= – 242 Jk-1 mol-1
∆G° = ∆H° – T∆S°
= – 890 – 300 × (- 242 × 10-3)
= – 890 + 72.6 = – 817.4 kJmol-1.
Question 44.
What is the equilibrium constant kc for the following reaction at 400 K?
Answer:
2NOCl (g) ⇌ 2 NO (g) + Cl2 (g)
Answer:
∆H° = 77.2 kJ and ∆S°
= 122 Jk-1 mol-1
∆G° = ∆H° – T∆S°
= 77.2 – 400 × 122 × 10-3
= 28.4 kJ = 28.4 × 103 J
We know, ∆G° = -2.303 RT log kc
log kc = \(\frac{-\Delta \mathrm{G}^{\circ}}{2.305 \times \mathrm{R} \times \mathrm{T}}\)
= \(\frac{-28.4 \times 10^{3}}{2.303 \times 8.314 \times 400}\) = 3.7081
kc = Antilog(-3.7081)
= 1.958 × 10-4
![]()
Question 45.
For the equilibrium
PCl (s) ⇌ PCl3 (g) + Cl2 (g) at 25°C.
kc = 1.8 × 10-7 R = 8.314 Jk-1 mol-1 Calculate ∆G° for the reaction.
Answer:
∆G° = – 2.303 RT log kc
= – 2.303 × 8.314 × 298 log (1.8 × 10-7)
= – 38484 J mol-1 = – 38.484 kJ mol-1
Question 46.
Calculate ∆G° for the reaction.
CO (g) + \(\frac{1}{2}\) O2 (g) → CO2 (g), ∆H° = -282.84 kJ
Answer:
Given, S°(CO2) = 213.8 Jk-1 mol-1
S°(CO) = 197.9 Jk-1 mol-1
S°(O2) = 205.0 Jk-1 mol-1
∆S° = Σ S°(products) – Σ S°(reactants)
= [S° (CO2) – S° (CO) + \(\frac{1}{2}\) S° (O2)]
= 213.8 – [197.9 + \(\frac{1}{2}\) × 205]
= – 86.6 JK-1 mol-1
We know,
∆G° = ∆H° – F∆S°
= – 282.84 – 298 × (- 86.6 × 10-3)
= – 282.84 + 25.807 = -257.033 kJ
![]()
Choose the correct answer:
Question 1.
When a liquid boils, there is:
(a) increase in entropy
(b) a decrease in entropy
(c) increase in heat of vaporization
(d) an increase in free energy
Answer:
(a) increase in entropy
Hint: When liquid boils, it becomes a gas vapour. The molecules in the gas vapour are randomly placed compared to the liquid i.e., randomness is high in gaseous state then in liquid.
∆s = SV – SL = positive
Question 2.
If ∆G for a reaction is negative, the change is:
(a) spontaneous
(b) non-spontaneous
(c) reversible
(d) equilibrium
Answer:
(a) spontaneous
Hint:
For a spontaneous reactions ∆G = negative
Question 3.
In which of the following process, the process is always non-feasible?
(a) ∆H > 0, ∆S > 0
(b) ∆H < 0, ∆S > 0
(c) ∆H > 0, ∆S < 0
(d) ∆H < 0, ∆S < 0
Answer:
(b) ∆H < 0, ∆S > 0
Hint:
For a spontaneous process, (b) ∆H < 0, ∆S > 0
![]()
Question 4.
Change in Gibbs free energy is given by:
(a) ∆G = ∆H + T∆S
(b) ∆G = ∆H – T∆S
(c) ∆G = ∆H × T∆S
(d) None of these
Ans:
(b) ∆G = ∆H – T∆S
Question 5.
Which of the following process is feasible at all temperatures?
(a) ∆H > 0, ∆S > 0
(b) ∆H > 0, ∆S < 0
(c) ∆H< 0, ∆S > 0
(d ∆H < 0, ∆S < 0
Answer:
(c) ∆H< 0, ∆S > 0
Hint:
When ∆H < 0 and ∆S > 0 at all temperatures, ∆G is negative.
Question 6.
Calculate the entropy change during the melting of one mole of ice into water at 0°C and 1 atm pressure. Enthalpy of fusion of ice is 6008 J mole-1.
(a) 22.007 J K-1 mole-1
(b) 22.007 J K mole-1
(c) 220.07 J K-1 mole-1
(d) 2.2007 J K-1 mole
Answer:
(a) 22.007 J K-1 mol-1
Hint:
∆S = \(\frac{\Delta \mathrm{H}_{f}}{\mathrm{~T}}=\frac{6008 \mathrm{~J} \mathrm{~mol}^{-1}}{273 \mathrm{~K}}\)
= 22.007 J K-1 mole-1
![]()
Question 7.
The final temperature of an engine whose initial temperature is 400K and having efficiency 25%.
(a) 200 K
(b) 400 K
(c) 300 K
(d) 450 K
Answer:
(c) 300 K
Hint:
% efficiency = \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{~T}_{1}}\)
T1 = initial temp.
T2 = final temp.
25 = \(\frac{400-T_{2}}{400}\) × 100
T2 = 300 K
Question 8.
When solid melts there is:
(a) an increase of entropy
(b) a decrease in entropy
(c) an increase in free energy
(d) an increase of heat of fusion
Answer:
(a) an increase of entropy
Hint:
∆S = SL – SS
Solid → liquid
∆S = SL – SS
SL > SS
∴ ∆S is positive
![]()
Question 9.
The unit of entropy is:
(a) J K-1 mol-1
(b) J mol-1
(c) J K mol-1
(d) J-1 K-1
Answer:
(a) J K-1 mol-1
Question 10.
If ∆G = 0, then the process is:
(a) Equilibrium
(b) Spontaneous
(c) Non Spontaneous
(d) None of the above
Answer:
(a) Equilibrium
Question 11.
The standard conditions for G° are:
(a) 1 mmHg / 25°C
(b) 1 atm / 25°K
(c) 1 atm / 298 K
(d) 1 atm / 0 K
Answer:
(c) 1 atm / 298 K
![]()
Question 12.
The efficiency of engine working between 100 to 400 K:
(a) 25 %
(b) 75 %
(c) 100 %
(d) 50 %
Answer:
(b) 75 %
Hint:
% efficiency = \(\frac{\mathrm{T}_{1}-\mathrm{T}_{2}}{\mathrm{~T}_{1}}\)
T1 = initial temp.
T2 = final temp.
25 = \(\frac{400-T_{2}}{300}\) × 100 (T1 > T2)
T2 = 100 K
Question 13.
Entropy is a _________ function.
(a) State
(b) Path
(c) Defined
(d) Undefined
Answer:
(a) State
Hint:
The value depends on initial and final state of the system and not on the path followed by the system.
Question 14.
An efficiency of an engine is always:
(a) = 0 %
(b) > 100 %
(c) < 100 %
(d) = 100 %
Answer:
(c) < 100 %
Hint:
According to second law of thermo-dynamics 100% conversion of energy to work is impossible.
![]()
Question 15.
If system moves from ordered state to disordered state, its entropy:
(a) Decreases
(b) Increases
(c) Become zero
(d) Increases then decreases
Answer:
(b) Increases
Hint:
Whenever there is greater disorderliness, greater is the entropy. Hence the increase in entropy.
Question 16.
In which of the following entropy increases?
(a) Condensation of water vapour
(b) Liquid freezes to solid
(c) Sublimation
(d) Gas freezes to a solid
Answer:
(c) Sublimation
Hint:
Solid → Vapour(sublimation)
∆S = S(vapour) – S(solid)
S(vap) > S(solid)= positive
i.e., entropy increases.
Question 17.
Which of the following is a state function?
(a) q
(b) ∆q
(c) w
(d) ∆S
Answer:
(d) ∆S
Hint:
∆S; The rest are path functions.
![]()
Question 18.
Which of the following will have highest ∆Hvap value?
(a) Acetone
(b) Ethanol
(c) Carbon tetrachloride
(d) Chloroform
Answer:
(c) Carbon tetrachloride
Hint:
When a liquid is converted to its vapour, the attraction between the molecules in the liquid should be less, so that they can readily escape into vapour. CCl4 being a non-polar liquid, has the least attraction and has lower vapour pressure and has highest ∆Hvap value.
Question 19.
Which of the following is not a state function?
(a) S
(b) H
(c) G
(d) q
Answer:
(d) q
Question 20.
The net work done by the system:
(a) w – P∆V
(b) w + P∆V
(c) -w + P∆V
(d) -w – P∆V
Answer:
(d) -w – P∆V
![]()
Question 21.
– ∆G is the net work done by the system except:
(a) Electrical work
(b) Expansion work
(c) Chemical work
(d) Photo chemical work
Answer:
(b) Expansion work
Hint:
The decrease in free energy (- ∆G) is the energy available with the system to perform work other than P – V work, (explanation / compression).
Question 22.
The enthalpy of vapourisation of a liquid is 30 kJ mol-1 and the entropy of vapourisation is 75 J K-1 mol-1. The boiling point of the liquid at 1 atm is:
(a) 250 K
(b) 400 K
(c) 450 K
(d) 600 K
Answer:
(b) 400 K
Hint:
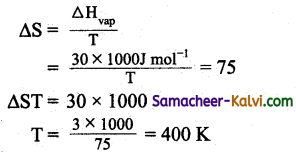
Question 23.
In a reversible process ∆S(system) + ∆S(surrounding) is:
(a) > 0
(b) < 0
(c) > 0
(d) = 0
Answer:
(d) = 0
Hint:
∆ST = 0 for a reversible (equilibrium)
= ∆S(system) + ∆S(surrounding) = 0
![]()
Question 24.
Which of the following does not result in an increase in the entropy?
(a) crystallisation of sucrose from solution
(b) rusting of Iron
(c) conversion of ice to water
(d) vapourisation of camphor
Answer:
(a) crystallisation of sucrose from solution
Hint:
Solution of sucrose > crystals of sucrose(solid)
∆S = S(solid) – S(solution)
= S(solution) < S(solid)
Question 25.
The standard free energy change (∆G°) is related to equilibrium constant (K) as:
(a) ∆G° = -2.303 RT lnK
(b) ∆G°= 2.303 RT log K
(c) ∆G° = RT ln K
(d) ∆G° = – 2.303 RT log K
Answer:
(d) ∆G° = – 2.303 RT log K
Question 26.
Entropy change involved in the conversion of 1 mole of liquid water at 373K to vapour at the same temperature will be ∆H = 2.257 kJ g-1
(a) 0.119 kJ
(b) 0.109 kJ
(c) 0.129 kJ
(d) 0.120 kJ
Answer:
(b) 0.109 kJ
Hint:
∆S = \(\frac{\Delta \mathrm{H}_{\mathrm{vap}}}{\mathrm{T}}\)
= \(\frac{2.257 \mathrm{~kJ} \mathrm{~g}^{-1} \times 18 \mathrm{~g} \mathrm{~mol}^{-1}}{373}\) = 0.109 kJ
![]()
Question 27.
Which of the following units represent largest amount of energy?
(a) calories
(b) Joule
(c) erg
(d) eV
Answer:
(a) calories
Hint:
1 calorie = 4.184 K; 1 erg = 10-7 J;
1 eV= 1.6 × 10-19 J
Question 28.
System in which there is no exchange of j matter , work or energy from surrounding:
(a) closed
(b) isolated
(c) adiabatic
(d isothermal
Answer:
(b) isolated
Question 29.
Identify the state quantity among the following:
(a) q
(b) q – w
(c) q + w
(d) q / w
Ans :
(c) q + w
Hint:
∆U = q + w; ∆U is a state function.
![]()
Question 30.
In general, for an exothermic reaction to be spontaneous :
(a) temperature should be high
(b) temperature should be zero
(c) temperature should be low
(d) temperature has no effect
Answer:
(c) temperature should be low
Hint:
∆G = ∆H – T∆S:
For exothermic reaction
∆H is negative,
∆S = positive and at low temperature
∆G = negative.
Hence temperature should be low.
Question 31.
Heat of neutralization of a strong acid by a j strong base is a constant value because:
(a) only H+ and OH– ions react in every case
(b) the strong base and strong acid react completely
(c) the strong base and strong acid react in aqueous solution
(d) salt formed does not hydrolyse
Answer:
(a) only H+ and OH– ions react in every case.
![]()
Question 32.
The heat absorbed at constant volume is equal to the system’s change in:
(a) enthalpy
(b) entropy
(c) internal energy
(d) free energy
Answer:
(c) internal energy
Hint:
qv</sub > = ∆U
Question 33.
Heat of neutralization of a strong acid by a base is always:
(a) positive
(b) negative
(c) zero
(d) positive or negative
Answer:
(b) negative
Hint:
The neutralisation of a strong acid by a base is always
H+ + OH– —> H2O, for which the value is – 57.32 kJ.
Question 34.
For the reaction H2 + I2 ⇌ 2HI, ∆H = 12.40 kcal the heat of formation of HI is:
(a) 12.4 kcal mol-1
(b) – 12.4 kcal mol-1
(c) – 6.20 kcal mol-1
(d) 6.20 kcal mol-1
Answer:
(d) 6.20 kcal mol-1
Hint:
12.4 kcal is the amount of heat absorbed for 2 mol of the formation of HI. By definition, j the heat of formation is for one mol of the formation of H is \(\frac{12.40}{2}\) = 6.20 kcal mol-1
![]()
Question 35.
Heat capacity is:
(a) dq / dT
(b) dq .dT
(c) Σ q.l / dT
(d) none of these
Ans :
(a) dq / dT
Question 36.
The relation between Cp and Cp is:
(a) Cp – Cv = R
(b) Cp + Cv = R
(c) – 285 KJ
(d) R – Cv = Cp
Answer:
(a) Cp – Cv = R
Question 37.
The heat required to raise the temperature of a body by 1 K is called:
(a) specific heat
(b) thermal capacity
(c) water equivalent
(d) none of these
Ans :
(b) thermal capacity
![]()
Question 38.
Heat liberated when 100 ml of 1 N NaOH is neutralized by 300 ml of 1 N HCl:
(a) 22.92 kJ
(b) 17.19 kJ
(c) 11.46 kJ
(d) 5.73 kcal
Ans :
(d) 5.73 kcal
Hint:
Number of equivalents of HCl = \(\frac{100 \times 1}{1000}\) = 0.1 equivalent
Number of equivalents of NaOH = \(\frac{300 \times 1}{1000}\) = 0.3 equivalent
Limiting reagent is HCl.
∴ 0.1 equivalent of HCl = 0.1 equivalent of NaOH
1 equivalent of HCl neutralised 1 equivalent of NaOH
heat liberated = 57.32 kcal
0.1 equivalent HCl, produce = \(\frac{57.32}{1}\) × 0.1 = 5.73 k cal
Question 39.
In order to decompose 9 g of water, 142.5 kJ of heat is required. Hence enthalpy of formation of water is:
(a) – 142.5 kJ
(b) 142.5 kJ
(c) – 285 kJ
(d) 285 kJ
Answer:
(d) 285 kJ
Hint:
Enthalpy of formation of 9 g of water = (-) 142.5 kJ
Enthalpy of formation of 18 g (1 mole) of water = -142.5/9 × 18 = – 285 kJ
Question 40.
The state of a system can be described by quoting the relationship between :
(a) pressure, volume, temperature
(b) temperature, amount, pressure
(c) amount, volume, temperature
(d) pressure, volume, temperature and amount
Answer:
(d) pressure, volume, temperature and amount
Hint:
Any thermodynamic property of a system is a function of pressure, temperature, volume and amount (number of moles).
![]()
Question 41.
During complete combustion of one mole of butane, 2658 kJ of heat is liberated. The thermo chemical reaction for the above change is:
(a) 2C4H10 (g) + 13 O2 (g) → 8 CO2 (g) + 10 H2O (l); ∆HC = – 2658 kJ mol-1
(b) C4H10 (g) + \(\frac{13}{2}\) O2 (g) → 4 CO2 (g) + 5 H2O (g); ∆HC = – 1329.0 kJ mol-1
(c) C4H10(g) + \(\frac{13}{2}\) O2 (g) → 4 CO2 (g) + 5H2O ∆HC = – 2658.0 kJ mol-1
(d) C4H10 + \(\frac{13}{2}\) O2 (g) → 4CO2 (g) + 5H2O (l) ∆HC = +2658.0 kJ mol-1
Answer:
(c) C4H10(g) + \(\frac{13}{2}\) O2 (g) → 4 CO2 (g) + 5H2O ∆HC = – 2658.0 kJ mol-1
Hint:
The enthalpy of combustion is heat released by one mol of butane an burning with oxygen. CO2 (g) and H2O7 (l) are formed.
Question 42.
If ∆U°f of formation of CH4 (g) at a certain temperature is -393 kJ mol-1, then, the value of ∆H/is:
(a) zero
(b) < ∆U°f
(c) > ∆U°f
(d) equal to ∆U°f
Answer:
(b) < ∆U°f
Hint:
The ∆U°f for CH4 (g) is
C(s) + 2 H2O(g) > CH4 ∆U°f = – 393kJ mol-1
∆H = ∆U + (RT)∆n
∆H= 1 – 2 = -1
∆H = ∆U + (RT)-1
![]()
Question 43.
In an adiabatic process, no transfer of heat takes place between the svstem and surroundings. Choose the correct option for free expansion of ideal gas under adiabatic conditions from the following:
(a) q = 0; ∆T ≠ 0; w = 0
(b) q ≠ 0; ∆T = 0; w = 0
(c) q = 0; ∆T = 0; w = 0
(d) q = 0; ∆T < 0; w ≠ 0
Answer:
(c) q = 0; ∆T = 0; w = 0
Hint:
For free expansion,
Pext = 0
W = -Pext ∆U
For adiabatic process; q = 0
∆U = q + w = 0.
This means that interval energy remains constant, which is so at constant temperature. Hence, ∆T = 0.
Question 44.
The pressure-volume work for an ideal gas can be calculated by using the expression.
w = – \(\int_{v_{I}}^{v_{f}}\) Pext . dNt
The work can also be calculated from the PV plot by using the area. Under the curve within the specified limits. When an ideal gas is compressed (a) reversibly or (b) irreversibly from volume Vi to Vf, choose the correct option:
(a) w(reversible) = w(irreversible)
(b) w(reversible) < w(irreversible)
(c) w(reversible) > w(irreversible)
(d) w(reversible) = w(irreversible)
Answer:
(b) w(reversible) < w(irreversible)
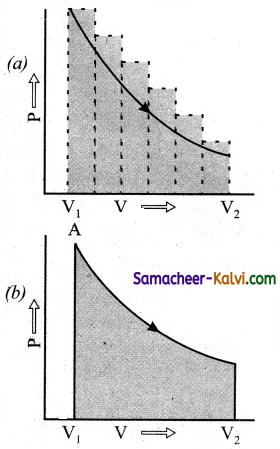
Hint:
Area under curve (a) which is for irreversible compression is more than area curve (b) which is for reversiblecompression. Hence, for compression w(reversible) < w(irreversible).
![]()
Question 45.
The entropy change can be calculated by using the expression, ∆S = \(\frac{q_{\text {rev }}}{\mathrm{T}}\). When water freezes in a glass beaker, choose the correct statement amongst the following:
(a) ∆S(system) decreases but ∆S(surroundings) remains same.
(b) ∆S(system) increases but ∆S(surroundings) decreases
(c) ∆S(system) decreases but ∆S(surroundings) increases
(d) ∆S(system) decreases and ∆S(surroundings) decreases.
Answer:
(c) ∆S(system) decreases but ∆S(surroundings) increases
Hint:
∆S (system) decreases because molecules of solid ice are less random than in liquid water. However, when water freezes to ice, heat is released which is absorbed by the surroundings. Hence entropy of the surroundings increases.
Question 46.
The enthalpies of elements in their standard states are taken as zero. The enthalpy of formation of a compound:
(a) is always negative
(b) is always positive
(c) may be positive or negative
(d) is never negative
Answer:
(c) may be positive or negative
![]()
Question 47.
The standard enthalpy of vapourisation, ∆H°vap for water at 100°C is 40.66 kJ mol-1, The internal energy change for water at 10i° C (in kJ mol-1) is:
(a) + 37.56
(b) – 43.76
(c) 43.76
(d) – 40.66
Answer:
(a) + 37.56
Hint:
H2O (l) → H2O
∆n = 1
∆H = ∆U – (RT)∆n
∆U = ∆H – (RT)∆n
= (40.66 × 1000 J mol-1 – (1 x 8.314Jk-1 mol-1 x 373 K)
= 40660 – 3101 JK-1 mol-1
= 37559 J mol-1 = 37.56 kJmol-1
Question 48.
Two similar reactions are given below:
H2 (g)+ O2 (g) >H2 (g); ∆H – ∆H1
H2 (g) + O2 (g) > H2 (l); ∆H = ∆H2
In terms of magnitude, of ∆H
(a) ∆H1 > ∆H2
(b) ∆H1 < ∆H2
(c) ∆H1 = ∆H2
(d) cannot be predicted
Answer:
(b) ∆H1 < ∆H2
Hint:
∆H2 > ∆H1 because when H2O (g) condenses to H2O (l), heat is evolved,. Hence, ∆H1 < ∆H2.
Question 49.
In the reaction, S + \(\frac{3}{2}\) O2 → SO3 + 2x kJ and SO2 + \(\frac{1}{2}\) O2 → SO3 + y kJ. The enthalpy of formation of SO2 is:
(a) x – y
(b) 2x + y
(c) x + y
(d) y – 2x
Answer:
(d) y – 2x
Hint:
Given, S + \(\frac{3}{2}\) O2 → SO3; ∆H = – 2x kJ (1)
SO2 + \(\frac{1}{2}\) O2 → SO3; ∆H = – y kJ (2)
The enthalpy of formation of SO2 is given by
S + O2 → SO3 ∆H = ? ………..(3)
Equation (1) – Equation (2) gives
S + O2 → SO3
i.e., ∆H = – 2x – (-y) = y – 2x
![]()
Question 50.
Calorific value of hydrogen gas is – 143 kJ mol-1. The standard enthalpy of formation of H2O will be:
(a) – 143 kJ mol-1
(b) + 143 kJ mol-1
(c) – 286 kJ mol-1
(d) + 286 kJ mol-1
Answer:
(c)
Hint:
H2 (g) + \(\frac{1}{2}\) O2 (g) → H2O (l)
Calorifìc value of a fuel is the amount of heat produced by 1 gm of the fuel.
1 g of H2O on combustion produces = 143 kJ
1 mol (2g) will produce 2 × 143 = 286 kJ
This is also the value of standard enthalpy of formation of water.
Question 51.
Based on first law of thermodynamics, which one of the following is correct?
(a) For an isochoric process, ∆U = -q
(b) For an adiabatic process, ∆U = -w
(c) For an isothermal process, q = + w
(d) For a cyclic process, q = -w
Answer:
(d) For a cyclic process, q = -w
Hint:
(a) ∆U = q + w; For an isochoric process, -w = P. ∆V = 0; Hence ∆U = qU
(b) For an adiabatic process, q = 0, Hence, ∆U = w.
(c) For an isothermal process, ∆U = 0, Hence, q = -w.
(d) For a cyclic process, ∆U = 0; Hence, q = – w.
![]()
Question 52.
The amount of heat evolved when 500 cm3 of 0.1 M hydrochloric acid is mixed with 200 cm3 of 0.2 M sodium hydroxide solution is:
(a) – 57.1 kJ
(b) + 57.1kJ
(c) 2.284 kJ
(d) -2.284 kJ
Answer:
(c) 2.284 kJ
Hint:
Number of mol of HCl = molarity × volume in cm-3 × 10-3
= 0.1 × 500 × 10-3 = 0.05
∴ Number of mol of H+ ions = 0.05 mol 6f H+ ions.
Number of mol of NaOH = 0.2 × 200 × 10-3 = 0.04 mol
number of mol of OH– ions = 0.04 mol
NaOH is the limiting reagent. Therefore 0.04 mol of OH– will combine with 0.04 mol of H+ ions
Heat evolved when 1 mol of OH– combine with 1 mol of H+ ion = 57.1 kJ
Heat evolved when 0.04 mol of OH– combine with 0.04 mol of H+ ion = 57.1 × 0.04
= 2.284 kJ
Question 53.
The following two reactions are known:
(i) Fe2O3 (s) + 3CO (g) → 2 Fe (s) + 3CO2 (g); ∆H = -26.8 kJ
(ii) FeO (s) + CO (g) → Fe (s) + CO2 (g); ∆H = -16.5kJ
The value for ∆H for the following reaction is
Fe2O3 (s) + CO (g) → 2 FeO (s) + CO2 (g) is
(a) + 10.3 kJ
(b) – 43.3 kJ
(c) -10.3kJ
(d) 6.2 kJ
Answer:
(d) 6.2 kJ
Hint:
Fe2O3 + 3CO → 2 Fe + 3CO2; ∆H = -26.8 kJ …………(1)
FeO + CO → Fe + CO2; ∆H = -16.5 kJ ……………..(2)
The required reactions is
Fe2O3 + CO → 2FeO + CO2; ∆H = ?
Multiply equation (2) by (1) and reverse it and add with equation (1)
Fe2O3 + 3CO → 2 Fe + 3CO2; ∆H = -26.8 kJ
2Fe + 2CO2 —> 2FeO + 2CO ; ∆H = +33.0 kJ
Fe2O3+ 3CO—> 2FeO + CO2; ∆H = 6.2 kJ
![]()
Question 54.
The heat of combustion of carbon to carbon-di-oxide is -393.5 kJ mol-1. The heat released upon formation of 35.2 g of CO2 from carbon and oxygen is:
(a) + 315 kJ
(b) – 630 kJ
(c) – 3.15 kJ
(d) – 315 kJ
Answer:
(d)
Hint:
C + O2 → CO2; ∆H = – 393.5 kJ
When 1 mol of CO2(44g of CO2) is formed heat evolved = – 393.5 kJ
When 35.2 g is formed, the amount of heat evolved is, = \(\frac{393.5}{44}\) × 35.2 = – 314.8 kJ
≈ – 315 kJ
Question 55.
For the reaction, 2H2 (g) + O2 (g) → 2H2O (g), the, ∆H = -571 kJ. Bond energy of H – H = 435 and O = O = 498. then the average bond energy of O – H bond will be:
(a) 484
(b) – 484
(c) 271
(d) – 271
Answer:
(a) 484
Hint:
2H2 + O2 → 2H2O
[∵ 2 × (H – O – H)]
∆H = 2 × BE(H -H) + BE(O = O) – 4(BE of O – H)
– 571 = (2 × 435 + 498 – (4 BE of O – H)
B.E (O – H) = 484
![]()
Question 56.
Enthalpy change for the reaction, 4H (g) → 2H2 (g) is – 869.6 kJ. The dissociation energy of H – H bond is:
(a) -217.4 kJ
(b) – 434.8 kJ
(c) – 896.6 kJ
(d) + 434.8 kJ
Ans :
(d) + 434.8 kJ
Hint:
2H2 (g) → 4H; ∆H = + 869.6 kJ
(or) H2 (g) → 2H (g)
∆H = \(\frac{869.6}{2}\) = 434.8 kJ
Question 57.
The direct conversion of A → B is difficult, Hence it is carried out by the following paths shown: . ..
∆S (A → C) = 50 e.u
∆S (C → D) = 30 e.u .
∆S (B → D) = 20 e.u.
where e.u. is entropy unit, then ∆S( A – B) is
(a) + 100 e.u.
(b) + 60 e.u
(c) – 100 e.u
(d) – 60 e.u.
Answer:
(b) + 60 e.u
Hint:
∆S (A – C)= SC – SA = 50e.u. …(1)
∆S (C → D) = SD – SA = 30 e.u. . . .(2)
∆S (B → D) = SD – SB = 20 e.u. .. .(3)
∆S (A → B) = SB – SA =?
Equation (1) + Equation (2) – Equation (3)
= ∆S(A – B)
= 50 + 30 – 20 = 60 e.u
![]()
Question 58.
In which of the following reaction, standard entropy change (∆S°) is positive and standard Gibb’s free energy change (∆G°) decreases sharply with increasing temperature?
(a) C(graphite) + \(\frac{1}{2}\) O2 (g) → CO (g)
(b) CO (g)+ \(\frac{1}{2}\) O2 (g) → CO2(g)
(c) Mg (s) + \(\frac{1}{2}\) O2 (g) → Mg (s)
(d) \(\frac{1}{2}\) C (graphite) + \(\frac{1}{2}\) O2 (g) → \(\frac{1}{2}\) CO2 (g)
Answer:
(a) C(graphite) + \(\frac{1}{2}\) O2 (g) → CO (g)
Hint:
The reaction (a) is accompanied increase in number of moles of gaseous substances. Hence entropy incre ases, i.e., ∆S° is + ve. From the relation, ∆G° = ∆H° – T∆S°, as temperature increases, T∆S° decreases sharply and hence ∆G° decreases sharply.
Question 59.
For the reaction, X2O4 (l) → 2 XO2 (g),
∆U = 2.1 kcal, ∆S = 20 cal Kr1 at 300 K. Hence, ∆G is:
(a) 2.7 kcal
(b) -2.7 kcal
(c) 9.3 kcal
(d) – 9.3 kcal
Answer:
(b) – 2.7 kcal
Hint:
∆H = ∆U + (RT)∆n
Given:
∆U = 2.1 kcal; ∆n = 2 – 0.2;
R = 2 × 10-3 kcal; T = 300K.
∴ ∆H= 2.1 + 2 × 2 × 10-3 × 300 = 3.3 kcal
Again, ∆G = ∆H – T∆S
Given, ∆S = 20 × 10-3 kcal K-1
∆H = 3.3 kcal (calculated above)
∆G = ?
∆S = 3.3 – 300 × (20 × 10-3)
= 3.3 – 6 = – 2.7 kcal.
![]()
Question 60.
Consider the following reactions:
(i) O2 (g) + 2 SO2 (g) → 2 SO3 (g)
(ii) CaC2O4 (s) → CaCO3 (s) + CO (g)
(iii) 2 H2 (g) + O2 (g) → 2H2O (g)
Choose the correct statement:
(a) In all the reactions entropy increases.
(b) In (i) and (iii) entropy decreases while in (ii) entropy increases
(c) In (i) and (ii) entropy decreases while in (in) entropy increases
(d) In (i) and (iii) entropy decreases while in (i) entropy increases.
Answer:
(b) In (i) and (iii) entropy decreases while in (ii) entropy increases
Hint:
In (i) ∆S = negative (because number of moles of gases decreases)
In (ii) ∆S = positive (because reactant is solid while the one of the productivity is a gas)
In (iii) ∆S = negative (because number of moles of gases decreases)
Question 61.
Which of the following is not correct?
(a) ∆G is zero for a reversible reaction
(b) ∆G is positive for a spontaneous reaction
(c) ∆G is negative for a spontaneous reaction
(d) ∆G is positive for a non-spontaneous reaction
Ans :
(b) ∆G is positive for a spontaneous reaction
Hint:
∆G is negative and net positive for a spontaneous reaction. ∆G = 0 for a reaction at equilibrium, ∆G is positive for a non-spontaneous reaction.
![]()
Question 62.
Examples for various types of system is given below. Identify the system which is different from others.
(a) Animals and plants
(b) Water kept in thermos flask
(c) Thermostat
(d) A refrigerator
Answer:
(a) Animals and plants
Hint:
Thermodynamically animals and plants | are considered as open system while others are closed system.
Question 63.
Examples of thermodynamic properties j are given. Among them one is an extensive | property and the others are intensive properties. Identify the extensive property.
(a) Temperature
(b) Pressure
(c) Mole fraction
(d) Gibb’s free energy ‘ v ‘
Answer:
(d) Gibb’s free energy ‘ v ‘
Question 64.
From the following pairs of properties identify the pair of property which is dependent on the quantity of matter present.
(a) Temperature, mass
(b) Mass, free energy
(c) Temperature and pressure
(d) Pressure and internal energy.
Answer:
(c) Temperature and pressure
Hint:
Both are intensive properties.
![]()
Question 65.
Work done in isothermal expansion of an ideal gas is given below.
From the following, identify the correct pairs which gives the expression for work done.
(a) w = +2.303 nRT log \(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\) and w = + 2.303 nRT log \(\frac{\mathrm{P}_{1}}{\mathrm{P}_{2}}\)
(b) w = -2.303 /?RT log \(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\) and w = – 2.303 nRT log \(\frac{\mathrm{P}_{2}}{\mathrm{P}_{1}}\)
(c) w = -2.303 nRT log \(\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}\) and A w = – 2 303 nRT log \(\frac{\mathrm{P}_{1}}{\mathrm{P}_{2}}\)
(d) w = +2.303 nRT log \(\frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}}\) and w = + 2.303 nRT log \(\frac{\mathrm{P}_{2}}{\mathrm{P}_{1}}\)
Answer:
(b) w = -2.303 /?RT log \(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\) and w = – 2.303 nRT log \(\frac{\mathrm{P}_{2}}{\mathrm{P}_{1}}\)
Question 66.
Assertion:
Heat energy is completely transformed into work during the isothermal expansion of an ideal gas.
Reason:
During an isothermal process, the changes in internal energy of a gas is due to decrease in pressure is nullified by the change due to increase in volume.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer:
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
![]()
Question 67.
Assertion:
Chlorine when solidifies does not have zero entropy ever at absolute zero.
Reason:
Chlorine is a pungent smelling gas and it is difficult to solidify it.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer:
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
Question 68.
Assertion:
Molar entropy of Vaporisation of water is different from ethanol.
Reason:
Water is more polar than ethanol.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer:
(c) If assertion is true but reason is false.
Question 69.
Assertion:
A process for which ∆Ssystem > 0 as well as ∆H > 0, passes from non spontaneous to spontaneous state as the temperature is increased.
Reason:
At higher temperatures T∆S exceeds ∆H.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer:
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
![]()
Question 70.
Assertion:
For the reaction,
2NH3 (g) → N2 (g) + 3H2 (g),
∆H > ∆E
Reason:
Enthalpy change is always greater than internal energy change.
(a) If both assertion and reason are true and reason is the correct explanation of the assertion.
(b) If both assertion ancj reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If both assertion and reason are false.
Answer:
(c) If assertion is true but reason is false.
Question 71.
Which of the following statements are not correct?
(i) The standard value of absolute entropy of elementary substance is taken as zero.
(ii) Work done in an isothermal expansion is greater than that in an adiabatic expansion for the same increase in volume.
(iii) During adiabatic expansion of a real gas, there is no change in the enthalpy of the system.
(iv) Expansion against vacuum is very large and hence work done is also very large.
(a) (i), (iv)
(b) (ii), (iii)
(c) (i), (iii)
(d) (ii), (iv)
Answer:
(a) (i), (iv)
![]()
Question 72.
Based on first law of thermodynamics, which one of the following is correct?
(a) For an isochoric process, ∆U = – q
(b) For an adiabatic process, ∆U = – w
(c) For an isothermal process, q = + w
(d) For a cyclic process, q = – w
Answer:
Question 73.
Choose the incorrect statement from among the following:
All statements under constant temperature.
(a) For a spontaneous process, ∆S(total) should be positive and also ∆G is negative.
(b) For a process at equilibrium, both ∆S(total) and ∆G should be equal to zero.
(c) For a non-spontaneous process ∆S(total)should be negative and ∆G should be positive,
(d) Spontaneous process ∆S negative and ∆G positive.
Answer:
(d) Spontaneous process ∆S negative and ∆G positive.
Question 74.
Which of the following statements is correct, when both ∆H and T∆S are positive?
(a) If ∆H > T∆S, the process is non-spontaneous and ∆G is positive.
(b) If ∆H < T∆S, the process is spontaneous and ∆G is positive.
(c) If ∆H > T∆S, the process is spontaneous and ∆G is positive.
(d) If ∆H = T∆S, the process is spontaneous and ∆G = 0 .
Answer:
(a) If ∆H > T∆S, the process is non-spontaneous and ∆G is positive.
![]()
Question 75.
Choose the correct statement from among the following:
(a) The standard enthalpy of methane gas is equal to its standard enthalpy of its formation.
(b) The standard enthalpy if diamond is zero.
(c) For the change H2O (l) → H2O (v) ∆S is negative.
(d) The lattice enthalpy of an ionic compound should always have high positive value.
Answer:
(a) The standard enthalpy of methane gas is equal to its standard enthalpy of its formation.
Question 76.
Match the entities in column I with appropriate entities in column II.
| Column I | Column II |
| (i) Isothermal process | (A) q = ∆U |
| (ii) Adiabatic process | (B) W = -P∆V |
| (iii) Isobaric process | (C) W = ∆U |
| (iv) Isochoric process | (D) W = nRT ln \(\frac{v_{2}}{v_{1}}\) |
(a) (i) – (D), (ii) – (B), (iii) – (C), (iv) – (A)
(b) (i) – (D), (ii) – (C), (iii) – (B), (iv) – (A)
(c) (i) – (A), (ii) – (C), (iii) – (B), (iv) – (D)
(d) (i) – (C), (ii) – (A), (iii) – (D), (iv) – (B)
Answer:
(b) (i) – (D), (ii) – (C), (iii) – (B), (iv) – (A)
![]()
Question 77.
Match the entities in column I with appropriate entities in column II.
| Column I | Column II |
| (i) Positive ∆U value | (A) Non – spontaneous at all temperature |
| (ii) Negative ∆H value | (B) Endothermic reaction |
| (iii) ∆H = -ve; ∆S = +ve | (C) Exothermic reaction |
| (iv) ∆H = +ve; ∆S = -ve | (D) Spontaneous at all temperatures |
(a) (i) – (B), (ii) – (C), (iii) – (D), (iv) – (A)
(b) (i) – (C), (ii) – (B), (iii) – (A), (iv) – (D)
(c) (i) – (D), (ii) – (C), (iii) – (B), (iv) – (A)
(d) (i) – (C), (ii) – (A), (iii) – (D), (iv) – (B)
Answer:
(a) (i) – (B), (ii) – (C), (iii) – (D), (iv) – (A)