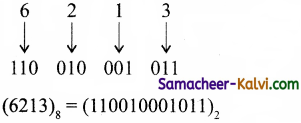
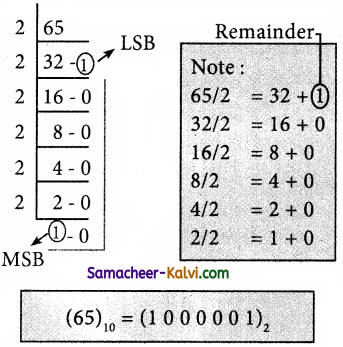
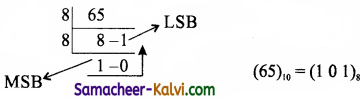
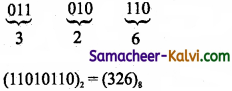
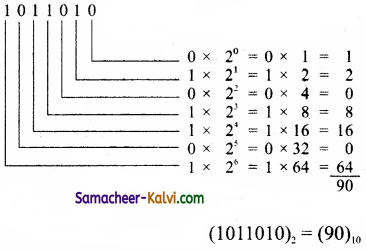
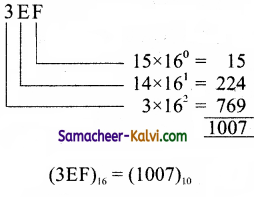
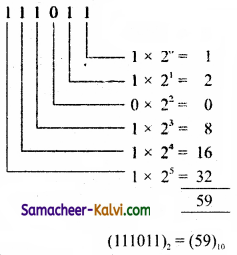
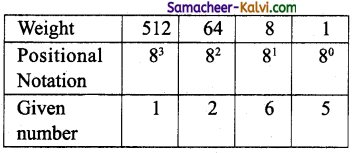
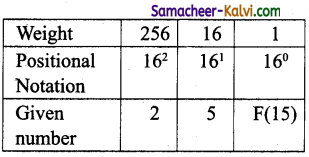
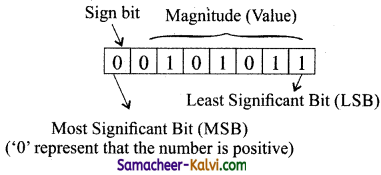
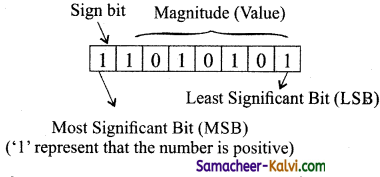
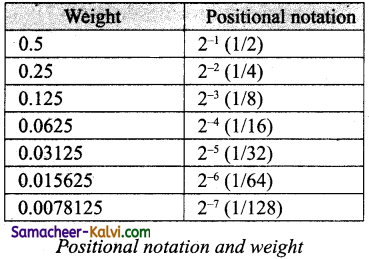
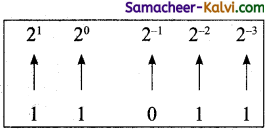
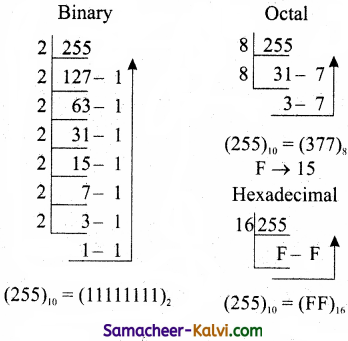
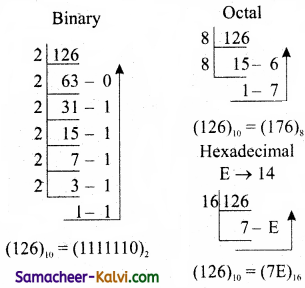
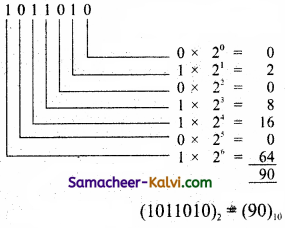
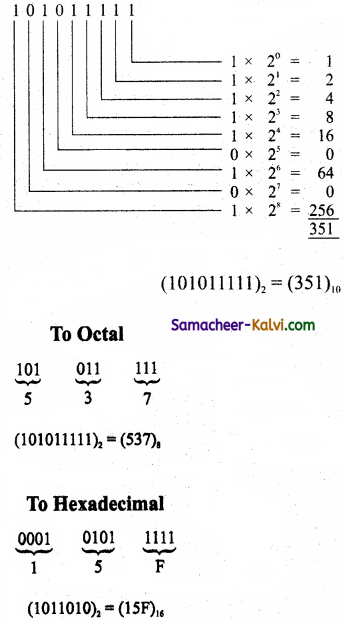
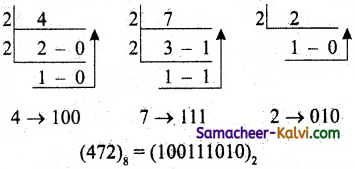
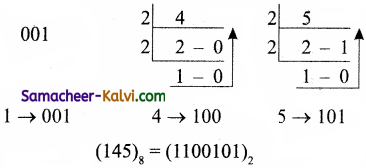
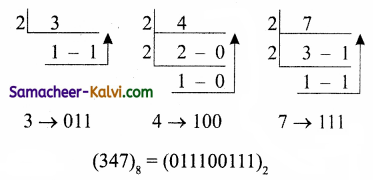
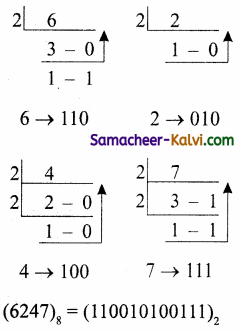
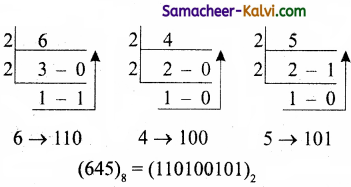
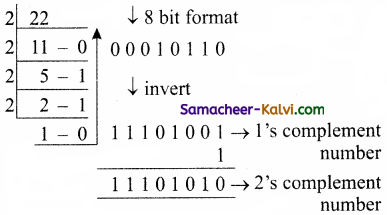
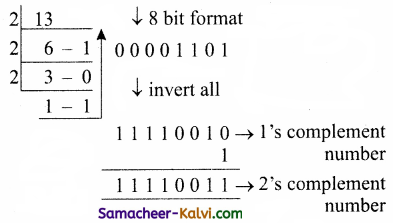
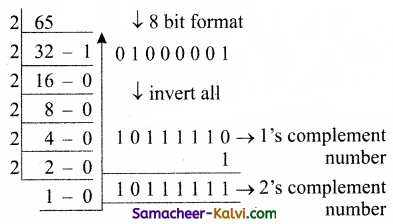
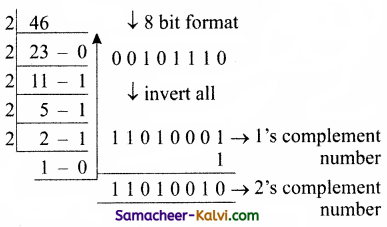
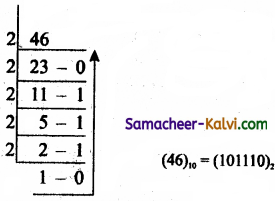
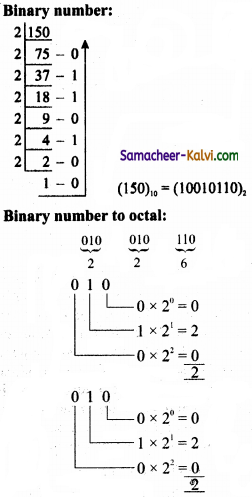
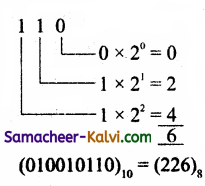
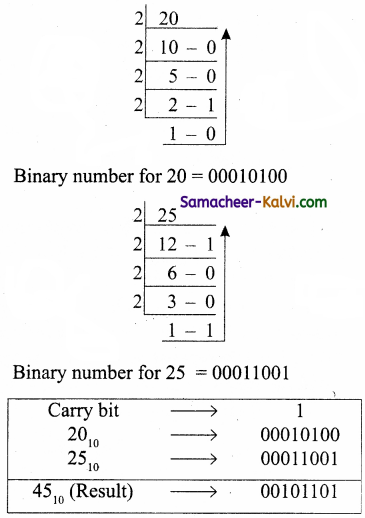
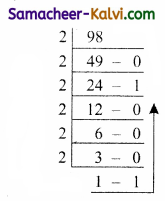
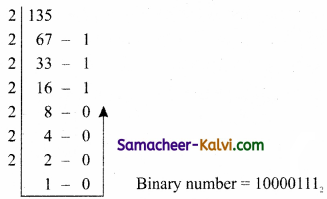
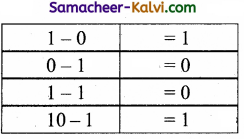
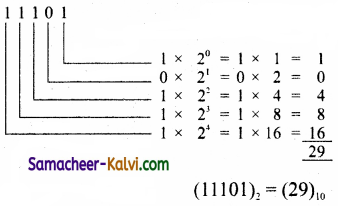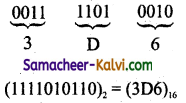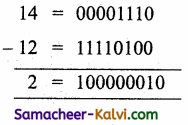TN State Board 11th Computer Science Important Questions Chapter 2 Boolean Algebra Part 2
Question 1.
Define Truth Table.
Answer:
A truth table represents all the possible values of logical variable or statements along with all the possible results of given combination of truth values.
Question 2.
What are logical operators?
Answer:
The basic logical operations are AND, OR and NOT, which are symbolically represented by dot (.), plus (+), and by over bar / single apostrophe respectively. These symbols are also called as “Logical Operators”.
![]()
Question 3.
Define AND operator?
Answer:
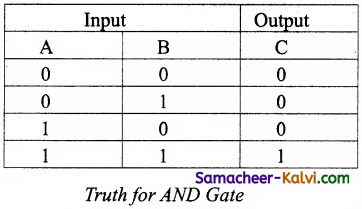
The AND operator is defined in Boolean algebra by the use of the dot (.) operator. It is similar to multiplication in ordinary algebra. The AND operator combines two or more input variables. So that the output is true only if all the inputs are true. The truth table for a 2-input AND operator is
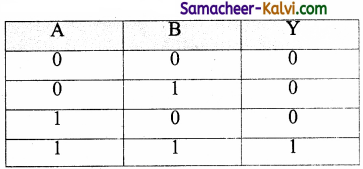
The above 2-input AND operation is expressed as: Y = A . B
Question 4.
What is OR operator?
Answer:
The plus sign is used to indicate the OR operator. The OR operator combines two or more input variables. So that the output is true if at least one input is true. The truth table for a 2-input OR operator is
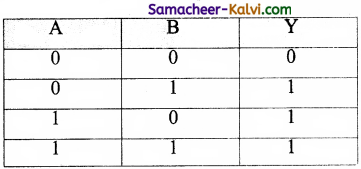
The above 2-input OR operation is expressed as: Y = A + B
![]()
Question 5.
What is NOT operator?
Answer:
The NOT operator has one input and one output. The input is either true or false, and the output is always the opposite, i.e., the NOT operator inverts the input. The truth table for a NOT operator where A is the input variable and Y is the output shown below:

The NOT operator is represented algebraically by the Boolean expression: Y = \(\overline{\mathrm{A}}\).
Question 6.
What is NAND operator?
Answer:
The NAND is the combination of NOT and AND. The NAND is generated by inverting the output of an AND operator. The algebraic expression of the NAND function is:
Y = \(\overline{\mathrm{A} \cdot \mathrm{B}}\)
The NAND function truth table is shown below:
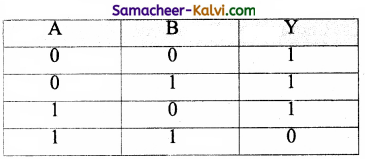
A NAND B = NOT (A AND B)
![]()
Question 7.
What is called basic logic gates?
Answer:
A gate is a basic electronic circuit which operates on one or more signals to produce an output signal. There are three fundamental gates namely AND, OR and NOT.
Question 8.
Write the Distributive law.
Answer:
A . (B + C) = A . B + A . C
A + (B . C) = (A + B) . (A + C)
Question 9.
Complete the following:
(i) A + \(\overline{\mathrm{A}}\) =
(ii) A. \(\overline{\mathrm{A}}\) =
(iii) \(\overline{\overline{\mathrm{A}}}\) =
(iv) A + A =
(v) A. A =
(vi) A + 1 =
Answer:
(i) A+ \(\overline{\mathrm{A}}\) = 1
(ii) A. \(\overline{\mathrm{A}}\) = 0
(iii) \(\overline{\overline{\mathrm{A}}}\) = A
(iv) A + A = A
(v) A . A = A
(vi) A + 1 = 1
![]()
Question 10.
Draw the logic circuit of Bubbled AND Gate and explain.
Answer:
The Logic Circuit of Bubbled AND Gate
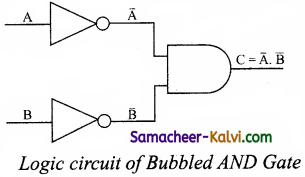
In the above circuit, invertors on the input lines of the above circuit, invertors on the input lines of the AND gate gives the output as C = (\(\overline{\mathrm{A}}\) . \(\overline{\mathrm{B}}\))This circuit can be redrawn as the bubbles on the inputs, where the bubbles represent inversion.
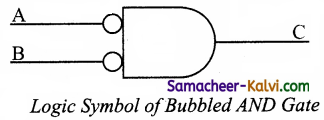
It is referred as bubbled AND gate.
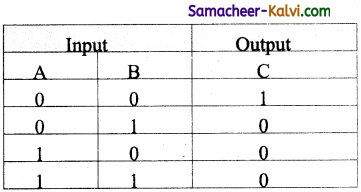
If A = 0 and B = 0 C = (\(\overline{0} . \overline{0}\)) = 1 . 1 = 1
If A = 0 and B = 1 C = (\(\overline{0} . \overline{1}\)) = 1 . 0 = 0
If A = 1 and B = 0 C = (\(\overline{1} . \overline{0}\)) = 0 . 1 = 0
If A = 1 and B = 1 C = (\(\overline{1} . \overline{1}\)) = 0 . 0 = 0
Here the truth table is
A bubbled AND gate produces the same output as a NOR gate. So, replace each NOR gate by a bubbled AND gate. The circuits are interchangeable.
Therefore,
\((\overline{\mathrm{A}+\mathrm{B}})=\overline{\mathrm{A}} \cdot \overline{\mathrm{B}}\)
Which establishes the De Morgan’s second theorem.
![]()
Question 11.
Draw the logic circuit of Bubbled OR Gate and explain.
Answer:
The logic circuit of bubbled OR gate is
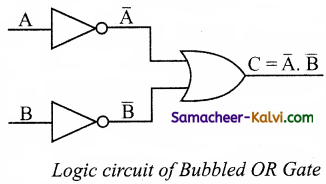
The output of this circuit can be written as
C = \(\overline{\mathrm{A}}\) + \(\overline{\mathrm{B}}\)
The above circuit can be redrawn as the bubbles on the input, where the bubbles represents the inversion.
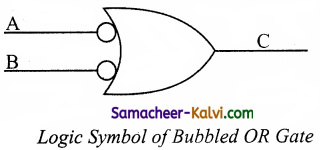
It is referred as bubbled OR gate. The truth table for the bubbled OR is
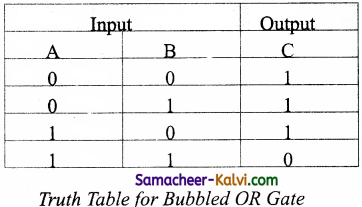
Comparing the truth tables of the bubbled OR gate with NAND gate, they are identical. So the circuits are interchangeable.
Therefore,
\((\overline{\mathrm{A} \cdot \mathrm{B}})=\overline{\mathrm{A}}+\overline{\mathrm{B}}\)which establishes the De Morgan’s second theorem.
![]()
Question 12.
Draw the symbol of logic agtes and their corresponding Truth tables.
Answer:
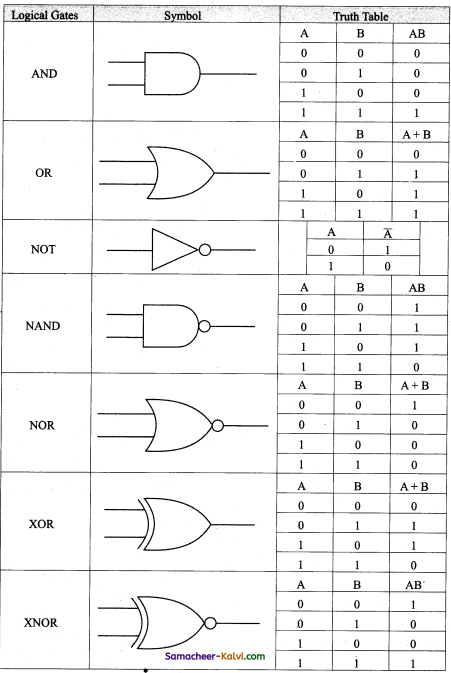
![]()
Question 13.
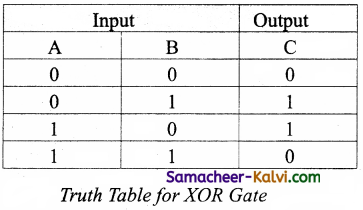
Explain XOR gate with truth table.
Answer:
The XOR (exclusive – OR) gate acts in the same way as the logical “either/or.” The output is “true” if either, but not both, of the inputs are “true”. The output is “false” if both inputs are “false” or if both inputs are “true”. The output is 1 if the inputs are different, but 0 if the inputs are the same. The logic circuit of XOR gate is
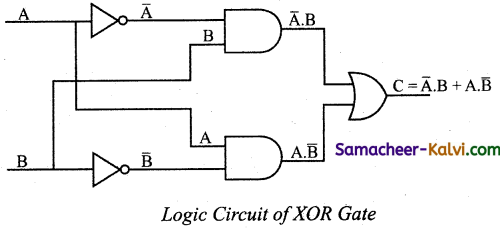
The output of the XOR gate is
The truth table for XOR gate is
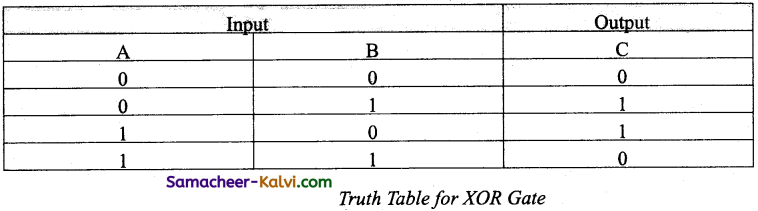
In boolean algebra, exclusive – OR operator © or “encircled plus”.
Hence, C = A © B
The logical symbol of XOR gate is
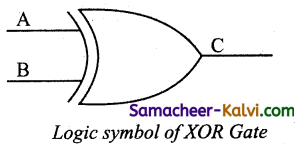
![]()
Question 14.
What is Boolean Algebra?
Answer:
It is a mathematical discipline that is used for designing digital circuits in a digital computer. It describes the relation between inputs and outputs of a digital circuit.
Question 15.
Write a short note on NAND Gate.
Answer:
The NAND gate operates an AND gate followed by a NOT gate. It acts in the manner of the logical operation “AND” followed by inversion. The output is “false” if both inputs are “true”, otherwise, the output is “true”. The output of the NAND gate is 0 if and only if both the inputs are 1, otherwise the output is 1.
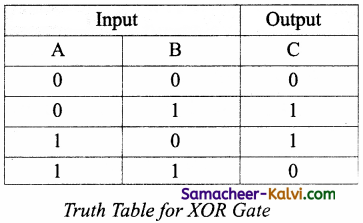
Question 16.
Draw the truth table for XOR gate.
Answer:
The truth table for XOR gate is
![]()
Question 17.
Write the associative laws?
Answer:
A + (B + C) = (A + B) + C
A. (B . C) = (A . B) . C
Question 18.
What are derived gates?
Answer:
Logic gates like NAND, NOR, XOR and XNOR are derived gates which are derived from the fundamental gates.
Question 19.
Write the truth table of fundamental gates.
Answer:
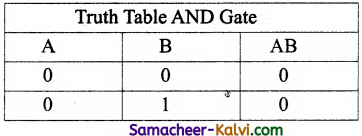
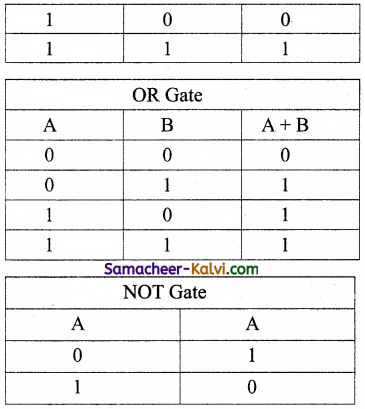
![]()
Question 20.
Write a short note on XNOR gate.
Answer:
The XNOR (exclusive – NOR) gate is a combination XOR gate followed by an inverter. Its output is “true” if the inputs are the same, and “false” if the inputs are different. In simple words, the output is 1 if the input are the same, otherwise the output is 0. The logic circuit of XNOR gate is
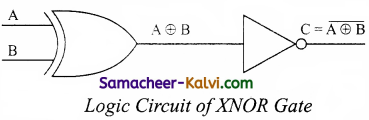
The output of the XNOR is NOT of XOR
C = A ⨁ B
= \(\overline{\mathrm{A}}\) . B + A . \(\overline{\mathrm{B}}\)
= A B + \(\overline{\mathrm{A}}\) \(\overline{\mathrm{B}}\)
(Using De Morgan’s Theorem)
In boolean algebra, ⊙ or “included dot” stands for the XNOR.
Therefore, C = A ⊙ B
The logical symbol is
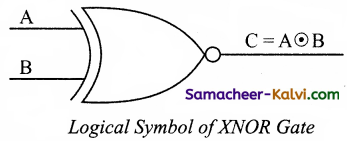
Truth Table for XOR Gate
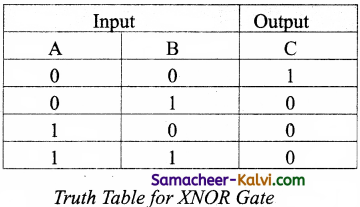
![]()
Question 21.
Reason out why the NAND and NOR are called universal gates?
Answer:
NAND and NOR gates are called Universal gates, because the fundamental logic gates can be realized through them.
Question 22.
Give the truth table of XOR gate.
Answer:
Question 23.
Write the De Morgan’s law.
Answer:
De Morgan’s law \(\overline{\mathrm{A}+\mathrm{B}}\) = A . \(\overline{\mathrm{B}}\)
(\(\overline{\mathrm{A} \cdot \mathrm{B}}\)) = \(\overline{\mathrm{A}}\) + \(\overline{\mathrm{B}}\)
![]()
Question 24.
Explain the fundamental gates with expression and truth table.
Answer:
The three fundamental gates namely AND, OR and NOT.
AND Gate:
The AND gate can have two or more input signals and produce an output signal. The output is “true” only when both inputs are “true”, otherwise, the output is “false”. The output will be 1 if and only if both inputs are 1; otherwise the output is 0. The output of the AND gate is represented by a variable say C, where A and B are two and if input boolean variables. In boolean algebra, a variable can take either of the values ‘0’ or ‘1’.
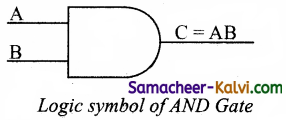
One way to symbolize the action of an AND gate is by writing the boolean function.
C = A AND B
In boolean algebra the multiplication sign stands for the AND operation. Therefore, the output of the AND gate is
C = A . B or simply C = AB
Read this as “C equals A AND B”. Since there are two input variables here, the truth table has four entries, because there are four possible inputs : 00, 01, 10 and 11.
For instance if both inputs are 0,
C = A .B = 0 . 0 = 0
The truth table for AND Gate is
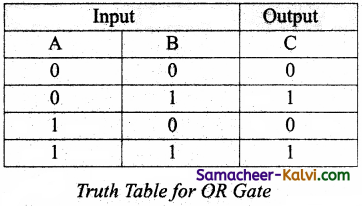
OR Gate:
The OR gate behaves like the logical inclusive “OR”. The output is “true” if either or both of the inputs are “true”. If both inputs are “false” then the output is “false”. The output will be 1 if and only if one or both inputs are 1; otherwise, the output is 0. The logical symbol of the OR gate is
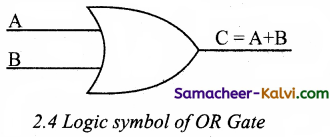
The OR gate output is
C = A OR B
We use the + sign to denote the OR function. Therefore,
C = A + B
Read this as “C equals A OR B”.
For instance, if both the inputs are 1
C = A + B = 1 + 1 = 1
The truth table for OR gate is
NOT Gate:
The NOT gate, called a logical inverter, has only one input. It reverses the logical state. The output C is always the complement of the input. The logical symbol of the NOT gate is
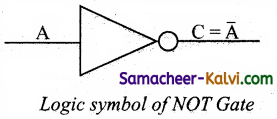
C = NOT A
In boolean algebra, the overbar stands for NOT operation. Therefore,
C = \(\overline{\mathrm{A}}\)
Read this as “C equals NOT A” or “C equals the complement of A”.
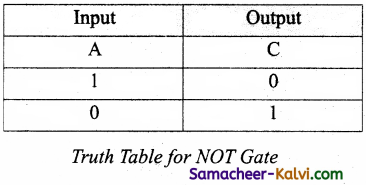
If A is 0,
C = \(\overline{1}\) = 0
On the otherhand, if A is 1,
C = \(\overline{1}\) = 0
The truth table for NOT gate is
![]()
Question 25.
How AND and OR can be realized using NAND and NOR gate.
Answer:
The output of NOR gate is
C = \(\overline{\mathrm{A}+\mathrm{B}}\)
The output of Bubbled AND gate is
C = \(\overline{\mathrm{A}}\) . \(\overline{\mathrm{B}}\)
The truth table for both Bubbled AND and NOR gate is
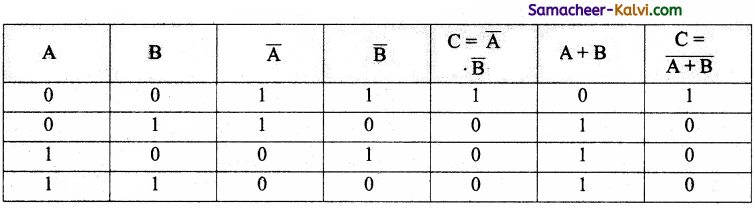
From the above table, a bubbled AND gate produces the same output as a NOR gate. In this way we can realised AND gate using NOR gate.
The output of NAND gate is C = \(\overline{\mathrm{A} \cdot \mathrm{B}}\)
The output of Bubbled OR gate is C = \(\overline{\mathrm{A}}\) + \(\overline{\mathrm{B}}\)
The truth table for both bubbled OR gate and NAND gate is

From the above table, a bubbled OR gate produces the same output as a NAND gate. In this way we can realised OR gate using NAND gate.
![]()
Question 26.
Explain the Derived gates with expression and truth table.
Answer:
The NAND gate operates an AND gate followed by a NOT gate. It acts in the manner of the logical operation “AND” followed by inversion. The output is “false” if both inputs are “true”, otherwise, the output is “true”. The output of the NAND gate is 0 if and only if both the inputs are 1, otherwise the output is 1. The logic circuit of NAND gate is
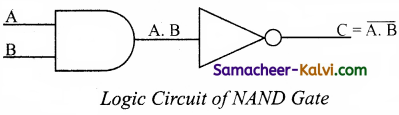
The logical symbol of NAND gate is
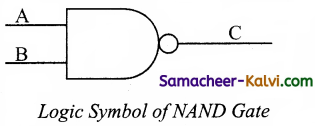
The output of the NAND gate is
C = (\(\overline{\mathrm{A} \cdot \mathrm{B}}\))
Read this as “C equals NOT of A AND B” or “C equals the complement of A and B”.
For example if both the inputs are 1
C = \((\overline{1.1})=\overline{1}\) = 0
The truth table for NAND gate is
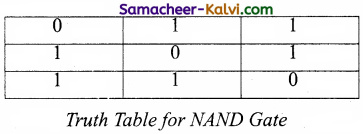
![]()
Choose the correct answer:
Question 1.
The AND operator is defined in Boolean algebra by the use of the operator
(a) +
(b) –
(c) *
(d) .
Answer:
(d) .
Question 2.
The plus sign is used to indicate the ______ operator.
(a) AND
(b) OR
(c) NOT
(d) NAND
Answer:
(b) OR
Question 3.
The _______ is the combination of NOT and AND.
(a) NAND
(b) XOR
(c) XNOR
(d) NOT
Answer:
(a) NAND
![]()
Question 4.
Which gate is the combination XOR gate followed by the inverter?
(a) XNOR
(b) XOR
(c) OR
(d) NOR
Answer:
(a) XNOR
Question 5.
How many fundamental logic gates?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(c) 3
Question 6.
A + 0 is:
(a) 1
(b) 0
(c) A
(d) \(\overline{\mathrm{A}}\)
Answer:
(c) A
![]()
Question 7.
A. \(\overline{\mathrm{A}}\) is:
(a) A
(b) 0
(c) \(\overline{\mathrm{A}}\)
(d) 1
Answer:
(b) 0
Question 8.
A + A is:
(a) 2A
(b) A2
(c) A
(d) +1
Answer:
(c) A
Question 9.
A + 1 is:
(a) 1A
(b) A
(c) 1
(d) 2A
Answer:
(c) 1
![]()
Question 10.
________ Gate is called logic inverter.
(a) OR
(b) NOT
(c) AND
(d) None
Answer:
(b) NOT
Question 11.
Who proposed the basic principles of Algebra?
(a) George Boole
(b) George William
(c) George Kingston
(d) George Barsley
Answer:
(a) George Boole
Question 12.
The variable which can stored truth values are called:
(a) Logical variable
(b) Binary valued variables
(c) Boolean variable
(d) All the above
Answer:
(d) All the above
![]()
Question 13.
The basic logical operations symbol are also called:
(a) Arithmetic operators
(b) Logical operators
(c) Conditional operators
(d) Relational operators
Answer:
(b) Logical operators
Question 14.
Which logical operator has one input and one output?
(a) AND
(b) OR
(c) NOT
(d) NAND
Answer:
(c) NOT
Question 15.
Which operator is generated by inverting the output of an AND operator?
(a) NAND
(b) NOT
(c) OR
(d) NOR
Answer:
(a) NAND
![]()
Question 16.
Which operator is the combination of NOT and OR?
(a) NAND
(b) NOT
(c) OR
(d) NOR
Answer:
(d) NOR
Question 17.
Which operator is generated by inverting the output of an OR operator?
(a) NOR
(b) NAND
(c) NOT
(d) OR
Answer:
(a) NOR
Question 18.
Which operator uses multiplication sign in boolean algebra?
(a) NOR
(b) NOT
(c) AND
(d) OR
Answer:
(c) AND
![]()
Question 19.
Which gate gets its name from its behaviour like the logical inclusive?
(a) OR
(b) AND
(c) NOT
(d) NAND
Answer:
(a) OR
Question 20.
Which gate circuit is an OR gate followed by an inverter?
(a) NAND
(b) NOR
(c) NOT
(d) AND
Answer:
(b) NOR
Question 21.
⊙ – (included dot) stands for the:
(a) XNOR
(b) XOR
(c) NAND
(d) NOR
Answer:
(a) XNOR
![]()
Question 22.
Which of the logic gates are found in digital integrated circuits?
(a) gates
(b) arrays
(c) operation
(d) physical space
Answer:
(b) arrays
Question 23.
A + \(\overline{\mathrm{A}}\) is:
(a) 0
(b) 1
(c) A
(d) \(\overline{\mathrm{A}}\)
Answer:
(b) 1
Question 24.
A.A is:
(a) 0
(b) 1
(c) A
(d) \(\overline{\mathrm{A}}\)
Answer:
(c) A
![]()
Question 25.
A.0 is:
(a) 0
(b) 1
(c) A
(d) \(\overline{\mathrm{A}}\)
Answer:
(a) 0
Question 26.
\((\overline{\overline{\mathrm{A}})}\) is:
(a) 0
(b) 1
(c) A
(d) \(\overline{\mathrm{A}}\)
Answer:
(c) A
Question 27.
The symbol of NOT gate is:
(a) 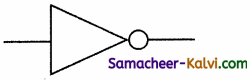
(b) 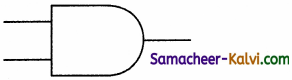
(c) 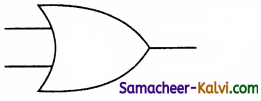
(d) 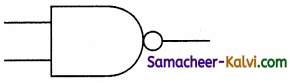
Answer:
(a) 
![]()
Question 28.
Choose the odd man out:
(a) F
(b) E
(c) D
(d) H
Answer:
(d) H
Question 29.
Choose the odd man out:
(a) AND
(b) OR
(c) NOR
(d) NOT
Answer:
(c) NOR
Question 30.
Match the following:
| (i) AND Operator | (a) Y = A + B |
| (ii) OR Operator | (b) Y= \(\overline{\mathrm{A}}\) |
| (iii) NOT Operator | (c) Y = \(\overline{\mathrm{A} \cdot \mathrm{B}}\) |
| (iv) NAND Operator | (d) Y = A . B |
Answer:
(a) (i) – (a); (ii) – (b); (iii) – (c); (iv) – (d)
(b) (i) – (b); (ii) – (a); (iii) – (c); (iv) – (d)
(c) (i) – (c); (ii) – (b); (iii) – (d); (iv) – (a)
(d) (i) – (d); (ii) – (a); (iii) – (b); (iv) – (c)
Answer:
(d) (i) – (d); (ii) – (a); (iii) – (b); (iv) – (c)
![]()
Question 31.
Match the following:
| (i) A + 0 | (a) A + B |
| (ii) A . \(\overline{\mathrm{A}}\) | (b) 1 |
| (iii) A + 1 | (c) 0 |
| (iv) A . \(\overline{\mathrm{A}}\) . B | (d) A |
(a) (i) – (d); (ii) – (c); (iii) – (b); (iv) – (a)
(b) (i) – (c); (ii) – (b); (iii) – (a); (iv) – (d)
(c) (i) – (d); (ii) – (b); (iii) – (a); (iv) – (c)
(d) (i) – (d); (ii) – (a); (iii) – (b); (iv) – (c)
Answer:
(a) (i) – (d); (ii) – (c); (iii) – (b); (iv) – (a)
Question 32.
Choose the incorrect pair:
| Column I |
Column II |
| (a) A + B | B + A |
| (b) A + (A . B) | A |
| (c) A + \(\overline{\mathrm{A}}\) . B | A . B |
| (d) \(\overline{\mathrm{A}+\mathrm{B}}\) | \(\overline{\mathrm{A}}\) . \(\overline{\mathrm{B}}\) |
Answer:
(c)
Question 33.
Assertion (A):
The NAND gate operates on OR gate followed by a NOT gate.
Reason (R):
It acts in the manner of the logical operation ‘AND’ followed by inversion.
(a) Both A and R are true, and R is the correct explanation for A.
(b) Both A and R are true, but R is not the correct explanation for A.
(c) A is true, but R is false.
(d) A is false, but R is true.
Answer:
(d) A is false, but R is true.
![]()
Question 34.
Assertion (A):
The XOR(exclusive-OR) gate acts in the same way as the logical ‘either/or’.
Reason (R):
The output is ‘true’ if either, but not both of the inputs are ‘true’.
(a) Both A and R are true, and R is the correct explanation for A.
(b) Both A and R are true, but R is not the correct explanation for A.
(c) A is true, but R is false.
(d) A is false, but R is true.
Answer:
(a) Both A and R are true, and R is the correct explanation for A.
Question 35.
Which is a basic electronic circuit which operates on one or more signals?
(a) Boolean algebra
(b) Gate
(c) Fundamental gates
(d) Derived gates
Answer:
(b) Gate
Question 36.
Which gate is called as the logical inverter?
(a) AND
(b) OR
(c) NOT
(d) XNOR
Answer:
(c) NOT
![]()
Question 37.
A + A = ?
(a) A
(b) O
(c) 1
(d) A
Answer:
(a) A
Question 38.
NOR is a combination of ?
(a) NOT(OR)
(b) NOT(AND)
(c) NOT(NOT)
(d) NOT(NOR)
Answer:
(a) NOT(OR)
![]()
Question 39.
NAND is called as ________ Gate.
(a) Fundamental Gate
(b) Derived Gate
(c) Logical Gate
(d) Electronic Gate
Answer:
(b) Derived Gate