Bhagya

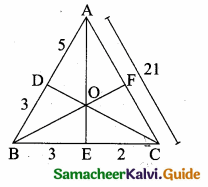
Students can download Maths Chapter 2 Measurements Ex 2.3 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 2 Measurements Ex 2.3

Miscellaneous practice problems

Question 1.
Two pipes whose lengths are 7 m 25 cm and 8 m 13 cm joined by welding and then a small piece 60 cm is cut from the whole. What is the remaining length of the pipe?
Solution:
Total length = 7 m 25 cm + 8 m 13 cm = 15 m 38 cm (or) 1538 cm
length detatched = 60 cm
Remaining length = 14 m 78 cm

Question 2.
The saplings are planted at a distance of 2 m 50 cm in the road of length 5 km by Saravanan. If he has 2560 saplings, how many saplings will be planted by him? how many saplings are left?
Solution:
Distance between two saplings = 2 m 50 cm = 250 cm
Total length of the road = 5000 m = 500000 cm

Question 3.
Put ✓ a mark in the circles which adds upto the given measure.

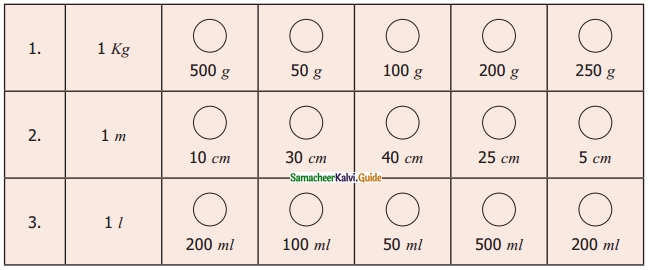
Solution:

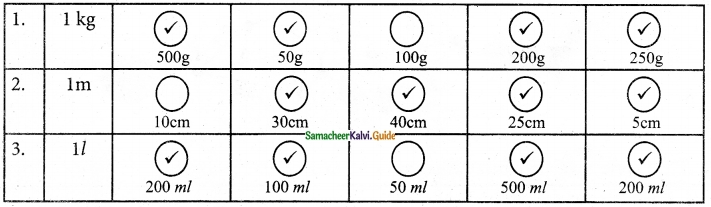
Question 4.
Make a calendar for the month of February 2020. (Hint: January 1st, 2020 is Wednesday)
Solution:
February 2020 is a leap year

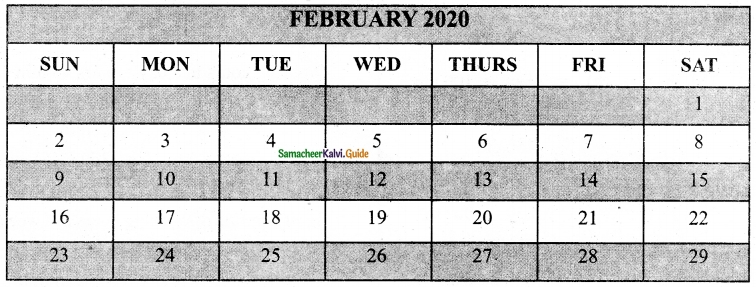
Question 5.
Observe and Collect the data for a minute

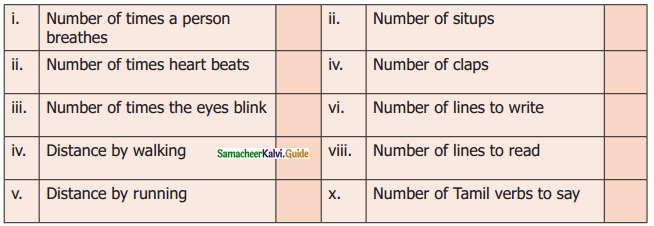
Solution:
Do your self.

Challenge Problems

Question 6.
A squirrel wants to eat the grains quickly. Help the Squirrel to find the shortest way to reach the grains. (Use your scale to measure the length of the line segments)

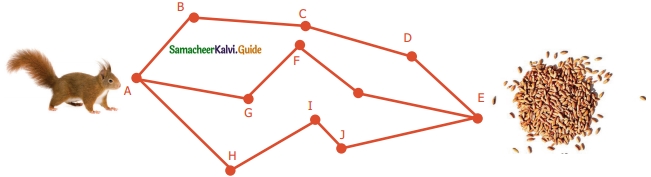
Solution:

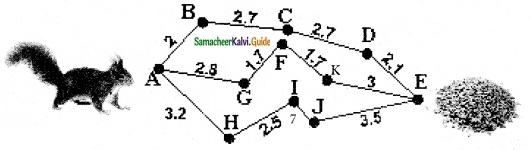
The Shortest way to reach the grains is the AGFKE path.

Question 7.
A room has a door whose measures are 1 m wide and 2 m 50 cm high.
Can we make a bed of 2 m and 20 cm in length and 90 cm wide into the room?
Solution:
Measures of the door length 2 m 50 cm width and lm (100 cm)
(i) Measures of the bed 2 m 20 cm width and 90 cm
Measures of the bed < measures of the door
∴ Yes, we can take the bed into the room.

Question 8.
A post office functions from 10 a.m. to 5.45 p.m. with a lunch break of 1 hour. If the post office works for 6 days a week, find the total duration of working hours in a week.
Solution:
Working hours in a day = 6 hrs 45 min
= (6 × 60 min) + 45 min
= (360 + 45) min
= 405 min
Total duration of working hours in a week
= 6 × 405 min
= 2430 min
= \(\frac{2430}{60}\)
= \(\frac{810}{20}\)
= 40 \(\frac{1}{2}\)
= 40 hours 30 minutes

Question 9.
Seetha wakes up at 5.20 a.m. She spends 35 minutes to get ready and travels 15 minutes to reach the railway station. If the train departs exactly at 6.00 am, will Seetha catch the train?
Solution:
No, Seetha will not catch the train
Time at Seetha wakes up = 5.20 am
Time is taken for getting ready = 35 min
Travelling time to station = 15 min
Reporting time = 5.20 am + 50 min = 6.10 am
But, the train departs exactly at 6.00 am
So, Seetha will not catch the train.

Question 10.
A doctor advised Vairavan to take one tablet every 6 hours once on the 1st day and once every 8 hours on the 2nd and 3rd day. If he starts to take 9.30 am the first dose. Prepare a time chart to take the tablet in railway time.
Solution:

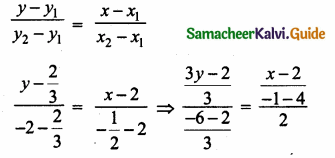
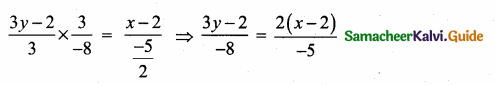
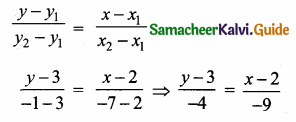
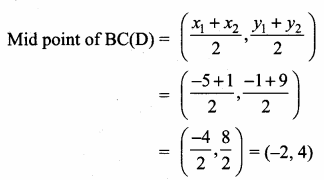
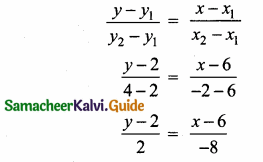
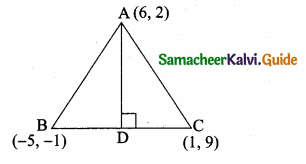
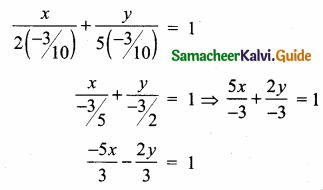
Students can download Maths Chapter 5 Coordinate Geometry Ex 5.3 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.3

Question 1.
Find the equation of a straight line passing through the mid-point of a line segment joining the points (1, -5), (4, 2) and parallel to (i) X axis (ii) Y axis
Solution:
Mid point of the line joining to points (1, -5), (4, 2)
Mid point of the line = (\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\))
= (\(\frac { 1+4 }{ 2 } \),\(\frac { -5+2 }{ 2 } \)) = (\(\frac { 5 }{ 2 } \),\(\frac { -3 }{ 2 } \))

(i) Any line parallel to X-axis. Slope of a line is 0.
Equation of a line is y – y₁ = m (x – x₁)
y + \(\frac { 3 }{ 2 } \) = 0 (x – \(\frac { 5 }{ 2 } \))
y + \(\frac { 3 }{ 2 } \) = 0 ⇒ \(\frac { 2y+3 }{ 2 } \) = 0
2y + 3 = 0

(ii) Equation of a line parallel to Y-axis is
x = \(\frac { 5 }{ 2 } \) ⇒ 2x = 5
2x – 5 = 0

Question 2.
The equation of a straight line is 2(x – y) + 5 = 0. Find its slope, inclination and intercept on the Y axis.
Solution:
Equation of a line is
2 (x – y) + 5 = 0
2 x – 2y + 5 = 0
-2y = -2x – 5
2y = 2x + 5
y = \(\frac { 2x }{ 2 } \) + \(\frac { 5 }{ 2 } \)
y = x + \(\frac { 5 }{ 2 } \)
Slope of line = 1
Y intercept = \(\frac { 5 }{ 2 } \)
tan θ = 1
tan θ = tan 45°
∴ angle of inclination = 45°

Question 3.
Find the equation of a line whose inclination is 30° and making an intercept -3 on the Y axis.
Solution:
Angle of inclination = 30°
Slope of a line = tan 30°
(m) = \(\frac{1}{\sqrt{3}}\)
y intercept (c) = -3
Equation of a line is y = mx + c
y = \(\frac{1}{\sqrt{3}}\) x – 3
\(\sqrt { 3 }\) y = x – 3 \(\sqrt { 3 }\)
∴ x – \(\sqrt { 3 }\) y – 3 \(\sqrt { 3 }\) = 0

Question 4.
Find the slope and y intercept of \(\sqrt { 3x }\) + (1 – \(\sqrt { 3 }\))y = 3.
Solution:
The equation of a line is \(\sqrt { 3 }\)x + (1 – \(\sqrt { 3 }\))y = 3
(1 – \(\sqrt { 3 }\))y = \(\sqrt { 3 }\) x + 3

Question 5.
Find the value of ‘a’, if the line through (-2,3) and (8,5) is perpendicular to y = ax + 2
Solution:
Given points are (-2, 3) and (8, 5)
Slope of a line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac { 5-3 }{ 8+2 } \) = \(\frac { 2 }{ 10 } \) = \(\frac { 1 }{ 5 } \)
Slope of a line y = ax + 2 is “a”
Since two lines are ⊥^r
m₁ × m₂ = -1
\(\frac { 1 }{ 5 } \) × a = -1 ⇒ \(\frac { a }{ 5 } \) = -1 ⇒ a = -5
∴ The value of a = -5

Question 6.
The hill in the form of a right triangle has its foot at (19,3). The inclination of the hill to the ground is 45°. Find the equation of the hill joining the foot and top.
Solution:
Slope of AB (m) = tan 45°
= 1
Equation of the hill joining the foot and the top is
y – y₁ = m(x – x₁)
y – 3 = 1 (x – 19)

y – 3 = x – 19
– x + y – 3 + 19 = 0
– x + y + 16 = 0
x – y – 16 = 0
The required equation is x – y – 16 = 0

Question 7.
Find the equation of a line through the given pair of points.
(i) (2,\(\frac { 2 }{ 3 } \)) and (\(\frac { -1 }{ 2 } \),-2)
(ii) (2,3) and (-7,-1)
Solution:
(i) Equation of the line passing through the point (2,\(\frac { 2 }{ 3 } \)) and (\(\frac { -1 }{ 2 } \),-2)


-5(3y – 2) = -8 × 2 (x – 2)
-15y + 10= -16 (x – 2)
-15y + 10= -16x + 32
16x – 15y + 10 – 32 = 0
16x – 15y – 22 = 0
The required equation is 16x – 15y – 22 = 0

(ii) Equation of the line joining the point (2, 3) and (-7, -1) is

-9 (y – 3) = -4 (x – 2)
-9y + 27 = – 4x + 8
4x – 9y + 27 – 8 = 0
4x – 9y + 19 = 0
The required equation is 4x – 9y + 19 = 0

Question 8.
A cat is located at the point(-6, -4) in xy plane. A bottle of milk is kept at (5,11). The cat wish to consume the milk travelling through shortest possible distance. Find the equation of the path it needs to take its milk.
Solution:

Equation of the line joining the point is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
\(\frac { y+4 }{ 11+4 } \) = \(\frac { x+6 }{ 5+6 } \)
\(\frac { y+4 }{ 15 } \) = \(\frac { x+6 }{ 11 } \)
15(x + 6) = 11(y + 4)
15x + 90 = 11y + 44
15x – 11y + 90 – 44 = 0
15x – 11y + 46 = 0
The equation of the path is 15x – 11y + 46 = 0

Question 9.
Find the equation of the median and altitude of AABC through A where the vertices are A(6,2), B(-5, -1) and C(1,9).
Solution:
(i) To find median


Equation of the median AD is

2(x – 6) = -8 (y – 2)
2x – 12= -8y + 16
2x + 8y – 28 = 0
(÷ by 2) x + 4y – 14 = 0
∴ Equation of the median is x + 4y – 14 = 0
Equation of the altitude is 3x + 5y – 28 = 0

(ii) To find the equation of the altitude

Slope of BC = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac { 9+1 }{ 1+5 } \)
= \(\frac { 10 }{ 6 } \) = \(\frac { 5 }{ 3 } \)
Slope of the altitude = – \(\frac { 3 }{ 5 } \)
Equation of the altitude AD is
y – y1 = m (x – x₁)
y – 2 = – \(\frac { 3 }{ 5 } \) (x – 6)
-3 (x – 6) = 5 (y – 2)
-3x + 18 = 5y – 10
-3x – 5y + 18 + 10 = 0
-3x – 5y + 28 = 0
3x + 5y – 28 = 0

Question 10.
Find the equation of a straight line which has slope \(\frac { -5 }{ 4 } \) and passing through the point (-1,2).
Solution:
Slope of a line (m) = \(\frac { -5 }{ 4 } \)
The given point (x₁, y₁) = (-1, 2)
Equation of a line is y – y₁ = m (x – x₁)
y – 2= \(\frac { -5 }{ 4 } \) (x + 1)
5(x + 1) = -4(y – 2)
5x +5 = -4y + 8
5x + 4y + 5 – 8 = 0
5x + 4y – 3 = 0
The equation of a line is 5x + 4y – 3 = 0

Question 11.
You are downloading a song. The percenty (in decimal form) of mega bytes remaining to get downloaded in x seconds is given by y = -0.1x + 1.
(i) graph the equation.
(ii) find the total MB of the song.
(iii) after how many seconds will 75% of the song gets downloaded?
(iv) after how many seconds the song will be downloaded completely?
Solution:
(i) y = – 0. 1x + 1

(ii) y = -0.1x + 1
x → seconds
y → Mega byte of the song.
The total mega byte of the song is at the beginning that is when x = 0
y = 1 mega byte

(iii) When 75% of song gets downloaded 25% remains.
In other words y = 25%
y = 0.25
By using the equation we get
0.25 = -0.1x + 1
0.1 x = 0.75
x = \(\frac { 0.75 }{ 0.1 } \) = 7.5 seconds

(iv) When song is downloaded completely the remaining percent is zero.
i.e y = 0
0 = -0.1 x + 1
0.1 x = 1 second
x = \(\frac { 1 }{ 0.1 } \) = \(\frac { 1 }{ 1 } \) × 10
x = 10 seconds

Question 12.
Find the equation of a line whose intercepts on the x and y axes are given below.
(i) 4, -6
(ii) -5, – 4
Solution:
(i) x intercept (a) = 4; y intercept (b) = – 6
Equation of a line is \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1
\(\frac { x }{ 4 } \) + \(\frac { y }{ -6 } \) = 1 ⇒ \(\frac { x }{ 4 } \) – \(\frac { y }{ 6 } \) = 1
(LCM of 4 and 6 is 12)
3x – 2y = 12
3x – 2y – 12 = 0
The equation of a line is 3x – 2y – 12 = 0

(ii) x intercept (a) = -5; y intercept (b) = \(\frac { 3 }{ 4 } \)
Equation of a line is \(\frac { x }{ a } \) + \(\frac { y }{ b } \) = 1 ⇒ \(\frac{x}{-5}+\frac{y}{\frac{3}{4}}=1\)
\(\frac { x }{ -5 } \) + \(\frac { 4y }{ 3 } \) = 1
(LCM of 5 and 3 is 15)
– 3x + 20y = 15
– 3x + 20y – 15 = 0
3x – 20y + 15 = 0
∴ Equation of a line is 3x – 20y + 15 = 0

Question 13.
Find the intercepts made by the following lines on the coordinate axes.
(i) 3x – 2y – 6 = 0
(ii) 4x + 3y + 12 = 0
Solution:
(i) 3x – 2y – 6 =0.
x intercept when y = 0
⇒ 3x – 6 = 0
⇒ x = 2
y intercept when x = 0
⇒ 0 – 2y – 6 = 0
⇒ y = -3
(ii) 4x + 3y + 12 = 0. x intercept when y = 0
⇒ 4x + 0 + 12 = 0
⇒ x = -3
y intercept when x = 0
⇒ 0 + 3y + 12 = 0
⇒ y = -4

Question 14.
Find the equation of a straight line.
(i) passing through (1,-4) and has intercepts which are in the ratio 2 : 5
(ii) passing through (-8, 4) and making equal intercepts on the coordinate axes.
Solution:
(i) Let the x-intercept be 2a and the y intercept 5 a
The equation of a line is
\(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1 ⇒ \(\frac { x }{ 2a } \) + \(\frac { y }{ 5a } \) = 1
The line passes through the point (1, -4)
\(\frac { 1 }{ 2a } \) + \(\frac { (-4) }{ 5a } \) = 1 ⇒ \(\frac { 1 }{ 2a } \) – \(\frac { 4 }{ 5a } \) = 1
Multiply by 10a
(L.C.M of 2a and 5a is 10a)
5 – 8 = 10a ⇒ -3 = 10a
a = \(\frac { -3 }{ 10 } \)
The equation of the line is

Multiply by 3
-5x – 2y = 3 ⇒ -5x – 2y – 3 = 0
5x + 2y + 3 = 0
The equation of a line is 5x + 2y + 3 = 0

(ii) Let the x-intercept andy intercept “a”
The equation of a line is
\(\frac { x }{ a } \) + \(\frac { y }{ a } \) = 1
The line passes through the point (-8, 4)
\(\frac { -8 }{ a } \) + \(\frac { 4 }{ a } \) = 1
\(\frac { -8+4 }{ a } \) = 1
-4 = a
The equation of a line is
\(\frac { x }{ -4 } \) + \(\frac { y }{ -4 } \) = 1
Multiply by -4
x + y = -4
x + y + 4 = 0
The equation of the line is x + y + 4 = 0

Students can download Maths Chapter 2 Measurements Ex 2.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 2 Measurements Ex 2.2

Question 1.
Say the time in two ways:

Solution:
(i) 10 : 15 hours; quarter past 10; 45 minutes to 11
(ii) 6 : 45 hours; quarter to 7; 45 minutes past 6
(iii) 4 : 10 hours; 10 minutes past 4; 50 minutes to 5
(iv) 3 : 30 hours; half-past 3; 30 minutes to 4
(v) 9 : 40 hours; 20 minutes to 10; 40 minutes past 9.

Question 2.
Match the following:

Solution:
(i) d
(ii) e
(iii) b
(iv) c
(v) a

Question 3.
Convert the following:
(i) 20 minutes into seconds
(ii) 5 hours 35 minutes 40 seconds into seconds
(iii) 3 ½ hours into minutes
(iv) 580 minutes into hours
(v) 25200 seconds into hours
Solution:
(i) 20 minutes into seconds:
1 min = 60 seconds
20 min = 20 × 60 seconds
= 1200 seconds

(ii) 5 hours 35 min 40 seconds into seconds
Solution:
1 hour = 60 min
1 min = 60 seconds
1 hour = 3600 seconds
5 hours = 5 × 3600 seconds
= 18000 seconds
35 min = 35 × 60 seconds
= 2100 seconds
5 hours 35 minutes 40 seconds
= (18000 + 2100 + 40) seconds
= 20140 seconds

(iii) 3 ½ hours into minutes
Solution:
1 hour = 60 minutes
3 ½ hours = 3 hours + 30 min
= (3 × 60 + 30) min
= (180 + 30)min
= 210 min

(iv) 580 minutes into hours
Solution:
1 hour = 60 min
580 min
= \(\frac{580}{60}\) hours
= \(\frac{290}{30}\) hours
= \(\frac{29}{3}\)
= 9 \(\frac{2}{3}\)
= 9 hours 40 min

(v) 25200 seconds into hours:
Solution:
25200 seconds = \(\frac{25200}{3600}\)
= \(\frac{126}{18}\) hours
= \(\frac{63}{9}\) hours
= 7 hours

Question 4.
The duration of electricity consumed by the farmer for his pump set on Monday and Tuesday was 7 hours 20 minutes 35 seconds and 3 hours 44 minutes 50 seconds respectively. Find the total duration of consumption of electricity.
Solution:
The total duration of electricity consumed on both days
= 7 hours 20 min 35 sec + 3 hours 44 min 50 sec
= (7 + 3) hours (20 + 44) min (35 + 50) sec
= 10 hours 64 min 85 seconds
= 11 hours 5 min 25 seconds

Question 5.
Subtract 10 hours 20 min 35 seconds from 12 hours 18 min 40 seconds.
Solution:
12 hours 18 min 40 seconds
= (12 × 3600) + (18 × 60) + 40 seconds
= 43200 + 1080 + 40 seconds
= 44320 seconds
10 hours 20 min 35 seconds
= (10 × 3600) + (20 × 60) + 35 seconds
= 36000 + 1200 + 35 seconds
= 37235 seconds
Difference:
44320 – 37235
= 7085
7085 seconds = (1 × 3600) + 3480 + 5 seconds
= 1 hour 58 minutes 5 seconds

Question 6.
Change the following into 12 hour format
(i) 02:00 hours
(ii) 08:45 hours
(iii) 21:10 hours
(iv) 11:20 hours
(v) 00:00 hours
Solution:
(i) 2 am
(ii) 08:45 am
(iii) 9:10 pm
(iv) 11:20 am
(v) 12 midrid

Question 7.
Change the following into 24-hour format.
(i) 3.15 am
( ii) 12.35 pm
(iii) 12.00 noon
(iv) 12.00 mid night
Solution:
(i) 03.15 hours
(ii) 12.35 hours
(iii) 12.00 hours
(iv) 24.00 hours

Question 8.
Calculate the duration of time
(i) from 5.30 am to 12.40 pm
(ii) from 1.30 pm to 10.25 pm
(iii) from 20.00 hours to 4.00 hours
(iv) from 17.00 hours to 5.15 hours
Solution:
(i) from 5.30 a.m. to 12 .40 p.m.
Duration of time from 5.30 a.m. to noon = 12 : 00 – 5 : 30 = 6 : 30 i.e 6 hours 30 minutes
From noon to 12.40 p.m the duration = 00 hours 40 minutes
Total duration = 6 hours 30 minutes + 00 hours 40 minutes
= 6 hours 70 minutes
= 6 hours + (60 + 10) minutes
= 6 hours + 1 hr 10 minutes
= 7 hours 10 minutes
∴ Duration of time from 5.30 am to 12.40 pm = 7 hours 10 minutes

(ii) From 1.30 pm to 10.25 pm
= (1.30 pm to 10.00 pm) + 25 min
= 8 hrs 30 min + 25 min
= 8 hrs 55 min

(iii) From 20.00 hours to 4.00 hours
= (20.00 hrs to 24.00 hrs) + (24.00 hrs to 4.00 hrs)
= 4 hrs + 4 hrs
= 8 hours

(iv) From 17.00 hrs to 5.15 hours
= (17.00 hrs to 05.00 hrs) + 15 min
= 12 hours + 15 min
= 12 hours 1.5 min

Question 9.
The departure and arrival timing of the Vaigai Superfast Express (No. 12635) from Chennai Egmore to Madurai Junction are given. Read the details and answer the following.

(i) At what time does the Vaigai Express start from Chennai and arrive at Madurai?
(ii) How many halts are there between Chennai and Madurai?
(iii) How long does the train halt at the Villupuram Junction?
(iv) At what time does the train come to Sholavandan?
(v) Find the journey time from Chennai Egmore to Madurai?
Solution:
(i) 13.40 hours – 21.20 hours
(ii) 8 halts
(iii) 5 minutes
(iv) 20.34 hours
(v) 7 hours 40 minutes

Question 10.
Manickam joined a chess class on 20.02.2017 and due to an exam, he left practice after 20 days. Again he continued to practice from 10.07.2017 to 31.03.2018. Calculate how many days did he practice?
Solution:
From the date of joining = 20 days From 10.07.2017 to 31.03.2018
July – 22
Aug – 31
Sep – 30
Oct – 31
Nov – 30
Dec – 31
Jan – 31
Feb – 28
Mar – 31
Total – 265
Total no of practice days = 265 + 20 = 285 days

Question 11.
A clock gains 3 minutes every hour. If the clock is set correctly at 5 am, find the time shown by the clock at 7 p.m?
Solution:
Time gained for 1 hour = 3 min
Time duration from 5 am to 7 pm = 14 hours
Time gained for 14 hours = 1 4 × 3 minutes
= 42 minutes
So, at 7 pm, the clock shows 7 hrs 42 minutes

Question 12.
Find the number of days between Republic day and Kalvi Valarchi Day in 2020.
Solution:
In 2020 Republic Day will be celebrated on 26th January and Kalvi Valarchi Day will be celebrated on 15th July.
Number of days between 26.01.2020 and 15.07.2020
January – 6 Days (from 26.01.2020)
February – 29 Days (2020 is a leap year)
March – 31 Days
April – 30 Days
May – 31 Days
June – 30 Days
July – 15 Days (upto 15.07.2020)
Total – 172 Days.
∴ Total number of days = 172

Question 13.
If the 11th of Jan 2018 is Thursday, what is the day on 20th July of the same year?
Solution:
Jan – 21
Feb – 28
Mar – 31
April – 30
May – 31
June – 30
July – 19
Total – 190 days
190 days = 27 weeks + 1 day
The required day is the first day after Thursday.
Therefore 20th July 2018 is Friday.

Question 14.
(i) Convert 480 days into years.
(ii) Convert 38 months into years
Solution:
(i) 480 days = \(\frac{480}{365}\)
= 1 year 115 days
= 1 year 3 months 25 days

(ii) 38 months = \(\frac{38}{12}\)
= 3 years 2 months

Question 15.
Calculate your age as on 01.06.2018
Solution:
My date of birth 20.11.1999
Convert in the format yyyy/mm/dd

My age is 18 yrs 6 months 11 days

Objective Type Questions

Question 16.
2 days = _____ hours.
(a) 38
(b) 48
(c) 28
(d) 40
Solution:
(b) 48

Question 17.
3 weeks = ……… days
(i) 21
(ii) 7
(iii) 14
(iv) 28
Solution:
(i) 21

Question 18.
The number of ordinary years between two consecutive leap years is _____.
(a) 4 years
(b) 2 years
(c) 1 year
(d) 3 years
Solution:
(d) 3 years

Question 19.
What time will it be 5 hours after 22:35 hours?
(i) 2:30 hours
(ii) 3:35 hours
(iii) 4:35 hours
(iv) 5:35 hours
Solution:
(ii) 3:35 hours

Question 20.
2\(\frac { 1 }{ 2 }\) years is equal to ______ months.
(a) 25
(b) 30
(c) 24
(d) 5
Solution:
(b) 30

Students can download Maths Chapter 2 Measurements Ex 2.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 2 Measurements Ex 2.1

Question 1.
Fill in the blanks.
(i) 250 ml + \(\frac{1}{2}\) ml = _____ l.
(ii) 150 kg 200 g + 55 kg 750 g = ____ kg ____ g.
(iii) 20 l – 1 l 500 ml = ____ l ___ ml
(iv) 450 ml × 5 = ____ l ____ ml.
(v) 50 Kg ÷ 100 g = ______
Solution:
(i) \(\frac{3}{4}\) l
(ii) 205 kg 950 g
(iii) 18 l 500 ml
(iv) 2l 250 ml
(v) 500

Question 2.
True or False.
(i) Pugazhenthi ate 100 g of nuts which is equal to 0.1 kg.
(ii) Meena bought 250 ml of buttermilk which is equal to 2.5 l.
(iii) Karkuzhali’s bag 1 kg 250 g and Poongkodi’s bag 2 kg 750 g. The total weight of their bags 4 kg.
(iv) Vanmathi bought 4 books each weighing 500 g. Total weight of 4 books is 2 kg.
(v) Gayathri bought 1 kg of birthday cake. She shared 450 g with her friends. The weight of cake remaining is 650 g.
Solution:
(i) True
(ii) False
(iii) True
(iv) True
(v) False

Question 3.
Convert into indicated units:
(i) 10 l and 50 ml into ml
(ii) 4 km and 300 m into m
(iii) 300 mg into g
Solution:
(i) 10 l and 50 ml
= 10 × 1000 ml + 50 ml
= (10000 + 50)ml
= 10050 ml

(ii) 4 km and 300 m
= 4 × 1000 + 300 m
= (4000 + 300) m
= 4300 m

(iii) 300 mg
= \(\frac{300}{1000}\)g
= 0.3 g

Question 4.
Convert into higher units:
(i) 13000 mm
(km, m, cm)
Solution:
13000 mm
= \(\frac{13000}{10}\) cm
= 1300 cm
= \(\frac{13000}{1000}\) m = 13000 mm
= 13 m
= \(\frac{13000}{1000000}\) km = 13000 mm
= 0.013 km

(ii) 8257 ml (kl, l)
Solution:
8257 ml
= \(\frac{8257}{1000}\) l
= 8.257 l
= 8257 ml
= \(\frac{8257}{1000000}\) kl
= 0.008257 kl

Question 5.
Convert into lower units:
(i) 15 km (m, cm, mm)
(ii) 12 kg (g, mg)
Solution:
(i) 15 km = 15 × 1000 m = 15000 m
15 km = 15 × 100000 cm
= 1500000 cm
15 km = 15 × 1000000 mm
= 15000000 mm

(ii) 12 kg (g, mg)
Solution:
12 kg = 12 × 1000 g
= 12000 g
12 kg = 12 × 1000000 mg
= 12000000 mg

Question 6.
Compare and put > or < or = in the following:
(i) 800 g + 150 g ____ 1 kg
(ii) 600 ml + 400 ml ____ 1 l
(iii) 6 m 25 cm ____ 600 cm + 25 cm
(iv) 88 cm ____ 8 m 8 cm
(v) 55 g ____ 550 mg
Solution:
(i) 800 g + 150g < 3kg
(ii) 600 ml + 400 ml = 1 l
(iii) 6 m 25 cm = 600 cm + 25 cm
(iv) 88 cm < 8 m 8 cm
(v) 55 g > 550 mg

Question 7.
Geetha brought 2 l and 250 ml of water in a bottle. Her friend drank 300 ml from it. How much of water is remaining in the bottle?
Solution:
Quantity of water Geetha brought = 2 l 250 ml
= 2 × 1000 + 250 ml
= 2000 + 250 ml
= 2,250 ml.
Quantity of water her friend drank = 300 ml
Remaining water = 2250 – 300 = 1950 ml. = 1 litre 950 ml.
Remaining water = 1 litre 950 ml.

Question 8.
Thenmozhi’s height is 1.25 m now she grows 5 cm every year. What would be her height after 6 years?
Solution:
Thenmozhi’s present height = 1.25 m
Rate of growth per year = 5 cm
Her growth in 6 years = 5 cm × 6 = 30 cm.
After 6 years her height = 1.25 m + 30 cm
= 1.25 × 100 + 30 cm
= 125 + 30 cm
= 155 cm.
∴ After 6 years Thenmozhi’s height will be 155 cm.

Question 9.
Priya bought 22\(\frac { 1 }{ 2 }\) kg of onion, Krishna bought 18\(\frac { 3 }{ 4 }\) kg of onion and Sethu bought 9 kg 250 g of onion. What is the total weight of onion did they buy?
Solution:
Priya’s weight = 22 kg 500 g
Krishna’s weight = 18 kg 750 g
Sethu’s weight = 9 kg 250 g
Total weight = 49 kg 1500 g = 49 kg + 1 kg 500 g = 50 kg + 500 g.
Their total weight = 50 kg 500 g.

Question 10.
Maran walks 1.5 km every day to reach the school while Mahizhan walks 1400 m. Who walks more distance and by how much?
Solution:
Distance which Maran walks = 1.5 km = 1.5 × 1000 m = 1500 m
The distance which Mahizhan walks = 1400 m.
Here 1500 > 1400
∴ Difference = 1500 – 1400 = 100 m.
∴ Maran walks more distance = 100 m.

Question 11.
In a JRC one day camp, 150 gm of rice and 15 ml oil are needed for a student. If there are 40 students to attend the camp how much rice and oil are needed?
Solution:
Rice needed for one student = 150 g
Rice needed for 40 students = 150 g × 40 = 6000 g. = \(\frac{6000}{1000}\) kg = 6 kg.
Oil needed for one student = 15 ml
Oil needed for 40 students = 15 ml × 40 = 600 ml. = \(\frac{600}{1000}\) l = 0.6 l
∴ For the camp 6 kg of rice and 0.6 l of oil needed.

Question 12.
In a school, 200 litres of lemon juice is prepared. If 250 ml lemon juice is given to each student, how many students get the juice?
Solution:
Total lemon juice prepared = 200 l = 200 × 1000 ml = 2,00,000 ml.
∴ Quantity of Lemon juice given to one student = 250 ml.
∴ Number of students can get = \(\frac{2,00,000}{250}\) = 800
∴ 800 students can get the lemon juice.

Question 13.
How many glasses of the given capacity will fill a 2 litre jug?
(i) 100 ml ___
(ii) 50 ml ____
(iii) 500 ml ____
(iv) 1 l ____
(v) 250 ml ____
Solution:
2 litre = 2 × 1000 ml = 2000 ml.
(i) 100 ml
\(\frac{2000}{100}=20\)
20 glasses of 100 ml.
(ii) 50 ml
\(\frac{2000}{50}=40\)
40 glasses of 50 ml
(iii) 500 ml
\(\frac{2000}{500}=4\)
4 glasses of 500 ml
(iv) 1 l
\(\frac{2 l}{1 l}=2\)
2 glasses of 1 l.
(v) 250 ml
\(\frac{2000}{250}=8\)
8 glasses of 250 ml can fill the jug.

Objective Type Questions

Question 14.
9 m 4 cm is equal to ……..
(i) 94 cm
(ii) 904 cm
(iii) 9.4 cm
(iv) 0.94 cm
Solution:
(ii) 904 cm

Question 15.
1006 g is equal to ____
(a) 1 kg 6 g
(b) 10 kg 6 g
(c) 100 kg 6 g
(d) 1 kg 600 g
Solution:
(a) 1 kg 6 g

Question 16.
Every day 150 l of water is sprayed in the garden. Water sprayed in a week is ……
(i) 700 l
(ii) 1000 l
(iii) 950 l
(iv) 1050 l
Solution:
(iv) 1050 l

Question 17.
Which is the greatest 0.007 g, 70 mg, 0.07 cg?
(a) 0.07 cg
(b) 0.007 g
(c) 70 mg
(d) all are equal
Solution:
(d) all are equal

Question 18.
7 km – 4200 m is equal to ……….
(i) 3 km 800 m
(ii) 2 km 800 m
(iii) 3 km 200 m
(iv) 2 km 200 m
Solution:
(ii) 2 km 800 m

Students can download Maths Chapter 4 Geometry Unit Exercise 4 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Unit Exercise 4

Question 1.
In the figure, if BD ⊥ AC and CE ⊥ AB , prove that
(i) ∆ AEC ~ ∆ADB
(ii) \(\frac { CA }{ AB } \) = \(\frac { CE }{ DB } \)

Solution:
(i) ∠AEC = ∠ADB = 90° ∠A is common By AA – Similarity.
∴ ∆AEC ~ ∆ADB
Since the two triangles are similar

(ii) \(\frac { AE }{ AD } \) = \(\frac { AC }{ AB } \) = \(\frac { EC }{ DB } \)
\(\frac { AC }{ AB } \) = \(\frac { CE }{ DB } \)

Question 2.
In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.

Solution:
In the given diagram ∆AEF and ∆ACD
∠AEF = ∠ACD = 90°
∠A is common
By AA – Similarity.
∴ ∆AEF ~ ∆ACD
\(\frac { AE }{ AC } \) = \(\frac { AF }{ AD } \) = \(\frac { EF }{ CD } \)
\(\frac { AE }{ AC } \) = \(\frac { EF }{ CD } \)
\(\frac { AE }{ AC } \) = \(\frac { 4 }{ x } \)
AC = \(\frac{\mathrm{AE} \times x}{4}\) …..(1)
In ∆EAB and ∆ECD,
∠EAB = ∠ECD = 90°
∠E is common
∆ ECD ~ ∆EAB
\(\frac { EC }{ EA } \) = \(\frac { ED }{ EB } \) = \(\frac { CD }{ AB } \)
\(\frac { EC }{ EA } \) = \(\frac { x }{ 6 } \)
EC = \(\frac{\mathrm{EA} \times x}{6}\) …….(2)
In ∆AEB; CD || AB
By Basic Proportionality Theorem
\(\frac { AB }{ CD } \) = \(\frac { EB }{ ED } \)
\(\frac { 6 }{ x } \) = \(\frac { 5+y }{ y } \)
x = \(\frac { 6y }{ y+5 } \) (EC = x) …….(3)
Add (1) and (2) we get
AC + EC = \(\frac{A E \times x}{4}+\frac{x \times E A}{6}\)
>
Substitute the value of x = 2.4 in (3)
2.4 = \(\frac { 6y }{ y+5 } \)
6y = 2.4y + 12
6y – 2.4y = 12 ⇒ 3.6 y = 12
y = \(\frac { 12 }{ 3.6 } \) = \(\frac { 120 }{ 36 } \) = \(\frac { 10 }{ 3 } \) = 3.3 cm
The value of x = \(\frac { 12 }{ 5 } \) (or) 2.4 cm and y = \(\frac { 10 }{ 3 } \) (or) 3.3 cm

Question 3.
O is any point inside a triangle ABC. The bisector of ∠AOB, ∠BOC and ∠COA meet the sides AB, BC and CA in point D, E and F respectively. Show that AD × BE × CF = DB × EC × FA.
Solution:
In ∆ABC the bisector meets AB at D, BC at E and AC at F.

The angle bisector AO, BO and CO intersect at “O”.
By Cevas Theorem
\(\frac { AD }{ DB } \) × \(\frac { BE }{ EC } \) × \(\frac { CF }{ AF } \) = 1
AD × BE × CF = DB × EC × AF
Hence it is proved

Question 4.
In the figure, ABC is a triangle in which AB = AC. Points D and E are points on the side AB and AC respectively such that AD = AE. Show that the points B, C, E and D lie on a same circle.

Solution:
∠B = ∠C (Given AB = AC)
AD + DB = AE + EC
BD = EC (Given AD = AE)
DE parallel BC Since AEC is a straight line.
∠AED + ∠CED = 180°
∠CBD + ∠CED = 180°
Similarly of the opposite angles = 180°
∴ BCED is a cyclic quadrilateral

Question 5.
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of 20 km/hr and the second train travels at 30 km/hr. After 2 hours, what is the distance between them?
Solution:
A is the position of the 1^st train.
B is the position of the 2^nd train.

Distance Covered in 2 hours
OA = 2 × 20 = 40 km
OB = 2 × 30 = 60 km
Distance between the train after 2 hours

Distance between
the two train = 72.11 km (or) 20\(\sqrt { 13 }\) km

Question 6.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that
(i) b² = p² + ax + \(\frac{a^{2}}{4}\)
(ii) c² = p² – ax + \(\frac{a^{2}}{4}\)
(iii) a² + c² = 2 p² + \(\frac{a^{2}}{2}\)
Solution:
(i) Given ∠AED = 90°

ED = x; DC = \(\frac { a }{ 2 } \)
(D is the mid point of BC)
∴ EC = x + \(\frac { a }{ 2 } \), BE = \(\frac { a }{ 2 } \) – x
∴ In the right ∆ AED
AD² = AE² + ED²
p² = h² + x²
In the right ∆ AEC,
AC² = AE² + EC²

(ii) In the right triangle ABE,
AB² = AE² + BE²
c² = h² + (\(\frac { a }{ 2 } \) – x)²
c² = h² + \(\frac{a^{2}}{4}\) + x² – ax
c² = h² + x² + \(\frac { 1 }{ 4 } \) a² – ax
c² = p² – ax + \(\frac{a^{2}}{4}\) (from 1)

(iii) By adding (2) and (3)
b² + c² = p² + ax + \(\frac{a^{2}}{4}\) + p² – ax + \(\frac{a^{2}}{4}\)
= 2p² + \(\frac{2a^{2}}{4}\)
= 2p² + \(\frac{a^{2}}{2}\)

Question 7.
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
Solution:
Let the height of the tree AD be “h”.

In ∆ ACD and ∆ BCF,
∠A = ∠B = 90°
∠C is common
∆ ACD ~ ∆ BCF by AA similarity
\(\frac { AD }{ BF } \) = \(\frac { AC }{ BC } \)
\(\frac { h }{ x } \) = \(\frac { 24 }{ 2 } \) = 6
h = 6x ………(1)
In ∆ ACE and ∆ ABF,
∠C = ∠B = 90°
∠A is common
∴ ∆ ACE ~ ∆ ABF
\(\frac { CE }{ BF } \) = \(\frac { AC }{ AB } \)
\(\frac { 2 }{ x } \) = \(\frac { 24 }{ 20 } \)
24x = 20 × 2
x = \(\frac{20 \times 2}{24}=\frac{5 \times 2}{6}=\frac{10}{6}\)
x = \(\frac { 5 }{ 3 } \)
Substitute the value of x in (1)
h = 6 × \(\frac { 5 }{ 3 } \) = 10 m
∴ Height of the tree is 10 m

Question 8.
An emu which is 8 ft tail is standing at the foot of a pillar which is 30 ft high. It walks away from the pillar. The shadow of the emu falls beyond emu. What is the relation between the length of the shadow and the distance from the emu to the pillar?
Solution:
Let the shadow of the emu AE be “x” and BE be “y” ED || BC

By basic proportionality theorem
\(\frac { AE }{ AB } \) = \(\frac { ED }{ BC } \)
\(\frac { x }{ x+y } \) = \(\frac { 8 }{ 30 } \)
30x = 8x + 8y
22x – 8y = 0
(÷ by 2) 11x – 4y = 0
11x = 4y
x = \(\frac { 4 }{ 11 } \) × y
x = \(\frac { 4 }{ 11 } \) × distance from the pillar to emu
Length of = \(\frac { 4 }{ 11 } \) × distance from the shadow the pillar to emu

Question 9.
Two circles intersect at A and B. From a point P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
Solution:
Proof:

A and B are the points intersecting the circles. Join AB.
∠P’PB = ∠PAB (alternate segment theorem)
∠PAB + ∠BAC = 180° …(1)
(PAC is a straight line)
∠BAC + ∠BDC = 180° …(2)
ABDC is a cyclic quadrilateral.
From (1) and (2) we get
∠P’PB = ∠PAB = ∠BDC
P’P and DC are straight lines.
PD is a transversal alternate angles are equal.
∴ P’P || DC.

Question 10.
Let ABC be a triangle and D, E, F are points on the respective sides AB, BC, AC (or their extensions).
Let AD : DB = 5 : 3, BE : EC = 3 : 2 and AC = 21. Find the length of the line segment CF.
Solution:

\(\frac { AD }{ DB } \) = \(\frac { 5 }{ 3 } \); \(\frac { BE }{ EC } \) = \(\frac { 3 }{ 2 } \); AC = 21
By Ceva’s theorem

Length of the line segment CF = 6 units

Students can download Maths Chapter 2 Introduction to Algebra Ex 2.2 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 2 Introduction to Algebra Ex 2.2

Question 1.
Find in the blanks.
(i) The algebraic statement of ‘f’ decreased by 5 is _______
(ii) The algebraic statement of ‘s’ divided by 5 is _______
(iii) The verbal statement of ‘2m – 10’ is _______
(iv) If A’s age is ‘n’ years now, 7 years ago A’s age was ______
(v) If ‘p – 5’ gives 12 then ‘p’ is ______
Solution:
(i) f – 5
(ii) \(\frac { s }{ 5 }\)
(iii) 10 less than 2 times m (or) Take away 10 from the product of 2 and m
(iv) n – 7
(v) 17
Hint: p – 5 = 12 ⇒ n = 12 + 5 = 17

Question 2.
Say True or False.
(i) 10 more to three times ‘c’ is ‘3c + 13’.
(ii) If the cost of 10 rice bags is ‘t’, then the cost of 1 rice bag is \(\frac { t }{ 10 }\)
(iii) The statements ‘x’ divided by 3 and 3 divided by ‘x’ are the same.
(iv) The product of ‘q’ and 20 is ’20q’
(v) 7 less to 7 times ‘y’ is ‘7 – 7y’
Solution:
(i) False
Hint: 3c + 10
(ii) True
(iii) False
(iv) True
(v) False
Hint: 7y – 7

Question 3.
Express the following verbal statement to an algebraic statement.
(i) ‘t’ is added to 100
(ii) 4 times ‘q’
(iii) 8 is reduced by ‘y’
(iv) 56 added to 2 times ‘x’
(v) 4 less to 9 times of ‘y’
Solution:
(i) t + 100
(ii) 4q
(iii) 8 – y
(iv) 2x + 56
(v) 9y – 4

Question 4.
Express the following algebraic statement to a verbal statement.
(i) x ÷ 3
(ii) 5n – 12
(iii) 11 + 10x
(iv) 70s
Solution:
(i) x divided by 3.
(ii) 12 less to 5 times n.
(iii) 11 added to 10 times x
(iv) 7 times s.

Question 5.
The teacher asked two students to write the algebraic statement for the verbal statement “8 more than a number”. Vetri wrote ‘8 + x’ but Maran wrote ‘8x’. Who gave the correct answer?
Solution:
Let the number be x; 8 more than the number = 8 + x.
Vetri gave the correct answer as 8 + x.

Question 6.
Answer the following questions.
(i) If ‘n’ takes the value 3 then find the value of ‘n + 10’?
(ii) If ‘g’ is equal to 300 what is the value of ‘g – 1’ and ‘g + 1’?
(iii) What is the value of ‘s’, if ‘2s – 6’ gives 30?
Solution:
(i) n = 3
n + 10 = 3 + 10 = 13

(ii) g = 300
g – 1 = 300 – 1
= 299
g + 1 = 300 + 1
=301

(iii) 2s – 6 = 30
2s = 30 + 6
2s = 36
s = 36/2
s = 18

Question 7.
Complete the table and find the value of ‘k’ for which ‘k/3’ gives 5.

Solution:

\(\frac{k}{3}\) = 5
k = 15

Question 8.
The value of ‘y’ in y + 7 = 13 is
(a) y = 5
(b) y = 6
(c) y = 7
(d) y = 8
Solution:
(b) y = 6
Hint: y = 13 – 7 = 6

Question 9.
6 less to ‘n’ gives 8 is represented as
(a) n – 6 = 8
(b) 6 – n = 8
(c) 8 – n = 6
(d) n – 8 = 6
Solution:
(a) n – 6 = 8

Question 10.
The value of ‘c’ for which \(\frac{3c}{4}\) gives 18 is
(a) c = 15
(b) c = 21
(c) c = 24
(d) c = 27
Solution:
(c) c = 24

Students can download Maths Chapter 1 Numbers Ex 1.6 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 1 Numbers Ex 1.6

Miscellaneous Practice Problems

Question 1.
Try to open my locked suitcase which has the biggest 5 digit odd number as the password comprising the digits 7, 5, 4, 3 and 8. Find the password.
Solution:
87543

Question 2.
As per the census of 2001, the population of four states are given below. Arrange the states in ascending and descending order of their population.

Solution:
Ascending Order: 6,85,48,437 < 7,21,47,030 < 7,26,26,809 < 9,12,76,115
Descending Order 9,12,76,115 > 7,26,26,809 > 7,21,47,030 > 6,85,48,437

Question 3.
Study the following table and answer the questions.

(i) How many tigers were there in 2011?
(ii) How many tigers were less in 2008 than in 1990?
(iii) Did the number of tigers increase or decrease between 2011 and 2014? If yes, by how much?
Solution:
(i) 1706
(ii) 2100
(iii) Yes, 2226 – 1706 = 520 tigers increased from 2011 to 2014

Question 4.
Mullaikodi has 25 bags of apples. In each bag, there are 9 apples. She shares them equally amongst her 6 friends. How many apples does each get? Are there any apples left over?
Solution:
No of apple bags = 25
Apples in each bag = 9
Total no of apples = 25 × 9 = 225
Apples shared among her 6 friends = 225 ÷ 6
So, among her 6 friends, each of them gets 37 apples and 3 apples are leftover.

Question 5.
Poultry has produced 15472 eggs and fits 30 eggs in a tray. How many trays do they need?
Solution:
No of eggs produced = 15472
No of eggs fits in a tray = 30
No of trays required = 15472 ÷ 30
Trays required = 515 + 1 (to fit the remaining 22 eggs) = 516
Quotient = 515
Remainder = 22

Challenging Problems

Question 6.
Read the table and answer the following questions.

(i) Write the Canopus star’s diameter in words, in the Indian and the International System.
(ii) Write the sum of the place values of 5 in Sirius star’s diameter in the Indian System.
(iii) Eight hundred sixty four million seven hundred thirty. Write in Indian System.
(iv) Write the diameter in words of Arcturus star in the International System
(v) Write the difference of the diameters of Canopus and Arcturus stars in the Indian and the International Systems.
Solution:
(i) 2,59,41,900
25,941,900
Indian System: Two crores fifty-nine lakh forty-one thousand nine hundred.
International System: Twenty-five million nine hundred forty-one thousand nine hundred.
(ii) 5,50,500
(iii) 864,000,730 (86,40,00,730)
(iii) Eighty-six crore forty lakh seven hundred thirty.
(iv) Nineteen million eight hundred eighty-eight thousand eight hundred. (19,888,800)
(v) Indian System: 60,53,100 – Sixty lakh fifty-three thousand one hundred International System: 6,053,100 – Six million fifty-three thousand one hundred.

Question 7.
Anbu asks Arivu Selvi to guess a five-digit odd number. He gives the following hints.
The digit in the 1000s place is less than 5
The digit in the 100s place is greater than 6
The digit in the 10s place is 8.
What is Arivu Selvi’s answer? Does she give more than one answer?
Solution:
There are more than one answers.
One of them is 54781
Some of the other numbers maybe 64783, 74785, 84787 and so on.

Question 8.
A Music concert is taking place in a stadium. A total of 7,689 chairs are to be put in rows of 90.
(i) How many rows will there be?
(ii) Will there be any chairs left over?
Solution:
Total no of chairs to be put = 7,689
Chairs in each row = 90
No of rows = 7689 ÷ 90
Hence, 84 + 1 = 85 rows are required to fill 7650 chairs
Chairs left over = 79 (If the no of rows = 84)

Question 9.
Round off the seven-digit number 29,75,842 to the nearest lakhs and ten lakhs. Are they the same?
Solution:
Yes. Both are same (30,00,000)

Question 10.
Find the 5 or 6 or 7 digit numbers from a newspaper or a magazine to get a rounded number to the nearest ten thousand.
Solution:
(i) 14276 \(\simeq\) 10000
(ii) 1,86945 \(\simeq\) 1,90000

Students can download Maths Chapter 1 Numbers Ex 1.5 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 1 Numbers Ex 1.5

Question 1.
Fill in the blanks.
(i) The difference between the smallest natural number and the smallest whole number is ……….
(ii) 17 × …….. = 34 × 17
(iii) When ……… is added to a number, it remains the same.
(iv) Division by ………. is not defined.
(v) Multiplication by ……… leaves a number unchanged.
Solution:
(i) 1
(ii) 34
(iii) Zero
(iv) 0
(v) 1

Question 2.
Say True or False.

1. 0 is the identity for multiplication of whole numbers.
2. The Sum of two whole numbers is always less than their product.
3. Both addition and multiplication are associative for whole numbers.
4. Both addition and multiplication are commutative for whole numbers.
5. Multiplication is distributive over addition for whole numbers.

Solution:

1. False
2. False
3. True
4. True
5. True

Question 3.
Name the property being illustrated in each of the cases given below.

1. 75 + 34 = 34 + 75
2. (12 × 4) × 8 = 12 × (4 × 8)
3. 50 + 0 = 50
4. 50 × 1 = 50
5. 50 × 42 = 50 × 40 + 50 × 2

Solution:

1. Commutativity for addition
2. Associativity for multiplication
3. Zero is the additive identity
4. One is the multiplicative identity
5. Distributivity of multiplication over addition

Question 4.
Use the properties of whole numbers and simplify.
(i) 50 × 102
(ii) 500 × 689 – 500 × 89
(iii) 4 × 132 × 25
(iv) 196 + 34 + 104
Solution:
(i) 50 × 102
= 50 × (100 + 2)
= (50 × 100) + (50 × 2)
= 5000 + 100 = 5100

(ii) 500 × 689 – 500 × 89
= 500 × (689 – 89)
= 344500 – 44500
= 300000
= 500 × (689 – 89)
= 500 × 600
= 3,00000

(iii) (4 × 132) × 25
= 4 × (132 × 25)
= (4 × 132) × 25
= 528 × 25
= 13200
= 4 × (132 × 25)
= 4 × 3300
= 13200

(iv) (196 + 34) + 104 = 196 + (34 + 104)
(196 + 34) + 104 = 230 + 104 = 334
196 + (34 + 104) = 196 + 138 = 334

Objective Type Questions

Question 5.
(53 + 49) × 0 is
(a) 102
(b) 0
(c) 1
(d) 53 + 49 × 0
Solution:
(b) 0

Question 6.
\(\frac{59}{1}\) is
(a) 1
(b) 0
(c) \(\frac{1}{59}\)
(d) 59
Solution:
(d) 59

Question 7.
The product of a non-zero whole number and its successor is always
(a) an even number
(b) an odd number
(c) zero
(d) none of these
Solution:
(a) an even number

Question 8.
The whole number that does not have a predecessor is
(a) 10
(b) 0
(c) 1
(d) none of these
Solution:
(b) 0

Question 9.
Which of the following expressions is not zero?
(a) 0 × 0
(b) 0 + 0
(c) \(\frac{2}{0}\)
(d) \(\frac{0}{2}\)
Solution:
(c) \(\frac{2}{0}\)
Dividing by 0 is not defined.

Question 10.
Which of the following is not true?
(a) (4237 + 5498) + 3439 = 4237 + (5498 + 3439)
(b) (4237 × 5498) × 3439 = 4237 × (5498 × 3439)
(c) 4237 + 5498 × 3439 = (4237 + 5498) × 3439
(d) 4237 × (5498 + 3439) = (4237 × 5498) + (4237 × 3439)
Solution:
(c) 4237 + 5498 × 3439 = (4237 + 5498) × 3439

Students can download Maths Chapter 1 Numbers Ex 1.4 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 1 Numbers Ex 1.4

Question 1.
Fill in the blanks.
(i) The nearest 100 of 843 is _____
(ii) The nearest 1000 of 756 is ______
(iii) The nearest 10,000 of 85654 is ______
Solution:
(i) 800.
The digit in tens place is 4 < 5
(ii) 1000.
The digit in hundred places is 7 ≥ 5
(iii) 90,000.
The digit in a thousand places is 5 ≥ 5

Question 2.
Say True or False
(i) 8567 is rounded off as 8600 to the nearest 10.
(ii) 139 is rounded off as 100 to the nearest 100.
(iii) 1,70,51,972 is rounded off as 1,70,00,000 to the nearest lakh.
Solution:
(i) False
Hint: In one’s place the digit is 7 ≥ 5. So 8580
(ii) True
Hint: In tens place, we have 3 < 5. So 100
(iii) False
Hint: In ten thousand places the digit is 5 ≥ 5. So 1,71,000,000

Question 3.
Round off the following to the given nearest place.
(i) 4,065; hundred
(ii) 44,555; thousand
(iii) 86,943; ten thousand
(iv) 50,81,739; lakh
(v) 33,75,98,482; ten crore
Solution:
(i) 4100
(ii) 45,000
(iii) 90,000
(iv) 51,00,000
(v) 30,00,00,000

Question 4.
Estimate the sum of 157826 and 32469 rounded off to the nearest ten thousand.
Solution:
= 157826 + 32469
= 190295
When rounded off to nearest ten thousand = 1,90,000

Question 5.
Estimate by rounding off each number to the nearest hundred.
(i) 8074 + 4178
(ii) 1768977 + 130589
Solution:
(i) 8074 + 4178 = 12,252
When rounded off to nearest hundred 12,300

(ii) 1768977 + 130589 = 18,99,566
When rounded off to nearest hundred = 18,99,600

Question 6.
The population of a city was 43,43,645 in the year 2001 and 46,81,087 in the year 2011. Estimate the increase in population by rounding off to the nearest thousands.
Solution:
Population in 2001 = 43,43,645
Population in 2011 = 46,81,087
Increase in population = 46,81,087 – 43,43,645 = 3,37,442
When rounded off to the nearest thousand = 3,37,000

Objective Type Questions

Question 7.
The number which on rounding off to the nearest thousand gives 11000 is
(a) 10345
(b) 10855
(c) 11799
(d) 10056
Solution:
(b) 10855

Question 8.
The estimation to the nearest hundredth of 76812 is
(a) 77000
(b) 76000
(c) 76800
(d) 76900
Solution:
(c) 76800
In tens place the digit is 1 < 5, So 76800

Question 9.
The number 9785764 is rounded off to the nearest lakh as
(a) 9800000
(b) 9786000
(c) 9795600
(d) 9795000
Solution:
(a) 9800000

Question 10.
The estimated difference of 167826 and 2765 rounded off to the nearest thousand is
(a) 180000
(b) 165000
(c) 140000
(d) 155000
Solution:
(b) 165000

Students can download Maths Chapter 1 Numbers Ex 1.3 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 1 Numbers Ex 1.3

Question 1.
Fill in the blanks.

1. If Arulmozhi saves ₹ 12 per day then she saves ₹ ____ in 30 days.
2. If a person ‘A’ earns ₹ 1800 in 12 days, then he earns ₹ ____ in a day.
3. 45 ÷ (7 + 8) – 2 = _____

Solution:

1. 12 × 30 = ₹ 360
2. \(\frac{1800}{12}=150\)
3. 45 ÷ 15 – 2 = 3 – 2 = 1

Question 2.
Say True or False

1. 3 + 9 × 8 = 96
2. 7 × 20 – 4 = 136
3. 40 + (56 – 6) ÷ 2 = 45

Solution:

1. False
   Hint: 3 + 9 × 8 = 3 + 72 = 75
2. True
   Hint: 7 × 20 – 4 = 140 – 4 = 136
3. False
   Hint: 40 + 50 ÷ 2 = 40 + 25 = 65

Question 3.
The number of people who visited the Public Library for the past 5 months was 1200, 2000, 2450, 3060 and 3200 respectively. How many people visited the library in the last 5 months.
Solution:
People visited the library for past 5 months = 1200 + 2000 + 2450 + 3060 + 3200 = 11910
Total people visited = 11910

Question 4.
Cheran had a bank savings of ₹ 7,50,250. He withdrew ₹ 5,34,500 for educational purposes. Find the balance amount in his account.
Solution:
Bank Savings of Cheran = ₹ 7,50,250
Withdrew Amount = ₹ 5,34,500
Balance Amount = ₹ 2,15,750

Question 5.
In a cycle factory, 1560 bicycles were manufactured every day. Find the number of bicycles manufactured in 25 days.
Solution:
Bicycles manufactured in one day = 1560
Bicycles manufactured in 25 days = 1560 × 25
= 39,000 bicycles

Question 6.
₹ 62,500 was equally distributed as a New Year bonus for 25 employees of a company. How much did each receive?
Solution:
Total amount = Rs 62500
Total number of employees = 25
Bonus amount received by each employee = Rs 62500 ÷ 25
= RS \(\frac{62500}{25}\)
= Rs 2500

Question 7.
Simplify the following numerical expressions:
(i) (10 + 17) ÷ 3
(ii) 12 – [3 – {6 – (5 – 1)}]
(iii) 100 + 8 ÷ 2 + {(3 × 2) -6 ÷ 2}
Solution:
(i) (10 + 17) ÷ 3
= 27 ÷ 3
= 9

(ii) 12 – [3 – {6 – (5 – 1)}]
= 12 – [3 – (6 – 4)]
= 12 – [3 – 2]
= 12 – 1
= 11

(iii) 100 + 8 ÷ 2 + {(3 × 2) – 6 ÷ 2}
= 100 + 8 ÷ 2 + {6 – 3}
= 100 + 8 ÷ 2 + 3
= 100 + 4 + 3
= 107

Objective Type Questions

Question 8.
The value of 3 + 5 – 7 × 1 is _____
(a) 5
(b) 7
(c) 8
(d) 1
Answer:
(d) 1
3 + 5 – 7 × 1 = 3 + 5 – 7 = 8 – 7 = 1

Question 9.
The value of 24 ÷ {8 – (3 × 2)} is ______
(a) 0
(b) 12
(c) 3
(d) 4
Answer:
(b) 12
24 ÷ {8 – 3 × 2} = 24 ÷ {8 – 6} = 24 ÷ 2 = 12

Question 10.
Use BIDMAS and put the correct operator in the box.
2 ….. 6 – 12 ÷ (4 + 2) = 10
(a) +
(b) –
(c) ×
(d) ÷
Answer:
(c) ×
2 ….. 6 – 12 ÷ 6 = 10
⇒ 2 ….. 6 – 2 = 10
⇒ 2 × 6 – 2 = 10