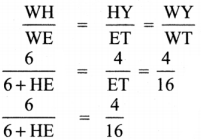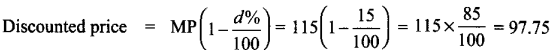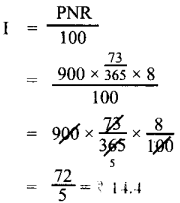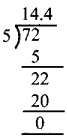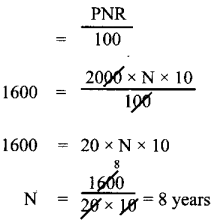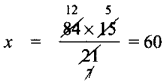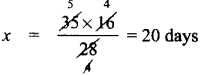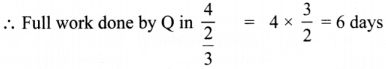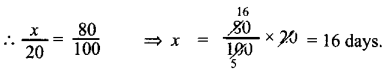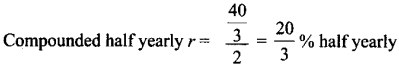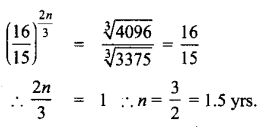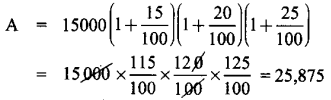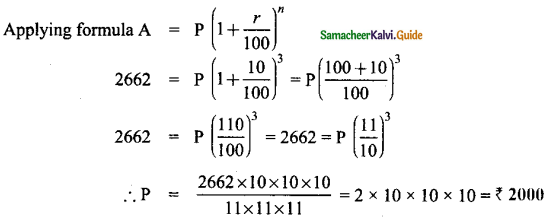Category: Class 8

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 Geometry InText Questions Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 5 Geometry InText Questions

Answer the following questions by recalling the properties of triangles:

Question 1.
The sum of the three angles of a triangle is _________ .
Answer:
180°

Question 2.
The exterior angle of a triangle is equal to the sum of the _______ angles to it.
Answer:
interior

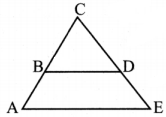
Question 3.
In a triangle, the sum of any two sides is ________ than the third side.
Answer:
greater

Question 4.
Angles opposite to equal sides are ________ and vice – versa.
Answer:
Equal

Question 5.
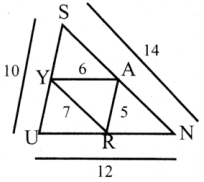
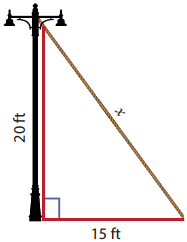
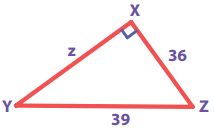
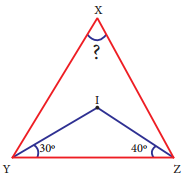
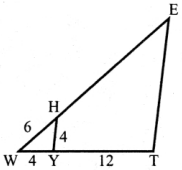
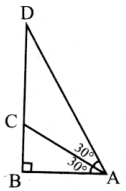
What is ∠A in the triangle ABC?

Answer:
The exterior angle = sum of interior opposite angles.
∴ ∠A + ∠C = 1500 in ∆ABC
But ∠C = 40°
[∵Vertically opposite angler are equal]
∴ ∠A + ∠C = 150°
⇒ ∠A + ∠40° = 150°
∠A = 150° – 40°
∠A = 1100

Try These (Text Book page No. 157)

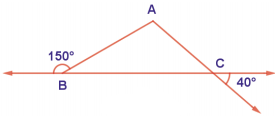
Identify the pairs of figures which are similar and congruent and write the letter pairs.

Answer:
Similar shapes:
(i) Wand L
(ii) B and J
(iii) A and G
(iv) B and J
(v) B and Y
(vi) E and N
(vii) H and Q
(viii) R and T
(ix) S and T

Congruent shapes:
(i) Z and I
(ii) J and Y
(iii) C and P
(iv) B and K
(v) R and S
(vi) I and Z
You can find more.

Try These (Text Book page No. 158)

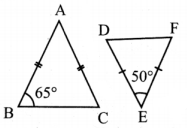
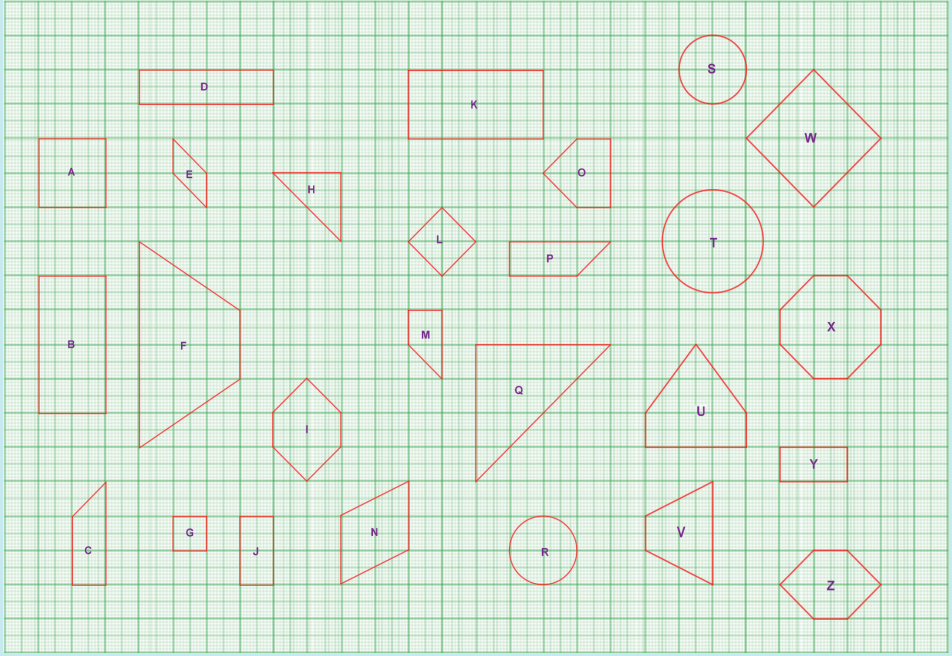
Question 1.
Match the following by their congruence property

Answer:
1. – (iv),
2. – (iii),
3. – (i),
4. – (ii)

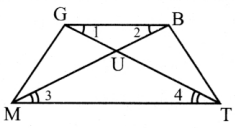
Think (Text Book page No. 160)

In the figure, DA = DC and BA = BC. Are the triangles DBA and DBC congruent? Why?

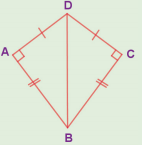
Answer:
Here AD = CD
AB = CB
DB = DB (common)
∆DB ≡ ∆DBC
[∵ By SSS congruency]
Also RHS rule also bind here to say their congruency.

Activity (Text Book page No. 169)

Question 1.
We can construct sets of Pythagorean triplets as follows.
Let m and n be any two positive integers (m > n):
(a, b, c) is a Pythagorean triplet if a = m² – n², b = 2mn and c = m² + n² (Think, why?)
Complete the table.

Answer:

Question 2.
Find all integer-sided right angled triangles with hypotenuse 85.
Answer:
(x + y)² – 2xy = 85²

Think (Text Book page No. 173)

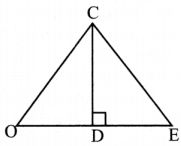
Question 1.
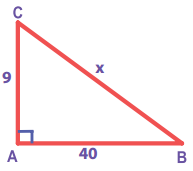
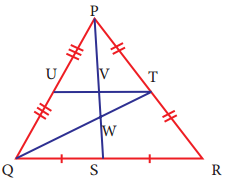
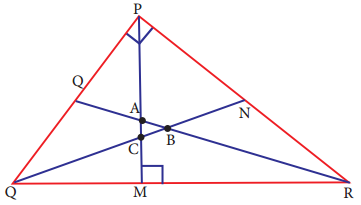
In any acute angled triangle, all three altitudes are inside the triangle. Where will be the orthocentre? In the interior of the triangle or in its exterior?

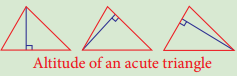
Answer:
Interior of the triangle

Question 2.
In any right angled triangle, the altitude perpendicular to the hypotenuse is inside the triangle; the other two altitudes are the legs of the triangle. Can you identify the orthocentre in this case?

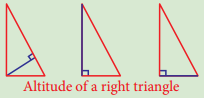
Answer:
Vertex containing 90°

Question 3.
In any obtuse angled triangle, the altitude connected to the obtuse vertex is inside the triangle, and the two altitudes connected to the acute vertices are outside the triangle. Can you identify the orthocentre in this case?

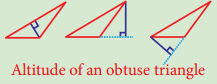
Answer:
Exterior of the triangle.

Try These (Text Book page No. 177)

Identify the type of segment required in each triangle:
(median, altitude, perpendicular bisector, angle bisector)

(i)

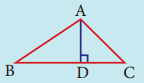
AD = _______
Answer:
AD = Altitude

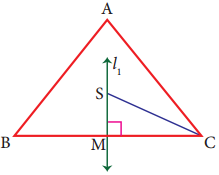
(ii)

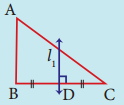
l₁ = _______
Answer:
l₁ = perpendicular bisector

(iii)

BD = _______
Answer:
BD = Median

(iv)

CD = _______
Answer:
CD = Angular bisector

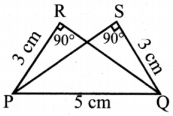
Think (Text Book page No. 187)

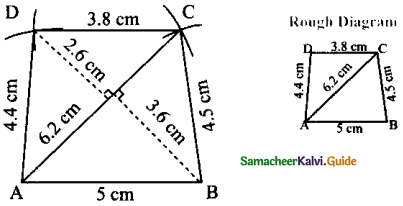
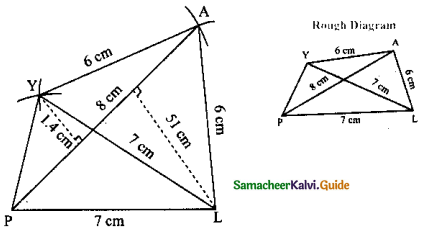
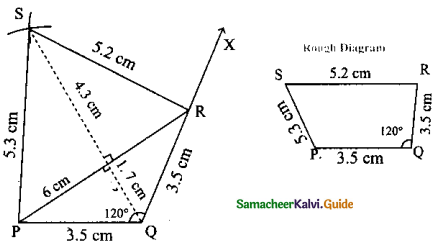
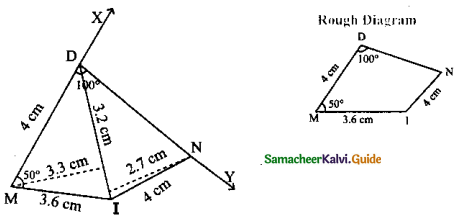
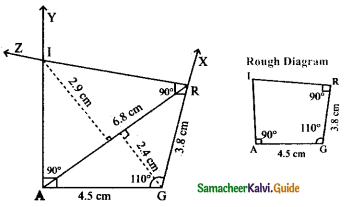
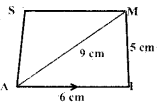
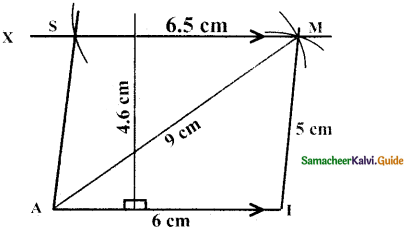
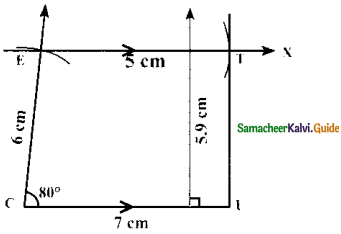
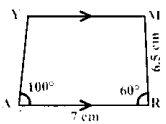
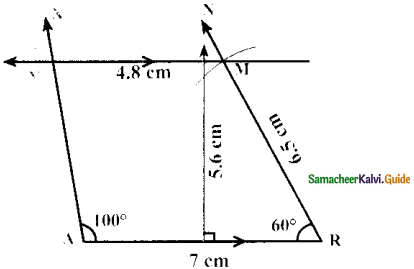
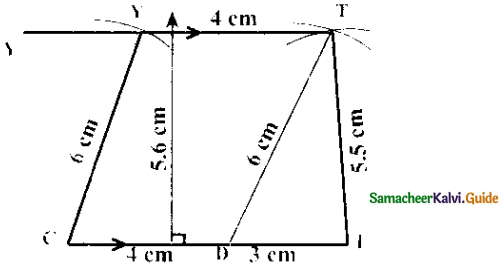
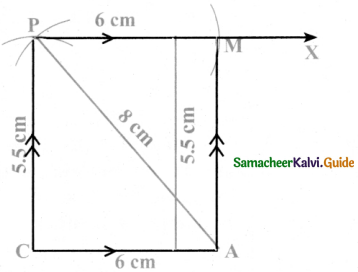
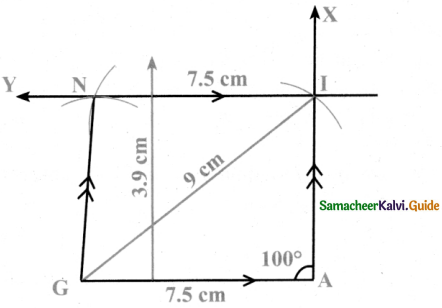
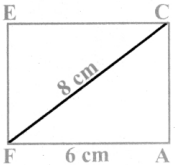
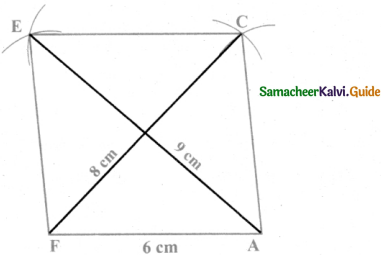
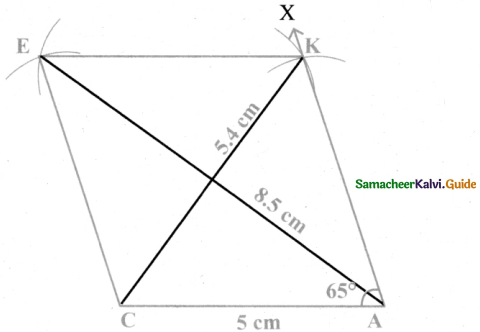
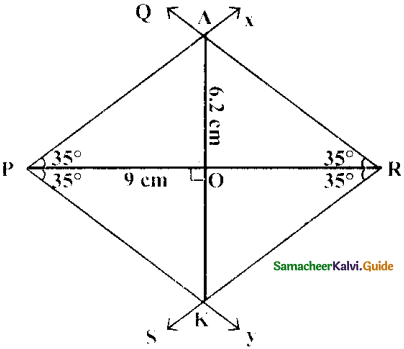
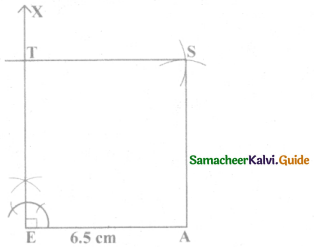
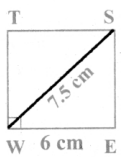
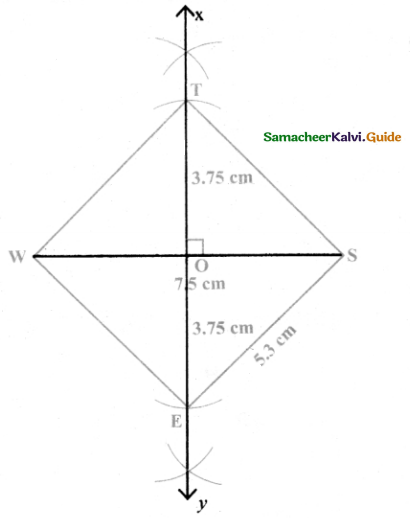
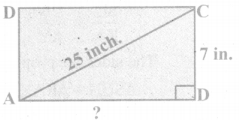
Is it possible to construct a quadrilateral PQRS with PQ = 5 cm, QR = 3cm, RS = 6cm, PS = 7cm and PR = 10cm. If not,why?
Answer:

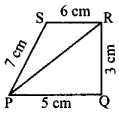
The lower triangle cannot be constructed as the sum of two sides 5 + 3 = 8 < 10 cm. So this quadrilateral cannot be constructed,

Try These (Text Book page No. 187)

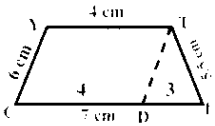
Question 1.
The area of the trapezium is ________ .
Answer:
\(\frac { 1 }{ 2 }\) × h × (a + b) sq. units

Question 2.
The distance between the parallel sides of a trapezium is called as ________ .
Answer:
its height

Question 3.
If the height and parallel sides of a trapezium are 5cm, 7cm and 5cm respectively, then
its area is ________ .
Answer:
30

Hints:
= \(\frac { 1 }{ 2 }\) × h × (a + b) sq. units
= \(\frac { 1 }{ 2 }\) × 5 × (7 + 5) = \(\frac { 1 }{ 2 }\) × 5 × 12 = 30 sq. cm

Question 4.
In an isosceles trapezium, the non-parallel sides are _________ in length.
Answer:
equal

Question 5.
To construct a trapezium, _________ measurements are enough.
Answer:
Four

Question 6.
If the area and sum of the parallel sides are 60 cm² and 12 cm, its height is ________ .
Answer:
10 cm
Hint:
Area of the trapezium = \(\frac { 1 }{ 2 }\) × h (a + b)
60 = \(\frac { 1 }{ 2 }\) × h × (12)
∴ h = \(\frac{60 \times 2}{12}\) = 10cm

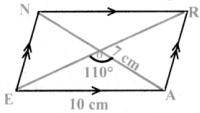
Activity (Text Book page No. 193 & 194)

Question 1.
A pair of identical 30° – 60° – 90° set-squares are needed for this activity. Place them as shown in the figure.

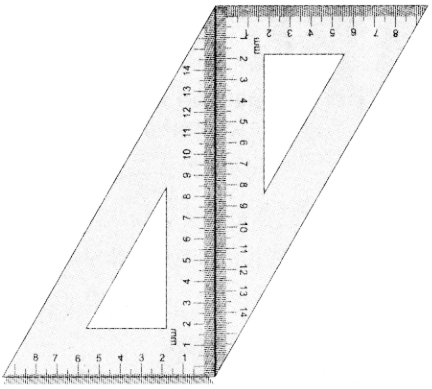
(i) What is the shape we get? It is a parallelogram.
Answer:

(ii) Are the opposite sides parallel?
Answer:
Yes

(iii) Are the opposite sides equal?
Ans:
Yes

(iv) Are the diagonals equal?
Answer:
No

(v) Can you get this shape by using any other pair of identical set-squares?
Answer:
Yes

Question 2.
We need a pair of 30° – 60° – 90° set- squares for this activity. Place them as shown in the figure.

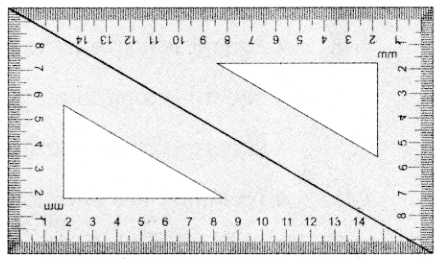
(i) What is the shape we get’?
Ans:
Rectangle

(ii) Is it a parallelogram?
Answer:
Yes

(iii) It is a quadrilateral; infact it is a rectangle. (How?)
Ans:
Opposits sides are equal.
All angles = 90°

(iii) What can we say about its lengths of sides, angles and diagonals?
Discuss and list them out.
Answer:
Opposite sides are equal
All angles are equal and are = 90°
Diagonals arc equal

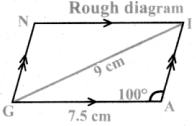
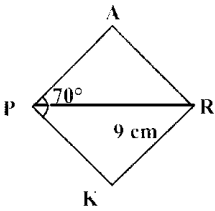
Question 3.
Repeat the above activity, this time with a pair of 45° – 45° – 90° set-squares.

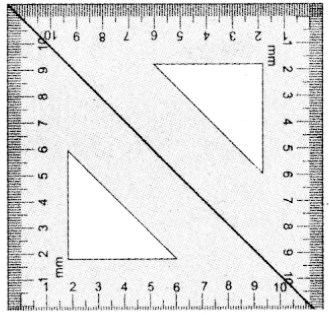
(i) How does the figure change now? Is it a parallelogram? It becomes a square! (How did it happen?)
Ans:
All sides are equal

(ii) What can we say about its lengths of sides, angles and diagonals? Discuss and list them out.
Answer:
All sides are equal
All angles = 90°
Diagonals equal

(iii) How does it differ from the list we prepared for the rectangle?
Answer:
All sides are equal.
Diagonals bisects each other.

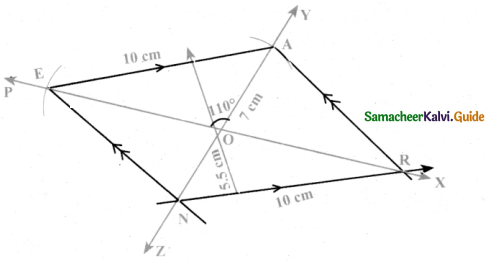
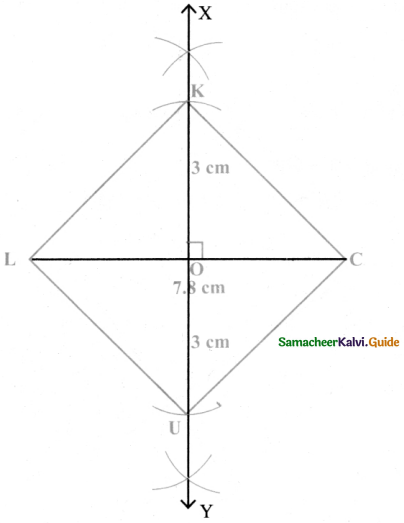
Question 4.
We again use four Identical 30° – 60° – 90° set- squares for this activity.
Note carefully how they are placed touching one another.

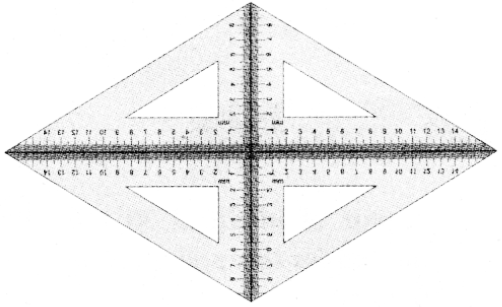
(j) Do we get a parallelogram now?
Answer:
Yes

(ii) What can we say about its lengths of sides, angles and diagonals’?
Answer:
All sides equal.
opposite sides arc equal and parallel.

(iii) What is special about their diagonals?
Answer:
Diagonals bisects perpendicularly.

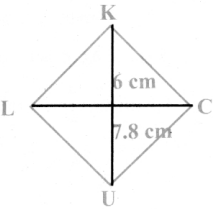
Try These (Text Book Page No. 195 & 196)

Question 1.
Say True or False:
(a) A square is a special rectangle.
Answer:
True

(b) A square is a parallelogram.
Answer:
True

(c) A square is a special rhombus.
Answer:
True

(d) A rectangle is a parallelogram
Answer:
True

Question 2.
Name the quadrilaterals

(a) Which have diagonals bisecting each other.
Answer:
Square, rectangle, parallelogram, rhombus.

(b) In which the diagonals are perpendicular bisectors of each other.
Answer:
Rhombus and square.

(c) Which have diagonals of different lengths.
Answer:
Parallelogram and Rhombus

(d) Which have equal diagonals.
Answer:
Rectangle, square.

(e) Which have parallel opposite sides.
Answer:
Square, Rectangle. Rhombus, parallelogram.

(f) In which opposite angles are equal.
Answer:
Square, rectangle. rhombus, parallelogram

Question 3.
Two sticks are placed on a ruled sheet as shown. What figure is formed if the four corners of the sticks are joined?

(a)

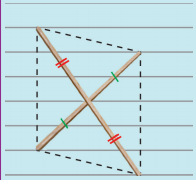
Two unequal sticks. Placed such that their midpoints coincide.
Answer:
parallelogram

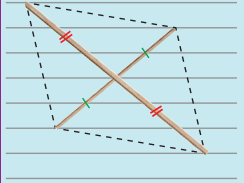
(b)

Two equal sticks. Placed such that their midpoints coincide.
Answer:
Rectangle

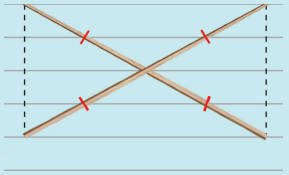
(c)

Two unequal sticks. Placed intersecting at mid points perpendicularly.
Answer:
Rhombus

(d)

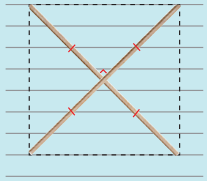
Two equal sticks. Placed intersecting at mid points perpendicularly.
Answer:
Square

(e)

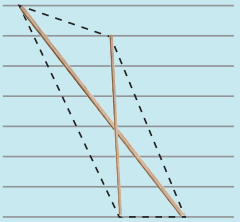
Two unequal sticks. Tops are not on the same ruling. Bottoms on the same ruling. Not cutting at the mid point of either.
Answer:
Quadrilateral

(f)

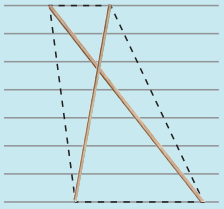
Two unequal sticks. Tops on the same ruling. Bottoms on the same ruling. Not necessarily cutting at
the mid point of either.
Answer:
Trapezium

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 Geometry Ex 5.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 5 Geometry Ex 5.4

I. Construct the following quadrilaterals with the given measurements and also find their area.

Question 1.
ABCD, AB = 5 cm, BC = 4.5 cm, CD = 3.8 cm, DA = 4.4 cm and AC = 6.2 cm.
Answer:
Given ABCD, AB = 5 cm, BC = 4.5 cm, CD = 3.8 cm, DA = 4.4 cm and AC = 6.2 cm.

Steps:

• Draw a line segment AB = 5 cm
• With A and B as centers drawn arcs of radii 6.2 cm and 4.5cm respectively and let them cut at C.
• Joined AC and BC.
• With A and C as centrers drawn arcs of radii 4.4cm and 3.8 cm respectively and let them at D.
• Joined AD and CD.
• ABCD is the required quadrilateral.

Calculation of Area:
Area of the quadrilateral ABCD = \(\frac { 1 }{ 2 }\) × d × (h₁1 + h₂) sq. units
= \(\frac { 1 }{ 2 }\) × 6.2 × (2.6 + 3.6)cm² = 3.1 × 6.2 = 19.22 cm²

Question 2.
PLAY, PL = 7cm, LA = 6cm, AY = 6cm, PA = 8cm and LY = 7cm.
Answer:
Given PLAY, PL = 7cm, LA = 6cm, AY = 6cm, PA = 8cm and LY = 7cm

Steps:

• Drawn a line segment PL = 7 cm
• With P and L as centers, drawn arcs of radii 8 cm and 6 cm respectively, let them cut at A.
• Joined PA and LA.
• With L and A as centers, drawn arcs of radii 7 cm and 6 cm respectively and let them cut at Y.
• Joined LY, PY and AY.
• PLAY is the required quadrilateral.

Calculation of Area:
Area of the quadrilateral PLAY = \(\frac { 1 }{ 2 }\) × d × (h₁ + h₂) sq. units = \(\frac { 1 }{ 2 }\) × 8 × (5.1 + 1.4) cm²
\(\frac { 1 }{ 2 }\) × 8 × 6.5 cm² = 26 cm²
Area of the quadrilateral = 26 cm²

Question 3.
PQRS, PQ = QR = 3.5 cm, RS = 5.2 cm, SP = 5.3 cm and ∠Q = 120°.
Answer:
Given PQ = QR = 3.5 cm, RS = 5.2 cm, SP = 5.3 cm and ∠Q = 120°

Steps:

• Draw a line segment PQ = 3.5 cm
• Made ∠Q = 120°. Drawn the ray QX.
• With Q as centre drawn an arc of radius 3.5 cm. Let it cut the ray QX at R.
• With R and P as centres drawn arcs of radii 5.2cm and 5.5 cm respectively and let them cut at S.
• Joined PS and RS.
• PQRS is the required quadrilateral.

Calculation of Area:
Area of the quadrilateral PQRS = \(\frac { 1 }{ 2 }\) × d × (h₁ + h₂) sq. units
= \(\frac { 1 }{ 2 }\) × 6 × (4.3 + 17)cm²
= 3 × 6cm²
= 18 cm²
Area of the quadrilateral PQRS = 18 cm²

Question 4.
MIND, MI = 3.6 cm, ND = 4 cm, MD = 4 cm, ∠M = 50° and ∠D = 100°.
Answer:
Given MI = 3.6 cm, ND = 4 cm, MD = 4 cm, ∠M = 50° and ∠D = 100°

Steps:

• Drawn a line segment MI = 3.6 cm
• At M on MI made an angle ∠IMX = 500
• Drawn an arc with center M and radius 4 cm let it cut MX it D
• At D on DM made an angle ∠MDY = 100°
• With I as center drawn an arc of radius 4 cm, let it cut DY at N.
• Joined DN and IN.
• MIND is the required quadrilateral.

Calculation of Area:
Area of the quadrilateral MIND = \(\frac { 1 }{ 2 }\) × d × (h₁ + h₂) sq. units = \(\frac { 1 }{ 2 }\) × 3.2 × (2.7 + 33) cm²
= \(\frac { 1 }{ 2 }\) × 3.2 × 6 cm² = 9.6 cm²
Area of the quadrilateral = 9.6 cm²

Question 5.
AGRI, AG = 4.5 cm, GR = 3.8 cm, ∠A = 60°, ∠G = 110° and ∠R = 90°.
Answer:
AG = 4.5 cm, GR = 3.8 cm, ∠A = 60°, ∠G = 110° and ∠R = 90°.

Steps:

• Draw a line segment AG = 4.5 cm
• At G on AG made ∠AGX = 110°
• With G as centre drawn an arc of radius 3.8 cm let it cut GX at R.
• At R on GR made ∠GRZ = 90°
• At A on AG made ∠GAY = 90°
• AY and RZ meet at I.
• AGRI is the required quadrilateral.

Calculation of Area:
Area of the quadrilateral AGRI = \(\frac { 1 }{ 2 }\) × d × (h₁ + h₂) sq. units = × 6.8 × (2.9 + 2.4) cm²
= \(\frac { 1 }{ 2 }\) × 6.8 × 5.3 × cm²
Area of the quadrilateral = 18.02 cm²

II. Construct the following trapeziums with the given measures and also find their area.

Question 1.
AIMS with \(\overline{\mathrm{AI}}\) || \(\overline{\mathrm{SM}}\), AI = 6cm, IM = 5cm, AM = 9cm and MS = 6.5cm.
Answer:
Given AI = 6 cm, IM = 5 cm
AM = 9 cm, and \(\overline{\mathrm{AI}}\) || \(\overline{\mathrm{SM}}\)
MS = 6.5 cm

Rough Diagram

Construction:
Steps:

• Draw a line segment AI = 6cm.
• With A and I as centres, draw arcs of radii 9 cm and 5 cm respectively and let them cut at M
• Join AM and IM.
• Draw MX parallel to AI
• With M as centre, draw an arc of radius 6.5 cm cutting MX at S.
• Join AS AIMS is the required trapezium.

Calculation of Area
Area of the trapezium AIMS = \(\frac { 1 }{ 2 }\) × h × (a + b) sq.units
= \(\frac { 1 }{ 2 }\) × 4.6 × (6 + 6.5)
= \(\frac { 1 }{ 2 }\) × 4.6 × 12.5
= 28.75 Sq.cm

Question 2.
CUTE with \(\overline{\mathrm{CD}}\) || \(\overline{\mathrm{ET}}\), CU = 7cm, ∠ UCE = 80° CE = 6cm and TE = 5cm.
Answer:
Given: In the trapezium CUTE,
CU = 7cm, ∠UCE = 80°,
CE = 6cm,TE = 5cm and \(\overline{\mathrm{CD}}\) || \(\overline{\mathrm{ET}}\)

Rough Diagram

Construction:
Steps:

• Draw a line segment CU = 7cm.
• Construct an angle ∠UCE = 80° at C
• With C as centre, draw an arc of radius 6 cm cutting CY at E
• Draw EX parallel to CU
• With E as centre, draw an arc 7 cm of radius 5 cm cutting EX at T
• Join UT. CUTE is the required trapezium.

Calculation of area:
Area of the trapezium CUTE = \(\frac { 1 }{ 2 }\) × h × (a + b) sq. units
= \(\frac { 1 }{ 2 }\) × 5.9 × (7 + 5)sq. units
= 35.4 sq.cm

Question 3.
ARMY with \(\overline{\mathrm{AR}}\) || \(\overline{\mathrm{YM}}\), AR = 7cm, RM = 6.5 cm ∠RAY = 100° and ∠ARM = 60°
Answer:
Given: In the trapezium ARMY
AR = 7cm,RM = 6.5cm,
∠RAY = 100° and ARM 60°, \(\overline{\mathrm{AR}}\) || \(\overline{\mathrm{YM}}\)

Rough Diagram

Construction:
Steps:

• Draw a line segment AR = 7 cm.
• Construct an angle ∠RAX = 100° at A
• Construct an angle ∠ARN = 60° at R
• With R as centre, draw an arc of radius 6.5 cm cutting RN at M
• Draw MY parallel to AR
• ARMY is the required trapezium.

Calcualtion of Area:
Area of the trapezium ARMY = \(\frac { 1 }{ 2 }\) × h × (a + b) sq. units
= \(\frac { 1 }{ 2 }\) × 5.6 × (7 + 4.8) sq. units
= \(\frac { 1 }{ 2 }\) × 5.6 × 1.18
= 33.04 sq.cm

Question 4.
CITY with \(\overline{\mathrm{CI}}\) || \(\overline{\mathrm{YT}}\), CI = 7cm, IT = 5 .5 cm, TY = 4cm and YC = 6cm.
Answer:
Given: In the trapezium CITY,
CI = 7cm,IT = 5.5cm, TY = 4cm
YC = 6cm, and \(\overline{\mathrm{CI}}\) || \(\overline{\mathrm{YT}}\)

Rough Diagram

Construction:
Steps:

• Draw a line segment CI = 7 cm.
• Mark a point D on CI such that CD = 4cm
• With D and I as centres, draw arcs of radii 6 cm and 5.5 cm respectively.
  Let them cut at T. Join DT and IT.
• With C as centre, draw an arc of radius 6 cm.
• Draw TY parallel to Cl. Let the line cut the previous arc at Y.
• Join CY. CITY is the required trapezium.

Construction of area:
Area of the trapezium CITY = \(\frac { 1 }{ 2 }\) × h × (a + b) sq. units
= \(\frac { 1 }{ 2 }\) × 5.5 × (7 + 4)sq.units
= \(\frac { 1 }{ 2 }\) × 5.5 × 11
= 30.25 sq.cm

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 Geometry Ex 5.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 5 Geometry Ex 5.5

I. Construct the following parallelograms with the given measurements and find their area.

Question 1.
ARTS, AR = 6cm, RT = 5cm and ∠ART = 70°.
Answer:
Given : In the Parallelogram ARTS,
AR = 6 cm, RT = 5 cm, and ∠ART = 70°

Rough Diagram

Construction:
Steps:

• Draw a line segment AR = 6 cm.
• Make an angle ∠ART = 70° at R on AR
• With R as centre, draw an arc of radius 5 cm cutting RX at T
• Draw a line TY parallel to AR through T.
• With T as centre, draw an arc of radius 6 cm cutting TY at S. Join AS
• ARTS is the required parallelogram.

Calculation of area:
Area of the parallelogram ARTS = b × h sq. units
= 6 × 4.7 = 28.2 sq.cm

Question 2.
CAMP, CA = 6cm, AP = 8cm and CP = 5.5cm.
Answer:
Given : In the parallelogram CAMP,
CA = 6 cm, AP = 8 cm, and CP = 5.5cm

Rough Diagram

Construction:
Steps:

• Draw a line segment CA = 6 cm.
• With C as centre, draw an arc of length 5.5 cm
• With A as centre, draw an arc of length 8 cm
• Mark the intersecting point of these two arcs as P
• Draw a line PX parallel to CA
• With P as centre draw an arc of radius 6 cm cutting PX at M. Join AM
• CAMP is the required parallelogram.

Calculation of area:
Area of the Parallelogram CAMP = b × h sq. units
= 6 × 5.5 = 33 sq.cm

Question 3.
EARN, ER = 10cm, AN = 7cm and ∠EOA = 110° where \(\overline{\mathrm{ER}}\) and \(\overline{\mathrm{AN}}\) intersect at O.
Answer:
Given: In the parallelogram EARN,
ER = 10 cm, AN = 7 cm, and LEOA = 1100
Where \(\overline{\mathrm{ER}}\) and \(\overline{\mathrm{AN}}\) intersect at 0

Rough diagram

Construction:
Steps:

• Draw a line segment PX. Mark a point O on PX
• Make an angle ∠EOA = 1100 on PX at O
• Draw arcs of radius 3.5 cm with O as centre on either side of PX. Cutting YZ on A and N
• With A as centre, draw an arc of radius 10 cm, cutting PX at E. Join AE
• Draw a line parallel to AE at N cutting PX at R. Join EN and AR
• EARN is the required parallelogram

Calculation of area:
Area of the Parallelogram EARN = b × h sq. units
= 10 × 5.5 = 55 sq.cm

Question 4.
GAIN, GA = 7.5cm, GI = 9cm and ∠GAI = 100°.
Answer:
Given : In the parallelogram GAIN,
GA = 7.5 cm, GI = 9 cm, and ∠GAI = 100°

Construction:
Steps:

• Draw a line segment GA = 7.5 cm.
• Make an angle GAI = 100° at A.
• With G as centre, draw an arc of radius 9 cm cutting AX at I. Join GI.
• Draw a line IY parallel to GA through I.
• With I as centre, draw an arc of radius 7.5 cm on IY cutting at N. Join GN
• GAIN is the required parallelogram.

Construction of area:
Area of the Parallelogram GAIN = b × h sq. units
= 7.5 × 39 = 29.25 sq. cm

II. Construct the following rhombuses with the given measurements and also find their area.

(i) FACE, FA = 6 cm and FC = 8 cm
Answer:
Given FA = 6 cm and FC = 8 cm

Rough Diagram

Steps:

• Drawn a line segment FA = 6 cm.
• With F and A as centres, drawn arcs of radii 8 cm and 6 cm respectively and let them cut at C.
• Joined FC and AC.
• With F and C as centres, drawn arcs of radius 6 cm each and let them cut at E.
• Joined FE and EC.
• FACE is the required rhombus.

Calculation of Area :
Area of the rhombus = \(\frac { 1 }{ 2 }\) × d₁ × d₂ sq.units = \(\frac { 1 }{ 2 }\) × 8 × 9 sq.units = 36 cm

(ii) CAKE, CA = 5 cm and ∠A = 65°
Answer:
Given CA = 5 cm and ∠A = 65°

Rough Diagram

Steps:

• Drawn a line segment CA = 5 cm.
• At A on AC, made ∠CAX = 65°
• With A as centre, drawn arc of radius 5 cm. Let it cut AX at K.
• With K and C as centres, drawn arcs of radius 5 cm each and let them cut at E.
• Joined KE and CE.
• CAKE is the required rhombus.

Calculation of Area:
Area of the rhombus = \(\frac { 1 }{ 2 }\) × d₁ × d₂ sq.units
= \(\frac { 1 }{ 2 }\) × 54 × 85cm²
= 22.95 cm²

(iii) LUCK, LC = 7.8 cm and UK = 6 cm
Answer:
Given LC = 7.8 cm and UK = 6 cm

Rough Diagram

Steps:

• Drawn a line segment LC = 7.8 cm.
• Drawn the perpendicular bisector XY to LC. Let it cut LC at ‘O’
• With O as centres, drawn arc of radius 3 cm on either side of O which cut OX at K and OY at U.
• Joined LU, UC, CK and LK.
• UCK is the required rhombus.

Calculation of Area:
Area of the rhombus = \(\frac { 1 }{ 2 }\) × d₁ × d₂ sq.units
= \(\frac { 1 }{ 2 }\) × 7.8 × 6 cm² = 23.4 cm²

(iv) PARK, PR = 9 cm and ∠P = 70°
Answer:
Given PR = 9 cm and ∠P = 70°

Rough Diagram

Steps:

• Drawn a line segment PR = 9 cm.
• At P, made ∠RPX ∠RPY = 35° on either side of PR.
• At R, made ∠PRQ = ∠PRS = 35° on either side of PR
• Let PX and RQ cut at A and PY and RS at K.
• PARK is the required rhombus

Constructon of Area:
Area of the rhombus = \(\frac { 1 }{ 2 }\) × d₁ × d₂ sq.units = \(\frac { 1 }{ 2 }\) × 9 × 6.2 cm²
= 27.9 cm²

III. Construct the following rectangles with the given measurements and also find their area.

(i) HAND,HA = 7cm and AN = 4 cm
Answer:
Given HA = 7cm and AN = 4 cm

Rough Diagram

Steps:

• Drawn a line segment HA = 7 cm.
• At H, constructed HX ⊥ HA.
• With H as centre, drawn an arc of radius 4 cm and let it cut at HX at D.
• With A and D as centres, drawn arcs of radii 4 cm and 7 cm respectively and let them cut at N.
• Joined AN and DN.
• HAND is the required rectangle.

calculation of’ area :
Area of the rectangle HAND = l × b sq.units
= 7 × 4 cm²
= 28 cm²

(ii) LAND, LA = 8cm and AD = 10 cm
Answer:
Given LA = 8cm and AD = 10 cm

Sleps :

• Drawn a line segment LA = 8 cm.
• At L, constructed LX ⊥ LA.
• With A as centre, drawn an arc of radius 10 cm and let it cut at LX at D.
• With A as centre and LD as radius drawn an arc. Also with D as centre and LA as radius drawn another arc. Let then cut at N.
• Joined DN and AN.
• LAND is the required rectangle.

Calcualtion of arca :
Area of the rectangle LAND = l × b sq.units
= 8 × 5.8 cm²
= 46.4 cm²

IV. Construct the following squares with the given measurements and also find their area.

(i) EAST, EA = 6.5 cm
Answer:
Given side = 6.5 cm

Rough diagram

Steps:

• Drawn a line segment EA = 6.5 cm.
• At E, constructed EX⊥ EA.
• With E as centre, drawn an arc of radius 6.5 cm and let it cut EX at T.
• With A and T as centre drawn an arc of radius 6.5 cm each and let them cut at S.
• Joined TS and AS.
• EAST is the required square.

Calcualtion of Area:
Area of the square EAST = a² sq.units
= 6.5 × 6.5 cm²
= 42.25 cm²

(ii) WEST, WS = 7.5 cm
Answer:
Given diagonal = 7.5 cm

Rough Diagram

Steps:

• Drawn a line segment WS = 7.5 cm.
• Drawn the perpendicular bisector XY to WS. Let it bisect BS at O.
• With O as centre, drawn an arc of radius 3.7 cm on either side of O which cut OX at T and OY at E
• Joined BE, ES, ST and BT.
• WEST is the required square.

Calculation of Area:
Area of the square WEST = a² sq.units
= 5.3 × 53 cm²
= 28.09 cm².

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 Geometry Ex 5.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 5 Geometry Ex 5.3

Question 1.
In the figure, given that ∠1 = ∠2 and ∠3 ≡ ∠4. Prove that ∆ MUG ≡ ∆TUB.

Answer:

Statements	Reasons
1. In △MUG and △TUG Mu = TU	∠3 = ∠4, opposite sides of equal angles
2. UG = UB	∠1 = ∠2 Side opposite to equal angles are equal
3. ∠GUM = ∠BUT	Vertically opposite angle
4. ∆MUG ≡  ∆TUG	SAS criteria By 1,2 and 3

Question 2.
From the figure, prove that ∆SUN ~ ∆RAY.

Answer:
Proof: from the ∆ SUN and ∆RAY
SU = 10
UN = 12
SN = 14
RA = 5
AY = 6
RY = 7

From (1), (2) and (3) we have

The sides are proportional
∴ ∆SUN ~ ∆RAY

Question 3.
The height of a tower is measured by a mirror on the ground at R by which the top of the tower’s reflection is seen. Find the height of the tower. If ∆PQR ~ ∆STR

Answer:
The image and its reflection make similar shapes
∴ ∆PQR ~ ∆STR

⇒ \(\frac{h}{8}=\frac{60}{10}\)
h = \(\frac{60}{10}\) × 8
= 48 feet
∴ Height of the tower = 48 feet.

Question 4.
Find the length of the support cable required to support the tower with the floor.

Answer:
From the figure, by Pythagoras theorem,
x² = 20² + 15²
= 400 + 225 = 625
x² = 25² ⇒ x = 25ft.
∴ The length of the support cable required to support the tower with the floor is 25ft.

Question 5.
Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Give reason.
Answer:

Take the sides of a right angled triangle ∆ABC as
a = 7 inches
b = 25 inches
c = ?
By Pythagoras theorem,
b² = a² + c²
25² = 7² + c²
⇒ c² = 25² – 7² = 625 – 49 = 576
∴ c² = 24²
⇒ c = 24 inches
∴ Width of TV cabinet is 20 inches which is lesser than the width of the screen ie.24 inches.
∴ The TV will not fit into the cabinet.

Challenging Problems

Question 6.
In the figure, ∠TMA ≡∠IAM and ∠TAM ≡ ∠IMA. P is the midpoint of MI and N is the midpoint of AI. Prove that Δ PIN ~ Δ ATM.

Answer:
proof:

Question 7.
In the figure, if ∠FEG ≡ ∠1 then, prove that DG² = DE.DF.

Answer:
Proof:

Question 8.
The diagonals of the rhombus is 12 cm and 16 cm. Find its perimeter. (Hint: the diagonals of rhombus bisect each other at right angles).
Answer:

Here AO = CO = 8cm
BO = DO = 6cm
(∴the diagonals of rhombus bisect each other at right angles)
∴ In ∆ AOB, AB² = AO² + OB²
= 8² + 6² = 64 + 36
= 100 = 10²
∴ AB = 10
Since it is a rhombus, all the four sides are equal.
AB = BC = CD = DA
∴ Its Perimeter = 10 + 10 + 10 + 10 = 40 cm

Question 9.
In the figure, find AR.

Answer:
∆ AFI, ∆ FRI are right triangles.
By Pythagoras theorem,
AF² = AI² – FI²
= 25² – 15²
= 625 – 225 = 400 = 20²
∴ AF = 20ft.
FR² = RI² – FI²
= 17² – 15² = 289 – 225 = 64 = 8²
FR = 8ft.
∴ AR = AF + FR
= 20 + 8 = 28 ft.

Question 10.
In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following.
(i) IF DE = 44, then DM = ?
(ii) IFPD=12, then PN= ?
(iii) IfDO = 8, then PD = ?
(iv) IF 0E = 36 then EP = ?

Answer:
Given DN, EO, FM are medians.
∴ FN = EN
DO = FO
EM = DM

(i) If DE = 44,then
DM = \(\frac{44}{2}\) = 22
DM = 22

(ii) If PD = 12,PN = ?
\(\frac{P D}{P N}=\frac{2}{1}\)
\(\frac{12}{\mathrm{PN}}=\frac{2}{1}\) ⇒ PN = \(\frac{12}{2}\) = 6.
PN = 6

(iii) If DO = 8, then
FD = DO + OF
= 8 + 8
FD = 16

(iv) If OE = 36

PE = 24

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 Geometry Ex 5.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 5 Geometry Ex 5.2

Question 1.
Fill in the blanks:
(i) If in a ∆ PQR, PR² = PQ² + QR², then the right angle of ∆ PQR is at the vertex _______ .
Answer:
Q
Hint:

(ii) If ‘l‘ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l² = _______ .
Answer:
n² – m²
Hint:

(iii) If the sides of a triangle are in the ratio 5:12:13 then, it is _______ .
Answer:
a right angled triangle
Hint:
13² = 169
5² = 25
12² = 144
169 = 25 + 144
∴ 13² = 5² + 12²

(iv) The medians of a triangle cross each other at _______ .
Answer:
Centroid

(v) The centroid of a triangle divides each medians in the ratio _______ .
Answer:
2 : 1

Question 2.
Say True or False.
(i) 8, 15, 17 is a Pythagorean triplet.
Answer:
True
Hint:
17² = 289
15² = 225
8² = 64
64 + 225 = 289 ⇒ 17² = 15² + 8²

(ii) In a right angled triangle, the hypotenuse is the greatest side.
Answer:
True
Hint:

(iii) In any triangle the centroid and the incentre are located inside the triangle.
Answer:
True

(iv) The centroid, orthocentre, and incentre of a triangle are collinear.
Answer:
True

(v) The incentre is equidistant from all the vertices of a triangle.
Answer:
False

Question 3.
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem.
(i) 8, 15, 17
Answer:
Take a = 8 b = 15 and c = 17
Now a² + b² = 8² + 15² = 64 + 225 = 289
172 = 289 = c²
∴ a² + b² = c²
By the converse of Pythagoras theorem, the triangle with given measures is a right angled triangle.
∴ Ans: yes

(ii) 12, 13, 15
Answer:
(ii) 12, 13. 15
Take a = 12,b = 13 and c = 15
Now a² + b² = 12² + 13² = 144 + 169 = 313
15² = 225 ≠ 313
By the converse of Pythagoras theorem, the triangle with given measures is not a right angled triangle.
∴ Ans: No.

(iii) 30, 40, 50
Answer:
Take a = 30, b = 40 and c = 50
Now a² + b² = 30² + 40² = 900 + 1600 = 2500
C² = 50² = 2500
∴ a² + b² = c²
By the converse of Pythagoras theorem, the triangle with given measures is a right
angled triangle.
∴ Ans: yes

(iv) 9, 40, 41
Answer:
Take a = 9, b = 40 and c = 41
Now a² + b² = 9² + 40² = 81 + 1600 = 1681
c² = 41² = 1681
∴ a² + b² = c²
By the converse of Pythagoras theorem, the triangle with given measures is a right
angled triangle.
∴ Ans: yes

(v) 24, 45, 51
Answer:
Take a = 24,b = 45 and c = 51
Now a² + b² = 24² + 45² = 576 + 2025 = 2601
c² = 51² = 2601
∴ a² + b² = c²
By the converse of Pyhtagoreas theorem, the triangle with given measure is a right angled triangle.
∴ Ans: yes

Question 4.
Find the unknown side in the following triangles.
(i)

Answer:
From ∆ ABC, by Pythagoras theorem
BC² = AB² + AC²
Take AB² + AC² = 9² + 40² = 81 + 1600 = 1681
BC² = AB² + AC² = 1681 = 41²
BC² = 41² ⇒ BC = 41
∴ x = 41

(ii)

Answer:
From ∆ PQR, by Pythagoras theorem.
PR² = PQ² + QR²
34² = y² + 30²
⇒ y² = 34² – 30²
= 1156 – 900
= 256 = 16²
y² = 16² ⇒ y = 16

(iii)

Answer:
From ∆ XYZ, by Pythagoras theorem,
= YZ² = XY² + XZ²
⇒ XY² = YZ² – XZ²
Z² = 39² – 36²
= 1521 – 1296
= 225 = 15²
z² = 15²
⇒ z = 15

Question 5.
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height.
Answer:

In an isosceles triangle the altitude dives its base into two equal parts.
Now in the figure, ∆ABC is an isosceles triangle with AD as its height
In the figure, AD is the altitude and ∆ABD is a right triangle.
By Pythagoras theorem,
AB² = AD² + BD²
⇒ AD² = AB² – BD²
= 13² – 12² = 169 – 144 = 25
AD² = 25 = 5²
Height: AD = 5cm

Question 6.
Find the distance between the helicopter and the ship.

Answer:
From the figure AS is the distance between the helicopter and the ship.
∆ APS is a right angled triangle, by Pythagoras theorem,
AS² = AP² + PS²
= 80² + 150² = 6400 + 22500 = 28900 = 170²
∴ The distance between the helicopter and the ship is 170 m

Question 7.
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12cm, SM = 8cm, find CS.

Answer:
Given l₁, is the perpendicular bisector of BC.
∴ ∠SMC = 90°and BM = MC
BC = 12cm
⇒ BM + MC = 12cm
MC + MC = 12cm
2MC = 12
MC = \(\frac{12}{2}\)
MC = 6cm
Given SM = 8 cm
By Pythagoras theorem SC² = SM² + MC²
SC² = 8² + 6²
SC² = 64 + 36
CS² = 100
CS² = 10²
CS = 10 cm

Question 8.
Identify the centroid of ∆PQR.

Answer:
In ∆PQR, PT = TR ⇒ QT is a median from vertex Q.
QS = SR ⇒ PS is a median from vertex P.
QT and PS meet at W and therefore W is the centroid of ∆PQR.

Question 9.
Name the orthocentre of ∆PQR.

Answer:
This is a right triangle
∴ orthocentre = P [∵ In right triangle orthocentre is the vertex containing 90°]

Question 10.
In the given figure, A is the midpoint of YZ and G is the centroid of the triangle XYZ. If the length of GA is 3 cm, find XA.

Answer:
Given A is the midpoint of YZ.
∴ ZA = AY
G is the centroid of XYZ centroid divides each median in a ratio 2 : 1 ⇒ XG : GA = 2:1
\(\frac{\mathrm{XG}}{\mathrm{GA}}=\frac{2}{1}\)
\(\frac{\mathrm{XG}}{3}=\frac{2}{1}\)
XG = 2 × 3
XG = 6 cm
XA = XG + GA = 6 + 3 ⇒ XA = 9cm

Question 11.
If I is the incentre of ∆XYZ, ∠IYZ = 30° and ∠IZY = 40°, find ∠YXZ.

Answer:
Since I is the incentre of AXYZ
∠IYZ = 30° ⇒ ∠IYX = 30°
∠IZY = 40° ⇒ ∠IZX = 40°
∴ ∠XYZ = ∠XYI + ∠IYZ = 30° + 30°
∠XYZ = 60°

∠XYZ = 80°
By angle sum property of a triangle
∠XZY + ∠XYZ + ∠YXZ = 180°
80° + 60° + ∠YXZ = 180°
140° + ∠YXZ = 180°
∠YXZ = 180° – 140°
∠YXZ = 40°

Objective Type Questions

Question 12.
If ∆GUT is isosceles and right angled, then ∠TUG is ______ .

(A) 30°
(B) 40°
(C) 45°
(D) 55°
Answer:
(C) 45°
Hint:
∠U ∠T = 45° (∵ GUT is an isosceles given)
∴ ∠TUG = 45°

Question 13.
The hypotenuse of a right angled triangle of sides 12cm and 16cm is ______ .
(A) 28 cm
(B) 20 cm
(C) 24 cm
(D) 21 cm
Answer:
(B) 20 cm
Hint:
Side take a = 12 cm
b = 16cm
The hypotenuse c² = a² + b²
= 12² + 16²
= 144 + 256
c² = 400 ⇒ c = 20 cm

Question 14.
The area of a rectangle of length 21cm and diagonal 29 cm is ______ .
(A) 609 cm²
(B) 580 cm²
(C) 420 cm²
(D) 210 cm²
Answer:
(C) 420 cm²

length = 21 cm
diagonal = 29 cm
By the converse of Pythagoras theorem,
AB² + BC² = AC²
21² + x² = 29²
x² = 841 – 441 400 = 20²
x = 20 cm
Now area of the rectangle = length × breadth.
ie AB × BC = 21 cm × 20 cm = 420 cm²

Question 15.
The sides of a right angled triangle are in the ratio 5:12:13 and its perimeter is 120 units then, the sides are .
(A) 25, 36, 59
(B) 10, 24, 26
(C) 36, 39, 45
(D) 20, 48, 52
Answer:
(D) 20,48,52
Hint:
The sides of a right angled triangle are in the ratio 5 : 12 : 13
Take the three sides as 5a, 12a, 13a
Its perimeter is 5a + 12a + 13a = 30a
It is given that 30a = 120 units
a = 4 units
∴ the sides 5a = 5 × 4 = 20 units
12a = 12 × 4 = 48 units
13a = 13 × 4 = 52 units

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 Geometry Ex 5.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 5 Geometry Ex 5.1

Question 1.
Fill in the blanks with the correct term from the given list.
(in proportion, similar, corresponding, congruent, shape, area, equal)
(i) Corresponding sides of similar triangles are _________ .
Answer:
in proportion

(ii) Similar triangles have the same ________ but not necessarily the same size.
Answer:
Shape

(iii) In any triangle _______ sides are opposite to equal angles.
Answer:
equal

(iv) The symbol is used to represent _________ triangles.
Answer:
congruent

(v) The symbol ~ is used to represent _________ triangles.
Answer:
similar

Question 2.
In the figure, ∠CIP ≡ ∠COP and ∠HIP ≡ ∠HOP. Prove that IP ≡ OP.

Answer:

Statements	Reasons
1. CI = CO	∵ CIP ≡ COP, by CPCTC
2. IP =  OP	By CPCTC
3. CP = CP	By CPCTC
4. Also HI = HO	CPCTC ∆HIP ≡ HOP given
5. IP = OP	By CPCTC and (4)
6. ∴ IP ≡ OP	By (2) and (4)

Question 3.
In the given figure, AC ≡ AD and ∠CBD ≡ ∠DEC. Prove that ∆ BCF ≡ ∆ EDF.

Answer:

Statements	Reasons
1. ∠BCF = ∠EFD	Vertically opposite angles
2. ∠CBD = ∠DEC	Angles on the same base given
3. ∠BCF = ∠EDF	Remaining angles of ∆BCF and ∆EDF
4. ∆BCF ≡ ∆EDF	By (1) and (2) AAA criteria

Question 4.
In the given figure, △ BCD is isosceles with base BD and ∠BAE ≡∠DEA. Prove that AB ≡ ED.

Answer:

Statements	Reasons
1. ∠BAE ≡ ∠DEA	Given
2. AC = EC	By (1) sides opposite to equal angles are equal
3. BC = DC	Given BCD is isosceles with base BD
4. AC – BC = EC – DC	2 – 3
5. AB ≡ ED	By 4

Question 5.
In the given figure, D is the midpoint of OE and ∠CDE = 90°. Prove that △ODC ≡ △EDC

Answer:

Statements	Reasons
1. OD = ED	D is the midpoint OE (given)
2. DC = DC	Common side
3. ∠CDE = ∠CDO = 90°	Linear pair and given ∠CDE = 90°
4. △ODC ≡ △EDC	By RHS criteria

Question 6.
Is △PRQ ≡ △QSP? Why?

Answer:
In △PRQ and △PSQ
∠PRQ = ∠PSQ = 90° given
PR = QS = 3 cm given
PQ = PQ = 5 cm common
It satisfies RHS criteria
∴ △PRQ congruent to △QSP.

Question 7.
From the given figure, prove that △ABC ~ △EDF

Answer:
From the △ABC, AB = AC
It is an isosceles triangle
Angles opposite to equal sides are equal
∴ ∠B = ∠C = 65°
∴ ∠B + ∠C = 65° + 65°
= 130°
We know that sum of three angles is a triangle = 180°
∠A + ∠B + ∠C = 180°
∠A + 130° = 180°
∠A = 180° – 130°
∠A = 50°
From △EDF, ∠E = 50°
∴ Sum of Remaining angles = 180° – 50° = 130°
DE = FD
∴ ∠D = ∠F
From △ABC and △EDF ∴ △D = \(\frac{130}{2}\) = 65°
∠A = ∠E = 50°
∠B = ∠D = 65°
∠C = ∠F = 65°
∴ By AAA criteria △EDF ~ △ABC

Question 8.
In the given figure YH || TE. Prove that △WHY ~ △WET and also find HE and TE.

Answer:

Statements	Reasons
1. ∠EWT = ∠HWY	Common angle
2.  ∠ETW = ∠HYW	Since YH || TE, corresponding angles
3. ∠WET = ∠WHY	Since YH || TE corresponding angles
4. △WHY ~ △WET	By AAA criteria

Also △ WHY ~ △WET
∴ Corresponding sides are proportionated

⇒ 6+HE = \(\frac{6}{4}\) × 16
⇒ 6 + HE = 24
∴ HE = 24 – 6
HE = 18
Again \(\frac{4}{\mathrm{ET}}=\frac{4}{16}\)
ET = \(\frac{4}{4}\)
ET = 16

Question 9.
In the given figure, if △EAT ~ △BUN, find the measure of all angles.

Answer:
Given △EAT ≡ △BUN
∴ Corresponding angles are equal
∴ ∠E = ∠B …… (1)
∠A = ∠U …… (2)
∠T = ∠N ……. (3)
∠E = x°
∠A = 2x°
Sum of three angles of a triangle = 180°
In △ EAT, x + 2x + ∠T = 180°
∠T = 180° – (x° + 2x°)
∠T = 180° – 3x°
Also in △BUN
(x + 40)° + x° + ∠U = 180°
x + 40° + x + ∠U = 180°
2x° + 40° + ∠U = 180°
∠U = 180° – 2x – 40° = 140° – 2x°
Now by (2)
∠A = ∠U
2x = 140° – 2x°
2x + 2x = 140°
4x = 140°
x = \(\frac{140}{4}\) = 35°
∠A = 2x° = 2 × 35° = 70°
∠N = x + 40° = 35° + 40° = 75°
∴ ∠T = ∠N = 75°
∠E = ∠8 = 35°
∠A = ∠U = 70°

Question 10.
In the given figure, UB || AT and CU ≡ CB Prove that △CUB ~ △CAT and hence △CAT is isosceles.

Answer:

Statements	Reasons
1. ∠CUB = ∠CBU	∵ In △CUB, CU = CB
2. ∠CUB = ∠CAB	∵ UB || AT, Corresponding angle if CA is the transversal.
3. ∠CBU = ∠CTA	CT is transversal UB || AT, Corresponding angle commom angle.
4. ∠UCB = ∠ACT	Common angle
5. △CUB ~ △CAT	By AAA criteria
6. CA = CT	∵ ∠CAT = ∠CTA
7. Also △CAT  is isoceles	By 1, 2 and 3 and sides opposite to equal angles are equal.

Objective Type Questions

Question 11.
Two similar triangles will always have _______ angles
(A) acute
(B) obtuse
(C) right
(D) matching
Answer:
(D) matching

Question 12.
If in triangles PQR and XYZ, \(\frac{\mathrm{PQ}}{\mathrm{XY}}=\frac{\mathrm{QR}}{\mathrm{ZX}}\) then they will be similar if
(A) ∠Q = ∠Y
(B) ∠P = ∠X
(C) ∠Q = ∠X
(D) ∠P ≡∠Z
Ans:
(C) ∠Q = ∠X

Question 13.
A flag pole 15 m high casts a shadow of 3m at 10 a.m. The shadow cast by a building at the same time is 18.6m. The height of the building is
(A) 90 m
(B) 91 m
(C) 92 m
(D) 93 m
Answer:
(D) 93 m

Question 14.
If ∆ABC – ∆PQR in which ∠A = 53° and ∠Q = 77°, then ∠R is
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Answer:
(A) 50°

Question 15.
In the figure, which of the following statements is true?

(A) AB = BD
(B) BD < CD
(C) AC = CD
(D) BC = CD
Answer:
(C) AC = CD

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 4 Life Mathematics InText Questions Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 4 Life Mathematics InText Questions

Try These (Text Book Page No. 122)

Find the indicated percentage value of the given numbers.

Answer:

Try These (Text Book Page No. 124)

Question 1.
What percentage ola day is 10 hours?
Answer:
In a day, there are 24 hours .
∴ 10 hrs out of 24 hrs is \(\frac{10}{24}\)
As a percentage, we need to multiply by 100
∴ Percentage = \(\frac{10}{24}\) × 100 = 41.67%

Question 2.
Divide ₹ 350 among P, Q and R such that P gets 50% of what Q gets and Q gets 50% of what R gets.
Answer:
Let R get x, Q gets 50% of what R gets
∴ Q gets = \(\frac{50}{100} \times x=\frac{x}{2}\)
P gets 50% of what Q gets .
∴ P gets = \(\frac{50}{100} \times \frac{x}{2}=\frac{x}{4}\)
Since 350 is divided among the three
∴ 350 = \(x+\frac{x}{2}+\frac{x}{4}\)
350 = \(\frac{4 x+2 x+x}{4}=\frac{7 x}{4}\) = 350
x = \(\frac{350 \times 4}{7}\)
Q gets = \(\frac{x}{2}=\frac{200}{2}\) = 100,
P gets = \(\frac{x}{4}=\frac{200}{4}\) = 50
∴ p = 50, Q = 100, R = 200

Think (Text Book Page No. 124)

With a lot of pride, the traffic police commissioner of a city reported that the accidents had decreased by 200% in one year. He came up with this number by stating that the increase in accidents from 200 to 600 is clearly a 200% rise and now that it had gone down from 600 last year to 200 this year should be a 200% fall. Is this decrease from 600 to 200, the same 200% as reported by him? Justify.

Answer:
Increase from original value 200 to 600

Decrease from original value 600 to 200

here original value is 600
% decrease = \(\frac{600-200}{600}\) × 100 = \(\frac{400}{600}\) × 100 = 66.67 % decrease
Increase from 200 → 600 and % decrease from 600 → 200 are not the same

Try These (Text Book Page No. 126)

Question 1.
If the selling price of an article is less than the cost price of the article, then there is a ________ .
Answer:
Loss

Question 2.
An article costing 5000 is sold for ₹ 4850. Is there a profit or loss? What percentage is it?
Answer:
Loss
Percentage of Loss

Question 3.
If the ratio of cost price and the selling price of an article is 5:7, then the profit / gain is ________ %.
Answer:
C.P = 5x
S.P = 7x
Profit = 7x – 5x = 2x

Think (Text Book Page No. 129)

A shopkeeper marks the price of a marker board 15% above the cost price and then allows a discount of 15% on the marked price. Does he gain or lose in the transaction?
Answer:
Let cost price of marker board be 100
CP = 100 Marks it 15% above CP
∴ Marked price MP = \(\frac{15}{100}\) × CP + CP
= \(\frac{15}{100}\) × 100 + 100 = 15 + 100 = 115
Discount % = 15 %

∴ He sells it 97.75 which is less than his cost price. Therefore he loses
Loss = 97.75 – 100 = – 2.25

Try These (Text Book Page No. 129)

Question 1.
The formula to find the simple interest for a given principal is ________ .
Answer:
\(\frac{\mathrm{PNR}}{100}\)

Question 2.
Find the simple interest on ₹ 900 for 73 days at 8% p.a.
Answer:

Question 3.
In how many years will ₹ 2000 become ₹ 3600 at 10% p.a simple interest?
Answer:
I = 3600 – 2000 = 1600

Try These (Text Book Page No. 141)

Question 1.
Classify the given examples as direct or inverse proportion:
(i) Weight of pulses to their cost.
Answer:
As weight increases cost also increases.
∴ Weight and cost are direct proportion.

(ii) Distance travelled by bus to the price of ticket.
Answer:
As the distance increases price to travel also increases,
∴ Distance and price are direct proportion.

(iii) Speed of the athelete to cover a certain distance.
Answer:
As the speed increases, the time to cover the distance become less.
So speed and üme are in indirect proportion.

(iv) Number of workers employed to complete a construction in a specified time.
Answer:
As the number of workers increases, the amount of work become less, so they are in indirect proportion.

(v) Area of a circle to its radius.
Answer:
If the radius of the circle increases its area also increases.
∴ Area and radius of circles are direct proportion.

Question 2.
A student can type 21 pages in 15 minutes. At the same rate, how long will it take student to type 84 pages?
Answer:
Direct proportion
No. of minutes = x
k = \(\frac{21}{15}\)
\(\frac{21}{15}=\frac{84}{x}\)

Question 3.
If 35 women can do a piece of work in 16 days, In how many days will 28 women do the same work?
Answer:
Inverse proportion
No. of days = x
k = 35 × 16
∴ 28 × x = 35 × 16

Try These (Text Book Page No. 145)

Question 1.
If x and y vary directly, find k when x = y = 5.
Answer:
I If x andy vary directly then \(\frac{x}{y}\) = k.
Here x = 5; y = 5
∴ k = \(\frac{5}{5}\)
k = 1

Question 2.
If x and y vary inversely, find the constant of proportionality when x = 64 and y = 0.75
Answer:
Gìven x = 64, y = 0.75
and also given x andy vary inversely.
∴ xy = k. the constant of variation.
∴ Constant = 64 × 0.75
Constant of variation = 48

Activity (Text Book Page No. 145)

Draw a circle of a given radius. Then, draw its radii in such a way that the angles between any two consecutive pair of radii are equal. Start drawing 3 radii and end with drawing 12 radii in the circle. List and prepare a table for the number of radii to the angle between a pair of consecutive radii and check whether they are in inverse proportion. What is the proportionality constant?
Answer:


As the number of radii increases angle decreases.
Hence they are in inverse proportion
∴ xy = 4 proportional constant
3 × 120° = 360° = k = 360°

Try These (Text Book Page No. 147)

Identify the different variations present in the following questions:

Question 1.
24 men can make 48 articles in 12 days. Then, 6 men can make _____ articles in 6 days.
Answer:
Let the required no. of articles be x

Men (P)	Days (D)	Articles (W)
24	12	48
6	6	x

(i) Mens and days are Indirect variables.
(ii) Men and Articles are direct vanables
(iii) Days and articles are also direct variables using formula.
Let
P₁ = 24
P₂ = 6

D₁ = 12
D₂ = 6

W₁ = 48
W₁ = x

x = 6 Articles

Question 2.
15 workers can lay a road of length 4 km in 4 hours. Then, _____ workers can lay a road of length 8 km in 8 hours.
Answer:
Let the required no. of workers be x

Length (work)	Hours	Workers
4 km	4 hrs	15
8 km	8 hrs	x

(i) Length and workers are direct variable as more length need more workers.
The proportion is 4 : 8 : : 15 : x ——– (1)
(ü) Hours and workers are indirect variables as more working hours need less men.
∴ The proportion is : 4 : : 15 : x ——– (2)
Combining (1) and (2)

Product of the extremes = Product of the mean
4 × 8 × x = 8 × 4 × 15
x = \(\frac{8 \times 4 \times 15}{4 \times 8}\)
x = 15 workers

Question 3.
25 women working 12 hours a day can complete a work in 36 days. Then, 20 women must work hours a day to complete the same work in 30 days.
Answer:
Let the required hours be x.

Women	Days	Hours
25	36	12
20	30	x

As women increases hours to work decreases
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{25}{20}\)
As days increases hours needed become less
∴ It is also an indirect variation.
∴ Multiplying factor is \(\frac{36}{30}\)
∴ x = \(12 \times \frac{25}{20} \times \frac{36}{30}\)
x = 18 hours

Question 4.
In a camp there are 420 kg of rice sufficient for 98 persons for 45 days. The number of days that 60 kg of rice will last for 42 persons is .
Answer:
Let the required number of days be x.

Rice (kg)	Men	Days
420	98	45
60	42	x

If amount of rice is more it will last for more days;
∴ It is Direct Proportion
∴ Multiplying factor is \(\frac{60}{420}\)
If men increases number of days the rice lasts decreases
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{98}{42}\)
x = \(45 \times \frac{60}{420} \times \frac{98}{42}\)

x = 15 days

Try These (Text Book Page No. 150)

Question 1.
Vikram can do one-third of work in p days. He can do th of work In ________ days.
Answer:
\(\frac{1}{3}\) of the work will be done mp days.
∴ Full work will be completed in 3p days
\(\frac{3}{4}\) th of the work will be done in = 3p x \(\frac{3}{4}\)
= \(\frac{9}{4}\)p = 2\(\frac{1}{4}\) p days.

Question 2.
If m persons can complete a work in n days, then 4m persons can complete the same
work in ______ days and \(\frac{m}{4}\) persons can complete the same work in ______ days.
Answer:
Givenm persons complete a work in n days
(i) Then work measured in terms of Man days = mn
4 m men do the work it will be completed in \(\frac{m n}{4 m}\) days = \(\frac{m}{4}\) days.

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 4 Life Mathematics Ex 4.5 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 4 Life Mathematics Ex 4.5

Question 1.
A fruit vendor bought some mangoes of which 10% were rotten. He sold 33\(\frac{1}{3}\) % of the rest. Find the total number of mangoes bought by him initially, if he still has 240 mangoes with him.

Answer:
Let the number of mangoes bought by fruit seller initially be x.
Given that 10% or mangoes were rotten
∴ Number of rotten mangoes = \(\frac{10}{100}\) × x
Number of good mangoes = x – no. of rotten mangoes
= \(x-\frac{10}{100} x=\frac{100 x-10 x}{100}=\frac{90}{100} x\) …….. (1)
Number of mangoes sold = 33\(\frac{1}{3}\)% of good mangoes = \(\frac{100}{3}\)%
∴ Mangoes sold = \(\frac{100}{3} \times \frac{90}{100} \times \times \frac{1}{100}=\frac{30}{100} x\) ……. (2)
Number of mangoes remaining = No. of good mangoes – No. of mangoes sold
From (1) and (2)

∴ Intially he had 400 mangoes

Question 2.
A student gets 31 % marks in an examination but fails by 12 marks. If the pass percentage is 35%, find the maximum marks of the examination.
Answer:
Let the maximum marks in the exam be ‘x’
Pass percentage is given as 35%
∴ Pass mark = \(\frac{35}{100} \times x=\frac{35}{100} x\)
Student gets 31% marks = \(\frac{31}{100} \times x=\frac{31}{100} x\)
But student fails by 12 marks → meaning his mark is 12 less than pass mark.

Maimum mark is 300

Question 3.
Sultana bought the following things from a general store. Calculate the total bill amount paid by her.
(i) Medicines costing ₹ 800 with GST at 5%

Answer:
Formula for bill amount is cost \(\left(1+\frac{\mathrm{GST} \%}{100}\right)\)
Medicine: bill amount is \(800\left(1+\frac{5}{100}\right)=800 \times \frac{105}{100}=840\)

(ii) Cosmetics costing ₹ 650 with GST at 12%

Answer:
Formula for bill amount is cost \(\left(1+\frac{\mathrm{GST} \%}{100}\right)\)
Cosmetics: Bill amount is \(550\left(1+\frac{12}{100}\right)=650 \times \frac{112}{100}=728\)

(iii) Cereals costing ₹ 900 with GST at 0%

Answer:
Formula for bill amount is cost \(\left(1+\frac{\mathrm{GST} \%}{100}\right)\)
Cereals: Bill amount is \(900\left(1+\frac{0}{100}\right)\) = 900

(iv) Sunglass costing ₹ 1750 with GST at 18%

Answer:
Formula for bill amount is cost \(\left(1+\frac{\mathrm{GST} \%}{100}\right)\)
Sunglass: Bill amount is \(1750\left(1+\frac{18}{100}\right)=1750 \times \frac{118}{100}=2065\)

(v) Air Conditioner costing ₹ 28500 with GST at 28 %

Answer:
Formula for bill amount is cost \(\left(1+\frac{\mathrm{GST} \%}{100}\right)\)
Air Conditioner: Bill amount is \(28500\left(1+\frac{28}{100}\right)=28500 \times \frac{128}{100}=36480\)
∴ Total Bill amount = 840 + 728 + 900 + 2065 + 36480
= ₹ 41,013 (total bill amount)

Question 4.
P’s income is 25 % more than that of Q. By what percentage is Q’s income less than P’s?
Answer:
Let Q’s income be 100.
P’s income is 25% more than that of Q.
∴ P’s income = 100 + \(\frac{25}{100}\) × 100 = 125
Q’s income is 25 less than that of P
In percentage terms, Q’s income is less than P’s with respect to P’s income is
\(\frac{\mathrm{P}-\mathrm{Q}}{\mathrm{P}}\) × 100 = \(\frac{125-100}{125}\) × 100 = \(\frac{25}{125}\) × 100 = 20%

Question 5.
Vaidegi sold two sarees for ₹ 2200 each. On one she gains 10% and on the other she loses 12%. Find her total gain or loss percentage in the sale of the sarees.

Answer:
Saree 1 :
The selling price is ₹ 2200, let cost price be CP₁, gain is 10%
Cost price? Using the formula

Saree 2 :
The selling price is 2200, let cost price be CP₂, loss is given as 12%. We need to find CP₂
using the formula as before,

∴ Cost price of both together is CP₁ + CP₂
= 2000 + 2500 = 4500 …….. (1)
Selling price of both together is 2 × 2200 = 4400 …… (2)
Since net selling price is less than net cost price, there is a loss.

Loss = Net cost price – Net selling price
(1) – (2) = 4500 – 4400 = 100
100 100 20 2
∴ loss % = \(\frac{100}{4500}\) × 100 = \(\frac{100}{45}=\frac{20}{9}=2 \frac{2}{9}\)%
= 2\(\frac{2}{9}\)%loss

Question 6.
If 32 men working 12 hours a day can do a work in 15 days, then how many men working 10 hours a day can do double that work in 24 days?
Answer:

Days (D)	Hours (H)	Men (P)
15	12	32
24	10	x

Let
P₁ = 32
P₂ = x

H₁ = 12
H₂ = 10

D₁ = 15
D₂ = 24

W₁ = 1
W₂ = 1


x = 24 persons
To complete the same work 24 men needed.
To complete double the work 24 × 2 = 48 men are required.

Question 7.
Amutha can weave a saree in 18 days. Anjali is twice as good a weaver as Amutha. If both of them weave together, then in how many days can they complete weaving the saree?
Answer:
Amutha can weave a saree in 18 days.
Anjali is twice as good as Amutha.
ie. 1f Amutha weave for 2 days, Anjali do the same work in 1 day.
If Anjali weave the saree she will take
\(\frac{18}{2}\) = 9 days.
Hence time taken by them together ab
= \(\frac{a b}{a+b}\) days
= \(\frac{18 \times 9}{18+9}=\frac{18 \times 9}{27}\) = 6 days

In 6 clays they complete weaving the saree.

Question 8.
P and Q can do a piece of work in 12 days and 15 days respectively. P started the work alone and then after 3 days, Q joined him till the work was completed. How long did the work last?
Answer:
P can do a piece of work in 12 days.
∴ P’s 1 day work = \(\frac{1}{12}\)
P’s 3 day’s work = 3 × \(\frac{1}{12}=\frac{3}{12}\)
Q can do a piece of work in 15 days.
∴ Q’s 1 day work = \(\frac{1}{15}\)
Remaining work after 3 days = 1 – \(\frac{3}{12}=\frac{9}{12}\)

∴ Number of days required to finish the remaining work 9

Remaining work lasts for 5 days
Total work lasts for 3 + 5 = 8 days.

Question 9.
If the numerator of a fraction is increased by 50% and the denominator is decreased by 20%, then it becomes \(\frac{3}{5}\). Find the original fraction.
Answer:
Original fraction = \(\frac{x}{y}\)
numerator increased by 50%
∴ Numerator = \(\frac{150}{100} x\)
Denominator decreased by 20%
∴ Denominator = \(\frac{80}{100} y\)
Hence

Question 10.
Gopi sold a laptop at 12% gain. If it had been sold for ₹ 1200 more, the gain would have been 20%. Find the cost price of the laptop.

Answer:
Let the cost price of the laptop be ‘x
Gain = 12%

If the selling price was 1200 more
i.e \(\frac{112}{100} x\) + 1200, the gain is 2o%

Cost price of the laptop is ₹ 15,000/-

Question 11.
A shopkeeper gives two successive discounts on an article whose marked price is ₹ 180 and selling price is ₹ 108. Find the first discount percentage if the second discount is 25%.
Answer:
Marked price is given as ₹ 180
Let 1 discount be d₁ % = ? (to find)
2nd discount be d₂ % = 25%
Selling price is 108 (given)
Price after 1^st discount = 180 \(\left(1-\frac{d_{1}}{100}\right)\) = P …… (1)
Price after 2^nd discount = P₁ \(\left(1-\frac{d_{2}}{100}\right)\) = 108
Substituting for P₁ from (1), we get

1st discount = 20%

Question 12.
Find the rate of compound interest at which a principal becomes 1.69 times itself in 2 years.
Answer:
Let principal be ‘P’
Amount is given to be 1.69 times principal
i.e 1.69 P
Time period is 2yrs. = (n)
Rate of interest = r = ?(required)
Applying the formula,

∴ rate of compound interest is 30%

Question 13.
A small – scale company undertakes an agreement to make 540 motor pumps in 150 days and employs 40 men for the work. After 75 days, the company could make only 180 motor pumps. How many more men should the company employ so that the work is completed on time as per the agreement?
Answer:
Let the number of men to be appointed more be x.

To produce more pumps more men required
∴ It is direct variation.
∴ The multiplying factor is \(\frac{360}{180}\)
More days means less employees needed.
∴ It is Indirect proportion. 75
∴ The multiplying factor is \(\frac{75}{75}\)
Now 40 + x = 40 × \(\frac{360}{180} \times \frac{75}{75}\)
40 + x = 80
x = 80 – 40
x = 40
40 more man should be employed to complete the work on time as per the agreement.

Question 14.
P alone can do \(\frac{1}{2}\) of a work in 6 days and Q alone can do \(\frac{2}{3}\) of the same work in 4 days. in how many days will they finish \(\frac{3}{4}\) of the work, working together?
Answer:
\(\frac{1}{2}\) of the work is done by P in 6 days

\(\frac{2}{3}\) of work done byQin4days.

(P + Q) will finish the whole work in \(\frac{a b}{a+b}\) days= \(\frac{12 \times 6}{12+6}=\frac{12 \times 6}{18}\)= 4 days
(P + Q) will finish \(\frac{-3}{4}\) of the work in 4 × \(\frac{3}{4}\) = 3 days.

Question 15.
X alone can do a piece of work in 6 days and Y alone in 8 days. X and Y undertook the work for ₹ 48000. With the help of Z, they completed the work in 3 days. How much is Z’s share?
Answer:
X can do the work in 6 days.
X’s I day work = \(\frac{1}{6}\)
X’s share for 1 day = \(\frac{1}{6}\) × 48000 = ₹ 800
X’s share for 3 days = 3 × 800 = ₹ 2400
Y can complete the work in 8 days.
Y’s 1 day work = \(\frac{1}{8}\)
Y’s I day share = \(\frac{1}{8}\) × 4800 = ₹ 600
Y’s 3 days share = ₹ 600 × 3 = ₹ 1800
(X+Y)’s 3days share = ₹ 2400 + ₹ 1800 = ₹ 4200
Remaining money is Z’s share
∴ Z’s share = ₹ 4800 – ₹ 4200 = ₹ 600

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 4 Life Mathematics Ex 4.4 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 4 Life Mathematics Ex 4.4

Question 1.
Fill in the blanks
(i) A can finish a job in 3 days whereas B finishes it in 6 days. The time taken to complete the job working together is __________days.
Answer:
2 days

(ii) If 5 persons can do 5 jobs in 5 days, then 50 persons can do 50 jobs in _________ days.
Answer:
5

(iii) A can do a work in 24 days. If A and B together can finish the work in 6 days, then B alone can finish the work in ________ days.
Answer:
8

(iv) A alone can do a piece of work in 35 days. If B is 40% more efficient than A, then B will finish the work in ___________days.
Answer:
25

(v) A alone can do a work in 10 days and B alone in 15 days. They undertook the work for ₹ 200000. The amount that A will get is .
Answer:
₹ 1,20,000

Question 2.
210 men working 12 hours a day can finish ajob in 18 days. How many men are required to finish the job in 20 days working 14 hours a day?
Answer:
Let the required number of men be x.

Hours	Day	Men
12	18	210
14	20	x

More working hours ⇒ less men required.
∴ It is inverse proportion.
∴ Multiplying factor is \(\frac{12}{14}\)
Also more number of days ⇒ less men
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{18}{20}\)
∴ x = \(210 \times \frac{12}{14} \times \frac{18}{20}\)

x = 162 men
162 men are required.

Question 3.
A cement factory makes 7000 cement bags in 12 days with the help of 36 machines. How many bags can be made in 18 days using 24 machines?
Answer:
Let he required number of cement bags be x.

Days	Machines	Cement bags
12	36	7000
18	24	x

Number of days more ⇒ More cement bags.
∴ It is direct variation.
∴ The multiplying factor = \(\frac{18}{12}\)
Number of machines more ⇒ More cement bags.
∴ It is direct variation.
∴ The multiplying factor = \(\frac{24}{36}\)
∴ x = \(7000 \times \frac{18}{12} \times \frac{24}{36}\)

x = 7000 cement bags
7000 cement bags can be made

Question 4.
A soap factory produces 9600 soaps in 6 days working 15 hours a day. In how many days will it produce 14400 soaps working 3 more hours a day?
Answer:
Let the required number of days be x.

Soaps	Hours	Days
9600	15	6
14400	(15 + 3) = 18	x

To produce more soaps more days required.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{14400}{9600}\)
If more hours spend, less days required.
∴ It is indirect proportion
∴ Multiplying factor = \(\frac{15}{18}\)
∴ x = \(6 \times \frac{14400}{9600} \times \frac{15}{18}\)

x = \(\frac{15}{2}\)
\(\frac{15}{2}\) days will be needed.

Question 5.
If 6 container lorries can transport 135 tonnes of goods in 5 days, how many more lorries are required to transport 180 tonnes of goods in 4 days?
Answer:
Let the number of lorries required more = x.

Container lorries	Goods (tonnes)	Days
6	135	5
6 + x	180	4

As the goods are more ⇒ More lorries are needed to transport.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{180}{135}\)
Again if more days ⇒ less number of lorries enough.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{5}{4}\)
∴ 6 + x = \(6 \times \frac{180}{135} \times \frac{5}{4}\)

6 + x = 10
x = 10 – 6
x = 4
∴ 4 more lorries are required.

Question 6.
A can do a piece of work in 12 hours, B and C can do it 3 hours whereas A and C can do it in 6 hours. How long will B alone take to do the same work?
Answer:
Time taken by A to complete the work = 12 hrs.
∴ A’s 1 hr work = \(\frac{1}{12}\) —— (1)
(B + C) complete the work in 3 hrs.
∴ (B + C)’s 1 hour work = \(\frac{1}{3}\) —— (2)
(1) + (2) ⇒
∴ (A + B + C)’s 1 hour work = \(\frac{1}{12}+\frac{1}{3}=\frac{1+4}{12}=\frac{5}{12}\)
Now (A + C) complete the work in 6 hrs.
∴(A + C)’s 1 hour work = \(\frac{1}{6}\)
∴ B’s 1 hour work = (A+ B + C)’s 1 hour work – (A + C)’s 1 hr work
\(=\frac{5}{12}-\frac{1}{6}=\frac{5-2}{12}=\frac{3}{12}=\frac{1}{4}\)
∴ B alone take 4 days to complete the work.

Question 7.
A and B can do a piece of work in 12 days, while B and C can do it in 15 days whereas A and C can do it in 20 days. How long would each take to do the same work?
Answer:
(A + B) complete the work in 12 days.
∴ (A + B)’s 1 day work = \(\frac{1}{12}\) —— (1)
(B + C) complete the work in 15 days
∴ (B + C)’s 1 day work = \(\frac{1}{15}\) —— (2)
(A + C) complete the work in 20 days
∴ (A + C)’s 1 day work = \(\frac{1}{20}\) —— (3)
Now (1) + (2) + (3) =
[(A + B)+ (B + C) + (A + C)]’s 1 day work = \(\frac{1}{12}+\frac{1}{15}+\frac{1}{20}\)
(2A + 2B + 2C)’s 1 day work = \(\frac{5}{60}+\frac{4}{60}+\frac{3}{60}\)
2(A + B + C)’s 1 day work = \(\frac{5+4+3}{60}\)

LCM = 5 × 4 × 3 = 60
(A + B + C)’s 1 day work = \(\frac{12}{60 \times 2}\)
(A + B + C)’s 1 day work = \(\frac{1}{10}\)
Now A’s I day’s work = (A + B + C)’s 1 day work – (B + C)’s 1 day work
\(=\frac{1}{10}-\frac{1}{15}=\frac{3}{30}-\frac{2}{30}=\frac{1}{30}\)
∴ A takes 30 days to complete the work.
B’s 1 day work – (A + B + C)’s 1 day’s work – (A + C)’s 1 day’s work
\(=\frac{1}{10}-\frac{1}{20}=\frac{6}{60}-\frac{3}{60}\)
\(=\frac{6-3}{60}=\frac{3}{60}=\frac{1}{20}\)
B takes 20 days to complete the work.
C’s 1 day work (A + B + C)’s I day work – (A + B)’s I day work
\(=\frac{1}{10}-\frac{1}{12}=\frac{6}{60}-\frac{5}{60}=\frac{6-5}{60}=\frac{1}{60}\)
∴ C takes 60 days to complete the work.

Question 8.
Carpenter A takes 15 minutes to fit the parts of a chair while Carpenter B takes 3 minutes more than A to do the same work. Working together, how long will it take for them to fit the parts for 22 chairs?
Answer:
Time taken by A to fit a chair = 15 minutes
Time taken by B = 3 minutes more than A
= 15 + 3 = 118 minutes
∴ As 1 minute work = \(\frac{1}{15}\)
B’s 1 minute work = \(\frac{1}{18}\)
(A+B)’s 1 minutes work = \(\frac{1}{15}+\frac{1}{18}\)
\(\frac{12}{180}+\frac{10}{180}=\frac{22}{180}=\frac{11}{90}\)
∴ Time taken by (A + B) to fit a chair

LCM = 3 × 5 × 6 = 180

∴ Time taken by (A + B) to fit a chair
= \(\frac{90}{11}\) × 22 = 180 minutes
= \(\frac{180}{60}\) = 3 hours

Question 9.
A can do a work In 45 days. He works at it for 15 days and then, B alone finishes the remaining work in 24 days. Find the time taken to complete 80% of the work, if they work together.
Answer:
A completes the work in 45 days.
∴ A’s 1 day work = \(\frac{1}{45}\)

Remaining work = \(1-\frac{1}{3}=\frac{3-1}{3}=\frac{2}{3}\)
B finishes \(\frac{2}{3}\) rd work in 24 days

Let x days required

Question 10.
A is thrice as fast as B. If B can do a piece of work in 24 days then, find the number of days they will take to complete the work together.
Answer:
If B does the work in 3 days, A will do it in I day.
B complete the work in 24 days.
∴ A complete the same work in \(\frac{24}{3}\) = 8 days.
∴ (A + B) complete the work in \(\frac{a b}{a+b}\) days
= \(\frac{24 \times 8}{24+8}\) days
= \(\frac{24 \times 8}{32}\) days = 6 days

They together complete the work in 6 days.

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 4 Life Mathematics Ex 4.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 4 Life Mathematics Ex 4.3

Question 1.
Fill in the blanks:
(i) The compound interest on ₹ 5000 at 12% p.a for 2 years, compounded annually is ________ .
Answer:
₹ 1272
Hint:
Compound Interest (CI) formula is
CI = Amount – Principal

∴ 6272 – 5000 = ₹ 1272

(ii) The compound interest on ₹8000 at 10% p.a for 1 year, compounded half yearly is ________ .
Answer:
₹ 820
Hint:
Compound interest (CI) = Amount – Principal
Amount = p \(\left(1+\frac{r}{100}\right)^{2 n}\) [2n as it is compounded half yearly]
r = 10% p.a, for half yearly r = \(\frac{10}{2}\) = 5
∴ A = 8000 \(\left(1+\frac{5}{100}\right)^{2 \times 1}\) = 8000 × \(\left(\frac{105}{100}\right)^{2}\) = 8820
CI = Amount – principal = 8820 – 8000 = ₹ 820

(iii) The annual rate of growth in population of a town is 10%. If its present population is 26620, then the population 3 years ago was ________ .
Answer:
₹ 20,000
Hint:
Rate of growth of population r = 10%
Present population = 26620
Let population 3 years ago be x
∴ Applying the formula for population growth which is similar to compound interest,

The population 3 years ago was ₹ 20,000

(iv) If the compound interest is calculated quarterly, the amount is found using the formula ________ .
Answer:
A = \(P\left(1+\frac{r}{400}\right)^{4 n}\)
Hint:
Quarterly means 4 times in a year.
∴ The formula for compound interest is
A = \(P\left(1+\frac{r}{400}\right)^{4 n}\)

(v) The difference between the C.I and S.I for 2 years for a principal of ₹ 5000 at the rate of interest 8% p.a is ________ .
Answer:
₹ 32
Hint:
Difference between S.I & C.I is given by the formula
CI – SI = \(\left(\frac{r}{100}\right)^{2}\)
Principal (P) = 5000. r = 8% p.a
∴ CI – SI = 5000\(\left(\frac{8}{100}\right)^{2}\) = 5000 × \(\left(\frac{8}{100}\right)^{2}\) × \(\left(\frac{8}{100}\right)^{2}\) = ₹ 32

Question 2.
Say True or False.
(i) Depreciation value is calculated by the formula, \(P\left(1-\frac{r}{100}\right)^{n}\).
Answer:
True
Hint:
Depreciation formula is \(P\left(1-\frac{r}{100}\right)^{n}\)

(ii) If the present population ola city is P and it increases at the rate of r% p.a, then the population n years ago would be \(P\left(1-\frac{r}{100}\right)^{n}\)
Answer:
False
Hint:
Let the population ‘n’ yrs ago be ‘x’
∴ Present popuLation (P) = x × \(\left(1+\frac{r}{100}\right)^{n}\)
∴ x = \(\frac{P}{\left(1+\frac{r}{100}\right)^{n}}\)

(iii) The present value of a machine is ₹ 16800. It depreciates at 25% p.a. Its worth after 2 years is ₹ 9450.
Answer:
True
Hint:
Present value of machine = ₹ 16800
Depreciation rate (n) = 25%

(iv) The time taken for ₹ 1000 to become ₹ 1331 at 20% p.a, compounded annually is 3 years.
Answer:
False
Hint:
Pnncipal money = 1000
rate of interest = 20%
Amount = 1331, applying in formula we get

(v) The compound interest on ₹ 16000 for 9 months at 20% p.a, compounded quarterly is ₹ 2522.
Answer:
True
Hint:
Principal (P) = 16000
n = 9 months = \(\frac{9}{12}\) years
r = 20% p.a
For compounding quarterly, we have to use below formula,
Amount(A) = P × \(\left(1+\frac{r}{100}\right)^{4 n}\)
Since quarterly we have to divide ‘r’ by 4

∴ Interest A – P = 18522 – 16000 = 2522 (True)

Question 3.
Find the compound interest on ₹ 3200 at 2.5 % p.a for 2 years, compounded annually.
Answer:
Principal (P) = ₹ 3200
r = 2.5% p.a
n = 2 years comp. annually
∴ Amount (A) = \(\left(1+\frac{r}{100}\right)^{n}\)
= 3200 \(\left(1+\frac{25}{100}\right)^{2}\)
= 3200 × (1.025)² = 3362
Compound interest (CI) = Amount – Principal
= 3362 – 3200 = 162

Question 4.
Find the compound interest for 2\(\frac { 1 }{ 2 }\) years on ₹ 4000 at 10% p.a, if the interest is compounded yearly.
Answer:
Principal (P) = ₹ 4000
r = 10 %p.a
Compounded yearly
n = 2\(\frac { 1 }{ 2 }\) years. Since it is of the form a \(\frac{b}{c}\) years

∴ CI = Amount – principal = 5082 – 4000 = 1082

Question 5.
A principal becomes ₹ 2028 in 2 years at 4% p.a compound interest. Find the principal.
Answer:
n = 2 years
r = rate of interest = 4% p.a
Amount A = ₹ 2028

Question 6.
In how many years will ₹ 3375 become ₹ 4096 at 13 % p.a if the interest is compounded half-yearly?
Answer:
Principal = ₹ 3375
Amount = ₹ 4096
r = 13\(\frac{1}{3}\)%p.a = \(\frac{40}{3}\)%p.a

Let no. of years be n
for compounding half yearly, formula is

Taking cubic root on both sides,

Question 7.
Find the CI on ₹ 15000 for 3 years if the rates of interest are 15%, 20% and 25% for the I, II and III years respectively.
Answer:
Principal (P) = ₹ 15000
rate of interest 1 (a) = 15% for year I
rate of interest 2 (b) = 20% for year II
rate of interest 3 (c) = 25% for year III
Formula for amount when rate of interest is different for different years is

Substituting in the above formula, we get

∴ Compound Interest(CI) = A – P = 25,875 – 15,000 = ₹ 10,875
CI = ₹ 10.875

Question 8.
Find the difference between C.I and S.I on ₹ 5000 for 1 year at 2% p.a, if the interest is compounded half yearly.
Answer:
Principal (P) = ₹ 5000
time period (n) = 1 yr.
Rate of interest (r) = 2%p.a
for half yearly r = 1%
Difference between CI & SI is given by the formula

Question 9.
Find the rate of interest if the difference between C.I and S.I on ₹ 8000 compounded annually for 2 years is ₹ 20.
Answer:
Principal (P) = ₹ 8000
time period (n) = 2 yrs.
rate of interest (r) = ?
Difference between CI & SI is given by the formula
CI – SI = \(p\left(1+\frac{r}{100}\right)^{n}\)
Difference between CI & SI is given as 20
∴ 20 = 8000 × \(\left(\frac{r}{100}\right)^{2}\)
∴ \(\left(\frac{r}{100}\right)^{2}=\frac{20}{8000}=\frac{1}{400}\)
Taking square root on both sides
\(\frac{r}{100}=\sqrt{\frac{1}{400}}=\frac{1}{20}\)
∴ r = \(\) = 5 %

Question 10.
Find the principal if the difference between C.I and S.l on it at 15% p.a for 3 years is ₹ 1134.
Answer:
Rate of interest (r) = 15% p.a
time period (n) = 3 years
Difference between CI & SI is given as 1134
Principal = ? → required to find
Using formula for difference
Simple Interest SI = \(\frac{P n r}{100}\)
Compound Interest CI = p(1 + i)ⁿ – p

1134 = P[(1.15)³ – 1 – 0.45] = P(1.52 – 1.45) = P (0.07)
∴ p = \(\frac{1134 \times 100}{0.07 \times 100}=\frac{113400}{7}\)
P = ₹ 16200

Objective Type Questions

Question 11.
The number of conversion periods in a year, if the interest on a principal is compounded every two months is _________ .
(A) 2
(B) 4
(C) 6
(D) 12
Answer:
(C) 6
Hint:
Conversion period is the time period after which the interest is added to the principal. If principal is compounded every two months then in a year, there will be 6\(\left(\frac{12}{2}\right)\) conversion periods.

Question 12.
The time taken for ₹ 4400 to become ₹ 4851 at 10%, compounded half yearly is _________ .
(A) 6 months
(B) 1 year
(C) 1\(\frac{1}{2}\) years
(D) 2 years
Answer:
(B) 1 year
Hint:
Principal = ₹ 4400
Amount = ₹ 4851
Rate of interest = 10% p.a
for half yearly, divide by 2,
r = \(\frac{10}{2}\) = 5 %
Compounded half yearly, so the formula is
A = P\(P\left(1+\frac{r}{100}\right)^{2 n}\)
Substituting in the above formula, we get

Taking square root on both sides, we get
\(\left(\frac{21}{20}\right)^{2 n}=\left(\frac{21}{20}\right)^{2}\)
Equating power on both sides
∴ 2n = 2, n = 1

Question 13.
The cost of a machine is ₹ 18000 and it depreciates at 16\(\frac{2}{3}\)% annually. Its value after 2 years will be _________ .
(A) ₹ 2000
(B) ₹ 12500
(C) ₹ 15000
(D) ₹ 16500
Answer:
(B) ₹ 12500
Hint:
Cost of machine = 18000
Depreciation rate = 16\(\frac{2}{3}\)% = \(\frac{50}{3}\)%p.a
time period = 2 years
∴ As per depreciation formula,
Depriciated value = Original value \(\left(1-\frac{r}{100}\right)^{n}\)
Substituting in above formula, we get
Depreciated value after 2 years

Question 14.
The sum which amounts to ₹ 2662 at 10% p.a in 3 years, compounded yearly is _________ .
(A) ₹ 2000
(B) ₹ 1800
(C) ₹ 1500
(D) ₹ 2500
Answer:
(A) ₹ 2000
Hint:
Amount = ₹ 2662
rate of interest = 10 % p.a
Time period = 3 yrs. Compounded yearly
Principal (P) → required to find?

Question 15.
The difference between compound and simple interest on a certain sum of money for 2 years at2%p.ais U. The sum of money is _________ .
(A) ₹ 2000
(B) ₹ 1500
(C) ₹ 3000
(D) ₹ 2500
Answer:
(D) ₹ 2500
Hint:
Difference between CI and SI is given as Re I
Time period (n) = 2 yrs.
Rate of interest (r) = 2 % p.a
Formula for difference is
CI – SI = \(P \times\left(1+\frac{r}{100}\right)^{n}\)
Substituting the values in above formula, we get
1 = p × \(\left(\frac{2}{100}\right)^{2}\)
∴ p = 1 × \(\left(\frac{100}{2}\right)^{2}\) = 1 × (50)² = ₹ 2500