Category: Class 9

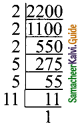
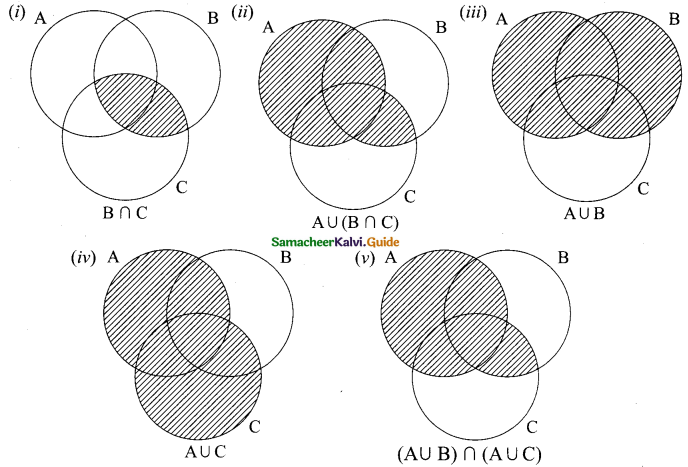
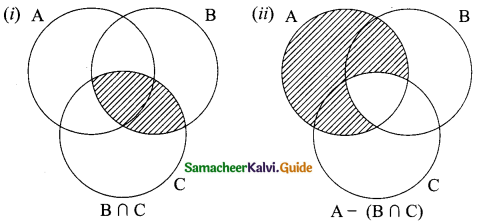
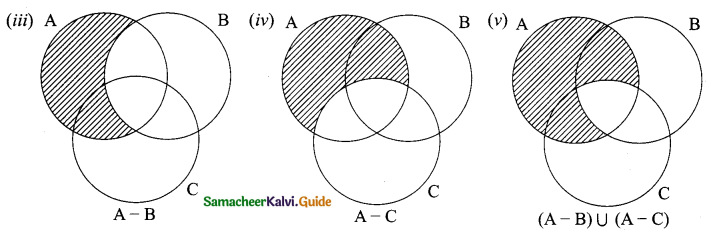
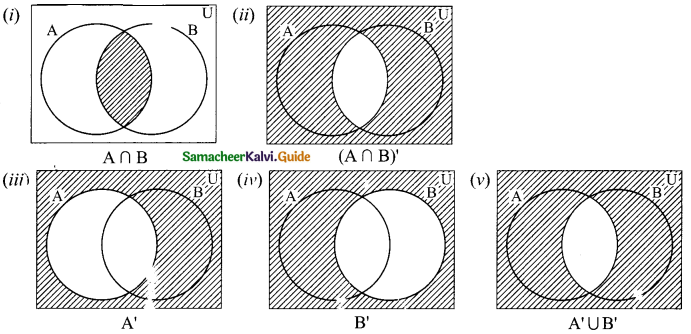
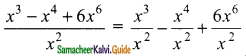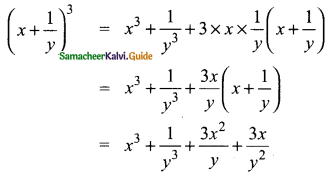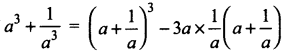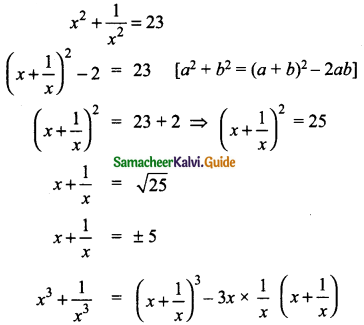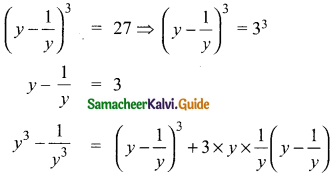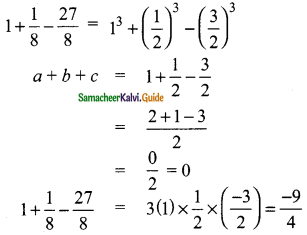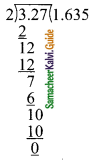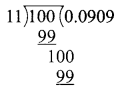Students can download Maths Chapter 3 Algebra Ex 3.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.2

Question 1.
Find the value of the polynomial f(y) = 6y – 3y² + 3 at
(i) y = 1
(ii) y = -1
(iii) y = 0
Solution:
(i) When y = 1
f(y) = 6y – 3y² + 3
f(1) = 6(1) – 3(1)² + 3
= 6 – 3 + 3 = 6

(ii) When y = – 1
f(y) = 6y – 3y² + 3
f(-1) = 6(-1) – 3(-1)² + 3
= – 6 – 3 + 3
= – 6

(iii) When y = 0
f(y) = 6y – 3y² + 3
f(0) = 6(0) – 3(0)² + 3
= 0 – 0 + 3
= 3

Question 2.
If p(x) = x² – 2√2x + 1, find p(2√2).
Solution:
p(x) = x² – 2√2x + 1
p(2√2) = (2√2)² – 2√2 (2√2) + 1
= 8 – 8 + 1
= 0 + 1
= 1

Question 3.
Find the zeros of the polynomial in each of the following.
(i) P(x) = x – 3
Solution:
p( 3) = 3 – 3
= 0
p(3) is the zero of p(x)

(ii) p(x) = 2x + 5
Solution:

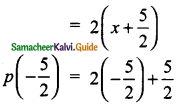
= -5 + 5
= 2(0)
= 0
Hence –\(\frac{5}{2}\) is the zero of p(x).

(iii) q(y) = 2y – 3
Solution:

= 2 × 0
= 0
Hence \(\frac{3}{2}\) is the zero of q(y).

(iv) f(z) = 8z
Solution:
f(0) = 8 × 0
= 0
Hence 0 is the zero of f(z)

(v) p(x) = ax when a ≠ 0
Solution:
p(0) = a(0)
= 0
Hence, 0 is the zero of p(x)

(vi) h(x) = ax + b, a ≠ 0, a, b∈R
Solution:

Hence –\(\frac{b}{a}\) is the zero of h(x).

Question 4.
Find the roots of the polynomial equations.
(i) 5x – 6 = 0
Solution:
5x = 6
x = \(\frac{6}{5}\)
\(\frac{6}{5}\) is the root of the polynomial.

(ii) x + 3 = 0
Solution:
x = -3
-3 is the root of the polynomial.

(iii) 10x + 9 = 0
Solution:
10x = -9
x = –\(\frac{9}{10}\)
–\(\frac{9}{10}\) is the root of the polynomial.

(iv) 9x – 4 = 0
Solution:
9x = 4
x = \(\frac{4}{9}\)
\(\frac{4}{9}\) is the root of the polynomial.

Question 5.
Verify whether the following are zeros of the polynomial, indicated against them,or not.
(i) p(x) = 2x – 1, x = \(\frac{1}{2}\)
Solution:
p (\(\frac{1}{2}\)) = 2(\(\frac{1}{2}\)) – 1
= 1 – 1
= 0
∴ \(\frac{1}{2}\) is the zero of the polynomial.

(ii) p(x) = x³ – 1, x = 1
Solution:
p(1) = 1³ – 1
= 1 – 1
= 0
∴ 1 is the zero of the polynomial

(iii) p(x) = ax + b, x = \(\frac{-b}{a}\)
Solution:
p(\(\frac{-b}{a}\)) = a(\(\frac{-b}{a}\)) + b
= -b + b
= 0
∴ \(\frac{-b}{a}\) is the zero of the polynomial. a

(iv) p(x) = (x + 3) (x – 4); x = -3, x = 4
Solution:
P(-3) = (-3 + 3) (-3 – 4)
= (0) (-7)
= 0
P( 4) = (4 + 3) (4 – 4)
= (7) (0)
= 0
∴ -3 and 4 are the zeros of the polynomial.

Question 6.
Find the number of zeros of the following polynomials represented by their graphs.

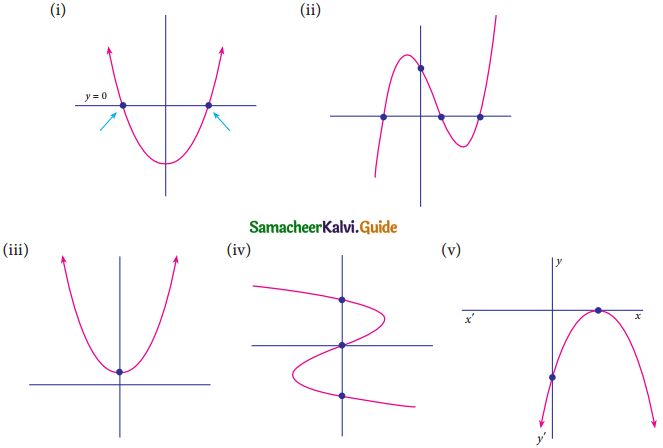
Solution:
(i) Number of zeros = 2 (The curve is intersecting the x-axis at 2 points)
(ii) Number of zeros = 3 (The curve is intersecting the x-axis at 3 points)
(iii) Number of zeros = 0 (The curve is not intersecting the x-axis)
(iv) Number of zeros = 1 (The curve is intersecting at the origin)
(v) Number of zeros = 1 (The curve is intersecting the x-axis at one point)

Students can download Maths Chapter 3 Algebra Ex 3.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.1

Question 1.
Which of the following expressions are polynomials. If not give reason:
(i) \(\frac{1}{x^2}\) + 3x – 4
Solution:
(i) \(\frac{1}{x^2}\) + 3x – 4 is not a polynomial. Since the exponent of x² is not a whole number, but it is (\(\frac{1}{x^2}\) = x^-2) negative number.

(ii) x² (x – 1)
Solution:
x² (x – 1) is a polynomial.

(iii) \(\frac{1}{x}\) (x + 5)
Solution:
\(\frac{1}{x}\) (x + 5) is not a polynomial. Since the exponent of x is not a whole number, but it is (\(\frac{1}{x}\) = x^-1) negative number.

(iv) \(\frac{1}{x^{-2}}\) + \(\frac{1}{x^{-1}}\) + 7
Solution:
\(\frac{1}{x^{-2}}\) + \(\frac{1}{x^{-1}}\) + 7 is a polynomial. (\(\frac{1}{x^{-2}}\) = x² and \(\frac{1}{x^{-1}}\) = x)

(v) √5x² + √3x + √2
Solution:
√5x² + √3x + √2 is a polynomial.

(vi) m² – \(\sqrt[3]{m}\) + 7m – 10
m² –\(\sqrt[3]{m}\) + 7m – 10 is not a polynomial. Since the exponent of m is not a whole number.
(\(\sqrt[3]{m}\) = m^1/3)

Question 2.
Write the coefficient of x² and x in each of the following polynomials.
(i) 4 + \(\frac{2}{5}\) x² – 3x
Solution:
Coefficient of x² is \(\frac{2}{5}\) and coefficient of x is -3.

(ii) 6 – 2x² + 3x³ – √7x
Solution:
Coefficient of x² is -2 and coefficient of x is -√7

(iii) π x² – x + 2
Solution:
Coefficient of x² is π and coefficient of x is -1.

(iv) √3x² + √2x + 0.5
Solution:
Coefficient of x² is √3 and coefficient of x is √2

(v) x² – \(\frac{7}{2}\) x + 8
Solution:
Coefficient of x² is 1 and coefficient of x is –\(\frac{7}{2}\)

Question 3.
Find the degree of the following polynomials.
(i) 1 – √2 y² + y⁷
(ii) \(\frac{x^{3}-x^{4}+6 x^{6}}{x^{2}}\)
(iii) x³ (x² + x)
(iv) 3x⁴ + 9x² + 27x⁶
(v) 2√5p⁴ \(-\frac{8 p^{3}}{\sqrt{3}}+\frac{2 p^{2}}{7}\)
Solution:
(i) 1 – √2 y² + y⁷
The degree of the polynomial is 7.

(ii)
= x – x² + 6x⁴
The degree of the polynomial is 4.

(iii) x³ (x² + x) = x⁵ + x⁴
The degree of the polynomial is 5.

(iv) 3x⁴ + 9x² + 27x⁶
The degree of the polynomial is 6.

(v) 2√5p⁴ \(-\frac{8 p^{3}}{\sqrt{3}}+\frac{2 p^{2}}{7}\)
The degree of the polynomial is 4.

Question 4.
Rewrite the following polynomial in standard form.
(i) x – 9 + √7x³ + 6x²
Solution:
The standard form is √7x³ + 6x² – x – 9
(or) – 9 + x + 6x² + √7x³

(ii) √2x² – \(\frac{7}{2}\) x⁴ + x – 5x³
Solution:
The standard form is – \(\frac{7}{2}\) x⁴ – 5x³ + √2x² + x
(or) x + √2x² – 5x³ – \(\frac{7}{2}\) x⁴

(iii) 7x³ – \(\frac{6}{5}\) x² + 4x – 1
Solution:
The given polynomial is in standard form (or) – 1 + 4x – \(\frac{6}{5}\) x² + 7x³

(iv) y² + √5y³ – 11 – \(\frac{7}{3}\) y + 9y⁴
Solution:
The standard form is 9y⁴ + √5y³ + y² – \(\frac{7}{3}\) y – 11
(or) – 11 – \(\frac{7}{3}\) y + y² + √5y³ + 9y⁴

Question 5.
Add the following polynomials and find the degree of the resultant polynomial
(i) p(x) = 6x² – 7x + 2; q(x) = 6x³ – 7x + 15
Solution:
p(x) + q(x) = 6x² – 7x + 2 + 6x³ – 7x + 15
= 6x³ + 6x² – 7x – 7x + 2 + 15
= 6x³ + 6x² – 14x + 17
The degree of the polynomial is 3.

(ii) h(x) = 7x³ – 6x + 1; f(x) = 7x² + 17x – 9
Solution:
h(x) + f(x) = 7x³ – 6x + 1 + 7x² + 17x – 9
= 7x³ + 7x² + 11x – 8
The degree of the polynomial is 3.

(iii) f(x) = 16x⁴ – 5x² + 9; g(x) = -6x³ + 7x – 15
Solution:
f(x) + g(x) = 16x⁴ – 5x² + 9 – 6x³ + 7x – 15
= 16x⁴ – 6x³ – 5x² + 7x + 9 – 15
= 16x⁴ – 6x³ – 5x² + 7x – 6
The degree of the polynomial is 4.

Question 6.
Subtract the second polynomial from the first polynomial and find the degree of the resultant polynomial.
(i) p(x) = 7x² + 6x – 1; q(x) = 6x – 9
Solution:
p(x) – q(x) = 7x² + 6x – 1 – (6x – 9)
= 7x² + 6x – 1 – 6x + 9
= 7x² + 6x – 6x – 1 + 9
= 7x² + 8
The degree of the polynomial is 2.

(ii) f(y) = 6y² – 7y + 2; g(y) = 7y + y³
Solution:
f(y) – g(y) = 6y² – 7y + 2 – (7y + y³)
= 6y² – 7y + 2 – 7y – y³
= -y³ + 6y² – 7y – 7y + 2
= -y³ + 6y² – 14y + 2
The degree of the polynomial is 3.

(iii) h(z) = z⁵ – 6z⁴ + z; f(z) = 6z² + 10z – 7
Solution:
h(z) – f(z) = z⁵ – 6z⁴ + z – (6z² + 10z – 7)
= z⁵ – 6z⁴ + z – 6z² – 10z + 7
= z⁵ – 6z⁴ – 6z² + z – 10z + 7
= z⁵ – 6z⁴ – 6z² – 9z + 7
The degree of the polynomial is 5.

Question 7.
What should be added to 2x³ + 6x² – 5x + 8 to get 3x³ – 2x² + 6x + 15?
Solution:
3x³ – 2x² + 6x + 15 – (2x³ + 6x² – 5x + 8)
= 3x³ – 2x² + 6x + 15 – 2x³ – 6x² + 5x – 8
= 3x³ – 2x³- 2x² – 6x² + 6x + 5x + 15 – 8
= x³ – 8x² + 11x + 7
x³ – 8x² + 11x + 7 must be added to get 3x³ – 2x² + 6x + 15.

Question 8.
What must be subtracted from 2x⁴ + 4x² – 3x + 7 to get 3x³ – x² + 2x + 1?
Solution:
2x⁴ + 4x² – 3x + 7 – (3x³ – x² + 2x + 1)
= 2x⁴ + 4x² – 3x + 7 – 3x³ + x² – 2x – 1
= 2x⁴ – 3x³ + 4x² + x² – 3x – 2x + 7 – 1
= 2x⁴ – 3x³ + 5x² – 5x + 6
2x⁴ – 3x³ + 5x² – 5x + 6 must be subtracted to get 3x³ – x² + 2x + 1.

Question 9.
Multiply the following polynomials and find the degree of the resultant polynomial:
(i) p(x) = x² – 9, q(x) = 6x² + 7x – 2
Solution:
p(x) × q(x) = (x² – 9) (6x² + 7x – 2)
= 6x⁴ + 7x³ – 2x² – 54x² – 63x + 18
= 6x⁴ + 7x³ – 56x² – 63x + 18
The degree of the polynomial is 4.

(ii) f(x) = 7x + 2, g(x) = 15x – 9
Solution:
f(x) × g(x) = (7x + 2) (15x – 9)
= 105x² – 63x + 30x – 18
= 105x² – 33x – 18
The degree of the polynomial is 2.

(iii) h(x) = 6x² – 7x + 1, f(x) = 5x – 7
Solution:
h(x) × f(x) = (6x² – 7x + 1) (5x – 7)
= 30x³ – 42x² – 35x² + 49x + 5x – 7
= 30x³ – 77x² + 54x – 7
The degree of the polynomial is 3.

Question 10.
The cost of a chocolate is Rs. (x + y) and Amir bought (x + y) chocolates. Find the total amount paid by him in terms of x and y. If x = 10, y = 5 find the amount paid by him.
Solution:
The cost of a chocolate = (x + y)
Number of chocolates bought by Amir = x + y
Total amount paid by him = (x + y) (x + y)
= x² + xy + xy + y²
= x² + 2xy + y²
When x = 10 and y = 5
The total amount paid by him = (10)² + 2(10)(5) + (5)²
= 100 + 100 + 25 = 225

Question 11.
The length of a rectangle is (3x + 2) units and it’s breadth is (3x – 2) units. Find its area in terms of x. What will be the area if x = 20 units.
Solution:
Length of the rectangle = 3x + 2 units
Breadth of the rectangle = 3x – 2 units
Area of the rectangle = (3x + 2) (3x – 2)
= 9x² – 6x + 6x – 4
= 9x² – 4
When x = 20
Area of the rectangle = 9(20)² – 4
= 9(400) – 4
= 3600 – 4
= 3596 sq.units.

Question 12.
p(x) is a polynomial of degree 1 and q(x) is a polynomial of degree 2. What kind of the polynomial is p(x) × q(x)?
Solution:
Degree of the polynomial p(x) = 1
Degree of the polynomial q(x) = 2
Degree of p(x) × q(x) = 3
The polynomial is a cubic polynomial (or) Polynomial of degree 3.

Students can download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.4

Question 1.
Expand the following:
(i) (2x + 3y + 4z)²
(ii) (-p + 2q + 3r)²
(iii) (2p + 3) (2p – 4) (2p – 5)
(iv) (3a + 1) (3a – 2) (3a + 4)
Solution:
We know that (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac
(i) (2x + 3y + 4z)² = (2x)² + (3y)² + (4z)² + 2(2x) (3y) + 2(3y) (4z) + 2(4z) (2x)
= 4x² + 9y² + 16z² + 12xy + 24yz + 16xz

(ii) (-p + 2q + 3r)² = (-p)² + (2q)² + (3r)² + 2(-p) (2q) + 2(2q)(3r) + 2(3r) (- p)
= p²+ 4q² + 9r² – 4pq + 12qr – 6pr

(iii) (2p + 3) (2p – 4) (2p – 5)
[Here x = 2p, a = 3, b = -4 and c = -5]
= (2p)³ + (3 – 4 – 5) (2p)² + [(3)(-4) + (-4)(-5) + (3) (-5)] 2p + (3) (-4) (-5)
= 8p³ + (-6)(4p²) + (-12 + 20 – 15) 2p + 60
= 8p³ – 24p² – 14p + 60

(iv) (3a + 1) (3a – 2) (3a + 4)
[Here x = 3a, a = 1, b = -2 and c = 4]
= (3a)³ + (1 – 2 + 4) (3a)² + [(1)(-2) + (-2) (4) + (4) (1)] (3a) + (1) (-2) (4)
= 27a³ + 3(9a²) + (-2 – 8 + 4) (3a) – 8
= 27a³ + 27a² – 18a – 8

Question 2.
Using algebraic identity, find the coefficients of x², x and constant term without actual expansion.
(i) (x + 5)(x + 6)(x + 7)
Solution:
[Here x = x, a = 5, b = 6, c = 7]
(x + a) (x + b) (x + c) = x³ + (a + b + c)x² + (ab + bc + ac)x + abc
coefficient of x² = 5 + 6 + 7
= 18
coefficient of x = 30 + 42 + 35
= 107
constant term = (5) (6) (7)
= 210

(ii) (2x + 3)(2x – 5) (2x – 6)
Solution:
[Here x = 2x, a = 3, b = -5, c = -6]
(x + a) (x + b) (x + c) = x³ + (a + b + c)x² + (ab + bc + ac)x + abc
coefficient of x² = (3 – 5 – 6)4 [(2x)² = 4x²]
= (-8) (4)
= -32
coefficient of x = [(3)(-5) + (-5)(-6) + (-6)(3)](2)
= (-15 + 30-18) (2)
= (-3) (2)
= -6
constant term = (3) (-5) (-6)
= 90

Question 3.
If (x + a)(x + b)(x + c) = x³ + 14x² + 59x + 70, find the value of
(i) a + b + c
(ii) \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\)
(iii) a² + b² + c²
(iv) \(\frac{a}{bc} + \frac{b}{ac} + \frac{c}{ab}\)
Solution:
(x + a) (x + b) (x + c) = x³ + 14x² + 59x + 70
x³ + (a + b + c)x² + (ab + bc + ac)x + abc = x³ + 14x² + 59x + 70
a + b + c = 14, ab + bc + ac = 59, abc = 70
(i) a + b + c = 14

(ii) \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\) = \(\frac{bc+ac+ab}{abc}\)
= \(\frac{59}{70}\)

(iii) a² + b² + c² = (a + b + c)² – 2 (ab + bc + ac)
= (14)² – 2(59)
= 196 – 118
= 78

Question 4.
Expand:
(i) (3a – 4b)³
Solution:
(a – b)³ = a³ – b³ – 3ab (a – b)
(3a – 4b)³ = (3a)³ – (4b)³ – 3(3a)(4b)(3a – 4b)
= 27a³ – 64b³ – 36ab (3a – 4b)
= 27a³ – 64b³ – 108a²b + 144ab²

(ii) [x + \(\frac{1}{y}]^{3}\)
Solution:
(a + b)³ = a³ + b³ + 3ab (a + b)

Question 5.
Evaluate the following by using identities:
(i) 98³
Solution:
98³ = (100 – 2)³ [(a – b)³ = a³ – b³ – 3ab (a – b)]
= 100³ – (2)³ – 3(100) (2) (100 – 2)
= 1000000 – 8 – 600(98)
= 1000000 – 8 – 58800
= 1000000 – 58808
= 941192

(ii) 1001³
Solution:
(1001)³ = (1000 + 1)³
[(a + b)³ = a³ + b³ + 3ab (a + b)]
= (1000)³ + 1³ + 3(1000) (1) (1000 + 1)
= 1000000000 + 1 + 3000 (1001)
= 1000000001 + 3003000
= 1003003001

Question 6.
If (x + y + z) = 9 and (xy + yz + zx) = 26, then find the value of x² + y² + z².
Solution:
x + y + z = 9; xy + yz + zx = 26
x² + y² + z² = (x + y + z)² – 2xy – 2yz – 2xz
= (x + y + z)² – 2 (xy + yz + zx)
= 9² – 2(26)
= 81 – 52
= 29

Question 7.
Find 27a³ + 64b³, If 3a + 4b = 10 and ab = 2
Solution:
3a + Ab = 10, ab = 2
27a³ + 64b³ = (3a)³ + (4b)³
[a³ + b³ = (a + b)³ – 3 ab (a + b)]
= (3a + 4b)³ – 3 × 3a × 4b (3a + 4b)
= 103 – 36ab (10)
= 1000 – 36(2)(10)
= 1000 – 720
= 280

Question 8.
Find x³ – y³, if x – y = 5 and xy = 14.
Solution:
x – y = 5, xy = 14
x³ – y³  = (x – y)³ + 3xy (x – y)
= 5³ + 3(14) (5)
= 125 + 210
= 335

Question 9.
If a + \(\frac{1}{a}\) = 6, then find the value of a³ +\(\frac{1}{a^3}\)
Solution:
a + \(\frac{1}{a}\) = 6 [a³ + b³ = (a + b)³ – 3ab (a + b)]

= 6³ – 3(6)
= 216 – 18
= 198

Question 10.
If x² + \(\frac{1}{x^2}\) = 23, then find the value of x + \(\frac{1}{x}\) and x³ + \(\frac{1}{x^3}\)
Solution:

When x = 5 [a³ + b³ = (a + b)³ – 3ab (a + b)]
= (5)³ – 3(5)
= 125 – 15
= 110
when x = -5
x³ + \(\frac{1}{x^3}\) = (-5)³ – 3(-5)
= -125 + 15
= -110
∴ x³ + \(\frac{1}{x^3}\) = ±110

Question 11.
If (y – \(\frac{1}{y})^{3}\) = 27 then find the value of y³ – \(\frac{1}{y^3}\)
Solution:

= 3³ + 3(3)
= 27 + 9
= 36

Question 12.
Simplify:
(i) (2a + 3b + 4c) (4a² + 9b² + 16c² – 6ab – 12bc – 8ca)
(ii) (x – 2y + 3z) (x² + 4y² + 9z² + 2xy + 6yz – 3xz)
Solution:
x³ + y³ + z³ – 3xyz ≡ (x + y + z) (x² + y² + z² – xy – yz – zx)
(i) (2a + 3b + 4c) (4a² + 9b² + 16c² – 6ab – 12bc – 8ea)
= (2a)³ + (3b)³ + (4c)³ – 3 (2a) (3b) (4c)
= 8a³ + 27b³ + 64c³ – 72abc

(ii) (x – 2y + 3z) (x² + 4y² + 9z² + 2xy + 6yz – 3xz)
= x³ + (-2y)³ + (3z)³ – 3(x) (-2y) (3z)
= x³ – 8y³ + 27z³ + 18xyz

Question 13.
By using identity evaluate the following:
(i) 7³ – 10³ + 3³
Solution:
x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² – xy – yz – zx)
We know that a + b + c = 0 then a³ + b³ + c³ = 3ab
a + b + c = 7 + (-10) + 3
= 10 – 10
= 0
∴ 7³ – 10³ + 3³ = 3(7) (-10) (3)
= -630

(ii) 1 + \(\frac{1}{8}\) – \(\frac{27}{8}\)
Solution:
We know that a³ + b³ + c³ = 0 then a + b + c = 3abc

Question 14.
If 2x -3y – 4z = 0, then find 8x³ – 27y³ – 64z³.
Solution:
We know x³ +y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² – xy – yz – zx)
x³ + y³ + z³ = (x + y + z) (x² +y² + z² – xy – yz – zx) + 3xyz
8x³ – 27y³ – 64z³ = (2x)³ + (-3y)³ + (-4z)³
= (2x – 3y- 4z) [(2x)² + (-3y)² + (-4z)² – (2x)(-3y) – (-3y) (-4z) -(-4z)(2x)] + 3(2x)(-3y)(-4z)
= 0 (4x² + 9y² + 16z² + 6xy – 12yz + 8xz) + 72xyz
= 72xyz
8x³ – 27y³ – 64z³ = 72xyz

Students can download Maths Chapter 2 Real Numbers Ex 2.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.3

Question 1.
Represent the following irrational numbers on the number line.
(i) \(\sqrt{3}\)
Solution:

Steps of construction:
1. Draw a line and mark a point A and B such that AB = 3 cm.
2. Mark a point C on this line such that BC = 1 cm.
3. Find the mid point of AC by drawing perpendicular bisector of AC and let it be “O”.
4. With O as centre and OC = OA as radius draw a semicircle.
5. Draw a line BD, which is perpendicular to AB at B.
6. Now BD = \(\sqrt{3}\) which can be marked in the number line as the value of BE = BD = \(\sqrt{3}\)

(ii) Represent \(\sqrt{4.7}\) on a number line.
Solution:

Steps of construction:
1. Draw a line and mark a point A and B such that AB = 4.7 cm.
2. Mark a point C on this line such that A BC = 1 cm.
3. Find the mid point of AC by drawing perpendicular bisector of AC and let it be “O”.
4. With O as centre and OC = OA as radius draw a semicircle.
5. Draw a line BD, which is perpendicular to AB at B.
6. Now BD = \(\sqrt{4.7}\), which can be marked in the number line as the value of BE = BD = \(\sqrt{4.7}\).

(iii) Represent \(\sqrt{6.5}\) on a number line.
Solution:

Steps of construction:
1. Draw a line and mark a point A and B such that AB = 6.5 cm.
2. Mark a point C on this line such that BC = 1 cm.
3. Find the mid point of AC by drawing perpendicular bisector of AC and let it be “O”.
4. With O as centre and OC = OA as radius draw a semicircle.
5. Draw a line BD, which is perpendicular to AB at B.
6. Now BD = \(\sqrt{6.5}\), which can be marked in the number line as the value of BE = BD = \(\sqrt{6.5}\)

Question 2.
Find any two irrational numbers between
(i) 0.3010011000111…. and 0.3020020002….
Solution:
Two irrational numbers between the given two rational numbers are 0.301202200222……. and 0.301303300333……..

(ii) \(\frac{6}{7}\) and \(\frac{12}{13}\)
Solution:
\(\frac{6}{7}\) = 0.\(\overline {857142}\)
\(\frac{12}{13}\) = 0.\(\overline {923076}\)
The two irrational numbers are 0.8616611666111…….. and 0.8717711777111………

(iii) \(\sqrt{2}\) and \(\sqrt{3}\)
Solution:

\(\sqrt{2}\) = 1.414
\(\sqrt{3}\) = 1.732
The two irrational numbers between \(\sqrt{2}\) and \(\sqrt{3}\) are 1.515511555……. and 1.616611666………..

Question 3.
Find any two rational numbers between 2.2360679……… and 2.236505500……….
Solution:
The two rational numbers are 2.2362 and 2.2363 (It has many answers)

Students can download Maths Chapter 2 Real Numbers Ex 2.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.2

Question 1.
Express the following rational numbers into decimal and state the kind of decimal expression.
(i) \(\frac{2}{7}\)
(ii) -5\(\frac{3}{11}\)
(iii) \(\frac{22}{3}\)
(iv) \(\frac{327}{200}\)
Solution:

(i) \(\frac{2}{7}\) = 0.2857142….
= 0.\(\overline {285714}\)
Non-terminating and recurring decimal expansion.

(ii) -5\(\frac{3}{11}\) = -5 + 0.272 = -5.272……..

= -5.\(\overline {27}\)
Non-terminating and recurring decimal expansion.

(iii) \(\frac{22}{3}\) = 7.333……..

= 7.\(\overline {3}\)
Non-terminating and recurring decimal expansion.

(iv) \(\frac{327}{200}\) = \(\frac{327}{2×100}\)

= \(\frac{3.27}{2}\)
= 1.635
Terminating decimal expansion.

Question 2.
Express \(\frac{1}{13}\) in decimal form. Find the length of the period of decimals.
Solution:

\(\frac{1}{13}\) = 0.07692307
= 0.\(\overline {076923}\)
Length of the period of decimal is 6.

Question 3.
Express the rational number \(\frac{1}{33}\) in recurring decimal form by using the recurring decimal expansion of \(\frac{1}{11}\). Hence write \(\frac{71}{33}\) in recurring decimal form.
Solution:

\(\frac{1}{11}\) = 0.0909……… = 0.\(\overline {09}\)
∴ \(\frac{1}{33}\) = \(\frac{1}{3}\) × \(\frac{1}{11}\)
= \(\frac{1}{3}\) × 0.0909 ……..
= 0.0303 …… = 0.\(\overline {03}\)
\(\frac{71}{33}\) = 2\(\frac{5}{33}\) = 2 + \(\frac{5}{33}\) = 2 + 5 × \(\frac{1}{33}\)
= 2 + 5 × 0.\(\overline {03}\)
2 + (5 × 0.030303 ……..)
2 + 0.151515 ………
2+ 0.\(\overline {15}\)
2.\(\overline {15}\)

Question 4.
Express the following decimal expression into rational numbers.
(i) 0.24
Solution:
Let x = 0.242424 ………. →(1)
100 x = 24.2424 ……… →(2)
(2) – (1) ⇒ 100 x – x = 24.2424 ……….. (-)
 0.2424 ……..
99 x = 24.0000
x = \(\frac{24}{99}\)
(or)
\(\frac{8}{33}\)

(ii) 2.327
Solution:
Let x = 2.327327327 ………. →(1)
1000 x = 2327.327327 ……… →(2)
(2) – (1) ⇒ 1000 x – x = 2327.327327 ……….. (-)
  2.327327 ……..
999 x = 2325.000
x = \(\frac{2325}{999}\)
(or)
\(\frac{775}{333}\)

(iii) – 5.132
Solution:
– 5.132 = -5 + \(\frac{1}{10}\) + \(\frac{3}{100}\) + \(\frac{2}{1000}\)
= \(\frac{-5000 + 100 +30 + 2}{1000}\) = \(\frac{-4868}{1000}\)
(or)
\(\frac{-1217}{250}\)

(iv) 3.17
Solution:
Let x = 3.1777 ………. →(1)
10 x = 31.777 ……… →(2)
100 x = 317.77 …….. →(3)
(3) – (2) ⇒ 100 x – 10 x = 317.77 ……….. (-)
 31.777 ……..
90 x = 286.000
x = \(\frac{286}{90}\)
(or)
\(\frac{143}{45}\)

(v) 17.215
Solution:
Let x = 17.2151515 ………. →(1)
10 x = 172.151515 ……… →(2)
100 x = 17215.1515 …….. →(3)
(3) – (2) ⇒ 1000 x – 10 x = 17215.1515 ……….. (-)
 17215.1515 ……..
990 x = 17043
x = \(\frac{17043}{990}\)
(or)
\(\frac{5681}{330}\)

(vi) -21.2137
Solution:
Let x = -21.213777 ………. →(1)
1000 x = -21213.777 ……… →(2)
100 x = -212137.77 …….. →(3)
(3) – (2) ⇒ 10000 x – 1000 x = -21213.777 ……….. (-)
-21213.777 ……..
9000 x = -190924
x = \(\frac{-190924}{9000}\)
(or)
\(\frac{-47731}{2250}\)

Question 5.
Without actual division, find which of the following rational numbers have terminating decimal expression.
(i) \(\frac{7}{128}\)
Solution:

\(\frac{7}{128}\) = \(\frac{7}{2^{7}}\)
∴ \(\frac{7}{128}\) has terminating decimal expression.

(ii) \(\frac{21}{15}\)
Solution:
\(\frac{21}{15}\) = \(\frac{7}{5}\) = \(\frac{7}{5^1}\)
\(\frac{21}{15}\) has terminating decimal expression.

(iii) 4\(\frac{9}{35}\)
Solution:
4\(\frac{9}{35}\) = \(\frac{149}{35}\)
4\(\frac{149}{5×7}\) (It is not in the form of \(\frac{P}{2^{m} × 5^{n}}\)
∴ 4\(\frac{9}{35}\) has non-terminating recurring decimal expression.

(iv) \(\frac{219}{2200}\)
Solution:

\(\frac{219}{2200}\) = \(\frac{219}{2^{3} × 5^{2} × 11}\) (It is not in the form of \(\frac{P}{2^{m} × 5^{n}}\)
∴ \(\frac{219}{2200}\) has non-terminating recurring decimal expression.

Students can download Maths Chapter 1 Set Language Ex 1.5 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.5

Question 1.
Using the adjacent Venn diagram, find the following sets:

(i) A – B
(ii) B – C
(iii) A’∪B’
(iv) A’∩B’
(v) (B∪C)’
(vi) A – (B∪C)
(vii) A – (B∩C)
Solution:
From the diagram we get
U = {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8},
A= {-2,-1, 3, 4, 6}, B = {-2,-1, 5, 7, 8}
C = {-3, -2, 0, 3, 8}
A’ = U – A = {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8} – {-2, -1, 3, 4, 6}
= {-3, 0, 1, 2, 5, 7, 8}
B’ = U – B = {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8} – {-2, -1, 5, 7, 8}
= {-3, 0, 1, 2, 3, 4, 6}
B∪C = {-2, -1, 5, 7, 8} ∪ {-3, -2, 0, 3, 8} = {-3, -2, -1, 0, 3, 5, 7, 8}
B∩C = {-2, -1, 5, 7, 8} ∩ {-3, -2, 0, 3, 8} = {-2, 8}

(i) A – B = {3, 4, 6}
(ii) B – C = {-1, 5, 7}
(iii) A’∪B’= {-3, 0, 1, 2, 5, 7, 8} ∪ {-3, 0, 1, 2, 3, 4, 6}
= {-3, 0, 1, 2, 3, 4, 5, 6, 7, 8}
(iv) A’∩B’ = {-3, 0, 1, 2, 5, 7, 8} ∩ {-3, 0, 1, 2, 3, 4, 6}
= {-3, 0, 1, 2}
(v) (B∪C)’ = U – (B∪C)= {-3,-2,-1,0, 1,2, 3,4, 5, 6, 7, 8} – {-3, -2, -1, 0, 3, 5, 7, 8}
= {1, 2, 4, 6}
(vi) A – (B∪C) = {-2, -1, 3, 4, 6} – {-3, -2, -1, 0, 3, 5, 7, 8} = {4, 6}
(vii) A – (B∩C) = {-2,-1, 3, 4, 6} – {-2, 8} = {-1, 3, 4, 6}

Question 2.
If K = {a, b, d, e, f}, L = {b, c, d, g} and M = {a, b, c, d, h} then find the following:
(i) K∪(L∩M)
(ii) K∩(L∪M)
(iii) (K∪L) ∩ (K∪M)
(iv) (K∩L) ∪ (K∩M)
and verify distributive laws.
Solution:
K = {a, b, d, e, f}, L = {b, c, d, g} and M = {a, b, c, d, h}
(i) K∪(L∩M)
(L∩M) = {b, c, d, g} ∩ [a, b, c, d, h}
= {b, c, d}
K∪(L∩M) = {a, b, d, e, f} ∪ {b, c, d}
= {a, b, c, d, e, f}

(ii) K∩(L∪M)
(L∪M) = {b, c, d, g} ∪ {a, b, c, d, h}
= {a, b, c, d, g, h}
K∩(L∪M) = {a, b, d, e, f} ∩ {a, b, c, d, g, h}
= {a, b, d }

(iii) (K∪L) ∩ (K∪M)
(K∪L) = {a, b, d, e, f} ∪ {b, c, d, g}
= {a, b, c, d, e, f, g}
(K∪M) = {a, b, d, e, f} ∪ {a, b, c, d, h}
= {a, b, c, d, e, f, h}
(K∪L) ∩ (K∪M) = {a, b, c, d, e, f, g} ∩ {a, b, c, d, e, f, h}
= {a, b, c, d, e, f}

(iv) (K∩L) ∪ (K∩M)
(K∩L) = {a, b, d, e, f) ∩ {b, c, d, g}
= {b, d}
(K∩M) = {a, b, d, e, f} ∩ {a, b, c, d, h}
= {a, b, d}
(K∩L) ∪ (K∩M) = {b, d} ∪ [a, b, d}
= {a, b, d}
From (ii) & (iv) we get, K∩(L∪M) = (K∩L) ∪ (K∩M)
From (i) & (iii) we get, K∪(L∩M) = (K∪L) ∩ (K∪M)

Question 3.
For A = {x : x ∈ Z, -2 < x ≤ 4}, B = {x : x ∈ W, x ≤ 5}, C = {-4, -1, 0, 2, 3, 4}
verify A∪(B∩C) = (A∪B) ∩ (A∪C).
Solution:
A = {-1, 0, 1, 2, 3, 4}, B = {0, 1, 2, 3, 4, 5} and C = {-4, -1, 0, 2, 3, 4}
B∩C = {0, 1, 2, 3, 4, 5} ∩ {-4, -1, 0, 2, 3, 4}
= {0, 2, 3, 4}
A∪(B∩C) = {-1, 0, 1, 2, 3, 4} ∪ {0, 2, 3, 4}
= {-1, 0, 1, 2, 3, 4} ……..(1)
A∪B = {-1, 0, 1, 2, 3, 4} ∪ {0, 1, 2, 3, 4, 5}
= {-1, 0, 1, 2, 3, 4, 5}
A∪C = {-1, 0, 1, 2, 3, 4} ∪ {-4, -1, 0, 2, 3, 4}
= {-4, -1, 0, 1, 2, 3, 4}
(A∪B) ∩ (A∪C) = {-1, 0, 1, 2, 3, 4, 5} ∩ {-4, -1, 0, 1, 2, 3, 4}
= {-1, 0, 1, 2, 3, 4} ……..(2)
From (1) and (2) we get A∪(B∩C) = (A∪B) ∩ (A∪C).

Question 4.
Verify A∪(B∩C) = (A∪B) ∩ (A∪C) using Venn diagrams.
Solution:

From (ii) and (v) we get A∪(B∩C) = (A∪B) ∩ (A∪C).

Question 5.
If A = {b, c, e, g, h}, B = {a, c, d, g, f}, and C = {a, d, e, g, h}, then show that A – (B∩C) = (A – B) ∪ (A – C).
Solution:
A = {b, c, e, g, h} ; B = {a, c, d, g, f}; C = {a, d, e, g, h}
B∩C = {a, c, d, g, i} ∩ {a, d, e, g, h}
= {a, d, g}
A – (B∩C) = {b, c, e, g, h} – {a, d, g}
= {b, c, e, h}…….(1)
A – B = {b, c, e, g, h} – {a, c, d, g, i}
= {b, e, h}
A – C = {b, c, e, g, h} – {a, d, e, g, h}
= {b, c}
(A – B) ∪ (A – C) = {b, e, h} ∪ {b, c}
= {b, c, e, h)……..(2)
From (1) and (2) we get A – (B∩C) = (A – B) ∪ (A – C)

Question 6.
If A= {x : x = 6n, n∈W and n < 6}, B = {x : x = 2n, n∈N and 2 < n ≤ 9} and
C = {x : x = 3n, n∈N and 4 ≤ n < 10}, then show that A – (B∩C) = (A – B) ∪ (A – C)
Solution:
A = {0, 6, 12, 18, 24, 30}; B = {6, 8, 10, 12, 14, 16, 18}; C = {12, 15, 18, 21, 24, 27}
B∩C = {6, 8, 10, 12, 14, 16, 18} ∩ {12, 15, 18, 21, 24, 27}
= {12, 18}
A – (B∩C) = {0, 6, 12, 18, 24, 30} – {12, 18}
= {0, 6, 24, 30}………(1)
A – B = {0, 6, 12, 18, 24, 30} – {6, 8, 10, 12, 14, 16, 18}
= {0, 24, 30}
A – C = {0, 6, 12, 18, 24, 30} – {12, 15, 18, 21, 24, 27}
= {0, 6, 30}
(A – B) ∪ (A – C) = {0, 24, 30} ∪ {0, 6, 30}
= {0, 6, 24, 30}……..(2)
From (1) and (2) we get A – (B∩C) = (A – B) ∪ (A – C).

Question 7.
If A = {-2, 0, 1, 3, 5}, B = {-1, 0, 2, 5, 6} and C = {-1, 2, 5, 6, 7}, then show that
A – (B∪C) = (A – B) ∩ (A – C).
Solution:
A= {-2, 0, 1, 3, 5}, B = {-1, 0, 2, 5, 6}, C = {-1, 2, 5, 6, 7}
B∪C = {-1, 0, 2, 5, 6} ∪ {-1, 2, 5, 6, 7}
= {-1, 0, 2, 5, 6, 7}
A – (B∪C) = {-2, 0, 1, 3, 5} – {-1, 0, 2, 5, 6, 7}
= {-2, 1, 3} ………(1)
A – B = {-2, 0, 1, 3, 5} – {-1, 0, 2, 5, 6}
= {-2, 1, 3}
A – C = {-2, 0, 1, 3, 5}- {-1, 2, 5, 6, 7}
= {-2, 0, 1, 3}
(A- B) ∩ (A- C) = {-2, 1, 3} ∩ {-2, 0, 1, 3}
= {-2, 1, 3} ….(2)
From (1) and (2) we get A – (B∪C) = (A – B) ∩ (A – C).

Question 8.
IF A = {y : y = \(\frac{a + 1}{2}\), a ∈ W and a ≤ 5}, B = {y : y = \(\frac{2n – 1}{2}\), n ∈ W and n < 5} and C = {-1, \(-\frac{1}{2}\), 1, \(\frac{3}{2}\), 2} then show that A – (B∪C) = (A – B) ∩ (A – C).
Solution:

From (1) and (2) we get A – (B∪C) = (A – B) ∩ (A – C).

Question 9.
Verify A- (B∩C) = (A – B) ∪ (A – C) using Venn diagrams.
Solution:


From (ii) and (v) we get A- (B∩C) = (A – B) ∪ (A – C).

Question 10.
If U = {4, 7, 8, 10, 11, 12, 15, 16} , A = {7, 8, 11, 12} and B = {4, 8, 12, 15}, then verify De Morgan’s Laws for complementation.
U= {4, 7, 8, 10, 11, 12, 15, 16} , A = {7, 8, 11, 12} and B = {4, 8, 12, 15}
(i) (A∪B)’ = A’∩B’
(ii) (A∩B)’ = A’∪B’
Solution:
(i) A∪B = {7, 8, 11, 12} ∪ {4, 8, 12, 15}
= {4, 7, 8, 11, 12, 15}
(A∪B)’ = {4, 7, 8, 10, 11, 12, 15, 16} – {4, 7, 8, 11, 12, 15}
= {10,16} ………(1)
A’ = {4, 7, 8, 10, 11, 12, 15, 16} – {7, 8, 11, 12}
= {4, 10, 15, 16}
B’ = {4, 7, 8, 10, 11, 12, 15, 16} – {4, 8, 12, 15}
= {7, 10, 11, 16}
A’∩B’ = {4, 10, 15, 16} ∩ {7, 10, 11, 16}
= {10,16} ………(2)
From (1) and (2) we get (A∪B)’ = A’∩B’

(ii) A∩B = {7, 8, 11, 12} ∩ {4, 8, 12, 15}
= {8, 12}
(A∩B)’ = {4, 7, 8, 10, 11, 12, 15, 16} – {8, 12}
= {4, 7, 10, 11, 15, 16} ………(1)
A’ = {4, 10, 15, 16}
B’ = {7, 10, 11, 16}
A’∪B’ = {4, 10, 15, 16} ∪ {7, 10, 11, 16}
= {4, 7, 10, 11, 15, 16} ………(2)
From (1) and (2) we get (A∩B)’ = A’∪B’

Question 11.
Verify (A∩B)’ = A∪B’ using Venn diagrams.
Solution:

From (ii) and (i) we get (A∩B)’ = A’∪B’

Students can download Maths Chapter 2 Real Numbers Ex 2.5 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.5

Question 1.
Write the following in the form of \(5^n\):
(i) 625
(ii) \(\frac{1}{5}\)
(iii) \(\sqrt{5}\)
(iv) \(\sqrt{125}\)
Solution:
(i) 625 = 5⁴

(ii) \(\frac{1}{5}\) = 5^-1
(iii) \(\sqrt{5}\) = \(5^\frac{1}{2}\)
(iv) \(\sqrt{125}\) = \(\sqrt{5^3}\) = \((5^3)^\frac{1}{2} = 5^\frac{3}{2}\)

Question 2.
Write the following in the form of \(4^n\):
(i) 16
(ii) 8
(iii) 32
Solution:
(i) 16
= 4 × 4
= 4²

(ii) 8
= 4 × 2
= 4 × \(\left(2^{2}\right)^{\frac{1}{2}} \)
= 4 \(\times 4^{\frac{1}{2}} \)
= 4\(^{1+\frac{1}{2}} \)
= 4\(^{\frac{2+1}{2}} \)
= 4\(^{3 / 2}\)

(iii) 32
= 4 × 4 × 2
= 4² × \(\left(2^{2}\right)^{\frac{1}{2}} \)
= 4\(^{2} \times 4^{\frac{1}{2}} \)
= 4\(^{2+\frac{1}{2}} \)
= 4\(^{\frac{4+1}{2}} \)
= 4\(^{\frac{5}{2}} \)

Question 3.
Find the value of
(i) (49)\(^\frac{1}{2}\)
(ii) (243)\(^\frac{2}{5}\)
(iii) (9)\(^\frac{-3}{2}\)
(iv) \((\frac{64}{125})^\frac{-2}{3}\)
Solution:
(i) 49\(^\frac{1}{2}\) = \((7^2)^\frac{1}{2}\) = 7\(^{2 × \frac{1}{2}}\) = 7
(ii) (243)\(^\frac{2}{5}\) = \((3^5)^\frac{2}{5}\) = 3\(^{5 × \frac{2}{5}}\) = 3² = 9

(iii) \(9^{\frac{-3}{2}}=\left(3^{2}\right)^{\frac{-3}{2}}=3^{2 \times \frac{-3}{2}}=3^{-3}=\frac{1}{3^{3}}=\frac{1}{27}\)
(iv) \(\left(\frac{64}{125}\right)^{\frac{-2}{3}}=\left(\frac{4^{3}}{5^{3}}\right)^{\frac{-2}{3}}=\left[\left(\frac{4}{5}\right)^{3}\right]^{\frac{-2}{3}}=\left(\frac{4}{5}\right)^{3 \times \frac{-2}{3}}=\left(\frac{4}{5}\right)^{-2}=\frac{4^{-2}}{5^{-2}}=\frac{5^{2}}{4^{2}}=\frac{25}{16} \)

Question 4.
Use a fractional index to write:
(i) \(\sqrt{5}\)
(ii) \(\sqrt[2]{7}\)
(iii) (\(\sqrt[3]{49})^{5}\)
(iv) \((\frac{1}{\sqrt[3]{100}})^{7}\)
Solution:
(i) \(\sqrt{5}\) = (5)\(^\frac{1}{2}\)
(ii) \(\sqrt[2]{7}\) = 7\(^\frac{1}{2}\)
(iii) \((\sqrt[3]{49})^{5}=\left[(49)^{\frac{1}{3}}\right]^{5}=\left[\left(7^{2}\right)^{\frac{1}{3}}\right]^{5}=\left(7^{\frac{2}{3}}\right)^{5}=7^{\frac{2}{3} \times 5}=7^{\frac{10}{3}}\)
(iv) \(\left(\frac{1}{\sqrt[3]{100}}\right)^{7}=\left[\frac{1}{\sqrt[3]{10^{2}}}\right]^{7}=\left[\frac{1}{\left(10^{2}\right)^{1 / 3}}\right]^{7}=\left[\frac{1}{10^{2 / 3}}\right]^{7}=\left(10^{\frac{-2}{3}}\right)^{7}=10^{\frac{-2}{3} \times 7}=10^{\frac{-14}{3}}\)

Question 5.
Find the 5th root of:
(i) 32
(ii) 243
(iii) 100000
(iv) \(\frac{1024}{3125}\)
Solution:
(i) \(\sqrt[5]{32}=(32)^{\frac{1}{5}}=\left(2^{5}\right)^{\frac{1}{5}}=2^{5 \times \frac{1}{5}} \) = 2

(ii) \(\sqrt[5]{243}=(243)^{\frac{1}{5}}=\left(3^{5}\right)^{\frac{1}{5}}=3^{5 \times \frac{1}{5}}\) = 3

(iii) \(\sqrt[5]{100000}=(100000)^{\frac{1}{5}}=\left(10^{5}\right)^{\frac{1}{5}}\)
= \(10^{5}\times{\frac{1}{5}}\)

Students can download Maths Chapter 2 Real Numbers Ex 2.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.4

Question 1.
Represent the following numbers on the number line.
(i) 5.348
Solution:
5.348 lies between 5 and 6.

Steps of construction:
1. Divide the distance between 5 and 6 into 10 equal intervals.
2. Mark the point 5.3 which is the sixth from the left of 6 and 3 from the right of 5.
3. 5.34 lies between 5.3 and 5.4. Divide the distance into 10 equal intervals.
4. Mark the point 5.34 which is sixth from the left of 5.40
5. 5.348 lies between 5.34 and 5.35. Divide the distance into 10 equal intervals.
6. Mark a point 5.348 which is second from the left of 5.350 and seventh form the right of 5.340

(ii) 6.\(\overline {4}\) upto 3 decimal places.
Solution:
6.\(\overline {4}\) = 6.4444
6.\(\overline {4}\) = 6.444 (correct to 3 decimal places)
The number lies between 6 and 7.

Steps of construction:
1. Divide the distance between 6 and 7 into 10 equal intervals.
2. Mark the point 6.4 which is the sixth from the left of 7 and fourth from the right of 6.
3. 6.44 lies between 6.44 and 6.45. Divide the distance into 10 equal intervals.
4. Mark the point 6.44 which is sixth from the left of 6.5 and fourth from the right of 6.40.
5. Mark the point 6.444 which is sixth from the left of 6.450 and fourth from the right of 6.440.

(ii) 4.\(\overline {73}\) upto 4 decimal places.
Solution:
4.\(\overline {73}\) = 4.737373……..
= 4.737374 (correct to 4 decimal places 4.7374 lies between 4 and 5)

Steps of construction:
1. Divide the distance between 4 and 5 into 10 equal parts.
2. Mark the point 4.7 which is third from the left of 5 and seventh from the right of 4.
3. 4.73 lies between 4.7 and 4.8. Divide the distance into 10 equal intervals.
4. Mark the point 4.73 which is seventh from the left of 4.80 and third from the left of 4.70.
5. 4.737 lies between 4.73 and 4.74. Divide the distance into 10 equal intervals.
6. Mark the point 4.737 which is third from the left of 4.740 and seventh from the right of 4.730.
7. 4.7374 lies between 4.737 and 4.738. Divide the distance into 10 equal intervals.
8. Mark the point 4.7374 which is sixth from the left of 4.7380 and fourth from the right of 4.7370.

Students can download Maths Chapter 1 Set Language Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Additional Questions

Choose the correct answer

Question 1.
A = {set of odd natural numbers}, B = {set of even natural numbers}, then A and B are……….
(a) equal set
(b) equivalent sets
(c) overlapping sets
(d) disjoint sets
Solution:
(d) disjoint sets

Question 2.
Number of subsets in set A = {1, 2, 3} is
(a) 3
(b) 6
(c) 8
(d) 9
Solution:
(c) 8

Question 3.
The set does not have a proper subset is
(a) Finite set
(b) Infinite set
(c) Null set
(d) Singleton set
Solution:
(c) Null set

Question 4.
Sets having the same number of elements are called
(a) overlapping sets
(b) disjoints sets
(c) equivalent sets
(d) equal sets
Solution:
(c) equivalent sets

Question 5.
The set (A – B) ∪ (B – A) is
(a) AΔB
(b) A∪B
(c) A∩B
(d) A’∪B’
Solution:
(a) AΔB

Question 6.
The set of (A∪B) – (A∩B) is
(a) (A∪B)’
(b) AΔB
(c) (A∩B)’
(d) A’∪B’
Solution:
(b) AΔB

Question 7.
The set {x : x ∈ A, x ∈ B, x ∉ A∩B} is
(a) A∩B
(b) A∪B
(c) A – B
(d) AΔB
Solution:
(d) AΔB

Question 8.
The number of elements of the set {x : x ∈ Z , x² = 1} is
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(c) 2

Question 9.
If A is a proper subset of B, then A∩B =…………..
(a) A
(b) B
(c) 0
(d)A∪B
Solution:
(a) A

Question 10.
The shade region with adjoint diagram represents ……….

(a) A – B
(b) B – A
(c) A’
(d) B’
Solution:
(c) A’

Question 11.
From the given venn diagram (A∪B)’ is ………..

(a) {5, 6}
(b) {1, 2, 3, 4, 7}
(c) {1, 2, 3, 4, 5, 6, 7}
(d) {8, 9}
Solution:
(d) {8, 9}

Question 12.
If n(A∪B∪C) = 73, n(A) = 2x, n(B) = 3x, n(C) = 5x, n(A∩B) = 10, n(B∩C) = 15, n(A∩C) = 5 and n(A∩B∩C) = 3, then the value of x is ………
(a) 9
(b) 10
(c) 5
(d) 18
Solution:
(b) 10

Question 13.
For any three sets, n(A∪B∪C) = 60, n(A) = 25, n(B) = 20, n(C) = 15, n(A∩B) = 10, n(B∩C) = 7, n(A∩C) = 3, then n(A∩B∩C) is……….
(a) 10
(b) 15
(c) 20
(d) 25
Solution:
(c) 20

Question 14.
If n(U) = 70, n(A) = 25, n(B) = 30, n(A∩B) = 5, then n(A∪B)’ is……….
(a) 5
(b) 10
(c) 15
(d) 20
Solution:
(d) 20

Question 15.
Which of the following is not correct?
(a) A – (B∪C) = (A – B) ∩ (A – C)
(b) A – (B∩C) = (A – B) ∪ (A – C)
(c) (A∪B)’ = A’∩B’
(d) A’∪B’ = (A – B)’
Solution:
(d) A’∪B’ = (A – B)’

Answer the following questions.

Question 1.
Write the following in “Roster” form?
(a) A = set of the months having 31 days.
(b) B = {x : x is a natural number of 2 digits divisible by 13}
(c) C = {set of vowels in the word “father”}
(d) D = {x : 5 < x ≤ 10; x ∈ N}
(e) E = {x : x is a square natural number less than 16}
Solution:
(a) A = {Jan, March, May, July, Aug, Oct, Dec}
(b) B = {13, 26, 39, 52, 65, 78, 91}
(c) C = {a, e}
(d) D = {6, 7, 8, 9, 10}
(e) E = {1, 4, 9}

Question 2.
Given that A = {1, 3, 5, 7} B = {1, 2, 4, 6, 8}. Find
(i) AΔB and
(ii) BΔA
Solution:
(i) A = {1, 3, 5, 7}; B = {1, 2, 4, 6, 8}
A – B = {1, 3, 5, 7} – {1, 2, 4, 6, 8}
= {3, 5, 7}
B – A = {1, 2, 4, 6, 8} – {1, 3, 5, 7}
= {2, 4, 6, 8}
AΔB = (A – B) ∪ (B – A)
= {3, 5, 7} ∪ {2, 4, 6, 8}
= {2, 3, 4, 5, 6, 7, 8}
(ii) BΔA = (B – A) ∪ (A – B)
= {2, 4, 6, 8} ∪ {3, 5, 7}
= {2, 3, 4, 5, 6, 7, 8}

Question 3.
From the venn-diagram, list the following:

(i) A
(ii) B
(iii) A∩B
(iv)A∪B
(v) A – B
(vi) B – A
(vii) (A – B) ∩ (B – A)
Solution:
(i) A = {1, 2, 5, 6, 7}
(ii) B = {3, 4, 5, 6}
(iii) A∩B = {5, 6}
(iv) A∪B = {1, 2, 3, 4, 5, 6, 7}
(v) A – B = {1, 2, 7}
(vi) B – A = {3, 4}
(vii) (A – B) ∩ (B – A) = { }

Question 4.
In a class there are 40 students. 26 have opted for Mathematics and 24 have opted for Science. How many student have opted for Mathematics and Science.
Solution:
Let M be the set of students opting for Mathematics.
Let S be the set of students opting for Science.
n (M∪S) = 40, n (M) = 26, n(S) = 24
n(M∪S) = n (M) + n (S)- n(M∩S)
40 = 26 + 24 – n(M∩S)
n (M∩S) = 26 + 24 – 40 = 50 – 40 = 10
∴ Number of students opted for Mathematics and Science = 10.
Another Method:
Let “x” be the number of students opted for Mathematics and Science.
Let M and S represent students opting Mathematics and Science.
n(M∪S) = 40, n(M) = 26, n(S) = 24

By venn-diagram, number of students in a class = 26 – x + x + 24 – x
40 = 50 – x
x = 50 – 40 = 10
x = 10
∴ Number of students opted for Mathematics and Science = 10.

Question 5.
If U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {4, 5, 7, 9}, B = {1, 3, 5, 7, 8}, Verify De Morgan’s Laws for complementation.
De Morgan’s Laws (i) (A∪B)’ = A’∩B’ (ii) (A∩B)’ = A’∪B’
Solution:
(i) A∪B = {4, 5, 7, 9} ∪ {1, 3, 5, 7, 8}
= {1, 3, 4, 5, 7, 8, 9}
(A∪B)’ = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 3, 4, 5, 7, 8, 9}
= {2, 6}……….(1)
A’= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {4, 5, 7, 9}
= {1, 2, 3, 6, 8}
B’ = {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 3, 5, 7, 8}
= {2, 4, 6, 9}
A’∩B’ = {1, 2, 3, 6, 8} ∩ {2, 4, 6, 9}
= {2, 6}………(2)
From (1) and (2) we get (A∪B)’ = A’∩B’.

(ii) A∩B = {4, 5, 7, 9} ∩ {1, 3, 5, 7, 8}
= {5, 7}
(A∩B)’= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {5, 7}
= {1, 2, 3, 4, 6, 8, 9}………(1)
A’ = {1, 2, 3, 6, 8}
B’ = {2, 4, 6, 9}
A’∪B’ = {1, 2, 3, 6, 8} ∪ {2, 4, 6, 9}
= {1, 2, 3, 4, 6, 8, 9}………(2)
From (1) and (2) we get (A∩B)’ = A’∪B’.

Students can download Maths Chapter 1 Set Language Ex 1.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.3

Question 1.
Using the given venn diagram, write the elements of

(i) A
(ii) B
(iii) A∪B
(iv) A∩B
(v) A – B
(vi) B – A
(vii) A’
(viii) B’
(ix) U
Solution:
(i) A = {2, 4, 7, 8, 10}
(ii) B = {3, 4, 6, 7, 9, 11}
(iii) A∪B = {2, 3, 4, 6, 7, 8, 9, 10, 11}
(iv) A∩B = {4, 7}
(v) A – B = {2, 8, 10}
(vi) B – A = {3, 6, 9, 11}
(vii) A’ = {1, 3, 6, 9, 11, 12}
(viii) B’ = {1,2, 8, 10, 12}
(ix) U = {1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12}

Question 2.
Find A∪B, A∩B, A – B and B – A for the following sets
(i) A = {2, 6, 10, 14} and B = {2, 5, 14, 16}
Solution:
A∪B = {2, 6, 10, 14} ∪ {2, 5, 14, 16}
= {2, 5, 6, 10, 14, 16}
A∩B = {2, 6, 10, 14} ∩ {2, 5, 14, 16}
= {2, 14}
A – B = {2, 6, 10, 14} – {2, 5, 14, 16}
= {6, 10}
B – A = {2, 5, 14, 16} – {2, 6, 10, 14}
= {5, 16}

(ii) A = {a, b, c, e, u} and B = {a, e, i, o, u}
Solution:
A∪B = {a, b, c, e, u} ∪ {a, e, i, o, u}
= {a, b, c, e, i, o, u}
A∩B = {a, b, c, e, u} ∩ {a, e, i, o, u}
= {a, e, u}
A – B = {a, b, c, e, u} – {a, e, i, o, u}
= {b, c}
B – A = {a, e, i, o, u} – {a, b, c, e, u}
= {i, o}

(iii) A = {x : x ∈ N, x ≤ 10} and B = {x : x ∈ W, x < 6}
Solution:
A = {1, 2, 3, 4, 5, 6,7, 8, 9, 10} and B = {0, 1, 2, 3, 4, 5}
A∪B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ∪ {0, 1, 2, 3, 4, 5}
= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A∩B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} ∩ {0, 1, 2, 3, 4, 5}
= {1, 2, 3, 4, 5}
A – B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {0, 1, 2, 3, 4, 5}
= {6, 7, 8, 9, 10}
B – A = {0, 1, 2, 3, 4, 5} – {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
= {0}

(iv) A = Set of all letters in the word “mathematics” and B = Set of all letters in the word “geometry”
Solution:
A = {m, a, t, h, e, i, c, s}
B = {g, e, o, m, t, r, y}
A∪B = {m, a, t, h, e, i, c, s} ∪ {g, e, o, m, t, r, y}
= {a, c, e, g, h, i, m, o, r, s, t, y}
A∩B= {m, a, t, h, e, i, c, s} ∩ {g, e, o, m, t, r, y}
= {e, m, t}
A – B = {m, a, t, h, e, i, c, 5} – {g, e, o, m, t, r, y}
= {a, c, h, i, s}
B -A = {g, e, o, m, t, r, y} – {m, a, t, h, e, i, c, s}
= {g, o, r, y}

Question 3.
If U = {a, b, c, d, e, f, g, h), A = {b, d, f, h} and B = {a, d, e, h}, find the following sets.
(i) A’
Solution:
A’ = U – A
= {a, b, c, d, e, f, g, h} – {b, d, f, h)
= {a, c, e, g}

(ii) B’
Solution:
B’ = U – B
= {a, b, c, d, e, f, g, h} – {a, d, e, h}
= {b, c, f, g}

(iii) A’∪B’
Solution:
A’∪B’ = {a, c, e, g} ∪ {b, c,f, g}
= {a, b, c, e, f, g}

(iv) A’∩B’
Solution:
A’∩B’ = {a, c, e, g} ∩ {b, c, f, g}
= {c, g}

(v) (A∪B)’
Solution:
A∪B = {b, d, f, h} ∪ {a, d, e, h}
= {a, b, d, e, f, h}
(A∪B)’ = U – (A∪B)
= {a, b, c, d, e, f, g, h} – {a, b, d, e, f, h}
= {c, g}

(vi) (A∩B)’
Solution:
(A∩B) = {b, d, f, h) ∩ {a, d, e, h)
= {d, h}
(A∩B)’ = U – (A∩B)
= {a, b, c, d, e, f, g, h} – {d, h}
= {a, b, c, e, f, g}

(vii) (A’)’
Solution:
A’ = {a, c, e, g}
(A’)’ = U – A’
= {a, b, c, d, e, f, g, h} – {a, c, e, g}
= {b, d, f, h}

(viii) (B’)’
Solution:
B’ = {b, c, f, g}
(B’)’ = U – B’
= {a, b, c, d, e, f, g, h) – {b, c, f, g)
= {a, d, e, h}

Question 4.
Let U = {0, 1, 2, 3, 4, 5, 6, 7} A = {1, 3, 5, 7} and B = {0, 2, 3, 5, 7}, find the following sets.
(i) A’
Solution:
A’ = U – A
= {0, 1, 2, 3, 4, 5, 6, 7} – {1, 3, 5, 7}
= {0, 2, 4, 6}

(ii) B’ = U – B
Solution:
= {0, 1, 2, 3, 4, 5, 6, 7} – {0, 2, 3, 5, 7}
= {1, 4, 6}

(iii) A’∪B’
Solution:
A’∪B’ = {0, 2, 4, 6,}∪{1, 4, 6}
{0, 1, 2, 4, 6}

(iv) A’∩B’
Solution:
A’∩B’ = {0, 2, 4, 6,}∩{1, 4, 6}
{4, 6}

(v) (A∪B)’
Solution:
A∪B = {1, 3, 5, 7}∪{0, 2, 3, 5, 7}
= {0, 1, 2, 3, 5, 7}
(A∪B)’ = U – (A∪B)
{0, 1, 2, 3, 4, 5, 6, 7} – {0, 1, 2, 3, 5, 7}
{4, 6}

(vi) (A∩B)’
Solution:
(A∩B)= {1, 3, 5, 7}∩{0, 2, 3, 5, 7}
= {3, 5, 7}
(A∩B)’ = U – (A∩B)
= {0, 1, 2, 3, 4, 5, 6, 7} – {3, 5, 7}
= {0, 1, 2, 4, 6}

(vii) (A’)’
A’ = {0, 2, 4, 6}
(A’)’ = U – A’
= {0, 1, 2, 3, 4, 5, 6, 7} – {0, 2, 4, 6}
= {1, 3, 5, 7}

(viii) (B’)’
B’ = {1, 4, 6}
(B’)’ = {0, 1, 2, 3, 4, 5, 6, 7} – {1, 4, 6}
= {0, 2, 3, 5, 7}

Question 5.
Find the symmetric difference between the following sets.
(i) P = {2, 3, 5, 7, 11} and Q = {1, 3, 5, 11}
Solution:
Use anyone of the formula to find A & B
AΔB = (A – B)∪(B – A) or AΔB = (A∪B) – (A∩B)
P∪Q = {2, 3, 5, 7, 11} ∪ {1,3,5, 11}
= {1, 2, 3, 5, 7, 11}
P∩Q = {2, 3, 5, 7, 11}∩{1, 3, 5,11}
= {3, 5, 11}
PΔQ = (P∪Q) – (P∩Q)
= {1, 2, 3, 5, 7, 11} – {3, 5, 11}
= {1, 2, 7}
(OR)
P – Q = {2, 3, 5, 7, 11} – {1, 3, 5, 11}
= {2,7}
Q – P = {1, 3, 5, 11} – {2, 3, 5, 7, 11}
= {1}
PΔQ = (P – Q)∪(Q – P)
= {2, 7} ∪ {1}
= {1, 2, 7}

(ii) R = {l, m, n, o, p} and S = {j, l, n, q}
Solution:
R- S = {l, m, n, o, p} – {j, l, n, q}
= {m, o, p}
S – R = {j, l, n, q} – {l, m, n, o, p}
= {j, q}
RΔS = (R – S)∪(S – R)
= {m, o, p} – {j, q} = {j, m, o, p, q)
(OR)
R∪S = {l, m, n, o, p} ∪ {j,l,n,q}
= {l, m, n, o, p, j, q}
R∩S = {l, m, n, o,p} ∩ {j, l, n, q}
= {l, n}
RΔS = (R∪S) – (R∩S)
= {l, m, n, o, p, j, q} – { l, n}
= {m, o, p, j, q}

(iii) X = {5, 6, 7} and Y = {5, 7, 9, 10}
Solution:
X∪Y = {5, 6, 7} ∪ {5, 7, 9, 10}
= {5 ,6, 7, 9, 10}
X∩Y = {5, 6, 7} ∩ {5, 7, 9, 10}
= {5, 7}
XΔY = (X∪Y) – (X∩Y)
= {5, 6, 7, 9, 10} – {5, 7}
= {6, 9, 10}
OR
X – Y = {5, 6, 7} – {5, 7, 9, 10} = {6}
Y – X = {5, 7, 9, 10} – {5, 6, 7} = {9, 10}
XΔY = (X – Y) ∪ (Y – X)
= {6}∪{9, 10}
= {6, 9, 10}

Question 6.
Using the set symbols, write down the expressions for the shaded region in the following

Solution:

Question 7.
Let A and B be two overlapping sets and the universal set U. Draw appropriate Venn diagram for each of the following,
(i) A∪B
(ii) A∩B
(iii) (A∩B)’
(iv) (B – A)’
(v) A’∪B’
(Vi) A’∩B’
(vii) What do you observe from the Venn diagram (iii) and (v)?
Solution:
(i) A∪B

(ii) A∩B

(iii) (A∩B)’

(iv) (B – A)’

(v) A’∪B’

(Vi) A’∩B’

(vii) What do you observe from the diagram (iii) and (v)?
From the diagram (iii) and (v) we get (A∩B)’ = A’∪B’