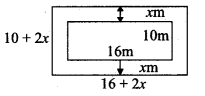
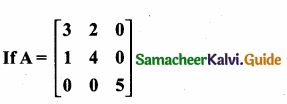
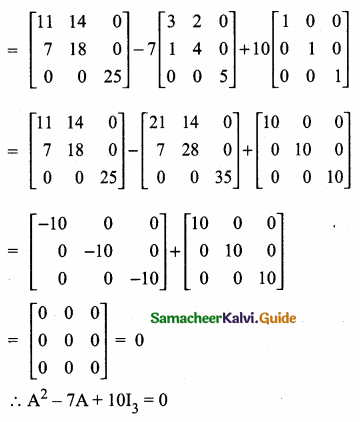
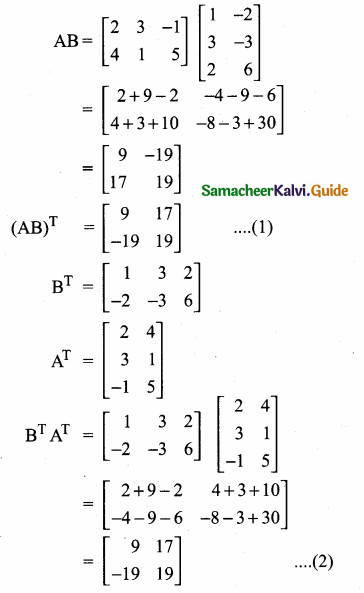
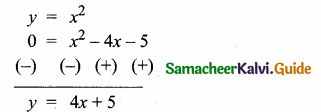
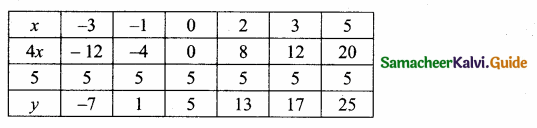
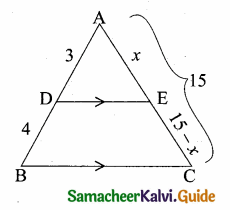
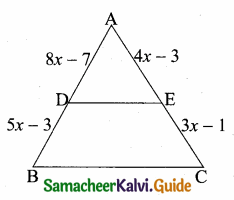
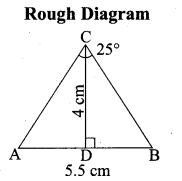
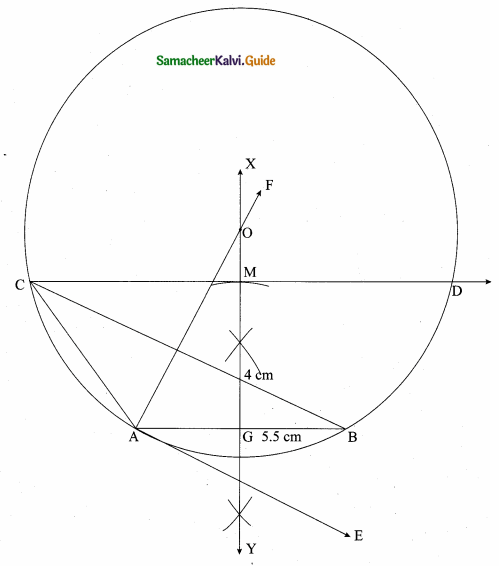
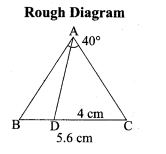
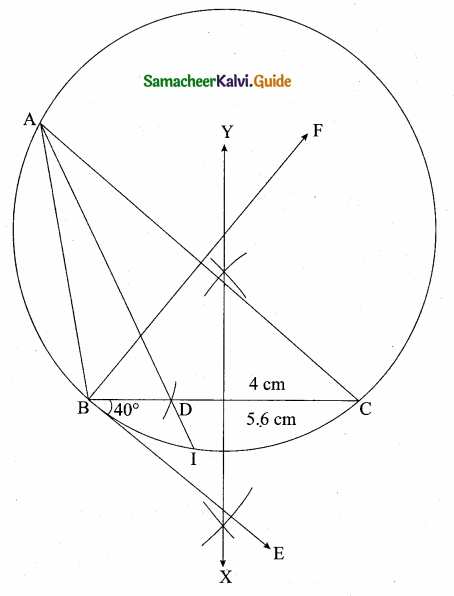
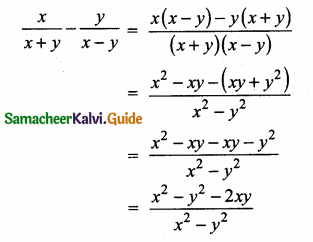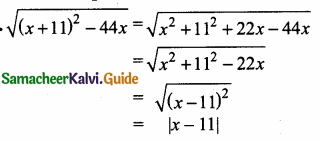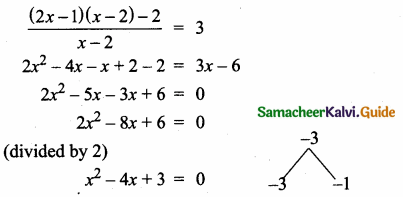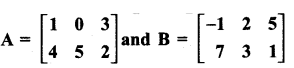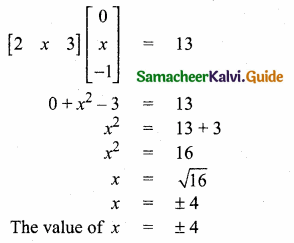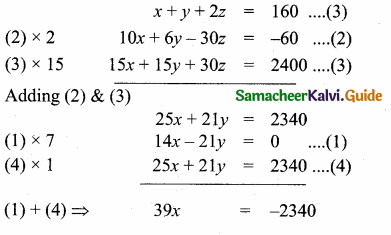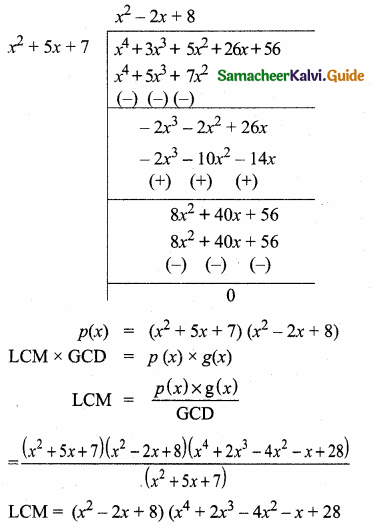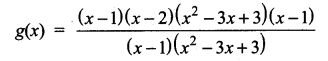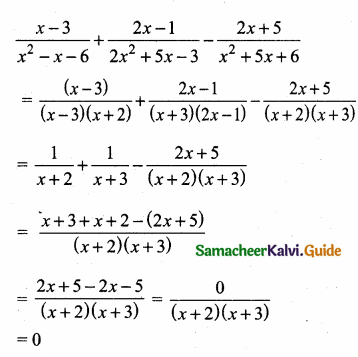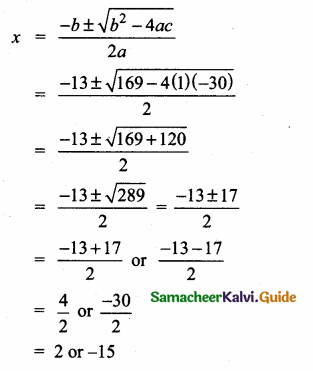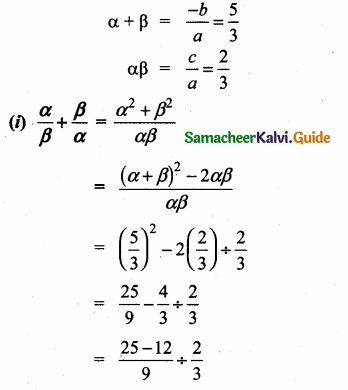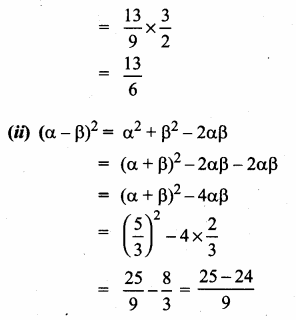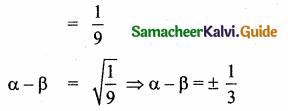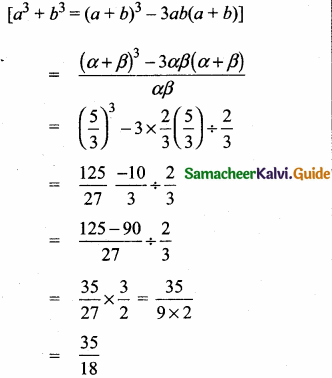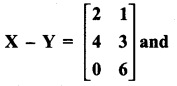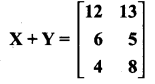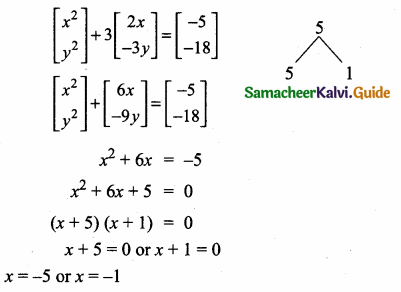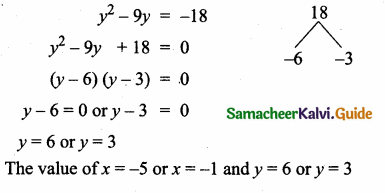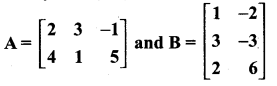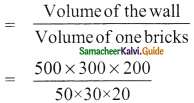Students can download Maths Chapter 3 Ratio and Proportion Ex 3.5 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Ex 3.5
Miscellaneous Practice Problems
Question 1.
The maximum speed of some of the animals are given below:
the Elephant = 20 km/h; the
Lion = 80 km/h;
the Cheetah =100 km/h
Find the following ratios of their speeds in simplified form and find which ratio is the least?
(i) the Elephant and the Lion
(ii) the Lion and the Cheetah
(iii) the Elephant and the Cheetah
Solution:
(i) The Elephant: the Lion
= 20 : 80 = \(\frac{20}{80}\) = \(\frac{1}{4}\) = 1 : 4
(ii) the Lion : the Cheetah
= 80 : 100 = \(\frac{80}{100}\) = \(\frac{4}{5}\) = 4 : 5
(iii) the Elephant: the Cheetah
= 20 : 100 = \(\frac{20}{100}\) = \(\frac{1}{5}\) = 1 : 5
The ratio of Elephant to Cheetah is the least.
![]()
Question 2.
A particular high school has 1500 students 50 teachers and 5 administrators. If the school grows to 1800 students and the ratios are maintained, then find the number of teachers and administrators.
Solution:
Administrators : teachers : students = 5 : 50 : 1500 = 1 : 10 : 300
If the school grows to 1800 students then 10 parts = teachers
1 part = administrators
300 parts = 1800
1 part = \(\frac{1800}{300}\) = 6
10 parts = 6 × 10 = 60
So, if the school grows to 1800 students the new ratio is administrators : teachers: students
6 : 60 : 1800
![]()
Question 3.
I have a box which has 3 green, 9 blue, 4 yellow, 8 orange coloured cubes in it.
(a) What is the ratio of orange to yellow cubes?
(b) What is the ratio of green to blue cubes?
(c) How many different ratios can be formed, when you compare each colour to any one of the other colours?
Solution:
Number of green cubes = 3
Number of blue cubes = 9
Number of yellow cubes = 4
Number of orange cubes = 8
(a) Ratio of orange to yellow cubes \(\frac{\text { Number of orange cubes }}{\text { Number of yellow cubes }}=\frac{8}{4}=\frac{2}{1}=2: 1\)
Ratio of orange to yellow cubes = 2 : 1
(b) \(\frac{\text { Number of green cubes }}{\text { Number of blue cubes }}=\frac{3}{9}=\frac{1}{3}\)
Ratio of green to blue cubes = 1 : 3
(c) The ratios can be Orange : Yellow, Orange: blue, Orange : green, Yellow : Orange, yellow : blue, yellow : green, blue : green, blue : orange, blue : yellow, green : orange, green : yellow, green : blue. Thus 12 ratios can be formed.
![]()
Question 4.
A gets double of what B gets and B gets double of what C gets. Find A : B and B : C and verify whether the result is in proportion or not.
Solution:
Let x be the part owned by C then A : B : C = 2(2x) : 2x : x = 4x : 2x : x
A : B = 4x : 2x = 2 : 1
B : C = 2x : x = 2 : 1
A : B : : B : C. i.e, They are in proportion.
Question 5.
The ingredients required for the preparation of Ragi Kali, a healthy dish of Tamilnadu is given below.
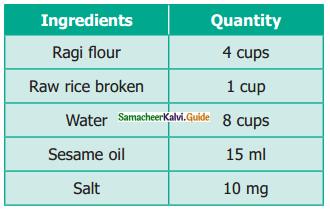
(a) If one cup of ragi flour is used then, what would be the amount of raw rice required?
(b) If 16 cups of water are used, then how much ragi flour should be used?
(c) Which of these ingredients cannot be expressed as a ratio? Why?
Solution:
(i) \(\frac{1}{4}\) cup
(ii) 8 cups
(iii) Ragi flour, Raw rice, and water are in one unit. Sesame oil and salt are in different units. These different units cannot be compared and cannot be expressed as a ratio because the two quantities of a ratio should be in the same unit.
![]()
Question 6.
Antony brushes his teeth in the morning and night on all days of the week. Shabeen brushes her teeth only in the morning. What is the ratio of the number of times they brush their teeth in a week?
Solution:
Number of times Antony brushes a day = 2
Number of times Antony brushes a week = 2 × 7 = 14
Number of times Shabeen brushes a day = 1
Number of times Shabeen brushes a week = 1 × 7 = 7
Number of times Antony brushes : Number of times Antony brushes = 14 : 7 = 2 : 1
The required ratio = 2 : 1
Question 7.
Thirumagal’s mother wears a bracelet made of 35 red beads and 30 blue beads. Thirumagal wants to make smaller bracelets using the same two coloured beads in the same ratio. In how many different ways can she make the bracelets?

Solution:
Red : blue = 35 : 30 = 7 : 6
Different ways (i) 7 : 6
(ii) 14 : 12;
(iii) 21 : 18;
(iv) 28 : 24
![]()
Question 8.
Team A wins 26 matches out of 52 matches. Team B wins three fourth of 52 matches played. Which team has a better winning record?
Solution:
Team A = \(\frac{26}{52}\) = \(\frac{1}{2}\)
Team B = \(\frac{3}{4}\) × 52 = 39
Team B has a better winning record.
Question 9.
In a school excursion, 6 teachers and 12 students from 6th standard and 9 teachers and 27 students from 7th standard, 4 teachers and 16 students from 8th standard took part. Which class has the least teacher to student ratio?
Solution:
Std VI – teachers: students = 6 : 12 = 1 : 2
Std VII – teachers : students = 9 : 27 = 1 : 3
Std VIII – teachers : students = 4 : 16 = 1 : 4
Std VIII has the least ratio.
![]()
Question 10.
Fill the boxes using any set of suitable numbers 6 : ___ : : ___ : 15
Solution:
6 : ……. = …….. : 15
Product of the extremes = 6 × 15 = 90
Set of suitable numbers
1 and 90, 2 and 45, 3 and 30, 5 and 18, 6 and 15
Question 11.
From your school diary, write the ratio of the number of holidays to the number of working days in the current academic year.
Solution:
Number of holidays = 145
Number of working days = 220
Holidays : working days = 145 : 220
= \(\frac{145}{220}\)
= \(\frac{29}{44}\)
= 29 : 44
![]()
Question 12.
If the ratio of Green, Yellow and Black balls in a bag is 4 : 3 : 5, then
(a) Which is the most likely ball that you can choose from the bag?
(b) How many balls in total are there in the bag if you have 40 black balls in it?
(c) Find the number of green and yellow balls in the bag.
Solution:
Green : Yellow : Black = 4 : 3 : 5
(i) Blackballs;
(ii) 96 balls (32 + 24 + 40);
(iii) green balls = 32
yellow balls = 24
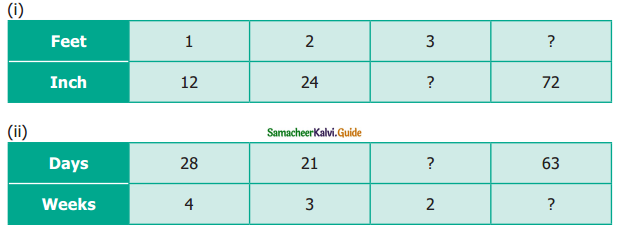
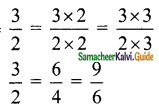
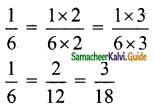
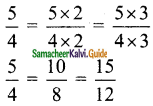
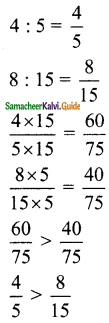
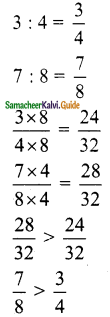
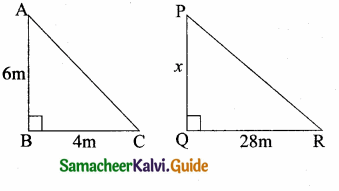
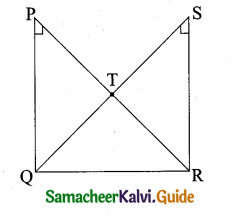
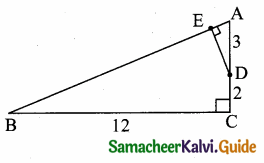
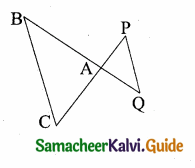
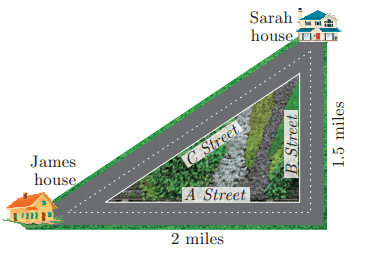

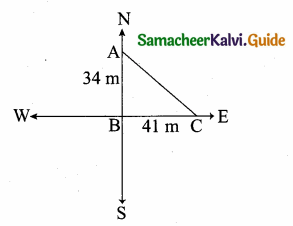

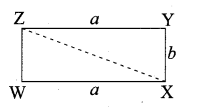
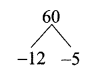
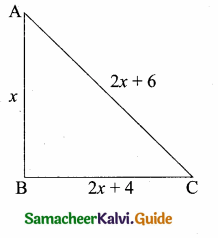
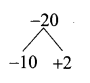
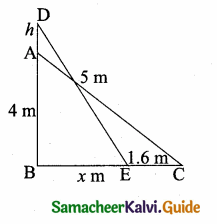
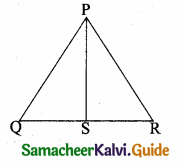
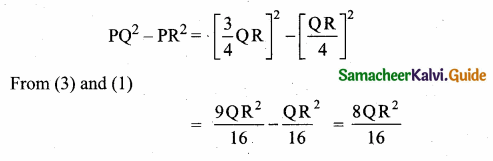
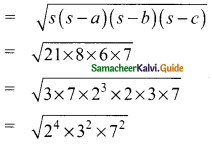
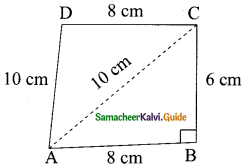
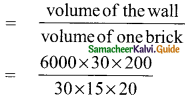
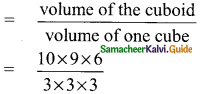
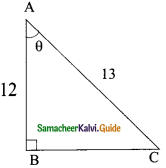

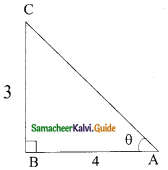
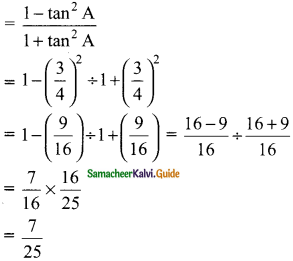
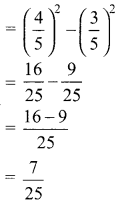
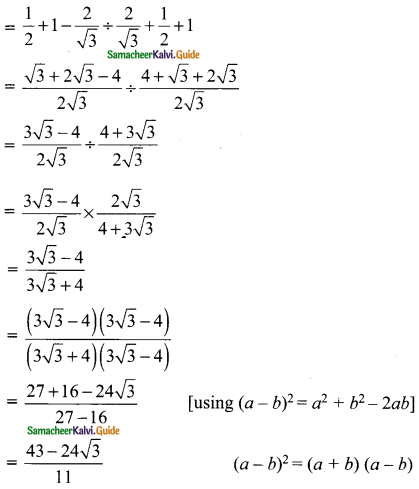
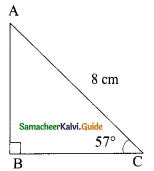
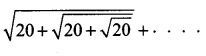 is ……….
is ……….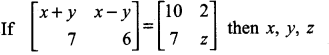
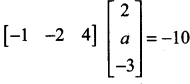 then the value of “a” is ………….
then the value of “a” is ………….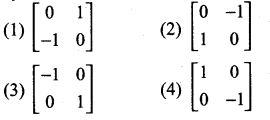

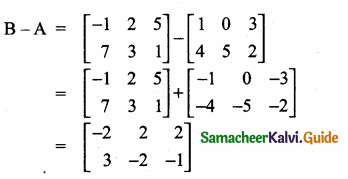
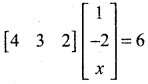 then “x” is ……………..
then “x” is ……………..