Bhagya

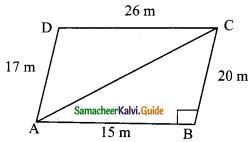
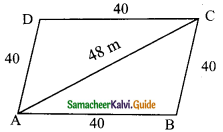
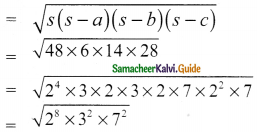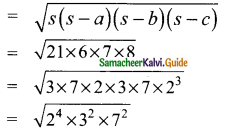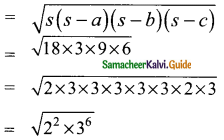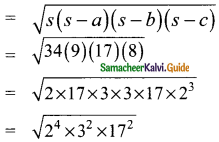Students can download Maths Chapter 7 Mensuration Ex 7.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 7 Mensuration Ex 7.3

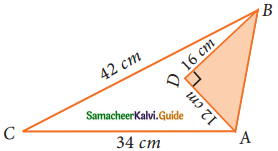
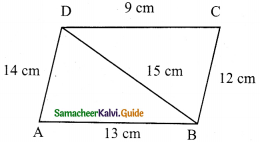
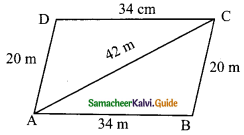
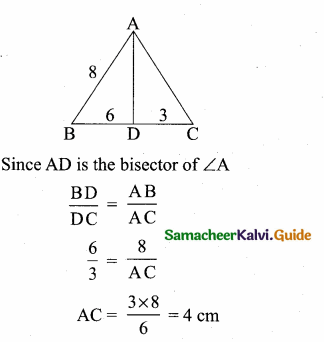
Question 1.
Find the volume of a cuboid whose dimensions are
(i) length = 12 cm, breadth = 8 cm, height = 6 cm
(ii) length = 60 m, breadth = 25 m, height = 1.5 m
Solution:
(i) Here l = 12 cm, b = 8 cm, h = 6 cm
Volume of a cuboid = l × b × h
= (12 × 8 × 6) cm³
= 576 cm³

(ii) Here l = 60 m, b = 25 m. h = 1.5 m
Volume of a cuboid = l × b × h
= 60 × 25 × 1.5 m³
= 2250 m³

Question 2.
The dimensions of a match box are 6 cm × 3.5 cm × 2.5 cm. Find the volume of a packet containing 12 such match boxes.
Solution:
Length of a match box (l) = 6 cm
Breadth of a match box (b) = 3.5 cm
Height of a match box (h) = 2.5 cm
Volume of one match box = l × b × h cu. units
= 6 × 3.5 × 2.5 cm³
= 52.5 cm³
Volume of 12 match box = 12 × 52.5 cm³
= 630 cm³

Question 3.
The length, breadth and height of a chocolate box are in the ratio 5 : 4 : 3. If its volume is 7500 cm³, then find its dimensions.
Solution:
Let the length of a chocolate be 5x, the breadth of a chocolate be 4x, and the height of a chocolate be 3x.
Volume of a chocolate = 7500 cm³
l × b × h = 7500
5x × 4x × 3x = 7500
5 × 4 × 3 × x³ = 7500
x³ = \(\frac{7500}{5×4×3}\)
x³ = 125 ⇒ x³ = 5³
x = 5
∴ Length of a chocolate = 5 × 5 = 25 cm
Breath of a chocolate = 4 × 5 = 20 cm
Height of a chocolate = 3 × 5 = 15 cm

Question 4.
The length, breadth and depth of a pond are 20.5 m, 16 m and 8 m respectively. Find the capacity of the pond in litres.
Solution:
Length of a pond (l) = 20.5 m
Breadth of a pond (b) = 16 m
Depth of a pond (h) = 8 m
Volume of the pond = l × b × h cu.units
= 20.5 × 16 × 8 m³
= 2624 m³ (1 cu. m = 1000 lit)
= (2624 × 1000) litres
= 2624000 lit

Question 5.
The dimensions of a brick are 24 cm × 12 cm × 8 cm. How many such bricks will be required to build a wall of 20 m length, 48 cm breadth and 6 m height?
Solution:
Length of a brick (l) = 24 cm
Breadth of a brick (b) = 12 cm
Depth of a brick (h) = 8 cm
Volume of a brick = lbh cu.units
Volume of one brick = 24 × 12 × 8 cm³
Length of a wall (l) = 20 m = 2000 cm
Breadth of a wall (b) = 48 cm
Height of a wall (h) = 6 m = 600 cm
Volume of a wall = l × b × h cu. units
= 2000 × 48 × 600 cm³
Number of bricks

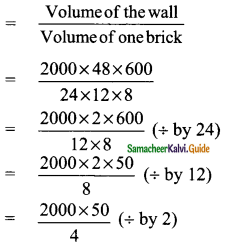
= 500 × 50 ( ÷ by 4)
= 25000 bricks
∴ Number of bricks = 25000

Question 6.
The volume of a container is 1440 m³. The length and breadth of the container are 15 m and 8 m respectively. Find its height.
Solution:
Let the height of the container be “h”
Length of the container (l) = 15 m
Breadth of the container (b) = 8 m
Volume of the container = 1440 m³
l × b × h = 1440
15 × 8 × h = 1440
h = \(\frac{1440}{15×8}\)
= 12 m
∴ Height of the container = 12 m

Question 7.
Find the volume of a cube each of whose side is
(i) 5 cm
(ii) 3.5 m
(iii) 21 cm
Solution:
(i) Side of a cube (a) = 5 cm
Volume of a cube = a³ cu. units
= 5 × 5 × 5 cm³
= 125 cm³

(ii) Side of a cube (a) = 3.5 m a³ cu. units
Volume of a cube = 3.5 × 3.5 × 3.5 m³
= 42.875 m³

(iii) Side of a cube (a) = 21 cm
Volume of a cube = a³ cu. units
= 21 × 21 × 21 cm³
= 9261 cm³

Question 8.
A cubical milk tank can hold 125000 litres of milk. Find the length of its side in metres.
Solution:
Volume of the cubical tank = 125000 liters
= \(\frac{125}{1000}\) m³ (1 cu.m = 1000 lit)
= 125 m³
a³ = 125 ⇒ a³ = 5³
a = 5
Side of a cube = 5 m

Question 9.
A metallic cube with side 15 cm is melted and formed into a cuboid. If the length and height of the cuboid is 25 cm and 9 cm respectively then find the breadth of the cuboid.
Solution:
Side of a cube (a) = 15 cm
Length of a cuboid (l) = 25 cm
Height of a cuboid (h) = 9 cm
Volume of the cuboid = Volume of the cube
l × b × h = a³
25 × b × 9 = 15 × 15 × 15
b = \(\frac{15 × 15 × 15}{25 × 9}\)
= 15 cm
Breadth of the cuboid = 15 cm

Students can download Maths Chapter 7 Mensuration Ex 7.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 7 Mensuration Ex 7.2

Question 1.
Find the Total Surface Area and the Lateral Surface Area of a cuboid whose dimensions are length = 20 cm, breadth = 15 cm, height = 8 cm.
Solution:
Here l = 20 cm, b = 15 cm, h = 8 cm
L.S.A. of the cuboid = 2(1 + b)h sq.m
= 2(20 + 15) × 8
= 2 × 35 × 8
= 560 sq.m
Total surface area of the cuboid = 2(lb + bh + lh) sq.units
= 2(20 × 15 + 15 × 8 + 8 × 20) sq. cm
= 2(300 + 120 + 160) sq. cm
= 2 × 580 sq. cm
= 1160 sq. cm

Question 2.
The dimensions of a cuboidal box are 6 m x 400 cm x 1.5 m. Find the cost of painting its entire outer surface at the rate of Rs 22 per m².
Solution:
Length of the cuboid box (l) = 6 m
Breadth of the cuboid box (b) = 400 cm = 4m
Height of the cuboid box (h) = 1.5 m
T.S.A. of the cuboid = 2(lb + bh + lh) sq.units
= 2(6 × 4 + 4 × 1.5 + 1.5 × 6) sq.units
= 2(24 + 6 + 9)
= 2 × 39 sq.m
= 78 sq.m
Cost of painting for one sq.m = Rs 22
Total cost of painting = Rs 78 × 22
= Rs 1716

Question 3.
The dimensions of a hall is 10 m × 9 m × 8 m. Find the cost of white washing the walls and ceiling at the rate of Rs 8.50 per m².
Solution:
Length of the hall (l) = 10 m
Breath of the hall (b) = 9 m
Height of the hall (h) = 8 m
Area to be white wash = L.S.A. + Ceiling of the building
= 2(l + b)h + lb sq.units
= 2(10 + 9)8 + 10 × 9 sq.m
= 2 × 19 × 8 + 10 × 9 sq. m
= (304 + 90) sq.m
= 394 sq.m
Cost of white washing one sq.m = Rs 8.50
Cost of white washing for 394 sq.m = Rs 394 × 8.50
= Rs 3349
Total cost of white washing = Rs 3349

Question 4.
Find the TSA and LSA of the cube whose side is
(i) 8 m
(ii) 21 cm
(iii) 7.5 cm
Solution:
(i) 8m
Side of a cube (a) = 8m
T.S.A. of the cube = 6a² sq.units
= 6 × 8 × 8 sq. m
= 384 sq.m
L.S.A. of the cube = 4a² sq.units
= 4 × 8 × 8 sq.m
= 256 sq.m

(ii) 21 cm
Solution:
Side of a cube (a) = 21 cm
T.S.A. of the cube = 6a² sq. units
= 6 × 21 × 21 cm²
= 2646 cm²
L.S.A. of the cube = 4a² sq.units
= 4 × 21 × 21 sq.cm
= 4 × 441 cm²
= 1764 cm²

(iii) 7.5 cm
Solution:
Side of a cube (a) = 7.5 cm
T.S.A. of the cube = 6a² sq.units
= 6 × 7.5 × 7.5 cm²
= 337.5 cm²
L.S.A. of the cube = 4a² sq.units
= 4 × 7.5 × 7.5 sq.cm
= 225 cm²

Question 5.
If the total surface area of a cube is 2400 cm² then, find its lateral surface area.
Solution:
T.S.A. of the cube = 2400 cm²
6a² = 2400
a² = \(\frac{2400}{6}\)
= 400 cm²
L.S.A. of the cube = 4a² sq.units
= 4 × 400 cm²
= 1600 cm²
(OR)
T.S.A. of the cube = 2400 cm²
6a² = 2400
a² = \(\frac{2400}{6}\)
= 400
a = \(\sqrt{400}\)
= 20 cm
Side of a cube (a) = 20 cm
L.S.A. of the cube = 4a² sq.units
= 4 × 20 × 20 cm²
= 1600 cm²

Question 6.
A cubical container of side 6.5 m is to be painted on the entire outer surface. Find the area to be painted and the total cost of painting it at the rate of Rs 24 per m².
Solution:
Side of a cube (a) = 6.5 m
Total surface area of the cube = 6a² sq.units
= 6 × 6.5 × 6.5 sq.m
= 253.50 sq.m
Cost of painting for 1 sq.m = Rs 24
Cost of painting for 253.5 sq.m = 253.5 × 24
= Rs 6084
∴ Area to be painted = 253.50 m²
Total cost of painting = Rs 6084

Question 7.
Three identical cubes of side 4 cm are joined end to end. Find the total surface area and lateral surface area of the new resulting cuboid.
Solution:
Joint the three identical cubes we get a new cuboid
Length of the cuboid (l) = (4 + 4 + 4) cm
l = 12 cm
Breadth of the cuboid (b) = 4 cm
Height of the cuboid (h) = 4 cm
Total surface area of the new cuboid = 2(lb + bh + lh) sq.units
= 2(12 × 4 + 4 × 4 + 4 × 12)
= 2(48 + 16 + 48) cm
= 2(112) cm²
= 224 cm²
Lateral surface area of the new cuboid = 2(l + b)h sq.units
= 2(12 + 4)4 cm²
= 2 × 16 × 4 cm²
= 128 cm²
∴ T.S.A of the new cuboid = 224 cm²
L.S.A of the new cuboid = 128 cm²

Students can download Maths Chapter 7 Mensuration Ex 7.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 7 Mensuration Ex 7.1

Question 1.
Using Heron’s formula, find the area of a triangle whose sides are
(i) 10 cm, 24 cm, 26 cm
Solution:
Let a = 10 cm, b = 24 cm and c = 26 cm
s = \(\frac{a + b + c}{2}\)
= \(\frac{10 + 24 + 26}{2}\)
s = \(\frac{60}{2}\)
= 30 cm
s – a = 30 – 10 = 20 cm
s – b = 30 – 24 = 6 cm
s – c = 30 – 26 = 4 cm
Area of a triangle

= 2³ × 3 × 5
= 8 × 3 × 5
= 120 cm²
Area of a triangle = 120 cm²

(ii) 1.8 m, 8 m, 8.2 m
Solution:
Here a = 1.8 m, b = 8 m, c = 8.2 m
s = \(\frac{a+b+c}{2}\)
= \(\frac{(1.8+8+8.2)m}{2}\)
= \(\frac{18}{2}\)
= 9 m
s – a = 9 – 1.8 = 7.2 m
s – b = 9 – 8 = 1 m
s – c = 9 – 8.2 m = 0.8 m
Area of triangle

= 3 × 2.4
= 7.2 m²
∴ Area of the triangle = 7.2 sq. m

Question 2.
The sides of the triangular ground are 22 m, 120 m and 122 m. Find the area and cost of levelling the ground at the rate of Rs 20 per m².
Solution:
The sides of the triangular ground are 22m, 120m and 122 m
a = 22 m, b = 120 m, c = 122 m
s = \(\frac{a+b+c}{2}\)
\(\frac{22+120+122}{2}\)m
= 132
s – a = 132 – 22 = 110 m
s – b = 132 – 120 = 12 m
s – c = 132 – 122 = 10 m

= 4 × 3 × 10 × 11
= 1320 sq.m
Cost of levelling for one sq.m = Rs 20
Cost of levelling the ground = Rs 1320 × 20
= Rs 26400
Area of the ground = Rs 1320 sq.m
Cost of levelling the ground = Rs 26400

Question 3.
The perimeter of a triangular plot is 600 m. If the sides are in the ratio 5 : 12 : 13, then find the area of the plot.
Solution:
Let the side of the triangle a, b and c be 5x, 12x and 13x
Perimeter of a triangular plot = 600 m
5x + 12x + 13x = 600
30x = 600 ⇒ x = \(\frac{600}{30}\)
x = 20
a = 5x = 5 × 20 = 100 m
b = 12x = 12 × 20 = 240 m
c = 13x = 13 × 20 = 260 m
s = \(\frac{600}{2}\)
= 300 m
s – a = 300 – 100 = 200 m
s – b = 300 – 240 = 60 m
s – c = 300 – 260 = 40 m
Area of triangle

= 10³ × 3 × 2 × 2 m²
= 1000 × 12 m²
= 12000 m²
Area of the triangular Plot = 12000 sq.m

Question 4.
Find the area of an equilateral triangle whose perimeter is 180 cm.
Solution:
Perimeter of an equilateral triangle = 180 cm
3a = 180
a = \(\frac{180}{3}\)
= 60 m
Area of an equilateral triangle
= \(\frac{√3}{4}\) a² sq.unit
= \(\frac{√3}{4}\) × 60 × 60 sq.m
= √3 × 15 × 60 sq.m
= 1.732 × 15 × 60 sq.m
= 1558.8 sq.m
Area of an equilateral triangle = 1558.8 sq.m

Question 5.
An advertisement board is in the form of an isosceles triangle with perimeter 36 m and each of the equal sides are 13 m. Find the cost of painting it at Rs 17.50 per square metre.
Solution:
Equal sides of a triangle = 13m
Perimeter of an isosceles triangle = 36 m
Length of the third side = 36 – (13 + 13) m
= 36 – 26
= 10 m
Here a = 13m, b = 13m and c = 10m
s = \(\frac{a+b+c}{2}\)
= \(\frac{36}{2}\)
= 18 m
s – a = 18 – 13 = 5 m
s – b = 18 – 13 = 5 m
s – c = 18 – 10 = 8 m

= 2² × 3 × 5
= 60 sq.m
Cost of painting for one sq. m = Rs 17.50
Cost of painting for 60 sq. m = Rs 60 × 17.50
= Rs 1050

Question 6.
Find the area of the unshaded region.

Solution:
Since ABD is a right angle triangle
AB² = AD² + BD²
= 12² + 16²
= 144 + 256
= 400
AB = \(\sqrt{400}\)
= 20 cm
Area of the right angle triangle = \(\frac{1}{2}\) bh sq.unit
= \(\frac{1}{2}\) × 12 × 16 cm²
= 6 × 16 cm²
= 96 cm²
To find the Area of the triangle ABC
Here a = 42 cm, b = 34 cm, c = 20 cm
s = \(\frac{a+b+c}{2}\)
= \(\frac{42+34+20}{2}\) cm
= \(\frac{96}{2}\)
= 48 cm
s – a = 48 – 42 = 6 cm
s – b = 48 – 34 = 14 m
s – c = 48 – 20 = 28 m
Area of triangle

= 16 × 3 × 7 cm²
= 336 cm²
Area of the unshaded region = Area of the ΔABC – Area of the ΔABD
= (336 – 96) cm²
= 240 cm²

Question 7.
Find the area of a quadrilateral ABCD whose sides are AB = 13 cm, BC = 12 cm, CD = 9 cm, AD = 14 cm and diagonal BD = 15 cm.
Solution:
In the triangle ABD,

Let a = 15 cm, b = 14 cm c = 13 cm
s = \(\frac{a+b+c}{2}\)
= \(\frac{15+14+13}{2}\) cm
= \(\frac{42}{2}\)
= 21 cm
s – a = 21 – 15 = 6 cm
s – b = 21 – 14 = 7 cm
s – c = 21 – 13 = 8 cm
Area of ΔABD

= 2² × 3 × 7 3
= 84 cm²
In the ΔBCD,
Let a = 15 cm, b = 9 cm, c = 12 cm
s = \(\frac{a+b+c}{2}\)
= \(\frac{15+9+12}{2}\) cm
= \(\frac{36}{2}\)
= 18 cm
s – a = 18 – 15 = 3 cm
s – b = 18 – 9 = 9 cm
s – c = 18 – 12 = 6 cm
Area of the ΔBCD

= 2 × 3³
= 2 × 27 sq.cm
= 54 sq. cm
Area of the quadrilateral ABCD = Area of ΔABD + Area of ΔBCD
= (84 + 54) sq.cm
= 138 sq.cm

Question 8.
A park is in the shape of a quadrilateral. The sides of the park are 15 m, 20 m, 26 m and 17 m and the angle between the first two sides is a right angle. Find the area of the park.
Solution:

In the right angle triangle ABC (Given ⌊B= 90°)
AC² = AB² + BC²
= 15² + 20²
= 225 + 400
AC² = 625
AC = \(\sqrt{225}\)
= 25 m
Area of the right ΔABC = \(\frac{1}{2}\) × AB × BC
= \(\frac{1}{2}\) × 15 × 20 sq.m
= 150 sq.m
In the triangle ACD
a = 25 m b = 17 m, c = 26 m
s = \(\frac{a+b+c}{2}\)
= \(\frac{25+17+26}{2}\) cm
= \(\frac{62}{2}\)
= 34 m
s – a = 34 – 25 = 9 m
s – b = 34 – 17 = 17 m
s – c = 34 – 26 = 8 m
Area of the triangle ACD

4 × 3 × 17
= 204 sq.m
Area of the quadrilateral = Area of the ΔABC + Area of the ΔACD
= (150 + 204) sq.m
= 354 sq.m
Area of the quadrilateral = 354 sq.m

Question 9.
A land is in the shape of rhombus. The perimeter of the land is 160 m and one of the diagonal is 48 m. Find the area of the land.
Solution:

Perimeter of the rhombus = 160 m
4 × side = 160
Side of a rhombus = \(\frac{160}{4}\)
= 40 m
In ΔABC, a = 40 m, b = 40 m, c = 48 m
s = \(\frac{a+b+c}{2}\)
= \(\frac{40+40+48}{2}\) cm
= \(\frac{128}{2}\)
= 64 m
s – a = 64 – 40 = 24 m
s – b = 64 – 40 = 24 m
s – c = 64 – 48 = 16m
Area of the ΔABC = \(\sqrt{64×24×24×16}\)
= 8 × 24 × 4
= 768 sq.m
Since ABCD is a rhombus Area of two triangles are equal.
Area of the rhombus ABCD = (768 + 768) sq.m
= 1536 sq.m
∴ Area of the land = 1536 sq.m

Question 10.
The adjacent sides of a parallelogram measures 34 m, 20 m and the measure of the diagonal is 42 m. Find the area of parallelogram.
Solution:
Since ABCD is a parallelogram opposite sides are equal.

In the ΔABC
a = 20 m, b = 42 m and c = 34 m
s = \(\frac{a+b+c}{2}\)
= \(\frac{20+42+34}{2}\) cm
= \(\frac{96}{2}\)
= 48 m
s – a = 48 – 20 = 28 m
s – b = 48 – 42 = 6 m
s – c = 48 – 34 = 14 m
Area of the ΔABC

= 2⁴ × 3 × 7 sq.m
= 16 × 3 × 7 sq.m
= 336 sq.m
Since ABCD is a parallelogram
Area of ΔABC and Area of ΔACD are equal
Area of the parallelogram ABCD = (336 + 336) sq.m
= 672 sq.m
∴ Area of the parallelogram = 672 sq.m

Students can download Maths Chapter 8 Statistics Ex 8.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Ex 8.1

Question 1.
In a week, temperature of a certain place is measured during winter are as follows 26°C, 24°C, 28°C, 31°C, 30°C, 26°C, 24°C. Find the mean temperature of the week.
Solution:
Mean temperature of the week

= 27°C
Mean temperature of the week 27° C

Question 2.
The mean weight of 4 members of a family is 60 kg. Three of them have the weight 56 kg, 68 kg and 72 kg respectively. Find the weight of the fourth member.
Solution:
Weight of 4 members = 4 × 60 kg
= 240 kg
Weight of three members = 56 kg + 68 kg + 72 kg
= 196 kg
Weight of the fourth member = 240 kg – 196 kg
= 44 kg

Question 3.
In a class test in mathematics, 10 students scored 75 marks, 12 students scored 60 marks, 8 students scored 40 marks and 3 students scored 30 marks. Find the mean of their score.
Solution:
Total marks of 10 students = 10 × 75 = 750
Total marks of 12 students = 12 × 60 = 720
Total marks of 8 students = 8 × 40 = 320
Total marks of 3 students = 3 × 30 = 90
Total marks of (10 + 12 + 8 + 3) 33 students
= 750 + 720 + 320 + 90
= 1880
Mean of marks = \(\frac{1880}{33}\)
= 56.97 (or) 57 approximately
Aliter:
Total number of students = 10+12 + 8 + 3
= 33
Mean of their marks

= 56.97 (or) 57 approximately

Question 4.
In a research laboratory scientists treated 6 mice with lung cancer using natural medicine. Ten days later, they measured the volume of the tumor in each mouse and given the results in the table.

find the mean.
Solution:

\(\bar { x }\) = \(\frac{Σfx}{Σf}\)
= \(\frac{2966}{21}\)
= 141.238
= 141.24
The Arithmetic mean = 141.24 mm³

Question 5.
If the mean of the following data is 20.2, then find the value of p.

Solution:

\(\bar { x }\) = \(\frac{Σfx}{Σf}\)
20.2 = \(\frac{610+20p}{30+p}\)
610 + 20 p = 20.2 (30 + p)
610 + 20 p = 606 + 20.2 p
610 – 606 = 20.2 p – 20 p
4 = 0.2 p
p = \(\frac{4}{0.2}\)
= \(\frac{4×10}{2}\)
= 20
The value of p = 20

Question 6.
In the class, weight of students is measured for the class records. Calculate mean weight of the class students using direct method.

Solution:

Arithmetic mean \(\bar { x }\) = \(\frac{Σfx}{Σf}\)
= \(\frac{2010}{50}\)
= 40.2
Arithmetic mean = 40.2

Question 7.
Calculate the mean of the following distribution using Assumed Mean Method.

Solution:
Assumed Mean (A) = 25

Arithmetic mean (\(\bar { x }\)) = A+\(\frac{Σfd}{Σf}\)
= 25 + \(\frac{270}{63}\)
= 25 + 4. 29
Assumed Mean = 29.29

Question 8.
Find the Arithmetic Mean of the following data using Step Deviation Method:

Solution:
Assumed Mean (A) = 32

Arithmetic mean = A+\(\frac{Σfd}{Σf}\) × c
= 32 + (\(\frac{-77.5}{105}\)×4)
= 32 – 2.95
= 29.05
Arithmetic mean = 29.05

Students can download Maths Chapter 9 Probability Ex 9.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 9 Probability Ex 9.3

I. Multiple choice questions.

Question 1.
A number between 0 and 1 that is used to measure uncertainty is called ……….
(a) Random variable
(b) Trial
(c) Simple event
(d) Probability
Solution:
(d) Probability

Question 2.
Probability lies between ………
(a) -1 and +1
(b) 0 and 1
(c) 0 and n
(d) 0 and ∞
Solution:
(b) 0 and 1

Question 3.
The probability based on the concept of relative frequency theory is called ………
(a) Empirical probability
(b) Classical probability
(c) Both (a) and (b)
(d) Neither (a) nor (b)
Solution:
(a) Empirical probability

Question 4.
The probability of an event cannot be ……….
(a) Equal to zero
(b) Greater than zero
(c) Equal to one
(d) Less than zero
Solution:
(d) Less than zero

Question 5.
The probability of all possible outcomes of a random experiment is always equal to ……..
(a) One
(b) Zero
(c) Infinity
(d) Less than one
Solution:
(a) One

Question 6.
If A is any event in S and its complement is A’ then P(A’) is equal to ………
(a) 1
(b) 0
(c) 1 – A
(d) 1 – P(A)
Solution:
(d) 1 – P(A)

Question 7.
Which of the following cannot be taken as probability of an event?
(a) 0
(b) 0.5
(c) 1
(d) -1
Solution:
(d) -1

Question 8.
A particular result of an experiment is called ………
(a) Trial
(b) Simple event
(c) Compound event
(d) Outcome
Solution:
(d) Outcome

Question 9.
A collection of one or more outcomes of an experiment is called ……….
(a) Event
(b) Outcome
(c) Sample point
(d) None of the above
Solution:
(a) Event

Question 10.
The six faces of the dice are called equally likely if the dice is ………
(a) Small
(b) Fair
(c) Six-faced
(d) Round
Solution:
(b) Fair

Students can download Maths Chapter 9 Probability Ex 9.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 9 Probability Ex 9.2

Question 1.
A company manufactures 10000 Laptops in 6 months. In that 25 of them are found to be defective. When you choose one Laptop from the manufactured, what is the probability that selected Laptop is a good one?
Solution:
Total number of laptops = 10000
∴ n(S) = 10000
Number of good laptops = 10000 – 25 = 9975
Let E be the event of getting good laptops
n(E) = 9975
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{9975}{10000}\)
= \(\frac{399}{400}\) (or)
= 0.9975

Question 2.
In a survey of 400 youngsters aged 16-20 years, it was found that 191 have their voter ID card. If a youngster is selected at random, find the probability that the youngster does not have their voter ID card.
Solution:
Here n(S) = 400
Number of persons having voter ID = 191
Number of persons does not have their voter ID
= 400 – 191
= 209
n(E) = 209
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{209}{400}\)
∴ The required probability is \(\frac{209}{400}\)

Question 3.
The probability of guessing the correct answer to a certain question is \(\frac{x}{3}\). If the probability of not guessing the correct answer is \(\frac{x}{5}\), then find the value of x.
Solution:
Probability of guessing the correct answer = \(\frac{x}{3}\)
P(E) = \(\frac{x}{3}\)
Probability of not guessing the correct answer = \(\frac{x}{5}\)
P(E)’ = \(\frac{x}{5}\)
But P(E) + P(E)’ = 1
\(\frac{x}{3}\) + \(\frac{x}{5}\) = 1
\(\frac{5x+3x}{15}\) = 1 ⇒ \(\frac{8x}{15}\) = 1
8x = 15
x = \(\frac{15}{8}\)
∴ The value of x = \(\frac{15}{8}\)

Question 4.
If a probability of a player winning a particular tennis match is 0.72. What is the probability of the player loosing the match?
Solution:
Probability of a player winning a tennis match = 0.72
P(E) = 0.72
Probability of a player loosing the match be P(E)’
But P(E) + P(E)’ = 1
0.72 + P(E)’ = 1
P(E)’ = 1 – 0.72
= 0.28
Probability of the player loosing the match = 0.28

Question 5.
1500 families were surveyed and following data was recorded about their maids at homes

A family selected at random. Find the probability that the family selected has
(i) Both types of maids
(ii) Part time maids
(iii) No maids
Solution:
Total number of families surveyed = 1500
n(S) = 1500
Number of families used maids = 860 + 370 + 250
= 1480
Number of families not using any maids = 1500 – 1480
= 20

(i) Let E₁ be the event of getting families use both types of maids
n(E₁) = 250
p(E₁) = \(\frac{n(E_{1})}{n(S)}\)
= \(\frac{250}{1500}\)
= \(\frac{25}{150}\)
= \(\frac{1}{6}\)
Probability of getting both types of maids = \(\frac{1}{6}\)

(ii) Let E₂ be the event of getting families use part time maids
n(E₂) = 860
p(E₂) = \(\frac{n(E_{2})}{n(S)}\)
= \(\frac{860}{1500}\)
= \(\frac{43}{75}\)
Probability of getting part time maids = \(\frac{43}{75}\)

(iii) Let E₃ be the event of getting family use no maids
n(E₃) = 20
p(E₃) = \(\frac{n(E_{3})}{n(S)}\)
= \(\frac{20}{1500}\)
= \(\frac{2}{150}\)
= \(\frac{1}{75}\)
Probability of getting no maids = \(\frac{1}{75}\)

Students can download Maths Chapter 4 Geometry Ex 4.5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 4 Geometry Ex 4.5

Question 1.
If in triangles ABC and EDF, \(\frac { AB }{ DE } \) = \(\frac { BC }{ FD } \) then they will be similar, when ……….
(1) ∠B = ∠E
(2) ∠A = ∠D
(3) ∠B = ∠D
(4) ∠A = ∠F
Answer:
(3) ∠B = ∠D
Hint:

Question 2.
In ∆LMN, ∠L = 60°, ∠M = 50°. If ∆LMN ~ ∆PQR then the value of ∠R is ……………
(1) 40°
(2) 70°
(3) 30°
(4) 110°
Answer:
(2) 70°
Hint:
Since ∆LMN ~ ∆PQR
∠N = ∠R
∠N = 180 – (60 + 50)
= 180 – 110°
∠N = 70° ∴ ∠R = 70°

Question 3.
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is ………
(1) 2.5 cm
(2) 5 cm
(3) 10 cm
(4) 5 \(\sqrt { 2 }\) cm
Answer:
(4) 5 \(\sqrt { 2 }\) cm
Hint:

AB² = AC² + BC²
AB² = 5² + 5²
(It is an isosceles triangle)
AB = \(\sqrt { 50 }\) = \(\sqrt{25 \times 2}\)
AB = 5 \(\sqrt { 2 }\)

Question 4.
In a given figure ST || QR, PS = 2 cm and SQ = 3 cm. Then the ratio of the area of ∆PQR to the area of ∆PST is …………….

(1) 25 : 4
(2) 25 : 7
(3) 25 : 11
(4) 25 : 13
Answer:
(1) 25 : 4
Hint. Area of ∆PQR : Area of ∆PST
\(\frac{\text { Area of } \Delta \mathrm{PQR}}{\text { Area of } \Delta \mathrm{PST}}=\frac{\mathrm{PQ}^{2}}{\mathrm{PS}^{2}}=\frac{5^{2}}{2^{2}}=\frac{25}{4}\)
Area of ∆PQR : Area of ∆PST = 25 : 4

Question 5.
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ =10 cm, then the length of AB is ………….
(1) 6 \(\frac { 2 }{ 3 } \) cm
(2) \(\frac{10 \sqrt{6}}{3}\)
(3) 66 \(\frac { 2 }{ 3 } \) cm
(4) 15 cm
Answer:
(4) 15 cm
Hint:

Question 6.
If in ∆ABC, DE || BC. AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm then the length of AE is ………..
(1) 1.4 cm
(2) 1.8 cm
(3) 1.2 cm
(4) 1.05 cm
Answer:
(1) 1.4 cm
Hint:

Question 7.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm.
The length of the side AC is ………….
(1) 6 cm
(2) 4 cm
(3) 3 cm
(4) 8 cm
Answer:
(2) 4 cm
Hint:

Question 8.
In the adjacent figure ∠BAC = 90° and AD ⊥ BC then ………..

(1) BD.CD = BC²
(2) AB.AC = BC²
(3) BD.CD = AD²
(4) AB.AC = AD²
Answer:
(3) BD CD = AD²
Hint:

Question 9.
Two poles of heights 6 m and 11m stand vertically on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?
(1) 13 m
(2) 14 m
(3) 15 m
(4) 12.8 m
Answer:
(1) 13 m
Hint:

AC² (Distance between the two tops)
= AE² + EC²
= 5² + 122
= 25 + 144= 169
AC = \(\sqrt { 169 }\) = 13 cm

Question 10.
In the given figure, PR = 26 cm, QR = 24 cm, ∠PAQ = 90°, PA = 6 cm and QA = 8 cm. Find ∠PQR.

(1) 80°
(2) 85°
(3) 75°
(4) 90°
Answer:
(4) 90°
Hint.
PR = 26 cm, QR = 24 cm, ∠PAQ = 90°
In the ∆PQR,

In the right ∆ APQ
PQ² = PA² + AQ²
= 6² + 8²
= 36 + 64 = 100
PQ = \(\sqrt { 100 }\) = 10
∆ PQR is a right angled triangle at Q. Since
PR² = PQ² + QR²
∠PQR = 90°

Question 11.
A tangent is perpendicular to the radius at the
(1) centre
(2) point of contact
(3) infinity
(4) chord
Solution:
(2) point of contact

Question 12.
How many tangents can be drawn to the circle from an exterior point?
(1) one
(2) two
(3) infinite
(4) zero
Answer:
(2) two

Question 13.
The two tangents from an external points P to a circle with centre at O are PA and PB.
If ∠APB = 70° then the value of ∠AOB is ……….
(1) 100°
(2) 110°
(3) 120°
(4) 130°
Answer:
(2) 110°
Hint.

∠OAP = 90°
∠APO = 35°
∠AOP = 180 – (90 + 35)
= 180 – 125 = 55
∠AOB = 2 × 55 = 110°

Question 14.
In figure CP and CQ are tangents to a circle with centre at 0. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm, then the length of BR is …….

(1) 6 cm
(2) 5 cm
(3) 8 cm
(4) 4 cm
Answer:
(4) 4 cm
Hint.
BQ = BR = 4 cm (tangent of the circle)
PC = QC = 11 cm (tangent of the circle)
QC = 11 cm
QB + BC = 11
QB + 7 = 11
QB = 11 – 7 = 4 cm
BR = BQ = 4 cm

Question 15.
In figure if PR is tangent to the circle at P and O is the centre of the circle, then ∠POQ is ………….

(1) 120°
(2) 100°
(3) 110°
(4) 90°
Answer:
(1) 120°
Hint.
Since PR is tangent of the circle.
∠QPR = 90°
∠OPQ = 90° – 60° = 30°
∠OQB = 30°
In ∆OPQ
∠P + ∠Q + ∠O = 180°
30 + 30° + ∠O = 180°
(OP and OQ are equal radius)
∠O = 180° – 60° = 120°

Students can download Maths Chapter 9 Probability Ex 9.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 9 Probability Ex 9.1

Question 1.
You are walking along a street. If you just choose a stranger crossing you, what is the probability that his next birthday will fall on a Sunday?
Solution:
Sample space = {M, T, W, Th, F, S, Sun}
n(S) = 7
Let E be the event of getting birthday on Sunday
n(E) = 1
p(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{1}{7}\)

Question 2.
What is the probability of drawing a King or a Queen or a Jack from a deck of cards?
Solution:
The outcomes n(S) = 52
Let E be the event of getting a king or a queen or a jack
= 4 + 4 + 4
n(E) = 12
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{12}{52}\)
= \(\frac{3}{13}\)

Question 3.
What is the probability of throwing an even number with a single standard dice of six faces?
Solution:
Sample space (S) = {1, 2, 3, 4, 5, 6}
n(S) = 6
Let E be the event of getting an even number
E = {2, 4, 6}
n(E) = 3
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{3}{6}\)
= \(\frac{1}{2}\)

Question 4.
There are 24 balls in a pot. If 3 of them are Red, 5 of them are Blue and the remaining are Green then, what is the probability of picking out (i) a Blue ball,
(ii) a Red ball and
(ii) a Green ball?
Solution:
Sample space n(S) = 24
Number of green ball = 24 – (3 + 5)
= 24 – 8
= 16

(i) Let E₁ be the event of getting a blue ball
n(E₁) = 5
p(E₁) = \(\frac{n(E_{1})}{n(S)}\)
= \(\frac{5}{24}\)

(ii) Let E₂ be the event of getting a red ball
n(E₂) = 3
p(E₂) = \(\frac{n(E_{2})}{n(S)}\)
= \(\frac{3}{24}\)
= \(\frac{1}{8}\)

(iii) Let E₃ be the event of getting a green ball
n(E₃) = 16
p(E₃) = \(\frac{n(E_{3})}{n(S)}\)
= \(\frac{16}{24}\)
= \(\frac{2}{3}\)

Question 5.
When two coins are tossed, what is the probability that two heads are obtained?
Solution:
Sample space (S) = {(H, H), (H, T), (T, H), (T, T)}
n(S) = 4
Let E be the event of getting two heads
n(E) = 1
p(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{1}{4}\)

Question 6.
Two dice are rolled, find the probability that the sum is

(i) equal to 1
(ii) equal to 4
(iii) less than 13
Solution:
Sample space (S) = {(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)}
n(S) = 36

(i) Let E₁ be the event of getting the sum is equal to 1
n(E₁) = 0
p(E₁) = \(\frac{n(E_{1})}{n(S)}\)
= \(\frac{0}{36}\)
= 0

(ii) Let E₂ be the event of getting the sum is equal to 4
E₂ = {(1,3), (2, 2) (3, 1)}
n(E₂) = 3
p(E₂) = \(\frac{n(E_{2})}{n(S)}\)
= \(\frac{3}{36}\)
= \(\frac{1}{12}\)

(iii) Let E₃ be the event of getting the sum is less than 13
n(E₃) = 36
p(E₃) = \(\frac{n(E_{3})}{n(S)}\)
= \(\frac{36}{36}\)
= 1

Question 7.
A manufacturer tested 7000 LED lights at random and found that 25 of them were defective. If a LED light is selected at random, what is the probability that the selected LED light is a defective one.
Solution:
Sample space n(S) = 7000
Let E₁ be the event of getting selected LED light is a defective one
n(E₁) = 25
p(E₁) = \(\frac{n(E_{1})}{n(S)}\)
= \(\frac{25}{7000}\)
= \(\frac{1}{280}\)

Question 8.
In a football match, a goalkeeper of a team can stop the goal, 32 times out of 40 attempts tried by a team. Find the probability that the opponent team can convert the attempt into a goal.
Solution:
Sample space n(S) = 40
Opponent team trying to attempt the goal = 40 – 32 = 8
Let E be the event of getting opponent team convert the attempt into a goal
n(E) = 8
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{8}{40}\)
= \(\frac{1}{5}\)

Question 9.
What is the probability that the spinner will not land on a multiple of 3?

Solution:
Sample space (S) = {1, 2, 3, 4, 5, 6, 7, 8}
n(S) = 8
Land in a multiple of 3 = {3, 6}
Land not a multiple of 3 = 8 – 2
= 6
Let E be the event of getting not a multiple of 6
n(E) = 6
P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{6}{8}\)
= \(\frac{3}{4}\)

Question 10.
Frame two problems in calculating probability, based on the spinner shown here.

Solution:
(i) What is the probability that the spinner will get an odd number?
(ii) What is the probability that the spinner will not land on a multiple of 2?

Students can download Maths Chapter 8 Statistics Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Additional Questions

I. Choose the Best Answer

Question 1.
The Arithmetic mean of all the factors of 10 is ………
(a) 4.5
(b) 5.5
(c) 10
(d) 55
Solution:
(a) 4.5

Question 2.
The mean of five numbers is 27, if one number is excluded, then mean is 25. Then the excluded number is ……..
(a) 0
(b) 15
(c) 25
(d) 35
Solution:
(d) 35

Question 3.
The mean of 8 numbers is 15. If each number is multiplied by 2, then the new mean will be ……..
(a) 7.5
(b) 30
(c) 10
(d) 25
Solution:
(b) 30

Question 4.
The median of 11, 8, 4, 9, 7, 5, 2, 4, 10 is ……..
(a) 1
(b) 8
(c) 4
(d) 11
Solution:
(a) 1

Question 5.
Median is …….
(a) the most frequent value
(b) the least frequent value
(c) middle most value
(d) mean of first and last values
Solution:
(c) middle most value

Question 6.
The mode of the distribution is …….

(a) 3
(b) 4
(c) 6
(d) 14
Solution:
(b) 4

Question 7.
Mode is …….
(a) the middle value
(b) extreme value
(c) minimum value
(d) the most repeated value
Solution:
(d) the most repeated value

Question 8.
The mode of the data 72, 33, 44, 72, 81, 72, 15 is ……..
(a) 12
(b) 33
(c) 81
(d) 15
Solution:
(a) 12

Question 9.
The Arithmetic mean of 10 number is -7. If 5 is added to every number, then the new arithmetic mean is ……..
(a) 17
(b) 12
(c) -2
(d) -7
Solution:
(c) -2

Question 10.
The Arithmetic mean of integers from -5 to 5 is ……..
(a) 25
(b) 10
(c) 3
(d) 0
Solution:
(d) 0

II. Answer the Following Questions

Question 1.
Find the Arithmetic mean for the following data.

Solution:

Arithmetic mean (\(\bar { X }\)) = \(\frac{Σfx}{Σf}\)
= \(\frac{5540}{96}\)
= 57.7
∴ Arithmetic mean = 57.7

Question 2.
Calculate the Arithmetic mean of the following data using step deviation method.

Solution:
Assumed mean = 35

Arithmetic mean (\(\bar { X }\)) = A + \(\frac{Σfd}{Σf}\) × c
= 35 + \(\frac{(-20)}{100}\) × 10
= 35 – 2
= 33
∴ Arithmetic mean = 33

Question 3.
Find the median for the following data.

Solution:
The given class intervals is inclusive type we convert it into exclusive type.

\(\frac{N}{2}\) = \(\frac{70}{2}\)
= 35
Median class is 25.5 – 30.5
Here l = 25.5, f = 26, m = 30, c = 5
Median = l + \(\frac{\frac{N}{2}-m}{f}\) × c
= 25.5 + \(\frac{35-30}{26}\) × 5
= 25.5 + \(\frac{5×5}{26}\)
= 25.5 + 0.96
= 26.46
∴ Median = 26.46

Question 4.
Calculate the mode of the following data.

Solution:

The highest frequency is 30. Corresponding class interval is the modal class.
Here l = 25, f = 30, f₁ = 18, f₂ = 20 and c = 5
Mode

∴ Arithmetic mean = 25 + 2.727
= 25 + 2.73
= 27.73
mode = 27.73

Question 5.
Find the mean, median and mode of marks obtained by 20 students in an examination. The marks are given below.

Solution:

Arithmetic mean:
Here Σfx = 560, Σf = 20
\(\bar { X }\) = \(\frac{Σfx}{Σf}\)
= \(\frac{560}{20}\)

Median:
Median class is 20 – 30
Here l = 20, \(\frac{N}{2}\) = 10, m = 5, c = 10, f = 5
Median

= 20 + 10
= 30

Mode:
The highest frequency is 8
Modal class is 30 – 40
Here, l = 30, f = 8, f₁ = 5, f₂ = 2, c = 10
Mode

= 33.33
Mean = 28, median = 30, mode = 33.33

Students can download Maths Chapter 2 Introduction to Algebra Ex 2.1 Questions and Answers, Notes, Samacheer Kalvi 6th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 2 Introduction to Algebra Ex 2.1

Question 1.
Fill in the blanks:
(i) The letters a, b, c, .., x, y, z are used to represent _____
(ii) A quantity that takes _____ values is called a variable.
(iii) If there are 5 students on a bench, then the number of students in ‘n’ benches is ‘5 × n’. Here _____ is a variable.
Solution:
(i) Variables
(ii) Different
(iii) n

Question 2.
Say True or False.

(iii) If there are 11 players in a team, then there will be ’11 + q’ players in ‘q’ teams.
Solution:
(i) False
(ii) True
(iii) False

Question 3.
Draw the next two patterns and complete the table

Solution:

Question 4.
Use a variable to write the rule, which gives the number of ice candy sticks required to make the following patterns.

Solution:
(a) No of ice candy sticks used = 3 × n = 3n
(b) No of ice candy sticks used = 4 × n = 4n

Question 5.
The teacher forms groups of five students in a class. How many students will be there in ‘p’ groups?
Solution:
No of students in a group = 5
No of students in ‘p’ groups = 5 × p = 5p

Question 6.
Arivazhagan is 30 years younger than his father. Write Arivazhagan’s age in terms of his father’s age.
Solution:
Let Arivazhagan’s father’s age be x years
According to the problem,
Arivazhagan’s age = (x – 30) years

Question 7.
If ‘u’ is an even number, how would you represent
(i) the next even number?
(ii) the previous even number?
Solution:
(i) Difference between two even numbers = 2
Given that ‘u’ is an even number.
Next, the even number is u + 2.
(ii) Previous even number is u – 2.

Objective Type Questions

Question 8.
Variable means that it
(a) can take only a few values
(b) has a fixed value
(c) can take different values
(d) can take only 8 values
Solution:
(c) can take different values

Question 9.
‘6y’ means
(a) 6 + y
(b) 6 – y
(c) 6 × y
(d) \(\frac{6}{7}\)
Solution:
(c) 6 × y

Question 10.
Radha is ‘x’ years of age now. 4 years ago, her age was
(a) x – 4
(b) 4 – x
(c) 4 + x
(d) 4x
Solution:
(a) x – 4

Question 11.
The number of days in ‘w’ weeks is
(a) 30 + w
(b) 30w
(c) 7 + w
(d) 7w
Solution:
(d) 7w

Question 12.
The value of ‘x’ in the circle is

(a) 6
(b) 8
(c) 21
(d) 22
Solution:
(d) 22