Bhagya

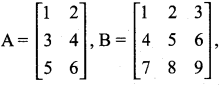
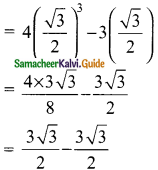
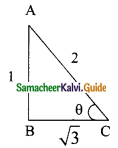
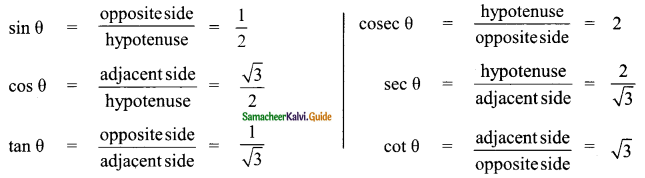
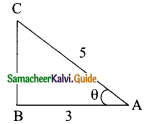
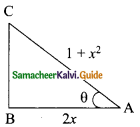
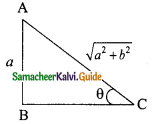
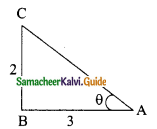
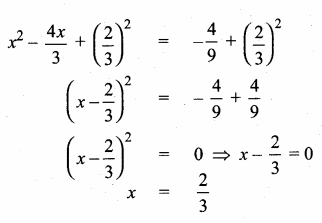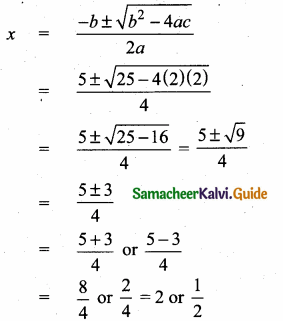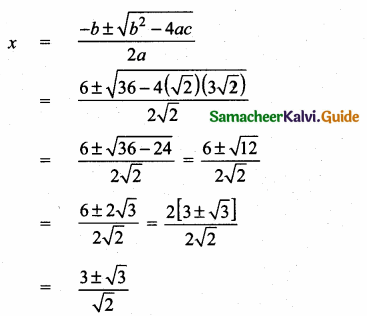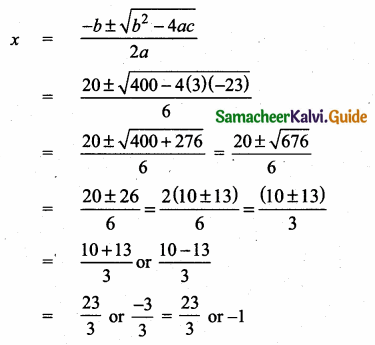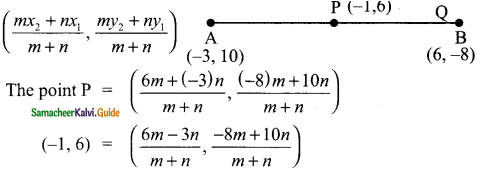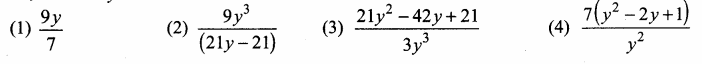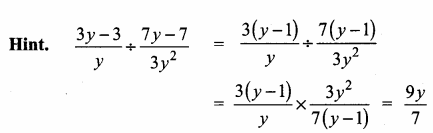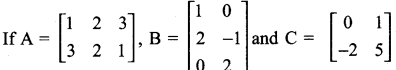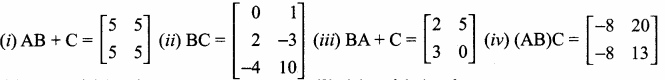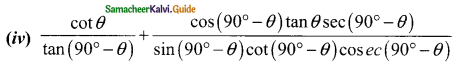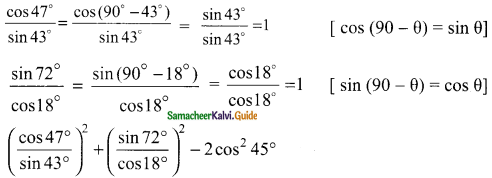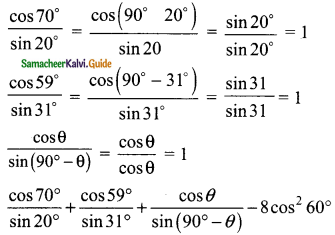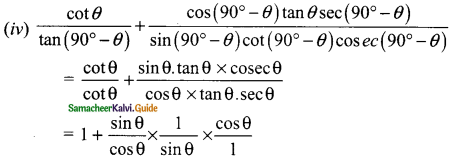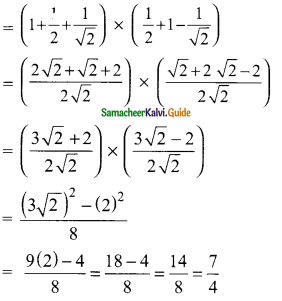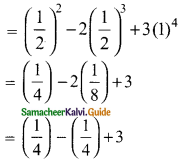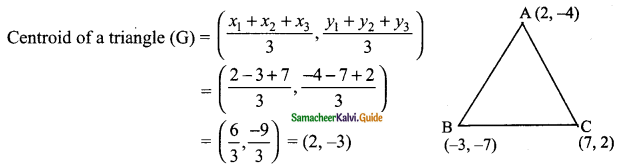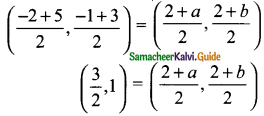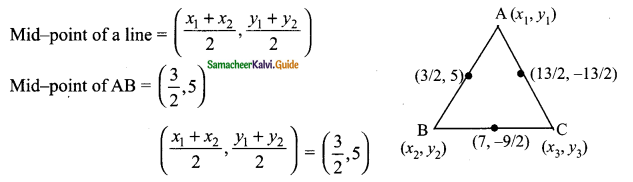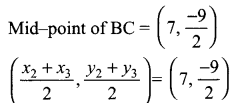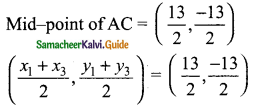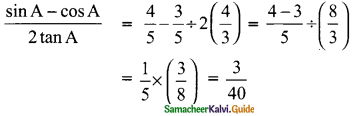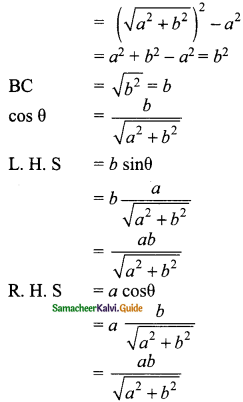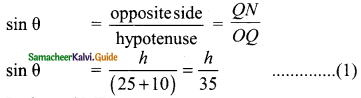Students can download Maths Chapter 4 Geometry Ex 4.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.4

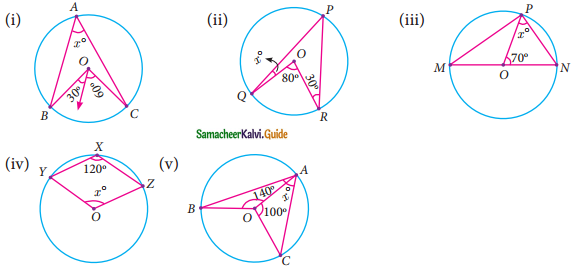
Question 1.
Find the value of x in the given figure.

Solution:
∠B = 180° – 120°
(Sum of the opposite angles of a quadrilateral are supplementary)
∠B = 60°
∠BCA = 90° (Angle in a semicircle)
∠BAC + ∠B + ∠BCA = 180°
x + 60° + 90° = 180°
x + 150° = 180°
x = 180° – 150°
= 30°
The value of x = 30°

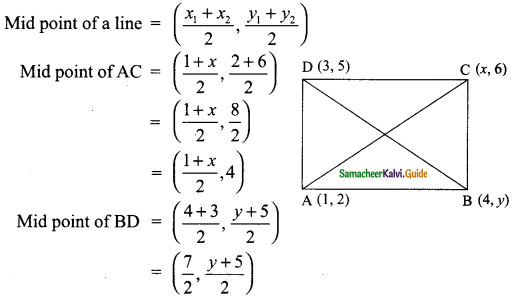
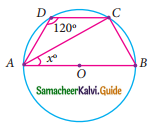
Question 2.
In the given figure, AC is the diameter of the circle with centre O.

If ∠ADE = 30°; ∠DAC = 35° and ∠CAB = 40°.
Find (i) ∠ACD
(ii) ∠ACB
(iii) ∠DAE
Solution:
(i) ∠ADC = 90° (Angle in a semi-circle)
∠ADC + ∠ACD + ∠DAC = 180° (Sum of the angles of a triangle is 180°)
90° + ∠ACD + 35° = 180°
∠ACD = 180° – 125°
∠ACD = 55°

(ii) ∠ABC = 90° (Angle in a semi-circle)
∠ACB + ∠CBA + ∠BAC = 180° (Sum of the angles of a triangle is 180°)
∠ACB + 90 °+ 40° = 180°
∠ACB = 180° – 130°
= 50°

(iii) In the cyclic quadrilateral ACDE,
∠AED = 180° – 55°
= 125°
In ΔAED,
∠DAE + ∠AED + ∠EDA = 180° (Sum of the angles of a triangle is 180°)
∠DAE + 125° + 30° = 180°
∠DAE = 180°- 155°
= 25°
∴ ∠DAE = 25°

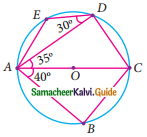
Question 3.
Find all the angles of the given cyclic quadrilateral ABCD in the figure.

Solution:
In a cyclic quadrilateral ABCD,
∠B + ∠D = 180° (Sum of the opposite angles of a cyclic quadrilateral is 180°)
6x – 4° + 7x + 2° = 180°
13x – 2° = 180°
13x = 182°
x = 182°
x = \(\frac{182°}{13}\)
x = 14°
∠B = 6x – 4°
= 6(14) – 4°
= 84 – 4
= 80°
∠D = 7x + 2°
7(14) + 2°
98 + 2
= 100°
180°
2y + 4° + 4y – 4° = (Sum of the opposite angles of a cyclic quadrilateral is 180°)
6y = 180°
y = \(\frac{180°}{6}\)
= 30°
∠A = 2y + 4°
= 2(30) + 4°
= 64°
∠C = 4y – 4°
= 4(30) – 4°
= 120° – 4°
= 116°
∴ ∠A = 64°, ∠B = 80°, ∠C = 116°, ∠D = 100°.

Question 4.
In the given figure, ABCD is a cyclic quadrilateral where diagonals intersect at P such that ∠DBC = 40° and ∠BAC = 60° find

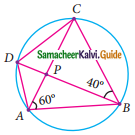
(i) ∠CAD
(ii) ∠BCD
Solution:
(i) ∠CAD = ∠DBC = 40° [Angles at the circumference to the same segment]
(ii) ∠BAC – ∠BDC = 60° [Angles at the circumference to the same segment]
∠BCD + ∠BDC + ∠CBD = 180° (Sum of the three angles of A is 180°)
∠BCD + 60° + 40° = 180°
∠BCD = 180° – 100°
= 80°

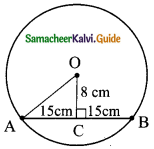
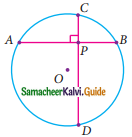
Question 5.
In the given figure, AB and CD are the parallel chords of a circle with centre O. Such that AB = 8 cm and CD = 6 cm. If OM ⊥ AB and OL ⊥ CD distance between LM is 7cm. Find the radius of the circle?

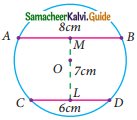
Solution:
Let OM be x.
∴ OL = 7 – x
In the right ΔAOM,
OA² = AM² + OM²
= 4² + x²
OA² = 16 + x²
r² = 16 + x² ……… (1) [r is the radius]
In the right ΔOCL,
OC² = OL² + CL²
r² = (7 – x)² + 3²
= 49 + x² – 14x + 9
= 58 + x² – 14x …….. (2)
From (1) and (2) we get,
16 + x² = 58 + x² – 14x
14x = 58 – 16
14x = 42
x = \(\frac{42}{14}\)
x = 3 cm
r² = 16 + x²
= 16 + 9
= 25
∴ r = \(\sqrt{25}\)
= 5
∴ radius of the circle = 5 cm.

Question 6.
The arch of a bridge has dimensions as shown, where the arch measure 2 m at its highest point and its width is 6 cm. What is the radius of the circle that contains the arch?

Solution:
AD = \(\frac{6}{2}\)
= 3 m
In the right ΔADC,

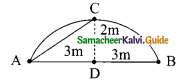
AC² = AD² + DC²
= 32 + 22
= 9 + 4
= 13
AC = \(\sqrt{13}\)
= 3.6m
radius = 3.6 m

Question 7.
In figure ∠ABC = 120°, where A, B and C are points on the circle with centre O. Find ∠OAC?

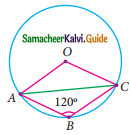
Solution:
Reflex ∠AOC = 2∠ABC
= 20 × 120°
= 240°
∴ ∠AOC = 360° – 240°
= 120°
∠OCA + ∠OAC = 180° – 120°
= 60°
∴ ∠OAC = \(\frac{60}{2}\)
= 30° (Since OA = OC)

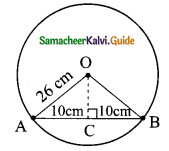
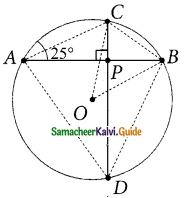
Question 8.
A school wants to conduct tree plantation programme. For this a teacher allotted a circle of radius 6m ground to nineth standard students for planting sapplings. Four students plant trees at the points A, B, C and D as shown in figure. Here AB = 8m, CD = 10m and AB ⊥ CD. If another student places a flower pot at the point P, the intersection of AB and CD, then find the distance from the centre to P.

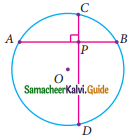
Solution:
OA = OD = 6 m
AB = 8 m (chord)
CD = 10 m (chord)
In Δ AOM, OM = \(\sqrt{6² – 4²}\) (∴ OM bisects the chord and ⊥ to the chord)
= \(\sqrt{36 – 16}\)
= \(\sqrt{20}\)m
In Δ CON, ON = \(\sqrt{6² – 5²}\)
= \(\sqrt{36 – 25}\)
= \(\sqrt{11}\)m (ON bisects the chord and ⊥ to the chord)
ONPM is a rectangle with all the angles 90° and with length \(\sqrt{20}\) m, breadth \(\sqrt{11}\)l m.
We need to find OP which is the diagonal of the rectangle ONPM.
∴ OP = \(\sqrt{ON² + NP²}\) = \(\sqrt{(\sqrt{11})² + (\sqrt{20})²}\)
(∴ OM = NP, opposite sides of the rectangle)
= \(\sqrt{11 + 20}\)
= \(\sqrt{31}\)
= 5.56 m

Question 9.
In the given figure, ∠POQ = 100° and ∠PQR° = 30°, then find ∠RPO.

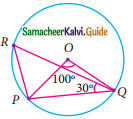
Solution:
∠PRQ = \(\frac{1}{2}\) ∠POQ (Angles at the circumference)
= \(\frac{1}{2}\) × 100°
= 50°
∠OPQ + ∠OQP = 180° – 100° (Total angles of A is 180°)
= 80°
∴ ∠OPQ = \(\frac{80}{2}\)
= 40° (Since OP = OQ, radius of the circle)
∠RPQ = 180°- (30 + 50)°
= 100°
∴ ∠RPO = ∠RPQ – ∠OPQ
= 100° – 40°
= 60°

Students can download Maths Chapter 3 Algebra Ex 3.11 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.11

Question 1.
Solve the following quadratic equations by completing the square method
(i) 9x² – 12x + 4 = 0
Answer:
9x² – 12x + 4 = 0
x² – \(\frac { 12x }{ 9 } \) + \(\frac { 4 }{ 9 } \) = 0 (Divided by 9)
x² – \(\frac { 4x }{ 3 } \) = \(\frac { -4 }{ 9 } \)
Add [\(\frac { 1 }{ 2 } \) (\(\frac { 4 }{ 3 } \))]² on both sides

The solution is \(\frac { 2 }{ 3 } \)

(ii) \(\frac { 5x+7 }{ x-1 } \) = 3x + 2
Answer:
(3x + 2) (x – 1) = 5x + 7
3x² – 3x + 2x – 2 = 5x + 7 ⇒ 3x² – x – 5x – 2 – 7 = 0
3x² – 6x – 9 = 0 ⇒ x² – 2x – 3 = 0 (divided by 3)
x² – 2x = 3
Adding (\(\frac { 1 }{ 2 } \) × 2)² on both sides
x² – 2x + 1 = 3 + 1
(x – 1)² = 4 ⇒ x – 1 = \(\sqrt { 4 }\)
x – 1 = ±2
x – 1 = 2 or x – 1 = -2
x = 3 or x = -1
The solution set is -1 and 3

Question 2.
Solve the following quadratic equations by formula method
(i) 2x² – 5x + 2 = 0
Answer:
a = 2, b = -5, c = 2

The solution set is \(\frac { 1 }{ 2 } \) and 2

(ii) \(\sqrt { 2 }\) f² – 6 f + 3 \(\sqrt { 2 }\) = 0
Answer:
Here a = \(\sqrt { 2 }\), b = -6 and c = 3\(\sqrt { 2 }\)

The solution set is \(\frac{3+\sqrt{3}}{\sqrt{2}}\) and \(\frac{3-\sqrt{3}}{\sqrt{2}}\)

(iii) 3y² – 20y – 23 = 0
Answer:
a = 3, b = -20, c = -23

The solution set is -1 and \(\frac { 23 }{ 3 } \)

(iv) 36y² – 12ay + (a² – b²) = 0
Answer:
Here a = 36, b = -12a, c = a² – b²

The solution set is \(\frac { (a+b) }{ 6 } \) and \(\frac { (a-b) }{ 6 } \)

Question 3.
A ball rolls down a slope and travels a distance d = t² – 0.75t feet in t seconds. Find the time when the distance travelled by the ball is 11.25 feet.
Answer:
Distance = t² – 0.75t
11.25 = t² – 0.75t
Multiply by 100
1125 = 100t² – 75t
100t² – 75t – 1125 = 0 (Divided by 25)
4t² – 3t – 45 = 0
a = 4,
b = -3,
c = -45

(time will not be negative)
The required time = \(\frac { 15 }{ 4 } \) seconds
= 3 \(\frac { 3 }{ 4 } \) second or 3.75 seconds

Students can download Maths Chapter 4 Geometry Ex 4.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.3

Question 1.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre.
Radius of a circle = \(\frac{56}{2}\) = 26 cm
Solution:

Length of the chord = 20 cm
AC = \(\frac{20}{2}\)
= 10 cm
In ΔOAC, OC² = OA² – AC²
= 26² – 10²
= (26 + 10) (26 – 10)
= 36 × 16
OC = \(\sqrt{30×16}\)
= 6 × 4 cm
= 24 cm
Distance of the chord from the centre = 24 cm.

Question 2.
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle.
Solution:

Distance AC = \(\frac{1}{2}\) × Length of chord
= \(\frac{1}{2}\) × 30
= 15 cm
Distance from the centre = 8 cm
In ΔOAC Radius (OA) = \(\sqrt{AC² + OC²}\)
= \(\sqrt{15² + 8²}\)
= \(\sqrt{224 + 64}\)
= \(\sqrt{289}\)
= 17
Radius of the circle = 17 cm.

Question 3.
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius 4√2 cm and also find ∠OAC and ∠OCA.
Solution:
Radius of a circle = 4√2 cm
In the right ΔAOC,

AC² = OA² + OC²
AC² = (4√2)² + (4√2)²
= 32 + 32 = 64
AC = \(\sqrt{64}\)
= 8
Length of the chord = 8 cm,
∠OAC = ∠OCA = 45°
Since OAC is an isosceles right angle triangle.

Question 4.
A chord is 12 cm away from the centre of the circle of radius 15cm. Find the length of the chord.
Solution:
Radius of a circle (OA) = 15 cm
Distance from centre to the chord (OC) = 12 cm
In the right ΔOAC,

AC² = OA² – OC²
= 15² – 12²
= 225 – 144
= 81
AC = \(\sqrt{81}\)
= 9
Length of the chord (AB) = AC + CB
= 9 + 9 = 18 cm.

Question 5.
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
Solution:
Length of the chord (AB) = 16 cm
∴ AF = \(\frac{1}{2}\) × 16
= 8 cm
Length of the chord (CD) = 12 cm
∴ CE = \(\frac{1}{2}\) × 12
= 6 cm

In the right ΔOCE,
OE² = OC² – CE²
= 10² – 6²
= 100 – 36
= 64
OE = \(\sqrt{64}\)
= 8 cm
In the right ΔOAF,
OF² = OA² – AF²
= 10² – 8²
= 100 – 64
= 36
OE = \(\sqrt{36}\)
= 6 cm
Distance between the two chords = OE + OF
= 8 + 6
= 14 cm.

Question 6.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Ans

Two circules intersect at C and D
CD is the common chord.
CD = AC + AD
= 3 + 3
= 6 cm
Length of the common chord = 6 cm.

Question 7.
Find the value of x° in the following figures:

Solution:
(i) ∠BOC = 30° + 60°
= 90°
∠BAC (x) = \(\frac{1}{2}\) ∠BOC (By theorem)
= \(\frac{1}{2}\) × 90°
x = 45°

(ii) Join OP
∠QPR = \(\frac{80}{2}\) = 40° (Angle of the circumference is \(\frac{1}{2}\) the angle at the centre)
∠RPO = 30° (OP and OR are equal sides)
∠OPQ = 40° – 30°
= 10°
∠OQP = 10° (OQ and OP are equal sides)
∴ x = 10°

(iii) ∠OPN = ∠ONP (ON and OP are the radius of the circle)
= 90°
In ΔOPN
∠PON + ∠ONP + ∠NPO = 180° (Sum of the angles of a triangle)
70° + x° + x° = 180°
2x° + 70° = 180°
2x = 180° – 70°
2x = 110°
X = \(\frac{110°}{2}\)
= 55°
The value of x = 55°

(iv) Reflex ∠YOZ = 2∠YXZ
= 2(120°)
= 240°
∠YOZ = 360° – reflex ∠YOZ
= 360° – 240°
= 120°
∴ x = 120°

(v) ∠OAC + ∠OCA = 180° – 100°
= 80°
∠OAC = \(\frac{1}{2}\) × 80° [Since OA = OC, (∴ ∠OAC = ∠OCA)]
= 40°
∠OBA + ∠OAB = 180° – 140°
= 40° [Since ∠OBA = ∠OAB, since OB = OA]
∴∠OAB = \(\frac{40°}{2}\)
= 20°
∠BAC = ∠OAB + ∠OAC
= 20° + 40°
x = 60°

Question 8.
In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB.

Solution:
In ΔACP,
∠ACP = 180° – (25° + 90°)
= 180° – 115°
= 65°
∠CBA = ∠CAB = 25° [Both the angles are standing in the same base]
∠DBA = 65° [∠DBA and ∠BCA standing in the same base]
∠COB = 50°

Students can download Maths Chapter 3 Algebra Ex 3.10 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.10

Question 1.
Solve the following quadratic equations by factorization method
(i) 4x² – 7x – 2 = 0
Answer:
4x² – 7x – 2 = 0
4x² – 8x + x – 2 = 0
4x(x – 2) + 1(x – 2) = 0
(x – 2) + (4x + 1) = 0

x – 2 = 0 or 4x + 1 = 0 (equate the product of factors to zero)
x = 2 or 4x = -1 ⇒ x = \(\frac { -1 }{ 4 } \)
The roots are 2; \(\frac { -1 }{ 4 } \)

(ii) 3(p² – 6) = p(p + 5)
Answer:
3p² – 18 = p² + 5p

2p² – 5p – 18 = 0
2p² – 9p + 4p – 18 = 0
p(2p – 9) + 2(2p – 9) = 0
(2p – 9)(p + 2) = 0
2p – 9 = 0 or p + 2 =
The roots are p = \(\frac { 9 }{ 2 } \), -2

(iii) \(\sqrt{a(a-7)}\) = 3 \(\sqrt{2}\)
Answer:
Squaring on both sides
a(a – 7) = (3\(\sqrt{2}\))²

a² – 7a = 18
a² – 7a – 18 = 0
(a – 9) (a + 2) = 0
a – 9 = 0 or a + 2 = 0
The roots are -2 and 9

(iv) \(\sqrt { 2 }\) x² + 7x + 5\(\sqrt { 2 }\) = 0
Answer:
\(\sqrt { 2 }\) x² + 7x + 5 \(\sqrt { 2 }\) = 0
\(\sqrt { 2 }\) x² + 2x + 5x + 5\(\sqrt { 2 }\) = 0
\(\sqrt { 2 }\) x (x + \(\sqrt { 2 }\)) + 5(x + \(\sqrt { 2 }\)) = 0

(x + \(\sqrt { 2 }\)) + (\(\sqrt { 2 }\)x + 5) = 0 (equate the product of factors to zero)
x + – \(\sqrt { 2 }\) = 0 or \(\sqrt { 2 }\)x + -5
x = \(\frac{-5}{\sqrt{2}}\)
The roots are – \(\sqrt { 2 }\), \(\frac{-5}{\sqrt{2}}\)

(v) 2x² – x + \(\frac { 1 }{ 8 } \) = 0
Answer:
2x² -x + \(\frac { 1 }{ 8 } \) = 0
16x² – 8x + 1 = (multiply by 8)

16x² – 4x – 4x + 1
4x(4x – 1) – 1 (4x – 1) = 0
(4x- 1) (4x- 1) = 0
4x = 1, 4x = 1
x = \(\frac { 1 }{ 4 } \), x = \(\frac { 1 }{ 4 } \)
The roots are \(\frac { 1 }{ 4 } \) and \(\frac { 1 }{ 4 } \)

Question 2.
The number of volleyball games that must be scheduled in a league with n teams is given by G(n) = \(\frac{n^{2}-n}{2}\) where each team plays with every other team exactly once. A league schedules 15 games. How many teams are in the league?
Solution:
G(n) = \(\frac{n^{2}-n}{2}\)
⇒ 15 = \(\frac{n^{2}-n}{2}\) ⇒ 30 = n² – n
n² – n – 30 = 0
⇒ n² – 6n + 5n – 30 = 0
n(n – 6) + 5 (n – 6) = 0
(n – 6)(n + 5) = 0 ⇒ n = 6, -5
As n cannot be (-ve), n = 6.
∴ There are 6 teams in the league.

Students can download Maths Chapter 5 Coordinate Geometry Additional Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Additional Questions

I. Multiple Choice Questions.

Question 1.
On which quadrant does the point (- 4, 3) lie?
(a) I
(b) II
(c) III
(d) IV
Solution:
(b) II

Question 2.
The point whose abscissa is 5 and lies on the x-axis is …….
(a) (-5, 0)
(b) (5, 5)
(c) (0, 5)
(d) (5, 0)
Solution:
(d) (5, 0)

Question 3.
A point which lies in the III quadrant is ……..
(a) (5, 4)
(b) (5, -4)
(c) (-5, -4)
(d) (-5, 4)
Solution:
(c) (-5, -4)

Question 4.
A point on the y-axis is ……..
(a) (1, 1)
(b) (6, 0)
(c) (0, 6)
(d) (-1, -1)
Solution:
(c) (0, 6)

Question 5.
The distance between the points (4, -1) and the origin is ……..
(a) \(\sqrt{24}\)
(b) \(\sqrt{37}\)
(c) \(\sqrt{26}\)
(d) \(\sqrt{17}\)
Solution:
(d) \(\sqrt{17}\)

Question 6.
The distance between the points (-1, 2) and (3, 2) is ……..
(a) \(\sqrt{14}\)
(b) \(\sqrt{15}\)
(c) 4
(d) 0
Solution:
(c) 4

Question 7.
The centre of a circle is (0, 0). One end point of a diameter is (5, -1), then the radius is …….
(a) \(\sqrt{24}\)
(b) \(\sqrt{37}\)
(c) \(\sqrt{26}\)
(d) \(\sqrt{17}\)
Solution:
(c) \(\sqrt{26}\)

Question 8.
The point (0, -3) lies on
(a) + ve x-axis
(b) + ve y-axis
(c) – ve x-axis
(d) – ve y-axis
Solution:
(d) – ve y-axis

Question 9.
The point which is on y-axis with ordinate -5 is ……..
(a) (0, -5)
(b) (-5, 0)
(c) (5, 0)
(d) (0, 5)
Solution:
(a) (0, -5)

Question 10.
The diagonal of a square formed by the points (1, 0), (0, 1), (-1, 0) and (0, -1) is …….
(a) 2
(b) 4
(c) √2
(d) 8
Solution:
(a) 2

Question 11.
The distance between the points (-2, 2) and (3, 2) is ……..
(a) 10 units
(b) 5 units
(c) 5√3 units
(d) 20 units
Solution:
(b) 5 units

Question 12.
The midpoint of the line joining the points (1, -1) and (-5, 3) is ……..
(a) (2, 1)
(b) (2, -1)
(c) (-2, -1)
(d) (-2, 1)
Solution:
(d) (-2, 1)

Question 13.
If the centroid of a triangle is at (1, 3) and two of its vertices are (-7, 6) and (8, 5) then the third vertex is ……..
(a) (-2, 2)
(b) (2, -2)
(c) (-2, -2)
(d) (2, 2)
Solution:
(b) (2, -2)

Question 14.
The ratio in which the X-axis divides the line segment joining the points (6, 4) and (1, -7) is ……..
(a) 1 : 2
(b) 2 : 3
(c) 4 : 7
(d) 7 : 4
Solution:
(c) 4 : 7

Question 15.
The centroid of a triangle (3, -5), (-7, 4) and (10, -2) is …….
(a) (2, -1)
(b) (2, 1)
(c) (-2, 1)
(d) (1, -2)
Solution:
(a) (2, -1)

II. Answer the Following Questions.

Question 1.
Show that the given points (1, 1), (5, 4), (-2, 5) are the vertices of an isosceles right angled triangle.
Solution:
Let A (1, 1), B (5, 4) and G (-2, 5)

AB = 5, AC = 5
∴ ABC is an isosceles triangle …….. (1)
BC² = AB² + AC²
50 = 25 + 25 ⇒ 50 = 50
∴ ∠A = 90° ……… (2)
From (1) and (2) we get ABC is an isosceles right angle triangle.

Question 2.
Show that the point (3, -2), (3, 2), (-1, 2) and (-1, -2) taken in order are the vertices of a square.
Solution:

= \(\sqrt{16}\)
= 4
AB = BC = CD = DA = 4. All the four sides are equal.
∴ ABCD is a Rhombus ……..(1)

Diagonal AC = Diagonal BD = \(\sqrt{32}\) ……..(2)
From (1) and (2) we get ABCD is a square.

Question 3.
Show that the point A (3, 7) B (6, 5) and C (15, -1) are collinear.
Solution:

AB + BC = AC ⇒ \(\sqrt{13}\) + 3\(\sqrt{13}\) = 4\(\sqrt{13}\)
∴ The points A, B, C are collinear.

Question 4.
Find the type of triangle formed by (-1, -1), (1, 1) and (-√, √3)
Solution:
Let the point A (-1, -1), B (1, 1) and C (-√3, √3)

AB = BC = AC = √8
∴ ABC is an equilateral triangle.

Question 5.
Find x such that PQ = QR where P(6, -1) Q(1, 3) and R(x, 8) respectively.
Solution:

But PQ = QR
\(\sqrt{(x-1)^{2}+25}\) = \(\sqrt{41}\)
Squaring on both sides
(x – 1)² + 25 = 41
(x – 1)² = 41 – 25 = 16
x – 1 = \(\sqrt{16}\) = ± 4
x – 1 = 4 (or) x – 1 = – 4
x = 5 (or) x = -4 + 1 = -3
The value of x = 5 or – 3

Question 6.
Find the coordinate of the point of trisection of the line segment joining (4, -1) and
Solution:
Let A (4, -1) and B (-2, -3) are the given points
Let P (a, b) and Q (c, d) be the points of trisection of AB.
∴ AP = PQ = QB

The required coordinate P is (2, –\(\frac{5}{3}\)) and Q is (0, –\(\frac{7}{3}\))

Question 7.
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
Solution:
Given points are A(-3, 10), B(6, -8) and P(-1, 6)
divides AB internally in the ratio m : n
By section formula.
A line divides internally in the ratio m : n the point P =

∴ \(\frac{6m-3n}{m+n}\) = -1
6m – 3n = -m – n
6m + m = 3n – n
7m = 2n ⇒ \(\frac{m}{n}\) = \(\frac{2}{7}\)
∴ m : n = 2 : 7
and
\(\frac{-8m+10n}{m+n}\) = 6
-8m + 10n = 6m + 6n
-8m – 6m = 6n – 10n
14m = 4n
∴ \(\frac{m}{n}\) = \(\frac{14}{4}\) = \(\frac{2}{7}\)
Hence P divides AB internally in the ratio 2 : 7

Question 8.
If (1, 2) (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find “x” and “y”.
Solution:
Let A(1, 2), B(4, y), C(x, 6) and D(3, 5)

Since ABCD is a parallelogram the diagonal bisect each other
Mid point of AC = Mid point of BD
(\(\frac{1+x}{2}\), 4) = (\(\frac{7}{2}\), \(\frac{y+5}{2}\))
\(\frac{1+x}{2}\) = \(\frac{7}{2}\)
1 + x = 7
x = 7 – 1
= 6
and
\(\frac{y+5}{2}\) = 4
y + 5 = 8
y = 8 – 5
= 3
∴ The value of x = 6 and y = 3

Students can download Maths Chapter 3 Algebra Ex 3.19 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.19

Question 1.
A system of three linear equations in three variables is inconsistent if their planes
(1) intersect only at a point
(2) intersect in a line
(3) coincides with each other
(4) do not intersect
Answer:
(4) do not intersect

Question 2.
The solution of the system x + y -3z = -6, -7y + 7z = 7,3z = 9 is
(1) x = 1, y = 2, z = 3
(2) x = -1, y = 2, z = 3
(3) x = -1, y = -2, z = 3
(4) x = 1, y = 2, z = 3
Solution:
(4) x = 1, y = 2, z = 3
Hint:
x + y – 3z = -6
-7y + 7z = 7
3z = 9
z = 3
-7y + 21 = 7
-7y = -14
y = 2
x + 2 -3 × 3 = -6
x + 2 – 9 = -6 .
x = -6 + 7 = 1

Question 3.
If (x – 6) is the HCF of x² – 2x – 24 and x² – kx – 6 then the value of k is ……………..
(1) 3
(2) 5
(3) 6
(4) 8
Answer:
(2) 5
Hint.
HCF = x – 6
p(x) = x² – 2x – 24
= (x – 6) (x + 4)
g(x) = x² – kx – 6
∴ x – 6 is the common factor.
g (6) = 6² – k(6) – 6
= 36 – 6k – 6
= 30 – 6k
g(6) = 0
30 – 6k = 0
30 = 6k ⇒ k = \(\frac { 30 }{ 6 } \) = 5
The value of k = 5

Question 4.
\(\frac { 3y-3 }{ y } \) + \(\frac { 7y-7 }{ 3y2 } \) is …………

Answer:
(1) \(\frac{9 y}{7}\)

Question 5.
y² + \(\frac{1}{y^{2}}\) is not equal to ………….
(1) \(\frac{y^{4}+1}{y^{2}}\)
(2) (y + \(\frac { 1 }{ y } \))²
(3) (y – \(\frac { 1 }{ y } \))²
(4) (y + \(\frac { 1 }{ y } \))² – 2
Answer:
(2) (y + \(\frac { 1 }{ y } \))²
Hint.

Question 6.
\(\frac{x}{x^{2}-25}-\frac{8}{x^{2}+6 x+5}\) gives …………..

Answer:

Hint.

Question 7.
The square root of \(\frac{256 x^{8} y^{4} z^{10}}{25 x^{6} y^{6} z^{6}}\) is equal to ………….

Answer:

Hint.

Question 8.
Which of the following should be added to make x⁴ + 64 a perfect square
(1) 4x²
(2) 16x²
(3) 8x²
(4) -8x²
Solution:
(2) 16x²
Hint:
x⁴ + 64 = (x²)² + 8² + 2 × 8x²
= (x² + 8)²

Question 9.
The solution of (2x – 1)² = 9 is equal to ………..
(1) -1
(2) 2
(3) -1, 2
(4) None of these
Answer:
(3) -1, 2
Hint.
(2x – 1)² = 9 ⇒ (2x – 1) = \(\sqrt { 9 }\)
2x – 1 = ± 3 ⇒ 2x – 1 = 3 or 2x – 1 = 3
2x – 1 = 3
2x = 4 ⇒ x = \(\frac { 4 }{ 2 } \) = 2
2x – 1 = -3 ⇒ 2x = -3 + 1
x = -1

Question 10.
The values of a and b if 4x⁴ – 24x³ + 76x² + ax + b is a perfect square are ………..
(1) 100,120
(2) 10,12
(3) -120,100
(4) 12,10
Answer:
(3) -120,100
Hint.
Since it is a perfect square
a + 120 = 0
a = -120
b – 100 = 0
b = 100

Question 11.
If the roots of the equation q²x² + p²x + r² = 0 are the squares of the roots of the equation qx² + px + r = 0 , then q,p,r are in ……………..
(1) A.P.
(2) G.P.
(3) Both A.P and G.P
(4) none of these
Answer:
(2) G.P.
Hint.
q²x² + p²x + r² = 0
Let the roots be α² + β²
α² + β² = \(\frac{-p^{2}}{q^{2}}\)
α²β² = \(\frac{r^{2}}{q^{2}}\)
qx² + px + r = 0
Let the root be α and β

Question 12.
Graph of a linear polynomial is a
(1) straight line
(2) circle
(3) parabola
(4) hyperbola
Solution:
(1) straight line

Question 13.
The number of points of intersection of the quadratic polynomial x2 + 4x + 4 with the X axis is …………….
(1) 0
(2) 1
(3) 0 or 1
(4) 2
Answer:
(2) 1
Hint:
(x + 2)² = 0 ⇒ (x + 2) (x + 2) = 0
x + 2 = 0 or x + 2 = 0 ⇒ x = -2 or x = -2
Number of points of intersection is 1 (both the values are same)

Question 14.
For the given matrix

the order of the matrix A^T is ……………
(1) 2 × 3
(2) 3 × 2
(3) 3 × 4
(4) 4 × 3
Answer:
(3) 3 × 4

Question 15.
If A is a 2 × 3 matrix and B is a 3 × 4 matrix, how many columns does AB have ………..
(1) 3
(2) 4
(3) 2
(4) 5
Answer:
(2) 4
Hint.
The order of AB is 2 × 4
∴ Number of columns is 4.

Question 16.
If the number of columns and rows are not equal in a matrix then it is said to be a
(1) diagonal matrix
(2) rectangular matrix
(3) square matrix
(4) identity matrix
Solution:
(2) rectangular matrix

Question 17.
Transpose of a column matrix is …………..
(1) unit matrix
(2) diagonal matrix
(3) column matrix
(4) row matrix
Answer:
(4) row matrix

Question 18.
Find the matrix X if


Answer:

Hint.

Question 19.
Which of the following can be calculated from the given matrices?

(i) A²
(ii) B²
(iii) AB
(iv) BA
(1) (i) and (ii) only
(2) (ii) and (iii) only
(3) (ii) and (iv) only
(4) all of these
Answer:
(3) (ii) and (iv) only
Hint: (i) A² is possible to find
(ii) B² is also possible to find
(iii) not possible: order of A= (3 × 2) order of B is (3 × 3). AB is not possible number of column of matrix A ≠ number of rows of the matrix B.
(iv) Possible number column of the matrix is equal to the number of the matrix A.

Question 20.

Which of the following statements are correct?

(1) (i) and (ii) only
(2) (ii) and (iii) only
(3) (iii) and (iv)
(4) all of these
Answer:
(1) (i) and (ii) only
Hint.
(i) AB + C : order of A = 2 × 3
order of B = 3 × 2
order of AB = 2 × 2
order of C = 2 × 2
It is possible to add AB + C

(ii) BC :
order of B = 3 × 2
order of C = 2 × 2
It is possible to find BC

(iii) BA is not possible
order of B = 3 × 2
order of A = 3 × 2
BA does not exist.
BA + C is not a correct statement

(iv) ABC is not possible
order of A = 2 × 3 order of
B = 3 × 2
order of AB = 2 × 2
order of C = 3 × 2
It is not possible to multiply AB and C.
∴ The statement ABC is not correct.

Students can download Maths Chapter 6 Trigonometry Ex 6.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.3

Question 1.
Find the value of the following:

(iii) tan 15° tan 30° tan 45° tan 60° tan 75°

Solution:
(i) cos 45° = \(\frac{1}{√2}\)

= 1² + 1² – 2(\(\frac{1}{√2}\))²
= 1 + 1 – 2(\(\frac{1}{2}\))
= 2 – 1
= 1

(ii) cos 60° = \(\frac{1}{2}\)

= 1 + 1 + 1 – 8(\(\frac{1}{2}\))²
= 3 – 8 × \(\frac{1}{4}\)
= 3 – 2
= 1

(iii) tan 30° = \(\frac{1}{√3}\), tan 45° = 1, tan 60° = √3
tan 15° . tan 30°. tan 45° . tan 60°. tan 75° = tan 15° . \(\frac{1}{√3}\) . 1 . √3 tan 75°
= tan 15° × tan 75° × \(\frac{1}{√3}\) × 1 × √3
= tan(90° – 75°) × \(\frac{1}{cot 75°}\) × 1 [tan 90° – θ = cot θ]
= cot 75° × \(\frac{1}{cot 75°}\) × 1
= 1

= 1 + 1
= 2

Students can download Maths Chapter 6 Trigonometry Ex 6.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.2

Question 1.
Verify the following equalities:
(i) sin² 60° + cos² 60° = 1
Solution:
sin 60° = \(\frac{√3}{2}\); cos 60° = \(\frac{1}{2}\)
L.H.S = sin² 60° + cos² 60°

L.H.S = R.H.S
Hence it is proved.

(ii) 1 + tan² 30° = sec² 30°
Solution:
tan 30° = \(\frac{1}{√3}\); sec 30° = \(\frac{2}{√3}\)
L.H.S = 1 + tan² 30°

∴ L.H.S = R.H.S
Hence it is proved.

(iii) cos 90° = 1 – 2sin² 45° = 2cos² 45° – 1
Solution:
cos 90° = 0, sin 45° = \(\frac{1}{√2}\), cos 45° = \(\frac{1}{√2}\)
cos 90° = 0 ……. (1)
1 – 2 sin² 45° = 1 – 2 (\(\frac{1}{√2}\))²
= 1 – 2 × \(\frac{1}{2}\)
= 1 – 1 = 0 → (2)
2 cos² 45° – 1 = 2(\(\frac{1}{√2}\))² – 1
= \(\frac{2}{2}\) – 1
= \(\frac{2 – 2}{2}\) = 0 → (3)
From (1), (2) and (3) we get
cos 90° = 1 – 2 sin² 45° = 2 cos² 45° – 1
Hence it is proved.

(iv) sin 30° cos 60° + cos 30° sin 60° = sin 90°
Solution:
sin 30° = \(\frac{1}{2}\); cos 60° = \(\frac{1}{2}\); cos 30° = \(\frac{√3}{2}\); sin 60° = \(\frac{√3}{2}\); sin 90° = 1
L.H.S = sin 30° cos 60° + cos 30° sin 60°

= 1
R.H.S = sin 90° = 1
L.H.S = R.H.S
Hence it is proved.

Question 2.
Find the value of the following:
(i) \(\frac{tan 45°}{cosec 30°}\) + \(\frac{sec 60°}{cot 45°}\) – \(\frac{5 sin 90°}{2 cos 0°}\)
(ii) (sin 90° + cos 60° + cos 45°) × (sin 30° + cos 0° – cos 45°)
(iii) sin²30° – 2 cos³ 60° + 3 tan⁴ 45°
Solution:
(i) tan 45° = 1, cosec 30° = 2; sec 60° = 2; cot 45° = 1; tan 45°, sin 90° = 1; cos 0° = 1

= 0

(ii) sin 90° = 1; cos 60° = \(\frac{1}{2}\); cos 45° = \(\frac{1}{√2}\); sin 30° = \(\frac{1}{2}\); cos 0° = 1
(sin 90° + cos 60° + cos 45°) × (sin 30° + cos 0° – cos 45°)

= \(\frac{7}{4}\)

(iii) sin 30° = \(\frac{1}{2}\); cos 60° = \(\frac{1}{2}\); tan 45° = 1
sin² 30° – 2 cos³ 60° + 3 tan⁴ 45°

= 3

Question 3.
Verify cos 3 A = 4 cos³ A – 3 cos A, when A = 30°
Solution:
L.H.S = cos 3 A
= cos 3 (30°)
= cos 90°
= 0
R.H.S = 4 cos³ A – 3 cos A
= 4 cos³ 30° – 3 cos 30°

= 0
∴ L.H.S = R.H.S
Hence it is proved.

Question 4.
Find the value of 8 sin2x, cos 4x, sin 6x, when x = 15°.
Solution:
8 sin 2x cos 4x sin 6x = 8 sin 2 (15°) × cos 4 (15°) × sin (6 × 15°)
= 8 sin 30° × cos 60° × sin 90°
= 8 × \(\frac{1}{2}\) × \(\frac{1}{2}\) × 1
= 2

Students can download Maths Chapter 5 Coordinate Geometry Ex 5.5 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.5

Question 1.
Find the centroid of the triangle whose vertices are
(i) (2, -4), (-3, -7) and (7, 2)
Solution:
Let the vertices of a triangle be A (2, -4), B (-3, -7) and C (7, 2) Centroid

Centroid is (2, -3)

(ii) (-5, -5), (1, -4) and (-4, -2)
Solution:
Let the vertices of a triangle be A (-5, -5), B (1, -4) and C (-4, -2)

Question 2.
If the centroid of a triangle is at (4, -2) and two of its vertices are (3, -2) and (5, 2) then find the third vertex of the triangle.
Solution:
Let the vertices of a triangle be A (3, -2), B (5, 2) and C (x₃, y₃)
Centroid of a triangle is (4, -2)

∴ \(\frac{8+x_{3}}{3}\) = 4
8 + x₃ = 12
x₃ = 12 – 8
= 4
and
\(\frac{y_{3}}{3}\) = -2
y₃ = -6
∴ The third vertex is (4, -6)

Question 3.
Find the length of median through A of a triangle whose vertices are A(-1, 3), B (1, -1) and C (5, 1).
Solution:
AD is the median of the ΔABC
D is the mid-point of BC

Length of the median AD is 5 units.

Question 4.
The vertices of a triangle are (1, 2), (h, -3) and (-4, k). If the centroid of the triangle is at the point (5, -1) then find the value of \(\sqrt{(h+k)^{2}+(h+3k)^{2}}\)
Solution:
Let the vertices A (1, 2), B (h, -3) and C (-4, k)


\(\frac{-3+h}{3}\) = 5
-3 + h = 15
h = 15 + 3 = 18
and
\(\frac{-1+k}{3}\) = -1
-1 + k = -3
k = -3 + 1
k = -2

Question 5.
Orthocentre and centroid of a triangle are A(-3, 5) and B(3, 3) respectively. If C is the circumcentre and AC is the diameter of this circle, then find the radius of the circle.
Solution:
Let PQR be any triangle orthocentre, centroid and circumcentre.

A orthocentre is (-3, 5)
B centroid is (3, 3)
C orthocentre is (a, 6)
Also \(\frac{AB}{BC}\) = \(\frac{2}{1}\)
B divides AC in the ratio 2 : 1
A line divides internally in the ratio point P is (\(\frac{mx_{2}+nx_{1}}{m+n}\), \(\frac{my_{2}+ny_{1}}{m+n}\))
m = 2
x₁ = 3
y₁ = 5
amd
n = 1
x₂ = a
y₂ = b
∴ The point B (\(\frac{2a-3}{2+1}\), \(\frac{2b+5}{2+1}\))
(3, 3) = (\(\frac{2a-3}{3}\), \(\frac{2b+5}{3}\))
\(\frac{2a-3}{3}\) = 3
2a – 3 = 9
2a = 9 + 3
2a = 12
a = \(\frac{12}{2}\) = 6
and
\(\frac{2b+5}{3}\)
2b + 5 = 9
2b = 9 – 5
2b = 4
b = \(\frac{4}{2}\) = 2
∴ Orthocentre C is (6, 2)

Question 6.
ABC is a triangle whose vertices are A (3, 4), B (-2, -1) and C (5, 3). If G is the centroid and BDCG is a parallelogram then find the coordinates of the vertex D.
Solution:
The vertices of a triangle are A (3, 4), B (-2, -1) and C (5, 3)

The point G is (2, 2)
Let the vertices D be (a, b)
Since BDCG is a parallelogram
Mid-point of BC = Mid-point of DG

\(\frac{2+a}{2}\) = \(\frac{3}{2}\)
4 + 2a = 6
2a = 6 – 4
2a = 2
a = 1
and
\(\frac{2+b}{2}\) = 1
2 + b = 2
b = 2 – 2 = 0
The vertices D is (1, 0).

Question 7.

Solution:
In ΔABC, Let A (x₁, y₁), B (x₂, y₁) and C (x₃, y₃)

x₁ + x₂ = 3 → (1)
y₁ + y₂ = 10 → (2)

x₂ + x₃ = 14 → (3)
y₂ + y₃ = 10 → (4)

x₁ + x₃ = 3 → (5)
y₁ + y₃ = 10 → (6)
Add (1) + (3) + (5) We get
2x₁ + 2x₂ + 2x₃ = 30
2(x₁ + x₂ + x₃) = 30
x₁ + x₂ + x₃ = 15
From (1), x₁ + x₂ = 3
∴ x₃ = 12
From (3), x₂ + x₃ = 14
∴ x₁ = 1
From (5), x₁ + x₃ = 13
∴ x₂ = 2
Add (2), (4) and (6) we get
2y₁ + 2y₂ + 2y₃ = -12
2(y₁ + y₂ + y₃) = – 12
∴ y₁ + y₂ + y₃ = -6
From (2), y₁ + y₂ = 10
∴ y₃ = -16
From (4) y₂ + y₃ = -9
∴ y₁ = 3
From (6) y₁ + y₃ = -13
∴ y₂ = 7
The vertices of the A are A (1, 3), B (2, 7) and C (12, -16)

The Centroid of Δ is (5, -2)

Students can download Maths Chapter 6 Trigonometry Ex 6.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.1

Question 1.
From the given figure, find all the trigonometric ratios of angle B.

Solution:

Question 2.
From the given figure, find the values of

(i) sin B
(ii) sec B
(iii) cot B
(v) tan C
(vi) cosec C
Solution:
In the right ΔABD,
AD² = AB² – BD²
= 13² – 5²
= 169 – 25
= 144
AD = \(\sqrt{144}\)
= 12
In the right ΔADC,
AC² = AD² + DC²
= 12² + 16²
= 144 + 256
= 400
AC = \(\sqrt{400}\)
= 20

Question 3.
If 2 cos θ = √3, then find all the trigonometric ratios of angle θ.
Solution:

2 cos θ = √3 ⇒ cos θ = \(\frac{√3}{2}\)
AB² = AC² – BC²
= 2² – (√3)² ⇒ = 4 – 3 = 1
AB = √1 = 1

Question 4.
If cos A =\(\frac{3}{5}\), then find the value of \(\frac{sin A-cos A}{2 tan A}\)
Solution:

cos A = \(\frac{3}{5}\)
ΔABC
BC² = AC² – AB²
= 5² – 3²
= 25 – 9
= 16
BC = \(\sqrt{16}\) = 4
sin A = \(\frac{4}{5}\); tan A = \(\frac{4}{3}\)

∴ The value of \(\frac{sin A-cos A}{2 tan A}\) = \(\frac{3}{40}\)

Question 5.
If cos A = \(\frac{2x}{1+x_{2}}\) then find the values of sin A and tan A in terms of x.
Solution:
cos A = \(\frac{2x}{1+x_{2}}\)
In the triangle ABC

BC² = AC² – AB²
= (1 + x²)² – (2x)²
= 1 + x⁴ + 2x² – 4x²
= x⁴ – 2x² + 1
= (x² – 1)² (or) (1 – x²)² (using (a – b)²)
BC = \(\sqrt{(x^{2}-1)^{2}}\) (or) \(\sqrt{(1-x^{2})^{2}}\)
BC = x² – 1
The value of sin A = \(\frac{BC}{AC}\) = \(\frac{x²-1}{x²+1}\)
tan A = \(\frac{BC}{AB}\) = \(\frac{x²-1}{2x}\)
and
BC = 1 – x²
The value of sin A = \(\frac{1-x²}{1+x²}\)
tan A = \(\frac{1-x²}{2x}\)

Question 6.
If sin θ = \(\frac{a}{\sqrt{a²+b²}}\) then show that b sin θ = a cos θ.
Solution:

sin θ = \(\frac{a}{\sqrt{a²+b²}}\)
In the triangle ΔABC
BC² = AC² – AB²

L. H. S = R. H. S

Question 7.
If 3 cot A = 2, then find the value of \(\frac{4sin A-3cos A}{2 sin A+3 Cos A}\)
Solution:

3 cot A = 2 ⇒ cot A = \(\frac{2}{3}\)
AC² = AB² + BC²
= 3² + 2²
= 9 + 4
AC = \(\sqrt{13}\)
cos A = \(\frac{AB}{AC}\) = \(\frac{3}{\sqrt{13}}\)
sin A = \(\frac{BC}{AC}\) = \(\frac{2}{\sqrt{13}}\)
The value of \(\frac{4sin A-3cos A}{2 sin A+3 Cos A}\)

The value is (\(\frac{-1}{13}\))

Question 8.
If cos θ : sin θ = 1 : 2, then find the value of \(\frac{8cos θ-2cos θ}{4 cos θ+2 sin θ}\)
Solution:
cos θ : sin θ = 1 : 2

Aliter:
cos θ : sin θ = 1 : 2
2 cos θ = sin θ ⇒ 2 = \(\frac{sin θ}{cos θ}\) ⇒ 2 = tan θ

∴ The value is \(\frac{1}{2}\)

Question 9.
From the given figure, prove that θ + ∅ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ∅.

Solution:
In the ΔABC,
AB = 9 + 16 = 25
AC = 15; BC = 20
AB² = 25²
= 625 ……. (1)
AC² + BC² = 15² + 20²
= 225 + 400
= 625 …….. (2)
From (1) and (2) we get
AB² = AC² + BC²
ABC is a right angle triangle at C (Pythagoras theorem)
∴ ∠C = 90°
θ + ∅ = 90°
Also ADC is a right angle triangle ∠ADC = 90° (Given)
BDC is also a right angle triangle ∠BDC = 90° (since ADB is a straight line sum of the two angle is 180°)
From the given diagram

Question 10.
A boy standing at a point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios).

Solution:
Let the angle O be “θ”
In ΔONQ

In ΔOMP
sin θ = \(\frac{PM}{OP}\) ⇒ sin θ = \(\frac{5}{25}\)
sin θ = \(\frac{1}{5}\) ……… (2)
From (1) and (2) we get
\(\frac{h}{35}\) = \(\frac{1}{5}\)
5 h = 35 ⇒ h = \(\frac{35}{5}\) = 7
The height of the kite from the ground is 7m.