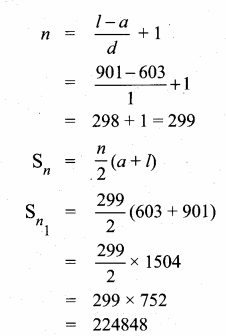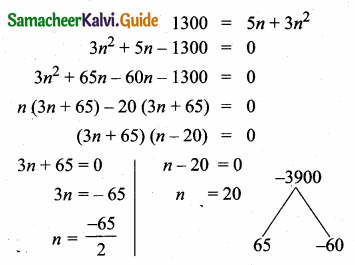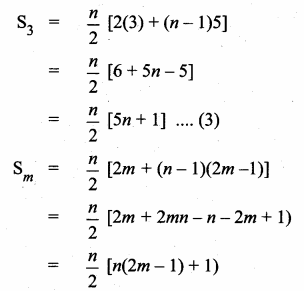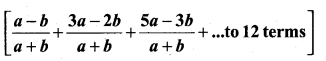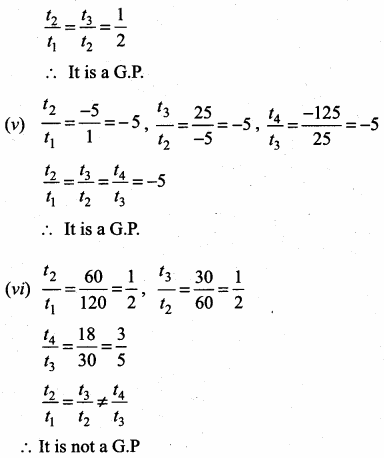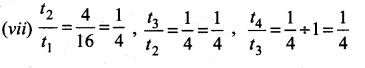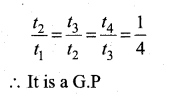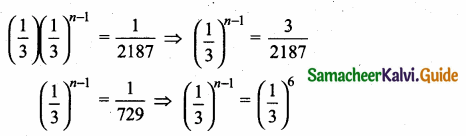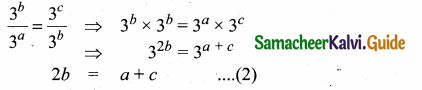Students can download Maths Chapter 3 Algebra Ex 3.19 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.19
Question 1.
A system of three linear equations in three variables is inconsistent if their planes
(1) intersect only at a point
(2) intersect in a line
(3) coincides with each other
(4) do not intersect
Answer:
(4) do not intersect
Question 2.
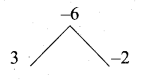
The solution of the system x + y -3z = -6, -7y + 7z = 7,3z = 9 is
(1) x = 1, y = 2, z = 3
(2) x = -1, y = 2, z = 3
(3) x = -1, y = -2, z = 3
(4) x = 1, y = 2, z = 3
Solution:
(4) x = 1, y = 2, z = 3
Hint:
x + y – 3z = -6
-7y + 7z = 7
3z = 9
z = 3
-7y + 21 = 7
-7y = -14
y = 2
x + 2 -3 × 3 = -6
x + 2 – 9 = -6 .
x = -6 + 7 = 1
![]()
Question 3.
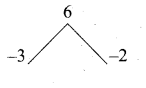
If (x – 6) is the HCF of x2 – 2x – 24 and x2 – kx – 6 then the value of k is ……………..
(1) 3
(2) 5
(3) 6
(4) 8
Answer:
(2) 5
Hint.
HCF = x – 6
p(x) = x2 – 2x – 24
= (x – 6) (x + 4)
g(x) = x2 – kx – 6
∴ x – 6 is the common factor.
g (6) = 62 – k(6) – 6
= 36 – 6k – 6
= 30 – 6k
g(6) = 0
30 – 6k = 0
30 = 6k ⇒ k = \(\frac { 30 }{ 6 } \) = 5
The value of k = 5
![]()
Question 4.
\(\frac { 3y-3 }{ y } \) + \(\frac { 7y-7 }{ 3y2 } \) is …………
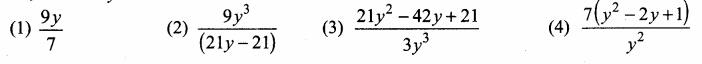
Answer:
(1) \(\frac{9 y}{7}\)
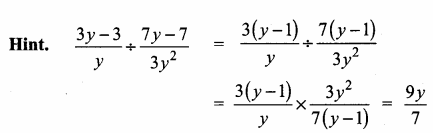
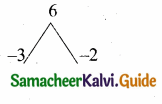
Question 5.
y2 + \(\frac{1}{y^{2}}\) is not equal to ………….
(1) \(\frac{y^{4}+1}{y^{2}}\)
(2) (y + \(\frac { 1 }{ y } \))2
(3) (y – \(\frac { 1 }{ y } \))2
(4) (y + \(\frac { 1 }{ y } \))2 – 2
Answer:
(2) (y + \(\frac { 1 }{ y } \))2
Hint.
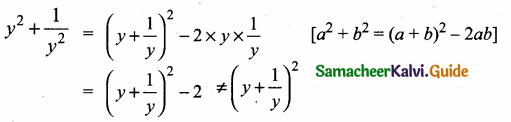
![]()
Question 6.
\(\frac{x}{x^{2}-25}-\frac{8}{x^{2}+6 x+5}\) gives …………..

Answer:
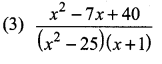
Hint.
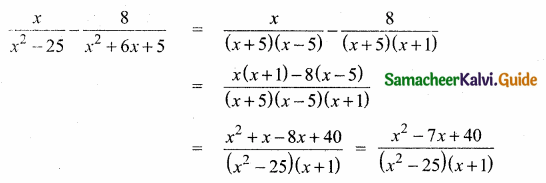
![]()
Question 7.
The square root of \(\frac{256 x^{8} y^{4} z^{10}}{25 x^{6} y^{6} z^{6}}\) is equal to ………….

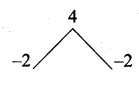
Answer:

Hint.
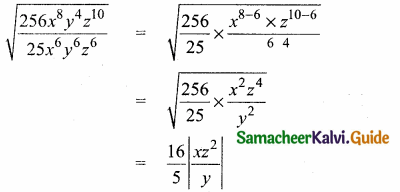
Question 8.
Which of the following should be added to make x4 + 64 a perfect square
(1) 4x2
(2) 16x2
(3) 8x2
(4) -8x2
Solution:
(2) 16x2
Hint:
x4 + 64 = (x2)2 + 82 + 2 × 8x2
= (x2 + 8)2
![]()
Question 9.
The solution of (2x – 1)2 = 9 is equal to ………..
(1) -1
(2) 2
(3) -1, 2
(4) None of these
Answer:
(3) -1, 2
Hint.
(2x – 1)2 = 9 ⇒ (2x – 1) = \(\sqrt { 9 }\)
2x – 1 = ± 3 ⇒ 2x – 1 = 3 or 2x – 1 = 3
2x – 1 = 3
2x = 4 ⇒ x = \(\frac { 4 }{ 2 } \) = 2
2x – 1 = -3 ⇒ 2x = -3 + 1
x = -1
![]()
Question 10.
The values of a and b if 4x4 – 24x3 + 76x2 + ax + b is a perfect square are ………..
(1) 100,120
(2) 10,12
(3) -120,100
(4) 12,10
Answer:
(3) -120,100
Hint.
Since it is a perfect square
a + 120 = 0
a = -120
b – 100 = 0
b = 100

![]()
Question 11.
If the roots of the equation q2x2 + p2x + r2 = 0 are the squares of the roots of the equation qx2 + px + r = 0 , then q,p,r are in ……………..
(1) A.P.
(2) G.P.
(3) Both A.P and G.P
(4) none of these
Answer:
(2) G.P.
Hint.
q2x2 + p2x + r2 = 0
Let the roots be α2 + β2
α2 + β2 = \(\frac{-p^{2}}{q^{2}}\)
α2β2 = \(\frac{r^{2}}{q^{2}}\)
qx2 + px + r = 0
Let the root be α and β
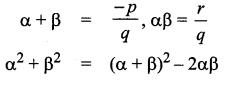

Question 12.
Graph of a linear polynomial is a
(1) straight line
(2) circle
(3) parabola
(4) hyperbola
Solution:
(1) straight line
![]()
Question 13.
The number of points of intersection of the quadratic polynomial x2 + 4x + 4 with the X axis is …………….
(1) 0
(2) 1
(3) 0 or 1
(4) 2
Answer:
(2) 1
Hint:
(x + 2)2 = 0 ⇒ (x + 2) (x + 2) = 0
x + 2 = 0 or x + 2 = 0 ⇒ x = -2 or x = -2
Number of points of intersection is 1 (both the values are same)
Question 14.
For the given matrix
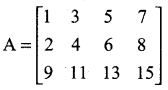
the order of the matrix AT is ……………
(1) 2 × 3
(2) 3 × 2
(3) 3 × 4
(4) 4 × 3
Answer:
(3) 3 × 4
Question 15.
If A is a 2 × 3 matrix and B is a 3 × 4 matrix, how many columns does AB have ………..
(1) 3
(2) 4
(3) 2
(4) 5
Answer:
(2) 4
Hint.
The order of AB is 2 × 4
∴ Number of columns is 4.
![]()
Question 16.
If the number of columns and rows are not equal in a matrix then it is said to be a
(1) diagonal matrix
(2) rectangular matrix
(3) square matrix
(4) identity matrix
Solution:
(2) rectangular matrix
Question 17.
Transpose of a column matrix is …………..
(1) unit matrix
(2) diagonal matrix
(3) column matrix
(4) row matrix
Answer:
(4) row matrix
Question 18.
Find the matrix X if
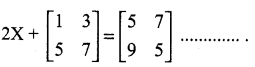

Answer:

Hint.
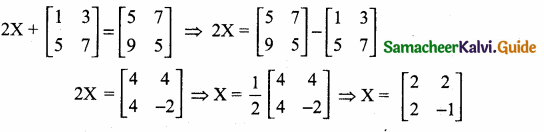
![]()
Question 19.
Which of the following can be calculated from the given matrices?
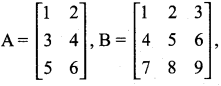
(i) A2
(ii) B2
(iii) AB
(iv) BA
(1) (i) and (ii) only
(2) (ii) and (iii) only
(3) (ii) and (iv) only
(4) all of these
Answer:
(3) (ii) and (iv) only
Hint: (i) A2 is possible to find
(ii) B2 is also possible to find
(iii) not possible: order of A= (3 × 2) order of B is (3 × 3). AB is not possible number of column of matrix A ≠ number of rows of the matrix B.
(iv) Possible number column of the matrix is equal to the number of the matrix A.
Question 20.
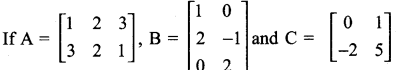
Which of the following statements are correct?
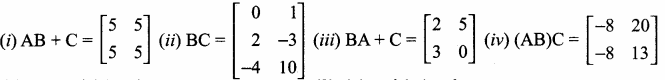
(1) (i) and (ii) only
(2) (ii) and (iii) only
(3) (iii) and (iv)
(4) all of these
Answer:
(1) (i) and (ii) only
Hint.
(i) AB + C : order of A = 2 × 3
order of B = 3 × 2
order of AB = 2 × 2
order of C = 2 × 2
It is possible to add AB + C
![]()
(ii) BC :
order of B = 3 × 2
order of C = 2 × 2
It is possible to find BC
(iii) BA is not possible
order of B = 3 × 2
order of A = 3 × 2
BA does not exist.
BA + C is not a correct statement
(iv) ABC is not possible
order of A = 2 × 3 order of
B = 3 × 2
order of AB = 2 × 2
order of C = 3 × 2
It is not possible to multiply AB and C.
∴ The statement ABC is not correct.
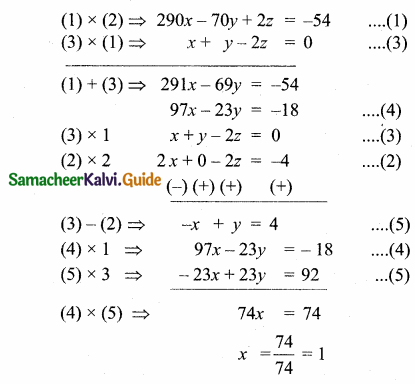


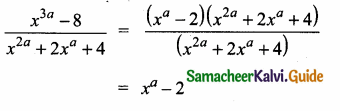
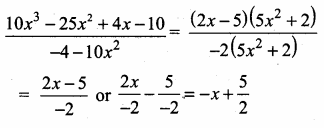
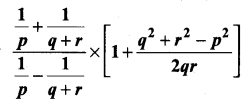
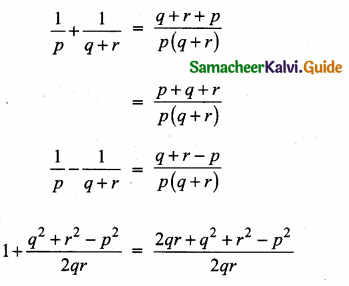
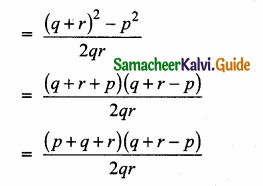
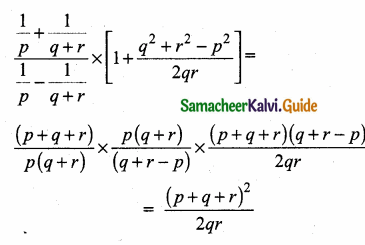
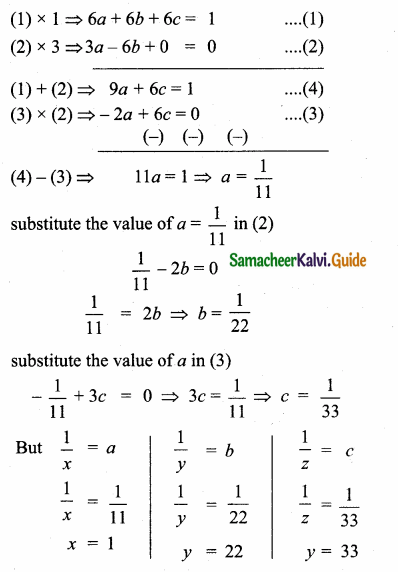

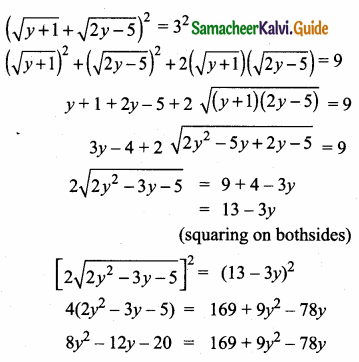


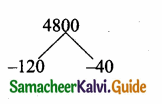
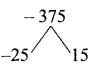

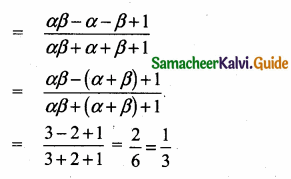



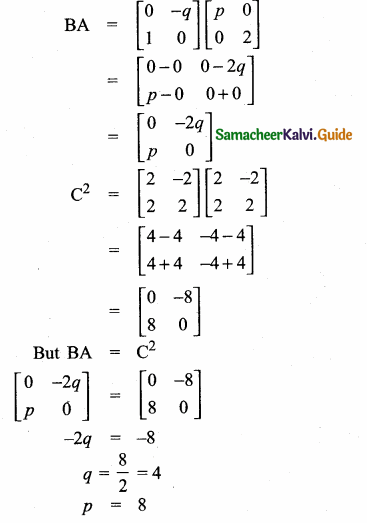
 = I2, find x.
= I2, find x.
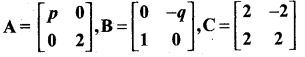
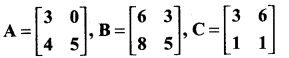

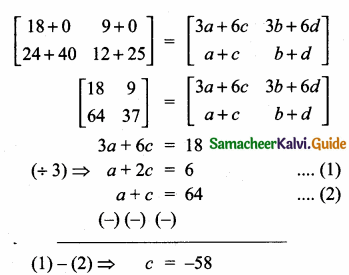
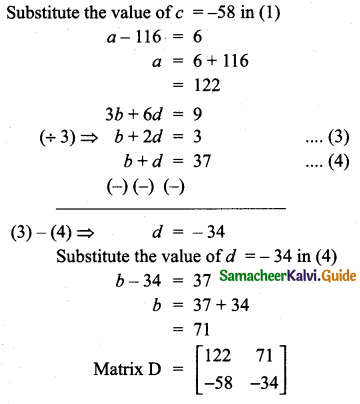


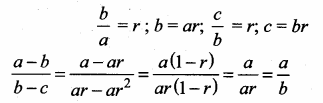

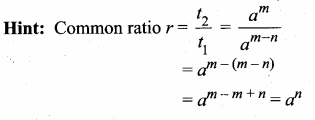
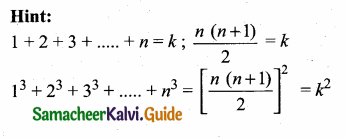

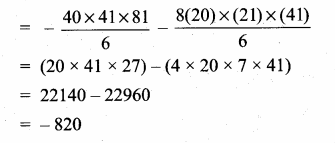
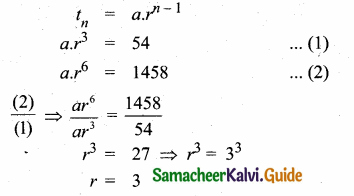
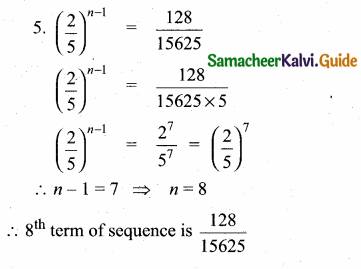
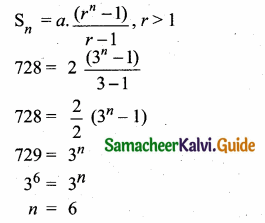
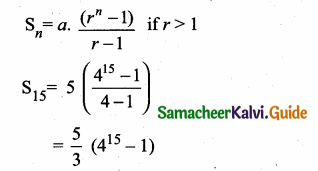
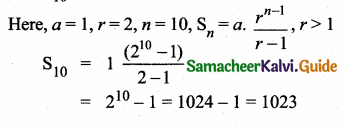
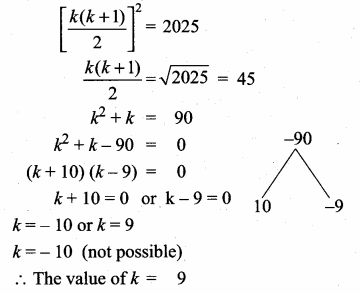
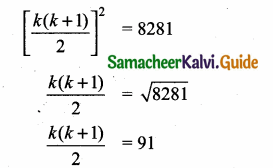
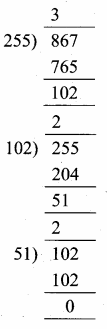
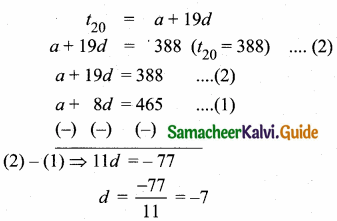
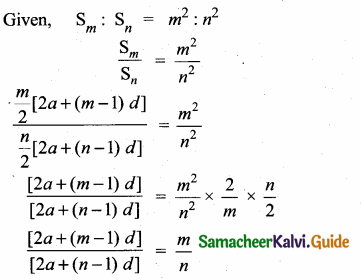
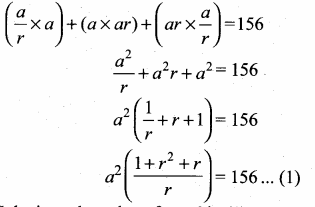


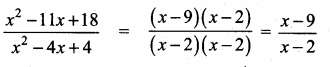
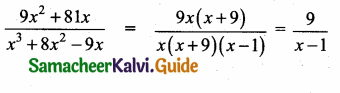
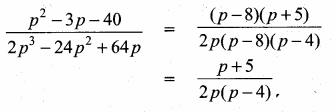
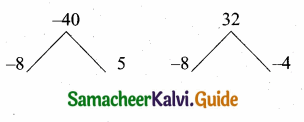
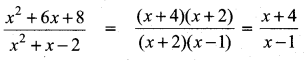
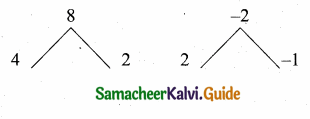
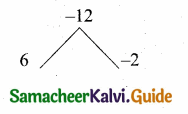
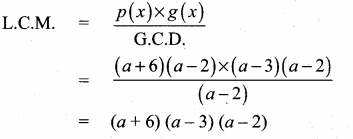
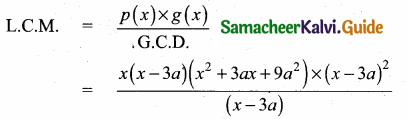
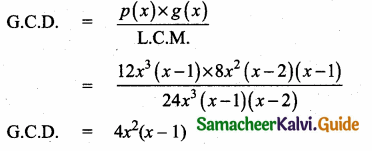
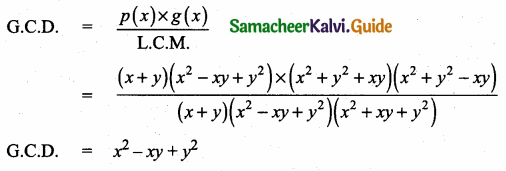

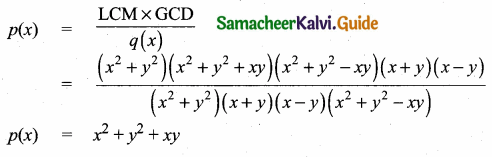

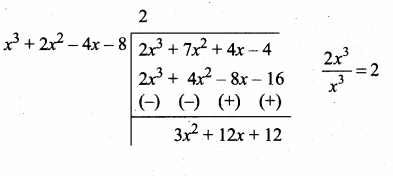
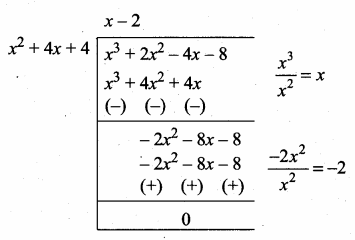
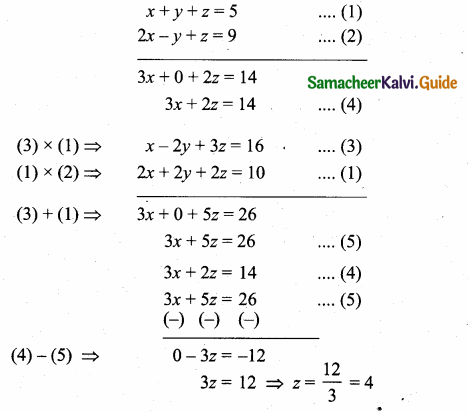
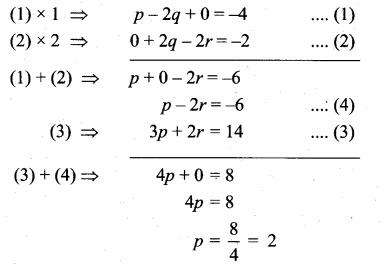
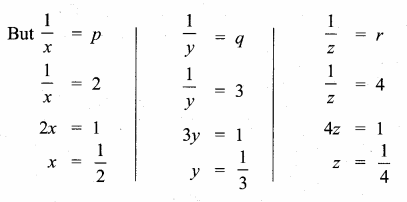

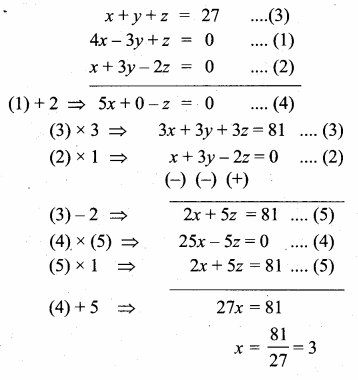
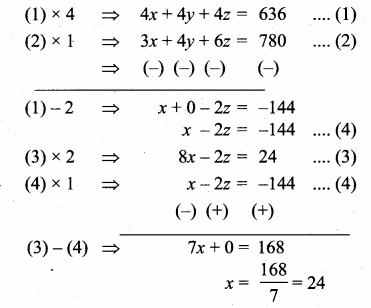
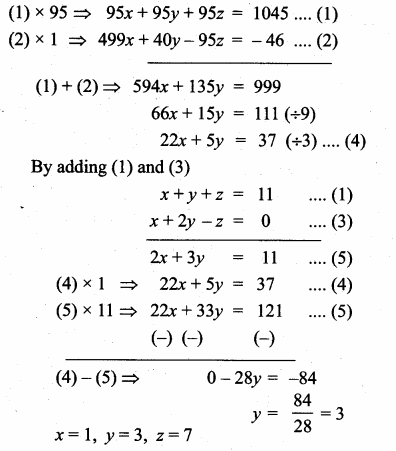
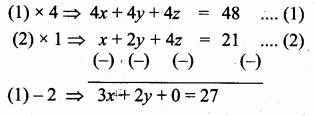
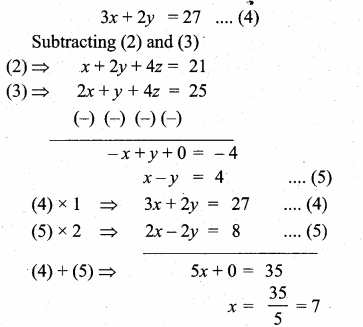
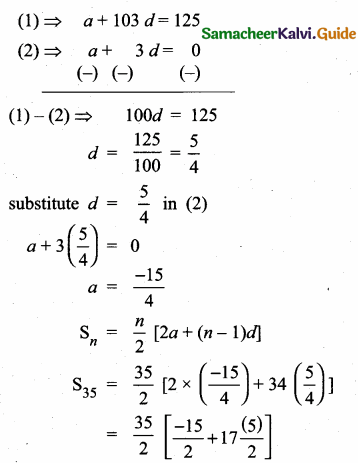
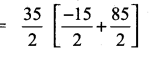
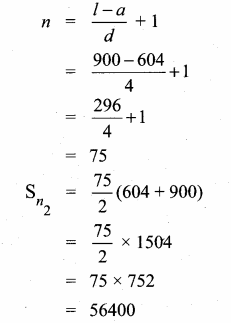
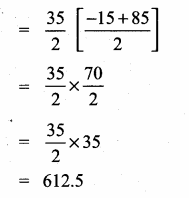 Sum of 35 terms = 612.5
Sum of 35 terms = 612.5