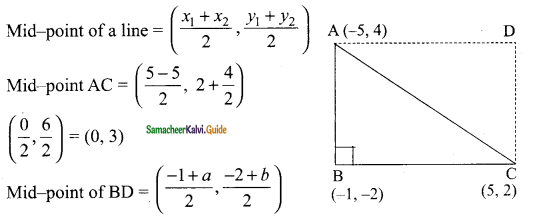
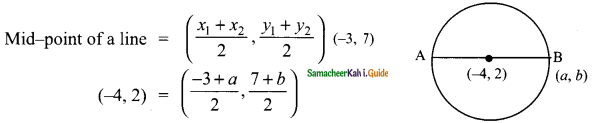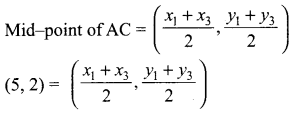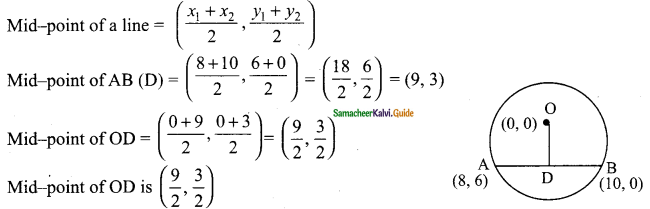Students can download Maths Chapter 2 Real Numbers Ex 2.6 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.6
Question 1.
Simplify the following using addition and subtraction properties of surds:
(i) 5\(\sqrt{3}\) + 18\(\sqrt{3}\) – 2\(\sqrt{3}\)
(ii) 4\(\sqrt[3]{5}\) + 2\(\sqrt[3]{5}\) – 3\(\sqrt[3]{5}\)
(iii) 3\(\sqrt{75}\) + 5\(\sqrt{48}\) – \(\sqrt{243}\)
(iv) 5\(\sqrt[3]{40}\) + 2\(\sqrt[3]{625}\) – 3\(\sqrt[3]{320}\)
Solution:
(i) 5\(\sqrt{3}\) + 18\(\sqrt{3}\) – 2\(\sqrt{3}\) = (5 + 18 – 2)\(\sqrt{3}\)
= (23 – 2) \(\sqrt{3}\) = 21\(\sqrt{3}\)
(ii) 4\(\sqrt[3]{5}\) + 2\(\sqrt[3]{5}\) – 3\(\sqrt[3]{5}\) = (4 + 2 – 3) \(\sqrt[3]{5}\)
= (6 – 3) \(\sqrt[3]{5}\) = 3\(\sqrt[3]{5}\)
![]()
(iii) 3\(\sqrt{75}\) + 5\(\sqrt{48}\) – \(\sqrt{243}\) = \(3\sqrt{5^{2}×3} + 5\sqrt{2^{4}×3} – \sqrt{3^{5}}\)
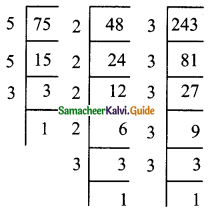
= 3 × 5\(\sqrt{3}\) + 5 × 2²\(\sqrt{3}\) – 3²\(\sqrt{3}\) = 15\(\sqrt{3}\) + 20\(\sqrt{3}\) – 9\(\sqrt{3}\)
= (15 + 20 – 9)\(\sqrt{3}\)
= (35 – 9)\(\sqrt{3}\)
= 26 \(\sqrt{3}\)
(iv) 5\(\sqrt[3]{40}\) + 2\(\sqrt[3]{625}\) – 3\(\sqrt[3]{320}\)
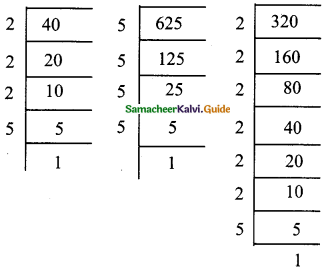
= 5\(\sqrt[3]{2^{3}×5} + 2\sqrt[3]{5^{3}×5} – 3\sqrt[3]{2^{3}×2^{3}×5}\)
5 × 2\(\sqrt[3]{5} + 2 × 5\sqrt[3]{5} – 3 × 2 × 2\sqrt[3]{5} \)
= 10\(\sqrt[3]{5} + 10\sqrt[3]{5} – 12\sqrt[3]{5} \)
= 20\(\sqrt[3]{5} – 12\sqrt[3]{5}\)
= 8\(\sqrt[3]{5}\)
![]()
Question 2.
Simplify the following using multiplication and division properties of surds:
(i) \(\sqrt{3}\) × \(\sqrt{5}\) × \(\sqrt{2}\)
(ii) \(\sqrt{35}\) ÷ \(\sqrt{7}\)
(iii) \(\sqrt[3]{27}\) × \(\sqrt[3]{8}\) × \(\sqrt[3]{125}\)
(iv) (7\(\sqrt{a}\) – 5\(\sqrt{b}\)) (7\(\sqrt{a}\) + 5\(\sqrt{b}\))
(v) (\(\sqrt{\frac{225}{729}} – \sqrt{\frac{25}{144}}\)) ÷ \(\sqrt{\frac{16}{81}}\)
Solution:
(i) \(\sqrt{3}\) × \(\sqrt{5}\) × \(\sqrt{2}\) = \(\sqrt{3×5×2} = \sqrt{30}\)
(ii) \(\sqrt{37} ÷ \sqrt{7} = \frac{\sqrt{35}}{\sqrt{7}} = \sqrt{\frac{35}{7}} = \sqrt{5}\)
(iii) \(\sqrt[3]{27}\) × \(\sqrt[3]{8}\) × \(\sqrt[3]{125}\) = \(\sqrt[3]{27×8×125}\)
= \(\sqrt[3]{3^{3}×2^{3}×5^{3}}\) = 3 × 2 × 5 = 30
(iv) (7\(\sqrt{a}\) – 5\(\sqrt{b}\)) (7\(\sqrt{a}\) + 5\(\sqrt{b}\))
[using a2 – b2 = (a + b) (a – b)]
(7\(\sqrt{a}\) – 5\(\sqrt{b}\)) (7\(\sqrt{a}\) + 5\(\sqrt{b}\)) = \((7\sqrt{a})^{2} – (5\sqrt{b})^{2}\) = 49a – 25b
(v) (\(\sqrt{\frac{225}{729}} – \sqrt{\frac{25}{144}}\)) ÷ \(\sqrt{\frac{16}{81}}\)
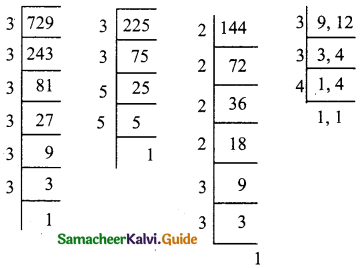
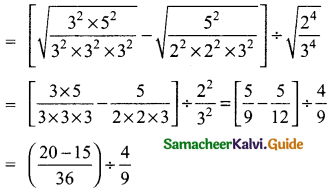
= \(\frac{5}{36}\) × \(\frac{9}{4}\)
= \(\frac{5×1}{4×4}\)
= \(\frac{5}{16}\)
![]()
Question 3.
If \(\sqrt{2}\) = 1.414, \(\sqrt{3}\) = 1.732, \(\sqrt{5}\) = 2.236, \(\sqrt{10}\) = 3.162, then find the values of the following correct to 3 places of decimals.
(i) \(\sqrt{40}\) – \(\sqrt{20}\)
(ii) \(\sqrt{300}\) + \(\sqrt{90}\) – \(\sqrt{8}\)
Solution:
(i) \(\sqrt{40}\) – \(\sqrt{20}\) = \(\sqrt{4×10} – \sqrt{4×5} = 2\sqrt{10} – 2\sqrt{5}\)
= 2 × 3.162 – 2 × 2.236 = 6.324 – 4.472 = 1.852
(ii) \(\sqrt{300}\) + \(\sqrt{90}\) – \(\sqrt{8}\) = \(\sqrt{3×100} + \sqrt{9×10} – \sqrt{4×2}\)
= 10\(\sqrt{3}\) + 3\(\sqrt{10}\) – 2\(\sqrt{2}\)
= 10 × 1.732 + 3 × 3.162 – 2 × 1.414
= 17.32 + 9.486 – 2.828
= 26.806 – 2.828
= 23.978
![]()
Question 4.
Arrange surds in descending order
(i) \(\sqrt[3]{5}\), \(\sqrt[9]{4}\), \(\sqrt[6]{3}\)
Solution:
LCM of 3, 9 and 6 is 18
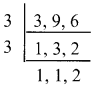
\(\sqrt[3]{5}\) = \(\sqrt[3×6]{5^{6}}\) = \(\sqrt[18]{15625}\)
\(\sqrt[9]{4}\) = \(\sqrt[2×9]{4^{2}}\) = \(\sqrt[18]{16}\)
\(\sqrt[6]{3}\) = \(\sqrt[3×6]{3^{3}}\) = \(\sqrt[18]{27}\)
\(\sqrt[18]{15625}\) > \(\sqrt[18]{27}\) > \(\sqrt[18]{16}\)
\(\sqrt[3]{5}\) > \(\sqrt[6]{3}\) > \(\sqrt[9]{4}\)
![]()
(ii) \(\sqrt[2]{\sqrt[3]{5}}\), \(\sqrt[3]{\sqrt[4]{7}}\), \(\sqrt{\sqrt{3}}\)
Solution:
\(\sqrt[2]{\sqrt[3]{5}}\) = \(\sqrt[6]{5}\); \(\sqrt[3]{\sqrt[4]{7}}\) = \(\sqrt[12]{7}\); \(\sqrt{\sqrt{3}}\) = \(\sqrt[4]{3}\)
LCM of 6, 12 and 4 is 12

\(\sqrt[2]{\sqrt[3]{5}}\) = \(\sqrt[6]{5}\) = \(\sqrt[12]{5^{2}}\) = \(\sqrt[12]{25}\)
\(\sqrt[3]{\sqrt[4]{7}}\) = \(\sqrt[12]{7}\) = \(\sqrt[12]{7}\)
\(\sqrt{\sqrt{3}}\) = \(\sqrt[4]{3}\) = \(\sqrt[12]{3^{3}}\) = \(\sqrt[12]{27}\)
\(\sqrt[12]{27}\) > \(\sqrt[12]{25}\) > \(\sqrt[12]{7}\)
\(\sqrt{\sqrt{3}}\) > \(\sqrt[2]{\sqrt[3]{5}}\) > \(\sqrt[3]{\sqrt[4]{7}}\)
Question 5.
Can you get a pure surd when you find:
(i) the sum of two surds
(ii) the difference of two surds
(iii) the product of two surds
(iv) the quotient of two surds
Justify each answer with an example.
Solution:
(i) Yes we can get a surd.
Example:
(a) 3\(\sqrt{2}\) + 5\(\sqrt{2}\) = (3 + 5)\(\sqrt{2}\) = 8\(\sqrt{2}\)
(b) 3\(\sqrt{6}\) + 2\(\sqrt{6}\) = (3 + 2)\(\sqrt{6}\) = 5\(\sqrt{6}\)
(ii) Yes we can get a surd.
Example:
(a) \(\sqrt{75}\) – \(\sqrt{48}\) = \(\sqrt{25×3}\) – \(\sqrt{16×3}\) = (5 – 4) \(\sqrt{3}\) = \(\sqrt{3}\)
(b) \(\sqrt{98}\) – \(\sqrt{72}\) = \(\sqrt{49×2}\) – \(\sqrt{36×2}\) = (7 – 6) \(\sqrt{2}\) = \(\sqrt{2}\)
![]()
(iii) Yes we can get a surd.
Example:
(a) \(\sqrt{8}\) × \(\sqrt{6}\) = \(\sqrt{8×6}\) = \(\sqrt{48}\)
(b) \(\sqrt{11}\) × \(\sqrt{3}\) = \(\sqrt{11×3}\) = \(\sqrt{33}\)
(iv) Yes we can get a surd.
Example:
(a) \(\sqrt{55}\) ÷ \(\sqrt{5}\) = \(\frac{\sqrt{11×5}}{\sqrt{5}} = \sqrt{11}\)
(b) \(\sqrt{65}\) ÷ \(\sqrt{5}\) = \(\frac{\sqrt{13×5}}{\sqrt{13}} = \sqrt{5}\)
Question 6.
Can you get a rational number when you compute:
(i) the sum of two surds
(ii) the difference of two surds
(iii) the product of two surds
(iv) the quotient of two surds
Justify each answer with an example.
Solution:
(i) Yes, the sum of two surds will give a rational number.
Example:
(a) (2 + \(\sqrt{3}\)) + (2 – \(\sqrt{3}\)) = 4
(b) (\(\sqrt{5}\) + 4) + (7 – \(\sqrt{5}\)) = 11
(ii) Yes, the difference of two surds will give a rational number.
Example:
(a) (5 + \(\sqrt{7}\)) – (- 5 + \(\sqrt{7}\)) = 10
(b) (\(\sqrt{11}\) + 5) – (-3 + \(\sqrt{11}\)) = 8
![]()
(iii) Yes, the product of two surds will give a rational number.
Example:
(a) \(\sqrt{125}\) × \(\sqrt{45}\) = \(\sqrt{25×5}\) × \(\sqrt{9×5}\) = 5\(\sqrt{5}\) × 3\(\sqrt{5}\) = 15 × 5 = 75
(b) \(\sqrt{150}\) × \(\sqrt{6}\) = \(\sqrt{25×6}\) × \(\sqrt{6}\) = 5\(\sqrt{6}\) × \(\sqrt{6}\) = 5 × 6 = 30
(iv) Yes. The quotient of two surds will give a rational number.
Example:
(a) \(\sqrt{32}\) ÷ \(\sqrt{8}\) = \(\frac{\sqrt{8×4}}{\sqrt{8}} = \sqrt{4}\) = 2
(b) \(\sqrt{50}\) ÷ \(\sqrt{2}\) = \(\frac{\sqrt{25×2}}{\sqrt{2}} = \sqrt{25}\) = 5
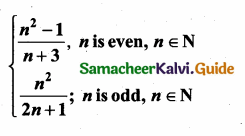
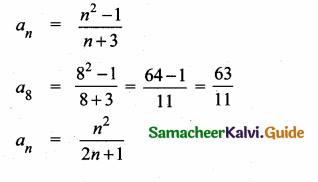
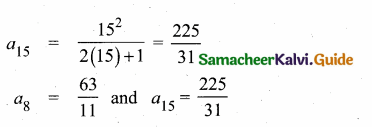
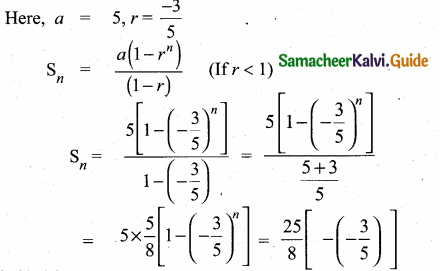
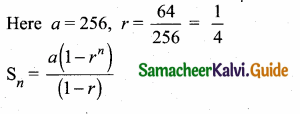
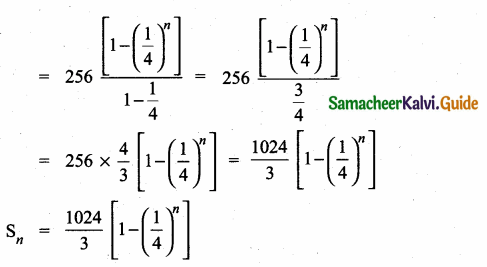
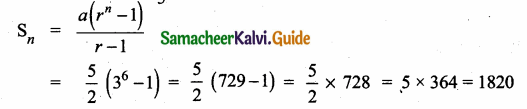

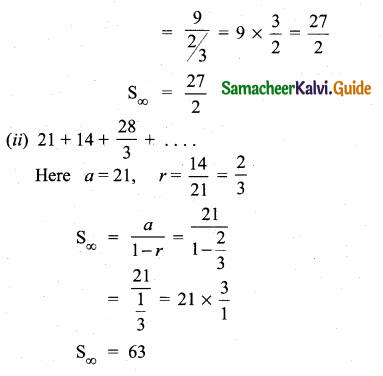



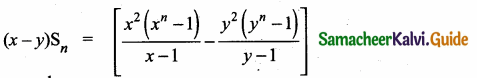
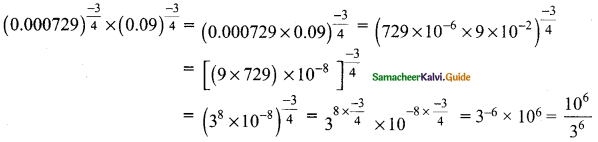
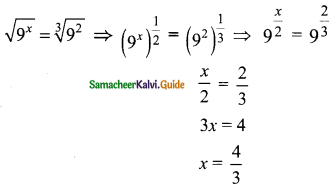
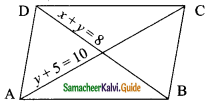



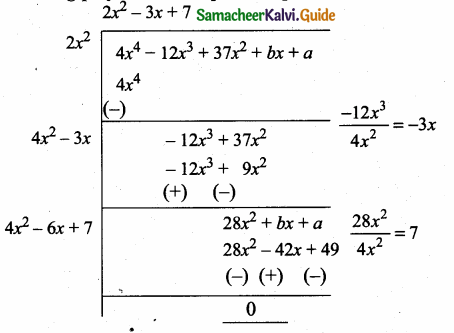


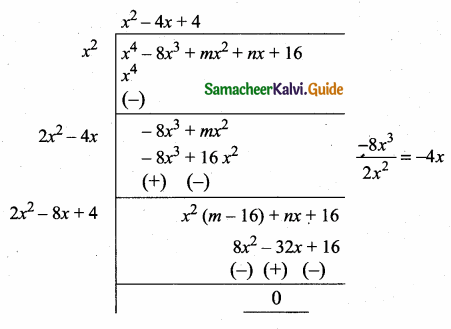
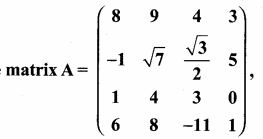
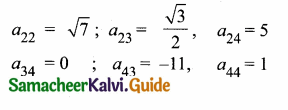

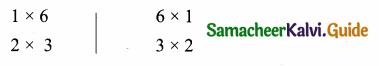
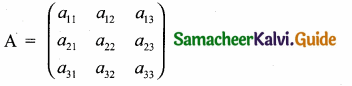
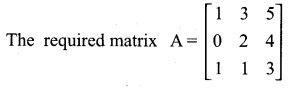
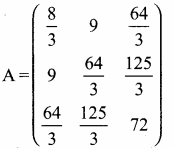
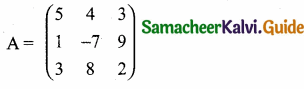 then find the tranpose of A.
then find the tranpose of A.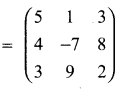
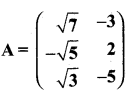 then find the tranpose of – A
then find the tranpose of – A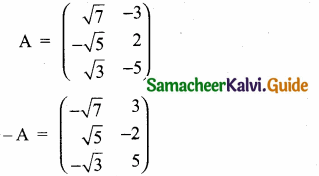
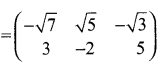
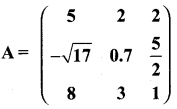 then verify (AT)T = A
then verify (AT)T = A