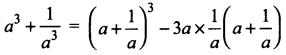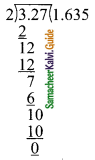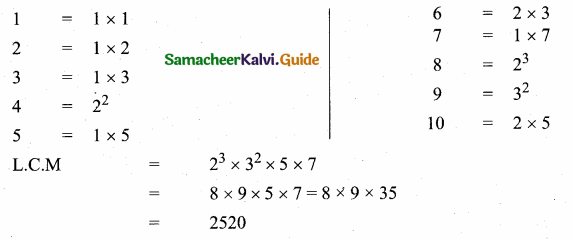Bhagya

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.9 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.9

Question 1.
Find the sum of the following series
(i) 1 + 2 + 3 + …….. + 60
(ii) 3 + 6 + 9 + …….. +96
(iii) 51 + 52 + 53 + …….. + 92
(iv) 1 + 4 + 9 + 16 + …….. + 225
(v) 6² + 7² + 8² + …….. + 21²
(vi) 10³ + 11³ + 12³ + …….. + 20³
(vii) 1 + 3 + 5 + …… + 71
Solution:
(i) 1 + 2 + 3 + …….. + 60 = \(\frac{60 \times 61}{2}\)
[Using \(\frac{n(n+1)}{2}\) formula]
= 1830

(ii) 3 + 6 + 9 + …….. + 96 = 3(1 + 2 + 3 + ……… + 32)
= \(\frac{3 \times 32 \times 33}{2}\)
= 1584

(iii) 51 + 52 + 53 + …….. + 92 = (1 + 2 + 3 + ……. + 92) – (1 + 2 + 3 + …… + 50)

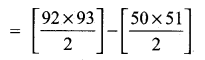
= 4278 – 1275
= 3003

(iv) 1 + 4 + 9 + 16 + …….. + 225 = 1² + 2² + 3² + 4² + ………… + 15²
\(\frac{15 \times 16 \times 31}{6}\)
[using \(\frac{n(n+1)(2 n+1)}{6}\)] formula
= 1240

(v) 6² + 7² + 8² + …….. + 21² = 1 + 2² + 3² + 4² + ………… + 21² – (1 + 2² + ………… + 5²)
= \(\frac{21 \times 22 \times 43}{6}\) – \(\frac{5 \times 6 \times 11}{6}\)
= 3311 – 55
= 3256

(vi) 10³ = 11³ + 12³ + …….. + 20³ = 1³ + 2³+ 3³ + ………… + 20³ – (1³ + 2³ + 3³ + …………. + 9³)

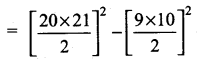
[Using (\(\frac{n(n+1)}{2}\))² formula]
= 210² – 45² = 44100 – 2025
= 42075

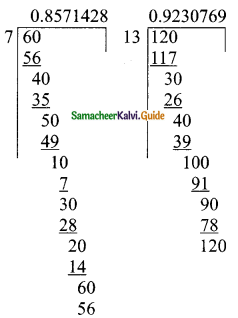
(vii) 1 + 3 + 5+ … + 71
Here a = 1; d = 3 – 1 = 2; l = 71

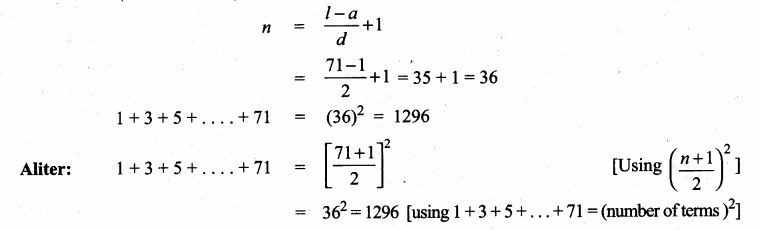
Question 2.
If 1 + 2 + 3 + …. + k = 325 , then find 1³ + 2³ + 3³ + …………. + k³
Answer:
1 + 2 + 3 + …. + k = 325
\(\frac{k(k+1)}{2}\) = 325 ……(1)

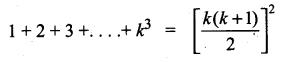
= 325² (From 1)
= 105625

Question 3.
If 1³ + 2³ + 3³ + ………… + K³ = 44100 then find 1 + 2 + 3 + ……. + k
Answer:
1³ + 2³ + 3³ + ………….. + k³ = 44100

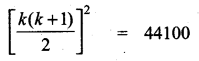
\(\frac{k(k+1)}{2}\) = \(\sqrt { 44100 }\) = 210
1 + 2 + 3 + …… + k = \(\frac{k(k+1)}{2}\)
= 210

Question 4.
How many terms of the series 1³ + 2³ + 3³ + …………… should be taken to get the sum 14400?
Answer:
1³ + 2³ + 3³ + ……. + n³ = 14400

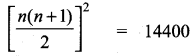
\(\frac{n(n+1)}{2}\) = \(\sqrt { 14400 }\)
\(\frac{n(n+1)}{2}\) = 120 ⇒ n² + n = 240

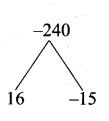
n² + n – 240 = 0
(n + 16) (n – 15) = 0
(n + 16) = 0 or (n – 15) = 0
n = -16 or n = 15 (Negative will be omitted)
∴ The number of terms taken is 15

Question 5.
The sum of the squares of the first n natural numbers is 285, while the sum of their cubes is 2025. Find the value of n.
Answer:
1² + 2² + 3² + …. + n² = 285

Question 6.
Rekha has 15 square colour papers of sizes 10 cm, 11 cm, 12 cm, …, 24 cm. How much area can be decorated with these colour papers?
Answer:
Area of 15 square colour papers
= 10² + 11² + 12² + …. + 24²
= (1² + 2² + 3² + …. + 24²) – (1² + 2² + 9²)
= \(\frac{24 \times 25 \times 49}{6}-\frac{9 \times 10 \times 19}{6}\)
= 4 × 25 × 49 – 3 × 5 × 19
= 4900 – 285
= 4615
Area can be decorated is 4615 cm²

Question 7.
Find the sum of the series (2³ – 1)+(4³ – 3³) + (6³ – 15³) + …….. to
(i) n terms
(ii) 8 terms
Answer:
Sum of the series = (2³ – 1) + (4³ – 3³) + (6³ – 15³) + …. n terms
= 2³ + 4³ + 6³ + …. n terms – (1³ + 3³ + 5³ + …. n terms) …….(1)
2³ + 4³ + 6³ + …. n = ∑(2³ + 4³ + 6³ + ….(2n)³]
∑ 2³ (1³ + 2³ + 3³ + …. n³)
= 8 (\(\frac{n(n+1)}{2}\))²
= 2[n (n + 1)]²
1³ + 3³ + 5³ + ……….(2n – 1)³ [sum of first 2n cubes – sum of first n even cubes]

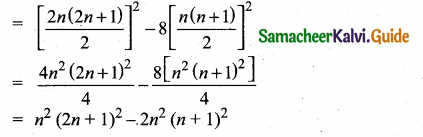
Substituting (2) and (3) in (1)
Sum of the series = 2n² (n + 1)² – n² (2n + 1)² + 2n²(n + 1)²
= 4n² (n + 1)² – n² (2n + 1)²
= n² [(4(n + 1)² – (2n + 1)²]
= n² [4n² + 4 + 8n – 4n² – 1 – 4n]
= n² [4n + 3]
= 4n³ + 3n²

(ii) when n = 8 = 4(8)³ + 3(8)²
= 4(512) + 3(64)
= 2240

Students can download Maths Chapter 3 Algebra Ex 3.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.2

Question 1.
Find the value of the polynomial f(y) = 6y – 3y² + 3 at
(i) y = 1
(ii) y = -1
(iii) y = 0
Solution:
(i) When y = 1
f(y) = 6y – 3y² + 3
f(1) = 6(1) – 3(1)² + 3
= 6 – 3 + 3 = 6

(ii) When y = – 1
f(y) = 6y – 3y² + 3
f(-1) = 6(-1) – 3(-1)² + 3
= – 6 – 3 + 3
= – 6

(iii) When y = 0
f(y) = 6y – 3y² + 3
f(0) = 6(0) – 3(0)² + 3
= 0 – 0 + 3
= 3

Question 2.
If p(x) = x² – 2√2x + 1, find p(2√2).
Solution:
p(x) = x² – 2√2x + 1
p(2√2) = (2√2)² – 2√2 (2√2) + 1
= 8 – 8 + 1
= 0 + 1
= 1

Question 3.
Find the zeros of the polynomial in each of the following.
(i) P(x) = x – 3
Solution:
p( 3) = 3 – 3
= 0
p(3) is the zero of p(x)

(ii) p(x) = 2x + 5
Solution:

= -5 + 5
= 2(0)
= 0
Hence –\(\frac{5}{2}\) is the zero of p(x).

(iii) q(y) = 2y – 3
Solution:

= 2 × 0
= 0
Hence \(\frac{3}{2}\) is the zero of q(y).

(iv) f(z) = 8z
Solution:
f(0) = 8 × 0
= 0
Hence 0 is the zero of f(z)

(v) p(x) = ax when a ≠ 0
Solution:
p(0) = a(0)
= 0
Hence, 0 is the zero of p(x)

(vi) h(x) = ax + b, a ≠ 0, a, b∈R
Solution:

Hence –\(\frac{b}{a}\) is the zero of h(x).

Question 4.
Find the roots of the polynomial equations.
(i) 5x – 6 = 0
Solution:
5x = 6
x = \(\frac{6}{5}\)
\(\frac{6}{5}\) is the root of the polynomial.

(ii) x + 3 = 0
Solution:
x = -3
-3 is the root of the polynomial.

(iii) 10x + 9 = 0
Solution:
10x = -9
x = –\(\frac{9}{10}\)
–\(\frac{9}{10}\) is the root of the polynomial.

(iv) 9x – 4 = 0
Solution:
9x = 4
x = \(\frac{4}{9}\)
\(\frac{4}{9}\) is the root of the polynomial.

Question 5.
Verify whether the following are zeros of the polynomial, indicated against them,or not.
(i) p(x) = 2x – 1, x = \(\frac{1}{2}\)
Solution:
p (\(\frac{1}{2}\)) = 2(\(\frac{1}{2}\)) – 1
= 1 – 1
= 0
∴ \(\frac{1}{2}\) is the zero of the polynomial.

(ii) p(x) = x³ – 1, x = 1
Solution:
p(1) = 1³ – 1
= 1 – 1
= 0
∴ 1 is the zero of the polynomial

(iii) p(x) = ax + b, x = \(\frac{-b}{a}\)
Solution:
p(\(\frac{-b}{a}\)) = a(\(\frac{-b}{a}\)) + b
= -b + b
= 0
∴ \(\frac{-b}{a}\) is the zero of the polynomial. a

(iv) p(x) = (x + 3) (x – 4); x = -3, x = 4
Solution:
P(-3) = (-3 + 3) (-3 – 4)
= (0) (-7)
= 0
P( 4) = (4 + 3) (4 – 4)
= (7) (0)
= 0
∴ -3 and 4 are the zeros of the polynomial.

Question 6.
Find the number of zeros of the following polynomials represented by their graphs.

Solution:
(i) Number of zeros = 2 (The curve is intersecting the x-axis at 2 points)
(ii) Number of zeros = 3 (The curve is intersecting the x-axis at 3 points)
(iii) Number of zeros = 0 (The curve is not intersecting the x-axis)
(iv) Number of zeros = 1 (The curve is intersecting at the origin)
(v) Number of zeros = 1 (The curve is intersecting the x-axis at one point)

Students can download Maths Chapter 3 Algebra Ex 3.1 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.1

Question 1.
Which of the following expressions are polynomials. If not give reason:
(i) \(\frac{1}{x^2}\) + 3x – 4
Solution:
(i) \(\frac{1}{x^2}\) + 3x – 4 is not a polynomial. Since the exponent of x² is not a whole number, but it is (\(\frac{1}{x^2}\) = x^-2) negative number.

(ii) x² (x – 1)
Solution:
x² (x – 1) is a polynomial.

(iii) \(\frac{1}{x}\) (x + 5)
Solution:
\(\frac{1}{x}\) (x + 5) is not a polynomial. Since the exponent of x is not a whole number, but it is (\(\frac{1}{x}\) = x^-1) negative number.

(iv) \(\frac{1}{x^{-2}}\) + \(\frac{1}{x^{-1}}\) + 7
Solution:
\(\frac{1}{x^{-2}}\) + \(\frac{1}{x^{-1}}\) + 7 is a polynomial. (\(\frac{1}{x^{-2}}\) = x² and \(\frac{1}{x^{-1}}\) = x)

(v) √5x² + √3x + √2
Solution:
√5x² + √3x + √2 is a polynomial.

(vi) m² – \(\sqrt[3]{m}\) + 7m – 10
m² –\(\sqrt[3]{m}\) + 7m – 10 is not a polynomial. Since the exponent of m is not a whole number.
(\(\sqrt[3]{m}\) = m^1/3)

Question 2.
Write the coefficient of x² and x in each of the following polynomials.
(i) 4 + \(\frac{2}{5}\) x² – 3x
Solution:
Coefficient of x² is \(\frac{2}{5}\) and coefficient of x is -3.

(ii) 6 – 2x² + 3x³ – √7x
Solution:
Coefficient of x² is -2 and coefficient of x is -√7

(iii) π x² – x + 2
Solution:
Coefficient of x² is π and coefficient of x is -1.

(iv) √3x² + √2x + 0.5
Solution:
Coefficient of x² is √3 and coefficient of x is √2

(v) x² – \(\frac{7}{2}\) x + 8
Solution:
Coefficient of x² is 1 and coefficient of x is –\(\frac{7}{2}\)

Question 3.
Find the degree of the following polynomials.
(i) 1 – √2 y² + y⁷
(ii) \(\frac{x^{3}-x^{4}+6 x^{6}}{x^{2}}\)
(iii) x³ (x² + x)
(iv) 3x⁴ + 9x² + 27x⁶
(v) 2√5p⁴ \(-\frac{8 p^{3}}{\sqrt{3}}+\frac{2 p^{2}}{7}\)
Solution:
(i) 1 – √2 y² + y⁷
The degree of the polynomial is 7.

(ii)
= x – x² + 6x⁴
The degree of the polynomial is 4.

(iii) x³ (x² + x) = x⁵ + x⁴
The degree of the polynomial is 5.

(iv) 3x⁴ + 9x² + 27x⁶
The degree of the polynomial is 6.

(v) 2√5p⁴ \(-\frac{8 p^{3}}{\sqrt{3}}+\frac{2 p^{2}}{7}\)
The degree of the polynomial is 4.

Question 4.
Rewrite the following polynomial in standard form.
(i) x – 9 + √7x³ + 6x²
Solution:
The standard form is √7x³ + 6x² – x – 9
(or) – 9 + x + 6x² + √7x³

(ii) √2x² – \(\frac{7}{2}\) x⁴ + x – 5x³
Solution:
The standard form is – \(\frac{7}{2}\) x⁴ – 5x³ + √2x² + x
(or) x + √2x² – 5x³ – \(\frac{7}{2}\) x⁴

(iii) 7x³ – \(\frac{6}{5}\) x² + 4x – 1
Solution:
The given polynomial is in standard form (or) – 1 + 4x – \(\frac{6}{5}\) x² + 7x³

(iv) y² + √5y³ – 11 – \(\frac{7}{3}\) y + 9y⁴
Solution:
The standard form is 9y⁴ + √5y³ + y² – \(\frac{7}{3}\) y – 11
(or) – 11 – \(\frac{7}{3}\) y + y² + √5y³ + 9y⁴

Question 5.
Add the following polynomials and find the degree of the resultant polynomial
(i) p(x) = 6x² – 7x + 2; q(x) = 6x³ – 7x + 15
Solution:
p(x) + q(x) = 6x² – 7x + 2 + 6x³ – 7x + 15
= 6x³ + 6x² – 7x – 7x + 2 + 15
= 6x³ + 6x² – 14x + 17
The degree of the polynomial is 3.

(ii) h(x) = 7x³ – 6x + 1; f(x) = 7x² + 17x – 9
Solution:
h(x) + f(x) = 7x³ – 6x + 1 + 7x² + 17x – 9
= 7x³ + 7x² + 11x – 8
The degree of the polynomial is 3.

(iii) f(x) = 16x⁴ – 5x² + 9; g(x) = -6x³ + 7x – 15
Solution:
f(x) + g(x) = 16x⁴ – 5x² + 9 – 6x³ + 7x – 15
= 16x⁴ – 6x³ – 5x² + 7x + 9 – 15
= 16x⁴ – 6x³ – 5x² + 7x – 6
The degree of the polynomial is 4.

Question 6.
Subtract the second polynomial from the first polynomial and find the degree of the resultant polynomial.
(i) p(x) = 7x² + 6x – 1; q(x) = 6x – 9
Solution:
p(x) – q(x) = 7x² + 6x – 1 – (6x – 9)
= 7x² + 6x – 1 – 6x + 9
= 7x² + 6x – 6x – 1 + 9
= 7x² + 8
The degree of the polynomial is 2.

(ii) f(y) = 6y² – 7y + 2; g(y) = 7y + y³
Solution:
f(y) – g(y) = 6y² – 7y + 2 – (7y + y³)
= 6y² – 7y + 2 – 7y – y³
= -y³ + 6y² – 7y – 7y + 2
= -y³ + 6y² – 14y + 2
The degree of the polynomial is 3.

(iii) h(z) = z⁵ – 6z⁴ + z; f(z) = 6z² + 10z – 7
Solution:
h(z) – f(z) = z⁵ – 6z⁴ + z – (6z² + 10z – 7)
= z⁵ – 6z⁴ + z – 6z² – 10z + 7
= z⁵ – 6z⁴ – 6z² + z – 10z + 7
= z⁵ – 6z⁴ – 6z² – 9z + 7
The degree of the polynomial is 5.

Question 7.
What should be added to 2x³ + 6x² – 5x + 8 to get 3x³ – 2x² + 6x + 15?
Solution:
3x³ – 2x² + 6x + 15 – (2x³ + 6x² – 5x + 8)
= 3x³ – 2x² + 6x + 15 – 2x³ – 6x² + 5x – 8
= 3x³ – 2x³- 2x² – 6x² + 6x + 5x + 15 – 8
= x³ – 8x² + 11x + 7
x³ – 8x² + 11x + 7 must be added to get 3x³ – 2x² + 6x + 15.

Question 8.
What must be subtracted from 2x⁴ + 4x² – 3x + 7 to get 3x³ – x² + 2x + 1?
Solution:
2x⁴ + 4x² – 3x + 7 – (3x³ – x² + 2x + 1)
= 2x⁴ + 4x² – 3x + 7 – 3x³ + x² – 2x – 1
= 2x⁴ – 3x³ + 4x² + x² – 3x – 2x + 7 – 1
= 2x⁴ – 3x³ + 5x² – 5x + 6
2x⁴ – 3x³ + 5x² – 5x + 6 must be subtracted to get 3x³ – x² + 2x + 1.

Question 9.
Multiply the following polynomials and find the degree of the resultant polynomial:
(i) p(x) = x² – 9, q(x) = 6x² + 7x – 2
Solution:
p(x) × q(x) = (x² – 9) (6x² + 7x – 2)
= 6x⁴ + 7x³ – 2x² – 54x² – 63x + 18
= 6x⁴ + 7x³ – 56x² – 63x + 18
The degree of the polynomial is 4.

(ii) f(x) = 7x + 2, g(x) = 15x – 9
Solution:
f(x) × g(x) = (7x + 2) (15x – 9)
= 105x² – 63x + 30x – 18
= 105x² – 33x – 18
The degree of the polynomial is 2.

(iii) h(x) = 6x² – 7x + 1, f(x) = 5x – 7
Solution:
h(x) × f(x) = (6x² – 7x + 1) (5x – 7)
= 30x³ – 42x² – 35x² + 49x + 5x – 7
= 30x³ – 77x² + 54x – 7
The degree of the polynomial is 3.

Question 10.
The cost of a chocolate is Rs. (x + y) and Amir bought (x + y) chocolates. Find the total amount paid by him in terms of x and y. If x = 10, y = 5 find the amount paid by him.
Solution:
The cost of a chocolate = (x + y)
Number of chocolates bought by Amir = x + y
Total amount paid by him = (x + y) (x + y)
= x² + xy + xy + y²
= x² + 2xy + y²
When x = 10 and y = 5
The total amount paid by him = (10)² + 2(10)(5) + (5)²
= 100 + 100 + 25 = 225

Question 11.
The length of a rectangle is (3x + 2) units and it’s breadth is (3x – 2) units. Find its area in terms of x. What will be the area if x = 20 units.
Solution:
Length of the rectangle = 3x + 2 units
Breadth of the rectangle = 3x – 2 units
Area of the rectangle = (3x + 2) (3x – 2)
= 9x² – 6x + 6x – 4
= 9x² – 4
When x = 20
Area of the rectangle = 9(20)² – 4
= 9(400) – 4
= 3600 – 4
= 3596 sq.units.

Question 12.
p(x) is a polynomial of degree 1 and q(x) is a polynomial of degree 2. What kind of the polynomial is p(x) × q(x)?
Solution:
Degree of the polynomial p(x) = 1
Degree of the polynomial q(x) = 2
Degree of p(x) × q(x) = 3
The polynomial is a cubic polynomial (or) Polynomial of degree 3.

Students can download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.4

Question 1.
Expand the following:
(i) (2x + 3y + 4z)²
(ii) (-p + 2q + 3r)²
(iii) (2p + 3) (2p – 4) (2p – 5)
(iv) (3a + 1) (3a – 2) (3a + 4)
Solution:
We know that (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac
(i) (2x + 3y + 4z)² = (2x)² + (3y)² + (4z)² + 2(2x) (3y) + 2(3y) (4z) + 2(4z) (2x)
= 4x² + 9y² + 16z² + 12xy + 24yz + 16xz

(ii) (-p + 2q + 3r)² = (-p)² + (2q)² + (3r)² + 2(-p) (2q) + 2(2q)(3r) + 2(3r) (- p)
= p²+ 4q² + 9r² – 4pq + 12qr – 6pr

(iii) (2p + 3) (2p – 4) (2p – 5)
[Here x = 2p, a = 3, b = -4 and c = -5]
= (2p)³ + (3 – 4 – 5) (2p)² + [(3)(-4) + (-4)(-5) + (3) (-5)] 2p + (3) (-4) (-5)
= 8p³ + (-6)(4p²) + (-12 + 20 – 15) 2p + 60
= 8p³ – 24p² – 14p + 60

(iv) (3a + 1) (3a – 2) (3a + 4)
[Here x = 3a, a = 1, b = -2 and c = 4]
= (3a)³ + (1 – 2 + 4) (3a)² + [(1)(-2) + (-2) (4) + (4) (1)] (3a) + (1) (-2) (4)
= 27a³ + 3(9a²) + (-2 – 8 + 4) (3a) – 8
= 27a³ + 27a² – 18a – 8

Question 2.
Using algebraic identity, find the coefficients of x², x and constant term without actual expansion.
(i) (x + 5)(x + 6)(x + 7)
Solution:
[Here x = x, a = 5, b = 6, c = 7]
(x + a) (x + b) (x + c) = x³ + (a + b + c)x² + (ab + bc + ac)x + abc
coefficient of x² = 5 + 6 + 7
= 18
coefficient of x = 30 + 42 + 35
= 107
constant term = (5) (6) (7)
= 210

(ii) (2x + 3)(2x – 5) (2x – 6)
Solution:
[Here x = 2x, a = 3, b = -5, c = -6]
(x + a) (x + b) (x + c) = x³ + (a + b + c)x² + (ab + bc + ac)x + abc
coefficient of x² = (3 – 5 – 6)4 [(2x)² = 4x²]
= (-8) (4)
= -32
coefficient of x = [(3)(-5) + (-5)(-6) + (-6)(3)](2)
= (-15 + 30-18) (2)
= (-3) (2)
= -6
constant term = (3) (-5) (-6)
= 90

Question 3.
If (x + a)(x + b)(x + c) = x³ + 14x² + 59x + 70, find the value of
(i) a + b + c
(ii) \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\)
(iii) a² + b² + c²
(iv) \(\frac{a}{bc} + \frac{b}{ac} + \frac{c}{ab}\)
Solution:
(x + a) (x + b) (x + c) = x³ + 14x² + 59x + 70
x³ + (a + b + c)x² + (ab + bc + ac)x + abc = x³ + 14x² + 59x + 70
a + b + c = 14, ab + bc + ac = 59, abc = 70
(i) a + b + c = 14

(ii) \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}\) = \(\frac{bc+ac+ab}{abc}\)
= \(\frac{59}{70}\)

(iii) a² + b² + c² = (a + b + c)² – 2 (ab + bc + ac)
= (14)² – 2(59)
= 196 – 118
= 78

Question 4.
Expand:
(i) (3a – 4b)³
Solution:
(a – b)³ = a³ – b³ – 3ab (a – b)
(3a – 4b)³ = (3a)³ – (4b)³ – 3(3a)(4b)(3a – 4b)
= 27a³ – 64b³ – 36ab (3a – 4b)
= 27a³ – 64b³ – 108a²b + 144ab²

(ii) [x + \(\frac{1}{y}]^{3}\)
Solution:
(a + b)³ = a³ + b³ + 3ab (a + b)

Question 5.
Evaluate the following by using identities:
(i) 98³
Solution:
98³ = (100 – 2)³ [(a – b)³ = a³ – b³ – 3ab (a – b)]
= 100³ – (2)³ – 3(100) (2) (100 – 2)
= 1000000 – 8 – 600(98)
= 1000000 – 8 – 58800
= 1000000 – 58808
= 941192

(ii) 1001³
Solution:
(1001)³ = (1000 + 1)³
[(a + b)³ = a³ + b³ + 3ab (a + b)]
= (1000)³ + 1³ + 3(1000) (1) (1000 + 1)
= 1000000000 + 1 + 3000 (1001)
= 1000000001 + 3003000
= 1003003001

Question 6.
If (x + y + z) = 9 and (xy + yz + zx) = 26, then find the value of x² + y² + z².
Solution:
x + y + z = 9; xy + yz + zx = 26
x² + y² + z² = (x + y + z)² – 2xy – 2yz – 2xz
= (x + y + z)² – 2 (xy + yz + zx)
= 9² – 2(26)
= 81 – 52
= 29

Question 7.
Find 27a³ + 64b³, If 3a + 4b = 10 and ab = 2
Solution:
3a + Ab = 10, ab = 2
27a³ + 64b³ = (3a)³ + (4b)³
[a³ + b³ = (a + b)³ – 3 ab (a + b)]
= (3a + 4b)³ – 3 × 3a × 4b (3a + 4b)
= 103 – 36ab (10)
= 1000 – 36(2)(10)
= 1000 – 720
= 280

Question 8.
Find x³ – y³, if x – y = 5 and xy = 14.
Solution:
x – y = 5, xy = 14
x³ – y³  = (x – y)³ + 3xy (x – y)
= 5³ + 3(14) (5)
= 125 + 210
= 335

Question 9.
If a + \(\frac{1}{a}\) = 6, then find the value of a³ +\(\frac{1}{a^3}\)
Solution:
a + \(\frac{1}{a}\) = 6 [a³ + b³ = (a + b)³ – 3ab (a + b)]

= 6³ – 3(6)
= 216 – 18
= 198

Question 10.
If x² + \(\frac{1}{x^2}\) = 23, then find the value of x + \(\frac{1}{x}\) and x³ + \(\frac{1}{x^3}\)
Solution:

When x = 5 [a³ + b³ = (a + b)³ – 3ab (a + b)]
= (5)³ – 3(5)
= 125 – 15
= 110
when x = -5
x³ + \(\frac{1}{x^3}\) = (-5)³ – 3(-5)
= -125 + 15
= -110
∴ x³ + \(\frac{1}{x^3}\) = ±110

Question 11.
If (y – \(\frac{1}{y})^{3}\) = 27 then find the value of y³ – \(\frac{1}{y^3}\)
Solution:

= 3³ + 3(3)
= 27 + 9
= 36

Question 12.
Simplify:
(i) (2a + 3b + 4c) (4a² + 9b² + 16c² – 6ab – 12bc – 8ca)
(ii) (x – 2y + 3z) (x² + 4y² + 9z² + 2xy + 6yz – 3xz)
Solution:
x³ + y³ + z³ – 3xyz ≡ (x + y + z) (x² + y² + z² – xy – yz – zx)
(i) (2a + 3b + 4c) (4a² + 9b² + 16c² – 6ab – 12bc – 8ea)
= (2a)³ + (3b)³ + (4c)³ – 3 (2a) (3b) (4c)
= 8a³ + 27b³ + 64c³ – 72abc

(ii) (x – 2y + 3z) (x² + 4y² + 9z² + 2xy + 6yz – 3xz)
= x³ + (-2y)³ + (3z)³ – 3(x) (-2y) (3z)
= x³ – 8y³ + 27z³ + 18xyz

Question 13.
By using identity evaluate the following:
(i) 7³ – 10³ + 3³
Solution:
x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² – xy – yz – zx)
We know that a + b + c = 0 then a³ + b³ + c³ = 3ab
a + b + c = 7 + (-10) + 3
= 10 – 10
= 0
∴ 7³ – 10³ + 3³ = 3(7) (-10) (3)
= -630

(ii) 1 + \(\frac{1}{8}\) – \(\frac{27}{8}\)
Solution:
We know that a³ + b³ + c³ = 0 then a + b + c = 3abc

Question 14.
If 2x -3y – 4z = 0, then find 8x³ – 27y³ – 64z³.
Solution:
We know x³ +y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² – xy – yz – zx)
x³ + y³ + z³ = (x + y + z) (x² +y² + z² – xy – yz – zx) + 3xyz
8x³ – 27y³ – 64z³ = (2x)³ + (-3y)³ + (-4z)³
= (2x – 3y- 4z) [(2x)² + (-3y)² + (-4z)² – (2x)(-3y) – (-3y) (-4z) -(-4z)(2x)] + 3(2x)(-3y)(-4z)
= 0 (4x² + 9y² + 16z² + 6xy – 12yz + 8xz) + 72xyz
= 72xyz
8x³ – 27y³ – 64z³ = 72xyz

Students can download Maths Chapter 1 Relations and Functions Ex 1.5 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.5

Question 1.
Using the functions f and g given below, find fog and gof Check whether fog = gof.

(i) f(x) = x – 6, g(x) = x²
Answer:
f(x) = x – 6, g(x) = x²
fog = fog (x)
= f(g(x))
fog = f(x)²
= x² – 6
gof = go f(x)
= g(x – 6)
= (x – 6)²
= x² – 12x + 36
fog ≠ gof

(ii) f(x) = \(\frac { 2 }{ x } \), g(x) = 2x² – 1
Answer:
f(x) – \(\frac { 2 }{ x } \); g(x) = 2x² – 1
fag = f[g (x)]
= f(2x² – 1)
= \(\frac{2}{2 x^{2}-1}\)
gof = g [f(x)]
= g (\(\frac { 2 }{ x } \))
= 2 (\(\frac { 2 }{ x } \))² – 1
\(=2 \times \frac{4}{x^{2}}-1\)
\(=\frac{8}{x^{2}}-1\)
fog ≠ gof

(iii) f(x) = \(\frac { x+6 }{ 3 } \), g(x) = 3 – x
Answer:
f(x) = \(\frac { x+6 }{ x } \), g(x) = 3 – x
fog = f[g(x)]
= f(3 – x)

(iv) f(x) = 3 + x, g(x) = x – 4
Answer:
f(x) = 3 + x ;g(x) = x – 4
fog = f[g(x)]
= f(x – 4)
= 3 + x – 4
= x – 1
gof = g[f(x)]
= g(3 + x)
= 3 + x – 4
= x – 1
fog = gof

(v) f(x) = 4x² – 1,g(x) = 1 + x
Answer:
f(x) = 4x² – 1 ; g(x) = 1 + x
fog = f[g(x)]
= 4(1 + x)
= 4(1 + x)² – 1
= 4[1 + x² + 2x] – 1
= 4 + 4x² + 8x – 1
= 4x² + 8x + 3
gof = g [f(x)]
= g (4x² – 1)
= 1 + 4x² – 1
= 4x²
fog ≠ gof

Question 2.
Find the value of k, such that fog = gof
(i) f(x) = 3x + 2, g(x) = 6x – k
(ii) f(x) = 2x – k, g(x) = 4x + 5
Solution:
(i) f(x) = 3x + 2, g(x) = 6x – k
fog(x) = f(g(x)) = f(6x – k) = 3(6x – k) + 2
= 18x – 3k + 2 …………… (1)
gof(x) = g(f(x)) = g(3x + 2) = 6(3x + 2) – k
= 18x + 12 – k ……………. (2)
(1) = (2)
⇒ 18x – 3k + 2 = 18x + 12 – k
2k = -10
k = -5

(ii) f(x) = 2x – k, g(x) = 4x + 5
fog(x) = f(g(x)) = f(4x + 5) = 2(4x + 5) – k
= 8x + 10 – k ……………… (1)
gof(x) = g(f(x)) = g(2x – k) = 4(2x – k) + 5
= 8x – 4k + 5 ……………. (2)
(1) = (2)
⇒ 8x + 10 – k = 8x – 4k + 5
3k = -5
k = \(\frac{-5}{3}\)

Question 3.
If f(x) = 2x – 1, g(x) = \(\frac { x+1 }{ 2 } \), show that f o g = g o f = x
Answer:
f(x) = 2x – 1 ; g(x) = \(\frac { x+1 }{ 2 } \)
fog = f[g(x)]

∴ fog = gof = x
Hence it is proved.

Question 4.
(i) If f (x) = x² – 1, g(x) = x – 2 find a, if gof(a) = 1.
(ii) Find k, if f(k) = 2k – 1 and fof (k) = 5.
Solution:
(i) f(x) = x² – 1, g(x) = x – 2
Given gof(a) = 1
gof(x) = g(f(x)
= g(x² – 1) = x² – 1 – 2
= x² – 3
gof(a) ⇒ a² – 3 = 1 =+ a² = 4
a = ± 2
(ii) f(k) = 2k – 1
fo f(k) = 5
f(f(k)m = f(2k – 1) = 5
⇒ 2(2k – 1) – 1 = 5
4 k – 2 – 1 = 5 ⇒ 4k = 8
k = 2

Question 5.
Let A,B,C ⊂ N and a function f: A → B be defined by f(x) = 2x + 1 and g: B → C be defined by g(x) = x² . Find the range of fog and gof.
Answer:
f(x) = 2x + 1 ; g(x) = x²
fog = f[g(x)]
= f(x²)
= 2x² + 1
2x² + 1 ∈ N
g o f = g [f(x)]
= g (2x + 1)
g o f = (2x + 1)²
(2x + 1)² ∈ N
Range = {y/y = 2x² + 1, x ∈ N};
{y/y = (2x + 1)², x ∈ N)

Question 6.
If f(x) = x² – 1. Find (i)f(x) = x² – 1, (ii)fofof
Solution:
(i) f(x) = x² – 1
fof(x) = f(fx)) = f(x² – 1)
= (x² – 1 )² – 1;
= x⁴ – 2x² + 1 – 1
= x⁴ – 2x²
(ii) fofof = f o f(f(x))
= f o f (x⁴ – 2x²)
= f(f(x⁴ – 2x²))
= (x⁴ – 2x²)² – 1
= x⁸ – 4x⁶ + 4x⁴ – 1

Question 7.
If f : R → R and g : R → R are defined by f(x) = x⁵ and g(x) = x⁴ then check if f, g are one – one and fog is one – one?
Answer:
f(x) = x⁵ – It is one – one function
g(x) = x⁴ – It is one – one function
fog = f[g(x)]
= f(x⁴)
= (x⁴)⁵
fag = x²⁰
It is also one-one function.

Question 8.
Consider the functions f(x), g(x), h(x) as given below. Show that (fog)oh = fo(goh) in each case.
(i) f(x) = x – 1, g(x) = 3x + 1 and h(x) = x²
(ii) f(x) = x², g(x) = 2x and h(x) = x + 4
(iii) f(x) = x – 4, g(x) = x² and h(x) = 3x – 5
Solution:
(i) f(x) = x – 1, g(x) = 3x + 1 and h(x) = x²
f(x) = x – 1
g(x) = 3x + 1
f(x) = x²
(fog)oh = fo(goh)
LHS = (fog)oh
fog = f(g(x)) = f(3x + 1) = 3x + 1 – 1 = 3x
(fog)oh = (fog)(h(x)) = (fog)(x² ) = 3²  ……………. (1)
RHS = fo(goh)
goh = g(h(x)) = g(x²) = 3x² + 1
fo(goh) = f(3x² + 1) = 3x² + 1 – 1= 3x² ………… (2)
LHS = RHS Hence it is verified.

(ii) f(x) = x², g(x) = 2x, h(x) = x + 4
(fog)oh = fo(goh)
LHS = (fog)oh
fog = f(g(x)) = f(2x) = (2x)² = 4x²
(fog)oh = (fog) h(x) = (fog) (x + 4)
= 4(x + 4)² = 4(x² + 8x+16)
= 4x² + 32x + 64 ………….. (1)
RHS = fo(goh) goh = g(h(x)) = g(x + 4)
= 2(x + 4) = (2x + 8)
fo(goh) = f(goh) = f(2x + 8) = (2x + 8)²
= 4x² + 32x + 64 ……………… (2)
(1) = (2)
LHS = RHS
∴ (fog)oh = fo(goh) It is proved.

(iii) f(x) = x – 4, g(x) = x², h(x) = 3x – 5
(fog)oh = fo(goh)
LHS = (fog)oh
fog = f(g(x)) = f(x²) = x² – 4
(fog)oh = (fog)(3x – 5) = (3x – 5)² – 4
= 9x² – 30x + 25 -4
= 9x² – 30x + 21 ………….. (1)
∴ RHS = fo(goh)
(goh) = g(h(x)) = g(3x – 5) = (3x – 5)²
= 9x² – 30x + 25
fo(goh) = f(9x² – 30 x + 25)
= 9x² – 30x + 25 – 4
= 9x² – 30x + 21 …………… (2)
(1) = (2)
LHS = RHS
∴ (fog)oh = fo(goh)
It is proved.

Question 9.
Let f = {(-1, 3), (0, -1), (2, -9)} be a linear function from Z into Z. Find f(x).
Answer:
The linear equation is f(x) = ax + b
f(-1) = 3
a(-1) + b = 3
-a + b = 3 ….(1)
f(0) = -1
a(0) + b = -1
0 + b = -1
b = -1
Substitute the value of b = -1 in (1)
-a – 1 = 3
-a = 3 + 1
-a = 4
a = -4
∴ The linear equation is -4(x) -1 = -4x – 1 (or) – (4x + 1)

Question 10.
In electrical circuit theory, a circuit C(t) is called a linear circuit if it satisfies the superposition principle given by C(at₁ + bt₂) = aC(t₁) + bC(t₂), where a,b are constants. Show that the circuit C(t) = 31 is linear.
Solution:
Given C(t) = 3t. To prove that the function is linear
C(at₁) = 3a(t₁)
C(bt₂) = 3 b(t₂)
C(at₁ + bt₂) = 3 [at₁ + bt₂] = 3at₁ + 3bt₂
= a(3t₁) + b(3t₂) = a[C(t₁) + b(Ct₂)]
∴ Superposition principle is satisfied.
Hence C(t) = 3t is linear function.

Students can download Maths Chapter 2 Real Numbers Ex 2.3 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.3

Question 1.
Represent the following irrational numbers on the number line.
(i) \(\sqrt{3}\)
Solution:

Steps of construction:
1. Draw a line and mark a point A and B such that AB = 3 cm.
2. Mark a point C on this line such that BC = 1 cm.
3. Find the mid point of AC by drawing perpendicular bisector of AC and let it be “O”.
4. With O as centre and OC = OA as radius draw a semicircle.
5. Draw a line BD, which is perpendicular to AB at B.
6. Now BD = \(\sqrt{3}\) which can be marked in the number line as the value of BE = BD = \(\sqrt{3}\)

(ii) Represent \(\sqrt{4.7}\) on a number line.
Solution:

Steps of construction:
1. Draw a line and mark a point A and B such that AB = 4.7 cm.
2. Mark a point C on this line such that A BC = 1 cm.
3. Find the mid point of AC by drawing perpendicular bisector of AC and let it be “O”.
4. With O as centre and OC = OA as radius draw a semicircle.
5. Draw a line BD, which is perpendicular to AB at B.
6. Now BD = \(\sqrt{4.7}\), which can be marked in the number line as the value of BE = BD = \(\sqrt{4.7}\).

(iii) Represent \(\sqrt{6.5}\) on a number line.
Solution:

Steps of construction:
1. Draw a line and mark a point A and B such that AB = 6.5 cm.
2. Mark a point C on this line such that BC = 1 cm.
3. Find the mid point of AC by drawing perpendicular bisector of AC and let it be “O”.
4. With O as centre and OC = OA as radius draw a semicircle.
5. Draw a line BD, which is perpendicular to AB at B.
6. Now BD = \(\sqrt{6.5}\), which can be marked in the number line as the value of BE = BD = \(\sqrt{6.5}\)

Question 2.
Find any two irrational numbers between
(i) 0.3010011000111…. and 0.3020020002….
Solution:
Two irrational numbers between the given two rational numbers are 0.301202200222……. and 0.301303300333……..

(ii) \(\frac{6}{7}\) and \(\frac{12}{13}\)
Solution:
\(\frac{6}{7}\) = 0.\(\overline {857142}\)
\(\frac{12}{13}\) = 0.\(\overline {923076}\)
The two irrational numbers are 0.8616611666111…….. and 0.8717711777111………

(iii) \(\sqrt{2}\) and \(\sqrt{3}\)
Solution:

\(\sqrt{2}\) = 1.414
\(\sqrt{3}\) = 1.732
The two irrational numbers between \(\sqrt{2}\) and \(\sqrt{3}\) are 1.515511555……. and 1.616611666………..

Question 3.
Find any two rational numbers between 2.2360679……… and 2.236505500……….
Solution:
The two rational numbers are 2.2362 and 2.2363 (It has many answers)

Students can download Maths Chapter 2 Real Numbers Ex 2.2 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.2

Question 1.
Express the following rational numbers into decimal and state the kind of decimal expression.
(i) \(\frac{2}{7}\)
(ii) -5\(\frac{3}{11}\)
(iii) \(\frac{22}{3}\)
(iv) \(\frac{327}{200}\)
Solution:

(i) \(\frac{2}{7}\) = 0.2857142….
= 0.\(\overline {285714}\)
Non-terminating and recurring decimal expansion.

(ii) -5\(\frac{3}{11}\) = -5 + 0.272 = -5.272……..

= -5.\(\overline {27}\)
Non-terminating and recurring decimal expansion.

(iii) \(\frac{22}{3}\) = 7.333……..

= 7.\(\overline {3}\)
Non-terminating and recurring decimal expansion.

(iv) \(\frac{327}{200}\) = \(\frac{327}{2×100}\)

= \(\frac{3.27}{2}\)
= 1.635
Terminating decimal expansion.

Question 2.
Express \(\frac{1}{13}\) in decimal form. Find the length of the period of decimals.
Solution:

\(\frac{1}{13}\) = 0.07692307
= 0.\(\overline {076923}\)
Length of the period of decimal is 6.

Question 3.
Express the rational number \(\frac{1}{33}\) in recurring decimal form by using the recurring decimal expansion of \(\frac{1}{11}\). Hence write \(\frac{71}{33}\) in recurring decimal form.
Solution:

\(\frac{1}{11}\) = 0.0909……… = 0.\(\overline {09}\)
∴ \(\frac{1}{33}\) = \(\frac{1}{3}\) × \(\frac{1}{11}\)
= \(\frac{1}{3}\) × 0.0909 ……..
= 0.0303 …… = 0.\(\overline {03}\)
\(\frac{71}{33}\) = 2\(\frac{5}{33}\) = 2 + \(\frac{5}{33}\) = 2 + 5 × \(\frac{1}{33}\)
= 2 + 5 × 0.\(\overline {03}\)
2 + (5 × 0.030303 ……..)
2 + 0.151515 ………
2+ 0.\(\overline {15}\)
2.\(\overline {15}\)

Question 4.
Express the following decimal expression into rational numbers.
(i) 0.24
Solution:
Let x = 0.242424 ………. →(1)
100 x = 24.2424 ……… →(2)
(2) – (1) ⇒ 100 x – x = 24.2424 ……….. (-)
 0.2424 ……..
99 x = 24.0000
x = \(\frac{24}{99}\)
(or)
\(\frac{8}{33}\)

(ii) 2.327
Solution:
Let x = 2.327327327 ………. →(1)
1000 x = 2327.327327 ……… →(2)
(2) – (1) ⇒ 1000 x – x = 2327.327327 ……….. (-)
  2.327327 ……..
999 x = 2325.000
x = \(\frac{2325}{999}\)
(or)
\(\frac{775}{333}\)

(iii) – 5.132
Solution:
– 5.132 = -5 + \(\frac{1}{10}\) + \(\frac{3}{100}\) + \(\frac{2}{1000}\)
= \(\frac{-5000 + 100 +30 + 2}{1000}\) = \(\frac{-4868}{1000}\)
(or)
\(\frac{-1217}{250}\)

(iv) 3.17
Solution:
Let x = 3.1777 ………. →(1)
10 x = 31.777 ……… →(2)
100 x = 317.77 …….. →(3)
(3) – (2) ⇒ 100 x – 10 x = 317.77 ……….. (-)
 31.777 ……..
90 x = 286.000
x = \(\frac{286}{90}\)
(or)
\(\frac{143}{45}\)

(v) 17.215
Solution:
Let x = 17.2151515 ………. →(1)
10 x = 172.151515 ……… →(2)
100 x = 17215.1515 …….. →(3)
(3) – (2) ⇒ 1000 x – 10 x = 17215.1515 ……….. (-)
 17215.1515 ……..
990 x = 17043
x = \(\frac{17043}{990}\)
(or)
\(\frac{5681}{330}\)

(vi) -21.2137
Solution:
Let x = -21.213777 ………. →(1)
1000 x = -21213.777 ……… →(2)
100 x = -212137.77 …….. →(3)
(3) – (2) ⇒ 10000 x – 1000 x = -21213.777 ……….. (-)
-21213.777 ……..
9000 x = -190924
x = \(\frac{-190924}{9000}\)
(or)
\(\frac{-47731}{2250}\)

Question 5.
Without actual division, find which of the following rational numbers have terminating decimal expression.
(i) \(\frac{7}{128}\)
Solution:

\(\frac{7}{128}\) = \(\frac{7}{2^{7}}\)
∴ \(\frac{7}{128}\) has terminating decimal expression.

(ii) \(\frac{21}{15}\)
Solution:
\(\frac{21}{15}\) = \(\frac{7}{5}\) = \(\frac{7}{5^1}\)
\(\frac{21}{15}\) has terminating decimal expression.

(iii) 4\(\frac{9}{35}\)
Solution:
4\(\frac{9}{35}\) = \(\frac{149}{35}\)
4\(\frac{149}{5×7}\) (It is not in the form of \(\frac{P}{2^{m} × 5^{n}}\)
∴ 4\(\frac{9}{35}\) has non-terminating recurring decimal expression.

(iv) \(\frac{219}{2200}\)
Solution:

\(\frac{219}{2200}\) = \(\frac{219}{2^{3} × 5^{2} × 11}\) (It is not in the form of \(\frac{P}{2^{m} × 5^{n}}\)
∴ \(\frac{219}{2200}\) has non-terminating recurring decimal expression.

Students can download Maths Chapter 2 Numbers and Sequences Ex 2.2 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.2

Question 1.
For what values of natural number n, 4th can end with the digit 6?
Answer:
4n = (2²)ⁿ = 2²ⁿ
= 2ⁿ × 2ⁿ
2 is a factor of 4ⁿ
∴ 4ⁿ is always even.

Question 2.
If m, n are natural numbers, for what values of m, does 2ⁿ × 5ⁿ ends in 5?
Solution:
2ⁿ × 5^m
2ⁿ is always even for all values of n.
5^m is always odd and ends with 5 for all values of m.
But 2ⁿ × 5^m is always even and ends in 0.
∴ 2ⁿ × 5^m cannot end with the digit 5 for any values of m. No value of m will satisfy 2ⁿ × 5^m ends in 5.

Question 3.
Find the H.C.F. of 252525 and 363636.
Answer:
To find the HCF of 252525 and 363636 by using Euclid’s Division algorithm.
363636 = 252525 × 1 + 111111
The remainder 111111 ≠ 0
By division of Euclid’s algorithm
252525 = 111111 × 2 + 30303
The remainder 30303 ≠ 0
Again by division of Euclid’s algorithm
111111 = 30303 × 3 + 20202
The remainder 20202 ≠ 0
Again by division of Euclid’s algorithm.
30303 = 20202 + 10101
The remainder 10101 ≠ 0
Again by division of Euclid’s algorithm.
20202 = 10101 × 2 + 0
The remainder is 0
∴ The H.C.F. is 10101

Question 4.
If 13824 = 2^a × 3^b then find a and b?
Answer:
Using factor tree method factorise 13824


13824 = 2⁹ × 3³
Given 13824 = 2a × 3b
Compare we get a = 9 and b = 3

Aliter:
13824 = 2⁹ × 3³
Compare with
13824 = 2^a × 3^b
The value of a = 9 b = 3

Question 5.
If p₁^x1 × p₂^x2 × p₃^x3 × p₄^x4 = 113400 where p₁ p₂, p₃, p₄ are primes in ascending order and x₁, x₂, x₃, x₄, are integers, find the value of p₁,p₂,p₃,p₄ and x₁,x₂,x₃,x₄.
Answer:
Given 113400 = p₁^x1 × p₂^x2 × p₃^x3 × p₄^x4
Using tree method factorize 113400

113400 = 23 × 34 × 52 × 7
compare with
113400 = p₁^x1 × p₂^x2 × p₃^x3 × p₄^x4
P₁ = 2, x₁ = 3
P₂ = 3, x₂ = 4
P₃ = 5, x₃ = 2
P₄ = 7, x₄ = 1

Question 6.
Find the L.C.M. and H.C.F. of 408 and 170 by applying the fundamental theorem of Arithmetic.
Answer:
Factorise 408 and 170 by factor tree method


408 = 2³ × 3 × 17
170 = 2 × 5 × 17
To find L.C.M. list all prime factors of 408 and 170 of their greatest exponents.
L.C.M. = 2³ × 3 × 5 × 17
= 2040
To find the H.C.F. list all common factors of 408 and 170.
H.C.F. = 2 × 17 = 34
L.C.M. = 2040 ; HCF = 34

Question 7.
Find the greatest number consisting of 6 digits which is exactly divisible by 24,15,36?
Answer:
The greatest number of 6 digits is 999999.
The greatest number must be divisible by L.C.M. of 24, 15 and 36

24 = 2³ × 3
15 = 3 × 5
36 = 2² × 3²
L.C.M = 2³ × 3² × 5
= 360
To find the greatest number 999999 must be subtracted by the remainder when 999999 is divided by 360
The greatest number in 6 digits = 999999 – 279
= 999720

Question 8.
What is the smallest number that when divided by three numbers such as 35, 56 and 91 leaves remainder 7 in each case?
Solution:
35 = 5 × 7
56 = 2 × 2 × 2 × 7
91 = 7 × 13
LCM of 35, 56, 91 = 5 × 7 × 2 × 2 × 2 × 13 = 3640
∴ Required number = 3647 which leaves remainder 7 in each case.

Question 9.
Find the least number that is divisible by the first ten natural numbers?
Answer:
Find the L.C.M of first 10 natural numbers

The least number is 2520

Modular Arithmetic
Two integers “a” and “b” are congruence modulo n if they differ by an integer multiple of n. That b – a = kn for some integer k. This can be written as a = b (mod n).

Euclid’s Division Lemma and Modular Arithmetic

Let m and n be integers, where m is positive. By Euclid’s division Lemma we can write n = mq + r where 0 < r < m and q is an integer.
This n = r (mod m)

Students can download Maths Chapter 1 Set Language Ex 1.5 Questions and Answers, Notes, Samacheer Kalvi 9th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.5

Question 1.
Using the adjacent Venn diagram, find the following sets:

(i) A – B
(ii) B – C
(iii) A’∪B’
(iv) A’∩B’
(v) (B∪C)’
(vi) A – (B∪C)
(vii) A – (B∩C)
Solution:
From the diagram we get
U = {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8},
A= {-2,-1, 3, 4, 6}, B = {-2,-1, 5, 7, 8}
C = {-3, -2, 0, 3, 8}
A’ = U – A = {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8} – {-2, -1, 3, 4, 6}
= {-3, 0, 1, 2, 5, 7, 8}
B’ = U – B = {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8} – {-2, -1, 5, 7, 8}
= {-3, 0, 1, 2, 3, 4, 6}
B∪C = {-2, -1, 5, 7, 8} ∪ {-3, -2, 0, 3, 8} = {-3, -2, -1, 0, 3, 5, 7, 8}
B∩C = {-2, -1, 5, 7, 8} ∩ {-3, -2, 0, 3, 8} = {-2, 8}

(i) A – B = {3, 4, 6}
(ii) B – C = {-1, 5, 7}
(iii) A’∪B’= {-3, 0, 1, 2, 5, 7, 8} ∪ {-3, 0, 1, 2, 3, 4, 6}
= {-3, 0, 1, 2, 3, 4, 5, 6, 7, 8}
(iv) A’∩B’ = {-3, 0, 1, 2, 5, 7, 8} ∩ {-3, 0, 1, 2, 3, 4, 6}
= {-3, 0, 1, 2}
(v) (B∪C)’ = U – (B∪C)= {-3,-2,-1,0, 1,2, 3,4, 5, 6, 7, 8} – {-3, -2, -1, 0, 3, 5, 7, 8}
= {1, 2, 4, 6}
(vi) A – (B∪C) = {-2, -1, 3, 4, 6} – {-3, -2, -1, 0, 3, 5, 7, 8} = {4, 6}
(vii) A – (B∩C) = {-2,-1, 3, 4, 6} – {-2, 8} = {-1, 3, 4, 6}

Question 2.
If K = {a, b, d, e, f}, L = {b, c, d, g} and M = {a, b, c, d, h} then find the following:
(i) K∪(L∩M)
(ii) K∩(L∪M)
(iii) (K∪L) ∩ (K∪M)
(iv) (K∩L) ∪ (K∩M)
and verify distributive laws.
Solution:
K = {a, b, d, e, f}, L = {b, c, d, g} and M = {a, b, c, d, h}
(i) K∪(L∩M)
(L∩M) = {b, c, d, g} ∩ [a, b, c, d, h}
= {b, c, d}
K∪(L∩M) = {a, b, d, e, f} ∪ {b, c, d}
= {a, b, c, d, e, f}

(ii) K∩(L∪M)
(L∪M) = {b, c, d, g} ∪ {a, b, c, d, h}
= {a, b, c, d, g, h}
K∩(L∪M) = {a, b, d, e, f} ∩ {a, b, c, d, g, h}
= {a, b, d }

(iii) (K∪L) ∩ (K∪M)
(K∪L) = {a, b, d, e, f} ∪ {b, c, d, g}
= {a, b, c, d, e, f, g}
(K∪M) = {a, b, d, e, f} ∪ {a, b, c, d, h}
= {a, b, c, d, e, f, h}
(K∪L) ∩ (K∪M) = {a, b, c, d, e, f, g} ∩ {a, b, c, d, e, f, h}
= {a, b, c, d, e, f}

(iv) (K∩L) ∪ (K∩M)
(K∩L) = {a, b, d, e, f) ∩ {b, c, d, g}
= {b, d}
(K∩M) = {a, b, d, e, f} ∩ {a, b, c, d, h}
= {a, b, d}
(K∩L) ∪ (K∩M) = {b, d} ∪ [a, b, d}
= {a, b, d}
From (ii) & (iv) we get, K∩(L∪M) = (K∩L) ∪ (K∩M)
From (i) & (iii) we get, K∪(L∩M) = (K∪L) ∩ (K∪M)

Question 3.
For A = {x : x ∈ Z, -2 < x ≤ 4}, B = {x : x ∈ W, x ≤ 5}, C = {-4, -1, 0, 2, 3, 4}
verify A∪(B∩C) = (A∪B) ∩ (A∪C).
Solution:
A = {-1, 0, 1, 2, 3, 4}, B = {0, 1, 2, 3, 4, 5} and C = {-4, -1, 0, 2, 3, 4}
B∩C = {0, 1, 2, 3, 4, 5} ∩ {-4, -1, 0, 2, 3, 4}
= {0, 2, 3, 4}
A∪(B∩C) = {-1, 0, 1, 2, 3, 4} ∪ {0, 2, 3, 4}
= {-1, 0, 1, 2, 3, 4} ……..(1)
A∪B = {-1, 0, 1, 2, 3, 4} ∪ {0, 1, 2, 3, 4, 5}
= {-1, 0, 1, 2, 3, 4, 5}
A∪C = {-1, 0, 1, 2, 3, 4} ∪ {-4, -1, 0, 2, 3, 4}
= {-4, -1, 0, 1, 2, 3, 4}
(A∪B) ∩ (A∪C) = {-1, 0, 1, 2, 3, 4, 5} ∩ {-4, -1, 0, 1, 2, 3, 4}
= {-1, 0, 1, 2, 3, 4} ……..(2)
From (1) and (2) we get A∪(B∩C) = (A∪B) ∩ (A∪C).

Question 4.
Verify A∪(B∩C) = (A∪B) ∩ (A∪C) using Venn diagrams.
Solution:

From (ii) and (v) we get A∪(B∩C) = (A∪B) ∩ (A∪C).

Question 5.
If A = {b, c, e, g, h}, B = {a, c, d, g, f}, and C = {a, d, e, g, h}, then show that A – (B∩C) = (A – B) ∪ (A – C).
Solution:
A = {b, c, e, g, h} ; B = {a, c, d, g, f}; C = {a, d, e, g, h}
B∩C = {a, c, d, g, i} ∩ {a, d, e, g, h}
= {a, d, g}
A – (B∩C) = {b, c, e, g, h} – {a, d, g}
= {b, c, e, h}…….(1)
A – B = {b, c, e, g, h} – {a, c, d, g, i}
= {b, e, h}
A – C = {b, c, e, g, h} – {a, d, e, g, h}
= {b, c}
(A – B) ∪ (A – C) = {b, e, h} ∪ {b, c}
= {b, c, e, h)……..(2)
From (1) and (2) we get A – (B∩C) = (A – B) ∪ (A – C)

Question 6.
If A= {x : x = 6n, n∈W and n < 6}, B = {x : x = 2n, n∈N and 2 < n ≤ 9} and
C = {x : x = 3n, n∈N and 4 ≤ n < 10}, then show that A – (B∩C) = (A – B) ∪ (A – C)
Solution:
A = {0, 6, 12, 18, 24, 30}; B = {6, 8, 10, 12, 14, 16, 18}; C = {12, 15, 18, 21, 24, 27}
B∩C = {6, 8, 10, 12, 14, 16, 18} ∩ {12, 15, 18, 21, 24, 27}
= {12, 18}
A – (B∩C) = {0, 6, 12, 18, 24, 30} – {12, 18}
= {0, 6, 24, 30}………(1)
A – B = {0, 6, 12, 18, 24, 30} – {6, 8, 10, 12, 14, 16, 18}
= {0, 24, 30}
A – C = {0, 6, 12, 18, 24, 30} – {12, 15, 18, 21, 24, 27}
= {0, 6, 30}
(A – B) ∪ (A – C) = {0, 24, 30} ∪ {0, 6, 30}
= {0, 6, 24, 30}……..(2)
From (1) and (2) we get A – (B∩C) = (A – B) ∪ (A – C).

Question 7.
If A = {-2, 0, 1, 3, 5}, B = {-1, 0, 2, 5, 6} and C = {-1, 2, 5, 6, 7}, then show that
A – (B∪C) = (A – B) ∩ (A – C).
Solution:
A= {-2, 0, 1, 3, 5}, B = {-1, 0, 2, 5, 6}, C = {-1, 2, 5, 6, 7}
B∪C = {-1, 0, 2, 5, 6} ∪ {-1, 2, 5, 6, 7}
= {-1, 0, 2, 5, 6, 7}
A – (B∪C) = {-2, 0, 1, 3, 5} – {-1, 0, 2, 5, 6, 7}
= {-2, 1, 3} ………(1)
A – B = {-2, 0, 1, 3, 5} – {-1, 0, 2, 5, 6}
= {-2, 1, 3}
A – C = {-2, 0, 1, 3, 5}- {-1, 2, 5, 6, 7}
= {-2, 0, 1, 3}
(A- B) ∩ (A- C) = {-2, 1, 3} ∩ {-2, 0, 1, 3}
= {-2, 1, 3} ….(2)
From (1) and (2) we get A – (B∪C) = (A – B) ∩ (A – C).

Question 8.
IF A = {y : y = \(\frac{a + 1}{2}\), a ∈ W and a ≤ 5}, B = {y : y = \(\frac{2n – 1}{2}\), n ∈ W and n < 5} and C = {-1, \(-\frac{1}{2}\), 1, \(\frac{3}{2}\), 2} then show that A – (B∪C) = (A – B) ∩ (A – C).
Solution:

From (1) and (2) we get A – (B∪C) = (A – B) ∩ (A – C).

Question 9.
Verify A- (B∩C) = (A – B) ∪ (A – C) using Venn diagrams.
Solution:


From (ii) and (v) we get A- (B∩C) = (A – B) ∪ (A – C).

Question 10.
If U = {4, 7, 8, 10, 11, 12, 15, 16} , A = {7, 8, 11, 12} and B = {4, 8, 12, 15}, then verify De Morgan’s Laws for complementation.
U= {4, 7, 8, 10, 11, 12, 15, 16} , A = {7, 8, 11, 12} and B = {4, 8, 12, 15}
(i) (A∪B)’ = A’∩B’
(ii) (A∩B)’ = A’∪B’
Solution:
(i) A∪B = {7, 8, 11, 12} ∪ {4, 8, 12, 15}
= {4, 7, 8, 11, 12, 15}
(A∪B)’ = {4, 7, 8, 10, 11, 12, 15, 16} – {4, 7, 8, 11, 12, 15}
= {10,16} ………(1)
A’ = {4, 7, 8, 10, 11, 12, 15, 16} – {7, 8, 11, 12}
= {4, 10, 15, 16}
B’ = {4, 7, 8, 10, 11, 12, 15, 16} – {4, 8, 12, 15}
= {7, 10, 11, 16}
A’∩B’ = {4, 10, 15, 16} ∩ {7, 10, 11, 16}
= {10,16} ………(2)
From (1) and (2) we get (A∪B)’ = A’∩B’

(ii) A∩B = {7, 8, 11, 12} ∩ {4, 8, 12, 15}
= {8, 12}
(A∩B)’ = {4, 7, 8, 10, 11, 12, 15, 16} – {8, 12}
= {4, 7, 10, 11, 15, 16} ………(1)
A’ = {4, 10, 15, 16}
B’ = {7, 10, 11, 16}
A’∪B’ = {4, 10, 15, 16} ∪ {7, 10, 11, 16}
= {4, 7, 10, 11, 15, 16} ………(2)
From (1) and (2) we get (A∩B)’ = A’∪B’

Question 11.
Verify (A∩B)’ = A∪B’ using Venn diagrams.
Solution:

From (ii) and (i) we get (A∩B)’ = A’∪B’

Students can download Maths Chapter 1 Relations and Functions Unit Exercise 1 Questions and Answers, Notes, Samacheer Kalvi 10th Maths Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Unit Exercise 1

Question 1.
If the ordered pairs (x² – 3x, y² + 4y) and (-2, 5) are equal, then find x and y.
Answer:
(x² – 3x, y² + 4y) = (-2, 5)
x² – 3x = -2
x² – 3x + 2 = 0
(x – 2) (x – 1) = 0
x – 2 = 0 or x – 1 = 0
x = 2 or 1

y² + 4y = 5
y² + 4y – 5 = 0
(y + 5) (y – 1) = 0
y + 5 = 0 or y – 1 = 0
y = -5 or y = 1
The value of x = 2, 1
and 7 = -5, 1

Question 2.
The Cartesian product A × A has 9 elements among which (-1, 0) and (0, 1) are found. Find the set A and the remaining elements of A × A.
Solution:
A = {-1, 0, 1}, B = {1, 0, -1}
A × B = {(-1, 1), (-1, 0), (-1, -1), (0, 1), (0, 0), (0, -1), (1, 1), (1, 0), (1, -1)}

Question 3.
Given that f(x) = \(\left\{\begin{array}{rl}
{\sqrt{x-1}} & {x \geq 1} \\
{4} & {x<1}
\end{array}\right.\).
Find
(i) f(0) (ii)f (3) (iii) f(a + 1) in terms of a.(Given that a > 0)
Answer:
f(x) = \(\sqrt { x-1 }\) ; f(x) = 4
(i) f(0) = 4
(ii) f(3) = \(\sqrt { 3-1 }\) = \(\sqrt { 2 }\)
(iii) f(a + 1) = \(\sqrt { a+1-1 }\) = \(\sqrt { a }\)

Question 4.
Let A = {9, 10, 11, 12, 13, 14, 15, 16, 17} and let f: A → N be defined by f(n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f.
Solution:
A = {9, 10, 11, 12, 13, 14, 15, 16, 17}
f: A → N
f(n) = the highest prime factor of n ∈ A
f = {(9, 3), (10, 5), (11, 11), (12, 3), (13, 13), (14, 7), (15, 5), (16, 2), (17, 17)}
Range = {3, 5, 11, 13, 7, 2, 17}
= {2, 3, 5, 7, 11, 13, 17}

Question 5.
Find the domain of the function

Answer:

Domain of f(x) = {-1, 0, 1}

Question 6.
If f(x)= x², g(x) = 3x and h(x) = x – 2 Prove that (fog)oh = fo(goh).
Solution:
f(x) = x²
g(x) = 3x
h(x) = x – 2
(fog)oh = x – 2
LHS = fo(goh)
fog = f(g(x)) = f(3x) = (3x)² = 9x²
(fog)oh = (fog) h(x) = (fog) (x – 2)
= 9(x – 2)² = 9(x² – 4x + 4)
= 9x² – 36x + 36 ……………. (1)
RHS = fo(goh)
(goh) = g(h(x)) = g(x – 2)
= 3(x – 2) = 3x – 6
fo(goh) = f(3x – 6) = (3x – 6)²
= 9x² – 36x + 36 ………….. (2)
(1) = (2)
LHS = RHS
(fog)oh = fo(goh) is proved.

Question 7.
Let A= {1,2} and B = {1,2,3,4}, C = {5,6} and D = {5,6,7,8}. Verify whether A × C is a subset of B × D?
Answer:
Given A = {1, 2}
B = {1, 2, 3, 4}
C = {5,6}
D = {5,6, 7,8}
A × C = {1,2} × {5,6}
= {(1,5) (1,6) (2, 5) (2, 6)}
B × D = {1,2, 3, 4} × {5, 6, 7, 8}
= {(1,5) (1,6) (1,7) (1,8)
(2, 5) (2, 6) (2,7) (2, 8)
(3, 5) (3, 6) (3, 7) (3, 8)
(4, 5) (4, 6) (4, 7) (4, 8)}
∴ A × C ⊂ B × D
Hence it is verified

Question 8.
If f(x) = \(\frac{x-1}{x+1}, x \neq 1\) Show that
f(f(x)) = – \(\frac { 1 }{ x } \), Provided x ≠ 0.
Answer:

Question 9.
The functions f and g are defined by f{x) = 6x + 8; g(x) = \(\frac { x-2 }{ 3 } \)
(i) Calculate the value of gg [latex]\frac { 1 }{ 2 } [/latex]
(a) Write an expression for gf (x) in its simplest form.
Answer:
f(x) = 6x + 8 ; g(x) = \(\frac { x-2 }{ 3 } \)

Question 10.
Write the domain of the following real functions

Answer:
(i) f (x) = \(\frac { 2x+1 }{ x-9 } \)
If the denominator vanishes when x = 9
So f(x) is not defined at x = 9
∴ Domain is x ∈ [R – {9}]

(ii) if p(x) = \(=\frac{-5}{4 x^{2}+1}\)
p(x) is defined for all values of x. So domain is x ∈ R.

(iii) g(x) = \(\sqrt { x-2 }\)
When x < 2 g(x) becomes complex. But given “g” is real valued function.
So x > 2
Domain x ∈ (2, α)

(iv) h (x) = x + 6
For all values of x, h(x) is defined. Hence domain is x ∈ R.