Bhagya

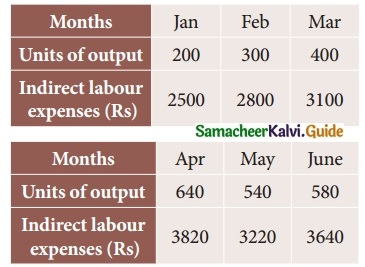
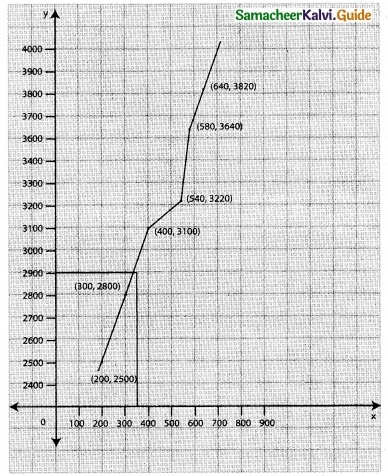
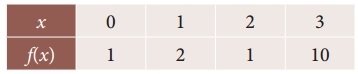
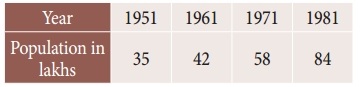
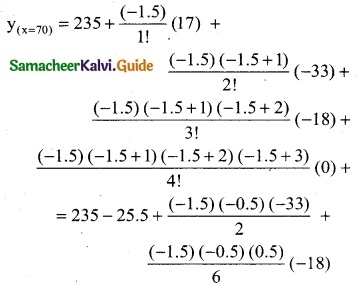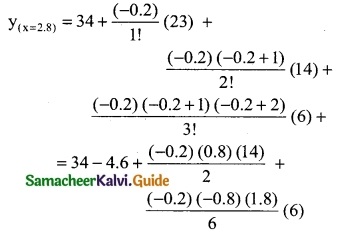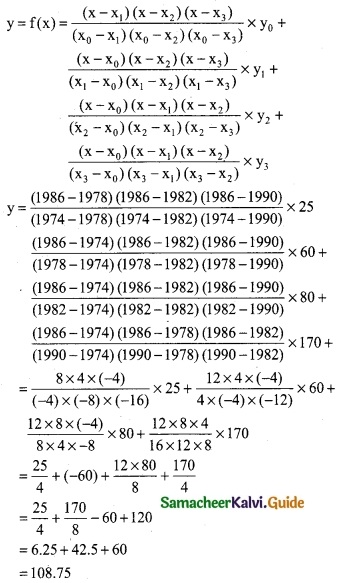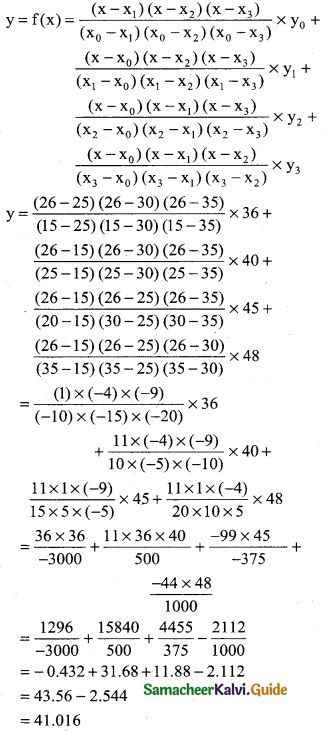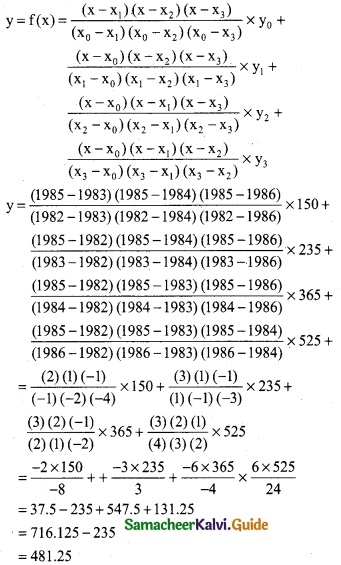Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 5 Numerical Methods Miscellaneous Problems Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 5 Numerical Methods Miscellaneous Problems

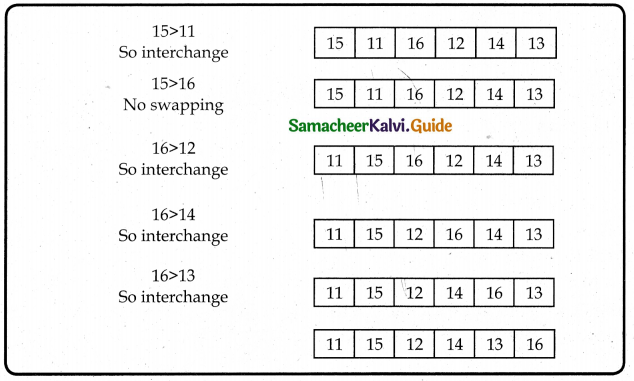
Question 1.
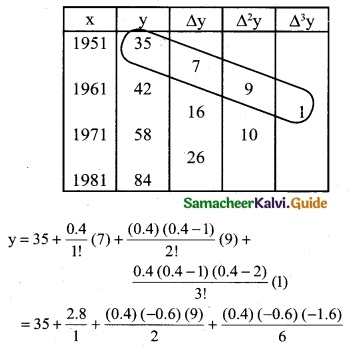
If f (x) = e^ax then show that f(0), Δf(0), Δ²f(0) are in G.P
Solution:
Given f(x) = e^ax
f(0) = e° = 1 ……… (1)
Δf(x) = e^a(x+h) – e^ax
= e ^ax+ah – e^ax
= e^ax. e^ah – e^ax
= e^ax (e^ah – 1)
Δf(0) = e° (e^ah – 1)
= (e^ah – 1) …….. (2)
Δ²f(x)= Δ [Δf(x)]
= Δ [e^a(x+h) – e^ax]
[e^a(x+h+h) – e^a(x+h)] – [e^a(x+h) – e^ax]
= e^a(x+2h) – e^a(x+h) – e^a(x+h) + e^ax
Δ²f(0) = Δ [Δf(x)]
= e^a(2h) – e^a(h) – e^a(h) + e⁰
= e^2ah – e^ah – e^ah + 1
= (e^ah)² – 2e^ah + 1
= [e^ah – 1]² ………… (3)
from (1), (2) & (3)
[t₂]² =[Δf(0)]² = (e^ah – 1)²
t₁ × t₃ = f(0) × Δ²f(0)
= (1)(e^ah – 1)² = (e^ah – 1)²
⇒ [Δf(0)]² = f(0) × Δ²f(0)
∴ f(0), Δf(0), Δ²f(0) an is G.P.

Question 2.
Prove that
(i) (1 + Δ) (1 – ∇) = 1
(ii) Δ∇ = Δ – ∇
(iii) EV = Δ = ∇E
Solution:
(i) LHS = (1 + Δ) (1 – ∇)
= (E) (E^-1) = E^1-1
= E° = 1
= RHS
Hence proved.

(ii) LHS = Δ∇
= (E – 1)(1 – E^-1)
= E – EE^-1 + E^-1
= E – 1 – 1 – E^-1
= E – 2 – E^-1 ………… (1)
RHS = Δ – ∇
= (E – 1) -(1 – E^-1)
= E – 1 – 1 + E^-1
= E – 2 + E^-1 ………. (2)
from (1) & (2) LHS = RHS
Hence proved.

(iii) E∇ = EE^-1Δ [∵ ∇ = E^-1Δ]
= Δ ……… (1)
∇E = E^-1 ΔE
= E^-1 EΔ
= Δ ………. (2)
from (1) (2)
E∇ = Δ = ∇E

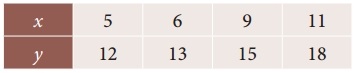
Question 3.
A second degree polynomial passes though the point (1, -1) (2, -1) (3, 1) (4, 5). Find the polynomial.
Solution:
Points are (1, -1), (2, -1), (3, 1) and (4, 5)

we will use Newton’s backward interpolation formula to find the polynomial.

= 5 + (x – 4) (4) + (x – 4) (x – 3) + 0
= 5 + 4x – 16 + x² – 7x + 12
y(x) = x² – 3x + 1

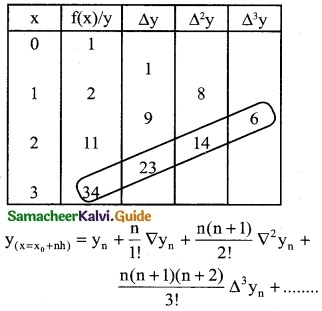
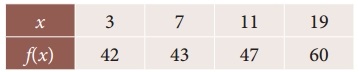
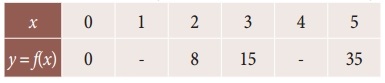
Question 4.
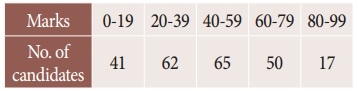
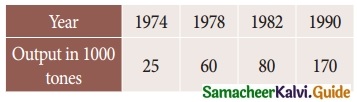
Find the missing figures in the following table

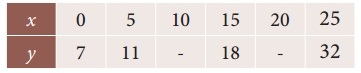
Solution:
Here y₀ = 7; y₁ = 11; y₂ = ?; y₃ = 18; y₄ = ?; y₅ = 32
Since only four values of f(x) are given, the polynomial which fits the data is of degree three. Hence fourth differences are zeros.
Δ⁴y_k = 0
(ie) (E – 1)⁴ y_k = 0
(i.e) (E⁴ – 4E³ + 6E² – 4E + 1)y_k = 0 ……….. (1)
Put k = 0 in (1)
(E⁴ – 4E³ + 6E² – 4E + 1)y₀ = 0
E⁴ y₀ – 4E³ y₀ + 6E² y₀ – 4E y₀ + y₀ = 0
y₄ – 4y₃ + 6y₂ – 4y₁ + y₀ = 0
y₄ – 4(18) + 6y₂ – 4(11) + 7 = 0
y₄ – 72 + 6y₂ – 44 + 7 = 0
y₄ + 6y₂ = 109
(2)
Put k = 1 in (1)
(E⁴ – 4E³ + 6E² – 4E + 1)y₁ = 0
[E⁴ y₁ – 4E y₁ + 6E² y₁ – 4Ey₁ + y] = 0
y₅ – 4y₄ + 6y₃ – 4y₂ + y₁ = 0
32 – 4 (y₄) + 6(18) — 4(y₂) + 11 = 0
32 – 4y₄ + 108 – 4y₂ + 11 = 0
-4y₄ – 4y₂ + 151 = 0
4y₄ + 4y₂ = 151 ,……. (3)
Solving equation (1) & (2)

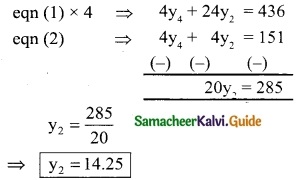
Substitute y₂ = 14.25 in eqn (1)
y₄ + 6(14.25) = 109
y₄ + 25.50 = 109
y₄ = 109 – 85.5
∴ y₄ = 23.5
∴ Required two missing values are 14.25 and 23.5.

Question 5.
Find f (0.5) if f(-1) = 202, f(0) = 175, f(1) = 82 and f(2) = 55
Solution:
From the given data

Here we have to apply Newton’s forward interpolation formula, since the value of f(x) is required near the beginning of the table.
y_{(x= x0+nh)} =f(x₀) + \(\frac { n }{1!}\) Δf(x₀) + \(\frac { n(n-1) }{2!}\) Δ²f(x₀) + \(\frac { n(n-1)(n-2) }{3!}\) Δ³f(x₀) + ………
Given:
x = 0.5 and h = 1
x₀ + nh = x
-1 + n(1) = 0.5
n = 1 + 0.5
∴ n = 1.5

= 202 – 40.5 – 24.75 – 8.25
= 202 – 73.5
f(0.5) = 128.5

Question 6.
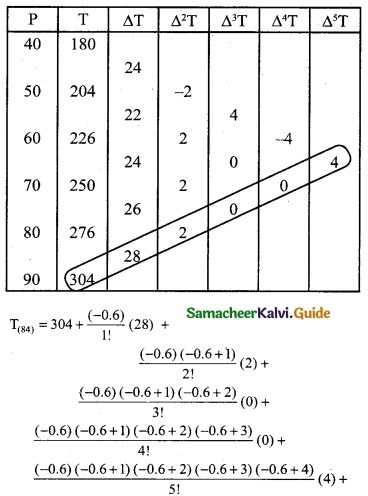
From the following data find y at x = 43 and x = 84

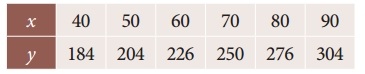
Solution:
To find y at x = 43
Since the value of y is required near the beginning of the table, we use the Newton’s forward interpolation formula.

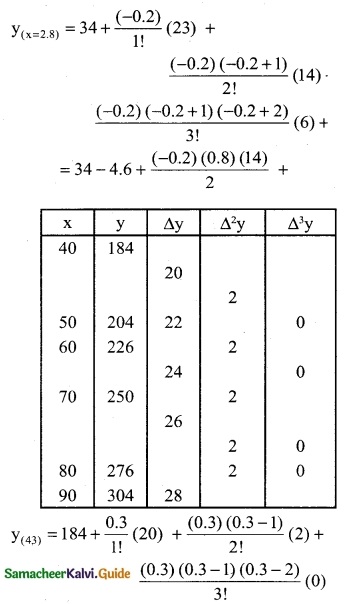
= 184 + (0.3) (20) + (0.3) (-0.7)
= 184 + 6.0 – 0.21
= 190 + 0.21
y_(x=43) = 189.79
To find y at x = 84
Since the value of y is required at the end of the table, we apply backward interpolation formula.

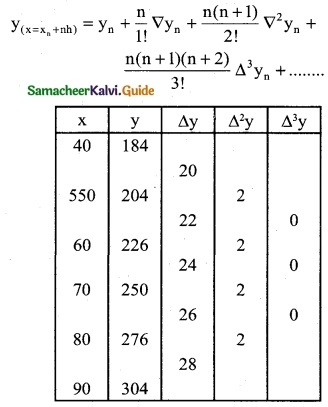
x_n + nh = x
90 + n(10) = 84
10n = 84 – 90
10n = -6
∴ n = -0.6
y_(x=84) = 304 + \(\frac { (0.6) }{1!}\) (28) + \(\frac {(0.6)(-0.6 + 1) }{2!}\)(2) +
= 304 + (0.6) (28) + \(\frac { (-0.6)(0.4) }{2}\) + 2
= 304 – 16.8 – 0.24
= 304 – 17.04
= 286.96

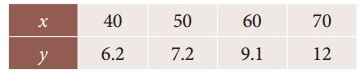
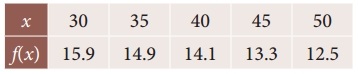
Question 7.
The area A of circle of diameter ‘d’ is given for the following values

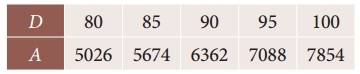
Find the approximate values for the areas of circles of diameter 82 and 91 respectively.
Solution:
To find A at D = 82
Since the value of A is required near the beginning of the table. We use the Newton’s forward interpolation formula.

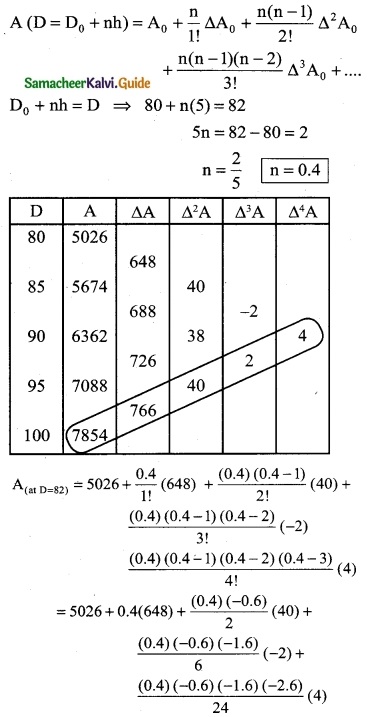
= 5026 + 259.2 – 4.8 – 0.128 – 0.1664
= 5285.2 – 5.0944
= 5280.1056
A = 5280.11
To find Δ at D = 91
Since the value of A is required near the beginning of the table. We use the Newton’s forward interpolation formula.

= 7854 – 1378.8 + 28.8 + 0.096 + 0.0576
= 7882.9536 – 1378.8
= 6504.1536
= 6504.15

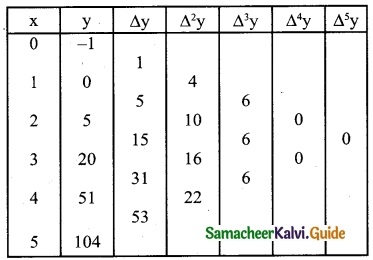
Question 8.
If u₀ = 560, u₁ = 556, u₂ = 520, u₄ = 385, show that u₃ = 465
Solution:
U₀ = 560; U₁ = 556; U₂ = 520; U₄ = 385
Since only four values of U are given, the polynomial which fits the data is of degree three. Hence fourth differences are zeros.
Δ⁴U₀
(E – 1)⁴ U₀ = 0
⇒ (E⁴ – 4E³ + 6E² – 4E + 1) U₀ = 0
⇒ E⁴U₀ – 4E³U₀ + 6E²U₀ – 4EU₀ + U₀ = 0
U₄ – 4U₃ + 6U₂ – 4U₁ + U₀ = 0
385 – 4(U₃) + 6 (520) – 4 (556) + 560 = 0
385 – 4(U₃) + 3120 – 2224 + 560 = 0
1841 – 4U₃ = 0
4U₃ = 1841 ⇒ U₃ = \(\frac { 1841 }{4}\)
U₃ = 460.25

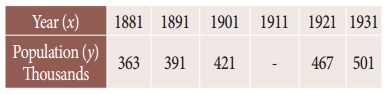
Question 9.
From the following table obtain a polynomial of degree y in x

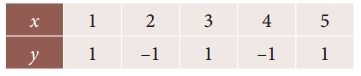
Solution:
We will use Newton’s backward interpolation formula to find the polynomial.

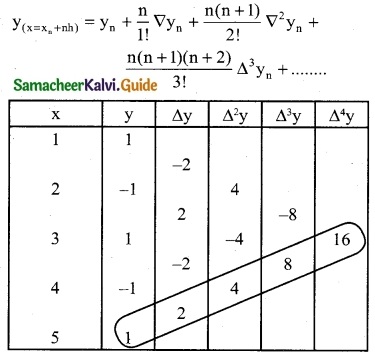
To find y in terms of x
x_n + nh = x
5 + n(1) = x
∴ n = x – 5

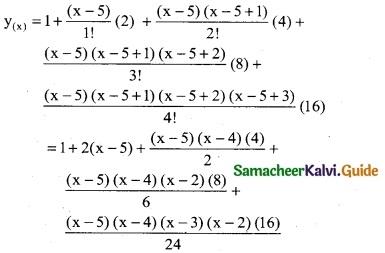
= 1 + 2x – 10 + 2 (x² – 9x + 20) + \(\frac { 4 }{3}\) (x – 5) (x² – 7x + 12) + \(\frac { 2 }{3}\)(x² – 9x + 20)(x² – 5x + 6)
= 1 + 2x – 10 + 2x² – 18x + 40 + \(\frac { 4 }{3}\)
[x³ – 7x² + 12x – 5x² + 35x – 60] + \(\frac { 2 }{3}\) [x⁴ – 5x³ + 6x² – 9x³ + 45x² – 54x + 20x² – 100x + 120]

Question 10.
Using Lagrange’s interpolation formula find a polynominal which passes through the points (0, -12), (1, 0), (3, 6) and (4, 12).
Solution:
We can construct a table using the given points.

Here x₀ = 0; x₁ = 1; x₂ = 3; x₃ = 4,
y₀ = -12; y₁ = 0; y₂ = 6; y₃ = 12

= (x³ – 7x² + 12x – x² + 7x – 12) – (x³ – 5x² + 4x) + (x³ – 4x² + 3x)
= (x³ – 8x² + 19x – 12) – (x³ – 5x² + 4x) + (x³ – 4x² + 3x)
= x³ – 8x² + 19x – 12 – x³ + 5x² – 4x + x³ – 4x² + 3x
∴ y = x³ – 7x² + 18x – 12

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Computer Science Guide Pdf Chapter 5 Python -Variables and Operators Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Computer Science Solutions Chapter 5 Python -Variables and Operators

12th Computer Science Guide Python -Variables and Operators Text Book Questions and Answers

I. Choose the best answer (1 Marks)

Question 1.
Who developed Python ?
a) Ritche
b) Guido Van Rossum
c) Bill Gates
d) Sunder Pitchai
Answer:
b) Guido Van Rossum

Question 2.
The Python prompt indicates that Interpreter is ready to accept instruction.
a) > > >
b) < < <
c) #
d) < <
Answer:
a) > > >

Question 3.
Which of the following shortcut is used to create a new Python Program?
a) Ctrl + C
b) Ctrl + F
c) Ctrl + B
d) Ctrl + N
Answer:
d) Ctrl + N

Question 4.
Which of the following character is used to give comments in Python Program?
a) #
b) &
c) @
d) $
Answer:
a) #

Question 5.
This symbol is used to print more than one item on a single line.
a) Semicolon(;)
b) Dollor($)
c) commaQ
d) Colon(:)
Answer:
c) commaQ

Question 6.
Which of the following is not a token?
a) Interpreter
b) Identifiers
c) Keyword
d) Operators
Answer:
a) Interpreter

Question 7.
Which of the following is not a Keyword in Python?
a) break
b) while
c) continue
d) operators
Answer:
d) operators

Question 8.
Which operator is also called a Comparative operator?
a) Arithmetic
b). Relational
c) Logical
d) Assignment
Answer:
b) Relational

Question 9.
Which of the following is not a Logical operator?
a) and
b) or
c) not
d) Assignment
Answer:
d) Assignment

Question 10.
Which operator is also called a Conditional operator?
a) Ternary
b) Relational
c) Logical
d) Assignment
Answer:
a) Ternary

II. Answer the following questions (2 Marks)

Question 1.
What are the different modes that can be used to test Python Program?
Answer:
In Python, programs can be written in two ways namely Interactive mode and Script mode. The Interactive mode allows us to write codes in Python command prompt (>>>) whereas in script mode programs can be written and stored as separate file with the extension .py and executed. Script mode is used to create and edit python source file.

Question 2.
Write short notes on Tokens.
Answer:
Python breaks each logical line into a sequence of elementary lexical components known as Tokens.
The normal token types are

1. Identifiers
2. Keywords
3. Operators
4. Delimiters
5. Literals

Question 3.
What are the different operators that can be used in Python?
Answer:
In computer programming languages operators are special symbols which represent computations, conditional matching etc. The value of an operator used is called operands. Operators are categorized as Arithmetic, Relational, Logical, Assignment etc.

Question 4.
What is a literal? Explain the types of literals?
Answer:

• Literal is raw data given in a variable or constant.
• In Python, there are various types of literals.

1. Numeric
2. String
3. Boolean

Question 5.
Write short notes on Exponent data.
Answer:
An Exponent data contains decimal digit part, decimal point, exponent part followed by one or more digits.
12.E04, 24.e04 # Exponent data

III. Answer the following questions (3 Marks)

Question 1.
Write short notes on the Arithmetic operator with examples.
Answer:

• An arithmetic operator is a mathematical operator that takes two operands and performs a calculation on them.
• They are used for simple arithmetic.
• Most computer languages contain a set of such operators that can be used within equations to perform different types of sequential calculations.
• Python supports the following Arithmetic operators.

Question 2.
What are the assignment operators that can be used in Python?
Answer:

• In Python,= is a simple assignment operator to assign values to variables.
• There are various compound operators in Python like +=, -=, *=, /=,%=, **= and / / = are also available.
• Let = 5 and = 10 assigns the values 5 to and 10 these two assignment statements can also be given a =5 that assigns the values 5 and 10 on the right to the variables a and b respectively.

Question 3.
Explain the Ternary operator with examples.
Answer:
Conditional operator:
Ternary operator is also known as a conditional operator that evaluates something based on a condition being true or false. It simply allows testing a condition in a single line replacing the multiline if-else making the code compact.
The Syntax conditional operator is,
Variable Name = [on – true] if [Test expression] else [on – false]
Example:
min = 50 if 49 < 50 else 70 # min = 50 min = 50 if 49 > 50 else 70 # min = 70

Question 4.
Write short notes on Escape sequences with examples.
Answer:

• In Python strings, the backslash “\” is a special character, also called the “escape” character.
• It is used in representing certain whitespace characters: “t” is a tab, “\n\” is a new line, and “\r” is a carriage return.
• For example to print the message “It’s raining”, the Python command is > > > print (“It \ ‘s raining”)
• output:
  It’s raining

Question 5.
What are string literals? Explain.
Answer:
String Literals:
In Python, a string literal is a sequence of characters surrounded by quotes. Python supports single, double and triple quotes for a string. A character literal is a single character surrounded by single or double-quotes. The value with triple – the quote is used to give multi-line string literal.
Strings = “This is Python”
char = “C”
multiline _ str = “This is a multiline string with more than one line code”.

IV. Answer the following questions (5 Marks)

Question 1.
Describe in detail the procedure Script mode programming
Answer:

• Basically, a script is a text file containing the Python statements.
• Python Scripts are reusable code.
• Once the script is created, it can be executed again and again without retyping.
• The Scripts are editable

Creating Scripts in Python:

• Choose File → New File or press Ctrl + N in the Python shell window.
• An untitled blank script text editor will be displayed on the screen.
• Type the code in Script editor
  a=100
  b=350
  c=a+b
  print(“The Sum=”,c)

Saving Python Script:

• Choose File →Save or press Ctrl+S
• Now, Save As dialog box appears on the screen
• In the Save As dialog box, select the location where you want to save your Python code, and type the File name box Python files are by default saved with extension by Thus, while creating Python scripts using Python Script editor, no need to specify the file extension.
• Finally, ‘click Save button to save your Python script.

Executing Python Script:

• Choose Run-Run Module or Press F5
• If code has any error, it will be shown in red color in the IDLE window,, and Python describes the type of error occurred. To correct the errors, go back to Script editor, make corrections, save the file using Ctrl + S or File→Save and execute it again.
• For all error-free code, the output will appear in the IDLE window of Python.

Question 2.
Explain input () and print() functions with examples.
Answer:
input () function:
In Python input() function is used to accept data as input at run time.
Syntax:
Variable = input (“prompt string”)

• where, prompt string in the syntax is a statement or message to the user, to know what input can be given.
• The input() takes whatever is typed from the keyboard and stores the entered data in the given variable.
• If prompt string is not given in input() no message is displayed on the screen, thus, the user will not know what is to be typed as input

Example:
> > > city=input(“Enter Your City: “)
Enter Your City: Madurai
> > > print(“I am from “, city)
I am from Madurai

• The input () accepts all data as string or characters but not as numbers.
• If a numerical value is entered, the input values should be explicitly converted into numeric data type.
• The int( ) function is used to convert string data as integer data explicitly.

Example:
x= int (input(“Enter Number 1: “))
y = int (input(“Enter Number 2: “))
print (“The sum =”, x+y)
Output
Enter Number 1: 34
Enter Number 2: 56
The sum = 90
print () function :
In Python, the print() function is used to display result on the screen. The syntax for print() is as follows:

Syntax:
print (“string to be displayed as output” )
print (variable)
print (“String to be displayed as output variable)
print (“String 1 “, variable, “String 2′”,variable, “String 3” )….)

Example
> > > print (“Welcome to Python Programming”)
Welcome to
Python Programming
> > > x= 5
> > > y= 6
> > > z=x+y
> > > print (z)
11
> > > print (“The sum =”,z)
The sum=11
> > > print (“The sum of”,x, “and “, y, “is “,z)
The sum of 5 and 6 is 11

• The print( ) evaluates the expressions before printing it on the monitor
• The print( ) displays an entire statement which specified within print ( )
• Comma (,) is used as a separator in print more than one time

Question 3.
Discuss in detail about Tokens in Python
Answer:
Python breaks each logical line into a sequence of elementary lexical components known as Token.
The normal token types are

1. Identifiers
2. Keywords
3. Operators
4. Delimiters and
5. Literals.

Identifiers:

• An Identifier is a name used to identify a variable, function, class, module or object.
• An identifier must start with an alphabet
  (A..Z or a..z) or underscore (_). Identifiers may contain digits (0 .. 9). „
• Python identifiers are case sensitive i.e. uppercase and lowercase letters are distinct. Identifiers must not be a python keyword.
• Python does not allow punctuation characters such as %,$, @, etc., within identifiers.

Keywords:
Keywords are special words used by Python interpreters to recognize the structure of the program. As these words have specific meanings for interpreters, they cannot be used for any other purpose.

Operators:

• In computer programming languages operators are special symbols which represent computations, conditional matching, etc.
• The value of an operator used is called operands.
• Operators are categorized as Arithmetic, Relational, Logical, Assignment, etc. Value and variables when used with the operator are known as operands

Delimiters:
Python uses the symbols and symbol combinations as delimiters in expressions, lists, dictionaries, and strings
Following are the delimiters knew as operands.

Literals:
Literal is raw data given in a variable or constant. In Python, there are various types of literals.

• Numeric
• String
• Boolean

12th Computer Science Guide Python -Variables and Operators Additional Questions and Answers

I. Choose the best answer (1 Mark)

Question 1.
Python language was released in the year
a) 1992
b) 1994
c) 1991
d) 2001
Answer:
c) 1991

Question 2.
CWI means ……………………………
Answer:
Centrum Wiskunde & Information

Question 3.
In Python, How many ways programs can be written?
a) 4
b) 2
c) 3 ‘
d) many
Answer:
b) 2

Question 4.
Find the wrong statement from the following.
(a) Python supports procedural approaches
(b) Python supports object-oriented approaches
(c) Python is a DBMS tool
Answer:
(c) Python is a DBMS tool

Question 5.
Which mode displays the python code result immediately?
a) Compiler
b) Script
c) Interactive
d) program
Answer:
c) Interactive

Question 6.
Which of the following command is used to execute the Python script?
a) Run → Python Module
b) File → Run Module
c) Run → Module Fun
d) Run → Run Module
Answer:
d) Run → Run Module

Question 7.
The extension for the python file is ……………………………
(a) .pyt
(b) .pt
(c) .py
(d) .pyth
Answer:
(c) .py

Question 8.
Which operator replaces multiline if-else in python?
a) Local
b) Conditional
c) Relational
d) Assignment
Answer:
b) Conditional

Question 9.
Which of the following is a sequence of characters surrounded by quotes?
a) Complex
b) String literal
c) Boolean
d) Octal
Answer:
b) String literal

Question 10.
What does prompt (>>>) indicator?
(a) Compiler is ready to debug
(b) Results are ready
(c) Waiting for the Input data
(d) Interpreter is ready to accept Instructions
Answer:
(d) Interpreter is ready to accept Instructions

Question 11.
In Python shell window opened by pressing.
a) Alt + N
b) Shift + N
c) Ctrl + N
d) Ctrl + Shift +N
Answer:
c) Ctrl + N

Question 12.
In Python, comments begin with …………..
a) /
b) #
c)\
d) //
Answer:
b) #

Question 13.
Which command is selected from the File menu creates a new script text editor?
(a) New
(b) New file
(c) New editor
(d) New Script file
Answer:
(b) New file

Question 14.
Python uses the symbols and symbol combinations as ……………. in expressions
a) literals
b) keywords
c) delimiters
d) identifiers
Answer:
c) delimiters

Question 15.
All data values in Python are ……………
a) class
b) objects
c) type
d) function
Answer:
b) objects

Question 16.
…………………………… command is used to execute python script?
(a) Run
(b) Compile
(c) Run ? Run Module
(d) Compile ? Compile Run
Answer:
(c) Run ? Run Module

Question 17.
Octal integer uses …………………………… to denote octal digits
(a) OX
(b) O
(c) OC
(d) Od
Answer:
(b) O

Question 18.
Find the hexadecimal Integer.
(a) 0102
(b) 0876
(c) 0432
(d) 0X102
Answer:
(d) 0X102

Question 19.
How many floating-point values are there is a complex number?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2

II. Answer the following questions (2 and 3 Marks)

Question 1.
Write a note on keywords. Give examples?
Answer:
Keywords are special words used by Python interpreters to recognize the structure of the program. As these words have specific meanings for interpreters, they cannot be used for any other purpose. Eg, While, if.

Question 2.
What are keywords? Name any four keywords in Python.
Answer:
Keywords are special words that are used by Python interpreters to recognize the structure of the program.

Question 3.
Write a note on the relational or comparative operator.
Answer:

• A Relational operator is also called a Comparative operator which checks the relationship between two operands.
• If the relation is true, it returns True otherwise it returns False.

Question 4.
Write a short note on the comment statement.
Answer:

• In Python, comments begin with hash symbol (#).
• The lines that begins with # are considered as comments and ignored by the Python interpreter.
• Comments may be single line or no multilines.
• The multiline comments should be enclosed within a set of # as given below.
  # It is Single line Comment
  # It is multiline comment which contains more than one line #

Question 5.
What are the key features of python?
Answer:
Key features of Python:
It is a general-purpose programming language which can be used for both scientific and non – scientific programming
It is a platform-independent programming language.
The programs written in Python are easily readable and understandable

Question 6.
What are the uses of the logical operators? Name the operators.
Answer:

• In python, Logical operators are used to performing logical operations on the given relational expressions.
• There are three logical operators they are and or not.
• 

III. Answer the following questions (5 Marks)

Question 1.
Explain data types in python?
Answer:
Python Data types:
All data values in Python are objects and each object or value has a type. Python has Built-in or Fundamental data types such as Numbers, String, Boolean, tuples, lists, and dictionaries.

Number Data type:
The built-in number objects in Python supports integers, floating-point numbers, and complex numbers.
Integer Data can be decimal, octal, or hexadecimal. Octal integers use O (both upper and lower case) to denote octal digits and hexadecimal integers use OX (both upper and lower case) and L (only upper case) to denote long integers.
Example:
102, 4567, 567 # Decimal integers
0102, o876, 0432 # Octal integers
0X102, oX876, 0X432 # Hexadecimal integers
34L, 523L # Long decimal integers
A floating-point data is represented by a sequence of decimal digits that includes a decimal point. An Exponent data contains decimal digit part, decimal point, exponent part followed by one or more digits.
Example :
123.34, 456.23, 156.23 # Floating point data
12.E04, 24.e04 # Exponent data
A complex number is made up of two floating-point values, one each for the real and imaginary parts.

Boolean Data type:
A Boolean data can have any of the two values: True or False.

Example:
Bool_varl = True
Bool_var2 = False

String Data type:
String data can be enclosed with a single quote or double quote or triple quote.

Example:
Char_data = ‘A’
String_data = “Computer Science”
Multiline_data= “““String data can be enclosed with single quote or double quote or triple quote.”””

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Computer Science Guide Pdf Chapter 4 Algorithmic Strategies Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Computer Science Solutions Chapter 4 Algorithmic Strategies

12th Computer Science Guide Algorithmic Strategies Text Book Questions and Answers

I. Choose the best answer (1 Mark)

Question 1.
The word comes from the name of a Persian mathematician Abu Ja’far Mohammed ibn-i Musa al Khwarizmi is called?
a) Flowchart
b) Flow
c) Algorithm
d) Syntax
Answer:
c) Algorithm

Question 2.
From the following sorting algorithms which algorithm needs the minimum number of swaps?
a) Bubble sort
b) Quick sort
c) Merge sort
d) Selection sort
Answer:
d) Selection sort

Question 3.
Two main measures for the efficiency of an algorithm are
a) Processor and memory
b) Complexity and capacity
c) Time and space
d) Data and space
Answer:
c) Time and space

Question 4.
The complexity of linear search algorithm is
a) O(n)
b) O(log n)
c) O(n2)
d) O(n log n)
Answer:
a) O(n)

Question 5.
From the following sorting algorithms which has the lowest worst-case complexity?
a) Bubble sort
b) Quick sort
c) Merge sort
d) Selection sort
Answer:
c) Merge sort

Question 6.
Which of the following is not a stable sorting algorithm?
a) Insertion sort
b) Selection sort
c) Bubble sort
d) Merge sort
Answer:
b) Selection sort

Question 7.
Time Complexity of bubble sort in best case is
a) θ (n)
b) θ (nlogn)
c) θ (n2)
d) θ n(logn)2)
Answer:
a) θ (n)

Question 8.
The Θ notation in asymptotic evaluation represents
a) Base case
b) Average case
c) Worst case
d) NULL case
Answer:
b) Average case

Question 9.
If a problem can be broken into sub problems which are reused several times, the problem possesses which property?
a) Overlapping sub problems
b) Optimal substructure
c) Memoization
d) Greedy
Answer:
a) Overlapping sub problems

Question 10.
In dynamic programming, the technique of storing the previously calculated values is called ?
a) Saving value property
b) Storing value property
c) Memoization
d) Mapping
Answer:
c) Memoization

II. Answer the following questions (2 Marks)

Question 1.
What is an Algorithm?
Answer:
An algorithm is a finite set of instructions to accomplish a particular task. It is a step-by-step procedure for solving a given problem. An algorithm can be implemented in any suitable programming language.

Question 2.
Define Pseudocode
Answer:

• Pseudocode is a notation similar to programming languages.
• Pseudocode is a mix of programming-language-like constructs and plain English.

Question 3.
Who is an Algorist?
Answer:
A person skilled in the design of algorithms is called Agorist.

Question 4.
What is Sorting?
Answer:
Sorting is a method of arranging a group of items in ascending or descending order. Various sorting techniques in algorithms are Bubble Sort, Quick Sort, Heap Sort, Selection Sort, Insertion Sort.

Question 5.
What is searching? Write its types.
Answer:

1. Searching is a process of finding a particular element present in given set of elements.
2. Some of the searching types are:

Linear Search
Binary Search.

III. Answer the following questions (3 Marks)

Question 1.
List the characteristics of an algorithm
Answer:
Input, Output, Finiteness, Definiteness, Effectiveness, Correctness, Simplicity, Unambiguous, Feasibility, Portable and Independent.

Question 2.
Discuss Algorithmic complexity and its types
Answer:

• The complexity of an algorithm f (n) gives the running time and/or the storage space required by the algorithm in terms of n as the size of input data.
• Time Complexity: The Time complexity of an algorithm is given by the number of steps taken by the algorithm to complete the process.
• Space Complexity: Space complexity of an algorithm is the amount of memory required to run to its completion.

The space required by an algorithm is equal to the sum of the following two components:

• A fixed part is defined as the total space required to store certain data and variables for an algorithm.
• Example: simple variables and constants used in an algorithm.
• A variable part is defined as the total space required by variables, which sizes depends on the problem and its iteration.
• Example: recursion used to calculate factorial of a given value n.

Question 3.
What are the factors that influence time and space complexity?
Answer:
Time Complexity:
The Time complexity of an algorithm is given by the number of steps taken by the algorithm to complete the process.

Space Complexity:
Space complexity of an algorithm is the amount of memory required to run to its completion. The space required by an algorithm is equal to the sum of the following two components:

A fixed part is defined as the total space required to store certain data and variables for an algorithm. For example, simple variables and constants used in an algorithm. A variable part is defined as the total space required by variables, which sizes depends on the problem and its iteration. For example, recursion used to calculate the factorial of a given value n.

Question 4.
Write a note on Asymptotic notation
Answer:

• Asymptotic Notations are languages that use meaningful statements about time and space complexity.
• The following three asymptotic notations are mostly used to represent time complexity of algorithms:

Big O:
Big O is often used to describe the worst -case of an algorithm.

Big Ω:

• Big O mega is the reverse Big O if Bi O is used to describe the upper bound (worst – case) of an asymptotic function,
• Big O mega is used to describe the lower bound (best-case).

Big Θ:
When an algorithm has complexity with lower bound = upper bound, say that an algorithm has a complexity 0 (n log n) and Ω (n log n), it actually has the complexity Θ (n log n), which means the running time of that algorithm always falls in n log n in the best-case and worst-case.

Question 5.
What do you understand by Dynamic programming?
Answer:
Dynamic programming is an algorithmic design method that can be used when the solution to a problem can be viewed as the result of a sequence of decisions. The dynamic programming approach is similar to divide and conquer. The given problem is divided into smaller and yet smaller possible subproblems.

IV. Answer the following questions (5 Marks)

Question 1.
Explain the characteristics of an algorithm.
Answer:

Question 2.
Discuss Linear search algorithm
Answer:

• Linear search also called sequential search is a sequential method for finding a particular value in a list.
• This method checks the search element with each element in sequence until the desired element is found or the list is exhausted. In this searching algorithm, list need not be ordered.

Pseudocode:

• Traverse the array using for loop
• In every iteration, compare the target search key value with the current value of the list.
• If the values match, display the current index and value of the array.
• If the values do not match, move on to the next array element.
• If no match is found, display the search element not found.

Example:

• To search the number 25 in the array given below, a linear search will go step by step in a sequential order starting from the first element in the given array if the search element is found that index is returned otherwise the search is continued till the last index of the array.
• In this example number 25 is found at index number 3.

Question 3.
What is Binary search? Discuss with example
Answer:
Binary Search:

• Binary search also called a half-interval search algorithm.
• It finds the position of a search element within a sorted array.
• The binary search algorithm can be done as a dividend- and -conquer search algorithm and executes in logarithmic time.

Example:

• List of elements in an array must be sorted first for Binary search. The following example describes the step by step operation of binary search.
• Consider the following array of elements, the array is being sorted so it enables to do the binary search algorithm.
  Let us assume that the search element is 60 and we need to search the location or index of search element 60 using binary search.

• First ‘we find index of middle element of the array by using this formula:
  mid = low + (high – low)/2
• Here it is, 0+(9 – 0)/2 = 4 (fractional part ignored)v So, 4 is the mid value of the array.

• Now compare the search element with the value stored at mid-value location 4. The value stored at location or index 4 is 50, which is not match with search element. As the search value 60 is greater than 50.

• Now we change our low to mid + land find the new mid-value again using the formula.
  low to mid + 1
  mid = low + (high -low) / 2
• Our new mid is 7 now. We compare the value stored at location 7 with our target value 31.

• The value stored at location or index 7 is not a match with search element, rather it is more than what we are looking for. So, the search element must be in the lower part from the current mid-value location

• The search element still not found. Hence, we calculated the mid again by using the formula.
  high = mid – 1
  mid = low + (high – low)/2
  Now the mid-value is 5.

• Now we compare the value stored at location 5 with our search element. We found that it is a match.

• We can conclude that the search element 60 is found at the location or index 5.
• For example, if we take the search element as 95, For this value this binary search algorithm returns the unsuccessful result.

Question 4.
Explain the Bubble sort algorithm with example
Answer:
Bubble sort:

• Bubble sort algorithm simple sorting algorithm.
• The algorithm starts at the beginning of the I list of values stored in an array.
• It compares each pair of adjacent elements and swaps them if they are in the unsorted order.
• This comparison and passed to be continued until no swaps are needed, which indicates that the list of values stored in an array is sorted.
• The algorithm is a comparison sort, is named for the way smaller elements “bubble” to the top of the list.
• Although the algorithm is simple, it is too slow and less efficient when compared to insertion sort and other sorting methods.
• Assume list is an array of n elements. The swap function swaps the values of the given array elements.

Pseudocode:

• Start with the first element i.e., index = 0, compare the current element with the next element of the array.
• If the current element is greater than the next element of the array, swap them.
  If the current element is less than the next or right side of the element, move to the next element. Go to Step 1 and repeat until the end of the index is reached.

Let’s consider an array with values {15, 11, 16, 12, 14, 13} Below, we have a pictorial representation of how bubble sort will sort the given array.

The above pictorial example is for iteration-d. Similarly, remaining iteration can be done. The final iteration will give the sorted array. At the end of all the iterations we will get the sorted values in an array as given below:

Question 5.
Explain the concept of dynamic programming with a suitable example.
Answer:
Dynamic programming:
Dynamic programming is an algorithmic design method that can be used when the solution to a problem can be viewed as the result of a sequence of decisions. The dynamic programming approach is similar to divide and conquer. The given problem is divided into smaller and yet smaller possible subproblems.

Dynamic programming is used whenever problems can be divided into similar sub-problems so that their results can be re-used to complete the process. Dynamic programming approaches are used to find the solution in an optimized way. For every inner subproblem, the dynamic algorithm will try to check the results of the previously solved sub-problems. The solutions of overlapped subproblems are combined in order to get a better solution.

Steps to do Dynamic programming:

1. The given problem will be divided into smaller overlapping sub-problems.
2. An optimum solution for the given problem can be achieved by using the result of a smaller sub-problem.
3. Dynamic algorithms use Memoization.

Fibonacci Series – An example:
Fibonacci series generates the subsequent number by adding two previous numbers. Fibonacci series starts from two numbers – Fib 0 & Fib 1. The initial values of fib 0 & fib 1 can be taken as 0 and 1.
Fibonacci series satisfies the following conditions:
Fibn = Fib_n-1 + Fib_n-2
Hence, a Fibonacci series for the n value 8 can look like this
Fib₈ = 0 1 1 2 3 5 8 13

Fibonacci Iterative Algorithm with Dynamic programming approach:
The following example shows a simple Dynamic programming approach for the generation of the Fibonacci series.
Initialize f0 = 0, f1 = 1
step – 1: Print the initial values of Fibonacci f0 and f1
step – 2: Calculate fibanocci fib ← f0 + f1
step – 3: Assign f0 ← f1, f1 ← fib
step – 4: Print the next consecutive value of Fibonacci fib
step – 5: Go to step – 2 and repeat until the specified number of terms generated
For example, if we generate Fibonacci series up to 10 digits, the algorithm will generate the series as shown below:
The Fibonacci series is: 0 1 1 2 3 5 8 1 3 2 1 3 4 5 5

12th Computer Science Guide Algorithmic Strategies Additional Questions and Answers

Choose the best answer: (1 Marks)

Question 1.
Which one of the following is not a data structure?
(a) Array
(b) Structures
(c) List, tuples
(d) Database
Answer:
(d) Database

Question 2.
Linear search is also called
a) Quick search
b) Sequential search
c) Binary search
d) Selection search
Answer:
b) Sequential search

Question 3.
Which is a wrong fact about the algorithm?
(a) It should be feasible
(b) Easy to implement
(c) It should be independent of any programming languages
(d) It should be generic
Answer:
(c) It should be independent of any programming languages

Question 4.
Which search algorithm can be done as divide and- conquer search algorithm?
a) linear
b) Binary search
c) Sequential
d) Bubble
Answer:
b ) Binary search

Question 5.
Which of the following sorting algorithm is too slow and less efficient?
a) Selection
b) Bubble
c) Quick
d) Merge
Answer:
b) Bubble

Question 6.
Which of the following programming is used whenever problems can be divided into similar sub-problems?
a) Object-oriented
b) Dynamic
c) Modular
d) Procedural
Answer:
b) Dynamic

Question 7.
Which of the following is the reverse of Big O?
a) Big μμ
b) Big Ω
c) Big symbol
d) Big ΩΩ
Answer:
b) Big Ω

Question 8.
How many different phases are there in the analysis of algorithms and performance evaluations?
(a) 1
(b) 2
(c) 3
(d) Many
Answer:
(b) 2

Question 9.
Which of the following is a finite set of instructions to accomplish a particular task?
a) Flowchart
b) Algorithm
c) Functions
d) Abstraction
Answer:
b) Algorithm

Question 10.
The way of defining an algorithm is called
a) Pseudo strategy
b) Programmatic strategy
c) Data structured strategy
d) Algorithmic strategy
Answer:
d) Algorithmic strategy

Question 11.
Time is measured by counting the number of key operations like comparisons in the sorting algorithm. This is called as ……………………………
(a) Space Factor
(b) Key Factor
(c) Priori Factor
(d) Time Factor
Answer:
(d) Time Factor

Question 12.
Efficiency of an algorithm decided by
a) Definiteness, portability
b) Time, Space
c) Priori, Postriori
d) Input/output
Answer:
b) Time, Space

Question 13.
Which of the following should be written for the selected programming language with specific syntax?
a) Algorithm
b) Pseudocode
c) Program
d) Process
Answer: c) Program

Question 14.
How many components required to find the space required by an algorithm?
a) 4
b) 3
c) 2
d) 6
Answer:
c) 2

Question 15.
Which of the following component is defined as the total space required to store certain data and variables for an algorithm?
a) Time part
b) Variable part
c) Memory part
d) Fixed part
Answer:
d) Fixed part

Question 16.
Which is true related to the efficiency of an algorithm?
(I) Less time, more storage space
(II) More time, very little space
(a) I is correct
(b) II is correct
(c) Both are correct
(d) Both are wrong
Answer:
(c) Both are correct

Question 17.
Time and Space complexity could be considered for an
a) Algorithmic strategy
b) Algorithmic analysis
c) Algorithmic efficiency
d) Algorithmic solution
Answer:
c) Algorithmic efficiency

Question 18.
Which one of the following is not an Asymptotic notation?
(a) Big
(b) Big \(\Theta\)
(c) Big Ω
(d) Big ⊗
Answer:
(d) Big ⊗

Question 19.
How many asymptotic notations are mostly used to represent time complexity of algorithms?
a) Two
b) Three
c) One
d) Many
Answer:
b) Three

II. Answer the following questions (2 and 3 Marks)

Question 1.
Define fixed part in the space complexity?
Answer:
A fixed part is defined as the total space required to store certain data and variables for an algorithm. For example, simple variables and constants used in an algorithm.

Question 2.
Write a pseudo code for linear search
Answer:

• Traverse the array using ‘for loop’
• In every iteration, compare the target search key value with the current value of the list.
• If the values match, display the current index and value of the array
• If the values do not match, move on to the next array element
• If no match is found, display the search element not found.

Question 3.
Design an algorithm to find the square of the given number and display the result?
Answer:
Problem: Design an algorithm to find the square of the given number and display the result. The algorithm can be written as:

• Step 1 – start the process
• Step 2 – get the input x
• Step 3 – calculate the square by multiplying the input value ie., square ← x* x
• Step 4 – display the resulting square
• Step 5 – stop

The algorithm could be designed to get a solution of a given problem. A problem can be solved in many ways. Among many algorithms, the optimistic one can be taken for implementation.

Question 4.
Write a pseudo code for bubble sort
Answer:

• Start with the first element i.e., index = 0, compare the current element with the next element of the array.
• If the current element is greater than the next element of the array, swap them.
• If the current element is less than the next or right side of the element, move to the next element.
• Go to Step 1 and repeat until end of the index is reached.

Question 5.
Write a pseudo code for selection sort.
Answer:

• Start from the first element i.e., index= 0, we search the smallest element in the array, and replace it with the element in the first position.
• Now we move on to the second element position, and look for smallest element present in the sub-array, from starting index to till the last index of sub-array.
• Now replace the second smallest identified in step-2 at the second position in the or original array, or also called first position in the sub-array.

Question 6.
Write a note on Big omega asymptotic notation
Answer:

• Big Omega is the reverse Big 0, if Big 0 is used to describe the upper bound (worst – case) of a asymptotic function,
• Big Omega is used to describe the lower bound (best-case).

Question 7.
Name the factors where the program execution time depends on?
The program execution time depends on:

1. Speed of the machine
2. Compiler and other system Software tools
3. Operating System
4. Programming language used
5. The volume of data required

Question 8.
Write a note on memoization.
Answer:
Memoization or memoisation is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again.

Question 9.
Give examples of data structures.
Answer:
Examples for data structures are arrays, structures, list, tuples, dictionary.

Question 10.
Define- Algorithmic Strategy?
Answer:
The way of defining an algorithm is called Algorithmic Strategy.

Question 11.
Define algorithmic solution?
Answer:
An algorithm that yields expected output for a valid input is called an algorithmic solution

Question 12.
Define- Algorithm Analysis?
Answer:
An estimation of the time and space complexities of an algorithm for varying input sizes is called Algorithm Analysis.

Question 13.
What are the different phases in the analysis of algorithms and performance?
Answer:
Analysis of algorithms and performance evaluation can be divided into two different phases:
A Priori estimates: This is a theoretical performance analysis of an algorithm. Efficiency of an algorithm is measured by assuming the external factors.
Posteriori testing: This is called performance measurement. In this analysis, actual statistics like running time and required for the algorithm executions are collected.

Question 14.
Define the Best algorithm?
Answer:
The best algorithm to solve a given problem is one that requires less space in memory and takes less time to execute its instructions to generate output.

Question 15.
Write a note Asymptotic Notations?
Answer:
Asymptotic Notations are languages that uses meaningful statements about time and space complexity.

III. Answer the following questions (5 Marks)

Question 1.
Differentiate Algorithm and program
Answer:

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 5 Numerical Methods Ex 5.3 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 5 Numerical Methods Ex 5.3

Choose the most suitable answer from the given four alternatives:

Question 1.
Δ²y₀ =
(a) y₂ – 2y₁ + y₀
(b) y₂ + 2y₁ – y₀
(c) y₂ + 2y₁ + y₀
(d) y₂ + y₁ + 2y₀
Solution:
(a) y₂ – 2y₁ + y₀
Hint:
Δ²y₀ = (E – 1)²y₀
= (E² – 2E + 1) y₀
= E²y₀ – 2Ey₀ + y₀
= y₂ – 2y₁ + y₀

Question 2.
Δf(x) =
(a) f (x + h)
(b) f (x) – f (x + h)
(c) f (x + h) – f(x)
(d) f(x) – f (x – h)
Solution:
(c) f (x + h) – f(x)
Hint:
Δf(x) = f (x + h) – f(x)

Question 3.
E≡
(a) 1 + Δ
(b) 1 – Δ
(c) 1 + ∇
(d) 1 – ∇
Solution:
(a) 1 + Δ

Question 4.
If h = 1, then Δ(x²) =
(a) 2x
(b) 2x – 1
(c) 2x + 1
(d) 1
Solution:
(c) 2x + 1
Hint:
Δ(x²) = (x + h)² – (x)²
= x² + 2xh + h² – x²
Δ(x²) = 2xh + h²
If h = 1 Δ (x²) = 2x + 1

Question 5.
If c is a constant then Δc =
(a) c
(b) Δ
(c) Δ²
(d) 0
Solution:
(d) 0

Question 6.
If m and n are positive integers then Δ^m Δⁿ f(x)=
(a) Δ^m+n f(x)
(b) Δ^m f(x)
(c) Δⁿ f(x)
(d) Δ^m-n f(x)
Solution:
(a) Δ^m+n f(x)

Question 7.
If ‘n’ is a positive integer Δⁿ[Δ^-n f(x)]
(a) f(2x)
(b) f(x + h)
(c) f(x)
(d) Δf(x)
Solution:
(c) f(x)
Hint:
Δⁿ [Δ^-n f(x)] = Δ^n-n f(x) = Δ⁰ f(x)
= f(x)

Question 8.
E f(x) =
(a) f(x – h)
(b) f(x)
(c) f(x + h)
(d) f(x + 2h)
Solution:
(c) f (x + h)

Question 9.
∇≡
(a) 1 + E
(b) 1 – E
(c) 1 – E^-1
(d) 1 + E^-1
Solution:
(c) 1 – E^-1

Question 10.
∇ f(a) =
(a) f(a) + f(a – h)
(b) f(a) – f(a + h)
(c) f(a) – f(a – h)
(d) f(a)
Solution:
(c) f(a) – f(a- h)

Question 11.
For the given points (x₀, y₀) and (x₁, y₁) the Lagrange’s formula is
(a) y(x) = \(\frac { x-x_1 }{x_0-x_1}\) y₀ + \(\frac { x-x_0 }{x_1-x_0}\) y₁
(b) y(x) = \(\frac { x_1-x}{x_0-x_1}\) y₀ + \(\frac { x-x_0 }{x_1-x_0}\) y₁
(c) y(x) = \(\frac { x-x_1 }{x_0-x_1}\) y₀ + \(\frac { x-x_0 }{x_1-x_0}\) y₀
(d) y(x) = \(\frac { x_1-x }{x_0-x_1}\) y₀ + \(\frac { x-x_0 }{x_1-x_0}\) y₀
Solution:
(a) y(x) = \(\frac { x-x_1 }{x_0-x_1}\) y₀ + \(\frac { x-x_0 }{x_1-x_0}\) y₁

Question 12.
Lagrange’s interpolation formula can be used for
(a) equal intervals only
(b) unequal intervals only
(c) both equal and unequal intervals
(d) none of these.
Solution:
(c) both equal and unequal intervals.

Question 13.
If f(x) = x² + 2x + 2 and the interval of differencing is unity then Δf(x)
(a) 2x – 3
(b) 2x + 3
(c) x + 3
(d) x – 3
Solution:
(b) 2x + 3
Hint:
Given:
f(x) = x² + 2x + 2
Δf(x) = f (x + h) – f (x)
since h = 1
Δf(x) = f (x – 1) – f (x)
= [(x + 1)² + 2(x + 1) + 2] – [x² + 2x + 2]
= [x² + 2x + 1 + 2x + 2 + 2] – [x² + 2x + 2]
= x² + 4x + 5 – x² – 2x – 2
= 2x + 3

Question 14.
For the given data find the value of Δ³y₀ is

(a) 1
(b) 0
(c) 2
(d) -1
Solution:
(b) 0
Hint:
From this data
y₀ = 12; y₁ = 13; y₂ = 15; y₃ = 18
Δ³y₀ = (E – 1)³ y₀
= (E³ – 3E² + 3E – 1) y₀
= E³y₀ – 3E²y₀ + 3Ey₀ – y₀
= y₃ – 3y₂ + 3y₁ – y₀
= 18 – 3 (15) + 3 (13) – 12
= 18 – 45 + 39 – 12
= 57 – 57 = 0

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 5 Numerical Methods Ex 5.2 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 5 Numerical Methods Ex 5.2

Question 1.
Using graphic method, find the value of y when x = 48 from the following data:

Solution:

The value of y when x = 48 is 6.8

Question 2.
The following data relates to indirect labour expenses and the level of output

Estimate the expenses at a level of output of 350 units, by using graphic method.
Solution:

Question 3.
Using Newton’s forward interpolation formula find the cubic polynomial.

Solution:
Since we use the Newton’s forward interpolation formula.
y_{(x= x0+nh)} = y₀ + \(\frac { n }{1!}\) Δy₀ + \(\frac { n(n-1) }{2!}\) Δ²y₀ + \(\frac { n(n-1)(n-2) }{3!}\) Δ³y₀ + ………
To find y at x
∴ x₀ + nh = x
0 + n(1) = x
∴ n = x

= 1 + x + (x² – x) (-1) + 2x (x² – 3x + 2)
y = 1 + x – x² + x + 2x³ – 6x² + 4x
y = 2x³ – 7x² + 6x + 1
∴ f(x) = 2x³ – 7x² + 6x + 1

Question 4.
The population of a city in a censes taken once in 10 years is given below. Estimate the population in the year 1955.

Solution:
Let the year be x and population be y. To find the population for the year 1955.
(ie) The value of y at x = 1955
Since the value of y is required near the beginning of the table, we use the Newton’s forward interpolation formula.
y_{(x= x0+nh)} = y₀ + \(\frac { n }{1!}\) Δy₀ + \(\frac { n(n-1) }{2!}\) Δ²y₀ + \(\frac { n(n-1)(n-2) }{3!}\) Δ³y₀ + ………
To find y at x = 1955
∴ x₀ + nh = 1955; x₀ = 1951, h = 10
⇒ 1951 + n(10) = 1955
10n = 1955 – 1951 ⇒ 10n = 4
n = \(\frac { 4 }{10}\) = 0.4

y = 35 + 2.8 – 1.08 + 0.064
= 37.864 – 1.08
y = 36.784
∴ Population in the year 1955 is 36.784 (lakhs)

Question 5.
In an examination the number of candidates who secured marks between certain interval were as follows:

Estimate the number of candidates whose marks are lessthan 70.
Solution:
Since the required mark is at the end of the table, we apply Backward interpolation formula. Let the marks be x and No. of candidates be y.

To find y at x = 70
x = x₀ + nh ⇒ 70 = 100 + n(20)
70 – 100 = 20n
20n = -30 ⇒ n = \(\frac { -30 }{20}\)
n = -1.5

= 235 – 25.5 – 12.375 – 1.125
= 235 – 39
= 196
∴ 196 candidates secured less than 70 marks

Question 6.
Find the value of f(x) when x = 32 from the following table

Solution:
Since the value of f(x) is required near the beginning of the table, we use the Newton’s forward interpolation formula.
y_{(x= x0+nh)} = y₀ + \(\frac { n }{1!}\) Δy₀ + \(\frac { n(n-1) }{2!}\) Δ²y₀ + \(\frac { n(n-1)(n-2) }{3!}\) Δ³y₀ + ………
To find y at x = 32
∴ x₀ + nh = 32;
30 + n(5) = 32
5n = 32 – 30 ⇒ 5n = 2
n = \(\frac { 2 }{5}\)
∴ n = 0.4

= 15.9 – 0.4 – 0.024 – 0.0128 – 0.00832
15.9 – 0.44512 = 15.45488
= 15.45
∴ when x = 32, f(x) = 15.45

Question 7.
The following data gives the melting point of a alloy of lead and zinc where ‘t’ is the temperature in degree c and p is the percentage of lead in the alloy

Find the melting point of the alloy containing 84 percent lead.
Solution:
Since the required value is at the end of the table, apply backward interpolation formula. To find T at p = 84
T_{(p= p0+nh)} = T_n + \(\frac { n }{1!}\) ∇T_n + \(\frac { n(n+1) }{2!}\) ∇²T₀ + \(\frac { n(n+1)(n+2) }{3!}\) Δ³T₀ + ………
To find T at P = 84
P_n + nh = 84
90 + n(10) = 84
10n = 84 – 90
10n = -6 ⇒ n = \(\frac { -6 }{10}\)
n = -0.6

= 304 – 16.8 – 0.24 – 0.091392
= 304 – 17.131392
= 286.86
Hence the melting point of the alloy is 286.86° c.

Question 8.
Find f(2.8) from the following

Solution:
Since the required value is at the end of the table, apply backward interpolation formula.

To find y at x = 2.8
∴ x₀ + nh = 2.8
∴ 3 + n(1) = 2.8
n = 2.8 – 3
n = -0.2

= 34 – 4.6 – 1.12 – 0.288
= 34 – 6.008
= 27.992
∴ f(2.8) = 27.992

Question 9.
Using interpolation estimate the output of a factory in 1986 from the following data

Solution:
Here the intervals are unequal. By Lagrange’s in-terpolation formula we have,
x₀ = 1974, x₁ = 1978, x₂ = 1982, x₃ = 1990
y₀ = 25, y₁ = 60, y₂ = 80, y₃ = 170, and x = 1986.

∴ output in 1986 is 108.75 (thousand tones)

Question 10.
Use lagrange’s formula and estimate from the following data the number of workers getting income not exceeding Rs. 26 per month.

Solution:
Here the intervals are unequal. By Lagrange’s In-terpolation formula we have,
x₀ = 15, x₁ = 25, x₂ = 30, x₃ = 35
y₀ = 36, y₁ = 40, y₂ = 45, y₃ = 48 and x = 26.

∴ Required No.of workers = 42 Persons (approximately)

Question 11.
Using interpolation estimate the business done in 1985 from the following data

Solution:
Here the intervals are unequal. By Lagrange’s formula we have,
x₀ = 1982, x₁ = 1983, x₂ = 1984, x₃ = 1986
y₀ = 150, y₁ = 235, y₂ = 365, y₃ = 525 and x = 1985.

∴ Business done in the year 1985 is 481.25 lakhs.

Question 12.
Using interpolation, find the value of f(x) when x = 15

Solution:
Here the intervals are unequal, By Lagrange’s in-terpolation formula we have,
x₀ = 3, x₁ = 7, x₂ = 11, x₃ = 19
y₀ = 42, y₁ = 43, y₂ = 47, y₃ = 60 and x = 15.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 5 Numerical Methods Ex 5.1 Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 5 Numerical Methods Ex 5.1

Question 1.
Evaluate Δ (log ax).
Solution:
Δ log (ax) = log (ax + h) – log ax
= log [ \(\frac { ax+h }{ax}\) ] = log[\(\frac { ax }{ax}\) + \(\frac { h }{ax}\)]
= log [1 + \(\frac { h }{ax}\)]

Question 2.
If y = x³ – x² + x -1 calculate the values of y for x= 0, 1, 2, 3, 4, 5 and form the forward differences table.
Solution:
Given y = x³ – x² + x – 1
when x = 0 y = -1
when x = 1
y = 1 – 1 + 1 – 1 = 0
when x = 2
y = 8 – 4 + 2 – 1 = 5
for x = 0, 1, 2, 3, 4, 5
when x = 3
y = 27 – 9 + 3 – 1 = 20
when x = 4
y = 64 – 16 + 4 – 1 = 51
when x = 5
y = 125 – 25 + 5 – 1 = 104

Question 3.
If h = 1 then prove that (E^-1 Δ)x³ = 3x² – 3x + 1
Solution:
h = 1 To prove (E^-1 ∆) x3 = 3×2 – 3x + 1
L.H.S = (E^-1 ∆) x³ = E^-1 (∆x³)
= E^-1[(x + h)³ – x³]
= E^-1( x + h)³ – E^-1(x³)
= (x – h + h)³ – (x – h)³
= x³ – (x – h)³
But given h = 1
So(E^-1 ∆) x³ = x³ – (x – 1)³
= x³ – [x³ – 3x² + 3x – 1]
= 3x² – 3x + 1
= RHS

Question 4.
If f(x) = x² + 3x than show that Δf(x) = 2x + 4
Solution:
Given f(x) = x³ + 3x; h = 1
Δf(x) = f (x + h) – f(x)
= (x + 1)² + 3 (x + 1) – (x² + 3x)
= x² + 2x + 1 + 3x + 3 – x² + 3x
= 2x + 4
∴ Δf(x) = 2x + 4

Question 5.
Evaluate Δ [ \(\frac { 1 }{(x+1)+(x+2)}\) ] by taking ‘1’ as the interval of differencing
Solution:

Question 6.
Find the missing entry in the following table

Solution:
Since only four values of f(x) are given the polynomial which fits the data is of degree three. Hence fourth differences are zeros.
(ie) Δ⁴ y₀ = 0
(E – 1)⁴ y₀ = 0
(E⁴ – 4E³ + 6E² – 4E + 1) y₀ = 0
E⁴y₀ – 4E³ y₀ + 6E²y₀ – 4E y₀ + 1y₀ = 0
y₄ – 4y₃ + 6y₂ – 4y₁+ y₀ = o
81 – 4y₃ + 6(9) – 4(3) + 1 = 0
81 – 4y₃ + 54 – 12 + 1 = 0
136 – 12 – 4y₃ = 0
4y₃ = 124
y₃ = \(\frac { 124 }{4}\)
∴ y₃ = 31

Question 7.
Following are the population of a district

Find the population of the year 1911
Solution:
Since only five values of fix) are given, the polynomial which fits the data is of degree four. Hence fifth differences are zeros.
(ie) Δ⁵ y₀ = 0
(E – 1)⁵ y₀ = 0
(E⁵ – 5E⁴ + 10E³ – 10E² + 5E – 1) y₀ = 0
E⁵y₀ – 5E⁴y₀ + 10E³y₀ – 10E²y₀ + 5E y₀ – y₀ = 0
y₅ – 5y₄ + 10y₃ – 10y₂ + 5y₁ – y₀ = 0
501 – 5 (467) + 10(y₃) -10 (421) + 5 (391) – 363 = 0
2456 – 6908 + 10y₃ = 0
-4452 + 10y₃ = 0 ⇒ 10y₃ = 4452
y = \(\frac { 4452 }{10}\) = 445.2
The population of the year 1911 is 445.2 thousands

Question 8.
Find the missing entries from the following.

Solution:
Since four values of f(x) are given we assume the polynomial of degree three. Hence fourth order differences are zeros.
(ie) Δ⁴y₀ = 0 (ie) (E – 1)⁴ y_k = 0
(E⁴ – 4E³ + 6E² – 4E + 1) y_k = 0 ……… (1)
Put k = 0 in (1)
(E⁴ – 4E³ + 6E² – 4E + 1) y₀ = 0
E⁴y₀ – 4E³y₀ + 6E³y₀ – 4Ey₀ + y₀ = 0
y₄ – 4y₃ + 6y₂ – 4y₁ + y₀ = 0
y₄ – 4 (15) + 6(8) – 4y₁ + 0 = 0
y₄ – 4y₁ = 12 …….. (2)
Put k = 1 in eqn (1)
(E⁴ – 4E³ + 6E² – 4E + 1) y₁ = 0
y₅ – 4y₄ + 6y₃ – 4y₂ + y₁ = 0
35 – 4 (y₄) + 6(15) – 4(8) + y₁ = 0
35 – 4y₄ + 90 – 32 + y₁ = 0
-4y₄ + y₁ + 125 – 32 = 0
-4y₄ + y₁ = -93 ………. (3)
Solving eqn (2) & (3)

Substitute y = 3 in eqn (2)
y₄ – 4(3) = 12
y₄ – 12 = 12
y₄ = 12 + 12
∴ y₄ = 24
The required two missing entries are 3 and 24.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Computer Science Guide Pdf Chapter 3 Scoping Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Computer Science Solutions Chapter 3 Scoping

12th Computer Science Guide Scoping Text Book Questions and Answers

I. Choose the best answer (I Marks)

Question 1.
Which of the following refers to the visibility of variables in one part of a program to another part of the same program.
a) Scope
b) Memory
c) Address
d) Accessibility
Answer:
a) Scope

Question 2.
The process of binding a variable name with an object is called
a) Scope
b) Mapping
c) late binding
d) early binding
Answer:
b) Mapping

Question 3.
Which of the following is used in programming languages to map the variable and obj ect?
a) ::
b) :=
c) =
d) ==
Answer:
c) =

Question 4.
Containers for mapping names of variables to objects is called
a) Scope
b) Mapping
c) Binding
d) Name spaces
Answer:
d) Name spaces

Question 5.
Which scope refers to variables defined in current function?
a) Local Scope
b) Global scope
c) Module scope
d) Function Scope
Answer:
a) Local Scope

Question 6.
The process of subdividing a computer program into separate sub-programs is called
a) Procedural Programming
b) Modular programming
c) Event Driven Programming
d) Object oriented Programming
Answer:
b) Modular programming

Question 7.
Which of the following security technique that regulates who can use resources in a computing environment?
a) Password
b) Authentication ‘
c) Access control
d) Certification
Answer:
c) Access control

Question 8.
Which of the following members of a class can be handled only from within the class?
a) Public members
b) Protected members
c) Secured members
d) Private members
Answer:
d) Private members

Question 9.
Which members are accessible from outside the class?
a) Public members
b) Protected members
c) Secured members
d) Private members
Answer:
a) Public members

Question 10.
The members that are accessible from within the class and are also available to its sub classes is called
a) Public members
b) Protected members
c) Secured members
d) Private members
Answer:
b) Protected members

II. Answer the following questions (2 Marks)

Question 1.
What is a scope?
Answer:
Scope refers to the visibility of variables, parameters, and functions in one part of a program to another part of the same program.

Question 2.
Why scope should be used for variables. State the reason
Answer:

• Every variable defined in a program has global scope.
• Once defined, every part of your program can access that variable.
• But it is a good practice to limit a variable’s scope to a single definition.
• This way, changes inside the function can’t affect the variable on the outside of the function in unexpected ways.

Question 3.
What is Mapping?
Answer:
The process of binding a variable name with an object is called mapping. = (equal to sign) is used in programming languages to map the variable and object.

Question 4.
What do you mean by Namespaces?
Answer:
Names paces are containers for mapping names of variables to objects.

Question 5.
How Python represents the private and protected Access specifiers?
Answer:
Private members of a class are denied access from the outside of the class. They can be handled only within the class.
Protected members of a class are accessible from within the class and are also available to its sub-classes. No other process is permitted access to it.

III. Answer the following questions (3 Marks)

Define Local scope with an example.
Answer:
Local scope:

• Local scope refers to variables defined in the current function.
• Always, a function will first lookup for a variable name in its local scope.
• Only if it does not find it there, the outer scopes are checked.

Example:

• On execution of the above code, the variable a displays the value 7, because it is defined and available in the local scope.

Question 2.
Define Global scope with an example
Answer:
Global variable:

• A variable which is declared outside of all the functions in a program is known as Global variable.
• Global variable can be accessed inside or outside of all the functions in a program

Example:

• On execution of the above code the variable a which is defined inside the, function displays the value 7 for the function call Disp() and then it displays 10, because a is defined in global scope.

Question 3.
Define Enclosed scope with an example
Answer:
Enclosed Scope:

• A variable which is declared, inside a function which contains another function definition with in it, the inner function can also access the variable of the outer function. This scope is called enclosed scope.
• When a compiler or interpreter search for a variable in a program, it first searches Local, and then searches Enclosing scopes.

Example:

Question 4.
Why access control is required?
Answer:
Access control is a security technique that regulates who or what can view or use resources in a computing environment.
It is a fundamental concept in security that minimizes risk to the object. In other words, access control is a selective restriction of access to data.
In Object-oriented programming languages, it is implemented through access modifies.
Classical object-oriented languages, such as C++ and Java, control the access to class members by the public, private, and protected keywords.

Question 5.
Identify the scope of the variables in the following pseudo-code and write its output
color:= Red
mycolor():
b:=Blue
myfavcolor():
g:=Green
printcolor, b, g
myfavcolor()
printcolor, b
mycolor()
print color
Answer:
Scopes:
g – Local scope
b – Enclosed scope
color – Global scope
Output:
Red Blue Green
Red Blue
Red

IV. Answer the following questions (5 Marks)

Question 1.
Explain the types of scopes for variable or LEGB rule with example.
Answer:
Types of Scope:
There are four types of Scope namely
Local Scope, Global Scope, Enclosed Scope and Built-in Scope:
Local Scope:

• Local scope refers to variables defined in the current function.
• Always, a function will first lookup for a variable name in its local scope.
• Only if it does not find it there, the outer scopes are checked.

Example:

• On execution of the above code the variable a displays the value 7, because it is defined and available in the local scope.

Global Scope:

• A variable which is declared outside of all the functions in a program is known as a global variable.
• This means global variable can be accessed inside or outside of all the functions in a program.

Example:

• On execution of the above code the variable ‘a’ which is defined inside the function displays the value 7 for the function call Disp() and then it displays 10; because a is defined in global scope.
• Enclosed Scope:
• All programming languages permit functions to be nested. A function (method) with in another function is called nested function.
• A variable which is declared inside a function which contains another function definition with in it, the inner function can also access the variable of the outer function. This scope is called enclosed scope.
• When a compiler or interpreter search for a variable in a program, it first search Local, and then search Enclosing scopes.

Example:

• In the above example Displ() is defined with in Disp().
• The variable ‘a’ defined in Disp( ) can be even used by Displ( ) because it is also a member of Disp().

Built-in Scope:

• The built-in scope has all the names that are pre-loaded into the program scope when we start the compiler or interpreter.
• Any variable or module which is defined in the library functions of a programming
  language has a Built-in or module scope. They are loaded as soon as the library files are imported to the program.

LEGB rule:

• The LEGB rule is used to decide the order in which the scopes are to be searched for scope resolution.
• The scopes are listed below in terms of hierarchy (highest to lowest).

Scope also defines the order in which variables have to be mapped to the object in order to obtain the value.

Example:
1. x:= ‘outer x variable’
2. display ():
3. x:= ‘inner x variable’
4. print x
5. display()

• When the above statements have executed the statement (4) and (5) display the result as

Output:
outer x variable
inner x variable

• Above statements give different outputs because the same variable name ‘x’ resides in different scopes, one inside the function display() and the other in the upper level.
• The value ‘outer x variable’ is printed when x is referenced outside the function definition.
• Whereas when display() gets executed, ‘inner x variable’ is printed which is the x value inside the function definition.
• From the above example, we can guess that there is a rule followed, in order to decide from which scope a variable has to be picked.

Question 2.
Write any Five Characteristics of Modules
Answer:

• Modules contain instructions, processing logic, and data.
• Modules can be separately compiled and stored in a library.
• Modules can be included in a program.
• Module segments can be used by invoking a name and some parameters.
• Module segments can be used by other modules.

Question 3.
Write any five benefits of using modular programming.
Answer:

• Less code to be written.
• A single procedure can be developed for reuse, eliminating the need to retype the code many times.
• Programs can be designed more easily because a small team deals with only a small part of the entire code.
• Modular programming allows many programmers to collaborate on the same application.
• The code is stored across multiple files.
• Code is short, simple, and easy to understand.
• Errors can easily be identified, as they are localized to a subroutine or function.
• The same code can be used in many applications.
• The scoping of variables can easily be controlled.

12th Computer Science Guide Scoping Additional Questions and Answers

I. Choose the best answer (1 Mark)

Question 1.
Names paces are compared with ……………………….
(a) Programs
(b) Dictionaries
(c) Books
(d) Notebooks
Answer:
(b) Dictionaries

Question 2.
The scope of a ……………. is that part of the code where it is visible
a) Variable
b) Keyword
c) Function
d) Operator
Answer:
a) Variable

Question 3.
Find the value of a.
1. a: = 5
2. b: = a
3. a: = 3
(a) 0
(b) 3
(c) 5
(d) 2
Answer:
(b) 3

Question 4.
The inner function can access the variable of the outer function. This is called ………… scope.
a) Local
b) Enclosed
c) Function
d) Global
Answer:
b) Enclosed

Question 5.
The duration for which a variable is alive is called its ……………………………
(a) Scale
(b) Life time
(c) Static
(d) Function
Answer:
(b) Lifetime

Question 6.
InObjectOrientedProgrammingLanguageAccesscontrolisimplementedthrough ………….
a) Access modules
b) Access modifiers
c) Access variables
d) Keywords
Answer:
b) Access modifiers

Question 7.
………… is a selective restriction of access to data in a program?
a) Control variable
b) Access control
c) System authentication
d) Module
Answer:
b) Access control

Question 8.
How many types of variable scopes are there?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4

Question 9.
How many variables can be mapped to the same instance?
a) 2
b) 3
c) Multiple
d) 4
Answer:
c) Multiple

Question 10.
A variable which is declared outside of all the functions in a program is known as …………………………… variable.
(a) L
(b) E
(c) G
(d) B
Answer:
(c) G

Question 11.
Which of the following rule is used to decide the order in which the scopes are to be searched for scope resolution?
a) LGEB
b) LEGB
c) LBEG
d) LGBE
Answer:
b) LEGB

Question 12.
How many types of variable scope are there?
a) 2
b) 3
c) 4
d) 6
Answer:
c) 4

Question 13.
A variable which is declared outside all the functions in a program is known as
a) Local
b) Enclosed
c) Global
d) Extern
Answer:
c) Global

Question 14.
The scope of a nested function is …………………………… scope
(a) Local
(b) Global
(c) Enclosed
(d) Built-in
Answer:
(c) Enclosed

Question 15.
Which of the following programming enables programmers to divide up the work and retry pieces of the program independently?
a) Procedural Programming
b) Modular Programming
c) Object-Oriented Programming
d) Structural Programming
Answer:
b) Modular Programming

Question 16.
Which of the following contain instructions, processing logic, and data?
a) Scopes
b) Indentation
c) Modules
d) Access control
Answer:
c) Modules

Question 17.
Which of the following members of a class are denied access from outside the class?
a) Protected
b) Private
c) Public
d) Enclosed
Answer:
b) Private

Question 18.
Variables of built-in scopes are loaded as …………………………… files.
(a) Exe
(b) Linker
(c) Object
(d) Library
Answer:
(d) Library

Question 19.
By default the Python class members are
a) Private
b) Protected
c) Public
d) Global
Answer:
c) Public

Question 20.
By default the C++ and Java class members are
a) Protected
b) Private
c) Public
d) Local
Answer:
b) Private

Question 21.
…………….. are composed of one or more independently developed Modules
a)’Access control
b) Programs
c) Encapsulation
d) Members of a class
Answer:
b) Programs

Question 22.
Identify which is not a module?
(a) Algorithm
(b) Procedures
(c) Subroutines
(d) Functions
Answer:
(a) Algorithm

II. Answer the following questions (2 and 3 Marks)

Question 1.
Define variable.
Answer:
Variable are addresses (references, or pointers, to an object in memory.

Question 2.
Define lifetime?
Answer:
The duration for which a variable is alive is called its ‘lifetime’.

Question 3.
Define Modular programming.
Answer:
The process of subdividing a computer program into separate sub-programs is called modular programming.

Question 4.
Define: module
Answer:

• A module is a part of a program.
• Programs are composed of one or more independently developed modules

Question 5.
Define nested function.
Answer:
A function (method) within another function is called a nested function.

Question 6.
Write a note on module
Answer:

• A module is a part of a program.
• Programs are composed of one or more independently developed modules.
• A single module can contain one or several statements closely related to each other.
• Modules work perfectly on an individual level and can be integrated with other modules.
• A software program can be divided into modules to ease the job of programming and debugging as well.
• A program can be divided into small functional modules that work together to get the output.
• The process of subdividing a computer program into separate subprograms is called Modular programming.
• Modular programming enables programmers to divide up the work and debug pieces of the program independently.
• The examples of modules are procedures, subroutines, and functions.

Question 7.
Write a note on modules?
Answer:
A module is a part of a program. Programs are composed of one or more independently developed modules. A single module can contain one or several statements closely related to each other. Modules work perfectly on an individual level and can be integrated with other modules.

III. Answer the following questions (5 Marks)

Question 1.
Explain how Access Specifiers are activated in Python, C++, and Java:
Answer:

• Python prescribes a convention of prefixing the name of the variable/ method with a single or double underscore to emulate the behaviour of protected and private access specifiers.
• C++ and Java, control the access to class members by the public, private, and protected
  keywords.
• All members in a Python class are public by default whereas by default in C++ and java all members are private.
• Any member can be accessed from outside the class environment in Python which is not. possible in C++ and java.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Business Maths Guide Pdf Chapter 4 Differential Equations Miscellaneous Problems Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Miscellaneous Problems

Question 1.
Suppose that Qd = 30 – 5P + 2\(\frac { dp }{dt}\) + \(\frac { d^2p }{dt^2}\) and Qs = 6 + 3P Find the equilibrium price for market clearance.
Solution :
Qd = 30 – 5P + 2\(\frac { dp }{dt}\) + \(\frac { d^2p }{dt^2}\) and
Qs = 6 + 3P
For market clearance, the required condition is
Qd = Qs

The auxiliary equation is m2 + 2m – 8 = 0
(m + 4) (m – 2) = 0
m = -4, 2
Roots are real and different
C.F = Ae^m₁x + Be^m₂x
C.F = Ae^-4t + Be^2t

The general solution is y = C.F + P.I
y = Ae^-ut + Be^2t + 3

Question 2.
Form the differential equation having for its general solution y = ax² + bx
Solution:
y = ax² + bx ……….. (1)
Since we have two arbitary constants, differentiative twice.

Question 3.
Solve yx²dx + e^-x dy = 0
Solution:
yx²dx + e^-x dy = 0
e^-x dy = -yx²dx
\(\frac { 1 }{y}\) dy = -x² e^x dx
Integrating on both sides

Question 4.
Solve (x² + y²) dx + 2xy dy = 0
Solution:
(x² + y²) dx + 2xy dy = 0
2xy dy = – (x² + y²) dx
\(\frac { dy }{dx}\) = \(\frac { -(x^2+y^2) }{2xy}\) ………. (1)
This is a homogeneous differential equation

\(\frac { 1 }{3}\) log(3v² + 1) = – logx + logc
log (3v² + 1)^1/3 + log x = log c
logx (3v² + 1)^1/3 = log c
⇒ x (3v² + 1)^1/3 = c
⇒ x[\(\frac { 3y^2 }{x^2}\) + 1]^1/3 = c

Question 5.
Solve x \(\frac { dy }{dx}\) + 2y = x⁴
Solution:

This solution is
y(I.F) = ∫Qx (I.F) dx + c
y(x²) = ∫(x³ × x²) dx + c
yx² = ∫x⁵ dx + c
⇒ yx² = \(\frac { x^6 }{6}\) + c

Question 6.
A manufacturing company has found that the cost C of operating and maintaining the equipment is related to the length’m’ of intervals between overhauls by the equation m² \(\frac { dc }{dm}\) + 2mc = 2 and c = 4 and whem m = 2. Find the relationship between C and m.
Solution:
m² \(\frac { dc }{dm}\) + 2mc = 2
÷ each term by m²
\(\frac { dc }{dm}\) + \(\frac { 2mc }{m^2}\) = \(\frac { 2 }{m^2}\)
\(\frac { dc }{dm}\) + \(\frac { 2c }{m}\) = \(\frac { 2 }{m^2}\)
This is a first order linear differential equation of the form
\(\frac { dc }{dm}\) + Pc = Q where P = \(\frac { 2 }{m}\) and Q = \(\frac { 2 }{m^2}\)
∫Pdm = 2 ∫\(\frac { 1 }{m}\)dm = 2 log m = log m²
I.F = e^∫Pdm = e^logm² = m²
General solution is
C (I.F) = ∫Q × (IF) dm + k
C(m²) = ∫\(\frac { 2 }{m^2}\) × (m²) dm + k
C(m²) = ∫2dm + k
Cm² = 2m + k ……….. (1)
when C = 4 and m = 2, we have
(4) (2)² = 2(2) + k
16 = 4 + k = 12
Equation (1)
Cm² = 2m + 12
Cm² = 2(m + 6)

Question 7.
Solve (D² – 3D + 2) y = e^4x
Solution:
(D² – 3D + 2) y = e^4x
The auxiliary equation is m² – 3m + 2 = 0
(m – 1) (m – 2) = 0
m = 1, 2
The roots are real and different
C.F = Ae^m₁x + Be^m₁x
C.F = Ae^x + Be^2x

The general solution is y = C.F + P.I
y = Ae^x + Be^2x + \(\frac { e^{4x} }{6}\) ………. (1)
When x = 0; y = 0

Question 8.
Solve \(\frac { dy }{dx}\) + y cos x = 2 cos x
Solution:
\(\frac { dy }{dx}\) + y cos x = 2 cos x
This is of the form \(\frac { dy }{dx}\) + Py = Q
Here P = cos x and Q = 2 cos x
∫Pdx = ∫cos x dx = sin x
I.F = e^∫pdx = e^{sin x}
The solution is
y (I.F) = ∫Q (I.F) dx + c
ye^{sin x} = ∫(2 cos x) e^{sin x} dx

Question 9.
Solve x²ydx – (x³ + y³) dy = 0
Solution:
x²ydx = (x³ + y³) dy = 0
x²ydx = (x³ + y³) dy
\(\frac { dy }{dx}\) = \(\frac { x^2y }{(x^3+y^3)}\) ……… (1)
This is a homogeneous differential equation, same degree in x and y

Question 10.
Solve \(\frac { dy }{dx}\) = xy + x + y + 1
Solution:

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Computer Science Guide Pdf Chapter 2 Data Abstraction Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Computer Science Solutions Chapter 2 Data Abstraction

12th Computer Science Guide Data Abstraction Text Book Questions and Answers

I. Choose the best answer (1 Marks)

Question 1.
Which of the following functions build the abstract data type?
a) Constructors
b) Destructors
c) recursive
d) Nested
Answer:
a) Constructors

Question 2.
Which of the following functions retrieve information from the data type?
a) Constructors
b) Selectors
c) recursive
d) Nested
Answer:
b) Selectors

Question 3.
The data structure which is a mutable ordered sequence of elements is called
a) Built-in
b) List
c) Tuple
d) Derived data
Answer:
b) List

Question 4.
A sequence of immutable objects is called
a) Built-in
b) List
c) Tuple
d) Derived data
Answer:
c) Tuple

Question 5.
The data type whose representation is known is called
a) Built-in data type
b) Derived data type
c) Concrete data type
d) Abstract data type
Answer:
c) Concrete data type

Question 6.
The data type whose representation is unknown are called
a) Built-in data type
b) Derived data type
c) Concrete data type
d) Abstract data type
Answer:
d) Abstract data type

Question 7.
Which of the following is a compound structure?
a) Pair
b) Triplet
c) single
d) quadrat
Answer:
a) Pair

Question 8.
Bundling two values together into one can be considered as
a) Pair
b) Triplet
c) single
d) quadrat
Answer:
a) Pair

Question 9.
Which of the following allows to name the various parts of a multi-item object?
a) Tuples
b) Lists
c) Classes
d) quadrats
Answer:
c) Classes

Question 10.
Which of the following is constructed by placing expressions within square brackets?
a) Tuples
b) Lists
c) Classes
d) quadrats
Answer:
b) Lists

II. Answer the following questions (2 Marks)

Question 1.
What is abstract data type?
Answer:
Abstract Data type (ADT) is a type (or class) for objects whose behavior is defined by a set of values and a set of operations. The definition of ADT only mentions what operations are to be performed but not how these operations will be implemented.

Question 2.
Differentiate constructors and selectors.
Answer:

Question 3.
What is a Pair? Give an example.
Answer:

• Pair is a compound structure which is made up of a list of Tuple
• The way of bundling two values together into one can be considered as a Pair.
• Example: Pr = [10,20]
  a,b :=Pr
  In the above example ‘a’ becomes 10,’ b’ becomes 20.

Question 4.
What is a List? Give an example.
Answer:
The list is constructed by placing expressions within square brackets separated by commas.
An example for List is [10, 20].

Question 5.
What is a Tuple? Give an example.
Answer:

• A tuple is a comma-separated sequence of values surrounded by parentheses.
• Example: colour^ (‘red’, ‘blue’, ‘Green’)

III. Answer the following questions (3 Marks)

Question 1.
Differentiate Concrete Data Type and Abstract Data Type
Answer:

Question 2.
Which strategy is used for program designing? Define that Strategy.
Answer:
We are using here a powerful strategy for designing programs: ‘wishful thinking’.
Wishful Thinking is the formation of beliefs and making decisions according to what might be pleasing to imagine instead of by . appealing to reality.

Question 3.
Identify Which of the following are constructors and selectors?
(a) N1=number()
(b) accetnum(n1)
(c)  displaynum(n1)
(d)  eval(a/b)
(e) x,y= makeslope (m), makeslope(n)
(f) display()
Answer:

Question 4.
What are the different ways to access the elements of a list. Give example
Answer:
List is constructed by placing expressions within square brackets separated by commas. An example for List is [10, 20].
The elements of a list can be accessed in two ways. The first way is via our familiar method of multiple assignments, which unpacks a list into its elements and binds each element to a different name.
1st: = [10, 20]
x, y: = 1st
In the above example, x will become 10 and y will become 20.
A second method for accessing the elements in a list is by the element selection operator, also expressed using square brackets. Unlike a list literal, a square – bracket expression directly following another expression does not evaluate to a list value but instead selects an element from the value of the preceding expression.
1st [0]
10
1st [1]
20

Question 5.
Identify Which of the following are List, Tuple and class ?
(a) arr [1, 2, 34]
(b) arr (1, 2, 34)
(c) student [rno, name, mark]
(d) day= (‘sun’, ‘mon’, ‘tue’, ‘wed’)
(e) x= [2, 5, 6.5, [5, 6], 8.2]
(f) employee [eno, ename, esal, eaddress]
Answer:

IV. Answer the following questions (5Marks)

Question 1.
How will you facilitate data abstraction? Explain it with a suitable example.
Answer:
To facilitate data abstraction we need to create two types of functions namely

1. Constructors
2. Selectors

Constructors:
Constructors are functions that build the abstract data type.
Selectors:
Selectors are functions that retrieve information from the data type.
Example:

• We have an abstract data type called a city.
• This city object will hold the city’s name, and its latitude and longitude.
• To create a city object, you’d use a function like
  city =makecity (name, lat, Ion)
• Here makecity (name, lat, Ion) is the constructor which creates the object city.
• To extract the information of a city object, we would use functions(Selectors) like getname( city)
  getlat( city)
  getlon(city)
• In the above example, makecity (name, lat, Ion) is the constructor and getname(city),getlat( city) and getlon(city) are the selectors.
• Because the above functions extract the information of the city object.

Question 2.
What is a List? Why List can be called as Pairs. Explain with suitable example
Answer:

• Some languages like Python provides a compound structure called Pair which is made up of List or Tuple.
  The first way to implement pairs is with the List construct.

List:

• The list is constructed by placing expressions within square brackets separated by commas.
• Such an expression is called a list literal. The list can store multiple values.
• Each value can be of any type and can even be another list.
• Example :List := [10,20],
  The elements of a list can be accessed in two ways.
• The first way is via our familiar method of multiple assignments, which unpacks a list into its elements and binds each element to a different name.
  1st := [10,20]
  x, y := 1st
  In the above example, x will become x and y will become 20.
• A second method for accessing the elements in a list is by the element selection operator, also expressed using square brackets.
• Unlike a list literal, a square-brackets expression directly following another expression does not evaluate a list value but instead selects an element from the value of the preceding expression.
  1st[0]
  10
  Ist[l]
  20
• In both the example mentioned above mathematically we can represent list similar to a set as 1st[(0,10),(l,20)]
  List [(0,10), (1,20)] – Where
  
• Any way of bundling two values together into one can be considered as a pair.
• Lists are a common method to do so. Therefore List can be called as Pairs.

Example: Representing rational numbers using list:

• We can now represent a rational number as a pair of two integers in pseudo-code: a numerator and a denominator.
  rational(n, d):
  return [n, d]
  numer(x):
  return x[0]
  denom(x):
  return x[l]

Question 3.
How will you access the multi-item? Explain with example.
Answer:
We can use the structure construct (In OOP languages it’s called class construct) to represent multi-part objects where each part is named (given a name).

Consider the following pseudo-code:
class Person:
creation()
firstName :=””
lastName :=””
id :=””
email :=””
The new data type Person is pictorially represented as

The class (structure) construct defines the form for multi-part objects that represent a person.

• Its definition adds a new data type, in this case, a type named Person.
• Once defined, we can create new variables (instances) of the type.
• In this example, Person is referred to as a class or a type, while pi is referred to as an object or an instance.

12th Computer Science Guide Data Abstraction Additional Questions and Answers

I. Choose the best answer (1 Mark)

Question 1.
How many types of functions are needed to facilitate abstraction?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2

Question 2.
Expansion of CDT is ………….
a) Collective Data Type
b) Class Data Type
c) Concrete Data Type
d) Central Data Type
Answer:
c) Concrete Data Type

Question 3.
To facilitate data abstraction we need to create types of functions
a) 2
b) 3
c) 4
d) 5
Answer:
a) 2

Question 4.
……………………………. is the representation for ADT.
(a) List
(b) Classes
(c) Int
(d) Float
Answer:
(b) Classes

Question 5.
Which of the following is contracted by placing expressions within square brackets separated by commas?
a) Tuple
b) List
c) Set
d) Dictionary
Answer:
b) List

Question 6.
The list is constructed by using …………….. and …………….
a) ();
b) [ ],
c) < >.;
d) [ ]
Answer:
b) [ ],

Question 7.
Identify the constructor from the following
(a) City = makecity(name, lat, lon)
(b) getname(city)
(c) getlat(city)
(d) getlon(city)
Answer:
(a) City = makecity(name, lat, lon)

Question 8.
Which of the following extract the information of the object?
a) Constructors
b) Selectors
c) Functions
d) Destructors
Answer:
b) Selectors

Question 9.
Which of the following is used to build the abstract data type?
a) Destructors
b) Constructors
c) Selectors
d) All of these
Answer:
b) Constructors

Question 10.
How many ways of representing pair data types are there?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2

Question 11.
The process of providing only the essentials and hiding the details is known as …………….
a) Functions
b) Encapsulation
c) Abstraction
d) Pairs
Answer:
c) Abstraction

Question 12.
A D T expansion is …………….
a) Abstract Data Type
b) Absolute Data Type
c) Abstract Data Template
d) Application Development Template
Answer:
a) Abstract Data Type

Question 13.
How many objects can be created from a class?
(a) 0
(b) 1
(c) 2
(d) many
Answer:
(d) many

Question 14.
A powerful concept that allows programmers to treat codes as objects?
a) Encapsulation
b) Inheritance
c) Data Abstraction
d) Polymorphism
Answer:
c) Data Abstraction

II. Answer the following questions (2 and 3 Marks)

Question 1.
What are the two parts of a program?
Answer:
The two parts of a program are, the part that operates on abstract data and the part that defines a concrete representation.

III. Answer the following questions (5 Marks)

Question 1.
Explain the representation of Abstract data type using rational numbers.
Answer:

• Any program consists of two parts – the part that operates on abstract data and the part that defines a concrete representation, which is connected by a small set of functions that implement abstract data in terms of the concrete representation.
• To illustrate this technique, let us consider an example to design a set of functions for manipulating rational numbers.

Example:

• A rational number is a ratio of integers, and rational numbers constitute an important sub-class of real numbers.
• A rational number such as 8/3 or 19/23 is typically written as : < numerator > /< denominator > where both the < numerator > and < denominator > are placeholders for integer values.
• Both parts are needed to exactly characterize the value of the rational number.
• Actually dividing integers produces a float approximation, losing the exact precision of integers.
• However, you can create an exact representation for rational numbers by combining together the numerator and denominator.
  – – constructor
  – – constructs a rational number with numerator n, denominator d
  rational (n, d)
  – – selector
  numer(x) → returns the numerator of rational number x
  denom(y) → returns the denominator of rational number y.
• We have the operations on rational numbers defined in terms of the selector functions numer and denom, and the constructor function rational, but you haven’t yet defined these functions.
• We have to glue together a numerator and a denominator into a compound value
• The pseudo-code for the representation of the rational number using the above constructor and selector is
  x,y:=8,3
  rational (n,d)
  numer(x)/numer(y)
  – – output: 2.6666666666666665

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Computer Science Guide Pdf Chapter 1 Function Text Book Back Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Computer Science Solutions Chapter 1 Function

12th Computer Science Guide Function Text Book Questions and Answers

I. Choose the best answer (I Marks)

Question 1.
The small sections of code that are used to perform a particular task is called
a) Subroutines
b) Files
c) Pseudo code
d) Modules
Answer:
a) Subroutines

Question 2.
Which of the following is a unit of code that is often defined within a greater code structure?
a) Subroutines
b) Function
c) Files
d) Modules
Answer:
b) Function

Question 3.
Which of the following is a distinct syntactic block?
a) Subroutines
b) Function
c) Definition
d) Modules
Answer:
c) Definition

Question 4.
The variables in a function definition are called as
a) Subroutines
b) Function
c) Definition
d) Parameters
Answer:
d) Parameters

Question 5.
The values which are passed to a function definition are called
a) Arguments
b) Subroutines
c) Function
d) Definition
Answer:
a) Arguments

Question 6.
Which of the following are mandatory to write the type annotations in the function definition
a) Curly braces
b) Parentheses
c) Square brackets
d) indentations
Answer:
b) Parentheses

Question 7.
Which of the following defines what an object can do?
a) Operating System
b) Compiler
c) Interface
d) Interpreter
Answer:
c) Interface

Question 8.
Which of the following carries out the instructions defined in the interface?
a) Operating System
b) Compiler
c) Implementation
d) Interpreter
Answer:
c) Implementation

Question 9.
The functions which will give exact result when same arguments are passed are called
a) Impure functions
b) Partial Functions
c) Dynamic Functions
d) Pure functions
Answer:
d) Pure functions

Question 10.
The functions which cause side effects to the arguments passed are called
a) Impure functions
b) Partial Functions
c) Dynamic Functions
d) Pure functions
Answer:
a) Impure functions

II. Answer the following questions (2 Marks)

Question 1.
What is a subroutine?
Answer:
Subroutines are the basic building blocks of computer programs. Subroutines are small sections of code that are used to perform a particular task that can be used repeatedly. In Programming languages, these subroutines are called Functions.

Question 2.
Define Function with respect to the Programming language.
Answer:

• A function is a unit of code that is often defined within a greater code structure.
• A function works on many kinds of inputs like variants, expressions and produces a concrete output.

Question 3.
Write the inference you get from X:=(78).
Answer:
Value 78 is bound to the name X.

Question 4.
Differentiate Interface and Implementation
Answer:

Question 5.
Which of the following is a normal function definition and which is a recursive function definition?
Answer:
(I) Let Recursive sum x y:
return x + y

(II) let disp:
print ‘welcome’

(III) let Recursive sum num:
if (num! = 0) then return num + sum (num – 1) else
return num

1. Recursive function
2. Normal function
3. Recursive function

III. Answer the following questions (3 Marks)

Question 1.
Mention the characteristics of Interface.
Answer:

• The class template specifies the interfaces to enable an object to be created and operated properly.
• An object’s attributes and behaviour is controlled by sending functions to the object.

Question 2.
Why strlen() is called pure function?
Answer:
strlen (s) is called each time and strlen needs to iterate over the whole of ‘s’. If the compiler is smart enough to work out that strlen is a pure function and that ‘s’ is not updated in the lbop, then it can remove the redundant extra calls to strlen and make the loop to execute only one time. This function reads external memory but does not change it, and the value returned derives from the external memory accessed.

Question 3.
What is the side effect of impure function? Give example.
Answer:

• Impure function has side effects when it has observable interaction with the outside world.
• The variables used inside the function may cause side effects through the functions which are not passed with any arguments. In such cases the function is called impure function.
• When a function depends on variables or functions outside of its definition block, you can never be sure that the function will behave the same every time it’s called.
• For example, the mathematical function random () will give different outputs for the same function call
  let random number
  let a:= random()
  if a> 10 then
  return: a
  else
  return 10
• Here the function random is impure as it not sure what the will be the result when we call
  the function

Question 4.
Differentiate pure and impure functions.
Answer:

Question 5.
What happens if you modify a variable outside the function? Give an example
Answer:
When a function depends on variables or functions outside of its definition block, you can never be sure that the function will behave the same every time it’s called.
For example let y: = 0
(int) inc (int) x
y: = y + x;
return (y)
In the above example the value of y get changed inside the function defintion due to which the result will change each time. The side effect of the inc ( ) function is it is changing the data ‘ of the external visible variable ‘y’.

IV. Answer the following questions (5 Marks)

Question 1.
What are called Parameters and Write a note on
1. Parameter Without Type
2. Parameter With Type
Answer:
Parameter:
Parameter is the variables in a function definition
Arguments:
Arguments are the values which are passed to a function definition
Parameters passing are of two types namely

1. Parameter without Type
2. Parameter with Type

1. Parameter without Type:
Let us see an example of a function definition.
(requires: b > =0 )
(returns: a to the power of b)
let rec pow a b:=
if b=0 then 1
else a pow a*(b-l)

• In the above function definition variable ‘b’ is the parameter and the value which is passed to the variable ‘b’ is the argument.
• The precondition (requires) and postcondition (returns) of the function is given.
• Note we have not mentioned any types (data types).
• Some language computer solves this type (data type) inference problem algorithmically, but some require the type to be mentioned.

2. Parameter with Type:
Now let us write the same function definition with types for some reason:
(requires: b > 0 )
(returns: a to the power of b )
let rec pow (a: int) (b: int): int: =
if b=0 then 1 else a * pow b (a-1)

• When we write the type annotations for ‘a’ and ‘b’ the parentheses are mandatory.
• There are times we may want to explicitly write down types.
• This useful on times when you get a type error from the compiler that doesn’t make sense.
• Explicitly annotating the types can help with debugging such an error message.

Question 2.
Identify in the following program
Answer:
let rec gcd a b : =
if b < > 0 then gcd b (a mod b) else return a
(I) Name of the function
gcd

(II) Identify the statement which tells it is a recursive function
let rec

(III) Name of the argument variable
a, b

(IV) Statement which invokes the function recursively
gcd b(a mod b) [when b < > 0]

(V) Statement which terminates the recursion
return a (when b becomes 0).

Question 3.
Explain with example Pure and impure functions.
Answer:
Pure functions:

• Pure functions are functions which will give exact result when the same arguments are passed.
• For example, the mathematical function sin (0) always results 0.
  Let us see an example.
  let square x
  return: x * x
• The above function square is a pure function because it will not give different results for the same input.

Impure functions:

• The variables used inside the function may cause side effects through the functions which are not passed with any arguments. In such cases, the function is called the impure function.
• When a function depends on variables or functions outside of its definition block, we can never be sure that the function will behave the same every time it’s called.
• For example, the mathematical functions random () will give different outputs for the same function call.
  let Random number
  let a := random() if a > 10 then
  return: a else
  return: 10
• Here the function Random is impure as it is not sure what will be the result when we call the function.

Question 4.
Explain with an example interface and implementation
Answer:
Interface Vs Implementation:
An interface is a set of actions that an object can do. For example, when you press a light switch, the light goes on, you may not have cared how it splashed the light. In an Object-Oriented Programming language, an Interface is a description of all functions that a class must have in order to be a new interface.

In our example, anything that “ACTS LIKE” a light, should have to function definitions like turn on ( ) and a turn off ( ). The purpose of interfaces is to allow the computer to enforce the properties of the class of TYPE T (whatever the interface is) must have functions called X, Y, Z, etc.

A class declaration combines the external interface (its local state) with an implementation of that interface (the code that carries out the behaviour). An object is an instance created from the class. The interface defines an object’s visibility to the outside world.

Characteristics of interface

• The class template specifies the interfaces to enable an object to be created and operated properly.
• An object’s attributes and behavior is controlled by sending functions to the object.

Example:

• • The person who drives the car doesn’t care about the internal working.
• To increase the speed of the car he just presses the accelerator to get the desired behaviour.
• Here the accelerator is the interface between the driver (the calling / invoking object) and the engine (the called object).
• In this case, the function call would be Speed (70): This is the interface.
• Internally, the engine of the car is doing all the things.
• It’s where fuel, air, pressure, and electricity come together to create the power to move the vehicle.
  All of these actions are separated from the driver, who just wants to go faster. Thus we separate interface from implementation.

12th Computer Science Guide Function Additional Questions and Answers

I. Choose the best answer (1 Mark)

Question 1.
……………………… are expressed using statements of a programming language.
(a) Algorithm
(b) Procedure
(c) Specification
(d) Abstraction
Answer:
(a) Algorithm

Question 2.
The recursive function is defined using the keyword
a) let
b) requires
c) name
d) let rec
Answer:
d) let rec

Question 3.
A function definition which calls itself is called
a) user-defined function
b) recursive function
c) built-in function
d) derived function
Answer:
b) recursive function

Question 4.
Find the correct statement from the following.
(a) a : = (24) has an expression
(b) (24) is an expression
Answer:
(a) a : = (24) has an expression

Question 5.
strlen() is an example of ………………. function.
a) pure
b) impure
c) user-defined
d) recursive
Answer:
a) pure

Question 6.
Evaluation of ………………. functions does not cause any side effects to its output?
a) Impure
b) built-in
c) Recursive
d) pure
Answer:
d) pure

Question 7.
The name of the function in let rec pow ab : = is …………………………
(a) Let
(b) Rec
(c) Pow
(d) a b
Answer:
(c) Pow

Question 8.
An …………….. is an instance created from the class.
a) Interface
b) object
c) member
d) function
Answer:
b) object

Question 9.
In object-oriented programs …………… are the interface.
a) classes
b) object
c) function
d) implementation
Answer:
a) classes

Question 10.
In b = 0, = is ……………………….. operator
(a) Assignment
(b) Equality
(c) Logical
(d) Not equal
Answer:
(b) Equality

II. Answer the following questions (2 and 3 Marks)

Question 1.
What are the two types of parameter passing?
Answer:

1. Parameter without type
2. Parameter with type

Question 2.
What is meant by Definition?
Answer:
Definitions are distinct syntactic blocks.

Question 3.
Write the syntax for the function definitions?
Answer:
let rec f_n a₁ a₂ … a_n : = k
f_n : Function name
a₁ … a_n – variable
rec: recursion

Question 4.
Define Argument.
Answer:
Arguments are the values which are passed to a function definition through the function definition

Question 5.
Write notes on Interface.
Answer:

• An interface is a set of actions that an object can do.
• Interface just defines what an object can do, but won’t actually do it

Question 6.
Define Implementation.
Answer:
Implementation carries out the instructions defined in the interface

Question 7.
Write notes on Pure functions.
Answer:

• Pure functions are functions which will give exact result when the same arguments are passed.
• Example: strlen(),sqrt()

Question 8.
Write notes on the Impure function.
Answer:

• The functions which cause side effects to the arguments passed are called
  Impure function.
• Example: random(), date()

Question 9.
What is a Recursive function?
Answer:
A function definition which calls itself is called a Recursive function.

Question 10.
Differentiate parameters and arguments.
Answer:

Question 11.
Give function definition for the Chameleons of Chromeland problem?
Answer:
let rec monochromatize abc : =
if a > 0 then
a, b, c : = a – 1, b – 1, c + 2
else
a: = 0, b: = 0, c: = a + b + c
return c

Question 12.
Define Object:
Answer:
An object is an instance created from the class.

III. Answer the following questions (5 Marks)

Question 1.
Explain the syntax of function definitions
Answer:

• The syntax to define functions is close to the mathematical usage.
• The definition is introduced by the keyword let, followed by the name of the function and its arguments; then the formula that computes the image of the argument is written after an = sign.
• If you want to define a recursive function: use “let rec” instead of “let”.

The syntax for function definitions:

• let rec fn al a2 … an := k
• Here the ‘fn’ is a variable indicating an identifier being used as a
  function name.
• The names ‘al’ to ‘an’ are variables indicating the identifiers used as parameters.
• The keyword ‘rec’ is required if ‘fn’ is to be a recursive function; otherwise, it may be omitted.

Question 2.
Write a short note and syntax for function types?
Answer:

• The syntax for function types
  x→→y
  x1 →→ x2→→y
  x1 →→….. →→xn→→ y
• The ‘x’ and ‘y’ are variables indicating types
• The type x →→ ‘y’ is the type of a function that gets an input of type ‘x’ and returns an output of type ‘y’ whereas xl→→ x2 →→y is a type of a function that takes two inputs, the first input is of type and the second input of type ‘xl’, and returns an output of type <y’.
• Likewise x1→→……. →→ >xn→→y has type ‘x’ as the input of n arguments and ‘y’ type as output

Question 3.
On the island, there are different types of chameleons. Whenever two different color chameleons meet they both change their colors to the third color. Suppose two types of chameleons are equal in number.
Construct an algorithm that arranges meetings between these two types so that they change their color to the third type. In the end, all should display the same color.
Answer:
let ree monochromatic a b c:=
if a > 0 then
a, b, c:= a -1, b -1, c + 2
else
a:= 0 b:= 0 c:= a + b + c
return c

HANDS-ON PRACTICE

Question 1.
Write the algorithmic function definition to find the minimum among 3 numbers.
Answer:
let min 3abc:=
if a < b then
if a < c then a else c
else
if b < c then b else c

Question 2.
Write the algorithmic recursive function definition to find the sum of ‘n ‘ natural numbers. Answer:
let rec sum num:
lf(num!=0)
then return num+sum(num-l)
else return num