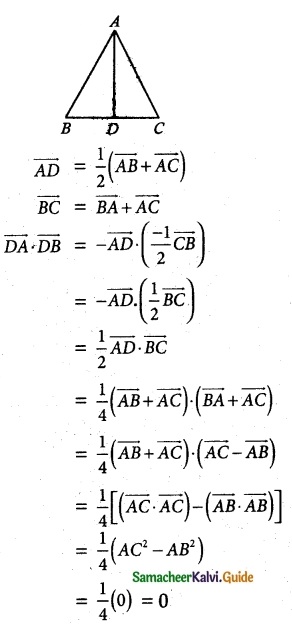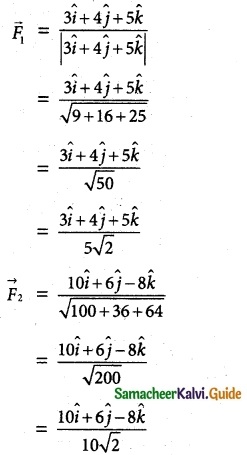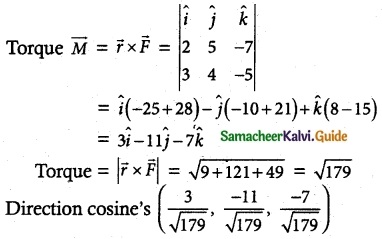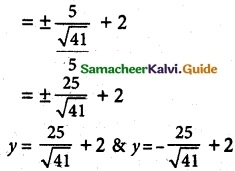Bhagya

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.3 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.3

Question 1.
If \(\overline { a }\) = \(\hat { i }\) – 2\(\hat { j }\) + 3\(\hat { k }\), \(\overline { b }\) = 2\(\hat { i }\) + \(\hat { j }\) – 2\(\hat { k }\), \(\overline { c }\) = 3\(\hat { i }\) + 2\(\hat { j }\) + \(\hat { k }\)
Find (i) (\(\overline { a }\) × \(\overline { b }\) ) × \(\overline { c }\)
(ii) \(\overline { a }\) × (\(\overline { b }\) × \(\overline { c }\))
Solution:
(i) \(\overline { a }\) × \(\overline { b }\) = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & -2 & 3 \\
2 & 1 & -2
\end{array}\right|\)
= \(\hat { i }\)(4 – 3) – \(\hat { j }\)(-2 – 6) + \(\hat { k }\)(1 + 4)
= \(\hat { i }\) + 8\(\hat { j }\) + 5\(\hat { k }\)
\(\overline { a }\) × \(\overline { b }\) × \(\overline { c }\) = \(\left|\begin{array}{lll}
\hat{i} & \hat{j} & \hat{k} \\
1 & 8 & 5 \\
3 & 2 & 1
\end{array}\right|\)
= \(\hat { i }\)(8 – 10) – \(\hat { j }\)(1 – 15) + \(\hat { k }\)(2 – 24)
= -2\(\hat { i }\) + 14\(\hat { j }\) – 22\(\hat { k }\)

(ii) \(\overline { b }\) × \(\overline { c }\) = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & 1 & -2 \\
3 & 2 & 1
\end{array}\right|\)
= \(\hat { i }\)(1 + 4) – \(\hat { j }\)(2 + 6) + \(\hat { k }\)(4 – 3)
= 5\(\hat { i }\) – 8\(\hat { j }\) + \(\hat { k }\)
\(\overline { a }\) × \(\overline { b }\) × \(\overline { c }\) = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & -2 & 3 \\
5 & -8 & 1
\end{array}\right|\)
= \(\hat { i }\)(-2 + 24) – \(\hat { j }\)(1 – 15) + \(\hat { k }\)(-8 + 10)
= 22\(\hat { i }\) + 14\(\hat { j }\) + 2\(\hat { k }\)

Question 2.
For any vector a, prove that
\(\hat { i }\)(\(\overline { a }\) × \(\hat { i }\)) + \(\hat { j }\) × (\(\overline { a }\) × \(\hat { j }\)) + \(\hat { k }\) × (\(\overline { a }\) × \(\hat { k }\)) = 2\(\overline { a }\).
Solution:
Let \(\overline { a }\) = a₁\(\hat { i }\) + a₂\(\hat { j }\) + a₃\(\hat { k }\)
\(\overline { a }\) × \(\hat { i }\) = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
a_{1} & a_{2} & a_{3} \\
1 & 0 & 0
\end{array}\right|\)
= \(\hat { i }\)(0) – \(\hat { j }\)(-a₃) + \(\hat { k }\)(0 – a₂)
\(\hat { i }\) × (\(\overline { a }\) × \(\hat { i }\)) = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & 0 & 0 \\
0 & a_{3} & -a_{2}
\end{array}\right|\)
= \(\hat { i }\)(0) – \(\hat { j }\)(-a₂) + \(\hat { k }\)(a₃)
= a₂\(\hat { j }\) + a₃\(\hat { k }\)
Similarly \(\hat { j }\) × (\(\overline { a }\) × \(\hat { j }\)) = a₁\(\hat { i }\) + a₃\(\hat { k }\)
\(\hat { k }\) × (\(\overline { a }\) × \(\hat { k }\)) = a₁\(\hat { i }\) + a₂\(\hat { j }\)
\(\hat { i }\) × (\(\overline { a }\) × \(\hat { i }\)) + \(\hat { j }\) × (\(\overline { a }\) × \(\hat { j }\)) + \(\hat { k }\) × (\(\overline { a }\) × \(\hat { k }\))
= 2a₁\(\hat { i }\) + 2a₂\(\hat { j }\) + 2a₃\(\hat { k }\)
= 2(a₁\(\hat { i }\) + a₂\(\hat { j }\) + a₃\(\hat { k }\))= 2 \(\overline { a }\)

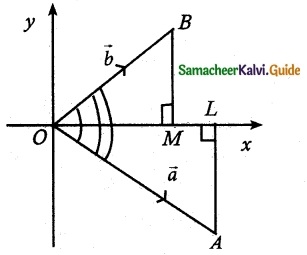
Question 3.
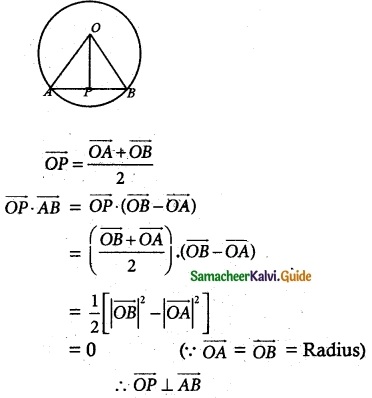
Prove that [\(\overline { a }\) – \(\overline { b }\), \(\overline { b }\) – \(\overline { c }\), c – a] = 0.
Solution:

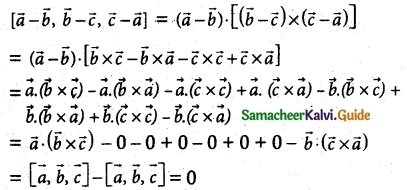
Hence proved.

Question 4.
If \(\overline { a }\) = 2\(\hat { i }\) + 3\(\hat { j }\) – \(\hat { k }\), \(\overline { b }\) = 3\(\hat { i }\) + 5\(\hat { j }\) + 2\(\hat { k }\), \(\overline { c }\) = –\(\hat { i }\) – 2\(\hat { j }\) + 3\(\hat { k }\)
(i) (\(\overline { a }\) × \(\overline { b }\)) × \(\overline { c }\) = (\(\overline { a }\). \(\overline { c }\))\(\overline { b }\) – (\(\overline { b }\).\(\overline { c }\))\(\overline { a }\)
(ii) \(\overline { a }\) (\(\overline { b }\) × \(\overline { c }\)) = (\(\overline { a }\). \(\overline { c }\))\(\overline { b }\) – (\(\overline { a }\).\(\overline { b }\))\(\overline { c }\)
Solution:

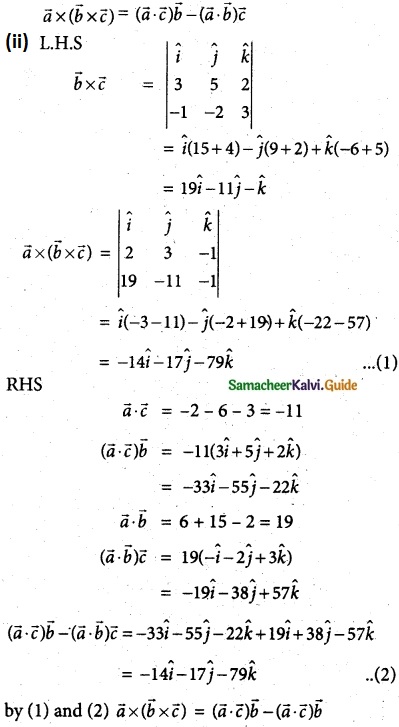
Question 5.
\(\overline { a }\) = 2\(\hat { i }\) + 3\(\hat { j }\) – \(\hat { k }\), \(\overline { b }\) = –\(\hat { i }\) + 2\(\hat { j }\) – 4\(\hat { k }\), \(\overline { c }\) = \(\hat { i }\) + \(\hat { j }\) + \(\hat { k }\) then find the value of (\(\overline { a }\) × \(\overline { b }\)) – (\(\overline { a }\) × \(\overline { c }\))
Solution:

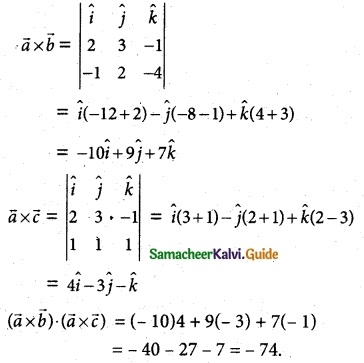
Question 6.
If \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) and \(\overline { d }\) are coplanar vectors, show that (\(\overline { a }\) × \(\overline { b }\)) × (\(\overline { c }\) × \(\overline { d }\)) = \(\overline { 0 }\)
Solution:

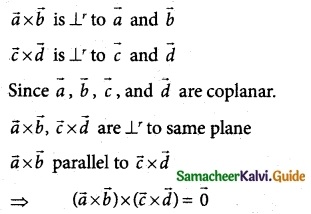
Question 7.
If \(\overline { a }\) = \(\hat { i }\) + 2\(\hat { j }\) + 3\(\hat { k }\), \(\overline { b }\) = 2\(\hat { i }\) – \(\hat { j }\) + \(\hat { k }\), \(\overline { c }\) = 3\(\hat { i }\) + 2\(\hat { j }\) + \(\hat { k }\) and \(\overline { a }\) × (\(\overline { b }\) × \(\overline { c }\)) = l\(\overline { a }\) + m\(\overline { b }\) + n\(\overline { c }\), find the values of l, m, n.
Solution:

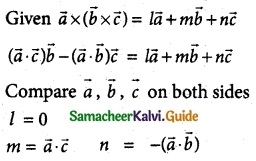
m = 3 + 4 + 3; n = -(2 – 2 + 3)
m = 10; n = -3
l = 0; m = 10; n = -3

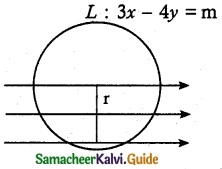
Question 8.
If \(\hat { a }\), \(\hat { b }\), \(\hat { c }\) are three unit vectors such that \(\hat { b }\) and \(\hat { c }\) are non-parallel and \(\hat { a }\) × (\(\hat { b }\) × \(\hat { c }\)) = \(\frac { 1 }{ 2 }\) \(\hat { b }\) find the angle between \(\hat { a }\) and \(\hat { c }\).
Solution:

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.2 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.2

Question 1.
If \(\overline { a }\) = \(\hat { i }\) – 2\(\hat { j }\) + 3\(\hat { k }\), b = 2\(\hat { i }\) + \(\hat { j }\) – 2\(\hat { k }\), c = 3\(\hat { i }\) + 2\(\hat { j }\) + \(\hat { k }\) find \(\overline { a }\).(\(\overline { b}\) × \(\overline { c }\)).
Solution:
\(\overline { a }\).(\(\overline { b}\) × \(\overline { c }\)) = [ \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) ] = \(\left|\begin{array}{ccc}
1 & -2 & 3 \\
2 & 1 & -2 \\
3 & 2 & 1
\end{array}\right|\)
= 1(1 + 4) + 2(2 + 6) + 3(4 – 3)
= 5 + 16 + 3 = 24

Question 2.
Find the volume of the parallelepiped whose coterminous edges are represented by the vectors -6\(\hat { i }\) + 14\(\hat { j }\) + 10\(\hat { k }\), 14\(\hat { i }\) – 10\(\hat { j }\) – 6\(\hat { k }\) and 2\(\hat { i }\) + 4\(\hat { j }\) – 2\(\hat { k }\)
Solution:
Volume of the parallelepiped = [ \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) ]
= \(\left|\begin{array}{ccc}
-6 & 14 & 10 \\
14 & -10 & -6 \\
2 & 4 & -2
\end{array}\right|\)
= -6(20 + 24) -14(-28 + 12) + 10(56 + 20)
= -6(44) -14(-16) + 10(76)
= -264 + 224 + 760
= 720 cu. units.

Question 3.
The volume of the parallelepiped whose coterminous edges are 7\(\hat { i }\) + λ\(\hat { j }\) – 3\(\hat { k }\), \(\hat { i }\) + 2\(\hat { j }\) – \(\hat { k }\), -3\(\hat { i }\) + 7\(\hat { j }\) + 5\(\hat { k }\) is 90 cubic units. Find the value of λ
Solution:
volume of the parallelepiped = [ \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) ]
\(\left|\begin{array}{ccc}
7 & \lambda & -3 \\
1 & 2 & -1 \\
-3 & 7 & 5
\end{array}\right|\) = 90
7(10 + 7) – λ(5 – 3) – 3(7 + 6) = 90
7(17) – λ(2) – 3(13) = 90
119 – 2λ – 39 = 90
2λ = 119 – 39 – 90
2λ = -10
λ = -5

Question 4.
If \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) are three non-coplanar vectors represented by concurrent edges of a parallelepiped of volume 4 cubic units, find the value of
(\(\overline { a }\) + \(\overline { b }\)).(\(\overline { b }\) × \(\overline { c }\)) + (\(\overline { b }\) + \(\overline { c }\)).(\(\overline { c }\) × \(\overline { a }\)) + (\(\overline { c }\) + \(\overline { a }\)).(\(\overline { a }\) × \(\overline { b }\)).
Solution:
Given [ \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) ] = ±4.
{(\(\overline { a }\) + \(\overline { b }\)).(\(\overline { b }\) × \(\overline { c }\)) + (\(\overline { b }\) + \(\overline { c }\)).(\(\overline { c }\) × \(\overline { a }\)) + (\(\overline { c }\) + \(\overline { a }\)).(\(\overline { a }\) × \(\overline { b }\)).}
= \(\overline { a }\)(\(\overline { b }\) × \(\overline { c }\)) + \(\overline { b }\) – (\(\overline { b }\) × \(\overline { c }\)) + \(\overline { b }\) – (\(\overline { c }\) × \(\overline { a }\)) + \(\overline { c }\) – (\(\overline { c }\) × \(\overline { a }\)) + \(\overline { c }\)(\(\overline { a }\) × \(\overline { b }\)) + \(\overline { a }\) – (\(\overline { a }\) × \(\overline { b }\))
= [ \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) ] + [ \(\overline { b }\), \(\overline { b }\), \(\overline { c }\) ] + [ \(\overline { p }\), \(\overline { c }\), \(\overline { a }\) ] + [ \(\overline { c }\), \(\overline { c }\), \(\overline { a }\) ] + [ \(\overline { c }\), \(\overline { a }\), \(\overline { b }\) ] + [ \(\overline { a }\), \(\overline { a }\), \(\overline { b }\) ]
= ± 4 + 0 ± 4 + 0 ± 4 + 0 = ± 12

Question 5.
Find the altitude of a parallelepiped determined by the vectors \(\overline { a }\) = -2\(\hat { i }\) + 5\(\hat { j }\) + 3\(\hat { k }\), \(\overline { b }\) = \(\hat { i }\) + 3\(\hat { j }\) – 2\(\hat { k }\) and \(\overline { c }\) = -3\(\hat { i }\) + \(\hat { j }\) + 4\(\hat { k }\) if the base is taken as the parallelogram determined by \(\overline { b }\) and \(\overline { c }\).
Solution:
V = \(\overline { a }\) -(\(\overline { b }\) × \(\overline { c }\)) = [ \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) ]
= \(\left|\begin{array}{ccc}
-2 & 5 & 3 \\
1 & 3 & -2 \\
-3 & 1 & 4
\end{array}\right|\)
= -2(12 + 2) -5(4 – 6) + 3(1 + 9)
= -2(14) -5(-2) + 3(10)
= -28 + 10 + 30 = 12
Area = |\(\overline { b }\) × \(\overline { c }\)| = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & 3 & -2 \\
-3 & 1 & 4
\end{array}\right|\)
= \(\hat { i }\)(12 + 2) – \(\hat { j }\)(4 – 6) + \(\hat { k }\)(1 + 9)
= 14\(\hat { i }\) + 2\(\hat { j }\) + 10\(\hat { k }\)
|\(\overline { b }\) × \(\overline { c }\)| = \(\sqrt { 196+4+100 }\) = \(\sqrt { 300 }\)
= 10√3
Altitude h = \(\frac { V }{ Area }\) = \(\frac { 12 }{ 10√3 }\) = \(\frac { 12×√3 }{ 10×3 }\) = \(\frac { 2√3 }{ 5 }\)

Question 6.
Determine whether the three vectors 2\(\hat { i }\) + 3\(\hat { j }\) + \(\hat { k }\), \(\hat { i }\) – 2\(\hat { j }\) + 2\(\hat { k }\) and 3\(\hat { i }\) + \(\hat { j }\) + 3\(\hat { k }\) are coplanar.
Solution:
If vectors are coplanar, [ \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) ] = 0
[ \(\overline { a }\), \(\overline { b }\), \(\overline { c }\) ] = \(\left|\begin{array}{ccc}
2 & 3 & 1 \\
1 & -2 & 2 \\
3 & 1 & 3
\end{array}\right|\)
= 2(-6 – 2) -3(3 – 6) + 1(1 + 6)
= -2(-8) -3(-3) + 1(7) = -16 + 9 + 7 = 0
∴ The given vectors are coplanar

Question 7.
Let \(\overline { a }\) = \(\hat { i }\) + \(\hat { j }\) + \(\hat { k }\), \(\overline { b }\) = \(\hat { i }\) and \(\overline { c }\) = c₁\(\hat { i }\) + c₂\(\hat { j }\) + c₃\(\hat { k }\). If c₁ = 1 and c₂ = 2, find c₃ such that \(\overline { a }\), \(\overline { b }\) and \(\overline { c }\) are coplanar.
Solution:
If \(\overline { a }\), \(\overline { b }\) and \(\overline { c }\) are coplanar [ \(\overline { a }\), \(\overline { b }\) and \(\overline { c }\) ] = 0
\(\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 0 \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\) = 0
1(0) – 1(c₃) + 1(c₂) = 0
-c₃ + c₂ = 0
c₃ = c₂ = 2

Question 8.
If \(\overline { a }\) = \(\hat { i }\) – \(\hat { k }\), \(\overline { b }\) = x\(\hat { i }\) + \(\hat { j }\) + (1 – x)\(\hat { k }\) c = y\(\hat { i }\) + x\(\hat { j }\) + (1 + x – y) \(\hat { k }\) Show that [ \(\overline { a }\), \(\overline { b }\) and \(\overline { c }\) ] = 0
Solution:
[ \(\overline { a }\), \(\overline { b }\) and \(\overline { c }\) ] = \(\left|\begin{array}{ccc}
1 & 0 & -1 \\
x & 1 & 1-x \\
y & x & 1+x-y
\end{array}\right|\)
= 1(1 + x – y – x + x²)-1(x² – y)
(1 + x – y – x + x² – x² + y)
= 1
There is no x and y terms
∴ [ \(\overline { a }\), \(\overline { b }\) and \(\overline { c }\) ] depends on neither x nor y.

Question 9.
If the vectors a\(\hat { i }\) + a\(\hat { j }\) + c\(\hat { k }\), \(\hat { i }\) + \(\hat { k }\) and c\(\hat { i }\) + c\(\hat { j }\) + b\(\hat { k }\) are coplanar, prove that c is the geometric mean of a and b.
Solution:
[ \(\overline { a }\), \(\overline { b }\) and \(\overline { c }\) ] = 0
\(\left|\begin{array}{lll}
a & a & c \\
1 & 0 & 1 \\
c & c & b
\end{array}\right|\) = 0
a(0 – c) – a(b – c) + c(c) = 0
-ac – ab + ac + c² = 0
c² – ab = 0
c² = ab
⇒ c in the geometric mean of a and b.

Question 10.
Let \(\overline { a }\), \(\overline { b }\) and \(\overline { c }\) be three non-zero vectors such that \(\overline { c }\) is a unit vector perpendicular to both \(\overline { a }\) and \(\overline { b }\). If the angle between \(\overline { a }\) and \(\overline { b }\) is \(\frac { π }{ 6 }\) show that [\(\overline { a }\), \(\overline { b }\) and \(\overline { c }\)]² = \(\frac { 1 }{ 4 }\) |\(\overline { a }\)|² |\(\overline { b }\)|²
Solution:

Hence proved

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 Applications of Vector Algebra Ex 6.1 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.1

Question 1.
Prove by vector method that if a line is drawn from the centre of a circle to the midpoint of a chord; then the line is perpendicular to the chord.
Solution:
A circle with centre at O. AB is chord of the circle and OP bisects AB (ie) AP = PB
To prove \(\overline { OP }\) ⊥ \(\overline { AB }\) O is the position vector
∴ \(\overline { OA }\) = \(\overline { OB }\) = Radius
Position vector of P

Hence proved

Question 2.
Prove by vector method that the median to the base of an isosceles triangle is perpendicular to the base.
Solution:
In isosceles ΔABC
Let AB = AC and AD is the median
D is the mid point of BC

\(\overline { DA }\).\(\overline { DB }\) = 0
\(\overline { DA }\) ⊥ \(\overline { DB }\)

Question 3.
Prove by vector method that an angle in a semi-circle is a right angle.
Solution:

Let us consider a circle with centre O and diameter AB.
Let P be any point on the semi-circle.
Let us prove that ∠APB = 90°
W.K.T OA = OB = OP (∵ radius)
\(\overline { PA }\) = \(\overline { PO }\) + \(\overline { OA }\)
\(\overline { PB }\) = \(\overline { PO }\) + \(\overline { OB }\)
= \(\overline { PO }\) – \(\overline { OA }\)
\(\overline { PA }\). \(\overline { PB }\) = (\(\overline { PO }\) + \(\overline { OA }\))(\(\overline { PO }\) – \(\overline { OA }\))
= \(\overline { PO }\)² – \(\overline { OA }\)² = 0
\(\overline { PA }\) ⊥ \(\overline { PB }\)
⇒ ∠APB = 90°. Hence proved.

Question 4.
Prove by vector method that the diagonals of a rhombus bisect each other at right angles.
Solution:
ABCD is a rhombus

\(\overline { AB }\) = \(\overline { a }\) and \(\overline { AD }\) = \(\overline { b }\)
Here AB = BC = CD = DA
(ie) |\(\overline { a }\)| = |\(\overline { b }\)|
\(\overline { AC }\) = \(\overline { AB }\) + \(\overline { BC }\)
= \(\overline { a }\) + \(\overline { b }\)
\(\overline { BD }\) = \(\overline { BC }\) + \(\overline { CD }\)
= \(\overline { AD }\) – \(\overline { AB }\)
= \(\overline { b }\) – \(\overline { a }\)
\(\overline { AC }\).\(\overline { BD }\) = (\(\overline { a }\) + \(\overline { b }\)).(\(\overline { b }\) – \(\overline { a }\))
= (\(\overline { b }\) + \(\overline { a }\)).(\(\overline { b }\) – \(\overline { a }\))
= (\(\overline { b }\))² – (\(\overline { a }\))² = 0 (∵ |\(\overline { a }\)| = |\(\overline { b }\)|)
\(\overline { AC }\).\(\overline { BD }\) = 0 ⇒ \(\overline { AC }\) ⊥ \(\overline { BD }\)
Hence proved.

Question 5.
Using vector method, prove that if the diagonals of a parallelogram are equal, then it is a rectangle.
Solution:

ABCD is a parallelogram with sides
\(\overline { AB }\) = \(\overline { a }\), \(\overline { AD }\) = \(\overline { b }\) and the diagonals are \(\overline { AC }\) and \(\overline { BD }\)
\(\overline { AC }\) = \(\overline { AB }\) + \(\overline { BC }\) = \(\overline { AB }\) + \(\overline { AD }\) = \(\overline { a }\) + \(\overline { b }\)
\(\overline { BD }\) = \(\overline { BA }\) + \(\overline { AD }\) = \(\overline { AD }\) – \(\overline { AB }\) = \(\overline { b }\) – \(\overline { a }\)
Since the diagonals are equal
|\(\overline { AC }\)| = |\(\overline { BD }\)|
|\(\overline { a }\) + \(\overline { b }\)| = |\(\overline { b }\) – \(\overline { a }\)|
(\(\overline { a }\) + \(\overline { b }\))² = (\(\overline { b }\) – \(\overline { a }\))²
\(\overline { a }\)² + 2\(\overline { a }\).\(\overline { b }\) + \(\overline { b }\)² = \(\overline { b }\)² – 2\(\overline { b }\) \(\overline { a }\) + \(\overline { a }\)²
4\(\overline { a }\) \(\overline { b }\) = 0
\(\overline { a }\).\(\overline { b }\) = 0
\(\overline { a }\) ⊥\(\overline { b }\) ⇒ ABCD is a rectangle. Since ∠A = 90°.

Question 6.
Prove by vector method that the area of the quadrilateral ABCD having diagonals AC and BD is \(\frac { 1 }{ 2 }\) |\(\overline { AC }\)| = |\(\overline { BD }\)|
Solution:
Vector area of a quadrilateral ABCD
= Vector area of ΔABC + Vector area of ΔACD

Area of quadrilateral
= \(\frac { 1 }{ 2 }\) |\(\overline { AC }\)| = |\(\overline { BD }\)|

Question 7.
Prove by vector method that the parallelograms on the same base and between the same parallels are equal in area.
Solution:
\(\overline { AB }\) = \(\overline { a }\), \(\overline { AD }\) = \(\overline { b }\)

Vector area of the parallelogram is \(\overline { b }\) × \(\overline { a }\) ……(1)
Consider the parallelogram ABB’A’
\(\overline { AB }\) = \(\overline { a }\), \(\overline { AB }\) = m\(\overline { a }\)
Because \(\overline { A’B }\) is parallel to \(\overline { AB }\)
Consider the triangle ADA’
By law of vectors AA’ = m\(\overline { a }\) + \(\overline { b }\)
Hence the vector area of parallelogram
ABB’A = \(\overline { a }\) × (m\(\overline { a }\) + \(\overline { b }\))
= m(\(\overline { a }\) × \(\overline { a }\)) + (\(\overline { a }\) × \(\overline { b }\))
= 0 + (\(\overline { a }\) × \(\overline { b }\))
= \(\overline { a }\) × \(\overline { b }\) ……..(2)
By (1) and (2) Area of ABCD = Area of ABB’A’
Hence proved.

Question 8.
If G is the centroid of a ΔABC, prove that (area of ΔGAB) = (area of ΔGBC) = (area of ΔGCA) = \(\frac { 1 }{ 3 }\) (area of ΔABC).
Solution:
W.K.T the median of a triangle divides it into two triangles of equal area.

In ΔABC, AD is the median
area (ΔABD) = area (ΔACD) ………. (1)
In ΔGBC, GD is die median
area (ΔGBD) = area (ΔGCD) ………. (2)
Sub (2) from (1) we get
area (ΔABD) – area (ΔGBD)
= area (ΔACD) – area (ΔGCD)
area(ΔAGB) = area(ΔAGC) ………… (3)
Similarly
area (ΔAGB) = area (ΔBGC) …………(4)
From (3) and (4) we get
area (ΔAGB) = area(ΔAGC) = area(ΔBGC) ……….. (5)
Now
area(ΔAGB) + area(ΔAGC) + area(ΔBGC) = area(ΔABC)
⇒ area(ΔAGB) + area(ΔAGB) + area(ΔAGB)
= area (ΔABC) (using 5)
⇒ 3area(ΔAGB) = area(ΔABC)
⇒ axea(ΔAGB) = \(\frac { 1 }{ 3 }\) area(ΔABC) ………..(6)
From (5) and (6) we get
area(ΔAGB) = area(ΔAGB) = area(ΔBGC)
= \(\frac { 1 }{ 3 }\) area(ΔABC)

Question 9.
Using vector method, prove that
cos(α – ß) = cos α cos ß + sin α sin ß.
Solution:
Let \(\overline { a }\) = \(\overline { OA }\), \(\overline { b }\) = \(\overline { OB }\) be the unit vectors and which make angles α and ß respectively with positive x-axis where A and B are as in diagram.

Draw AL and BM perpendicular to the X axis, then
\(\overline { OL }\) = \(\overline { OA }\) = cos α
|\(\overline { OL }\)| = |\(\overline { OA }\)| cos α = cos α
|\(\overline { LA }\)| = |\(\overline { OA }\)| sin α = sin α
\(\overline { OL }\) = |\(\overline { OL }\)|\(\hat { i }\) = cos α \(\hat { i }\)
\(\overline { LA }\) = sin α (+\(\hat { j }\))
\(\overline { a }\) = \(\overline { OA }\) = \(\overline { OL }\) + \(\overline { LA }\)
= cosα \(\hat { i }\) + sinα \(\hat { j }\) ……… (1)
Similarly \(\overline { b }\) = cos ß \(\hat { i }\) + sin ß \(\hat { j }\) ……… (2)
The angle between \(\overline { a }\) and \(\overline { b }\) is α – ß and so \(\overline { a }\).\(\overline { b }\) = |\(\overline { a }\)||\(\overline { b }\)| cos(α – ß) = cos(α – ß) ……..(3)
From (1) and (2)
\(\overline { a }\).\(\overline { b }\) = (cosα\(\hat { i }\) + sinα \(\hat { j }\)).(cosß\(\hat { i }\) + sinß\(\hat { j }\))
= cos α cos ß + sin α sin ß ………. (4)
From (3) and (4)
cos(α – ß) = cos α cos ß + sin α sin ß

Question 10.
Prove by vector method that
sin(α + ß) = sin α cos ß +cos α sin ß.
Solution:
Let \(\overline { a }\) = \(\overline { OA }\), \(\overline { b }\) = \(\overline { OB }\) be the unit vectors making angles α and ß respectively with positive x axis where A and B are as shown in the diagram

Draw AL and BM perpendicular to the X axis, then
\(\overline { OL }\) = \(\overline { OA }\) cos α
|\(\overline { OL }\)| = |\(\overline { OA }\)| cos α = cos α
|\(\overline { LA }\)| = |\(\overline { OA }\)| sin α = sin α
|\(\overline { OL }\)| = |\(\overline { OL }\)| \(\hat { i }\) = cos α \(\hat { i }\)
\(\overline { LA }\) = sin α(-\(\hat { j }\))
\(\overline { a }\) = \(\overline { OA }\) = \(\overline { OL }\) + \(\overline { LA }\)
= cos α \(\hat { i }\) + sin α \(\hat { j }\) ………… (1)
similarly \(\overline { b }\) = cos ß \(\hat { i }\) – sin ß \(\hat { j }\) ………… (2)
The angle between \(\overline { a }\) and \(\overline { b }\) is α + ß and the vectors \(\overline { b }\), \(\overline { a }\), \(\overline { k }\) from a right handed system.
\(\overline { b }\) × \(\overline { a }\) = |\(\overline { b }\)||\(\overline { a }\)| sin(α + ß)\(\hat { k }\) = sin(α + ß)\(\hat { k }\) ………..(1)
\(\overline { b }\) × \(\overline { a }\) = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
\cos \beta & -\sin \beta & 0 \\
\cos \alpha & \sin \alpha & 0
\end{array}\right|\)
= (sin α cos ß + cos α sin ß)\(\hat { k }\) ……… (2)
From (1) & (2)
sin(α + ß) = sin α cos ß + cos α sin ß

Question 11.
A particle acted on by constant forces 8\(\hat { i }\) + 2\(\hat { j }\) – 6\(\hat { k }\) and 6\(\hat { i }\) + 2\(\hat { j }\) – 2\(\hat { k }\) is displaced from the point (1, 2, 3) to the point (5, 4, 1). Find the total work done by the forces.
Solution:
\(\overline { OA }\) = \(\hat { i }\) + 2\(\hat { j }\) + 3\(\hat { k }\)
\(\overline { OB }\) = 5\(\hat { i }\) + 4\(\hat { j }\) + \(\hat { k }\)
\(\overline { d }\) = \(\overline { AB }\) = \(\overline { OB }\) – \(\overline { OA }\)
= 4\(\hat { i }\) + 2\(\hat { j }\) – 2\(\hat { k }\)
\(\overline { F_1 }\) = 8\(\hat { i }\) + 2\(\hat { j }\) – 6\(\hat { k }\)
and \(\overline { F_2 }\) = 6\(\hat { i }\) + 2\(\hat { j }\) – 2\(\hat { k }\)
\(\overline { F }\) = \(\overline { F_1 }\) + \(\overline { F_2 }\) = 14\(\hat { i }\) + 4\(\hat { j }\) – 8\(\hat { k }\)
Work done = \(\overline { F }\) \(\overline { d }\)
= (14\(\hat { i }\) + 4\(\hat { j }\) – 8\(\hat { k }\)).(4\(\hat { i }\) + 2\(\hat { j }\) – 2\(\hat { k }\))
= 56 + 8 + 16
= 80 units

Question 12.
Forces of magnitudes 5√2 and 10√2 units acting in the directions 3\(\hat { i }\) + 4\(\hat { j }\) + 5\(\hat { k }\) and 10\(\hat { i }\) + 6\(\hat { j }\) – 8\(\hat { k }\), respectively, act on a particle which is displaced from the point with position vector 4\(\hat { i }\) – 3\(\hat { j }\) – 2\(\hat { k }\) to the point with position vector 6\(\hat { i }\) – \(\hat { j }\) – 3\(\hat { k }\). Find the work done by the forces.

Resultant force \(\overline { F }\) = \(\overline { F_1 }\) + \(\overline { F_2 }\)
= 5√2\(\overline { F_1 }\) + 10√2 \(\overline { F_2 }\)
= 3\(\hat { i }\) + 4\(\hat { j }\) + 5\(\hat { k }\) + 10\(\hat { i }\) + 6\(\hat { j }\) – 8\(\hat { k }\)
= 13\(\hat { i }\) + 10\(\hat { j }\) – 3\(\hat { k }\)
\(\overline { OA }\) = 4\(\hat { i }\) – 3\(\hat { j }\) – 2\(\hat { k }\)
\(\overline { OB }\) = 6\(\hat { i }\) + \(\hat { j }\) – 3\(\hat { k }\)
\(\overline { d }\) = \(\overline { AB }\) = \(\overline { OB }\) – \(\overline { OA }\) = 2\(\hat { i }\) + 4\(\hat { j }\) – \(\hat { k }\)
\(\overline { F }\).\(\overline { d }\) = (13\(\hat { i }\) + 10\(\hat { j }\) – 3\(\hat { k }\)).(2\(\hat { i }\) + 4\(\hat { j }\) – \(\hat { k }\))
= 26 + 40 + 3
= 69 units

Question 13.
13. Find the magnitude and direction cosines of the torque of a force represented by 3\(\hat { i }\) + 4\(\hat { j }\) – 5\(\hat { k }\) about the point with position vector 2\(\hat { i }\) – 3\(\hat { j }\) + 4\(\hat { k }\) acting through a point whose position vector is 4\(\hat { i }\) + 2\(\hat { j }\) – 3\(\hat { k }\)
Solution:
\(\overline { OA }\) = 2\(\hat { i }\) – 3\(\hat { j }\) + 4\(\hat { k }\)
\(\overline { OB }\) = 4\(\hat { i }\) + 2\(\hat { j }\) – 3\(\hat { k }\)
\(\hat { r }\) = \(\overline { AB }\) = \(\overline { OB }\) – \(\overline { OA }\)
= 2\(\hat { i }\) + 5\(\hat { j }\) – 7\(\hat { k }\)
= 3\(\hat { i }\) + 4\(\hat { j }\) – 5\(\hat { k }\)

Question 14.
Find the torque of the resultant of the three forces represented by -3\(\hat { i }\) + 6\(\hat { j }\) – 3\(\hat { k }\), 4\(\hat { i }\) – 10\(\hat { j }\) + 12\(\hat { k }\) and 4\(\hat { i }\) + 7\(\hat { j }\) acting at the point with position vector 8\(\hat { i }\) – 6\(\hat { j }\) – 4\(\hat { k }\) about the point with position vector 18\(\hat { i }\) + 3\(\hat { j }\) – 9\(\hat { k }\)
Solution:
\(\overline { F_1 }\) = -3\(\hat { i }\) + 6\(\hat { j }\) – 3\(\hat { k }\)
\(\overline { F_2 }\) = 4\(\hat { i }\) – 10\(\hat { j }\) + 12\(\hat { k }\)
\(\overline { F_3 }\) = 4\(\hat { i }\) + 7\(\hat { j }\)
\(\overline { F }\) = \(\overline { F_1 }\) + \(\overline { F_2 }\) + \(\overline { F_3 }\)
= 5\(\hat { i }\) + 3\(\hat { j }\) + 9\(\hat { k }\)
\(\overline { OB }\) = 8\(\hat { i }\) – 6\(\hat { j }\) – 4\(\hat { k }\)
\(\overline { OA }\) = 18\(\hat { i }\) + 3\(\hat { j }\) – 9\(\hat { k }\)
\(\overline { AB }\) = \(\overline { OB }\) – \(\overline { OA }\)
= -10\(\hat { i }\) – 9\(\hat { j }\) + 5\(\hat { k }\)
\(\overline { t }\) = \(\overline { r }\) × \(\overline { F }\) = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
-10 & -9 & 5 \\
5 & 3 & 9
\end{array}\right|\)
= \(\hat { i }\)(-81 – 15) – \(\hat { j }\)(-90 – 25) + \(\hat { k }\)(-30 + 45)
= -96\(\hat { i }\) + 115\(\hat { j }\) + 15\(\hat { k }\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.6 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.6

Choose the most suitable answer from the given four alternatives:

Question 1.
The equation of the circle passing through (1, 5) and (4, 1) and touching y-axis is x² + y² – 5x – 6y + 9 + λ (4x + 3y – 19) = 0 where λ is equal to
(a) 0, –\(\frac {40}{9}\)
(b) 0
(c) \(\frac {40}{9}\)
(d) –\(\frac {40}{9}\)
Solution:
(a) 0, –\(\frac {40}{9}\)
Hint:
x² + y² – 5x – 6y + 9 + λ(4x + 3y – 19) = 0
x² + y² + x (-5 + 4λ) + y (- 6 + 3λ) + 9 – 19λ = 0
It touches the y-axis put x = 0.
y² + (3λ – 6) y + 9 – 19λ = 0
Now, b² – 4ac = 0
⇒ (3λ – 6)² – 4 (1) (9 – 19λ) = 0
Solving this equation we get
λ = 0 or λ = –\(\frac {40}{9}\)

Question 2.
The eccentricity of the hyperbola whose latus rectum is 8 and conjugate axis is equal to half the distence between the foci is
(a) \(\frac {4}{3}\)
(b) \(\frac {4}{√3}\)
(c) \(\frac {2}{√3}\)
(d) –\(\frac {3}{2}\)
Solution:
(c) \(\frac {2}{√3}\)
Hint:
Length of Latus Rectum \(\frac {2b^2}{a}\) = 8
⇒ b² = 4a …….. (1)
Length of conjugate axes
2b = \(\frac {1}{2}\)(2ae)
⇒ b = \(\frac {1}{2}\) …….. (2)
b² = \(\frac {a^2e^2}{4}\)
Now b² = a²(e² – 1)
\(\frac {a^2e^2}{4}\) = a²(e² – 1)
e² = 4e² – 4
3e² = 4
e² = \(\frac {4}{3}\)
∴ e = \(\frac {2}{√3}\)

Question 3.
The circle x² + y² = 4x + 8y + 5 intersects the line 3x – 4y = m at two distinct points if
(a) 15 < m < 65
(b) 35 < m < 85
(c) -85 < m < -35
(d) -35 < m < 15
Solution:
(d) -35 < m < 15
Hint:

C : x² + y² – 4x – 8y – 5 = 0
(x – 2)² + (y – 4)² = 25
C (2, 4); r = 5
Distance from centre < r

-25 < 10 + m < 25
⇒ -25 – 10 < m < 25 – 10
-35 < m < 15

Question 4.
The length of the diameter of the circle which touches the x-axis at the point (1, 0) and passes through the point (2, 3).
(a) \(\frac {6}{5}\)
(b) \(\frac {5}{3}\)
(c) \(\frac {10}{3}\)
(d) \(\frac {3}{5}\)
Solution:
(c) \(\frac {10}{3}\)
Hint:

CA = CB
CA² = CB²
(1 – 1)² + (h – 0)² = (1 – 2)² + (h – 3)²
h² = 1 + h² + 9 – 6h
6h = 10
h = \(\frac {10}{6}\) = \(\frac {5}{3}\)
Diameter is 2h = 2(\(\frac {5}{3}\)) = \(\frac {10}{3}\)

Question 5.
The radius of the circle 3x² + by² + 4bx – 6by + b² = 0 is
(a) 1
(b) 3
(c) \(\sqrt {10}\)
(d) \(\sqrt {11}\)
Solution:
(c) \(\sqrt {10}\)
Hint:
Equation of circle
3x² + by² + 4 bx – 6by + b² = 0
a = b ⇒ b = 3
3x² + 3y² + 12x – 18y + 9 = 0
÷ by 3 x² + y² + 4x – 6y + 3 = 0
2g = 4; 2f = -6; c = 3
g = 2; f = -3
r = \(\sqrt {g^2+f^2-c}\)
= \(\sqrt {4+9-3}\)
= \(\sqrt {10}\)

Question 6.
The centre of the circle inscribed in a square formed by the lines x² – 8x – 12 = 0 and y² – 14y + 45 = 0 is
(a) (4, 7)
(b) (7, 4)
(c) (9, 4)
(d) (4, 9)
Solution:
(a) (4, 7)
Hint:
Equation of lines
x² – 8x – 12 = 0
(x – 6)(x – 2) = 0
x = 2, 6
Another lines
y² – 14y + 45 = 0
(y – 5 )(y – 9) = 0
y = 5, 9
Hence the extremities of the diameter are (6, 9) and (2, 5).
Centre is mid point of (6, 9) and (2, 5)
Centre = (\(\frac {6+2}{2}\),\(\frac {9+5}{2}\))
= (4, 7)

Question 7.
The equation of the normal to the circle x² + y² – 2x – 2y + 1 = 0 which is parallel to the line 2x + 4y = 3 is
(a) x + 2y = 3
(b) x + 2y + 3 = 0
(c) 2x + 4y + 3 = 0
(d) x – 2y + 3 = 0
Solution:
(a) x + 2y = 3
Hint:

x² + y² – 2x – 2y + 1 = 0
2g = -2 2f = -2
g = -1 f = -1
Parallel line be 2x + 4y + λ = 0
Centre be (-g, -f) = (1, 1)
Which lies on line
2 + 4 + λ = 0 ⇒ λ = -6
∴ 2x + 4y – 6 = 0 ⇒ x + 2y = 3

Question 8.
If P(x, y) be any point on 16x² + 25y² = 400 with foci F(3, 0) then PF₁ + PF₂ is
(a) 8
(b) 6
(c) 10
(d) 12
Solution:
(c) 10
Hint:
16x² + 25y² = 400
\(\frac {x^2}{25}\) + \(\frac {y^2}{16}\) = 1
a² = 25
⇒ ∴ a = ±5
PF₁ + PF₂ = major axis = 2a
= 2 × 5 = 10.

Question 9.
The radius of the circle passing through the points (6,2) two of whose diameter are x + y = 6 and x + 2y = 4 is
(a) 10
(b) 2√5
(c) 6
(d) 4
Solution:
(b) 2√5
Hint:
x + y = 6 …….. (1)
x + 2y = 4 ……… (2)
(1) – (2) -y = 2 ⇒ y = -2
(1) ⇒ x – 2 = 6 ⇒ x = 8.
point be (8, -2)
another point (6, 2)
radius = \(\sqrt {(x_2-x_1)^2+(y_2-y_1)^2}\)
= \(\sqrt {(8-6)^2+(2+2)^2}\)
= \(\sqrt {2^2+4^2}\) = \(\sqrt {4+16}\)
= \(\sqrt {20}\) = 2√5.

Question 10.
The area of quadrilateral formed with foci of the hyperbolas \(\frac {x^2}{a^2}\) – \(\frac {y^2}{b^2}\) = 1 and \(\frac {x^2}{a^2}\) – \(\frac {y^2}{b^2}\) = -1 is
(a) 4(a² + b²)
(b) 2(a² + b²)
(c) a² + b²
(d) \(\frac {1}{2}\)(a²+ b²)
Solution:
(b) 2(a² + b²)
Hint:

Question 11.
If the normals of the parabola y² = 4x drawn at the end points of its latus rectum are tangents to the circle (x – 3)² + (y + 2)² = r², then the value of r² is
(a) 2
(b) 3
(c) 1
(d) 4
Solution:
(a) 2
Hint:
y² = 4x
4a = 4
a = 1
End points of latus rectum = (a, ±2a)
= (1, ±2)
Normal equation
xyx + 2ay = x₁y₁ + 2 ay₁
Equation of normal at points (1, ±2)
y = -x + 3, y = x + 3
x + y – 3 = 0, x – y + 3 = 0

Question 12.
If x + y = k is a normal to the parabola y² = 12x, then the value of k is 14.
(a) 3
(b) -1
(c) 1
(d) 9
Solution:
(d) 9
Hint:
y² = 12x ⇒ 4a = 12
⇒ a = 3
y = mx + c ∴ x + y = k
⇒ y = -x + k
∴ m = -1, c = k.
c = -2am – am² ⇒ k = -2a(-1) – a(-1)³
k = -6(-1) – 3(-1) = 6 + 3 = 9
k = 9

Question 13.
The ellipse E₁ : \(\frac {x^2}{9}\) + \(\frac {y^2}{4}\) = 1 is inscribed in a rectangle R whose sides are parallel to the co-ordinate axes. Another ellipse E₂ passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse is
(a) \(\frac {√2}{2}\)
(b) \(\frac {√3}{2}\)
(c) \(\frac {1}{2}\)
(d) \(\frac {3}{4}\)
Solution:
(c) \(\frac {1}{2}\)
Hint:

Question 14.
Tangents are drawn to, the, hyperbola \(\frac {x^2}{9}\) – \(\frac {y^2}{4}\) = 1 parallel to the straight line 2x – y – 1. One of the points of contact of tangents on the hyperbola is
(a) (\(\frac {9}{2√2}\), \(\frac {-1}{√2}\))
(b) (\(\frac {-9}{2√2}\), \(\frac {1}{√2}\))
(c) (\(\frac {9}{2√2}\), \(\frac {1}{√2}\))
(d) (3√3, -2√2)
Solution:
(c) (\(\frac {9}{2√2}\), \(\frac {1}{√2}\))
Hint:
a² = 9 b² = 4, 2x – y = 1
y = 2x – 1
m = 2

Question 15.
The equation of the circle passing through the foci of the ellipse \(\frac {x^2}{16}\) + \(\frac {y^2}{9}\) = 1 having centre at (0, 3) is
(a) x² + y² – 6y – 7 = 0
(b) x² + y² – 6y + 7 = 0
(c) x² + y² – 6y – 5 = 0
(d) x² + y² – 6y + 5 = 0
Solution:
(a) x² + y² – 6y – 7 = 0
Hint:
a² = 16, b² = 16
(h, k) = (0, 3)
e = \(\sqrt{1-\frac {b^2}{a^2}}\) = \(\sqrt{1-\frac {9}{16}}\)
= \(\sqrt{\frac {7}{16}}\) = \(\frac {√7}{4}\)
ae = 4\(\frac {√7}{4}\) = √7.
F(√7, 0) lies on circle.
(x – h)² + (y – k)² = r²
(√7 – 0)² + (0 – 3)² = r² ⇒ √7² + 3² = r²
7 + 9 = r²
⇒ r² = 16.
∴ (x – 0)² + (y – 3)² = 16
x² + y² – 6y + 9 = 16
x² + y² – 6y – 7 = 0

Question 16.
Let C be the circle with centre at (1, 1) and radius = 1. If T is the circle centered at (0, y) passing through the origin and touching the circle C externally, then the radius of T is equal to
(a) \(\frac {√3}{√2}\)
(b) \(\frac {√3}{2}\)
(c) \(\frac {1}{2}\)
(d) \(\frac {1}{4}\)
Solution:
(d) \(\frac {1}{4}\)
Hint:

ΔOO’A
(1 + y)² = (1 – y)² + 1
1 + y² + 2y = 1 + y² – 2y + 1
4y = 1 ⇒ y = \(\frac {1}{4}\)

Question 17.
Consider an ellipse whose centre is of the origin and its major axis is a long x-axis. If its eccentricity is \(\frac {3}{5}\) and the distance between its foci is 6, then the area of the quadrilateral’ inscribed in the ellipse with diagonals as major and minor axis, of the ellipse is
(a) 8
(b) 32
(c) 80
(d) 40
Solution:
(d) 40
Hint:

e = \(\frac {3}{5}\)
2ae = 6 ⇒ 2a(\(\frac {3}{5}\)) = 6
a = 5; b = 4
Area = 4 × \(\frac {1}{2}\) × ab = 2 ab
= 2 × 5 × 4
= 40

Question 18.
Area of the greatest rectangle inscribed in the ellipse \(\frac {x^2}{16}\) + \(\frac {y^2}{9}\) = 1 is
(a) 2ab
(b) ab
(c) \(\sqrt {ab}\)
(d) \(\frac {a}{b}\)
Solution:
(a) 2ab
Hint:

x = a cosθ; y = b sinθ
length = 2acosθ; breadth = 2bsinθ
A = l × b = 4absinθcosθ
A = 2ab sin2θ
\(\frac {dA}{dt}\) = 2ab cos2θ (2)
= 4ab cos2θ
\(\frac {dA}{dt}\) = 0
cos2θ = 0
2θ = \(\frac {π}{2}\)
θ = \(\frac {π}{4}\)
∴ A = 2ab sin²(\(\frac {π}{4}\))
= 2ab sin \(\frac {π}{2}\)
A = 2ab

Question 19.
An ellipse has OB as semi minor axes, F and F’ its foci and the angle FBF’ is a right angle. Then the eccentricity of the ellipse is
(a) \(\frac {1}{√2}\)
(b) \(\frac {1}{2}\)
(c) \(\frac {1}{4}\)
(d) \(\frac {1}{√3}\)
Solution:
(a) \(\frac {1}{√2}\)
Hint:

Distance between foci and end of minor axes = a
∴ F₁B = F₂ = a
F₁F₂ = 2ae
In right angle F₁BF₂
F₁B² + F₂B² = F₁F₂²
a² + a² = (2ae)²
2a² = 4a²e²
e² = \(\frac {2}{4}\) = \(\frac {1}{2}\)
∴ e = \(\frac {1}{√2}\)

Question 20.
The eccentricity of the ellipse
(x – 3)² + (y – 4)² = \(\frac {y²}{9}\) is
(a) \(\frac {√3}{2}\)
(b) \(\frac {1}{3}\)
(c) \(\frac {1}{3√2}\)
(d) \(\frac {1}{√3}\)
Solution:
(b) \(\frac {1}{3}\)
Hint:
PF = e²p³
(x – h)² + (y – k)² = e²(\(\frac {ax+by+c}{\sqrt{a^2+b^2}}\))
(h, k) = (3, 4),
a = 0, c = 0
e² = \(\frac {1}{3}\)
e = \(\frac {1}{3}\)

Question 21.
If the two tangents drawn from a point P to the parabola y2 = 4r are at right angles then the locus of P is {SEA
(a) 2x + 1 = 0
(b) x = -1
(c) 2x – 1 = 0
(d) x = 1
Solution:
(b) x = -1
Hint:
Locus of P = Directrix of y² = 4x; 4a = 4
∴ a = 1
Equation of directrix x = -a = -1
∴ -x = -1

Question 22.
The circle passing through (1, -2) and touching the axis of x at (3, 0) passing through the point
(a) (-5, 2)
(b) (2, -5)
(c) (5, -2)
(d) (-2, 5)
Solution:
(c) (5, -2)
Hint:
(x – 3)² + (y – 0)² + λy = 0
At (1, -2), (1 – 3)² + (-2 – 0)² + λy = 0
4 + 4 – 2λ = 0
8 = 2λ
λ = 4
x² – 6x + 9 + y² + 4y = 0
Apply all the point which satisfied that passes through the circle At (+5, -2),
25 – 30 + 9 + 4 – 8 = 0

Question 23.
The locus of a point whose distance from (- 2, 0) is \(\frac {2}{3}\) times its distance from the line x = \(\frac {-9}{2}\) is
(a) a parabola
(b) a hyperbola
(c) an ellipse
(d) a circle
Solution:
(c) an ellipse
Hint:
P(h, k) Q(-2, 0)
x = –\(\frac {9}{2}\) PQ = \(\frac {2}{3}\)
2x + 9 = 0
\(\sqrt {(h+2)^2+k^2}\) = \(\frac {2}{3}\)|\(\frac {2h+9}{2}\)|
(h + 2)² + k² = \(\frac {1}{9}\)(2h + 9)²
h² + 4 + 4h + k² = \(\frac {1}{9}\)(4h² + 36h + 81)
9h² + 36 + 36h + 9k² = 4h² + 36h + 81
5h² + 9k² = 45
\(\frac {h^2}{9}\) + \(\frac {k^2}{5}\) = 1
\(\frac {x^2}{9}\) + \(\frac {y^2}{5}\) = 1
Which is ellipse.

Question 24.
The values of m for which the line y = mx + 2√5 touches the hyperbola 16x² – 9y² = 144 are the roots of x² – (a + b)x – 4 = 0, then the value of (a + b) is
(a) 2
(b) 4
(c) 0
(d) -2
Solution:
(c) 0
Hint:
a² = 9; b² = 16
a = 3; b = 4
c² = a²m² – b²
(2√5)² = 9m² – 16
20 + 16 = 9m²; m² = \(\frac {36}{9}\)
∴ m = 2 which is roots of x² -(a + b)x – 4 = 0
2² -(a + b)2 – 4 = 0
a + b = 0

Question 25.
If the coordinates at one end of a diameter of the circle x² + y² – 8x – 4y + c = 0 are (11, 2) the cordinates of the other end are
(a) (-3, 2)
(b) (2, -5)
(c) (5, -2)
(d) (-2, 5)
Solution:
(a) (-3, 2)
Hint:

2g = -g; 2f = -4
g = -4; f = -2
c(-g, -f) = (4, 2)
\(\frac {x_1+x_2}{9}\) = 4; \(\frac {y_1+y_2}{2}\) = 2
\(\frac {x_1+11}{2}\) = 4; \(\frac {y_1+2}{2}\) = 2
x₁ = 8 – 11; y₁ = 4 – 2
x₁ = -3; y₁ = 2
∴ Other end be (-3, 2)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.5 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.5

Question 1.
A bridge has a parabolic arch that is 10 m high in the centre and 30 m wide at the bottom. Find the height of the arch 6 m from the centre, on either sides.
Solution:

PQ = 2a = 30 m
a = 15 m
Point Q be (15 , -10)
Equation of the parabola
x² = -4 ay …….. (1)
Q lies on parabola
15² = -4a( -10)
a = \(\frac {225}{40}\)
(1) ⇒ x² = -4(\(\frac {225}{40}\))y
x² = \(\frac {225}{10}\)y
Let B(6, y) lies on parabola
6² = \(\frac {225}{10}\) y₁
y₁ = –\(\frac {36×10}{225}\) = \(\frac {-8}{5}\) = \(\frac {8}{5}\) m
AB = AC – BC = 10 – \(\frac {8}{5}\)
= \(\frac {50-8}{5}\) = \(\frac {42}{5}\)
AB = 8.4 m
∴ The height of the arch 6 m from the centre is 8.4 m.

Question 2.
A tunnel through a mountain for a four lane highway is to have a elliptical opening. The total width of the highway (not the opening) is to be 16 m and the height at the edge of the road must be sufficient for a truck 4 m high to clear if the highest point of the opening is to be 5 m approximately. How wide must the opening be?
Solution:

Let the equation of the ellipse be
\(\frac {x^2}{a^2}\) + \(\frac {y^2}{b^2}\) = 1
Length of semi minor axis b = 5
i,e., \(\frac {x^2}{a^2}\) + \(\frac {y^2}{5^2}\) = 1
Let BB’ be the road width and AA’ be the end points of the opening of the tunnel.
Let CB = 8, BD = 4
∴ D is (8, 4) lies on the ellipse
\(\frac {8^2}{a^2}\) + \(\frac {4^2}{5^2}\) = 1
⇒ a² = \(\frac {25}{9}\) × 64
⇒ a = \(\frac {40}{3}\)
The width AA’ = 2a
= \(\frac {80}{3}\) = 26.66 m
The required width is 26.66 m.

Question 3.
At a water fountain, water attains a maximum height of 4 m at horizontal distance of 0.5 m from its origin. If the path of water is a parabola, find the height of water at a horizontal distance of 0.75 m from the point of origin.
Solution:

Let the equation of parabola be
(x – h)² = -4a (y – k)
Here vertex B (0.5, 4)
∴ Equation of parabola
(x – 0.5)² = -4a(y – 4)
Parabola passes through origin (0, 0)
(0 – 0.5)² = -4a(0 – 4)
(-\(\frac {1}{2}\))² = 16a
∴ \(\frac {1}{4}\) = 16a ⇒ a = \(\frac {1}{64}\)
∴ Equation of parabola
(x – 0.5)² = -4(\(\frac {1}{64}\))(y- 4)
This Parabola passes again through D(0.75, y₁)
∴ (0.75 – 0.5)² = –\(\frac {1}{16}\) (y₁ – 4)
(0.25)² = –\(\frac {1}{16}\) (y₁ – 4)
(\(\frac {1}{4}\))² = –\(\frac {1}{16}\) (y₁ – 4)
\(\frac {1}{16}\) = –\(\frac {1}{16}\) (y₁ – 4)
1 = -y₁ + 4
y₁ = 3
Height of water at a horizontal distance of 0.75 m is 3 m.

Question 4.
An engineer designs a satellite dish with a parabolic cross section. The dish is 5 m wide at the opening and the focus is placed 1.2 m from the vertex
(a) Position a co-ordinate system with the origin at the vertex and the x-axis on the parabola’s axis of symmetry and find an equation of the parabola.
(b) Find the depth of the satellite dish at the vertex.
Solution:

(a) Consider the satellite dish is open rightward parabola
y² = 4 ax ……….. (1)
Clearly a = 1.2m
(1) ⇒ y² = 4(1.2)
y² = 4.8x
(b) Use the point (x₁, 2.5) in (1)
(2.5)² = 4(1.2)x₁
\(\frac{(2.5)^{2}}{4(1.2)}\) = y₁
x₁ = 1.3 m
∴ The depth of the satellite dish at vertex is 1.3 m

Question 5.
The parabolic cable of a 60 m portion of the roadbed of a suspension bridge are positioned as shown below. Vertical cables are to be spaced every 6 m along this portion of the roadbed. Calculate; the lengths of first two of these vertical cables: from the vertex.

Solution:

From the diagram, the equation is x² = 4 ay and it passes through C(30, 13)
Equation of Parabola x² = 4ay.
30² = 4a × 13
4a = \(\frac {30^2}{13}\)
∴ Equation of the parabola is
x² = \(\frac {30^2}{13}\)y
(i) Let VG = 6 and GE = y
∴ E is (6, y) and it lies on the parabola
36 = \(\frac {30^2}{13}\)y
⇒ y = 0.52
Gable from the road = 3 + 0.52
= 3.52 m.

(ii) Let VH = 12 and HF = y
∴ F (12, y) lies on the parabola
12² = \(\frac {30^2}{13}\)y
⇒ y = \(\frac {144×13}{900}\)
= \(\frac {208}{100}\)y
y = 2.08
Cable from the road = 3 + 2.08 = 5.08
The heights of the first two vertical cables from the vertex are 3.52 m and 5.08 m

Question 6.
Cross-section of a Nuclear cooling tower is in the shape of a hyperbola with equation \(\frac {x^2}{30^2}\) – \(\frac {y^2}{44^2}\) = 1. The tower is 150 m tall and the distance from the top of the tower to the centre of the hyperbola is half the distance from the base of the tower to the centre of the hyperbola. Find the diameter of the top and base of the tower.

Solution:

Equation of hyperbola is \(\frac {x^2}{30^2}\) – \(\frac {y^2}{44^2}\) = 1
Given OC = \(\frac {1}{2}\) OD and CD = 150
∴ OC = 50 m and OD = 100 m
Let the Radius of top of the tower be x₁ and bottom of the tower be x₂.
∴ Points A(x₁, 50) and B(x₂, 100)
Hyperbola passes through A(x₁, 50)

∴ Radius of the top = 45.41 m.
Diameter of the top = 90.82 m
Also
The hyperbola again passes through B(x₂, 100)

∴ Radius of the base = 74.48 m.
Diameter of the base = 148.96 m
∴ Diameter of the top and base of the tower are 90.82 m and 148.96 m.

Question 7.
A rod of length 1.2 m moves with its ends always touching the co-ordinate axes. The locus of a point P on the rod, which is
0. 3 m from the end in contact with x axis is an ellipse. Find the eccentricity.
Solution:

Length of rod BD = 1.2 m
Let P(x, y) be any point on the Rod such
that PB = 0.3 m
∴ PD = 1.2 – 0.3 = 0.9 m
Let ΔPAB and ΔPCD are similar triangles
In ΔPAB sin θ = \(\frac {y}{0.3}\)
In A PCB cos θ = \(\frac {y}{0.9}\)
We know that sin² θ + cos² θ = 1

Question 8.
Assume that water’issuing from the end of a horizontal pipe, 7.5 m. above the ground, describes a parabolic path. The vertex of the parabolic path is at The end of the pipe. At position 2.5 in below the line of the pipe, the flow of water has curved outward 3 m beyond the vertical, line through the end of the pipe. How far beyond this vertical line will the water strike the ground?
Solution:

Equation of the water path is
x² = – 4 ay
Use the point (3, – 2.5) in (1)
(3)² = – 4a(- 2.5)
9 = 10a
a = \(\frac{9}{10}\) substituting in (1)
(1) ⇒ x² = -4\(\frac{9}{10}\)y …………. (2)
Use the point (x₁, -7.5) in (2)
(2) ⇒ x₁² = -4 \(\frac{9}{10}\)(-7.5) ⇒ x₁² = 30(\(\frac{9}{10}\))
x₁ = \(\sqrt{3 \times 9}\)
x₁ = \(3 \sqrt{3}\) m
∴ The water strikes the ground \(3 \sqrt{3}\) m beyond the vertical line.

Question 9.
On lighting a rocket cracker it gets projected in a parabolic path and reaches a maximum height of 4 in when it is 6 m away from the point of projection. Finally, it reaches the ground 12 in away from the starting-point. Find the angle of! projection.
Solution:

Equation of the parabola be x² = – 4ay ……. (1)
B(6, -4) lies on parabola
6² = -4a(-4)
\(\frac {36}{16}\) = a ⇒ a = \(\frac {9}{4}\)
(1) ⇒ x² = -(\(\frac {9}{4}\))y
x² = -9y ………. (2)
Now need tofind slope at (-6, -4)
Diff (2) w.r.to x
2x = -9 \(\frac {dy}{dx}\)
\(\frac {dy}{dx}\) = \(\frac {2x}{-9}\)
At(-6, -4), \(\frac {dy}{dx}\) = \(\frac {2(-6)}{-9}\) = \(\frac {12}{9}\) = \(\frac {4}{3}\)
tan θ = \(\frac {4}{3}\)
θ = tan^-1(\(\frac {4}{3}\))

Question 10.
Points A and B are 10 km apart and it is determined from the sound of an explosion heard at those points at different times that the location of the explosion is 6 km closer to A than 5. Show that the location of the explosion is restricted to a particular curve and find an equation of it.
Solution:
As shown in figure, A and B are on both sides of x-axis at Co-ordinates (-5, 0) and (5, 0)
The distance between A and B is 10. A point C is on the graph at Co-ordinates (x, y)
C is 6 km closer to A than B.

Squaring on both sides we get,
(x – 5)² + y² = 36 + (x + 5)² + y² + 12(\(\sqrt {(x+5)^2+y^2}\))
x² + 25 – 10x + y² = x² + 10x + y² + 36 + 25 + 12\(\sqrt {(x+5)^2+y^2}\)
-20x – 36 = 12\(\sqrt {(x+5)^2+y^2}\)
(÷ by 4) ⇒ -5x – 9 = 3\(\sqrt {(x+5)^2+y^2}\)
Squaring both sides we get,
25x² + 81 + 90x = 9(x² + 25 + 10x + y²)
25x² + 81 + 90x – 9x² – 90x – 9y² – 225 = 0
16x² – 9y² – 144 = 0
16x² – 9y² = 144
(÷ by 144) ⇒ \(\frac {x^2}{9}\) – \(\frac {y^2}{16}\) = 1 is the required equation of hyperbola.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.4 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.4

Question 1.
Find the equations of the two tangents that can be drawn from (5, 2) to the ellipse 2x² + 7y² = 14.
Solution:
2x² + 7y² = 14
(÷ by 14) ⇒ \(\frac{x^{2}}{7}+\frac{y^{2}}{2}\) = 1
comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
we get a² = 7 and b² = 2
The equation of tangent to the above ellipse will be of the form
y = mx + \(\sqrt{a^{2} m^{2}+b^{2}}\) ⇒ y = mx + \(\sqrt{7 m^{2}+2}\)
Here the tangents are drawn from the point (5, 2)
⇒ 2 = 5m + \(\sqrt{7 m^{2}+2}\) ⇒ 2 – 5m = \(\sqrt{7 m^{2}+2}\)
Squaring on both sides we get
(2 – 5m)² = 7m² + 2
25m² + 4 – 20m – 7m² – 2 = 0
18m² – 20m + 2 = 0
(÷ by 2) ⇒ 9m² – 10m + 1 = 0
(9m – 1) (m – 1) = 0
‘ m = 1 (or) m = 1/9
When m = 1, the equation of tangent is
y = x + 3 or x – y + 3 = 0
When m = \(\frac{1}{9}\) the equation of tangent is 9
y = \(=\frac{x}{9}+\sqrt{\frac{7}{81}+2}\) (i.e.) y = \(\frac{x}{9}+\frac{13}{9}\)
9y = x + 13 or x – 9y + 13 = 0

Question 2.
Find the equations of tangents to the hyperbola \(\frac {x^2}{16}\) – \(\frac {y^2}{64}\) = 1 which are parallel to 10x – 3y + 9 = 0.
Solution:
Equation of Hyperbola \(\frac {x^2}{16}\) – \(\frac {y^2}{64}\) = 1
∴ a² = 16, b² = 64
Tangent is parallel to the line
10x – 3y + 9 = 0 is
10x – 3y + k = 0
∴ 3y = 10x + k
y = \(\frac {10}{3}\)x + \(\frac {k}{3}\)
∴ m = \(\frac {10}{3}\) c = \(\frac {k}{3}\)
Condition that the line y = mx + c to be tangent to the hyperbola is
c² = a²m² – b²

k² = 1024
k = ±32
∴ Equation of tangent
⇒ 10x – 3y ± 32 = 0

Question 3.
Show that the line x – y + 4 = 0 is a tangent to the ellipse x² + 3y² = 12. Also find the co-ordinates of the point of contact.
Solution:
The given ellipse is x² + 3y² = 12
(÷ by 12) ⇒ \(\frac{x^{2}}{12}+\frac{y^{2}}{4}\) = 1
(ie.,) Here a² = 12 and b² = 4
The given line is x – y + 4 = 0
(ie.,) y = x + 4
Comparing this line with y = mx + c
We get m = 1 and c = 4
The condition for the line y = mx + c
To be a tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 is c² = a²m² + b²
LHS = c² = 4² = 16
RHS: a²m² + b² = 12( 1 )² + 4 = 16
LHS = RHS The given line is a tangent to the ellipse. Also the point of contact is
\(\left(\frac{-a^{2} m}{c}, \frac{b^{2}}{c}\right)=\left[-\left(\frac{12(1)}{4}\right), \frac{4}{4}\right]\) (i.e.,) (-3, 1)

Question 4.
Find the equation of the tangent to the parabola y² = 16x perpendicular to 2x + 2y + 3 = 0.
Solution:
Equation of the parabola
y² = 16x
4 a = 16
a = 4
Tangent is perpendicular to the line
2x + 2y + 3 = 0 is 2x – 2y + k = 0
2x – 2y + k = 0
2y = 2x + k
y = x + \(\frac {k}{2}\)
m = 1 c = \(\frac {k}{2}\)
Condition that the line y = mx + c to be tangent to the parabola is
c = \(\frac {a}{m}\)
\(\frac {k}{2}\) = \(\frac {4}{1}\)
k = 8
Equation of the tangent
2x – 2y + 8 = 0
÷ by 2 ⇒ x – y + 4 = 0

Question 5.
Find the equation of the tangent at t = 2 to the parabola y² = 8x (Hint: use parametric form).
Solution:
y² = 8x
Comparing this equation with y² = 4ax
we get 4a = 8 ⇒ a = 2
Now, the parametric form for y² = 4ax is x = at², y = 2at
Here a = 2 and t = 2
⇒ x = 2(2)² = 8 and y = 2(2) (2) = 8
So the point is (8, 8)
Now eqution of tangent to y² = 4 ax at (x₁, y₁) is yy₁ = 2a(x + x₁)
Here (x₁, y₁) = (8, 8) and a = 2
So equation of tangent is y(8) = 2(2) (x + 8)
(ie.,) 8y = 4 (x + 8)
(÷ by 4) ⇒ 2y = x + 8 ⇒ x – 2y + 8 = 0
Aliter
The equation of tangent to the parabola y² = 4ax at ‘t’ is
yt = x + at²
Here t = 2 and a = 2
So equation of tangent is
(i.e.,) y(2) = x + 2(2)²
2y = x + 8 ⇒ x – 2y + 8 = 0

Question 6.
Find the equations of the tangent and normal to hyperbola 12x² – 9y² = 108 at θ = \(\frac {π}{3}\) .
(Hint: use parametric form)
Solution:
(i) Equation of the tangent to hyperbola be

⇒ 4x – 3y = 6
⇒ 4x – 3y – 6 = 0

(ii) Equation of the normal to hyperbola be

⇒ 3x + 4y – 42 = 0

Question 7.
Prove that the point of intersection of the tangents at ‘t₁‘ and ‘t₂‘ on the parabola y² = 4ax is [at₁t₂, a(t₁ + t₂)].
Solution:
Equation of the tangent of parabola y² = 4ax be
at t₁ yt₁ = x + at₁² ……….. (1)
at t₂ yt₂ yt = x + at₂² ……….. (2)
(1) – (2) ⇒ y(t₁ – t₂) = a(t₁² – t₂²)
y(t₁ – t₂) = a(t₁ + t₂)(t₁ – t₂)
y = a(t₁ + t₂)
(1) ⇒ t₁a(t₁ + t₂) = x + at₁²
x = at₁² + at₁t₂ – at₁²
x = at₁t₂
Point of intersection be [at₁t₂, a(t₁ + t₂)]

Question 8.
If the normal at the point ‘t₁‘ on the parabola y² = 4ax meets the parabola again at the point t₂ then prove that t₂ = -(t₁ + \(\frac {2}{t_1}\))
Solution:
Equation of normal to y² = 4at’ t’ is y + xt = 2at + at³.
So equation of normal at ‘t₁’ is y + xt₁ = 2at₁ + at₁³
The normal meets the parabola y² = 4ax at ‘t₂’ (ie.,) at (at₂², 2at₂)
⇒ 2at₂ + at₁t₂² = 2at₁ + at₁³
So 2a(t₂ – t₁) = at₁³ – at₁t₂²
⇒ 2a(t₂ – t₁) = at₁(t₁² – t₂²)
⇒ 2(t₂ – t₁) = t₁(t₁ + t₂)(t₁ – t₂)
⇒ 2= -t₁(t₁ + t₂)
⇒ t₁ + t₂ = \(\frac{-2}{t_{1}}\)
⇒ t₂ = \(-t_{1}-\frac{2}{t_{1}}=-\left(t_{1}+\frac{2}{t_{1}}\right)\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.3 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.3

Question 1.
Identify the type of conic section of each of the equations.
(1) 2x² – y² = 7
(2) 3x² + 3y² – 4x + 3y + 10 = 0
(3) 3x² + 2y² = 14
(4) x² + y² + x – y = 0
(5) 11x² – 25y² – 44x + 50y – 256 = 0
(6) y² + 4x + 3y + 4 = 0
Solution:
(1) 2x² – y² = 7
Comparing this equation with the general equation of the conic
Ax² + Bxy + Cy² + Dx + Ey + F = 0
We get A = 2, C = – 1
Elere A ≠ C also A and C are of opposite signs.
So the conic is a hyperbola.

(2) 3x² + 3y² – 4x + 3y + 10 = 0
A = 3, B = 0, C = 3, D = -4, E = 3, F = 10
A = C and B = 0 (No xy term)
∴ It is a circle.

(3) 3x² + 2y² = 14
A = 3, B = 0, C = 2, F = -14
A ≠ C and A & C are the same signs.
∴ It is an ellipse.

(4) x² + y² + x – y = 0
Comparing this equation with the general equation of the conic
Ax² + Bxy + Cy² + Dx + Ey + F = 0
We get A = C and B = 0
So the given conic is a circle.

(5) 11x² – 25y² – 44x + 50y – 256 = 0
A =11, B = 0, C = -25, D = -44, E = 50, F = -256
A ≠ C and A & C are the opposite signs.
∴ It is a hyperbola.

(6) y² + 4x + 3y + 4 = 0
Comparing this equation with the general equation of the conic
Ax² + Bxy + Cy² + Dx + Ey + F = 0
We get A = 0 and B = 0
So the conic is a parabola.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.2 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.2

Question 1.
Find the equation of the parabola in each of the cases given below:
(i) focus (4, 0) and directrix x = -4.
(ii) passes through (2, – 3) and symmetric about y axis.
(iii) vertex (1,-2) and focus (4, – 2).
(iv) end points of latus rectum (4, -8) and (4, 8).
Solution:
(i) focus (4, 0) and directrix x = -4
Parabola is open rightwards vertex (0, 0)

a = 4
(Distance AS = 4 unit)
f² = 4(4) x
Equation of parabola
y² = 16x.

(ii) passes through (2, – 3) and symmetric about y-axis

x² = 4ay
It passes through (2, -3)
⇒ 2² = 4a(-3)
4 = -12a ⇒ a = \(-\frac{1}{3}\) ⇒ 4a = \(-\frac{4}{3}\)
∴ Equation of parabola is x² = \(-\frac{4}{3}\) y
3x²= – 4y.

(iii) vertex (1,-2) and focus (4, – 2)

In given data the parabola is open rightwards and symmetric about the line parallel to x-axis.
Equation of parabola
(y – k)² = 4a(x – h)
Vertex (h, k) = (1, -2)
(y + 2)² = 4a(x – 1)
a = AS = 3
Equation of parabola
(y + 2)² = 4(3)(x – 1)
(y + 2)² = 12(x – 1)

(iv) end points of latus rectum (4, -8) and (4, 8)

Focus = (4, 0)
Equation of the parabola will be of the form y² = 4ax
Here a = 4
⇒ y² = 16x

Question 2.
Find the equation of the ellipse in each of the cases given below:
(i) foci (± 3, 0), e = \(\frac {1}{2}\)
(ii) foci (0, ±4) and end points of major axis are (0, ±5).
(iii) length of latus rectum 8, eccentricity = \(\frac {3}{5}\) and major axis on x-axis.
(iv) length of latus rectum 4, distance between foci and major axis as y axis.
Solution:
(i) foci (± 3, 0), e = \(\frac {1}{2}\)
foci (± c, 0) = (± 3, 0)

e = \(\frac {1}{2}\)
c = ae = 3
a(\(\frac {1}{2}\)) = 3
a = 6 ⇒ a² = 36
b² = a² – c²
b² = 36 – 9 = 27
b² = 27
Equation of the ellipse be \(\frac {x^2}{a^2}\) + \(\frac {y^2}{b^2}\) = 1
\(\frac {x^2}{36}\) + \(\frac {y^2}{27}\) = 1

(ii) foci (0, ±4) and end points of major axis are (0, ±5)

foci (0, ±c) = (0, +4)
vertex (0, ±a) = (0, ±5)
∴ c = 4, a = 5
ae = 4
5e = 4
e = \(\frac {4}{5}\)
b² = a² – c²
= 25 – 16
b² = 9
Equation of the ellipse be \(\frac {x^2}{b^2}\) + \(\frac {y^2}{a^2}\) = 1
\(\frac {x^2}{9}\) + \(\frac {y^2}{25}\) = 1

(iii) length of latus rectum 8, eccentricity = \(\frac {3}{5}\) and major axis on x-axis.
e = \(\frac {3}{5}\)
Latus rectum \(\frac {2b^2}{a}\) = 8

(iv) length of latus rectum 4, distance between foci 4√2 and major axis as y-axis

Given \(\frac{2 b^{2}}{a}\) = 4 and 2ae = \(4 \sqrt{2}\)
Now \(\frac{2 b^{2}}{a}\) = 4 2b² = 4a
⇒ b² = 2a
2ae = \(4 \sqrt{2}\) ae = \(2 \sqrt{2}\)
So a²e² = 4(2) = 8
We know b² = a²(1 – e²) = a² – a²e²
⇒ 2a = a² – 8 ⇒ a² – 2a -8 = 0
⇒ (a – 4) (a +2) = 0 ⇒a = 4 or -2
As a cannot be negative
a = 4 So a² = 16 and b² = 2(4) = 8
Also major axis is along j-axis
So equation of ellipse is \(\frac{x^{2}}{8}+\frac{y^{2}}{16}\) = 1

Question 3.
Find the equation of the hyperbola in each of the cases given below:
(i) foci (± 2, 0), eccentricity = \(\frac {3}{2}\)
(ii) centre (2, 1) one of the foci (8, 1) and corresponding directrix x = 4.
(iii) passing through (5, -2) and length of the transverse axis along x axis and length 8 units.
Solution:
(i) foci (± 2, 0), eccentricity = \(\frac {3}{2}\)

(ii) centre (2, 1) one of the foci (8, 1) and corresponding directrix x = 4.
Distance CS = ae = 6 …….. (1)
Directrix \(\frac {a}{e}\) = 4 ……… (2)
(1) × (2) ⇒ ae × \(\frac {a}{e}\) = 24
a² = 24

∴ c = ae = 6
b² = c² – a²
= 36 – 24 = 12
The transverse axis is parallel to x-axis
∴ \(\frac {(x-h)^2}{a^2}\) – \(\frac {(y – k)^2}{b^2}\) = 1 (h, k) = (2, 1)
\(\frac {(x-2)^2}{24}\) – \(\frac {(y – 1)^2}{12}\) = 1

(iii) passing through (5,-2) and length of the transverse axis along x axis and of length 8 units.
Transverse axis along x-axis
\(\frac {x^2}{a^2}\) – \(\frac {y^2}{b^2}\) = 1
Length of transverse axis 2a = 8
⇒ a = 4

Question 4.
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
(i) y² = 16x
(ii) x² = 24y
(iii) y² = -8x
(iv) x² – 2x + 8y + 17 = 0
(v) y² – 4y – 8x + 12 = 0
Solution:
(i) y² = 16x

4a = 16
a = 4
(a) Vertex V (0, 0)
(b) Focus S(a, 0) = S(4, 0)
(c) Equation of the directrix x = – a
x = -4 ⇒ x + 4 = 0
(d) Length of the latus rectum = 4a = 4(4)
= 16

(ii) x² = 24y

(a) Vertex V (0, 0),
(b) Focus S (0, a) = S(0, 6)
(c) Equation of the directrix y = -a = -6
⇒ y + 6 = 0
(d) Length of the latus rectum = 4a
= 4 (6) = 24

(iii) y² = -8x
4a = 8,
a = 2

(a) Vertex V(0, 0) = ( 0, 0)
(b) Focus S(-a, 0) = (-2, 0)
(c) Equation of the directrix x = a = 2
x – 2 = 0
(d) Length of the latus rectum 4a = 8
(iv) x² – 2x + 8y + 17 = 0
x² – 2x = -8y – 17
(x – 1)² = -8y – 17 + 1
(x – 1)² = -8y – 16
(x – 1)² = -8(y + 2)
It is form of (x – h)² = -4a(y – k)
4a = 8 ⇒ a = 2
(a) Vertex be (h, k) = (1, -2)

(b) Foeus = (0 +h, -a + k) = (0 + 1, -2 – 2) = (1, -4)
(c) Equation of the directrix is y + k + a = 0
y – 2 + 2= 0
y = 0
(d) Length of latus rectum is 4a = 4 × 2 = 8 units,

(v) y² – 4y – 8x + 12 = 0

y² – 4y = 8x – 12
(y – 2)² = 8x – 12 + 4
= 8x – 8
= 8 (x – 1)
(y – 2)² = 8 (x – 1)
It is form of (y – k)² = Aa(x – h)
4a = 8 ⇒ a = 2
(a) Vertex (h, k) = (1, 2)
(b) Focus = (a+h, 0 + k) = (2 + 1, 0 + 2) = (3, 2)
(c) Equation of the directrix x = -a + h
= -2 + 1
= -1
x + 1 = 0
(d) Length of latus rectum is
4a = 4 × 2 = 8 units.

Question 5.
Identify the type of conic and find centre, foci, vertices and directrices of each of the following:
(i) \(\frac {x^2}{25}\) + \(\frac {y^2}{9}\) = 1
(ii) \(\frac {x^2}{3}\) + \(\frac {y^2}{10}\) = 1
(iii) \(\frac {x^2}{25}\) – \(\frac {y^2}{144}\) = 1
(iv) \(\frac {y^2}{16}\) – \(\frac {x^2}{9}\) = 1
Solution:
(i) \(\frac{x^{2}}{25}+\frac{y^{2}}{9}\) = 1
It is of the form \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, which is an ellipse
Here a² = 25, b² = 9
a = 5, b = 3
e² = \(\frac{a^{2}-b^{2}}{a^{2}}=\frac{25-9}{25}=\frac{16}{25}\) ⇒ e = \(\frac{4}{5}\)
Now e = \(\frac{4}{5}\) and a = 5 ⇒ ae = 4 and \(\frac{a}{e}=\frac{5}{4 / 5}=\frac{25}{4}\)
Here the major axis is along x axis
∴ Centre = (0, 0)
Foci = (± ae, 0) = (± 4, 0)
Vertices = (± a, 0) = (±5, 0)
Equation of directrix x = ± \(\frac{a}{e}\) (ie.,) x = ± \(\frac{25}{4}\)

(ii) \(\frac {x^2}{3}\) + \(\frac {y^2}{10}\) = 1
It is an ellipse. The major axis is along y axis

a² = 10 b² = 3
a = \(\sqrt {10}\) b = √3
c² = a² – b²
= 10 – 3 = 7
c = √7
ae = √7 .
\(\sqrt {10}\) = √7
e = \(\sqrt {\frac{7}{10}}\)
(a) Centre (0, 0)
(b) Vertex (0, ±a) = (0, ±\(\sqrt {10}\))
(c) Foci (0, ±c) – (0, ±√7)
(d) Equation of the directrix a
y = ±\(\frac{a}{e}\)
= ±\(\frac{\sqrt {10}}{√7}\).\(\sqrt {10}\) = ±\(\frac {10}{√7}\)
y = ±\(\frac {10}{√7}\)

(iii) \(\frac {x^2}{25}\) – \(\frac {y^2}{144}\) = 1
It is Hyperbola. The transverse axis the x axis.

a² = 25; b² = 144
a = 5; b = 12
c² = a² + b²
= 25 + 144 = 169
c = 13
ae = 13
5e = 13
e = \(\frac {13}{5}\)
(a) Centre (0, 0)
(b) Vertex (± a, 0) = (± 5, 0)
(c) Foci (± c, 0) = (± 13, 0)
(d) Equation of the directrix
x = ±\(\frac {a}{e}\) = ±\(\frac {5}{\frac{13}{5}}\) = ±\(\frac {25}{13}\)
x = ±\(\frac {25}{13}\)

(iv) \(\frac {y^2}{16}\) – \(\frac {x^2}{9}\) = 1
It is Hyperbola. The transverse axis the y axis.

a² = 16; b² = 9
a = 4; b = 3
c² = a² + b²
= 16 + 6 = 25
c = 5
ae = 5
4e = 5
e = \(\frac {5}{4}\)
(a) Centre (0, 0)
(b) Vertex (0, ±a) = (0, ±4)
(c) Foci (0, ±ae) = (0, ±5)
(d) Equation of the directrix
y = ±\(\frac {a}{e}\) = ±\(\frac {4}{\frac{5}{4}}\) = ±\(\frac {16}{5}\)
y = ±\(\frac {16}{5}\)

Question 6.
Prove that the length of the latns rectum of the hyperbola \(\frac {x^2}{a^2}\) – \(\frac {y^2}{b^2}\) = 1 is \(\frac {2b^2}{a}\)
Solution:
The latus rectum LL’ of an hyperbola \(\frac {x^2}{a^2}\) – \(\frac {y^2}{b^2}\) = 1 passes through S(ae, 0)
Hence L is (ae, y₁)

Hence proved

Question 7.
Show that the absolute value of the difference of the focal distances of any point P on the hyperbola is the length of its transverse axis.
Solution:

Let P be a point on the hyperbola.
Definition of conic
\(\frac {SP}{PM}\) = e; \(\frac {S’P}{PM’}\) = e
SP = e(PM) ……..(1)
S’P = e (PM’) ……….(2)
(2) – (1) ⇒ S’P – SP = e PM’- e PM
= e(PM’ – PM)
= e MM’
= e ZZ’
[∵ MM’ = ZZ’ = \(\frac {2a}{e}\) ]
= e(\(\frac {2a}{e}\))
S’P – SP = 2a (constant)
= length of the transverse axis.

Question 8.
Identify the type of conic and find centre, foci, vertices and directrices of each of the following:

(v) 18x² + 12y² – 144x + 48y + 120 = 0
(vi) 9x² – y² – 36x – 6y + 18 = 0
Solution:
(i) \(\frac {(x-3)^2}{225}\) + \(\frac {(y-4)^2}{289}\) = 1

It is an ellipse. The major axis is parallel to y axis
a² = 289, b² = 225
a = 17, b = 15
c² = a² – b²
= 289 – 225 = 64
c = 8
ae = 8
17e = 8
e = \(\frac {8}{17}\)
Centre (h, k) = (3, 4)
Vertices (h, ±a + k) = (3, 17 + 4) & (3, -17 + 4)!
= (3, 21) and (3, -13)
Foci (h + 0, ± c + k) = (3, 8 + 4) & (3, -8 + 4)
= (3, 12) and (3, -4)

(ii) \(\frac {(x+1)^2}{100}\) + \(\frac {(y-2)^2}{64}\) = 1
It is an ellipse. The major axis is parallel to the x-axis.
a² = 100, b² = 64
a = 10, b = 8
c² = a² – b²
= 100 – 64 = 36
c = 6
ae = 6
10 e = 6
e = \(\frac {6}{10}\) = \(\frac {3}{5}\)
centre (h, k) = (-1, 2)
vertices (h±a, k) = (-1±10, 2)
= (-1+10, 2) & (-1-10, 2)
= (9, 2) & (-11, 2)
foci (h±c, k) = (-1±6, 2)
= (-1+6, 2) & (-1-6, 2)
= (5, 2) & (-7, 2)
directrix x = ±\(\frac {a}{e}\) + h

(iii) \(\frac {(x+3)^2}{225}\) + \(\frac {(y-4)^2}{64}\) = 1
It is an hyperbola. The transverse axis is parallell to x axis.
a² = 225, b² = 64
a = 15, b = 8
c² = a² – b²
= 225 + 64
c² = 289
c = 17
ae = 17
5e = 17
e = \(\frac {17}{15}\)
centre (h, k) = (-3, 4)
vertices (h±a, k) = (-3±15, 4)
= (-3+15, 4) & (-3-15, 4)
= (12, 4) & (-18, 4)
foci (h±c, k) = (-3±17, 4)
= (-3+17, 4) & (-3-17, 4)
= (14, 4) & (-20, 4)
directrix x = ±\(\frac {a}{e}\) + h

(iv) \(\frac {(y-2)^2}{25}\) + \(\frac {(x+1)^2}{16}\) = 1
It is an hyperbola. The transverse axis is parallell to y axis.
a² = 25, b² = 16
a = ±5, b = 4
c² = a² + b²
= 25 + 16
= 41
c = \(\sqrt {41}\)
ae = \(\sqrt {41}\)
5 e = \(\sqrt {41}\)
e = \(\frac {\sqrt {41}}{5}\)
centre (h, k) = (-1, 2)
vertices (h, ±a + k) = (-1, ±5 + 2)
= (-1, 5 + 2) & (-1, -5 + 2)
= (-1, 7) & (-1, -3)
foci (h, ±c + k) = (-1, ±\(\sqrt {41}\) + 2)
= (-1, \(\sqrt {41}\) + 2) & (-1, –\(\sqrt {41}\) + 2)
directrix x = ±\(\frac {a}{e}\) + k

(v) 18x² + 12y² – 144x + 48y + 120 = 0
18x² – 144x + 12y² + 48y = -120
18 (x² – 8x) + 12 (y² + 4y) = -120
18 (x – 4)² + 12 (y + 2)² = -120 + 288 + 48
18(x – 4)² + 12 (y + 2)² = 216
\(\frac {18(x-4)^2}{216}\) + \(\frac {12(y+2)^2}{216}\) = 1
\(\frac {(x-4)^2}{12}\) + \(\frac {(y+2)^2}{18}\) = 1
It is an ellipse. The major axis is parallell to y axis.
a² = 18, b² = 12
a = \(\sqrt {18}\), b = 2√3
= 3 √2
c² = a² + b²
= 18 – 12
= 6
c = √6
ae = √6
3√2 e = √6
e = \(\frac {√6}{3√2}\) = \(\frac {√3}{3}\) = \(\frac {1}{√3}\)
centre (h, k) = (4, -2)
vertices (h, ±a + k) = (4, ±3√2 – 2)
= (4, 3√2 – 2) & (4, -3√2 – 2)
foci (h, ±c + k) = (4, ±√6 – 2)
= (4, ±√6 – 2) & (4, -√6 – 2)
directrix y = ±\(\frac {a}{e}\) + k
= ±\(\frac {3√2}{1}\) – 2
= ±3√6 – 2
y = 3√6 – 2 & y = -3√6 – 2

(vi) 9x² – y² – 36x – 6y + 18 = 0
9x² – 36x – y² – 6y = – 18
9(x² – 4x) – (y² + 6y) = -18
9(x – 2)² – (y + 3)² = -18 + 36 – 9
9(x – 2)² – (y + 3)² = 9
\(\frac {(x-2)^2}{1}\) – \(\frac {(y+3)^2}{9}\) = 1
It is hyperbola. The transverse axis is parallel to x axis.
a² = 1; b² = 9
a = 1; b = 3
c² = a² + b²
= 1 + 9
= 10
c = \(\sqrt {10}\)
ae = \(\sqrt {10}\)
e = \(\sqrt {10}\)
centre (h, k) = (2, -3)
vertices (h ± a, k) = (2 ± 1, -3)
= (2 + 1, -3) & (2 – 1, -3)
= (3, -3) & (1, -3)
foci (h ± c, k) = (2 ±\(\sqrt {10}\), -3)
= (2 + \(\sqrt {10}\), -3) & (2 –\(\sqrt {10}\), -3)
directrix x = ±\(\frac {a}{e}\) + h
= ±\(\frac {1}{\sqrt {10}}\) + 2 & x = –\(\frac {1}{\sqrt {10}}\) + 2

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.1 Textbook Questions and Answers, Notes.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.1

Question 1.
Obtain the equation of the circles with a radius of 5 cm and touching the x-axis at the origin in a general form.
Solution:

Given radius = 5 cm and the circle is touching x axis
So centre will be (0, ± 5) and radius = 5
The equation of the circle with centre (0, ± 5) and radius 5 units is
(x – 0)² + (y ± 5)² = 5²
(i.e) x² + y² ± 10 y + 25 – 25 = 0
(i.e) x² + y² ± 10y = 0

Question 2.
Find the equation of the circle with centre (2, – 1) and passing through the point (3, 6) in standard form.
Solution:
Centre = (2, -1) = (h, k)
Passing through the point (3, 6)
Equation of the circle (x – h)² + (y – k)² = r² ………. (1)
(3 – 2)² + (6 + 1)² = r²
1² + 7² = r²
1 + 49 = r²
r² = 50
(1) ⇒ (x – 2)² + (y + 1)² = 50

Question 3.
Find the equation of circles that touch both the axes and pass-through (-4, -2) in a general form.
Solution:

Since the circle touches both the axes, its centre will be (r, r) and the radius will be r.
Here centre = C = (r, r) and point on the circle is A = (-4, -2)
CA = r ⇒ CA² = r²
(i.e) (r + 4)² + (r + 2)² = r²
⇒ r² + 8r +16 + r² + 4r + 4 – r² = 0
(i.e) r² + 12r + 20 = 0
(r + 2) (r + 10) = 0
⇒ r = -2 or -10
When r = -2, the equation of the circle will be (x + 2)² + (y + 2)² = 2²
(i.e) x² + y² + 4x + 4y + 4 = 0
When r = -10, the equation of the circle will be (x + 10)² + (y + 10)² = 10²
(i.e) x² + y² + 20x + 20y + 100 = 0

Question 4.
Find the equation of the circles with centre (2, 3) and passing through the intersection of the lines 3x – 2y – 1 =0 and 4x + y – 27 = 0.
Solution:
centre (2, 3) = (h, k)
Point of intersection
Solve 3x – 2y – 1 = 0 ………. (1)
4x + y – 27 = 0 ……… (2)
(1) ⇒ 3x – 2y = 1
(2) × 2 ⇒ 8x + 2y = 54
11x = 55
x = 5
put in (1)
15 – 2y – 1 = 0
14 = 2y
y = 7
Passing-through point is (5, 7)
Equation of circle be (x – h)² + (y – k)² = r² ……….(3)
(5 – 2)² + (7 – 3)² = r²
3² + 4² = r²
r² = 25
∴ (3) ⇒ (x – 2)² + (y – 3)² = 25
x² – 4x + 4 + y² – 6y + 9 – 25 = 0
x² + y² – 4x – 6y – 12 = 0

Question 5.
Obtain the equation of the circle for which (3, 4) and (2, -7) are the ends of a diameter.
Solution:
The equation of a circle with (x₁ , y₁) and (x₂ , y₂ ) as end points of a diameter is
(x – x₁ )(x – x₂) + (y – y₁ )(y – y₂) = 0
Here the end points of a diameter are (3, 4) and (2, -7)
So equation of the circle is (x – 3 )(x – 2 ) + (y – 4) (y + 7.) = 0
x² + y² – 5x + 37 – 22 = 0

Question 6.
Find the equation of the circle through the points (1, 0), (-1, 0) and (0, 1).
Solution:
Let the general equation of the circle be
x² + y² + 2gx + 2fy + c = 0
It passes through the points (1, 0), (-1, 0) and (0,1)
1 + 0 + 2g + c = 0
2g + c = -1 ………(1)
1 + 0 – 2g + c = 0
-2g + c = -1 …………(2)
0 + 1 + 0 + 2f + c = 0
2f + c = -1
(1) + (2) ⇒ 2c = -2
c = -1
substitute in eqn (1)
2g – 1 = -1
2g = 0
g = 0
substitute in eqn (3)
2f – 1 = -1
2f = -1 + 1
2f = 0
f = 0
Therefore, the required equation of the circle
x² + y² – 1 = 0

Question 7.
A circle of area 9π square units has two of its diameters along the lines x + y = 5 and: x – y = 1. Find the equation of the circle.
Solution:

Area of the circle = 9π
(i.e) πr² = 9π
⇒ r² = 9 ⇒ r = 3
(i.e) radius of the circle = r = 3
The two diameters are x + y = 5 and x – y = 1
The point of intersection of the diameter is the centre of the circle = C
To find C: Solving x + y = 5 ……… (1)
x – y = 1 ………. (2)
(1) + (2) ⇒ 2x = 6 ⇒ x = 3
Substituting x = 3 in (1) we get
3 + y = 5 ⇒ y = 5 – 3 = 2
∴ Centre = (3, 2) and radius = 3
So equation of the circle is (x – 3)² + (y – 2)² = 3²
(i.e) x² + y² – 6x – 4y + 4 = 0

Question 8.
If y = 2√2 x + c is a tangent to the circle x² + y² = 16, find the value of c.
Solution:
The condition of the line y = mx + c to be a tangent to the circle x² + y² = a² is
c² = a²( 1 + m²)
a² = 16; m = 2√2 ⇒ m² = 4 × 2 = 8
c² = 16(1+8)
c² = 16(9)
c = ±4 × 3 = ±12
∴ c = ± 12.

Question 9.
Find the equation of the tangent and normal to the circle x² + y² – 6x + 6y – 8 = 0 at (2, 2).
Solution:
The equation of the tangent to the circle x² + y² + 2 gx + 2fy + c = 0 at (x₁, y₁) is
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 9
So the equation of the tangent to the circle
x² + y² – 6x + 6y – 8 = 0 at (x₁, y₁) is
xx₁ + yy₁ – \(\frac{6\left(x+x_{1}\right)}{2}+\frac{6\left(y+y_{1}\right)}{2}\) – 8 = 0
(i.e) xx₁ + yy₁ – 3(x + x₁) + 3(y + y₁) – 8 = 0
Here (x₁, y₁) = (2, 2)
So equation of the tangent is
x(2) + y(2) – 3(x + 2) + 3(y + 2) – 8 = 0
(.i.e) 2x + 2y – 3x – 6 + 3y + 6 – 8 = 0
(i.e) -x + 5y – 8 = 0 or x – 5y + 8=0
Normal is a line ⊥r to the tangent
So equation of normal circle be of the form 5x + y + k = 0
The normal is drawn at (2, 2)
⇒ 10 + 2 + k = 0 ⇒ k = -12
So equation of normal is 5x + y – 12 = 0

Question 10.
Determine whether the points (- 2, 1), (0, 0) and s (- 4, – 3) lie outside, on or inside the circle x² + y² – 5x + 2y – 5 = 0.
Solution:
x² + y² – 5x + 2y – 5 = 0
(i) At (-2, 1) ⇒ (-2)² + 1² – 5(-2) + 2(1) – 5
= 4 + 1 + 10 + 2 – 5 = 12 > 0
∴ (-2, 1) lies outside the circle.

(ii) At(0, 0) ⇒ 0 + 0 – 0 + 0 – 5 = -5 < 0
(0, 0) lies inside the circle.

(iii) At (-4, -3) ⇒ (-4)² + (- 3)² – 5(-4) + 2(-3) – 5 = 16 + 9 + 20 – 6 – 5 = 34 > 0
(-4, -3) lies outside the circle.

Question 11.
Find the centre and radius of the following circles.
(i) x² + (y + 2)² = 0
(ii) x² + y² + 6x – 4y + 4 = 0
(iii) x² + y² – x + 2y – 3 = 0
(iv) 2x² + 2y² – 6x + 4y + 2 = 0
Solution:
(i) x² + (y + 2)² = 0
(i.e) x² + y² + 4y + 4 = 0
Comparing this equation with the general form x² + y² + 2gx + 2fy + c = 0
we get 2g = 0 ⇒ g = 0
2f = 4 ⇒ f= 2 and c = 4
Now centre = (-g, -f) = (0, -2)
Radius = r = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{0+4-4}\)
∴ Centre = (0, -2) and radius = 0

(ii) x² + y² + 6x – 4y + 4 = 0
Comparing with the general form we get
2g = 6, 2f = -4
⇒ g = 3, /= -2 and c = 4
Centre = (-g, -f) = (-3, 2)
Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{9+4-4}\)= 3
∴ Centre = (-3, 2) and radius = 3

(iii) x² + y² – x + 2y – 3 = 0
2g = -1; 2f = 2; c = -3
g = \(\frac{-1}{2}\) f = 1
Centre (-g, -f) = (\(\frac{1}{2}\), -1)
Radius = \(\sqrt{g^2+f^2-c}\) = \(\sqrt{\frac{1}{4}+1+3}\)
\(\sqrt{\frac{1+4+12}{4}}\)
\(\sqrt{\frac{17}{4}}\) = \(\frac{\sqrt{17}}{2}\)

(iv) 2x² + 2y² – 6x + 4y + 2 = 0
(÷ by 2) ⇒ x² + y² – 3x + 2y + 1 =0
Comparing this equation with the general form of the circle we get
2g = -3, 2f= 2
g = \(-\frac{3}{2}\), g= 1 and c = 1
So centre = (-g, -f) = (\(\frac{3}{2}\), -1)
and radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{\frac{9}{4}+1-1}=\frac{3}{2}\)
∴ Centre = (\(\frac{3}{2}\), -1) and radius = \(\frac{3}{2}\)

Question 12.
If the equation 3x² + (3 – p) xy + qy² – 2px = 8pq represents a circle, find p and q. Also determine the centre and radius of the circle.
Solution:
3x² + (3 – p) xy + qy² – 2px = 8pq represent a circle means,
Co-efficient of x² = co-efficient of y²
3 = q ⇒ q = 3
Co-efficient of xy = 0
3 – p = 0 ⇒ p = 3
3x² + 3y² – 6x = 8 (3)(3)
3x² + 3y² – 6x – 72 = 0
(÷3) x² + y² – 2x – 24 = 0
2g = -2; 2f = 0; c = -24
g = -1 f = 0
Centre (-g, -f) = (1, 0)
Radius = \(\sqrt{g^2+f^2-c}\) = \(\sqrt{1+0+24}\)
= \(\sqrt{25}\) = 5

Students can Download Tamil Nadu 11th English Model Question Paper 5 Pdf, Tamil Nadu 11th English Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus, helps students complete homework assignments and to score high marks in board exams.

TN State Board 11th English Model Question Paper 5

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
7. Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 3:00 Hours
Maximum Marks: 90

PART – I

I. Answer all the questions. [20 × 1 = 20]
Choose the correct synonyms for the underlined words from the options given.

Question 1.
The place was a bedlam for birds.
(a) pandemonium
(b) peace
(c) serenity
(d) transition
Answer:
(a) pandemonium

Question 2.
He enlightened them with bon-mots.
(a) repartee
(b) wit
(c) challenges
(d) goodies
Answer:
(b) wit

Question 3.
Words of praise and adulation were showered on the debut artist.
(a) blasphemy
(b) condemnation
(c) aversion
(d) exaltation
Answer:
(d) exaltation

Choose the correct antonyms for the underlined words from the options given.

Question 4.
The princely sum was a stumbling block for her career.
(a) generous
(b) substantial
(c) prime
(d) meagre
Answer:
(d) meagre

Question 5.
Retaining my world cup was one of my greatest achievements.
(a) holding
(b) rescuing
(c) losing
(d) reviving
Answer:
(c) losing

Question 6.
I was so relieved to get my transfer order.
(a) delighted
(b) worried
(c) pleased
(d) comforted
Answer:
(b) worried

Question 7.
Choose the blended form of, “telecast”.
(a) television + broad cast
(b) television + cast
(c) tele + broad cast
(d) tele + cast
Answer:
(a) television + broad cast

Question 8.
Choose the right definition for the given term “choreography”.
(a) The art of designing steps in ballet or another staged dance, or the written steps for such movements
(b) The process of giving some of your work, duties, or responsibilities to a less senior person or a less powerful person
(c) A student of bees
(d) One who accumulates; one who collects
Answer:
(a) The art of designing steps in ballet or another staged dance, or the written steps for such movements

Question 9.
Choose the meaning of the idiom ‘At the drop of a hat’.
(a) To hear rumours about someone
(b) Do or say something exactly right
(c) To go to bed
(d) Without any hesitation; instantly
Answer:
(d) Without any hesitation; instantly

Question 10.
Choose the meaning of the foreign word in the sentence.
Leo was disappointed, but his losing the election for class president was a fait accompli.
(a) faithful friend
(b) established fact
(c) accomplished scholar
(d) standard issue
Answer:
(b) established fact

Question 11.
Choose the word from the options given to form a compound word with “child”.
(a) person
(b) hood
(c) bed
(d) call
Answer:
(b) hood

Question 12.
Form a new word by adding a suitable prefix to the root word “taken”.
(a) un
(b) mis
(c) dis
(d) en
Answer:
(b) mis

Question 13.
Choose the expanded form of “IIM”.
(a) Indian Institute of Minorities
(b) Indian Institute of Managers
(c) Indian Institute of Marine
(d) Indian Institute of Management
Answer:
(d) Indian Institute of Management

Question 14.
Choose the correct sentence pattern.
He loves his profession.
(a) SVO
(b) SVOC
(c) SVOA
(d) SVC
Answer:
(a) SVO

Question 15.
A collection of selected literary passages is known as ………….
(a) Phenomenology
(b) Anthology
(c) Phrenology
(d) Homology
Answer:
(b) Anthology

Question 16.
Fill in the blank with the suitable preposition.
Many people travel to Kerala to work ………… small companies.
(a) in
(b) under
(c) on
(d) with
Answer:
(a) in

Question 17.
Add a suitable question tag to the following statement.
Priyanka dances well,………?
(a) isn’t she
(b) doesn’t she
(c) won’t she
(d) will she
Answer:
(b) doesn’t she

Question 18.
Substitute the underlined word with the appropriate polite alternative.
The shoes looked like they had been stolen.
(a) theft
(b) lost
(c) damaged
(d) had fallen off the back of a truck
Answer:
(d) had fallen off the back of a truck

Question 19.
Substitute the phrasal verb in the sentence with a single word.
Your statement will not stand up as proof in the court of law.
(a) oppose
(b) accept
(c) deny
(d) support
Answer:
(d) support

Question 20.
Fill in the blank with a suitable relative pronoun
Tell me the name of the student ………….. you want to meet.
(a) whom
(b) which
(c) that
(d) whose
Answer:
(a) whom

PART – II

II. Answer any seven of the following: [7 × 2 = 14]
(i) Read the following sets of poetic lines and answer any four of the following. [4 × 2 = 8]

Question 21.
“I have learned to wear many faces Like dresses – home face”
(а) What has the poet learned?
(b) Mention the figure of speech employed in this line.
Answer:
(a) The poet has learned to put on appearances to conform to the changed attitude of people in modem times.
(b) Simile

Question 22.
“For he’s a fiend in feline shape, a monster of depravity.”
(a) Identify the poem and the poet.
(b) Explain the phrase ‘monster of depravity’.
Answer:
(a) The poem is ‘Macavity – The Mystery Cat’ written by T.S. Eliot.
(b) Satan is called the master of depravity. T.S. Eliot calls Macavity, the master of depravity. He means that the cat is an embodiment of evil. He is wicked and all the time involved in doing something evil.

Question 23.
“A life that knows no kneeling and bending.
We are proud and feel so tall”
(a) Who does we refer to?’
(b) What has life never experienced?
Answer:
(a) ‘We’ refers to ordinary people who live noble lives.
(b) The life of ordinary people who have not experienced kneeling or bending before the mighty. They are able to stand firm on defending the truth.

Question 24.
“Infusing him with self and vain conceit,
As if this flesh which walls about our life”
(a) Who has vain conceit?
(b) Explain the above lines.
Answer:
(a) The king has vain conceit.
(b) Death knows that all great kings must come to him. For a brief time death is generous and allows kings to rule and to be feared by their subjects. Death allows them to feel conceited and proud with an inflated image of ‘self’.

Question 25.
“And I must think, do all I can,
That there was pleasure there…”
(a) What did the poet notice about the twigs?
(b) What was the poet’s thought about then?
Answer:
(a) The budding twigs spread out their fan to catch the breezy air.
(b) The poet thought the twigs were experiencing the joy of their contact with the breezy air.

Question 26.
“This one the prize ring hates to enter
That one becomes a tackle or center,”’
(a) What game/sports is associated with “prize ring”?
(b) Which game is discussed in the second line?
Answer:
(a) Prize ring is associated with boxing.
(b) Football is discussed in the second line.

(ii) Do as Directed: (Answer any three) [3 × 2 = 6]

Question 27.
Report the following dialogue:
Tara: I went to Hyderabad to attend a seminar on environmental pollution.
Harsha: I am going to the library. Are you coming with me?
Answer:
Tara asked Harsha where he was going then. Harsha replied that he was going to the library and asked if I were coming with him.

Question 28.
Change into active voice of the following sentence.
Answer:
Alas! Her voice shall not be heard by his friends anymore.
Alas! His friends will not hear her voice anymore.

Question 29.
I did not know that you are going to visit us. I would have come to the airport. (Combine using ‘if’)
Answer:
If I had known that you were going to visit us, I would have come to the airport.

Question 30.
He was ill, but he came for practice. (Change into a compound sentence)
Besides being a good writer he is an outstanding lecturer.
Answer:
He is not only a good writer but also an outstanding lecturer.

PART – III

III. Answer any seven of the following: [7 × 3 = 21]
(i) Explain any two of the following with Reference to the Context: [2 × 3 = 6]

Question 31.
Once upon a time, son
They used to laugh with their eyes:
Answer:
Reference: These lines are from the poem, “Once upon a time” written by Gabriel Okara.

Context: The poet says these words to his son while discussing his own happy childhood days.

Explanation: The poet compares the behaviour of people in the past and those in modern . times. He tells his son that people in the past used to laugh with their eyes. There was an expression of genuine warmth among people when they laughed.

Question 32.
We deem it our duty and mission in life,
To bless and praise the deserving ones;
Answer:
Reference: These lines are from the poem “Everest is not the Only Peak” written by Kulothungan.

Context: The poet says these words highlighting the virtues of unsung heroes, who adhere to their ethical principles in life.

Explanation: They consider it their duty and mission to identify deserving people with natural talents and bless and appreciate them.

Question 33.
Let’s talk of graves, of worms, and epitaphs.
Answer:
Reference: These lines are from the poem “The Hollow Crown” by William Shakespeare. The poem is an excerpt from the play “Richard II”.

Context: King Richard II says these words while waiting for death. He is totally dejected.

Explanation: King Richard II thinks of words which could figure in the epitaph (i.e.) on his tomb stone. Being sure of death in the hands of Bolingbroke he requests his loyal courtiers to talk about death and about burial.

(ii) Answer any two of the following briefly: [2 × 3 = 6]

Question 34.
Why did Mary Kom think that she should not return empty-handed?
Answer:
Mary Korn’s dad had given all he had for her trip to USA. Besides, her friends had raised funds through MPs. They had pinned their hopes on her. So, she thought she should not return empty handed.

Question 35.
What made people wonder about the absentmindedness of their fellow-beings?
Answer:
The publication of articles lost by train travellers astonished many readers. Old people did not forget much. In fact, young men have forgotten bats and balls on their return from matches.

Question 36.
Enumerate the values instilled in the students by the Universities.
Answer:
Universities instill the values of robust optimism, respect for democracy and appreciation of others’ point of view. It also develops adjustment of differences through discussion; develop patience, perseverance, confidence, faith in themselves and others. They also instill confidence in their ability to shoulder responsibilities.

(iii) Answer any three of the following briefly: [3 × 3 = 9]

Question 37.
Re-arrange the shuffled words and frame into meaningful sentences, (change to pie chart/graph or table)

1. you/where/have/this/all/while/been?
2. this/we/visiting/Shimla/are/summer.
3. the/all/of/art/the/of/science/questions/is/and/knowledge/asking/source/

Answer:

1. Where have you been all this while?
2. We are visiting Shimla this summer.
3. The art and science of asking questions is the source of all knowledge!

Question 38.
Describe the process of Book-binding.
Answer:

1. Firstly, the pages are carefully arranged page wise. Any folding found is removed.
2. They are then arranged into sections and stitched.
3. The sides of the book are cut neatly and covered with a suitable brown paper.
4. Two card board sheets slightly bigger than the book must be pasted on both sides.
5. A calico cloth should be pasted on the closed side of the book to hold the cardboards and be allowed to dry.

Question 39.
Expand the news headlines in a sentence each.
(a) Suman Rao selected the new Miss India.
(b) 12 Injured as Buses Collide.
(c) Indian Team on the high in T20s in England.
Answer:
(a) 20-year old Miss Rajasthan 2019, Suman Rao, was awarded the most covetous crown Miss India at the finals held at Sardar Vallabhbhai Patel Indoor Stadium, Mumbai.

(b) Due to poor visibility of street lights and negligence of the State Transport Drivers two buses collided on the narrow stretch of Nammakal district near Ambedkar statue. 12 passengers including a six month old baby boy were rushed to the nearby Government hospital for treatment.

(c) Indian Team bagged the winner’s trophy and is expected to return next Monday at the Mumbai airport.

Question 40.
Complete the proverbs using the words given below.
(а) The harder you ………… the luckier you get. (throw, work, try)
(b) There is no time like the ……….. (present, future, past)
(c) ……….. and tide wait for no man. (Wind, Sea, Time)
Answer:
(a) work
(b) present
(c) Time

PART – IV

IV. Answer the following: [7 × 5 = 35]

Question 41.
How does the speaker highlight the importance of giving back to the society?
Answer:
The graduates have drawn largely from the social chest. The largest taken from the society needs to be replenished. If graduates fail to pay back, ordinary people’s coffer will be empty. The supervisor’s education enjoins greater responsibility to society. Apart from their own individual advancement, society has got a right to expect an adequate return from the graduates.

The society does not expect them to payback in cash. But they must pay back in terms of service. They should tone up the society by bringing a light into the dark alleys. They should herald sunshine into dingy places. They must give solace to the affiliated people. They should also give hope unto the despondent and thus ensure a new life unto every one.

[OR]

As a narrator, make a diary entry about the tight corner you faced at Christie’s and how you were saved from the dire situation.
Answer:
Thursday, 17th Nov. 20xx
I was lunching at a club in King James’s street. While passing along Kingstreet later, my friend suggested that we peeped in at Christie’s where an auction of Barbizon pictures was going on. The pieces of the paintings were pertaining to forest scenes, pools at evening, shepherdesses, and the regular subjects were tremendous for each ranging from two to three thousand guineas each. The remarkable thing was that nothing was sold at three figures.

After watching the auction for fun for a while I found myself bidding. I had exactly sixty three pounds in my account in the bank. I knew that any bidder must have a minimum of five hundred pounds in the bank to stand as security to bid for the artistic works. I enthusiastically participated in many bids as the starting price for each painting was a modest fifty to hundred guineas. Things went on well for me for quite sometime. But a cruel fate awaited me. A short red-faced man electrified the room by fixing the starting price at 4000 guineas. There was a rustle of excitement followed by terrible silence. But I found myself saying “and fifty”.

The dealer looked at the opener and at the company. To my surprise and horror, the dealer shot his bolt. My heart stopped and my blood congealed. I was in possession of the picture I did not want to buy. I was the top purchaser in the auction with just 63 pounds in the bank account. I turned to my friend for some moral support but he had deserted me to have a hearty laugh at a distance. With great alarm, I saw many other Barbizon pictures being put up and sold.

The auction came to an end. The bidders stood in a queue to pay the price and collect the pictures. I stayed behind at the end of the queue as I could not recall the name of any uncle, aunt or even a relative who could offer me 4050 guineas to buy the painting. I wished that a firing squad could give me a welcome relief by shooting me down. I preferred death to public disgrace.

But something divine turned my tragedy into a comedy. Just then one gentleman enquired if I was the gentlemen who bought “big Daubigny”. I admitted. The mediator asked if I could take 50 guineas for my interest and give up my claim. I would have hugged him and wept for joy of relief from the tight comer. But I had the guile/presence of mind to ask, “Is that the most he would offer?”

The mediator said that there was no harm in trying for a bit more. I said, “Tell him I will take hundred” myself and my friend started laughing. But when I saw the cheque for hundred guineas, I became grave. My friend said to me that it was he who brought me to Christie. I admitted, “I shall never forget it. It is indelibly branded in letters of fire on my heart”.

Question 42.
Describe the various reasons for King Richard’s grief and distress.
Answer:
King Richard II is a popular king. He has many nobles at the service. His rebellious cousin Bolingbroke attacks him with 10,000 men on his side. He sends message to the Welsh King for sending his army to defeat Bolingbroke. But to his shock, Welsh army is not sent. He realizes with alarm the terrible fate he would suffer in the hands of his foe and his most impending death in captivity. King Richard is reminded of the power of death that overshadows everything else. Death scoffs at the power of rulers.

Losing the battle, non¬receipt of Welsh army and the prospect of being jailed and killed worries Richard II. He realizes that in the hollow crown death had reigned him. In fact, death, a jester had misled him to believe that he was monarchising England. He can now only own a small patch of barren land. He is not an impregnable castle of brass anymore. He is an ordinary mortal. He too needs friends and needs to taste grief and face death.

[OR]

The poem ’Everest is not the only peak’ does not focus on the destination but the journey towards it. Discuss.
Answer:
The poet discusses the merits of efforts, duty and devotion and values of honesty, uprightness and service-mindedness. He does not have any special appreciation to those who reach great peaks like Himalayas. He appreciates the process, the journey and not the destination. When the whole world has a perspective of seeking glory using any foul method or underhand dealing, the poet differs from it.

For him the means is more important than the end. However modest may be one’s position is, it is adorable if attained by competence and merit. Pride is not in heights one reaches but in a life that knows no bending or kneeling. The poet respects one who does not stoop as a king. Thus the poet pays importance to the journey of life not the destination.

Question 43.
Write an essay of about 150 words by developing the following hints.
“After Twenty Years,” – time – 10 o’clock at night, – depeopled the streets – Only two men – on street – that night – policeman approaches – lurking man – light from his match – shows a pale face – keen eyes, a scar in eyebrow – a scarf pin – diamond – expensive watch – all hints as to the man’s past.
Answer:
The short story “After Twenty Years” Jakes place around 10 p.m. along a dark, windy New York City business avenue, mostly within the darkened doorway of a closed hardware-store.- This particular location had been a restaurant until five years ago. The plot begins with a policeman “on the beat” who discovers a.man standing in the dark doorway. The man then proceeds to explain why he is there. He and his best friend, Jimmy Wells had parted exactly twenty years ago to make their fortunes and had promised to meet at that spot “After Twenty Years”. He had gone west and gotten rich and was sure his friend, Jimmy would meet him if he were alive.

They talked a while and the policeman carried on. The man from the west wonders if his friend will come. The drama increases in anticipation of the rendezvous. Twenty minutes later, another man, whom we assume is his long lost friend, greets him warmly and they walk arm in arm discussing careers until they come to a well-lit comer near a drug store.

The man from the west gets a good look at his companion and discovers that he is not his friend, Jimmy. We are treated to several surprises for the man from the west is under arrest and secondly he is actually ‘Silky Bob’, a gangster from Chicago and finally the stranger is a plainclothes policeman. However, it seems that these three surprises are not enough. We get the “real” surprise when Jimmy Wells, the original policeman didn’t have the heart to arrest Bob, because he was his friend.

[OR]

Narrator – wants – photograph – photographer wait for an hour – comments – angry – called on Saturday – proof – Narrator shocked – photograph – not like him – worthless bauble.
Answer:
‘With the Photographer’ by Stephen Leacock is narrated in the first person. The narrator while sitting in the photographer’s studio begins to read some magazines and sees how other people look and the narrator begins to feel insecure about his appearance. It is also noticeable that the photographer takes a dislike to his face judging it to be wrong. What should have been a simple process of taking a photograph becomes something of a nightmare for the narrator. How confident the narrator becomes is noticeable when he returns to the photographer’s studio the following Saturday.

He realises that the photograph that has been taken of him looks nothing like him. This angers the narrator as he was simply looking for a photograph that would show his likeness. He accepts that he may not be to everybody’s liking when it comes to his physical appearance but is angered by the changes made. The photographer has retouched the photograph so much that the narrator does not recognise himself. The end of the story is also interesting as the reader realises that it is just a worthless bauble when he begins to cry. He has been judged solely by his appearance by the photographer whose job was to simply take a life like photograph.

Question 44.
Write a summary or Make notes of the following passage.
Answer:
The greatness of a country depends upon its people. India is fortunate to have vast human resources. Our countrymen are second to none in intelligence and in doing hard work. From the ancient period Indians excelled in art, architecture, knowledge of metals, medicines, literature etc., After our independence in 1947, the Government took steps to improve our country in all sphere. By the first Five-Year Plan was specially designed to improve our irrigational methods.

By the five year plans, provisions are made for the development of the country. The first Five-Year Plan was specially designed to improve our irrigational methods. By the green revolution we attained self sufficiency in the field of agricultural production. The present age is the atomic age. India too established an Atomic Energy Commission under the guidance of Dr. BhabhaI India made the first successful nuclear explosion on 18th Mary, 1974 which made India the sixth member of the world nuclear club. No other country’s scientists helped; it was purely Indian efforts. We have sent our Indian cosmonaut to space also. On April 3, 1984 Shri Rakesh Sharma, the best pilot of Indian Air Forse, travelled into space with two Soviet spacemen in Spyuz II spaceship.
Answer:
Summary
No. of words given in the original passage: 199
No. of words to be written in the summary: 199/3 = 66 ± 5

Rough Draft
India is fortunate to have vast human resources. Our countrymen are second to none in inteIligence and in doing hard work. Ancient Indians excelled in art, architecture, metallurgy, medicine, literature etc., After Independence, by the five year plans, provisions are made for the development of the country. By the green revolution self sufficiency in agricultural production was attained. Present age is the atomic age. An Atomic Energy Commission under the guidance of Dr. Babha. Due to the successful nuclear explosion in 1974, India the sixth member of the world nuclear club. It was purely Indian efforts. We have to sent Rakesh Sharma to space in Soyuz II.

Fair Draft
Greatness of India
India is fortunate to have vast human resources. Ancient Indians excelled in art, architecture, metallurgy, medicine, literature etc. After Independence by the green revolution self sufficiency in agricultural production was attained. Present age is the atomic age. Atomic Energy Commission was established under the guidance of Dr. Bhabha. Due to the successful nuclear explosion in 1974, India is the sixth member of the world nuclear club.

No. of words in the summary: 64

[OR]

Note-making
Title: Greatness of India
Answer:
1. Greatness of the country
people
our country men are second to none
from the ancient times Indians excelled in arts, architecture, metallurgy, medicine, literature etc.

2. Post Independence
government took steps to improve in all spheres
the first five-year plan was designed
Green Revolution attained self sufficiency

3. Present age
atomic age
India made the first nuclear explosion in 1974
sixth member of the world nuclear club
India sent cosmonaut, Shri Rakesh Sharma to space with two Soviet spacemen in Soyuz II spaceship.

Question 45.
You are Anita. You recently visited a hill station along with your parents. It was an exhilarating, adventurous and joyful experience. Write a letter to your friend sharing your experience in 150-200 words.
Answer:

25th June, 2020

From
Anitha
6, West street,
Chennai
To
Mercy
6, Abraham Street
PeriyarNagar
Chennai – 600 014

Dear Mercy,
Hope my letter finds you in the best of your health. Have you been to your grandparents house for vacation? I had recently gone to Matheran with my parents and really missed you. Matheran is the smallest hill station in the Indian state of Maharashtra and is located on the Western Ghats range at an elevation of around 800 m above sea level. It is about 90 km from Mumbai. Matheran’s proximity to many metropolitan cities makes it a popular weekend getaway for urban residents. Matheran, which means “forest on the forehead” is an eco-sensitive region declared by the Government of India.

It is Asia’s only automobile-free hill station. Doesn’t that spark an exhilarating, adventurous and joyful experience? Yes, from the foothills of the mountain, you either need to walk up the mountain to lodges and cottages there for your accommodation or need to hire Cycle rickshaws or ponies to travel. We all took a horse each and my little brother got on to a pony. Our baggage was loaded on to a wheel barrow to be brought up to our destination.

There are around 38 designated viewpoints in Matheran, including the Panorama Point that provides a 360-degree view of the surrounding area and also the Neral town. From this point, the view of sunset and sunrise is dramatic. The Louisa Point offers crystal clear view of the Prabal Fort. The other points are the One Tree Hill Point, Heart Point, Monkey Point, Porcupine Point, Rambagh Point, and more. We stayed in a Parsi bungalow. Beautiful old British-style architecture is preserved in Matheran. The roads are not metalled and are made of red laterite earth. As anticipated, there are many monkeys around and even the summer season was very pleasant.

I hope to visit the place again and I hope we will get an opportunity to visit it together. Why don’t you ask your parents if both our families could go to Matheran during our next vacation? My parents too were talking about going there again since it’s such a pollution free spot to relax and enjoy. Looking forward to meeting you in person to share the photographs we have taken here.

Yours loving friend,
Anita
Address on the Envelope
To
Mercy
6, Abraham Street
PeriyarNagar
Chennai – 600 014

[OR]

Write an essay in about 150 words on ‘Punctuality’
Answer:
Punctuality is essential to succeed in one’s career. In business schools, Time management is also taught. Those who are punctual prove that they respect the time of those whom they visit. Those who have missed interviews, flights, Olympic golds and even the opportunity to win goes by milliseconds know the value of time. We should cultivate the quality of being punctual right from our student days. Maintaining a calendar of action and keeping track of time all the time would help one to be punctual. God gives twenty four hours to each one of us, if we are punctual and make most of the given time we would definitely succeed in life.

Question 46.
Read the following sentences, spot the errors and rewrite the sentences correctly.
(a) There is an University at Madurai.
(b) He is confident on his success.
(c) Though he is old but he walks steadily.
(d) Sam is junior than me.
(e) His father is a honest man.
Answer:
(a) There is a University at Madurai.
(b) He is confident of his success.
(c) Though he is old he walks steadily.
(d) Sam is junior to me.
(e) His father is an honest man.

[OR]

Fill in the blanks appropriately.
(a) The story told by the ……….. fat man is not ………… (credible/credulous)
(6) My keys ……….. be in the car. (Fill in with a modal verb)
(c) This watch …………. belong to my father, (use semi-modal)
(d) The strike was announced ………… the disagreement between the management and the employees on the bonus issue. (Use a suitable link word)
Answer:
(a) credulous, credible
(b) must
(c) used to
(d) on account of

Question 47.
Identify each of the following sentences with the fields given below.
(a) Robots are steadily moving from fiction to fact.
(b) Examination should evaluate all aspects of learning.
(c) Indian players have performed well in the Commonwealth Games.
(d) Napoleon Bonaparte was considered an enlightened monarch of France.
(e) “Health is Wealth” but pollution takes it all away.
(Sports, Environment, History, Science, Education)
Answer:
(a) Science
(b) Education
(c) Sports
(d) History
(e) Environment

[OR]

Read the following passage carefully and answer the questions that follow.

I have always been attracted by people of unusual habits. By this, I do not imply hippies and drop-outs or anyone of that band of unhappy people for whom modem society is too sick and uncivilized to bear. No, I mean those quiet, orderly people, living apparently blameless lives, who enrich their har humdrum existences by adopting odd quirks and passions, unlikely, routines or harmless manias for useless objects. Like the secretary I had, who collected earwigs, though what she did with them I never knew, I believe that she loved them because they were small and thin like herself and had a way of scuttling about in very much the same way she did. Life, I am sure, would be very much poorer without such people in it. Sometimes, I feel I am lacking in personality, since I have none of these strange habits.. Unless you count the fact that I never eat eggs unless they are boiled in milk.
Questions.

1. What attracted the author?
2. According to the author, who are the people who have unusual habits?
3. What did the author’s secretary collect?
4. Why did she love them, according to the author?
5. Do you think that the author has any strange habit? If so, what is it?

Answer:

1. Unusual habits of others attracted the author.
2. Quite orderly people living blameless lives have unusual habits.
3. The author’s secretary collected ‘earwigs’.
4. They were small and thin like herself scuttling about.
5. Yes, he has a habit of eating eggs which are only boiled in milk.